Journal of Artificial Evolution and Applications
Volume 2008, Issue 1 827401
Research Article
Open Access

Novel Orthogonal Momentum-Type Particle Swarm Optimization Applied to Solve Large Parameter Optimization Problems

Jenn-Long Liu, 

Corresponding Author

Jenn-Long Liu

Department of Information Management College of Electrical Engineering and Information Science I-Shou University No. 1, Section 1, Syuecheng Road Kaohsiung County 840, Taiwan

Search for more papers by this author
Chao-Chun Chang, 

Chao-Chun Chang

Department of Information Management College of Electrical Engineering and Information Science I-Shou University No. 1, Section 1, Syuecheng Road Kaohsiung County 840, Taiwan

Search for more papers by this author
First published: 31 March 2008
https://doi.org/10.1155/2008/827401
Citations: 3
Academic Editor: Jim Kennedy

Abstract

This study proposes an orthogonal momentum-type particle swarm optimization (PSO) that finds good solutions to global optimization problems using a delta momentum rule to update the flying velocity of particles and incorporating a fractional factorial design (FFD) via several factorial experiments to determine the best position of particles. The novel combination of the momentum-type PSO and FFD is termed as the momentum-type PSO with FFD herein. The momentum-type PSO modifies the velocity-updating equation of the original Kennedy and Eberhart PSO, and the FFD incorporates classical orthogonal arrays into a velocity-updating equation for analyzing the best factor associated with cognitive learning and social learning terms. Twelve widely used large parameter optimization problems were used to evaluate the performance of the proposed PSO with the original PSO, momentum-type PSO, and original PSO with FFD. Experimental results reveal that the proposed momentum-type PSO with an FFD algorithm efficiently solves large parameter optimization problems.

1. Introduction

Many well-known representative evolutionary computation (EC) techniques, such as genetic algorithms (GAs) [1–3], genetic programming (GP) [4], evolutionary programming (EP) [5, 6], evolutionary strategies (ESs) [7, 8], and particle swarm optimization (PSO) [9], have emerged as efficient computational tools for solving global optimization problems, especially for large parameter optimization problems (LPOPs). These EC techniques are sufficiently robust when coping with discontinuous, vast multimodal problems or with noisy search spaces since they do not depend on derivatives of objective functions and constraints. Among these techniques, PSO is easily implemented and computationally inexpensive as it has low memory and CPU costs. The PSO methodology involves creation of a population of particles such that each particle is capable of adjusting its flying velocity, according to its flying experience and the best experience of the group. Therefore, each particle in the PSO can be regarded as a cooperating agent.

The original PSO algorithm, developed by Kennedy and Eberhart in 1995 [9], was inspired by the swarm behaviors of flocks of birds and schools of fish. Thus, the PSO method is a swarm intelligence method [10] for solving global optimization problems, and it compares favorably to other evolutionary algorithms [11]. The original PSO is effective in determining optimal solutions in static environments, but performs poorly in locating a changing extremum. In addition, imposing a maximum value Vmax⁡ is necessary to limit the particle velocity. Shi and Eberhart introduced a parameter called inertia weight (w), which dampens particles’ velocities over time, allowing a swarm to converge efficiently and with increased accuracy [12, 13]. Furthermore, Clerc proposed using a constriction factor (K), which improves the ability of PSO to constrain and control velocities [14]. Eberhart and Shi found that K, combined with constraints on the maximum allowable velocity vector (Vmax⁡), improved the PSO performance significantly [15]. Additionally, when utilizing PSO with a constriction factor setting, the Xmax⁡ for each dimension is the best approach. Constriction factor (K) implements velocity control for effectively erasing the tendency of some particles to spiral into ever-increasing velocity oscillations. Parsopoulos and Vrahatis presented an overview of recent approaches for solving global optimization problems using PSOs [16].

This work presents a novel orthogonal momentum-type PSO algorithm for locating the best position for each particle efficiently. The momentum-type PSO, proposed in previous work [17], has a delta momentum rule in the velocity-updating equation, and efficiently determines the physical motion of particles more reasonably than other PSO versions. The momentum-type PSO markedly outperformed the original PSO [9] and modified PSO [13] versions. Furthermore, this study incorporates the momentum-type PSO and well-known fractional factorial analysis, which utilize several factorial experiments, according to classical orthogonal tables, to identify intelligently the best combination of factors from two-level variables to enhance algorithmic search efficiency. The novel combination of the momentum-type PSO and fractional factorial design (FFD) is termed the momentum-type PSO with FFD herein. Ho et al. [18] and Lin [19] developed Taguchi orthogonal tables for their GA and PSO for constructing an orthogonal GA and orthogonal PSO. Their strategies markedly improved the search ability of their GA and PSO. In 1991, Bhote reported that classical fractional factorial analysis combined with evolutionary optimization is superior to the Taguchi method [20]. Consequently, this study proposes orthogonal PSO using the FFD, rather than Taguchi tables, for a velocity-updating equation of momentum-type PSO to analyze the best factor related to cognitive learning and social learning terms with the goal of enhancing algorithmic efficiency. This work also developed the original PSO with FFD, which combines the original Kennedy and Eberhart PSO and classical orthogonal arrays, to enhance the performance of the original PSO. Performance of the original PSO, momentum-type PSO, original PSO with FFD, and proposed momentum-type PSO with FFD were compared using 12 benchmark LPOPs.

2. Methodology of the Proposed Particle Swarm Optimization

2.1. Description of an Objective Function

The general form of an objective function with variable vector is expressed as . The variable represents the solution vector with N variables, and is defined as the set {xi,   i = 1, N}. In PSO computation, each particle is assigned a fitness value based on the calculation of objective function. Moreover, the fitness value of a particle determines the best position of each particle over time and determines which particle has the best global value in the current swarm.

2.2. Momentum-Type Particle Swarm Optimization

The original PSO developed by Kennedy and Eberhart [9] supposed that the ith particle flies over a hyperspace; its position and velocity are given by and , respectively. Initial particle position and velocity are chosen randomly. At time step k, the best position of the current and previous moves for the ith particle is denoted by pbesti; the best particle with the best function value in the swarm is denoted by gbest. Consequently, the next flying velocity and position of particle i at time step k + 1 is updated using the following heuristic equations:
()
()
where c1 and c2 are cognitive and social learning rates, respectively. These two parameters control the relative importance of memory (position) of a particle itself and the neighborhood memory, and are both set to 2.0 [9, 12, 21] for multiplying random values by a mean of 1, such that agents would “overfly” the target about half the time [9]. Random function rand() is uniformly distributed in the range [0,1]. As in (1), the two random values are generated independently, and the velocity vector of a particle is updated based on variations on its current position, its previous best position, and the previous best position of its neighbors. After particle velocity is updated using (1), its new position is updated by adding the velocity vector to the current position. Analyses of algorithmic stability and convergence of the PSO have been examined theoretically by Clerc and Kennedy [22] and by Trelea [23] who used dynamic system theory.
The goal of the momentum-type PSO [17], which includes a delta term for the velocity vector for detecting particle-velocity variation, is to express the physical motion of particles more accurately than current PSO algorithms do. According to [17], the difference between a particle’s current position and pbesti (as shown in (1)) represents the first external effect on the particle and causes it to move, and the difference between a particle’s current position and gbest, which represents the second external effect on a particle. The two effects propelling particle i to move can be expressed in delta position forms as follows:
()
where p = c1×rand() and q = c2 × rand(). Combining the two terms and using the velocity to represent the variation of positions the composed velocity can be obtained as follows:
()
Since is particle-composed velocity, velocity of particle i at next time step k + 1 may include a delta form for velocity as rather than the velocity as employed in the original PSO, the Shi and Eberhart PSO, and many other PSOs. Generally, denotes the difference of velocities between time steps k + 1 and k, that is, Thus, the momentum-type form for velocity updating with parameter β can be written as
()
where β is a positive number (0 ≤ β < 1) termed the momentum constant, which controls velocity vector rate of change. The momentum constant has characteristics that are reminiscent of the stabilizing effect in backpropagation neural networks [24] and accelerating convergence in numerical algorithms [25]. Similarly, position of particle i at time step k + 1 can be written as the current position plus a delta form of the position :
()
Parameter α is another momentum constant for adjusting the rate of change of particle position. Consequently, (5) and (6) correspond to each other, and both are consistent with the physical behavior for variations in velocity and position of particle motion. Hence, (5) and (6) can be combined to form a matrix of the generalized delta rule:
()
where
()
Equation (7) allows each particle the ability of dynamic self-adaptation in the search space over time, that is, the ith particle can memorize the previous velocity variation state and automatically adjust the next velocity value during movement. The delta momentum term in the PSO algorithm stabilizes searching, and an appropriate value for β = 0.1 improves convergence and the optimal solution [17]. Parameter α was set to 1 such that variable ν could be interpreted as true velocity, that is, the change between two successive particle positions [23]. Thus (7) satisfies the zero-velocity variation () and zero velocity () conditions for the particle considered.

2.3. Proposed Momentum-Type PSO with Fractional Factorial Design

This study integrates FFD into the momentum-type PSO to determine the combination of factors associated with cognitive learning and social learning terms. This study defined the two states of orthogonal momentum-type PSO as follows:
()
where and indicate two possible new positions related to cognitive learning and social learning for particle i. Thus, updating rules for velocity and position using the proposed momentum-type PSO with FFD can be expressed as
()
()
The expression represents the implementation of OR operator via fractional factorial analysis using variables and . Therefore, the new flying position of particle i is determined by (11), namely, the best position of particle i on the next time k + 1 can be obtained using FFD.

2.4. Fractional Factorial Design (FFD)

To solve the operator shown in (10) and (11), the FFD used in this work is based on classical full factorial analysis with two-level, multivariable orthogonal tables [20]. Applying the fractional factorial analysis to the operator yields an arrangement of two-level factors that corresponds to the two possible states of the design variables. In the classical factorial experiments, the two levels of a design variable are labeled by “−” and “+”. Hence, and represent the two levels of the design variable Xi in this work. Table 1 lists the level distribution of seven factors with the same number of levels “−” and “+” at each column to retain the balance of a statistically designed experiment. The detailed steps of the numerical procedure for the fractional factorial analysis are as follows.

Table 1. Orthogonal table with seven factors.
Factor A B AB C AC BC ABC Output
Factor level
Experiment 1 − − + − + + − f1
2 + − − − − + + f2
3 − + − − + − + f3
4 + + + − − − − f4
5 − − + + − − + f5
6 + − − + + − − f6
7 − + − + − + − f7
8 + + + + + + + f8
  
Contribution C1 C2 C3 C4 C5 C6 C7
Select level + or − + or − + or − + or − + or − + or − + or −
Best factor or or or or or or or

(1) First, if N factors (termed by design variables in the PSO) each has two levels, build a table of m rows and m − 1 columns. The value m is defined by the integer . For example, if seven factors (N = 7) are associated with vector , then eight experiments (m = 8) are conducted for factorial analysis. As shown in Table 1, the levels “−” and “+” in columns A, B, and C are assigned to each cell position according to the classical full factorial principle [20]. In columns AB, AC, BC, and ABC, each level in the cells is determined from the inner products of columns A and B, columns A and C, columns B and C, and columns A, B, and C.

(2) The first experiment has a factor set to , obtained by combining the factors A to ABC with the assigned levels. In the following, its objective function, f1, is computed, and put it into the first position of column “Output”. Repeat the computations for the remaining seven experiments with function values f2, f3, …, and f8; then, the eight experiments for seven factors are finished.

(3) In column A, multiply the function values f1, f2, …, and f8 by the corresponding algebraic value −1 for level “−”, and 1 for level “+”, as listed in Table 1. The effect of factor A on the level is determined by adding the eight products together. The mathematical form for each factor i is . Here, Ui,j equals −1 when the cell level is at level “−”, and equals 1 when it is at level “+”. The summation C1 is placed in the first position in the row “Contribution” which is associated with factor A. Repeat the multiplication and summation operations for the remaining six values, C2, C3, …, and C7, and put them in corresponding positions in the row “Contribution”; the effects of factors B, C,…, and ABC on the levels are thus obtained.

(4) Check the signs of the seven values C1, C2, …, and C7 listed in the row “Contribution”; if the sign of Ci is negative, then place the symbol “−” in the row “Selected level” (Table 1). Otherwise, select symbol “+”. The dominant levels of the seven factors are thus determined.

(5) The best combination of for the seven factors is determined from the factors with selected levels, presented in the row “Best factor” (Table 1), and the best value of the function is obtained by calculating the objective function . The choice principle for each best factor is expressed as follows:
()
Thus the new position of the particle i at time step k + 1 shown in (11) can be set equal to .

3. Results and Discussion

3.1. Effect of Number of Particles

This work applied FFD to several factorial experiments to determine the best position of particles. When the dimension of design variables is high, that is, a large parameter optimization problem, FFD usually required numerous function evaluations for factorial analysis. Therefore, few particles for the proposed PSO with FFD should reduce CPU cost if the good performance of searching of the PSO can be retained. To determine how many particles are appropriate when using the momentum-type PSO with FFD and original PSO with FFD algorithms, adequate size of Nparticle is investigated by conducting the following large parameter optimization problem with low and high dimensions:
()

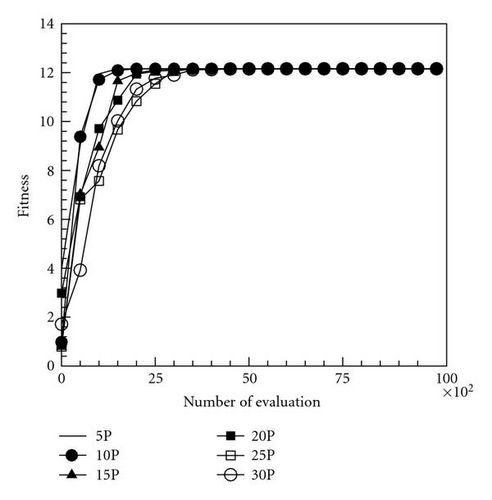
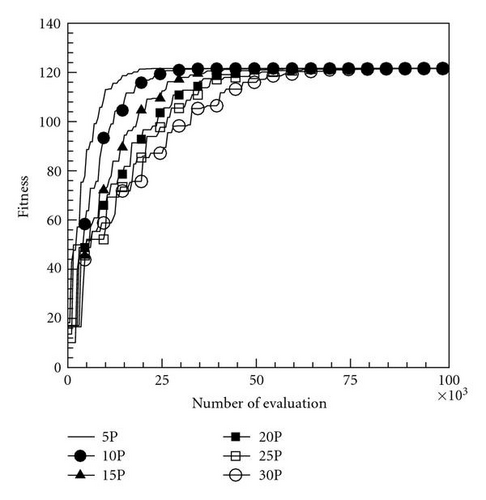
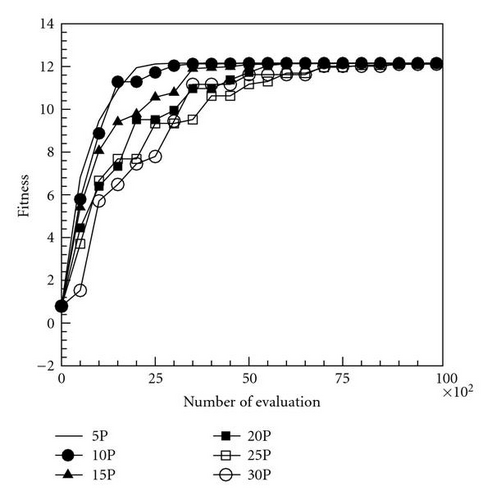
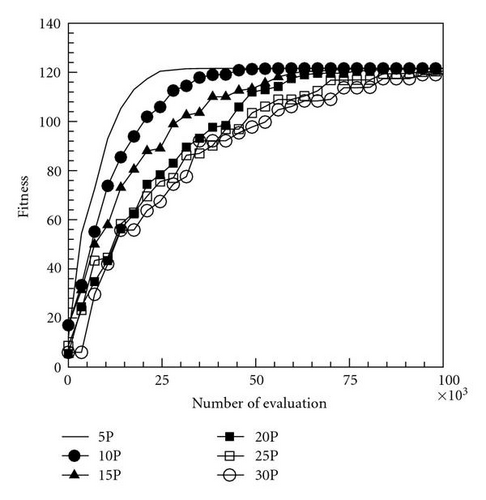
This function is a multimodal problem and has an analytical optimum of 1.216N. In this computation, dimensions were set at 10 and 100, and the maximum numbers of function evaluation for the two cases were set at 10000 and 100000, respectively. Moreover, the number of particles was 5, 10, 15, 20, 25, and 30 to investigate the effects of different swarm sizes of particles to orthogonal PSOs. Figures 1(a) and 1(b) reveal that the proposed momentum-type PSO with the FFD algorithm and few particles achieved a favorable convergence rate and numerical accuracy; nevertheless, many particles resulted in poor convergence. Using the proposed momentum-type PSO with FFD and few particles for N = 10 and N = 100 cases rapidly converges to optimal values 12.1598 and 121.598, respectively. In this study, numerical performance using Nparticle = 5 is better than other cases using large number sizes of particles. Similar results shown in Figures 2(a) and 2(b) are observed when using the original PSO with the FFD technique. Accordingly, this work set Nparticle = 5 for the momentum-type PSO with FFD and the original PSO with FFD algorithms in the following computations.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Effect of number of particles using the momentum-type PSO with FFD for solving the LPOP at (a) N = 5 and (b) N = 100 dimensions.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Effect of number of particles using the momentum-type PSO with FFD for solving the LPOP at (a) N = 5 and (b) N = 100 dimensions.
Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Effect of number of particles using the original PSO with FFD for solving the LPOP at (a) N = 5 and (b) N = 100 dimensions.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Effect of number of particles using the original PSO with FFD for solving the LPOP at (a) N = 5 and (b) N = 100 dimensions.

3.2. Experiments for 12 Large Parameter Optimization Problems (LPOPs)

Twelve benchmark LPOPs presented in [18] are evaluated to further examine the performance of the proposed momentum-type PSO with FFD. This study sets Nparticle = 5 for the original PSO with FFD and the proposed momentum-type PSO with FFD, and Nparticle = 30 for the original PSO and momentum-type PSO. The number of dimensions for all benchmark LPOPs was set to 100, and the terminated number of function evaluations for the four PSO algorithms was set to 100000. Twenty independent runs were conducted for each problem. Algorithmic performance was assessed by the best solution, averaged best solution, mean absolute error (MAE, and standard deviation. The MAE was used as the measurement of error in this work with the following form:
()

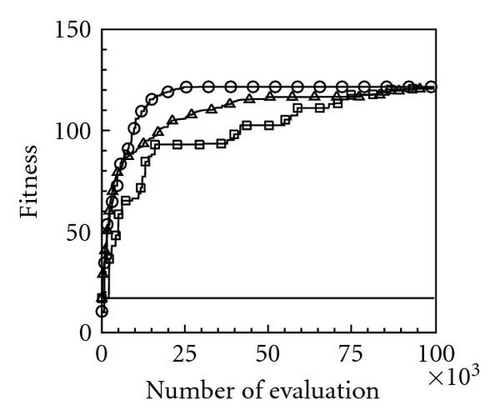
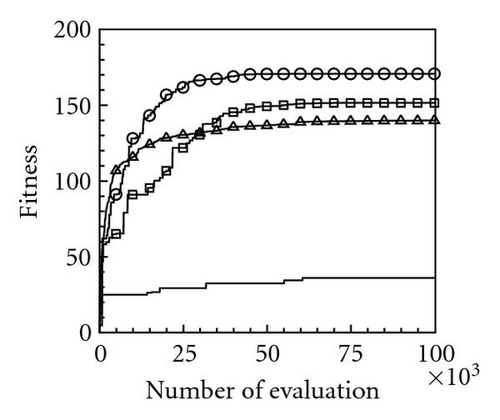
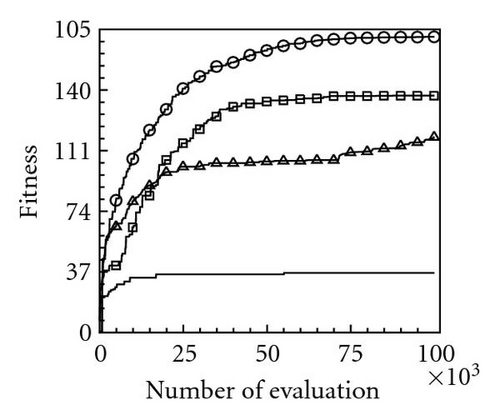
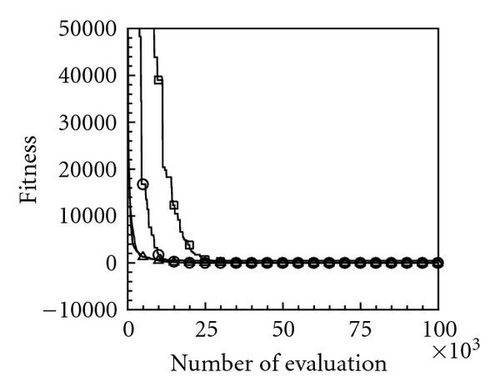
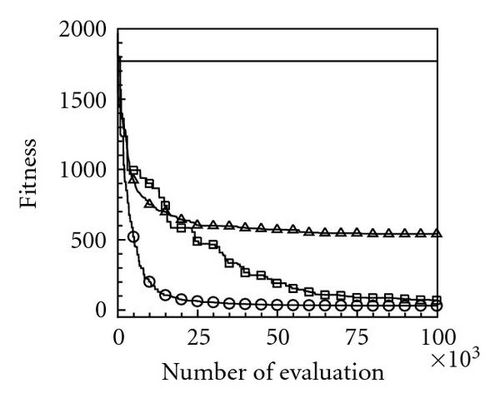
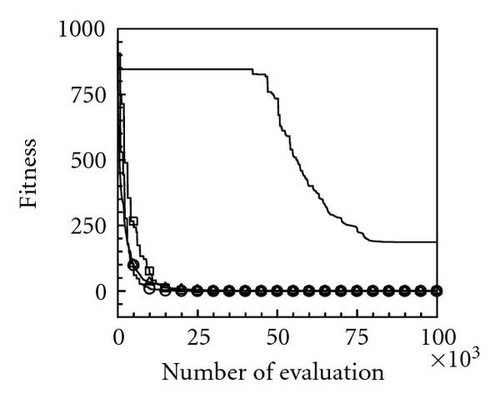
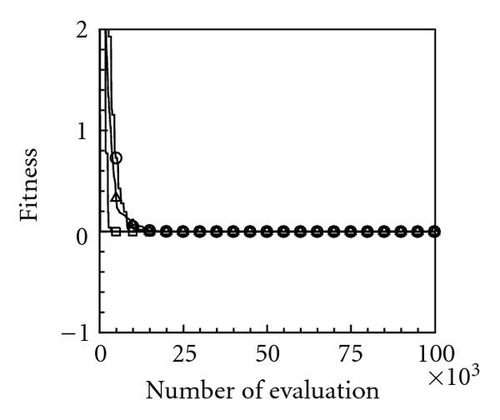
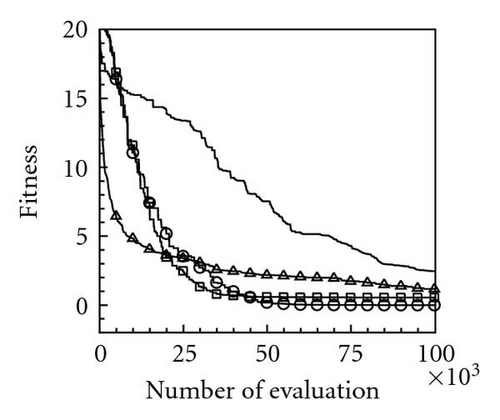
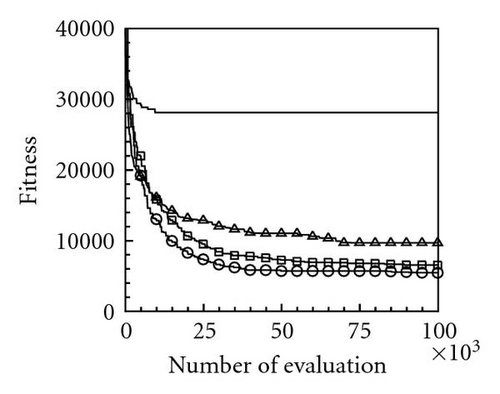
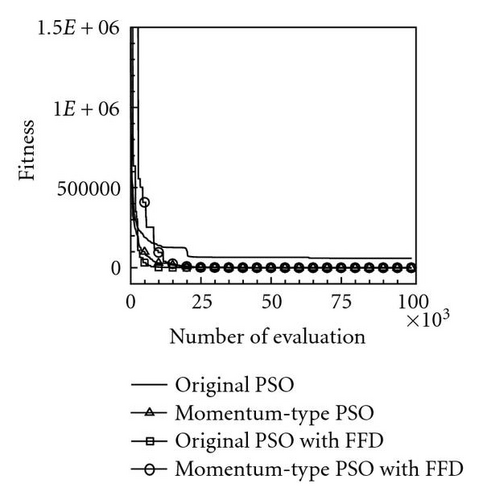
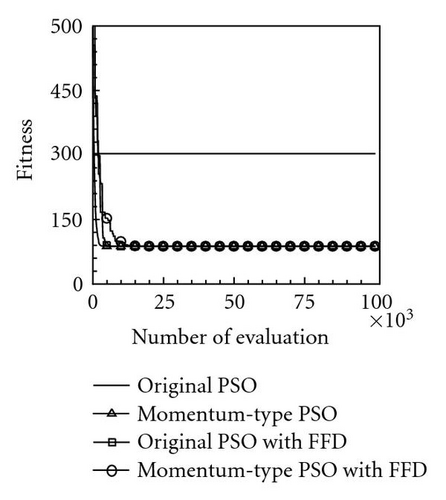
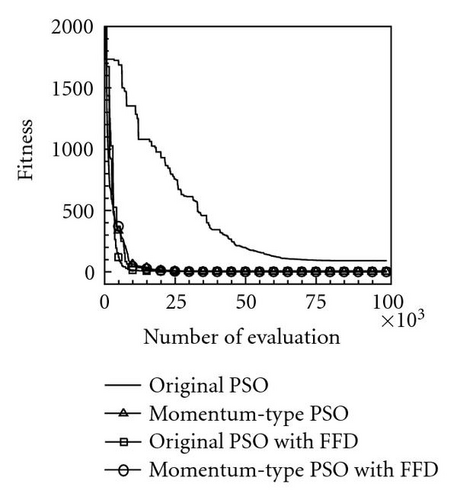
Table 2 lists the 12 objective functions with range constraints and their global optima [18]. Notably, the objectives of problems 1–3 are set to maximize the objective functions f1–3, and other problems are set to minimize the objective functions f4–12. The optima of the first three maximal functions f1, f2, and f3 are 121.598, 200, and 185, respectively, and the minimal functions f4–12 are all zero. Table 3 lists the computational results for the 12 functions at a dimension of N = 100 using the four PSOs. Computational results reveal that the evaluation results for maximal functions f1, f2, and f3 using the proposed momentum-type PSO with FFD were 121.598, 174.452, and 182.798, respectively. These computational results are better than those computed by the other three PSOs. Additionally, the algorithmic performance of the PSOs with FFD is superior to that of PSOs without FFD. Consequently, the proposed PSO with FFD promoted solution searches more effectively than the PSO does without FFD. For the remaining nine minimal function evaluations, f4–12, the optima obtained using the proposed momentum-type PSO with FFD were 0.0, 11.946, 0.0, 0.00005, 0.000039, 3781.879, 92.874, 88.0, and 0.000059, respectively, and the average solutions were 0.0, 32.4641, 0.0, 0.0001, 0.0139, 5676.0005, 181.8753, 88.2285, and 0.1009, respectively. Both the best and average results are the best when compared with solutions obtained by the other three PSOs. Additionally, all MAEs and standard deviations are lowest for the nine optimization functions evaluated by the proposed momentum-type PSO with FFD over 20 independent runs. From the computational results (Table 3), the proposed momentum-type PSO with FFD performed well in solving LPOPs. Figures 3(a)–3(l) represent the convergence histories of the 12 objection functions obtained by the four PSOs. The proposed momentum-type PSO is superior to the other PSOs in terms of convergence rate and optimal solution (Figures 3(a)–3(c)). Although the convergence rate of the original PSO is relatively poor for solving LPOPs, it can be significantly improved by introducing FFD into the PSO algorithm. Figures 3(d)–3(l) present results similar to the maximization cases.

Table 2. Twelve objective functions with range constraints and their optima.
Problems Objective functions and ranges Optima
1 1.21598N
  
2 ≈ 2N
  
3 1.85N
  
4 0
  
5 0
  
6 0
  
7 0
  
8 0
  
9 0
  
10 0
  
11 0
  
12 0
Table 3. Results obtained using the original PSO, momentum-type PSO, original PSO with FFD, and momentum-type PSO with FFD algorithms to solve the 12 benchmark LPOPs.
f(x) Algorithms fopt fbest favg |fopt − favg| MAE SD (20 runs)
f1 Original PSO 121.598 26.5864 15.3709 106.2271 1.0623 5.8322
Momentum-type PSO 121.5966 119.6452 1.9528 0.0195 3.2968
Original PSO with FFD 121.5730 120.6245 0.9735 0.0097 2.7499
Momentum-type PSO with FFD 121.5980 120.3738 1.2242 0.0122 2.2866
  
f2 Original PSO 200 41.3325 35.9429 164.0571 1.6406 2.9219
Momentum-type PSO 147.5408 135.8634 64.1366 0.6414 8.0647
Original PSO with FFD 163.7965 150.1892 49.8108 0.4981 6.3295
Momentum-type PSO with FFD 174.4516 166.6228 33.3772 0.3338 6.0346
  
f3 Original PSO 185 41.7656 36.0755 148.9245 1.4892 5.6901
Momentum-type PSO 128.7731 116.8754 68.1246 0.6812 11.8977
Original PSO with FFD 165.4799 140.0511 44.9489 0.4495 25.4287
Momentum-type PSO with FFD 182.7978 174.9624 10.0376 0.1004 7.8354
  
f4 Original PSO 0 1.3102 462.9955 462.9955 4.6300 461.6853
Momentum-type PSO 0.0001 1.9415 1.9415 0.0194 1.9413
Original PSO with FFD 3.6828 9.2072 9.2072 0.0921 5.5244
Momentum-type PSO with FFD 0.0000 0.0000 0.0000 0.0000 0.0000
  
f5 Original PSO 0 1685.8392 1774.6315 1774.6315 17.7463 88.7923
Momentum-type PSO 408.6802 565.3514 565.3514 56.5351 156.6713
Original PSO with FFD 35.6695 76.3567 76.3567 0.7636 40.6872
Momentum-type PSO with FFD 11.9463 32.4641 32.4641 0.3246 20.5178
  
f6 Original PSO 0 52.4517 186.2910 186.2910 1.8629 133.8393
Momentum-type PSO 0.0000 1.3711 1.3711 0.0137 1.3711
Original PSO with FFD 0.0000 0.0000 0.0000 0.0000 0.0000
Momentum-type PSO with FFD 0.0000 0.0000 0.0000 0.0000 0.0000
  
f7 Original PSO 0 0.0001 0.0001 0.0001 0.0000 0.0000
Momentum-type PSO 0.0001 0.0211 0.0211 0.0002 0.0210
Original PSO with FFD 0.0001 0.0001 0.0001 0.0000 0.0000
Momentum-type PSO with FFD 0.0001 0.0001 0.0001 0.0000 0.0000
  
f8 Original PSO 0 0.4069 3.9570 3.9570 0.0396 3.5501
Momentum-type PSO 0.0520 1.3377 1.3377 0.0134 1.2857
Original PSO with FFD 0.0000 0.6476 0.6476 0.0065 0.6476
Momentum-type PSO with FFD 0.0000 0.0139 0.0139 0.0001 0.0139
  
f9 Original PSO 0 28122.4766 29843.7729 29843.7729 298.4377 1721.2964
Momentum-type PSO 7731.2314 9897.2021 9897.2021 98.9720 2165.9706
Original PSO with FFD 5363.7783 6583.7198 6583.7198 65.8372 1219.9415
Momentum-type PSO with FFD 3781.8799 5676.0005 5676.0005 56.7600 1894.1206
  
f10 Original PSO 0 577.8867 64444.4250 64444.4250 644.4443 63866.5383
Momentum-type PSO 373.7911 635.0241 635.0241 6.3502 261.2330
Original PSO with FFD 341.0312 1292.7659 1292.7659 12.9277 951.7347
Momentum-type PSO with FFD 92.8743 181.8753 181.8753 1.8188 89.0009
  
f11 Original PSO 0 231.3600 319.4241 319.4241 3.1942 88.0640
Momentum-type PSO 88.0000 89.7067 89.7067 0.8971 1.7067
Original PSO with FFD 88.0000 89.3653 89.3653 0.8937 1.3653
Momentum-type PSO with FFD 88.0000 88.2285 88.2285 0.8823 0.2285
  
f12 Original PSO 0 0.2118 171.7896 171.7896 1.7179 171.5778
Momentum-type PSO 0.0183 3.2176 3.2176 0.0322 3.1992
Original PSO with FFD 0.8876 7.6815 7.6815 0.0768 6.7939
Momentum-type PSO with FFD 0.0001 0.1009 0.1009 0.0010 0.1008
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (e)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (f)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (g)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (h)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (i)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (j)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (k)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.
Details are in the caption following the image
Figure 3 (l)
Open in figure viewerPowerPoint
Evaluated results obtained using the four PSOs for solving functions (a) f1, (b) f2, (c) f3, (d) f4, (e) f5, (f) f6, (g) f7, (h) f8, (i) f9, (j) f10, (k) f11, and (l) f12.

4. Conclusion

This study examined the performance of the proposed momentum-type PSO with the FFD algorithm, which uses the delta momentum rule to update particle velocity and FFD to locate a particle’s best location for handling LPOPs. Using the momentum-type PSO, each particle can adjust its velocity vector according to its previous velocity change rate. The new location of a particle is then determined by analyzing the best combination of cognitive and social learning terms via several factorial experiments based on the FFD. Moreover, this work modified the original PSO by incorporating with FFD, which also employs the classical orthogonal tables, and improved significantly the efficiency of the original Kennedy and Eberhart PSO. Through 12 benchmark function assessments, the proposed momentum-type PSO algorithm outperformed the original PSO, momentum-type PSO and original PSO with FFD in terms of solution accuracy, numerical error and standard deviation. This work also determined that algorithmic performance of the proposed PSO with FFD is superior to that without FFD. Numerical results show that the proposed momentum-type PSO with FFD algorithm is efficient and is a promising method for solving LPOPs.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.