Volume 2008, Issue 1 753518

Research Article

Open Access

Numerical Blow-Up Time for a Semilinear Parabolic Equation with Nonlinear Boundary Conditions

Louis A. Assalé,

Louis A. Assalé

Institut National Polytechnique Houphouët-Boigny de Yamoussoukro BP 1093, Yamoussoukro, Cote D′Ivoire , inphb.edu.ci

Search for more papers by this author

Théodore K. Boni,

Théodore K. Boni

Institut National Polytechnique Houphouët-Boigny de Yamoussoukro BP 1093, Yamoussoukro, Cote D′Ivoire , inphb.edu.ci

Search for more papers by this author

Diabate Nabongo,

Corresponding Author

Diabate Nabongo

[email protected]

Département de Mathématiques et Informatiques Université d′Abobo-Adjamé, UFR-SFA 16 BP 372 Abidjan 16, Cote D′Ivoire , uabobo.ci

Search for more papers by this author

Louis A. Assalé,

Louis A. Assalé

Institut National Polytechnique Houphouët-Boigny de Yamoussoukro BP 1093, Yamoussoukro, Cote D′Ivoire , inphb.edu.ci

Search for more papers by this author

Théodore K. Boni,

Théodore K. Boni

Institut National Polytechnique Houphouët-Boigny de Yamoussoukro BP 1093, Yamoussoukro, Cote D′Ivoire , inphb.edu.ci

Search for more papers by this author

Diabate Nabongo,

Corresponding Author

Diabate Nabongo

[email protected]

Département de Mathématiques et Informatiques Université d′Abobo-Adjamé, UFR-SFA 16 BP 372 Abidjan 16, Cote D′Ivoire , uabobo.ci

Search for more papers by this author

First published: 12 April 2009

https://doi.org/10.1155/2008/753518

Citations: 5

Academic Editor: Jacek Rokicki

Share a link

Email
Wechat
Bluesky

Abstract

We obtain some conditions under which the positive solution for semidiscretizations of the semilinear equation u_t = u_xx − a(x, t)f(u), 0 < x < 1, t ∈ (0, T), with boundary conditions u_x(0, t) = 0, u_x(1, t) = b(t)g(u(1, t)), blows up in a finite time and estimate its semidiscrete blow-up time. We also establish the convergence of the semidiscrete blow-up time and obtain some results about numerical blow-up rate and set. Finally, we get an analogous result taking a discrete form of the above problem and give some computational results to illustrate some points of our analysis.

1. Introduction

In this paper, we consider the following boundary value problem:

(1.1)

where f : [0, ∞)→[0, ∞) is a C¹ function, f(0) = 0, g : [0, ∞)→[0, ∞) is a C¹ convex function, g(0) = 0, a ∈ C⁰([0, 1] × ℝ₊), a(x, t) ≥ 0 in [0, 1] × ℝ₊, a_t(x, t) ≤ 0 in [0, 1] × ℝ₊, b ∈ C¹(ℝ₊), b(t) > 0 in ℝ₊, b^′(t) ≥ 0 in ℝ₊. The initial data u₀ ∈ C²([0, 1]),

Here (0, T) is the maximal time interval on which the solution u of (1.1) exists. The time T may be finite or infinite. Where T is infinite, we say that the solution u exists globally. When T is finite, the solution u develops a singularity in a finite time, namely

(1.2)

where ∥u(⋅, t)∥_∞ = max_0≤x≤1 | u(x, t)|.

In this last case, we say that the solution u blows up in a finite time and the time T is called the blow-up time of the solution u.

In good number of physical devices, the boundary conditions play a primordial role in the progress of the studied processes. It is the case of the problem described in (1.1) which can be viewed as a heat conduction problem where u stands for the temperature, and the heat sources are prescribed on the boundaries. At the boundary x = 0, the heat source has a constant flux whereas at the boundary x = 1, the heat source has a nonlinear radition haw. Intensification of the heat source at the boundary x = 1 is provided by the function b. The function g also gives a dominant strength of the heat source at the boundary x = 1.

The theoretical study of blow-up of solutions for semilinear parabolic equations with nonlinear boundary conditions has been the subject of investigations of many authors (see [1–7], and the references cited therein).

The authors have proved that under some assumptions, the solution of (1.1) blows up in a finite time and the blow-up time is estimated. It is also proved that under some conditions, the blow-up occurs at the point 1. In this paper, we are interested in the numerical study. We give some assumptions under which the solution of a semidiscrete form of (1.1) blows up in a finite time and estimate its semidiscrete blow-up time. We also show that the semidiscrete blow-up time converges to the theoretical one when the mesh size goes to zero. An analogous study has been also done for a discrete scheme. For the semidiscrete scheme, some results about numerical blow-up rate and set have been also given. A similar study has been undertaken in [8, 9] where the authors have considered semilinear heat equations with Dirichlet boundary conditions. In the same way in [10] the numerical extinction has been studied using some discrete and semidiscrete schemes (a solution u extincts in a finite time if it reaches the value zero in a finite time). Concerning the numerical study with nonlinear boundary conditions, some particular cases of the above problem have been treated by several authors (see [11–15]). Generally, the authors have considered the problem (1.1) in the case where a(x, t) = 0 and b(t) = 1. For instance in [15], the above problem has been considered in the case where a(x, t) = 0 and b(t) = 1. In [16], the authors have considered the problem (1.1) in the case where a(x, t) = λ > 0, b(t) = 1, f(u) = u^p, g(u) = u^q. They have shown that the solution of a semidiscrete form of (1.1) blows up in a finite time and they have localized the blow-up set. One may also find in [17–22] similar studies concerning other parabolic problems.

The paper is organized as follows. In the next section, we present a semidiscrete scheme of (1.1). In Section 3, we give some properties concerning our semidiscrete scheme. In Section 4, under some conditions, we prove that the solution of the semidiscrete form of (1.1) blows up in a finite time and estimate its semidiscrete blow-up time. In Section 5, we study the convergence of the semidiscrete blow-up time. In Section 6, we give some results on the numerical blow-up rate and Section 7 is consecrated to the study of the numerical blow-up set. In Section 8, we study a particular discrete form of (1.1). Finally, in the last section, taking some discrete forms of (1.1), we give some numerical experiments.

2. The Semidiscrete problem

Let I be a positive integer and define the grid x_i = ih, 0 ≤ i ≤ I, where h = 1/I. We approximate the solution u of (1.1) by the solution U_h(t) = (U₀(t), U₁(t), …, U_I(t)) ^T of the following semidiscrete equations

(2.1)

(2.2)

(2.3)

where φ_i+1 ≥ φ_i, 0 ≤ i ≤ I − 1,

(2.4)

Here

is the maximal time interval on which ∥U_h(t)∥_∞ is finite where ∥U_h(t)∥_∞ = max_0≤i≤IU_i(t). When

is finite, we say that the solution U_h(t) blows up in a finite time and the time

is called the blow-up time of the solution U_h(t).

3. Properties of the Semidiscrete Scheme

In this section, we give some lemmas which will be used later.

The following lemma is a semidiscrete form of the maximum principle.

Lemma 3.1. Let a_h(t) ∈ C⁰([0, T), ℝ^I+1) and let V_h(t) ∈ C¹([0, T), ℝ^I+1) such that

(3.1)

Then we have V_i(t) ≥ 0, 0 ≤ i ≤ I, t ∈ (0, T).

Proof. Let T₀ < T and define the vector Z_h(t) = e^λtV_h(t) where λ is large enough that a_i(t) − λ > 0 for t ∈ [0, T₀], 0 ≤ i ≤ I. Let . Since for i ∈ {0, …, I}, Z_i(t) is a continuous function, there exists t₀ ∈ [0, T₀] such that for a certain i₀ ∈ {0, …, I}. It is not hard to see that

(3.2)

A straightforward computation reveals that

(3.3)

We observe from (3.2) that

which implies that

because

. We deduce that V_h(t) ≥ 0 for t ∈ [0, T₀] and the proof is complete.

Another form of the maximum principle for semidiscrete equations is the following comparison lemma.

Lemma 3.2. Let V_h(t),U_h(t) ∈ C¹([0, T), ℝ^I+1) and f ∈ C⁰(ℝ × ℝ, ℝ) such that for t ∈ (0, T)

(3.4)

(3.5)

Then we have V_i(t) < U_i(t), 0 ≤ i ≤ I, t ∈ (0, T).

Proof. Define the vector Z_h(t) = U_h(t) − V_h(t). Let t₀ be the first t ∈ (0, T) such that Z_i(t) > 0 for t ∈ [0, t₀), 0 ≤ i ≤ I, but for a certain i₀ ∈ {0, …, I}. We observe that

(3.6)

which implies that

(3.7)

But this inequality contradicts (3.4) and the proof is complete.

4. Semidiscrete Blow-Up Solutions

In this section under some assumptions, we show that the solution U_h of (2.1)–(2.3) blows up in a finite time and estimate its semidiscrete blow-up time.

Before starting, we need the following two lemmas. The first lemma gives a property of the operator δ² and the second one reveals a property of the semidiscrete solution.

Lemma 4.1. Let U_h ∈ ℝ^I+1 be such that U_h ≥ 0. Then we have

(4.1)

Proof. Apply Taylor′s expansion to obtain

(4.2)

where θ_i is an intermediate between U_i and U_i+1 and η_i the one between U_i−1 and U_i. The first and last equalities imply that

(4.3)

Combining the second and third equalities, we see that

(4.4)

Use the fact that g^′′(s) ≥ 0 for s ≥ 0 and U_h ≥ 0 to complete the rest of the proof.

Lemma 4.2. Let U_h be the solution of (2.1)–(2.3). Then we have

(4.5)

Proof. Let t₀ be the first t > 0 such that U_i+1(t) > U_i(t) for 0 ≤ i ≤ I − 1 but for a certain i₀ ∈ {0, …, I − 1}. Without loss of generality, we may suppose that i₀ is the smallest integer which satisfies the equality. Introduce the functions Z_i(t) = U_i+1(t) − U_i(t) for 0 ≤ i ≤ I − 1. We get

(4.6)

which implies that

(4.7)

But this contradicts (2.1)-(2.2) and we have the desired result.

The above lemma says that the semidiscrete solution is increasing in space. This property will be used later to show that the semidiscrete solution attains its minimum at the last node x_I.

Now, we are in a position to state the main result of this section.

Theorem 4.3. Let U_h be the solution of (2.1)–(2.3). Suppose that there exists a positive integer A such that

(4.8)

Assume that

(4.9)

Then the solution U_h blows up in a finite time

and we have the following estimate

(4.10)

Proof. Since is the maximal time interval on which ∥U_h(t)∥_∞ < ∞, our aim is to show that is finite and satisfies the above inequality. Introduce the vector J_h such that

(4.11)

A straightforward calculation gives

(4.12)

From Lemma 4.1, we have δ²g(U_I) ≥ g^′(U_I)δ²U_I which implies that

(4.13)

Using (2.1), we get

(4.14)

It follows from the fact that

, b^′(t) ≥ 0 and dU_i/dt = J_i + Ag(U_i) that

(4.15)

We deduce from (4.9) that

(4.16)

From (4.8), we observe that

(4.17)

We deduce from Lemma 3.1 that J_i(t) ≥ 0, 0 ≤ i ≤ I, which implies that dU_I/dt ≥ g(U_I), 0 ≤ i ≤ I. Obviously we have

(4.18)

Integrating this inequality over

, we arrive at

(4.19)

which implies that

(4.20)

Since the quantity on the right hand side of the above inequality is finite, we deduce that the solution U_h blows up in a finite time. Use the fact that ∥U_h(0)∥_∞ = ∥φ_h∥_∞ to complete the rest of the proof.

Remark 4.4. The inequality (4.19) implies that

(4.21)

where H(s) is the inverse of

Remark 4.5. If g(s) = s^q, then G(s) = s^1−q/(q − 1) and H(s) = ((q − 1)s) ^1/(1−q).

5. Convergence of the Semidiscrete Blow-Up Time

In this section, we show the convergence of the semidiscrete blow-up time. Now we will show that for each fixed time interval [0, T] where u is defined, the solution U_h(t) of (2.1)–(2.3) approximates u, when the mesh parameter h goes to zero.

Theorem 5.1. Assume that (1.1) has a solution u ∈ C^4,1([0, 1]×[0, T]) and the initial condition at (2.3) satisfies

(5.1)

where u_h(t) = (u(x₀, t), …, u(x_I, t)) ^T. Then, for h sufficiently small, the problem (2.1)–(2.3) has a unique solution U_h ∈ C¹([0, T], ℝ^I+1) such that

(5.2)

Proof. Let α > 0 be such that

(5.3)

The problem (2.1)–(2.3) has for each h, a unique solution

. Let

the greatest value of t > 0 such that

(5.4)

The relation (5.1) implies that t(h) > 0 for h sufficiently small. By the triangle inequality, we obtain

(5.5)

which implies that

(5.6)

Let e_h(t) = U_h(t) − u_h(t) be the error of discretization. Using Taylor′s expansion, we have for t ∈ (0, t(h)),

(5.7)

where θ_I(t) is an intermediate value between U_I(t) and u(x_I, t) and ξ_i(t) the one between U_i(t) and u(x_i, t). Using (5.3) and (5.6), there exist two positive constants K and L such that

(5.8)

Consider the function

where M, C, Q are constants which will be determined later. We get

(5.9)

By a semidiscretization of the above problem, we may choose M, C, Q large enough that

(5.10)

It follows from Lemma 3.2 that

(5.11)

By the same way, we also prove that

(5.12)

which implies that

(5.13)

We deduce that

(5.14)

Let us show that t(h) = T. Suppose that T > t(h). From (5.4), we obtain

(5.15)

Since the term on the right hand side of the above inequality goes to zero as h tends to zero, we deduce that 1 ≤ 0, which is impossible. Consequently t(h) = T, and the proof is complete.

Now, we are in a position to prove the main result of this section.

Theorem 5.2. Suppose that the problem (1.1) has a solution u which blows up in a finite time T_b such that u ∈ C^4,1([0, 1]×[0, T_b)) and the initial condition at (2.3) satisfies

(5.16)

Under the assumptions of Theorem 4.3, the problem (2.1)–(2.3) admits a unique solution U_h which blows up in a finite time

and we have the following relation

(5.17)

Proof. Let ε > 0. There exists a positive constant N such that

(5.18)

Since the solution u blows up at the time T_b, then there exists T₁ ∈ (T_b − ε/2, T_b) such that ∥u(⋅, t)∥_∞ ≥ 2N for t ∈ [T₁, T_b). Setting T₂ = (T₁ + T_b)/2, then we have

. It follows from Theorem 5.1 that

(5.19)

Applying the triangle inequality, we get

(5.20)

which leads to ∥U_h(T₂)∥_∞ ≥ N. From Theorem 4.3, U_h(t) blows up at the time

. We deduce from Remark 4.4 and (5.18) that

(5.21)

and the proof is complete.

6. Numerical Blow-Up Rate

In this section, we determine the blow-up rate of the solution U_h of (2.1)–(2.3) in the case where b(t) = 1. Our result is the following.

Theorem 6.1. Let U_h(t) be the solution of (2.1)–(2.3). Under the assumptions of Theorem 4.3, U_h(t) blows up in a finite time and there exist two positive constants C₁, C₂ such that

(6.1)

where H(s) is the inverse of the function

Proof. From Theorem 4.3 and Remark 4.4, U_h(t) blows up in a finite time and there exists a constant C₂ > 0 such that

(6.2)

From Lemma 4.2, U_I−1 < U_I. Then using (2.2), we deduce that dU_I/dt ≤ (2/h)b(t)g(U_I) − a_I(t)f(U_I), which implies that dU_I/dt ≤ (2b(t)/h)g(U_I). Integration this inequality over

, there exists a positive constant C₁ such that

(6.3)

which leads us to the result.

7. Numerical Blow-Up Set

In this section, we determine the numerical blow-up set of the semidiscrete solution. This is stated in the theorem below.

Theorem 7.1. Suppose that there exists a positive constant C₀ such that sF^′(s) ≤ C₀ and

(7.1)

Assume that there exists a positive constant C such

(7.2)

Then the numerical blow-up set is B = {1}.

Proof. Let v(x) = 1 − x² and define

(7.3)

where δ is small enough. We have

(7.4)

and for t ≥ t₀, we get

(7.5)

A straightforward computation yields

(7.6)

This implies that there exists α > 0 such that

(7.7)

Using Taylor′s expansion, there exists a constant K > 0 such that

(7.8)

which implies that

(7.9)

The maximum principle implies that

(7.10)

Hence, we get

(7.11)

Therefore U_i(T)<+∞, 0 ≤ i ≤ I − 1, and we have the desired result.

8. Full Discretization

In this section, we consider the problem (1.1) in the case where a(x, t) = 1, b(t) = 1, f(u) = u^p, g(u) = u^p with p = const >1. Thus our problem is equivalent to

(8.1)

where p > 1, u₀ ∈ C¹([0, 1]),

and

We start this section by the construction of an adaptive scheme as follows. Let I be a positive integer and let h = 1/I. Define the grid x_i = ih, 0 ≤ i ≤ I and approximate the solution u(x, t) of the problem (8.1) by the solution

of the following discrete equations

(8.2)

(8.3)

(8.4)

where n ≥ 0, φ_i+1 ≥ φ_i, 0 ≤ i ≤ I − 1,

(8.5)

In order to permit the discrete solution to reproduce the property of the continuous one when the time t approaches the blow-up time, we need to adapt the size of the time step so that we take

, 0 < τ < 1/p.

Let us notice that the restriction on the time step ensures the nonnegativity of the discrete solution. The lemma below shows that the discrete solution is increasing in space.

Lemma 8.1. Let be the solution of (8.2)–(8.4). Then we have

(8.6)

Proof. Let , 0 ≤ i ≤ I − 1. We observe that

(8.7)

Using the Taylor′s expansion, we find that

(8.8)

where

is an intermediate value between

and

. If

, 0 ≤ i ≤ I − 1, we deduce that

(8.9)

Using the restriction

, we find that

(8.10)

We observe that 1 − 3(Δt_n/h²) − pτ is nonnegative and by induction, we deduce that

, 0 ≤ i ≤ I − 1. This ends the proof.

The following lemma is a discrete form of the maximum principle.

Lemma 8.2. Let be a bounded vector and let a sequence such that

(8.11)

(8.12)

Then

for n ≥ 0, 0 ≤ i ≤ I if

Proof. If then a routine computation yields

(8.13)

Since

, we see that

is nonnegative. From (8.12), we deduce by induction that

which ends the proof.

A direct consequence of the above result is the following comparison lemma. Its proof is straightforward.

Lemma 8.3. Suppose that and two vectors such that is bounded. Let and two sequences such that

(8.14)

Then

for n ≥ 0, 0 ≤ i ≤ I if

Now, let us give a property of the operator δ_t.

Lemma 8.4. Let U⁽ⁿ⁾ ∈ ℝ be such that U⁽ⁿ⁾ ≥ 0 for n ≥ 0. Then we have

(8.15)

Proof. From Taylor′s expansion, we find that

(8.16)

where θ⁽ⁿ⁾ is an intermediate value between U⁽ⁿ⁾ and U⁽ⁿ⁺¹⁾. Use the fact that U⁽ⁿ⁾ ≥ 0 for n ≥ 0 to complete the rest of the proof.

To handle the phenomenon of blow-up for discrete equations, we need the following definition.

Definition 8.5. We say that the solution of (8.2)–(8.4) blows up in a finite time if

(8.17)

The number

is called the numerical blow-up time of

The following theorem reveals that the discrete solution of (8.2)–(8.4) blows up in a finite time under some hypotheses.

Theorem 8.6. Let be the solution of (8.2)–(8.4). Suppose that there exists a constant A ∈ (0, 1] such that the initial data at (8.4) satisfies

(8.18)

Then

blows up in a finite time

which satisfies the following estimate

(8.19)

where

Proof. Introduce the vector defined as follows

(8.20)

A straightforward computation yields

(8.21)

Using (8.2), we arrive at

(8.22)

Due to the mean value theorem, we get

(8.23)

where

is an intermediate value between

and

. On the other hand, from Lemmas 2.4 and 2.5, we deduce that

(8.24)

It follows from (8.3) that

(8.25)

which implies that

(8.26)

From (8.18), we observe that

. It follows from Lemma 8.2 that

which implies that

(8.27)

From Lemma 8.1, we see that

which implies that

(8.28)

It is not hard to see that

(8.29)

From (8.28), we get

. By induction, we arrive at

, which implies that

. Therefore, we find that

(8.30)

Consequently, we arrive at

(8.31)

and by induction, we get

(8.32)

Since the term on the right hand side of the above equality tends to infinity as n approaches infinity, we conclude that

tends to infinity as n approaches infinity. Now, let us estimate the numerical blow-up time. Due to (8.32), the restriction on the time step ensures that

(8.33)

Using the fact that the series on the right hand side of the above inequality converges towards

, we deduce that

and the proof is complete.

Remark 8.7. Apply Taylor′s expansion to obtain , which implies that

(8.34)

If we take τ = h², we see that

(8.35)

We deduce that τ/τ^′ is bounded from above. We conclude that

is bounded from above.

Remark 8.8. From (8.31), we get

(8.36)

which implies that

(8.37)

We deduce that

(8.38)

In the sequel, we take τ = h².

9. Convergence of the Blow-Up Time

In this section, under some conditions, we show that the discrete solution blows up in a finite time and its numerical blow-up time goes to the real one when the mesh size goes to zero. To start, let us prove a result about the convergence of our scheme.

Theorem 9.1. Suppose that the problem (1.1) has a solution u ∈ C^4,2([0, 1]×[0, T]). Assume that the initial data at (8.4) satisfies

(9.1)

Then the problem (8.2)–(8.4) has a solution

for h sufficiently small, 0 ≤ n ≤ J and we have the following relation

(9.2)

where J is such that

and

Proof. For each h, the problem (8.2)–(8.4) has a solution . Let N ≤ J be the greatest value of n such that

(9.3)

We know that N ≥ 1 because of (9.1). Due to the fact that u ∈ C^4,2, there exists a positive constant K such that ∥u∥_∞ ≤ K. Applying the triangle inequality, we have

(9.4)

Since u ∈ C^4,2, using Taylor′s expansion, we find that

(9.5)

Let

be the error of discretization. From the mean value theorem, we get

(9.6)

where

is an intermediate value between u(x_i, t_n) and

. Hence, there exist positive constants L and K such that

(9.7)

Consider the function

where M, C, Q are positive constants which will be determined later. We get

(9.8)

By a discretization of the above problem, we obtain

(9.9)

We may choose M, C, Q large enough that

(9.10)

It follows from Comparison Lemma 8.3 that

(9.11)

By the same way, we also prove that

(9.12)

which implies that

(9.13)

Let us show that N = J. Suppose that N < J. From (9.3), we obtain

(9.14)

Since the term on the right hand side of the second inequality goes to zero as h goes to zero, we deduce that 1 ≤ 0, which is a contradiction and the proof is complete.

Now, we are in a position to state the main theorem of this section.

Theorem 9.2. Suppose that the problem (1.1) has a solution u which blows up in a finite time T₀ and u ∈ C^4,2([0, 1]×[0, T₀)). Assume that the initial data at (2.3) satisfies

(9.15)

Under the assumption of Theorem 8.6, the problem (8.2)–(8.4) has a solution

which blows up in a finite time

and the following relation holds

(9.16)

Proof. We know from Remark 8.7 that is bounded. Letting ε > 0, there exists a constant R > 0 such that

(9.17)

Since u blows up at the time T₀, there exists T₁ ∈ (T₀ − ε/2, T₀) such that ∥u(⋅, t)∥_∞ ≥ 2R for t ∈ [T₁, T₀). Let T₂ = (T₁ + T₀)/2 and let q be a positive integer such that

for h small enough. We have 0 < ∥u_h(t_n)∥_∞ < ∞ for n ≤ q. It follows from Theorem 4.3 that the problem (2.1)–(2.3) has a solution

which obeys

for n ≤ q, which implies that

(9.18)

From Theorem 8.6,

blows up at the time

. It follows from Remark 8.8 and (9.17) that

because

. We deduce that

, which leads us to the result.

10. Numerical Experiments

In this section, we present some numerical approximations to the blow-up time of (1.1) in the case where a(x, t) = λ > 0, f(u) = u^p, g(u) = u^q, b(t) = 1 with p = const >1, q = const >1. We approximate the solution u of (1.1) by the solution

of the following explicit scheme

(10.1)

We also approximate the solution u of (1.1) by the solution

of the implicit scheme below

(10.2)

For the time step, we take n ≥ 0,

for the explicit scheme and

for the implicit scheme.

The problem described in (10.1) may be rewritten as follows

(10.3)

Let us notice that the restriction on the time step Δt_n ≤ h²/2 ensures the nonnegativity of the discrete solution.

The implicit scheme may be rewritten in the following form

(10.4)

where

(10.5)

The matrix

satisfies the following properties

(10.6)

It follows that

exists for n ≥ 0. In addition, since

is nonnegative,

is also nonnegative for n ≥ 0. We need the following definition.

Definition 10.1. We say that the discrete solution of the explicit scheme or the implicit scheme blows up in a finite time if and the series converges. The quantity is called the numerical blow-up time of the solution .

In Tables 1, 2, 3, 4, 5, 6, 7, and 8, in rows, we present the numerical blow-up times, values of n, the CPU times and the orders of the approximations corresponding to meshes of 16, 32, 64, 128, 256. For the numerical blow-up time we take

which is computed at the first time when

(10.7)

The order (s) of the method is computed from

(10.8)

Table 1. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the explicit Euler method defined in (10.1).

I	Tⁿ	n	CPU time	s
16	0.047927	451	—	—
32	0.044695	1260	0.5	—
64	0.043583	4075	5	1.54
128	0.043225	14555	60	1.64
256	0.043115	55061	1816	1.71

Table 2. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the implicit Euler method defined in (10.2).

I	Tⁿ	n	CPU time	s
16	0.047631	423	—	—
32	0.044645	1234	1	—
64	0.043576	4050	5	1.49
128	0.043224	14533	99	1.61
256	0.043113	55035	2000	1.67

Table 3. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the explicit Euler method defined in (10.1).

I	Tⁿ	n	CPU time	s
16	0.018286	21750	3	—
32	0.017181	83838	17	—
64	0.016729	329960	108	1.30
128	0.016412	1298750	1570	0.51
256	0.016324	6447649	27049	1.85

Table 4. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the implicit Euler method defined in (10.2).

I	Tⁿ	n	CPU time	s
16	0.018283	21741	6	—
32	0.017181	83831	37	—
64	0.016729	3299953	347	1.30
128	0.016617	1208495	4640	2.01
256	0.016526	6348765	29957	0.30

Table 5. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the explicit Euler method defined in (10.1).

I	Tⁿ	n	CPU time	s
16	0.024197	1649	—	—
32	0.022570	6103	2	—
64	0.021950	23583	8	1.40
128	0.021734	92985	200	1.52
256	0.021712	369250	3243	3.30

Table 6. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the implicit Euler method defined in (10.2).

I	Tⁿ	n	CPU time	s
16	0.024169	1602	—	—
32	0.022566	6066	5	—
64	0.021950	23551	65	1.38
128	0.021734	92985	1140	1.52
256	0.021713	370240	6709	3.37

Table 7. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the explicit Euler method defined in (8.2)–(8.4).

I	Tⁿ	n	CPU time	s
16	0.054342	422	—	—
32	0.050346	1130	—	—
64	0.049027	3539	4	1.60
128	0.048615	12020	28	1.68
256	0.048491	46439	937	1.74

Table 8. Numerical blow-up times, numbers of iterations, CPU times (seconds) and orders of the approximations obtained with the implicit Euler method defined in (10.2).

I	Tⁿ	n	CPU time	s
16	0.054158	364	—	—
32	0.050332	1077	0.6	—
64	0.049030	3491	7	1.56
128	0.048616	12358	79	1.66
256	0.048519	36919	1123	2.10

Case 1. p = 0, q = 2, φ_i = 10 + 10 * cos (πih), λ = 1.

Case 2. p = 2, q = 4, φ_i = 10 + 10 * cos (πih), λ = 1.

Case 3. p = 2, q = 3, φ_i = 10 + 10 * cos (πih), λ = 1.

Case 4. p = 2, q = 2, φ_i = 10 + 10 * cos (πih), λ = 1.

Remark 10.2. The different cases of our numerical results show that there is a relationship between the flow on the boundary and the absorption in the interior of the domain. Indeed, when there is not an absorption on the interior of the domain, we see that the blow-up time is slightly equal to 0.043 for q = 2 whereas if there is an absorption in the interior of the domain, we observe that the blow-up time is slightly equal to 0.048 for q = 2 and p = 2. We see that there is a diminution of the blow-up time. We also remark that if the power of flow on the boundary increases then the blow-up time diminishes. Thus the flow on the boundary make blow-up occurs whereas the absorption in the interior of domain prevents the blow-up. This phenomenon is well known in a theoretical point of view.

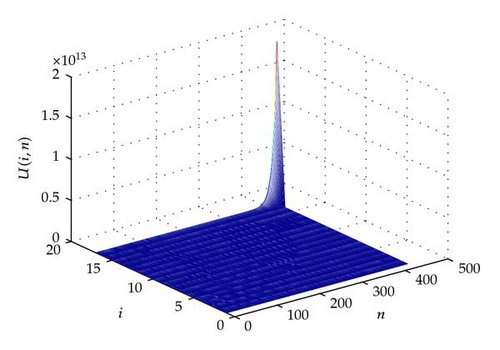
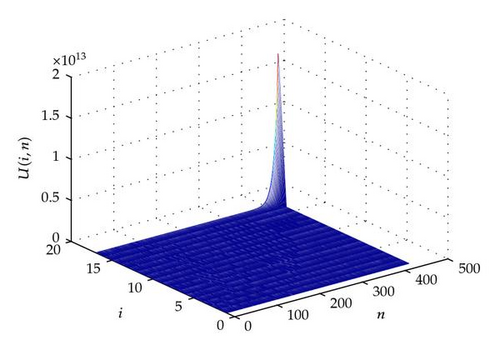
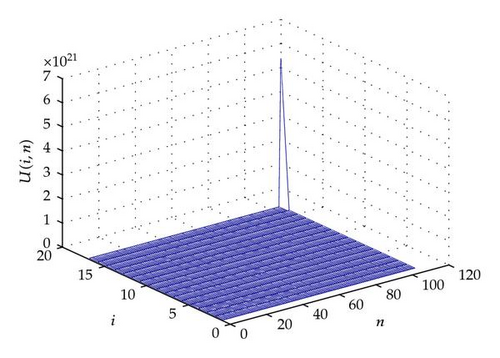
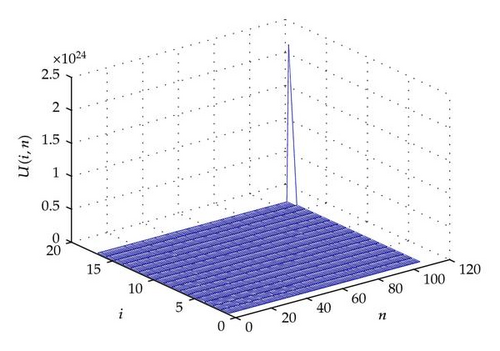
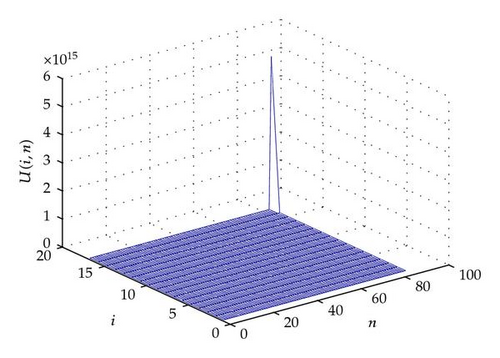
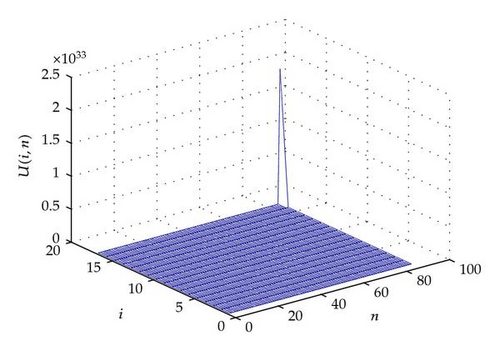
For other illustrations, in what follows, we give some plots to illustrate our analysis. In Figures 1, 2, 3, 4, 5, and 6, we can appreciate that the discrete solution blows up in a finite time at the last node.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Evolution of the discrete solution, q = 2, p = 2 (explicit scheme).

Acknowledgments

We want to thank the anonymous referee for the throughout reading of the manuscript and several suggestions that help us to improve the presentation of the paper.

References

1 Boni T. K., Sur l′explosion et le comportement asymptotique de la solution d′une équation parabolique semi-linéaire du second ordre, Comptes Rendus de l′Académie des Sciences. Série I. (1998) 326, no. 3, 317–322, MR1648453, https://doi.org/10.1016/S0764-4442(97)82987-4, ZBL0913.35069.
10.1016/S0764-4442(97)82987-4
Google Scholar
2 Boni T. K., On blow-up and asymptotic behavior of solutions to a nonlinear parabolic equation of second order with nonlinear boundary conditions, Commentationes Mathematicae Universitatis Carolinae. (1999) 40, no. 3, 457–475, MR1732489, ZBL1011.35078.
Google Scholar
3 Chipot M., Fila M., and Quittner P., Stationary solutions, blow up and convergence to stationary solutions for semilinear parabolic equations with nonlinear boundary conditions, Acta Mathematica Universitatis Comenianae. (1991) 60, no. 1, 35–103, MR1120596, ZBL0743.35038.
Google Scholar
4 Galaktionov V. A. and Vázquez J. L., The problem of blow-up in nonlinear parabolic equations, Discrete and Continuous Dynamical Systems. Series A. (2002) 8, no. 2, 399–433, MR1897690, https://doi.org/10.3934/dcds.2002.8.399, ZBL1010.35057.
10.3934/dcds.2002.8.399
Web of Science® Google Scholar
5 Quittner P. and Souplet P., Superlinear Parabolic Problems: Blow-up, Global Existence and Steady States, 2007, Birkhäuser, Basel, Switzerland, Birkhäuser Advanced Texts. Basler Lehrbücher, MR2346798, ZBL1128.35003.
Google Scholar
6 Samarskii A. A., Galaktionov V. A., Kurdyumov S. P., and Mikhailov A. P., Blow-up in Problems for Quasilinear Parabolic Equations, 1987, Nauka, Moscow, Russia, MR919951.
Google Scholar
7 Samarskii A. A., Galaktionov V. A., Kurdyumov S. P., and Mikhailov A. P., Blow-up in Problems for Quasilinear Parabolic Equations, 1995, Walter de Gruyter, Berlin, Germany, MR1330922.
10.1515/9783110889864
Google Scholar
8 Abia L. M., López-Marcos J. C., and Martínez J., On the blow-up time convergence of semidiscretizations of reaction-diffusion equations, Applied Numerical Mathematics. (1998) 26, no. 4, 399–414, MR1612360, https://doi.org/10.1016/S0168-9274(97)00105-0, ZBL0929.65070.
10.1016/S0168-9274(97)00105-0
Web of Science® Google Scholar
9 Nakagawa T., Blowing up of a finite difference solution to u_t = u_xx + u², Applied Mathematics and Optimization. (1975) 2, no. 4, 337–350, MR0423823, ZBL0357.65075, https://doi.org/10.1007/BF01448176.
10.1007/BF01448176
Web of Science® Google Scholar
10 Boni T. K., Extinction for discretizations of some semilinear parabolic equations, Comptes Rendus de l′Académie des Sciences. Série I. (2001) 333, no. 8, 795–800, MR1868956, https://doi.org/10.1016/S0764-4442(01)02078-X, ZBL0999.35004.
10.1016/S0764-4442(01)02078-X
Google Scholar
11 Acosta G., Fernández Bonder J., Groisman P., and Rossi J. D., Simultaneous vs. non-simultaneous blow-up in numerical approximations of a parabolic system with non-linear boundary conditions, M2AN. (2002) 36, no. 1, 55–68, MR1916292, https://doi.org/10.1051/m2an:2002003, ZBL1003.65097.
10.1051/m2an:2002003
Google Scholar
12 Acosta G., Fernández Bonder J., Groisman P., and Rossi J. D., Numerical approximation of a parabolic problem with a nonlinear boundary condition in several space dimensions, Discrete and Continuous Dynamical Systems. Series B. (2002) 2, no. 2, 279–294, MR1898142, https://doi.org/10.3934/dcdsb.2002.2.279, ZBL0997.35025.
10.3934/dcdsb.2002.2.279
Google Scholar
13 Brändle C., Groisman P., and Rossi J. D., Fully discrete adaptive methods for a blow-up problem, Mathematical Models & Methods in Applied Sciences. (2004) 14, no. 10, 1425–1450, MR2095297, ZBL1065.35022.
10.1142/S0218202504003751
Google Scholar
14 Brändle C., Quirós F., and Rossi J. D., An adaptive numerical method to handle blow-up in a parabolic system, Numerische Mathematik. (2005) 102, no. 1, 39–59, MR2206671, https://doi.org/10.1007/s00211-005-0638-x, ZBL1082.65094.
10.1007/s00211-005-0638-x
Web of Science® Google Scholar
15 Duran R. G., Etcheverry J. I., and Rossi J. D., Numerical approximation of a parabolic problem with a nonlinear boundary condition, Discrete and Continuous Dynamical Systems. (1998) 4, no. 3, 497–506, MR1612760, https://doi.org/10.3934/dcds.1998.4.497, ZBL0951.65088.
10.3934/dcds.1998.4.497
Google Scholar
16 Fernández Bonder J. and Rossi J. D., Blow-up vs. spurious steady solutions, Proceedings of the American Mathematical Society. (2001) 129, no. 1, 139–144, MR1712866, https://doi.org/10.1090/S0002-9939-00-05663-X, ZBL0970.35003.
10.1090/S0002-9939-00-05663-X
Google Scholar
17 de Pablo A., Pérez-Llanos M., and Ferreira R., Numerical blow-up for the p-Laplacian equation with a nonlinear source, Proceedings of the 11th International Conference on Differential Equations (Equadiff ′05), July 2005, Bratislava, Slovakia, 363–367.
Google Scholar
18 Le Roux M. N., Semidiscretization in time of nonlinear parabolic equations with blowup of the solution, SIAM Journal on Numerical Analysis. (1994) 31, no. 1, 170–195, MR1259971, https://doi.org/10.1137/0731009, ZBL0803.65095.
10.1137/0731009
Google Scholar
19 Le Roux M. N., Semi-discretization in time of a fast diffusion equation, Journal of Mathematical Analysis and Applications. (1989) 137, no. 2, 354–370, MR984965, https://doi.org/10.1016/0022-247X(89)90251-5, ZBL0693.65085.
10.1016/0022-247X(89)90251-5
Google Scholar
20 Nabongo D. and Boni T. K., Numerical blow-up and asymptotic behavior for a semilinear parabolic equation with a nonlilnear boundary condition, Albanian Journal of Mathematics. (2008) 2, no. 2, 111–124, MR2415487, ZBL1144.35416.
10.51286/albjm/1210658677
Google Scholar
21 Nabongo D. and Boni T. K., Numerical blow-up solutions of localized semilinear parabolic equations, Applied Mathematical Sciences. (2008) 2, no. 21–24, 1145–1160, MR2443797.
Google Scholar
22 N′gohissé F. K. and Boni T. K., Numerical blow-up solution for some semilinear heat equation, Electronic Transactions on Numerical Analysis. (2008) 30, 247–257.
Google Scholar

Citing Literature

All articles

Numerical Blow-Up Time for a Semilinear Parabolic Equation with Nonlinear Boundary Conditions

Abstract

1. Introduction

2. The Semidiscrete problem

3. Properties of the Semidiscrete Scheme

4. Semidiscrete Blow-Up Solutions

5. Convergence of the Semidiscrete Blow-Up Time

6. Numerical Blow-Up Rate

7. Numerical Blow-Up Set

8. Full Discretization

9. Convergence of the Blow-Up Time

10. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Blow-Up Time for a Semilinear Parabolic Equation with Nonlinear Boundary Conditions

Abstract

1. Introduction

2. The Semidiscrete problem

3. Properties of the Semidiscrete Scheme

4. Semidiscrete Blow-Up Solutions

5. Convergence of the Semidiscrete Blow-Up Time

6. Numerical Blow-Up Rate

7. Numerical Blow-Up Set

8. Full Discretization

9. Convergence of the Blow-Up Time

10. Numerical Experiments

Acknowledgments

References

Citing Literature

Figures

References

Related

Information