Particle swarm optimisation (PSO) is an innovative and competitive optimisation technique for numerical optimisation with real-parameter representation. In this paper, we examine the working mechanism of PSO in a principled manner with forma analysis and investigate the applicability of PSO on the permutation problem domain. Particularly, our derived PSO schemes are empirically studied based on the quadratic assignment problem (QAP) benchmarks to justify its comparable performance, which in turn implies the benefits of our approach in applying PSO to the discrete problem domain.

1. Introduction

PSO was originally designed as a numerical optimisation technique based on swarm intelligence. In the literature, there are a few attempts to exploit its usage in the discrete problem domain [1–4], which are mostly performed using a binary encoding. However, research on the transformation of the working mechanism of PSO to the permutation problem domain, where the representations are highly constrained, has been relatively limited [3, 5, 6]. This limitation is mainly caused by the lack of a principled generalisation of PSO to guide its adaptation to discrete combinatorial problems [3].

In this paper, we aim to design PSO operators for permutation problems without losing the underlining principles of the original PSO. A PSO operator template will be formally defined with forma analysis in form of equivalence relations. Following the introduction of formal descriptions of permutations, concrete PSO operators are then formally derived based on the PSO operator template. Empirical study of the derived PSO schemes is also carried out based on the QAP benchmarks.

2. Particle Swarm Optimisation

PSO was initially introduced by Kennedy and Eberhart [7] as a function optimisation technique inspired by the behaviors of fish schooling and bird flocking. The PSO approach simulates the social behavior of particles/agents moving in a multidimensional search space, while each particle has its position and velocity. Each particle is treated as a potential solution to the optimisation problem. Usually, the position is represented as a vector:

()

while the velocity is represented as another vector:

()

where i represents the index of the particle, t is the time step, and D is the dimensionality of the search space.

For each generation, the particle compares its current position with the goal (global best/personal best) position, adjusting its velocity accordingly towards the goal with the help of the explicit memory of the best position ever found both globally and individually.

The most popular formulation of how particle adjusts its velocity and position [8, 9] is shown in

()

Alternatively, we may have

()

In the above formulation, d is the index of dimension in the search space, w represents the inertia weight of the “flying” dynamic, which describes the degree of maintaining its previous velocity vector against the attraction point. c₁ and c₂ are regarded as cognitive and social parameters for the algorithm, respectively, while r₁ and r₂ are random numbers within the interval [0, 1]. Pb_i is the personal best position which is recorded by particle i, while Gb is the global best position obtained by any particle in the population.

Adapting standard PSO to permutation problems has been a rather interesting task, as researchers are curious about its performance in the discrete domain. In this paper, we suggest that forma analysis gives a possible solution to achieve such task in a principled manner.

3. Forma Analysis

Forma analysis [10] is a formal but practical method that allows the problem representation and its operators to be structured in a formal manner by using equivalence relations. Each equivalence relation Ψ divides the search space into disjoint equivalence classes Ξ_ψ (depending on which value the solutions match), with individual equivalence classes being denoted by ξ, which gathers solutions that are equivalent under a certain equivalence relation.

The initial aim of forma analysis [10] was to codify knowledge of the problem domain using a set of equivalence classes (or formae) which is assumed to be able to cluster solutions with related performance in order to guide the search process more effectively, for example, edges if we are considering the travelling salesman problem. Since equivalence relations/classes have the ability to capture the properties of solutions, concrete operators can thus be mathematically derived with regards to how these equivalence relations are formally manipulated by the operator templates.

Figure 1 illustrates briefly the approach we adopt here in this paper, which can be explained as follows. Given an operator template, any suitable description of the considered problem domain gives rise to a concrete operator, whose behavior and performance are related to the assumption adopted to describe the search space. This approach effectively allows PSO to be adapted to arbitrary problem domain with the underlying working mechanism retained. Taking a step further, this approach is applicable across different problem domains and different optimisation techniques.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of the methodology based on forma analysis.

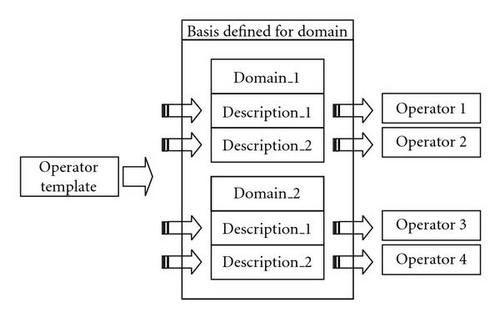
Some of the characteristics and operator templates related to forma analysis [10–12] are given below to facilitate our generalisation of PSO.

3.1. Describing the Search Space

The key concept is that of a basis: a set of equivalence relations that allows us to describe the search space S.

Definition 1. A subset Ψ of a set of equivalence relations is termed as a basis for the set of equivalence relations, if Ψ spans the set and Ψ is independent.

An encoding can thus be derived by taking the image of the basis equivalence classes corresponding to a particular solution in the search space.

3.2. Domain Independent Operator Templates

Forma analysis can derive operators that explicitly manipulate the given equivalence relations. This is achieved by combining the basis with domain independent operators for specifying operator behavior in terms of basis.

One such (domain independent) operator template, which is related to the work presented in this paper, corresponds to the (strict) k-change operator template [12], formally as

()

where x and y represent the solution to be perturbed and the produced child, respectively, while dis_Ψ(x,y) represents the forma distance [13] between x and y under basis Ψ. This operator template can be interpreted as changing the values for k equivalence relations in x produces solution y.

The other operator template, random transmitting recombination (RTR) [10], is defined to select a child solution z out of the dynastic potential of the parent solutions x and y. RTR(x,y,Ψ) can be formally defined as

()

where the actual child solution z is chosen from the set above uniformly at random. The underlying idea of RTR is to randomly generate child solution using parental equivalence classes (genetic material).

3.3. Applicability

Although the above concepts of forma analysis are developed under genetic algorithms, it has been shown that the forma analysis methodology itself is generalisable to other evolutionary optimisers based on (theoretically) any problem domain from the knowledge-based system (KBS) design standpoint [12]. Also, the underlying idea proposed by Surry [11] on defining formal representation in order to derive domain specific operators has also been justified to be rather successful. Furthermore, our previous work on adapting PSO to the binary search space following the forma analysis approach has provided some preliminary positive results and expectations. In summary, the proposed forma analysis-based operator design approach is applicable in the context of PSO and permutation problem domain, considering the previous theoretical and practical evidence.

4. Formal Descriptions of Permutation

As previously studied in [12, 14], there are mainly three different representations for permutation that we can adopt to describe the permutation problems:

(1)
position-based representation, which decides the absolute position of an item (e.g., item 5 is at position 4),
(2)
precedence-based representation, which decides whether one task is performed before another (e.g., task 5 appears before task 4),
(3)
adjacency-based representation, which decides whether two items are next to each other (e.g., item 4 is next to item 5).

In the following sections, formal descriptions for permutation with a set of n elements N = {e₁, … ,e_n} will be reviewed in form of equivalence relations, followed by some formal definitions of their induced constraints and their distance measurements [12, 15].

4.1. Position-Based Description of Permutation

For position-based description, each position in the permutation i (i = 1, …,n) is defined as an equivalence relation ψ_pos(i) to form the basis of position equivalence relations such that

()

The equivalence classes (formae) for each position i are the set of n elements:

()

As an example, the permutation (1, 4, 3, 2) can be described by the set of equivalence classes

()

In addition, an induced feasibility constraint for this description C_pos needs to be added to ensure that different elements do not occupy the same position, and no two different positions can take the same element, formally as follows.

Definition 2. Given any two equivalence relations ψ_pos(i) and ψ_pos(j) for a permutation, the position-based constraintC_pos can be defined as

()

A direct implication of this constraint is that the 1-change neighborhood structure should be prevented as this would involve placing two elements in the same position.

The distance metric for this formal description is simply the number of positions in the permutation that have different elements (i.e., the hamming distance) according to the definition of forma distance [13]. For example, the distance between (1, 4, 3, 2) and (1, 4, 2, 3) is 2, since they are different in two positions.

4.2. Precedence-Based Description of Permutation

For precedence-based description, a set of basis precedence equivalence relations Ψ_prec between any two different elements in the permutation will be considered formally as

()

However, by considering the fact (constraint) that

and

are reverse relations:

()

we can remove unnecessary relations by enforcing a sequence (e.g., e₁ < e₂ < …<e_n) in the definition of the relation, such that

()

Obviously, the equivalence classes are simply true/false for whether element e_i precedes element e_j in the permutation formally as

()

In addition, the feasibility constraint C_prec needs to be added that a valid permutation exists if and only if the relationship between the precedences is consistent (in that the transitivity condition is preserved), as shown below.

Definition 3. Given any two equivalence relations, and , for a permutation, the precedence-based constraintC_prec can be defined as

()

The distance metric can be specified as the number of different precedence relations between two solutions. For example, the distance between permutation (1, 2, 3, 4) and (1, 4, 2, 3) can be obtained by comparing the following two sets:

()

In practice, bubble sort will be sufficient to calculate the distance from one permutation towards another. This can be achieved by sorting one permutation towards another, when setting one as the initial permutation and the other as the goal permutation which represents the right “order.” If we are looking at the previous example with two permutations, to calculate the distance from (1, 2, 3, 4) (i.e., the initial permutation) to (1, 4, 2, 3) (i.e., the goal permutation), the “priority” information can be obtained from (1, 4, 2, 3):

()

Thus, the initial permutation can be represented (or more closely, implemented) in terms of (e_i,order(e_i)):

()

and it should be sorted according to the values of order(e_i) in order to “transform" to the goal permutation with a certain number of basic swap adjacency mutations.

4.3. Adjacency-Based Description of Permutation

For adjacency-based description, a set of basis adjacency equivalence relations Ψ_adj is considered for any two elements to decide whether they are adjacent formally as

()

Due to the fact that

and

are equivalent relations for symmetric problems (Surry presented an extensive study about directed edge representation for permutation in his work [11]):

()

we can remove redundant relations by enforcing a sequence (e.g., e₁ < e₂ < …<e_n) in the definition of the relation, such that

()

As undirected edges are considered for adjacency-based description, the equivalence classes are simply true/false for whether there exists an edge between element e_i and element e_j formally as

()

In this case,

represents a positive edge so that edge (e_i,e_j) must exists in the solution (e.g., a tour), while

stands for a negative edge so that edge (e_i,e_j) cannot be included into the solution.

In addition, the feasibility constraint C_adj needs to be added so that each vertex of the undirected graph corresponding to the permutation can only participate in two edges and still be a valid permutation as follows.

Definition 4. Given an equivalence relation for a permutation, the adjacency-based constraintC_adj can be defined as

()

The distance between any two solutions in the search space under adjacency basis is thus calculated as the number of different edges that they possess. For instance, the distance between permutation (1, 2, 3, 4) and (1, 2, 4, 3) can be obtained by calculating the number of different adjacency relations between the following two sets:

()

However, on the “phenotypical” level this forma distance reduces to the number of different positive edges (n minus common positive edges), which should be 2 in this case. This is mainly because negative edges do not directly affect the quality of solution, although they implicitly affect the selection of positive edges through the feasibility constraints.

5. PSO Operator Template—A Generalisation

The generalisation of PSO is not as straightforward as some other optimisation techniques, such as the generalisation of Differential Evolution [16]. This is mainly because, besides the generalisation of position in a multi-dimensional space, we also need to generalise the velocity of particle in a multi-dimensional space.

By observing the update equation (as shown in (4)), we can easily find out that

()

in which case the velocity is effectively the step size to perturb one solution towards another (in other words, the distance between the two solutions), which is jointly decided by the inertia component w∗v_it(d), the bias towards its personal best c₁r₁[Pb_i(d) − x_it(d)], and the bias towards the global best c₂r₂[Gb(d) − x_it(d)].

5.1. PSO Operator Template

By revealing the fact that velocity is the distance between the previous and current positions of the particle, we can define the operator template (under the basis Ψ) as follows.

Definition 5. Given a current position X_t (if one temporarily ignores the index i of this particle in the population), its position for the next time step X_t+1 can be produced according to (27):

()

where dis_Ψ(X_t,X_t−1) is used to formalise the previous velocity of the particle, while dis_Ψ(X_t+1,X_t) represents the current velocity for perturbing the current solution X_t.

5.2. Stochastic Interpretation of Accumulation

In the context of real-vectors, the accumulation of distances is straightforward to understand. However, for permutation problems the consideration of “directionality” becomes rather complex from the practical standpoint. By taking into account the fact that forma distance includes domain-specific distance magnitude and direction which cause certain difficulties in the context of permutation problems, a reasonable interpretation of the PSO operator template is required to facilitate the derivation of suitable PSO operators for permutation problems. From this perspective, the original PSO operator template (before interpretation), which abstracts how solutions are manipulated, can be regarded as an operator design guideline embedded with the PSO working mechanism. As a matter of fact, various interpretations and approximations have also been made in the previous work of forma analysis for the purpose of facilitating operator derivations [11, 12] (such as the derivation of RTR operator template to blend crossover/line recombination crossover for continuous domain).

By understanding the fact that the perturbation of the current individual is jointly decided by three components (with their degrees of influence distributed proportionally), we can give a stochastic interpretation of the PSO operator template as follows.

The perturbation dis_Ψ(X_t+1,X_t) can be interpreted separately in three cases:

Case 1
if rand()≤(w/b), dis_Ψ(X_t,X_t−1);
Case 2
else if rand()≤(w/b)+(c₁r₁/b), dis_Ψ(Pb,X_t);
Case 3
else, dis_Ψ(Gb,X_t),

where b equals (w + c₁r₁ + c₂r₂). In this interpretation, the parameters w and c₁/c₂ are used to represent the probabilities of the current particle′s commitment to each of the components. In other words, the new velocity has a probability of (w/b) to stay the same as previous value, a probability of (c₁r₁/b) to converge towards its personal best record, and a probability of (c₂r₂/b) to converge towards the global best record.

The decomposition of the flying dynamics of a particle is illustrated in Figure 2. The current particle has three options: a random k-change according to the magnitude of its previous velocity, change towards its personal best record, or change towards the global best record. (Strictly according to the original PSO working mechanism, this should not be a random k-change. Instead it should be a directed perturbation following the previous direction. However, since this direction is difficult to “replicate” practically, we choose to simplify this to a random k-change with the magnitude maintained only.)

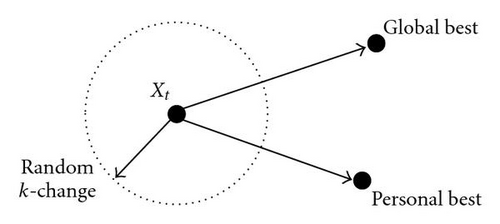
However, the mixing effect of several distances with different directions is hard to represent in the context of permutation. Modelling the accumulation from a stochastic perspective helps us avoid this unnecessary complication.

5.3. Incorporation of Direction-A Crossover Perspective

Given that we already have the mechanism to separate each distance component, the next question is how to incorporate direction to guide our PSO operator so that the particles can converge towards superior records.

As aforementioned, if a greedy component with superior record considered is selected to perturb the current particle, we directly have

()

which means that the particle should jump to the attraction point (i.e., Pb/Gb) without any reservations. However, this is the situation we should try to avoid in practice, since the search may stagnate at a very early stage dominated by the initial superior component. Thus, we desire the current particle to converge somewhere between itself and the attraction point along the right direction.

By taking a closer look at the guided PSO operator, we can actually find that the effect of perturbing one individual towards another is the same as making a crossover (e.g., RTR) between these two individuals where the direction can be naturally retained. Understanding the greedy components of PSO operator in terms of crossover makes the practical incorporation of direction in the operator much easier.

5.4. Understanding PSO Operator Template

From the above discussion, we can evolve a new interpretation of the PSO operator template. The new position X_t+1 can be generated according to three cases separately:

Case 1
if rand()≤(w/b), O_k(X_t, |dis_Ψ(X_t,X_t−1)|);
Case 2
else if rand()≤(w/b)+(c₁r₁/b), RTR (X_t,Pb,Ψ);
Case 3
else, RTR (X_t,Gb,Ψ),

where for the first case a random k-change, with k = |dis_Ψ(X_t,X_t−1)|, is adopted to perturb the current particle, while for the second and the third cases a RTR operator template is used to perturb the current particle towards the attraction point (i.e., Pb/Gb). For the first case, only the magnitude of the previous velocity is considered to parameterise the random k-change. For the second and the third cases, the magnitude of velocity should be updated according to the difference between the new position and the previous position of the particle after the RTR “move.”

5.5. Brief Comparisons with Geometric PSO

In this section, our forma analysis framework is compared with the geometric framework [3] which has also been proposed for generalising PSO.

5.1.1. Comparisons on the Framework

On the framework level, both frameworks aim to generalise PSO based on underlying optimisation components (e.g., solution representation or distance notion) so that the abstraction of optimisers, either in the form of standard operator template RTR/RRR/RAR or in the form of line segment/ball [3], can be further generalised to arbitrary problem domain. In both cases, these abstractions need to be instantiated to concrete operators by embedding domain knowledge into the corresponding abstraction. In other words, these abstractions all carry some form of domain knowledge, either by using equivalence relations or by using distance notions, so that they can be applied to concrete problem instances.

The main difference on the design concept level lies in the choice of such abstractions and the “carrier” of domain knowledge. For our forma analysis approach, the solution representation is generalised with equivalence relations/classes so that formal representation can be defined in an unified manner, while operators that manipulate the solutions are abstracted as operator templates that process equivalence relations. In contrast, the geometric framework is more about generalising optimisers based on a notion of distance where different distance metrics give rise to different operators with regards to the predefined geometric operators using the notions of line segment and ball [3]. Each framework looks at operator design through abstraction and formal description (of either solutions or distance) at different levels, with potentially equivalence relations lying at a slightly lower level than distance notion as distance notion is effectively a derivative of equivalence relations once forma distance [13, 15] is defined under the forma analysis framework.

5.1.2. Comparisons on PSO Generalisation

On the practical PSO generalisation level, both approaches are generally different in two places as well.

First of all, the concept of velocity has been removed from the geometric framework (thus, including the simplification of the concept of inertia as a component in geometric crossover), while a random mutation is added to the geometric PSO as a potential replacement for perturbation purposes. In our forma analysis approach, velocity has been interpreted and formulated as distance (more precisely forma distance) in the previous time step. However, velocity itself is a rather complicated concept to formulate as it involves the interpretation of both magnitude and direction which are hard to represent in the context of permutation problems. Certain simplifications and compromises have been made to maintain this concept for future research.

Secondly, the accumulation of greediness toward personal best and global best, balanced by previous velocity (or position), is interpreted differently as well. In geometric PSO, multiparental geometric crossover is used to linearly recombine these positions to produce the next position with different weights taken into account through the concept of product geometric crossover. In contrast, in our forma analysis approach, different convergence components are treated stochastically according to their different weights where higher weight represents higher probability of being treated as the convergence direction for the next time step (and vice versa). By looking at the full picture, different components (personal best, global best, or previous velocity) all share the probability of being selected to guide the next move. Standard RTR operator template is used to converge towards superior solutions with the direction of distance naturally maintained, while standard k-change operator template is used to represent the inertia component.

6. “Blended” PSO Operators for Permutation Problems

As mentioned earlier, the formal descriptions of permutation problems implicitly introduces some feasibility constraints to produce a valid solution. When we design PSO operators for permutation problems, these constraints must be satisfied (or handled properly) which is effectively a subproblem to solve. (Of course, these constraints only exist if we are only interested in searching feasible regions, while search techniques making use of infeasible regions are out of the scope in this discussion.) In our previous work [15], we have presented that the application of standard genetic operators for permutation problems can be viewed as a process of constraint satisfaction, so as to instantiate the declarative nature of forma analysis in a systematic manner and bring forma analysis to a more practical level. In this section, we will show how the PSO operators for permutation problems can be obtained procedurally based on the operator template from a constraint satisfaction problem (CSP) [17] solving perspective.

According to the aforementioned stochastic interpretation of PSO operator template, the outcome is effectively a blended operator with three different “phases”: k-change according to k = |dis_Ψ(X_t,X_t−1)|, RTR (X_t,Pb,Ψ), and RTR (X_t,Gb,Ψ). The separate instantiations of k-change and RTR in the context of different formal descriptions of permutation should directly give rise to the instantiations of the corresponding blended PSO operators.

6.1. Instantiations of k-Change

6.1.1. Position-Based k-Change: O_k-pos

For the position-based description,

can be obtained as the hamming distance between X_t+1 and X_t under basis Ψ_pos. Thus, we only need to apply a distance of k based on X_t to generate X_t+1 such that

. For example, given that X_t represents a permutation (1, 2, 3, 4) such that

()

what would be the potential candidates for the permutation X_t+1 so that they have a distance of k (e.g., k = 2)?

The most straightforward thought would be to randomly select k equivalence relations and change the equivalence classes they fall into. However, the feasibility constraint C_pos induced by position-based description must be satisfied to produce a valid permutation. In this case, the k-change operator for permutation following the position-based description should involve a constraint satisfaction subproblem, where C_pos must be satisfied to guarantee a valid permutation.

The CSP we consider here is defined as the k-change operator itself with C_pos satisfied. Classical CSP techniques can be directly utilised to implement the operator. Now, we will follow the above example to illustrate how CSP can be effectively used in the position-based PSO operator design.

Given X_t (), we can first uninstantiate k (e.g., k = 2) equivalence relations to produce a partial permutation for a potential distance of 2. This gives us options from which we can uniformly select one to serve as the base (partial permutation) of X_t+1 (e.g., ).

Then, what we need to do is simply to reinstantiate these 2 equivalence relations to suitable classes such that C_pos is satisfied. The first position of the partial solution (−,2, − ,4) is considered first. The domain of the first position is {1, 3}, while the domain of the third position is {1, 3} as well. After an equivalence class (1 or 3) is chosen for the first position, the domain is reduced for the third position through constraint propagation. After instantiating all the possible solutions, X_t+1 can be randomly selected among the whole set of feasible solutions to the CSP.

In fact, the working mechanism of O_k-pos has a similar effect as the scramble mutation [18], which rearranges a certain number of positions. The only difference is that the selection of these positions should be purely random, other than inside a continuous block. Thus, O_k-pos can be defined as the modified scramble mutation operator with k random positions, where k is decided by the magnitude of the current velocity .

6.1.2. Precedence-Based k-Change: O_k-prec

For the precedence-based description of permutation, the distance of two permutations is the number of different precedence relations . As aforementioned, the bubble sort algorithm is sufficient to calculate the precedence distance of two permutations, with the distance decided as the number of adjacency-swap to sort one permutation towards another.

Assuming k = 3 which should be applied to X_t = (2, 3, 4, 1) as an example, X_t+1 can be obtained by solving the CSP as shown in Figure 3.

Given that X_t can be represented as

()

to apply a distance of 3 will be a reinstantiation of 3 equivalence relations. This gives us

options from which we can uniformly select one as the partial permutation to generate X_t+1. For example, the partial permutation can be

()

Reinstantiating these 3 precedence relations to suitable classes such that C_prec is satisfied can give us potential candidates for X_t+1.

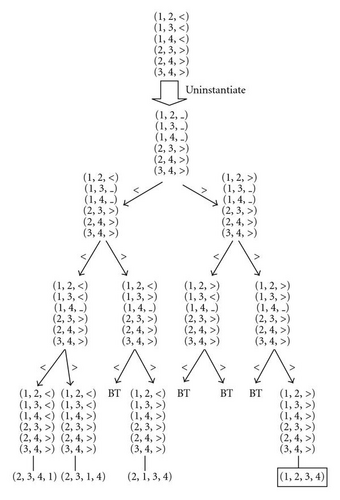
As shown in Figure 3, the reinstantiation of precedence relations is carried out one after another. The domain of each relation is simply {0, 1}. Alternatively, we use “<” and “>” to represent the precedence such that symbol “(i,j, >)” means element i is before element j while “(i,j, <)” means otherwise. X_t+1 can be randomly selected among the set of feasible solutions to the CSP.

By observing the effect of changing a single precedence equivalence class, it is not difficult to find that a 1-change (minimal mutation) reduces to the adjacent swap mutation [18], which swaps two contiguous elements. Thus, O_k-prec can be approximately regarded as equivalent to a k-iterated adjacent swap mutation with k decided by the magnitude of the current velocity , which can be effectively calculated through bubble sort.

6.1.3. Adjacency-Based k-Change: O_k-adj

Since each potential edge is defined as an equivalence relation for the adjacency-based description of permutation, the distance of two permutations corresponds to the “edge-difference” between them.

For the simplicity of illustration, we assume that k = 4, which should be applied to X_t to generate X_t+1. As an example, given the base permutation (1, 2, 3, 4) being represented as

()

we first uninstantiate 4 relations (randomly chosen from

options) to produce the partial permutation for X_t+1, for example:

()

By solving the CSP to generate X_t+1 such that C_adj is satisfied, we can get a solution permutation (1, 3, 2, 4) with a distance of 4 to X_t:

()

The minimal mutation implied by the adjacency-based description is an edge 2-change mutation, because 1-change automatically violates the feasibility constraint C_adj. (A standard edge2-change mutation involves the “replacement” of 2 edges which in turn results in the change of 4 adjacency equivalence relations, since there are also changes involving negative edges. However, from the implementation perspective only phenotypical (or positive) edges are considered.) This operator is equivalent to the edge-reverse mutation in the literature [18], which reverses the positions of a segment in the permutation in such a manner that the feasibility constraint C_adj can be satisfied automatically. Due to the fact that any edge-reverse mutation involves the change of 2 edges, O_k-adj can be generally approximated by a k^∗-iterated edge-reverse mutation with k^∗ decided by k as follows:

()

where any function that rounds k/2 to its nearest integer is sufficient.

6.2. Instantiations of RTR

6.2.1. Position-Based RTR: RTR_pos

For the position-based description Ψ_pos, its feasibility constraint C_pos largely reduces the number of feasible solutions to the basic CSP, where RTR is interpreted as recombination of parental equivalence classes, because not all combinations of them lead to valid permutations. By satisfying C_pos while instantiating P_c, we can obtained all potential candidates for RTR_pos as a result of solving the CSP.

For example, given P_p1 = (1, 2, 3, 4) and P_p2 = (4, 3, 2, 1), RTR_pos can produce potential candidate(s) for P_c by reinstantiating it (as shown in Figure 4) with corresponding equivalence classes, as shown in (37)

()

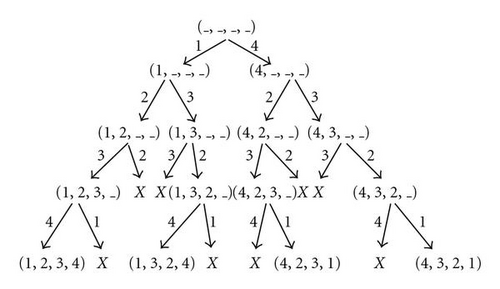
To transmit position features from parents to children and interpret the feasibility constraint C_pos in a more natural way, we produce a fully-transmitting crossover for permutation, namely position transmitting crossover (PTX), by identifying the constraint satisfaction process of operator as a CSP.

In PTX, both C_pos and transmitting C_t have to be satisfied as an interpretation of its CSP. (Transmitting can be regarded as an additional constraint imposed by operator.) In this sense, constrained positions are clustered to function separately. For example, given two permutations

()

we are able to construct the constraint graph implied by both C_pos and transmitting C_t, as shown in Figure 5 with constrained positions linked together.

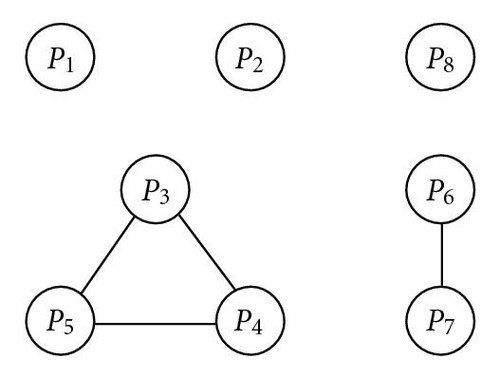
The construction of the constraint graph is straightforward to understand—a value that has been taken for one position must be forbidden (constrained) for another position. For example, for position 3 (P₃ in Figure 5) either 5 or 2 should be chosen to achieve transmitting. However, choosing either of them will forbid another position (e.g., P₄ or P₅ in Figure 5) from taking the same value, which effectively reduces the domain for another position.

The only possibility that the value taken by one position does not constrain the value taken by another is that the parents both take the same value for that position (e.g., P₁ in Figure 5), where taking (the only) one value automatically satisfies the constraint.

Thus, as long as the constrained positions are transmitted all-together to the child, PTX always satisfies both C_pos and C_t, and the child solution is always a valid permutation. Following the above example, the child produced by PTX could be

()

In fact, PTX works in an equivalent manner as cycle crossover [19] in the literature, which preserves absolute positions in parents and guarantees feasibility of child solutions.

6.2.2. Precedence-Based RTR: RTR_prec

To achieve transmitting in precedence-based crossover, both transmitting C_t and C_prec should be satisfied from the CSP viewpoint. It is easy to verify that this CSP is solvable, since (in the worst case) taking all the equivalence classes for either parent to produce child always gives one possible solution such that constraints (C_t and C_prec) are satisfied.

Furthermore, precedence relation is special in that its equivalence class is either 1 or 0. This means that in the case when two parents are different for a certain equivalence relation , the domain of for the child is always {0, 1}, which implicitly means that can take any value for the child. In the case when two parents are the same for , the corresponding equivalence class is fixed for the child to achieve transmitting.

For example, given permutations (3, 1, 2, 4) and (4, 2, 3, 1) such that

()

the partial permutation as a child to achieve transmitting can be

()

while the uninstantiated relations can be reinstantiated randomly to produce the child permutation, by solving a CSP such that simply C_prec should be satisfied.

In fact, strictly transmitting crossover is also possible for precedence-based description. Due to the fact that the reinstantiation process of precedence relations is equivalent to the topological sorting problems [20], where a partial order needs to be completed to a linear order (in a directed acyclic graph (DAG) based on precedence) with a complexity of O(edges + vertices), we argue that the reinstantiation of precedence relations in the considered CSP can be solved in a deterministic polynomial-time in terms of topological sorting problems. (The partial order is defined by the equivalence relations where the parents are equivalent—the order that must be enforced for the child.)

In the literature, precedence preservative crossover (PPX) [18] was found to be strictly transmitting. The underlining principle in PPX is that the precedence equivalence classes of parents are passed to the child in such an order (from left to right or more specifically from the node with no incoming edges in the precedence graph) that both C_t and C_prec are satisfied automatically. Practically, this order is implemented using a “from” table which indicates the switching process between the two parents.

Many readers may find that this is rather similar to the most popular algorithm used for topological sorting where the order can be completed by starting from the node(s) with no incoming edges. Switching between two parents simply aims at recombining the precedence equivalence classes of the two parents.

It is also easy to find that the set of all possible solutions produced by PPX is in fact a subset of the set of solutions produced by the above CSP approach. In other words, for each of the solution produced by PPX, there is always a corresponding reinstantiation of the partial child permutation.

6.2.3. Adjacency-Based RTR: RTR_adj

Regarding the adjacency-based description of permutation which has been proved to be non g-separable [10], literature [11, 12] pointed out that transmission cannot be achieved without sacrificing assortment. From the CSP viewpoint, this implies that C_adj and C_t all together may make the corresponding CSP not strictly solvable (if the original parental permutations are not allowed to be repeated as a child permutation). Through investigation, we can also find that it is the case when two parents are the same for some equivalence relations that makes the CSP NP-complete in “strict” sense. For those adjacency relations that two parents are different, no restriction will be applied to the child solution for that relation (as both {1, 0} are allowed).

Furthermore, for those edges which are absent in both parents (“negative edges” ), transmitting automatically forbids them from being included in the children. In this sense, the induced CSP is equivalent to the Hamiltonian cycle problem [21] in an incomplete graph, which is NP-complete. (It should be pointed out that this Hamiltonian cycle problem is NP-complete only if the parental permutations are forbidden for the child, since the parents automatically gives 2 possible solutions. However, finding the third solution is still NP-complete.) Those edges which are common for both parents (“positive edges” ) effectively enforce that some edges must be included in the Hamiltonian cycles (solutions). This is actually a constrained version of the original Hamiltonian cycle problem induced by “negative edges,” which is also NP-complete.

Thus, approximation through relaxation of C_t may be required to produce a valid new child permutation. In the literature, enhanced edge recombination devised by [22] has been noticed as an effective “edge-aware” recombination operator which has a high rate (98%) of adjacency transmission. The transmitting of adjacency formae is approximated by creating an edge table with the related edge information for both parents and selecting edges in a heuristic manner to construct the child solution.

6.3. The Blended PSO Schemes

In summary, the derived blended PSO schemes with different formal descriptions of permutation can be described in the following Algorithms 1, 2, and 3.

Algorithm 1: Position-based blended PSO scheme (PSO_pos).

1. for all particle ido
2. initialize P_i (with its velocity V_i) and evaluate P_i;
3. endfor
4. do
5. for all particle ido
6. setPb_i as best position found by particle i so far;
7. setGb as best position found by all particles so far;
8. if (rand() < w/b):
9. modified scramble mutation according to |V_i|;
10. elseif (rand()<(w + c₁r₁)/b):
11. cycle crossover CX (P_i,Pb_i);
12. else:
13. cycle crossover CX (P_i,Gb);
14. endif
15. evaluate P_i and update |V_i|;
16. endfor
17. until (halting criterion met);

Algorithm 2: Precedence-based blended PSO scheme (PSO_prec).

1. for all particle ido
2. initialize P_i (with its velocity V_i) and evaluate P_i;
3. endfor
4. do
5. for all particle ido
6. setPb_i as best position found by particle i so far;
7. setGb as best position found by all particles so far;
8. if (rand() < w/b):
9. k-iterated adjacent-swap with k = |V_i|;
10. elseif (rand()<(w + c₁r₁)/b):
11. precedence preservative crossover PPX (P_i,Pb_i);
12. else:
13. precedence preservative crossover PPX (P_i,Gb);
14. endif
15. evaluate P_i and update |V_i|;
16. endfor
17. until (halting criterion met);

Algorithm 3: Adjacency-based blended PSO scheme (PSO_adj).

1. for all particle ido
2. initialize P_i (with its velocity V_i) and evaluate P_i;
3. endfor
4. do
5. for all particle ido
6. setPb_i as best position found by particle i so far;
7. setGb as best position found by all particles so far
8. if (rand() < w/b):
9. k-iterated edge-reverse mutation with k = round(|V_i | /2)
10. elseif (rand()<(w + c₁r₁)/b):
11. enhanced edge crossover EX (P_i,Pb_i);
12. else:
13. enhanced edge crossover EX (P_i,Gb);
14. endif
15. evaluate P_i and update |V_i|;
16. endfor
17. until (halting criterion met);

7. Experiments of PSO Schemes on Quadratic Assignment Problems

To illustrate the search dynamics of the derived blended PSO schemes, we evaluated the performance of these PSO schemes on the quadratic assignment problem (QAP) benchmarks. However, due to the fact that for QAP the absolute positioning of element is more related to the quality of solution [14], it is estimated that the PSO scheme with position-based description (i.e., PSO_pos) should perform better than the other PSO schemes.

After a brief description of the problem formulation, we show both the experiment configurations and the experimental results, followed by a few discussions to help the understanding of the benefits of our approach.

7.1. Problem Formulation of QAP

The quadratic assignment problem (QAP) is an important problem in both practice and theory. Many practical problems can be formulated as QAPs [23–25]. The QAP can be described as the problem of assigning a set of facilities to a set of locations with the given distances between the locations and the given flows between the facilities. The goal is to place the facilities on locations such that the sum of the product between flows and distances is minimised. Formally, given n facilities and n locations, two n × n matrices A = [a_ij] and B = [b_rs], where a_ij is the distance between locations i and j, and b_rs is the flow between facilities r and s, the QAP can be formally defined as

()

The QAP is a class of NP-hard optimisation problems. It is considered as one of the hardest optimisation problems as general instances of size larger than 20 cannot be solved to optimality. Therefore, to practically solve QAP with high quality solutions various heuristic algorithms have been proposed [26–28] trying to find high quality solution with limited computational resources.

7.2. Benchmarks and Experimental Settings

The benchmarks for this experimental study are acquired from QAP-LIB [29]. It has been pointed out [30] that there are four types of QAP instances: unstructured, randomly generated instances, unstructured instances with grid-distances, real-life instances, real-life like instances. We select 2 instances for each type of QAP as our benchmarks, with size no smaller than 20. For type 1, we choose and Tai40a. For type 2, we choose Nug20 and Sko56. For type 3, we choose Bur26a and Ste36a. For type 4, we choose Tai20b and Tai40b.

For each of the instances, fine tuning is carried out for each of the algorithms to reach its best performance among different combinations of parameter settings with equal number of generations. The parameter settings with the best performance over 20 independent runs for each algorithm will be used to get the execution results. (The performance is evaluated by considering both its average best solution found and its average number of generations to reach its best solution. The number of generation to reach its best solution is only considered when two parameter settings have the same average best solution.)

The original free parameters for each instances are W and C, where W represents the parameter to control the inertia weight and C represents the value taken by c₁ and c₂ (as in literature c₁ and c₂ often adopt the same value). By taking a closer look, it is not difficult to realise that in our PSO schemes for QAP, the probability of taking each branch can be simplified to

()

The above simplification means that the essential element controlling the search dynamics is (W/C). This implies that (W/C) is effectively the only parameter we need to deal with for our PSO scheme, where a relatively larger (W/C) would encourage a more explorative search, while a relatively smaller (W/C) would favour a greedier search towards either one of the superior attraction points (i.e., Pb/Gb).

The population size is fixed to be an appropriate number (100) for each instance through observations. Since we do not have preknowledge about the discrete PSO operators, the tuning process is only carried out in a coarse manner, where the options for W and C are both formatively set to be {1, 2, 3, …, 9, 10} (although only W/C matters).

7.3. Observations and Experimental Results

According to the tuned parameter settings, 50 independent runs were executed for each PSO scheme under each instance to produce experimental results.

7.3.1. Comparisons Among PSO Schemes

To examine the search behavior of the proposed PSO schemes, we track three components of each scheme that are felt to be essential to the search dynamics of PSO. These three components are: the mean cost of the population; the average best of the population; the average velocity of the population. The mean cost and average best of the population are plotted together to reveal the convergence pattern, while the average velocity is plotted to track the exploration power. Only the search patterns for are illustrated here (as shown in Figure 6), since the patterns for all the other instances are quite similar. In addition, the execution results are also shown in Table 1.

Table 1. Experimental results over 50 independent runs for different PSO schemes.

	SIZE	GEN #	POP_size	Tai40a	SIZE	GEN #	POP_size
	20	5000	100	Tai40a	40	10000	100
Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS	749292.1871		12172.79199	PSO_POS	3332304		27611.47461
PSO_PREC	756756.8125		6750.588867	PSO_PREC	3475673		23905.56437
PSO_ADJ	778401.8125		10900.51661	PSO_ADJ	3547892		17521.19283

Nug20	SIZE	GEN #	POP_size	Sko56	SIZE	GEN #	POP_size
Nug20	20	5000	100	Sko56	65	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS	2680.120117		34.834686	PSO_POS	35955.64063		309.11557
PSO_PREC	2717.847864		27.325028	PSO_PREC	36078.96543		257.68971
PSO_ADJ	2746.896391		25.121398	PSO_ADJ	38423.78542		375.67864

Bur26a	SIZE	GEN #	POP_size	Ste36a	SIZE	GEN #	POP_size
Bur26a	26	5000	100	Ste36a	36	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS	5445906.1		8688.298828	PSO_POS	10808.51953		436.841125
PSO_PREC	5462411.9		8622.741697	PSO_PREC	11356.24567		553.488941
PSO_ADJ	5489783.6		7989.741787	PSO_ADJ	11667.04213		604.555.718

Tai20b	SIZE	GEN #	POP_size	Tai40b	SIZE	GEN #	POP_size
Tai20b	20	5000	100	Tai40b	40	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS	124803488		1190690.75	PSO_POS	696782272		28186792
PSO_PREC	125760656		1622274.93	PSO_PREC	706244099		17986929
PSO_ADJ	128727848		1379135.25	PSO_ADJ	722001585		18978233

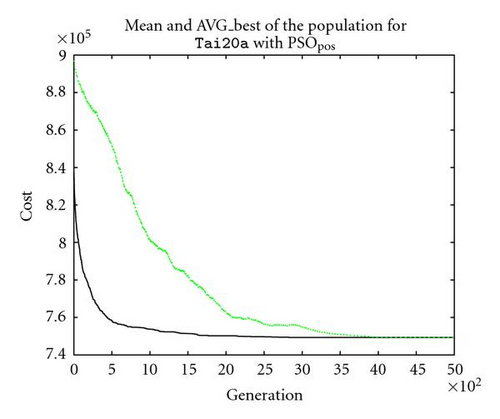
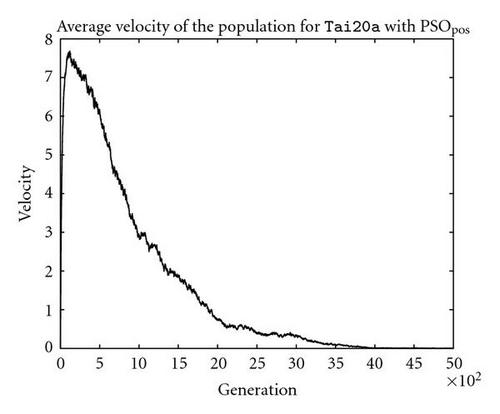
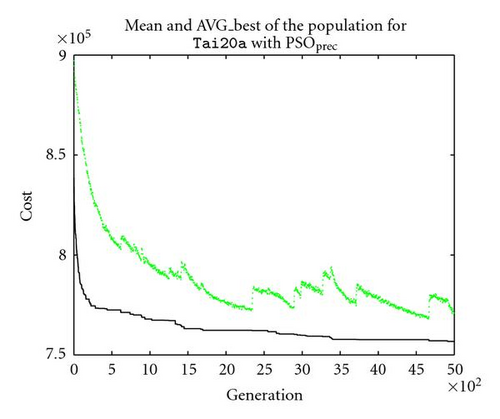
Through observation shown in Figure 6(a), we can find that for position-based PSO (PSO_pos) both the mean cost and the average velocity of population are changing throughout the search process smoothly, as the whole population is constantly converging towards the attraction point(s). The pattern of the corresponding velocity (as shown in Figure 6(b)) implies that the exploration power of the whole population initially increases to a relatively higher level, before it decreases constantly as the search goes to a later stage. These searching patterns are generally very similar as those in the traditional PSO in the real-vector space.

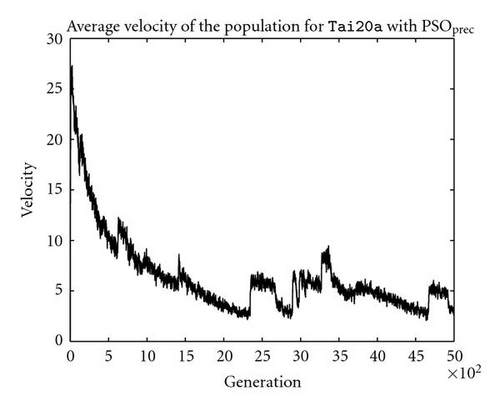
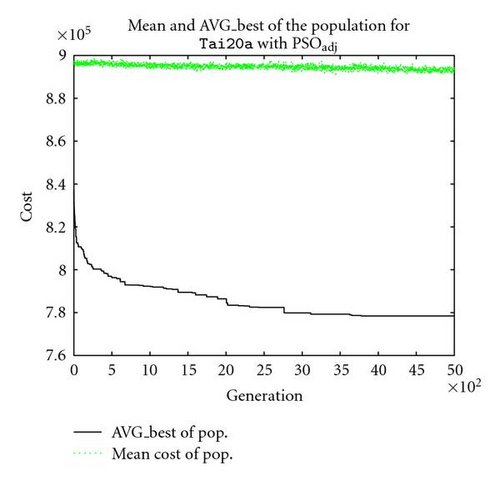
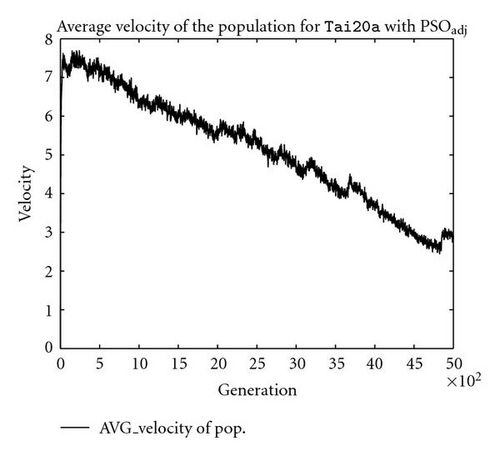
The situation for PSO_prec is however slightly different from PSO_pos according to the patterns shown in Figures 6(c) and 6(d). Although the mean quality of the whole population still converge towards the superior individuals (i.e., the global/local best solutions) and the average velocity decreases with the generation number, it is observed that there are some “resistances” in its convergence process. The situation is even worse for PSO_adj (as shown in Figures 6(e) and 6(f)), as the mean quality of the whole population hardly converges, and the average velocity of the population decreases more slowly relative to the average velocity for PSO_pos. Presumably, the degree of such resistance is the main cause for performance loss/gain, considering the fact that both PSO_prec and PSO_adj are outperformed by PSO_pos (as shown in Table 1).

This can be mainly explained by the different information transfer efficiencies with different descriptions for QAP. The position-based PSO scheme (PSO_pos) is the most efficient scheme among the three since absolute positioning is being processed for its corresponding position-based description, which is most related to the quality of solution for QAP. From the implementation standpoint, the “recombination” of the position-based equivalence classes from both the current individual and its superior records serves as the main drive for convergence.

However, the information processing of absolute positioning is disrupted by both precedence description and adjacency description to different degrees. This is also quite obvious from the implementation standpoint, since the “recombination” of precedence/adjacency information certainly will not produce the convergence of solution quality efficiently in terms of absolute positioning. The degree of such “disruption/deviation” is mainly decided by its correlations to the positional description. This can be further illustrated by the fact that precedence-based PSO performs better than adjacency-based PSO. As a matter of fact, precedence relations are more correlated to positional relations, which can be easily understood by inspecting the shift operator—as the number of precedences changed by the shift operator increases, so does the number of positions in a smooth progression. In contrast, adjacency relations are found to be poorly correlated with positional relations, since the number of adjacency relations changed by edge-reverse mutation is poorly correlated with the changes in the absolute positioning of permutations.

The above results also reflect the main argument we are making for the methodology in this paper: the search behavior and performance of the derived operator depend on the description for the specific problem. Further estimations can be that PSO_prec should perform well in those problems where precedence information processing in permutation is essential (e.g., JSSP), while PSO_adj should perform well in those problems where adjacency/edge information is related to solution quality (e.g., TSP).

7.3.2. Extended Comparisons

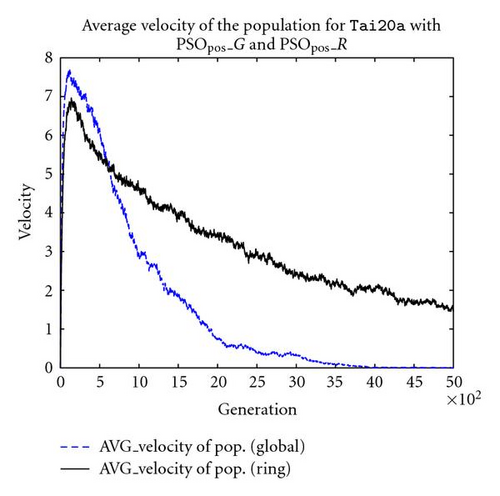
In addition, another PSO scheme for QAP is also implemented with ring topology based on PSO_pos to illustrate the benefits of changing topology. As shown clearly in Figure 7(a), the position-based PSO scheme with ring topology (PSO_pos_R) outperforms the position-based PSO scheme with global topology (PSO_pos_G) by enhancing the exploration power through the implicit search control introduced by ring topology. In order to compare the exploration power of both PSOs, the average velocities of both schemes are plotted in Figures 7(b). From Figure 7(b), we can easily find that the ring structured PSO (PSO_pos_R) has a greater persistence in maintaining its velocity level than the global PSO (PSO_pos_G), which in turn enables a better exploration of the search space. Another observation is that, by the end of the execution, the average velocity of PSO_pos_R has not decreased to 0 yet, which means that given a larger number of generation an even better performance can be expected.

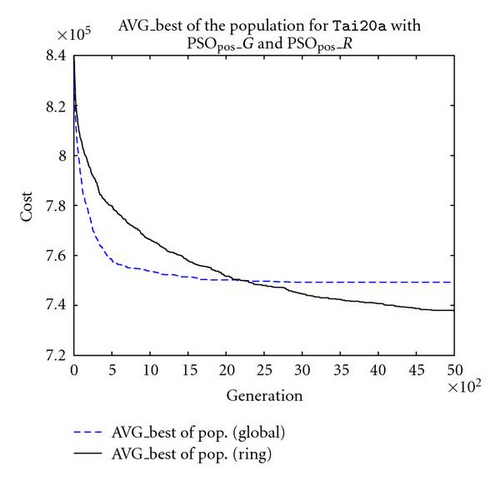
The mean-best and standard deviation produced by our PSO schemes for each instance are presented in Table 2 under algorithms PSO_pos_G (for global structure) and PSO_pos_R (for ring structure). The results are also compared against a steady state standard GA using cycle crossover, with swap mutation (mutation rate = 0.1).

Table 2. Experimental results over 50 independent runs for PSO schemes with different topologies against a standard GA.

	SIZE	GEN #	POP_size	Tai40a	SIZE	GEN #	POP_size
	20	5000	100	Tai40a	40	10000	100
Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS_G	749292.1871		12172.79199	PSO_POS_G	3332304		27611.47461
PSO_POS_R	737858.2491		9983.63476	PSO_POS_R	3307909		28703.17578
GA	721765.0625		6995.33252	GA	3232640		14233.77148

Nug20	SIZE	GEN #	POP_size	Sko56	SIZE	GEN #	POP_size
Nug20	20	5000	100	Sko56	65	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS_G	2680.120117		34.834686	PSO_POS_G	35955.64063		309.11557
PSO_POS_R	2629.800049		24.587896	PSO_POS_R	35452.19922		179.47287
GA	2606.199951		21.662531	GA	35040.23828		184.824081

Bur26a	SIZE	GEN #	POP_size	Ste36a	SIZE	GEN #	POP_size
Bur26a	26	5000	100	Ste36a	36	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS_G	5445906.1		8688.298828	PSO_POS_G	10808.51953		436.841125
PSO_POS_R	5434604.5		3932.839611	PSO_POS_R	10252.40039		235.487991
GA	5436641.5		5282.220703	GA	10061.67969		219.714996

Tai20b	SIZE	GEN #	POP_size	Tai40b	SIZE	GEN #	POP_size
Tai20b	20	5000	100	Tai40b	40	10000	100

Algorithms	Mean best		Std Dev	Algorithms	Mean best		Std Dev
PSO_POS_G	124803488		1190690.75	PSO_POS_G	696782272		28186792
PSO_POS_R	123274304		783373.25	PSO_POS_R	662772480		13308939
GA	125778728		5234746.11	GA	679525504		18660756

From the results, we can see that PSO_pos_R with ring topology overall outperforms PSO_pos_G with global topology, while generally GA still performs slightly better than the PSO schemes we have for some cases. We understand that this inferiority is mainly caused by the simplification of the inertia component in the PSO operator template, since a random k-change is not good enough to represent a directed k-change which should be parameterised by its previous velocity. This drawback requires our further research on how to replicate and apply distance, so that the previous distance/velocity can be retained and applied during the next generation. If we are able to implement this, the PSO should display a better convergence pattern. Also, further tuning and exploration of PSO options will inevitably lead to improved performance. However, we should point out that the main aim of this paper is certainly not to produce sophisticated PSO schemes with competitive results. Instead, the intent of this work is to generalise PSO in a formal manner, adapt its working mechanism to the permutation problem domain with reasonably good performance, and hopefully show some future research directions on generalising PSO. In this case, performance comparison at a competitive level is not performed due to the fact that most of those results were produced by highly tuned/adapted hybrid algorithms [5, 31] where the separate contribution of each component is usually hard to justify, and comparisons against them would be of limited value.

8. Conclusions and Future Work

In this paper, we have presented how the original PSO operator can be generalised in a formal manner to the permutation problem domain using forma analysis, with both the formal descriptions of permutation and a stochastic PSO operator template defined. By considering the application of operators as a process of constraint satisfaction, we derived several concrete PSO schemes for permutation problem, each of which involves a different assumption made on the description of the search space. Through observations of the search patterns of the derived PSO schemes together with the ring structured extension of position-based PSO on the QAP benchmarks, it is clear that the description choice is a critical issue in operator design, and the position-based PSO scheme for QAP achieves a certain degree of convergence towards the optimum in a similar manner as the traditional PSO for real-vector space, with results comparable to a standard GA.

More importantly, we have presented in this paper a principled approach to formally derive algorithms with regard to the actual problem domain, in which case the behaviors and the performance of the derived algorithms are directly related to the assumption we make to describe the search space.

In the future, efforts on the improvement of these discrete PSO schemes are possible by considering additional issues (e.g., topological search control, local search, and even parameter selections). Application of our methodology to a wider range of problems and optimisation techniques can also be explored. In addition, the interpretation of applying a directed k-change (e.g., distance replication) in the context of permutation problems should be studied in the future to give a better understanding of the working mechanism of PSO for those problems.

References

1 Kennedy J. and Eberhart R. C., A discrete binary version of the particle swarm algorithm, 5, Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, October 1997, Orlando, Fla, USA, IEEE Press, 4104–4108, https://doi.org/10.1109/ICSMC.1997.637339.
10.1109/ICSMC.1997.637339
Google Scholar
2 Clerc M., The swarm and the queen: towards a deterministic and adaptive particle swarm optimization, 3, Proceedings of the IEEE Congress of Evolutionary Computation (CEC ′99), July 1999, Washington, DC, USA, https://doi.org/10.1109/CEC.1999.785513.
10.1109/CEC.1999.785513
Google Scholar
3 Moraglio A., Chio C. D., and Poli R., Geometric particle swarm optimization, Proceedings of the 10th European Conference Genetic Programming (EuroGP ′07), April 2007, Valencia, Spain, 125–136, https://doi.org/10.1007/978-3-540-71605-1_12.
10.1007/978-3-540-71605-1_12
Google Scholar
4 Gong T. and [email protected], Tuson A. L., [email protected], Binary particle swarm optimization: a forma analysis approach, Proceedings of 9th Annual Conference on Genetic and Evolutionary Computation (GECCO ′07), July 2007, London, UK, ACM, https://doi.org/10.1145/1276958.1276986.
10.1145/1276958.1276986
Google Scholar
5 Tasgetiren M. F., [email protected], Liang Y.-C., Sevkli M., and Gencyilmaz G., A particle swarm optimization algorithm for makespan and total flowtime minimization in the permutation flowshop sequencing problem, European Journal of Operational Research. (2007) 177, no. 3, 1930–1947, https://doi.org/10.1016/j.ejor.2005.12.024.
10.1016/j.ejor.2005.12.024
Web of Science® Google Scholar
6 Clerc M., Particle Swarm Optimization, 2006, ISTE, London, UK.
10.1002/9780470612163
Google Scholar
7 Kennedy J. and Eberhart R. C., Particle swarm optimization, 4, Proceedings of the IEEE International Conference on Neural Networks, November-December 1995, Perth, WA, Australia, 1942–1948, https://doi.org/10.1109/ICNN.1995.488968.
10.1109/ICNN.1995.488968
Google Scholar
8 Shi Y. and Eberhart R. C., A modified particle swarm optimizer, Proceedings of the IEEE Congress on Evolutionary Computation (ICEC ′98), May 1998, Anchorage, Alaska, USA, IEEE Press, 69–73, https://doi.org/10.1109/ICEC.1998.699146.
10.1109/ICEC.1998.699146
Google Scholar
9 Shi Y. and Eberhart R. C., Parameter selection in particle swarm optimization, Proceedings of the 7th Annual Conference on Evolutionary Programming (EP ′98), March 1998, San Diego, Calif, USA, 591–600.
Google Scholar
10 Radcliffe N. J., The algebra of genetic algorithms, Annals of Mathematics and Artificial Intelligence. (1994) 10, no. 4, 339–384, https://doi.org/10.1007/BF01531276.
10.1007/BF01531276
Google Scholar
11 Surry P. D., A prescriptive formalism for constructing domain-specific evolutionary algorithm, Ph.D. thesis, University of Edinburgh, 1998, Edinburgh, Scotland, UK.
Google Scholar
12 Tuson A. L., No optimization without representation: a knowledge based systems view of evolutionary/neighbourhood search optimization, Ph.D. thesis, University of Edinburgh, 1999, Edinburgh, Scotland, UK.
Google Scholar
13 Gong T. and [email protected], Tuson A. L., [email protected], Formal descriptions of real parameter optimisation, Proceedings of the IEEE Congress on Evolutionary Computation (CEC ′06), July 2006, Vancouver, BC, Canada, IEEE Press, 2119–2126, https://doi.org/10.1109/CEC.2006.1688568.
10.1109/CEC.2006.1688568
Google Scholar
14 Bierwirth C., Mattfeld D. C., and Kopfer H., On permutation representations for scheduling problems, Proceedings of the 4th International Conference on Parallel Problem Solving from Nature (PPSN ′96), September 1996, Berlin, Germany, Springer, 310–318.
Google Scholar
15 Gong T. and [email protected], Tuson A. L., [email protected], Enhanced forma analysis of permutation problems, Proceedings of 9th Annual Conference on Genetic and Evolutionary Computation (GECCO ′07), July 2007, London, UK, ACM, 923–930, https://doi.org/10.1145/1276958.1277146.
10.1145/1276958.1277146
Google Scholar
16 Gong T. and Tuson A. L., A. Saad, E. Avineri, K. Dahal, M. Sarfraz, and R. Roy, Differential evolution for binary encoding, 39, Proceedings of the 11th Online World Conference on Soft Computing in Industrial Applications (WSC ′06), September-October 2006, Springer, Advances in Soft Computing.
Google Scholar
17 Tsang E. P. K., Foundations of Constraint Satisfaction, 1993, Academic Press, London, UK.
Google Scholar
18 Bäck T., Fogel D. B., and Michalewicz Z., Evolutionary Computation 1: Basic Algorithms and Operators, 2000, Institute of Physics, Bristol, UK.
10.1887/0750306645
Google Scholar
19 Oliver I. M., Smith D. J., and Holland J. R. C., J. J. Grefenstette, A study of permutation crossover operators on the traveling salesman problem, Proceedings of the 2nd International Conference on Genetic Algorithms on Genetic Algorithms and Their Application (ICGA ′87), July 1987, Cambridge, Mass, USA, Lawrence Erlbaum Associates.
Google Scholar
20 Cormen T. H., Leiserson C. E., Rivest R. L., and Stein C., Introduction to Algorithms, 2001, 2nd edition, MIT Press, Cambridge, Mass, USA.
CAS PubMed Google Scholar
21 DeLeon M., A study of sufficient conditions for hamiltonian cycles, 2000, Department of Mathematics and Computer Science, Seton Hall University, South Orange, NJ, USA.
Google Scholar
22 Starkweather T., McDaniel S., Mathias K., Whitley C., and Whitley D., R. Belew and L. Booker, A comparison of genetic sequencing operators, Proceedings of the 4th International Conference on Genetic Algorithms (ICGA ′91), July 1991, San Diego, Calif, USA, Morgan Kaufmann.
Google Scholar
23 Steinberg L., The backboard wiring problem: a placement algorithm, SIAM Rview. (1961) 3, no. 1, 37–50, https://doi.org/10.1137/1003003.
10.1137/1003003
Web of Science® Google Scholar
24 Elshafei A., Hospital layout as a quadratic assignment problem, Operational Research Quarterly. (1977) 28, no. 1, 167–179.
10.1057/jors.1977.29
Web of Science® Google Scholar
25 Geoffrion A. and Graves G., Scheduling parallel production lines with changeover costs: practical application of a quadratic assignment/lp approach, Operations Research. (1976) 24, no. 4, 595–610.
10.1287/opre.24.4.595
Web of Science® Google Scholar
26 Stützle T. and Dorigo M., D. Corne, M. Dorigo, and F. Glover, ACO algorithms for the quadratic assignment problem, New Ideas in Optimization, 1999, McGraw-Hill, London, UK, 33–50.
Google Scholar
27 Battiti R. and Tecchiolli G., The reactive tabu search, ORSA Journal on Computing. (1994) 2, no. 6, 126–140.
10.1287/ijoc.6.2.126
Google Scholar
28 Burkard R. E. and Rendl F., A thermodynamically motivated simulation procedure for combinatorial optimization problems, European Journal of Operational Research. (1984) 17, no. 2, 169–174, https://doi.org/10.1016/0377-2217(84)90231-5.
10.1016/0377-2217(84)90231-5
Web of Science® Google Scholar
29 Burkard R. E., Karisch S., and Rendl F., QAPLIB-A quadratic assignment problem library, European Journal of Operational Research. (1991) 55, no. 1, 115–119, https://doi.org/10.1016/0377-2217(91)90197-4.
10.1016/0377-2217(91)90197-4
Web of Science® Google Scholar
30 Taillard E. D., Comparison of iterative searches for the quadratic assignment problem, Location Science. (1994) 3, no. 2, 87–105, https://doi.org/10.1016/0966-8349(95)00008-6.
10.1016/0966-8349(95)00008-6
Google Scholar
31 Lim M.-H., Yuan Y., and Omatu S., Extensive testing of a hybrid genetic algorithm for solving quadratic assignment problems, Computational Optimization and Applications. (2002) 23, no. 1, 47–64, https://doi.org/10.1023/A:1019972523847.
10.1023/A:1019972523847
Web of Science® Google Scholar

Citing Literature

All articles

Forma Analysis of Particle Swarm Optimisation for Permutation Problems

Abstract

1. Introduction

2. Particle Swarm Optimisation

3. Forma Analysis

3.1. Describing the Search Space

3.2. Domain Independent Operator Templates

3.3. Applicability

4. Formal Descriptions of Permutation

4.1. Position-Based Description of Permutation

4.2. Precedence-Based Description of Permutation

4.3. Adjacency-Based Description of Permutation

5. PSO Operator Template—A Generalisation

5.1. PSO Operator Template

5.2. Stochastic Interpretation of Accumulation

5.3. Incorporation of Direction-A Crossover Perspective

5.4. Understanding PSO Operator Template

5.5. Brief Comparisons with Geometric PSO

5.1.1. Comparisons on the Framework

5.1.2. Comparisons on PSO Generalisation

6. “Blended” PSO Operators for Permutation Problems

6.1. Instantiations of k-Change

6.1.1. Position-Based k-Change: Ok-pos

6.1.2. Precedence-Based k-Change: Ok-prec

6.1.3. Adjacency-Based k-Change: Ok-adj

6.2. Instantiations of RTR

6.2.1. Position-Based RTR: RTRpos

6.2.2. Precedence-Based RTR: RTRprec

6.2.3. Adjacency-Based RTR: RTRadj

6.3. The Blended PSO Schemes

7. Experiments of PSO Schemes on Quadratic Assignment Problems

7.1. Problem Formulation of QAP

7.2. Benchmarks and Experimental Settings

7.3. Observations and Experimental Results

7.3.1. Comparisons Among PSO Schemes

7.3.2. Extended Comparisons

8. Conclusions and Future Work

References

Citing Literature

Figures

References

Related

Information

6.1.1. Position-Based k-Change: O_k-pos

6.1.2. Precedence-Based k-Change: O_k-prec

6.1.3. Adjacency-Based k-Change: O_k-adj

6.2.1. Position-Based RTR: RTR_pos

6.2.2. Precedence-Based RTR: RTR_prec

6.2.3. Adjacency-Based RTR: RTR_adj