Genetic Algorithm for Finding Minimal Cost Light Forest of Multicast Routing on WDM Networks
Abstract
Wavelength division multiplexing (WDM) is an important technique to make use of the large amount of bandwidth in optical fibers to meet the bandwidth requirements of applications. Multicast is the transmission of information from one source to multiple destinations simultaneously. Given a multicast request in a WDM network, the goal is to find a set of light trees, the assigned wavelengths of light trees, and construct a light forest. In this paper, the minimal cost multicast routing problem (MCMRP) on WDM networks with tap-and-continue (TaC) nodes is defined and studied. A new cost model which consists of the wavelength usage and communication cost is defined. The objective is to minimize the sum of the cost of used wavelengths and the communication cost of the light forest. Specifically, the formulation for the WDM multicast routing problem is given. Because the MCMRP is NP-hard, two genetic algorithms (GAs) are proposed to solve this problem. In the proposed GAs, a path-oriented encoding chromosome is used to represent the routing paths. These routing paths are used to construct source-based light forests to represent a feasible solution to the multicast request. Moreover, to speed up the convergence of GAs, a farthest-first greedy heuristic algorithm is proposed and used to generate one of the initial chromosomes. Simulation results demonstrate that the proposed GAs can run efficiently.
1. Introduction
1.1. WDM
Wavelength division multiplexing (WDM) is an important technique to make use of the large amount of bandwidths in optical fibers to meet the bandwidth requirements of applications. There is a growing consensus that the next generation Internet will employ an IP-over-WDM architecture [1]. In this architecture, IP routers are attached to the optical cross-connects (OXCs) and IP links are realized by light paths in a WDM optical network. Communication requests are transmitted by sending packets on a dedicated wavelength of the light path between the source node′s transmitter and the destination node′s receiver [2, 3]. Because there is no electrooptic (E/O) or optic-electronic (O/E) conversion in OXCs, all-optical networks greatly increase the throughput capacity [4]. In addition, because the network requires not only transmission line capacity enhancement, but also cross-connect node processing capability enhancement. The WDM should be used in combination with wavelength routing [5, 6].
In wavelength routing, data signals are carried on a unique wavelength from a source node to a destination node passing through nodes where the signals are optically routed and switched without regeneration in the electrical domain. When a physical network is given and connections among the nodes in the network are required, an optical path (light path) with a dedicated wavelength for each required connection should be established. The routing and wavelength assignment (RWA) problem is a problem to select suitable paths and wavelengths among the many possible choices for the required connections. To avoid collision, no two paths using the same wavelength pass through the same link called a wavelength continuity constraint [5]. By practical limitations on transmission technology, the number of available wavelengths on a fiber is restricted. So, a good solution to the RWA problem is important to increase the efficiency of the WDM network.
In order to solve various applications on WDM networks, mechanisms must be developed to handle not only point-to-point communications but also multicast. Multicast is the transmission of information from one source to multiple destinations simultaneously, for example, a one-to-many communication technique. Many broadband services such as video conferences, distance learning, and web casting employ multicast for data delivery. The support of multicast in future WDM networks is essential for these applications. Thus, issues concerning supporting multicast on WDM networks need to be studied.
1.2. Multicast
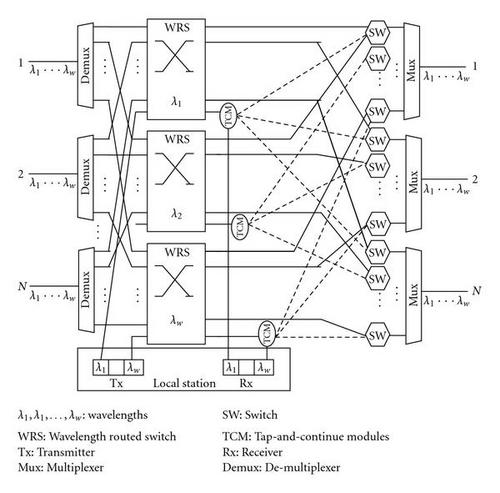
Recently, several researchers studied the multicast problem over WDM networks [7–12]. A comprehensive survey has been done by Ding and Poo [12]. Several researchers studied the multicast problem on WDM with all or sparse multicast capable (MC) [7, 8]. But the drawback of the problem studied in [7, 8] is that the MC node is expensive. To overcome this problem, Ali and Deogun have proposed a low-cost novel architecture called Tap-and-Continue (TaC), shown in Figure 1, for realizing multicast [9]. This architecture provides a natural evolution from current unicast cross-connects and is based on tapping devices. The proposed device can reduce the cost of MC cross-connects at the expense of more fiber links used in the routing structure. In the TaC cross-connect, optical signals are passed through a set of Tap-and-Continue Modules (TCMs). In a TCM, an extremely small fraction of the input signal is tapped and forwarded to the local station. The remaining power on the order of 99.9% is switched to any one of the other outputs [9].
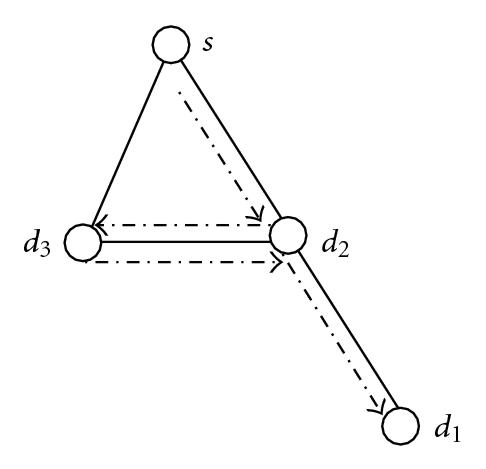
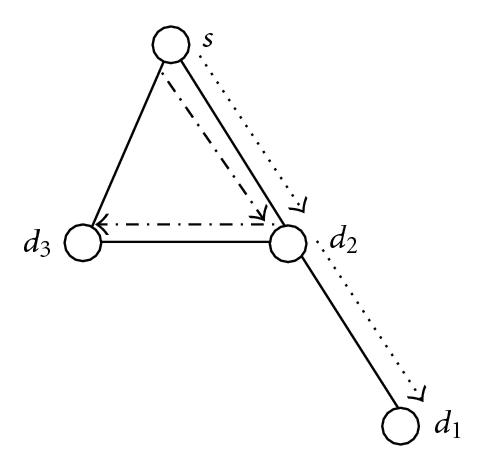
In [9], the route from source to destination is constructed as a trial, but this is impractical. For example, consider the network shown in Figure 2(a), where node s is the source and nodes d1, d2, and d3 are the destinations. The trial s → d2 → d3 → d2 → d1 goes through d3 by way of passing directed link (d2,d3) and immediately forwards the light back to d2 through the reverse link (d3,d2), which is impractical. This is because the delay between source and the farthest destination may be too large. In the WDM with TaC nodes, the trial can be replaced by a light tree which consists of light paths s → d2 → d3 and s → d2 → d1, as shown in the Figure 2(b). After this replacement, the delay between the source and the farthest destination can be reduced. But on the other hand, the wavelength usage is greater than the original trial. From this, there is a tradeoff between cost and wavelength usage.
In [10, 11], another version of multicast problems on the WDM network is studied. Nodes in the WDM network are further subdivided into four types [10, 11]: Drop and Continue node (DaC-node), Wavelength Conversion node (WC-node), Light-Splitting node (split-node), and virtual source (VS). A DaC-node, which is the same as the TaC node in [9], is capable of tapping a small amount of optical power from the wavelength channel and transmitting the remainder. The VS is capable of both split-node and WC-node. The VS plays a key role in the construction of a multicast forest. A heuristic algorithm is proposed to construct the multicast tree [11].
In this paper, the multicast routing problem on WDM networks, whose nodes are TaCs, is studied. Given the WDM network and a multicast request, the goal is to find a light forest which consists of one or more light trees rooted at the multicast source and to their destinations, in such a way that the objective can be minimized. The usual goals to the multicast routing optimization problem [13] in traditional networks are the minimization of: (1) the path delay [14] due to blocking and (2) the cost of the path tree to reach the destinations. Often, the total cost minimization of the routing tree of networks with data replication is equivalent to the classical NP-Hard problem: the minimum Steiner tree [15]. Because both the routing paths and the wavelength assignments are considered in the multicast problem on WDM networks, the multicast routing optimization problem in general networks is a special case. This means that the multicast routing problem on WDM networks is a NP-hard problem.
1.3. Genetic Algorithm
For a NP-hard problem, designing an algorithm to find an optimal solution is impractical, due to the exponential growth in execution time. Genetic algorithms (GAs) proposed by Holland [16] have been trusted as a class of general-purpose search strategies that strike a reasonable balance between exploration and exploitation. GAs have been constructed as robust stochastic search algorithms for various optimization problems. GAs are implemented as computer simulations to gain better solutions in a population of chromosomes of candidate solutions to an optimization problem. The evolution usually starts from a population of randomly generated individuals and this occurs in generations. In each generation, the fitness of each individual in the population is evaluated; multiple individuals are stochastically selected from the current population, based on their fitness. And individuals are modified, recombined, and possibly randomly mutated to form a new population. The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either the maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. If the algorithm has terminated due to the maximum number of generations, a satisfactory solution may or may not have been reached. GAs find applications in computer science, engineering, and other fields [16]. The structure of the GA is shown in Algorithm 1.
-
Algorithm 1: Genetic algorithm.
-
BEGIN
-
generate initial population;
-
evaluate the fitness and penalty function of each individual in the population.
-
WHILE (not terminated) DO
-
select individuals form parent to reproduce;
-
generate offspring through crossover and mutation;
-
evaluate the individual fitness of the offspring;
-
replace the worst ranked part of the population with offspring.
-
END of WHILE
-
END
GAs search by exploiting information sampled from different regions of the solution space. The combination of crossover and mutation helps GA escape from local optima. These properties of GA provide a good global search methodology for the multicast problem. In this paper, two GAs are proposed to find the light forest for the multicast request on WDM networks so as to minimize the objective cost. The performance of the proposed algorithms is evaluated in terms of the costs associated with the light forest and the number of wavelengths they construct.
1.4. Contributions and Outline
The major contributions of this research are briefly described here. First, a new cost model of the WDM multicast problem is introduced and a new problem is defined. Second, a smart coding method of GAs for the multicast problem on WDM networks is constructed. Two GAs are proposed to solve the WDM multicast problem. Then, a Farthest-first greedy algorithm is used to generate the initial population and speed up the convergence of the GA.
The rest of this paper is organized as follows. In Section 2, the assumptions and definitions of the multicast problem are described. In Sections 3 and 4, a simple genetic algorithm (SGA) and an extended genetic algorithm (TLGA) are proposed to solve this problem. Experimental results are given in Section 5. Finally, conclusions are given in Section 6.
2. Assumption, Formulation, and Related Works
2.1. Network Model
In this paper, all nodes in a WDM network are TaC nodes. The functions of the TaC nodes are listed as follows [17]:
- (i)
drop only: when the locally attached router is a destination and there is no need to forward a copy to any downstream node;
- (ii)
continues only: when the locally attached router is not a destination and there is a down-stream destination;
- (iii)
drop and continue: when the locally attached router is a destination and there is a down-stream destination.
For the given WDM network, the unique source node is able to send multiple “copies” to the same output using different wavelengths along different paths. That is, the source node of the multicast request has multiple transmitters, and therefore packets can be transmitted to as many children as needed when constructing a multicast tree, rooted at itself. Similarly, a source can transmit to its children on different wavelengths using different transmitters.
2.2. Problem Definition
In this paper, a multicast request r(s,D) is given, the request is for setting up a multicast channel from the source s to a group of destinations D = {d1,d2, …, d|D|}, where s ∈ V, s ∉ D, and D⊆V. The problem studied in this paper is called the minimal cost multicast routing problem (MCMRP). The goal of MCMRP is to find the routing trees (or tree) and the assigned wavelengths for the multicast request such that the total cost, consisting of routing cost and wavelength cost, can be minimized.
In this paper, the input optical signal of a TaC node can only be forwarded to an output port leading to its child. A node in the WDM network can perform a “drop and continue” function to transmit the signal to its child until all nodes in Dk receive it. That is, no light splitting function is enabled on node. Therefore the degree of nodes, expect for source node, of light tree on each wavelength network is less than or equal to 2.
Another important goal of the model is to minimize the number of wavelengths to serve the multicast request without causing wavelength conflicts. Since wavelength is one of the most important resources in the WDM network, if the number of used wavelengths can be reduced, the consequent multicast requests can find the light tree or light forest easily in the WDM network. Thus, the blocking probability of the multicast request can be reduced. Otherwise, the multicast request will be blocked or rejected. In the equation described above, if the number of wavelengths used to route the multicast request is not restricted, the routing path may tend to consume more wavelengths.
2.3. Light-Splitting Constraint
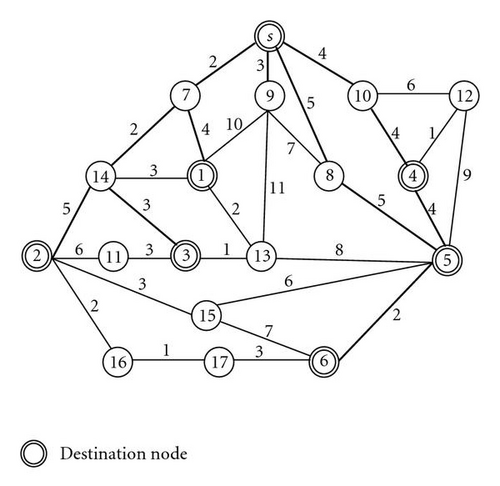
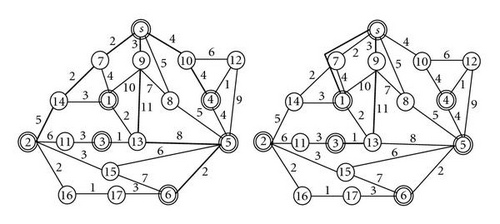
A key observation is that, due to the light-splitting constraint of the WDM node, a single light tree may not be sufficient to transmit the multicast message to all destinations in a multicast session. Consider the example shown in Figure 3, a WDM network with 18 nodes and a multicast request r(s,D) = r(s, {1, 2, 3, 4, 5, 6}) are given. The number near the edge represents the cost of edge. When the shortest path heuristic algorithm is used to find the shortest tree from s to D, node 7 is used to forward data to nodes 1, 2, and 3 as the bold lines show in Figure 3. This shortest path tree violates the light-splitting constraint. To solve this problem, path P(s,3) or P(s,2) may be reassigned another wavelength. Once destinations 2 and 3 are reassigned to other wavelengths, source node s needs to send out three “copies” on link (s,7), and three wavelengths are needed on link (s,7) in a wavelength-routed network. Alternately, paths P(s,2) and P(s,3) may be rerouted to satisfy the light-splitting constraint.
2.4. GA-Based Approaches in Multicast Routing
For the multicast problem on general networks, there were several multicast routing algorithms [18–24]. For example, KMB algorithm (proposed by Kou et al.)[18], minimum path cost heuristic (MPH) [19], dynamic center-based heuristic (DCBH) [20], and best effort residual delay (BERD) [20] belong to traditional heuristic algorithms. In [21], the minimum cost Steiner tree is constructed based on GAs to form the QoS-driven multicast routing tree with the lowest cost of network resources. In [22], a multicast routing algorithm based on chaotic neural networks was proposed. In [23], a hybrid approach based on neural networks and GAs was proposed to solve the QoS multicast routing problem. In [24], a QoS multicast routing algorithm based on the tabu search was proposed, speeding up the convergence to the optimal solution. In [8], a QoS multicast routing algorithm based on a tabu-hierarchy GA (THGA) in IP/DWDM optical Internet was designed. This constructs a QoS, and cost optimized or suboptimized multicast routing tree with network load balance was supported.
Recently, GAs were used to find the multicast routing so as to reduce the total cost from the multicast delivery tree. Examples are the multimedia multicast routing [25, 26], WDM multicast network routing [27, 28], QoS-based multicast routing [28–30], WDM ring multicast [31], WDM anycast [32], group multicast [33], and others related to Steiner trees. In [28], authors considered the problem of minimizing the number of split-capable nodes in the network for a given set of multicast requests. A GA that exploits the combination of alternative shortest paths for the given multicast request, in order to minimize the number of required split-capable nodes, was proposed. Several GA-based algorithms have been proposed to solve the Steiner tree problem with QoS constraints. In [34], the authors considered the framework of multicast routing in wireless ad hoc networks. An unconstrained problem was also addressed in [35], where the authors apply GAs to the calculation of optimal link weights. These are then used to automatically generate multicast routes. Another genotype representation scheme was proposed in [36]. In [14], the authors considered the bandwidth-delay-constrained least-cost multicast routing problem by proposing several novel solutions based on GAs.
3. Simple Genetic Algorithm (SGA) for Wdm Multicast Routing
In this section, a simple genetic algorithm (SGA) is proposed to solve MCMRP. The development of the SGA requires: (1) a chromosomal coding scheme, (2) crossover operators, (3) mutation operators, (4) a fitness definition, (5) a replacement strategy, and (6) termination rules. The outline of the SGA is shown in Algorithm 2.
-
Algorithm 2: Simple genetic algorithm.
-
BEGIN
-
Initialize population randomly;
-
generate randomly the routing paths for destinations;
-
call Light-forest construct algorithm to generate feasible light forests;
-
compute the fitness of light forests.
-
WHILE (not terminated) DO
-
choose parents from population; /* Selection */
-
generate offspring through crossover and mutation;
-
call Light-forest construct algorithm to generate feasible light forests;
-
compute the fitness of light forest;
-
replace the worst ranked part of population with offspring.
-
END of WHILE
-
END
3.1. Chromosomal Coding
A pair of source-destination nodes can be connected by a path. There are usually many possible paths between any pair of nodes in a given network. For example, consider the network shown in Figure 3; the possible paths between the node s and the node 1 include s → 7 → 1, s → 9 → 1, s → 7 → 14 → 1, …, and so on. For each destination di in D, there is a path table which consists of Ri possible paths associated with it. These paths in the path table are sorted and indexed in the nondescending order according to the cost of the path. The encoding method, denoted as path-oriented encoding, was first proposed in [37] for the point-to-point routing problem and used by Hwang et al. [38] to solve the multicast routing problem in a general network. In the MCMRP, because both routing paths and assigning wavelengths are considered simultaneously, the encoding method proposed in [38] cannot be applied directly. Thus, an adjustment algorithm and/or extended coding method should be developed to generate a feasible solution.
Let Ri be an integer which represents the size of the path table from s to destination di, for i = 1, 2, …, |D|. The value of Ri is a parameter of the algorithm and is initially set to a small number (R = R1 = R2 = ⋯ = R|D| = 16 or 64). For a given source node s and destination set D = {d1, d2, d3, …, d|D|}, the chromosome of SGA can be represented by an array of integers with length |D|. A path gene pi, i = 1, 2, …, |D|, of the chromosome is an integer in {1, 2, …, Ri}, which represents a possible path between s and di. For example, Figure 4 shows the path table for the source-destination pair (s,1). The relationship between the path gene and path table is explained in Figure 4.
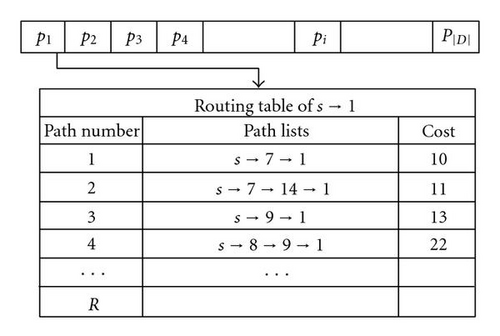
Obviously, a chromosome represents a candidate solution for the multicast routing problem, because it guarantees a path between the source node and any of the destination nodes. However, a chromosome does not necessarily represent a light tree, because a chromosome may violate the light-splitting constraint. Thus, a decoding method called Light-Forest Constructing Algorithm (LFCA) is proposed to transform the chromosome to the corresponding light forest. Given a path-oriented encoding chromosome, after performing the LFCA, the corresponding light forest on the WDM network G(V,E,c,w) is constructed. Moreover, the cost of the light forest is also computed. Let A = {p1,p2, …, p|D|} be the set of paths represented by the chromosome, which are extracted from respective path tables. For each path p, let Bypass(p) be the set of paths contained in A whose destination nodes are passed by path p. The details of the Light-Forest Construct Algorithm (LFCA) are shown as in Algorithm 3 .
-
Algorithm 3: Light-forest construct
algorithm.
-
Sort paths which are represented by the chromosomes in the descending order according to the cost
-
of paths and reindex;
-
let A = {p1, p2, …, p|D|} be the set of paths and c(p1) ≥ c(p2)≥⋯≥c(p|D|);
-
k = 1;
-
T1 = T2 = ⋯ = Tw = ∅;
-
select and remove a path pk from A;
-
WHILE (A ≠ ∅) DO
-
flag = FALSE;
-
j = 1;
-
WHILE (flag ≠ TRUE) DO
-
IF (Tj ∪ pk satisfies light-splitting constraint and does not form a cycle) THEN
-
Tj = Tj ∪ pk;
-
flag = TRUE ;
-
path pk is assigned wavelength j;
-
compute Bypass(pk);
-
A = A∖Bypass(pk);
-
ELSE
-
j ++;
-
IF (j > w) THEN
-
print(“not enough wavelengths");
-
exit();
-
END IF
-
END IF
-
WHILE (pk ∉ A)
-
k++;
-
select and remove a path pk from A;
-
END of WHILE
-
k++;
-
END of WHILE
-
END of WHILE
-
Algorithm 4: Chromosome adjustment algorithm.
-
BEGIN
-
Perform wavelength mapping algorithm;
-
let B be the set of wavelength networks which violate the light-splitting constraint;
-
let j be the minimal index of new wavelengths.
-
WHILE (B ≠ ∅) DO
-
T = ∅;
-
randomly select and remove a wavelength network from B;
-
let P be the set of paths assigned to the wavelength network;
-
sorted paths in P in the increasing order according to the cost of paths;
-
WHILE (P ≠ ∅) DO
-
select and remove a path p(s,d) from P;
-
If (p(s,d) ∪ T violates the light-splitting constraint or forms a cycle), then
-
perform path rerouting (T,p(s,d)) to find path p′(s,d);
-
If (path p′(s,d) is found), then
-
if (p′(s,d) is a new path), then
-
insert path p′(s,d) into the path table;
-
increasing the table size of respective destination d by 1;
-
else
-
path p(s,d) is assigned wavelength j;
-
increase j by 1;
-
END IF
-
END IF
-
ELSE
-
Tj = p ∪ Tj;
-
END IF
-
END of WHILE
-
END of WHILE
-
Perform wavelength packing algorithm;
-
END
Assume the paths extracted from path tables of all destinations of the chromosome are shown in Figure 5(a). After performing LFCA, the final light trees on first and second wavelength networks are shown in Figure 5(b). Observe the result shown in Figure 5; destination 5 is reached by the routing path P(s,6). Two wavelengths are used to transmit the multicast request. The cost of the light forest is equal to 62 + 2 × α. It is noteworthy that the tests of “Is there any conflict between path pk and tree Tj ?” and “Does adding path pk to Tj form a cycle?” can provide knowledge by adding edge of path pk into Tj edge-by-edge and test “Whether the degree of the endvertices of edge is greater than 2?” If no, path pk is added into light tree Tj to form a new light forest, such as Tj = Tj ⋃ pk. Otherwise, pk is in conflict with light tree Tj and pk tries to be assigned to the next light forest Tj+1 if possible. This process is repeated until a wavelength is found for the path.

3.2. Crossover Operator
The crossover operator used in the development of SGA is two point crossover (TPC). The TPC randomly selects two chromosomes for crossover from previous generation and then uses a random number generator, in which two integers i1, i2 (i1 ≠ i2) are generated in the interval [1, |D|]. These integers are used as the crossover sites.
It is worth noting that after performing the TPC crossover, LFCA should be used to construct the new light forest and the cost of the new light forest should be recomputed.
3.3. Mutation
Two types of mutations are used to develop this algorithm; they are single routing path mutation (SRPM) and multiple routing paths mutation (MRPM).
- (i)
Single routing path mutation (SRPM): first, a destination di (i = 1, 2, …, |D|) is selected randomly from a chromosome. Then the SRPM changes the value of path gene pi to an integer z which is selected randomly from [1, Ri]. After performing SRPM, the light forest may be changed. Thus, the LFCA should be used to construct the new light forest and evaluate the cost of the new chromosomes.
- (ii)
Multiple routing paths mutation (MRPM): first, select an integer z between 1 and |D|. A set Z of z destinations is randomly generated from a chromosome. Then, MRPM changes the value of the destination node di in Z to a random integer, which is randomly generated between 1 and Ri. After performing the MRPM, the light forest may be changed. Thus, the LFCA should be used to construct the new light forest and evaluate the cost of the new chromosome.
3.4. Fitness Definition
3.5. Replacement Strategy and Termination Rules
Initially, assume that Npopulation is the number of chromosomes to be generated and Nparent connection chromosomes are randomly constructed. In the process of selection, Npopulation/2 pairs of connections are randomly selected for crossover to generate the new generation of chromosomes. After crossover, chromosomes are sorted according to the fitness in the increasing order; Nparent chromosomes with the smallest fitness are selected to construct the new generation. The values of Npopulation and Nparent will be determined through experiments. Execution of SGA can be terminated when the number of generations exceeds an upper bound (ng), specified by the user.
4. Two-Level Genetic Algorithm (TLGA)
In this section, another genetic algorithm, named two-level genetic algorithm (TLGA), is proposed to solve the MCMRP. In the TLGA, the encoding method of the SGA is extended by adding an assigning gene which represents the assigned wavelengths of the paths. Because this extension may cause the chromosome generated by the TLGA to be an infeasible solution, some heuristics are developed to modify the chromosome into a constraint-satisfied solution. The outline of TLGA is shown in Algorithm 3 and the details of TLGA are described in the following subsections.
4.1. Chromosome Encoding
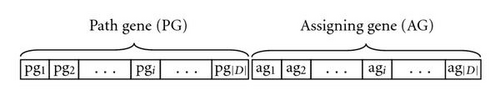
Because the problem involves representing routing paths of multicast and assigning wavelengths, a coding scheme that uses positive integral number is employed. A chromosome of one-dimensional array with size 2×|D| is introduced to represent the routing paths and assigned wavelengths of paths.
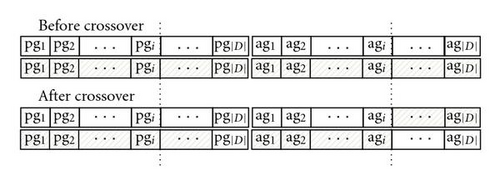
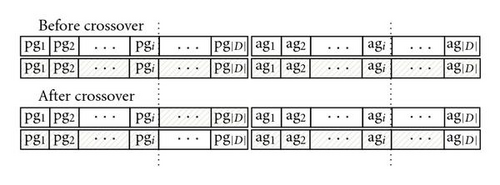
The structure of the chromosome is divided into two parts, as shown in Figure 6(a). The first part denoted as the PG (path gene), PG = {pg1,pg2, …, pg|D|}, is the same as the PG of SGA described in Section 3.1. The second part of the chromosome is used to represent the assigned wavelength of the respective path, denoted as the AG (Assigning Gene), AG = {ag1,ag2, …, ag|D|}, where each element agi (i = 1, 2, …, |D|) falls in {1, 2, …, w}.
Let Edge(P(s,di)) be the set of edges that compose the path P(s,di) and all the edges with at least one of its endpoints, not be s, be on P(s,di). Let G′ = G∖Edge(P(s,di)) be the remaining graph by removing those edges and nodes in Edge(P(s,di)). For example, assume that G is the network shown in Figure 3. If P(s,2) = s → 7 → 14 → 2, then Edge(P(s,2)) = {(s,7), (7, 14), (14, 2), (1, 7), (1, 14), (3, 14), (2, 11), (2, 15), (2, 16)}. To generate the initial values of the chromosomes, first the content of the chromosome is selected randomly. Then, the content is modified by performing the chromosome adjustment algorithm (CAA) to form a feasible solution. There are several algorithms called by the CAA; they are (1) the wavelength mapping algorithm, (2) the wavelength packing algorithm, and (3) the path rerouting algorithm. The details of these algorithms are described as follows.
- (i)
The wavelength mapping algorithm (WMA) is used to map the set of used wavelengths to the new set {1, 2, …, |Wold|}, where Wold = {w(p(s,di))∣ with di being a leaf node of the light tree} is the set of wavelengths used by the routing paths. To do the mapping, only a bijective function should be found.
- (ii)
The wavelength packing algorithm (WPA) is used to reduce the number of used wavelengths of the light forest. To do this, first for the given light forest, which consists of several light trees on different wavelength network, a bipartite graph BG(U,V,E) is constructed. Then node in the set (U and V) of BG is the light tree; edge in BG is established for two nodes if the respective light trees can be merged without violating the light-splitting constraint. Second, the maximal matching finding algorithm is performed to find the maximal matching. Finally, two light trees connected by the matching edge are merged to form a new light tree, the two original light trees are deleted, and the wavelength mapping algorithm is performed. This process is repeated until no matching edge is found.
- (iii)
Given a light tree T and a source-destination pair (s, d), the path rerouting algorithm tries to find the new minimal cost path p(s,d) such that T ∪ p(s,d) satisfies the light-splitting constraint.
Because the routing paths and the assigned wavelengths in the TLGA are generated randomly, this may generate an infeasible solution. Thus, the chromosome should be adjusted to a constraint-satisfied solution by performing the CAA. The details of CAA are described in Algorithm 5.
-
Algorithm 5: Two-level genetic algorithm.
-
BEGIN
-
Initialize population randomly;
-
generate routing paths for destinations randomly;
-
generate assigning wavelengths of routing paths randomly;
-
call chromosome adjustment algorithm to generate feasible light forests;
-
compute the fitness of light forests.
-
WHILE (not terminated) DO
-
choose parents from population; /* Selection */
-
generate offspring through crossover and mutation;
-
call chromosome adjustment algorithm to generate feasible light forests;
-
compute the fitness of light forests;
-
replace the worst ranked part of the population with offspring.
-
END of WHILE
-
END
-
Algorithm 6: Wavelength packing algorithm.
-
BEGIN
-
let TS be the set of light trees on wavelengths networks;
-
perform wavelength mapping algorithm;
-
mm = |Wold|; // maximal matching initial value
-
WHILE (mm > 0) DO
-
Construct a bipartite graph BG(U,V,E) of the set of the TS;
-
nodes in U and V represent the light tree in TS;
-
let E be the set of edges e = (ui,vj) ∈ E, where ui ∈ U and vj ∈ V, and Ti ∪ Tj
-
satisfies the light-splitting constraint;
-
perform maximal matching algorithm to find the maximal matching mm of BG;
-
for each matching edge, merge two light trees Ti and Tj which are connected by it;
-
perform wavelength mapping algorithm.
-
END of WHILE
-
END
4.2. Crossover Operator
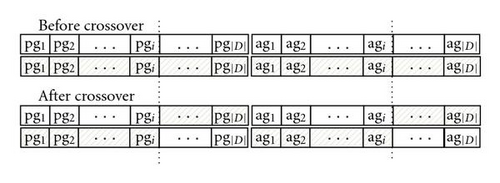
Four types of crossover operators are used to develop this TLGA. They are (1) the single point crossover (SPC), (2) the single point wavelength crossover (SPWC), (3) the single point routing path crossover (SPRPC), and (4) the wavelength exchanging operator (WEO). The details of the crossover operators are described as follows.
- (i)
Single point crossover (SPC): randomly select a crossover site integer i from interval [1, |D|]. Two chromosomes are mated as shown in Figure 6(b). In SPC, the operator is applied on both the path gene and the wavelength gene.
- (ii)
Single point wavelength crossover (SPWC): randomly select a crossover site integer i from interval [1, |D|]. Two chromosomes are mated as shown in Figure 6(c). In SPWC, the operator is only applied on the wavelength gene.
- (iii)
Single point routing path crossover (SPRPC): randomly select a crossover site integer i from interval [1, |D|]. Two chromosomes are mated as shown in Figure 6(d). In SPRPC, the operator is only applied on the path gene.
- (iv)
Wavelength exchanging operator (WEO): randomly select two wavelength assignments of assigning genes agi and agi, 1 ≤ i,j≤|D| (i ≠ j); and the assigned wavelengths of these two paths are exchanged.
4.3. Mutation
Three types of mutations are used to develop the TLGA. They are (1) the single routing path mutation (SRPM), (2) the single wavelength mutation (SWM), and (3) the wavelength packing mutation (WPM).
- (i)
Single routing path mutation (SRPM): randomly select an integer i in the interval [1, |D|], the single routing path mutation (SRPM) changes the value of pgi to an integer randomly selected from {1, 2, …, Ri}.
- (ii)
Single wavelength mutation (SWM): randomly select an integer i in the interval [1, |D|], the single wavelength mutation (SWM) changes the value of agi to an integer randomly selected from {1, 2, …, w}.
- (iii)
Wavelength packing mutation (WPM): WPM changes the assigned wavelengths of paths in the selected chromosome by performing the wavelength packing algorithm(see Algorithm 7).
-
Algorithm 7: Wavelength mapping algorithm.
-
BEGIN
-
let w(p(s,di)) be the assigned wavelength of the path p(s,di);
-
let Wold = {w(p(s,di))∣di is a leaf node of the light tree} be the set of wavelengths used by
-
the routing paths; (|Wold | ≤ w)
-
find a one-to-one and onto (bijective) mapping function wm:Wold → {1, 2, …, |Wold|};
-
for each path p(s,di), the assigned wavelength w(p(s,di)) is changed to wm(w(p(s,di));
-
END
-
Algorithm 8: Path rerouting algorithm.
-
Input: tree T, path p(s,d)
-
Output: return path or NULL
-
BEGIN
-
For each leaf node di in T, find the set Edge(P(s,di));
-
for each leaf node di in T, remove Edge(P(s,di)) from G, let the remaining graph be G′;
-
find a minimal cost path p′(s,d) from source s to destination d on graph G′.
-
IF (path p′(s,d) is found), then
-
return path p′(s,d);
-
else
-
return NULL.
-
END IF
-
END
5. Heuristic Initialization
Because finding the optimal solution for the MCMRP with a large problem size is impractical, GAs can be used to find the near optimal solution. But, only using random initialization the GA may take a lot of time to converge. Therefore, heuristic algorithms are used to find the better initial solution, instead of random initialization, to speed up the convergence of GAs. In this section, a shortest path-based heuristic algorithm is proposed to find the minimal cost path from source to destinations.
Assume that P(s,di), i = 1, 2, …, |D|, is the minimal cost path from the source node s to the destination di ∈ D. Paths P(s,di), i = 1, 2, …, |D| are combined to form P, such that . It is worth noting that P should be a tree. If P satisfies the light-splitting constraint, then P is the minimal cost light tree of the multicast request. Otherwise, a heuristic algorithm is needed to modify it to a light tree or light forest which satisfies the light-splitting constraint.
Before introducing the proposed algorithm, some notations are introduced and stated here. Let degree(s) be the degree of the source node s on tree P, then tree P can be divided into degree(s) subtrees. Let v1, v2, …, vdegree(s) be the nodes in P which are directly adjacent to the source node s; the subtree rooted at vi is represented by PT(vi), for i = 1, 2, …, vdegree(s). This is due to the fact that the routing tree in a wavelength network cannot contain cycle(s) and must satisfy the light-splitting constraint. Thus, it is easy to find that if there is more than one destination on the leaves in one of the subtrees, only one of these destinations can be selected to route by this subtree and the other destinations should be rerouted. To determine the rerouting paths of the destinations in the leaves, a heuristic method is developed and used. For each subtree PT(vi), i = 1, 2, …, vdegree(s), only the farthest destination v with c(P(s,v))≥{c(P(s,u))} is routed by the path P(s,v) on PT(vi) and the others should be rerouted. This is denoted as the farthest-first greedy (FG).
Consider the network shown in Figure 3, there are three destinations in the subtree PT(7) with nodes 1, 2, and 3. The farthest (maximal cost) destination is node 2, thus the routing paths to destination nodes 1 and 3 should be rerouted. The farthest destinations in the subtrees PT(8) and PT(10) are nodes 6 and 4, respectively. Now, the problem is “how to find the reroute paths?”, because the routed paths and nodes used by the farthest path in each subtree cannot be used twice in the same wavelength network. Moreover, the rerouting paths together with the existing paths cannot form a cycle (or cycles) or violate the light-splitting constraint. Thus, the path P(s,v) to the farthest destinations and Edge(P(s,v)) in each subtrees should be removed. Let UNREACH be the set of all destinations that have not been routed and which are sorted in the descending order according to the minimal cost of path on G.
According to the above discussions, the rerouting path can be determined to be more complex. Let G1, G2, …, Gw be the w wavelength graphs of a WDM network, the script index i of Gi means that the routing path is on the ith wavelength network. Let k be an integer which indicates the maximal index of the currently used wavelength network. To find a rerouting path of a destination v, k + 1(≤w) wavelength graphs (G1, G2, …, Gk, Gk+1) are considered in the proposed algorithm. Let Pi(s,v) be the minimal cost path from source s to destination v in the wavelength graph Gi, the cost of the path Pi(s,v) is defined as c(Pi(s,v)), i = 1, 2, …, k + 1(≤w) and is determined as follows.
- (i)
If Pi(s,v) passes destinations, {v1,v2, …, vk} in UNREACH on Gi, then the costs of P(s,v1), P(s,v2), …, P(s,vk) on G should be subtracted from the cost of path Pi(s,v). That is, c(Pi(s,v)) = c(Pi(s,v)) − c(P(s,v1)) − c(P(s,v2))−⋯−c(P(s,vk)).
- (ii)
If Pi(s,v) uses the wavelength graph the (k + 1)th (≤w), where i is equal to k + 1, then the cost of path Pi(s,v) should be increased by α.
- (iii)
If path from s to v cannot be found in the wavelength network Gi, then c(Pi(s,v)) = ∞.
After finding and computing the paths and costs of the possible paths, the path with the minimal cost is selected to be the rerouting path. If i is equal to k + 1, then increase k by 1. Find the set Edge(Pi(s,v)) and remove those edges in Edge(Pi(s,v)) from Gi. Let dest(vi) be the farthest destination node in subtree PT(vi). Let Live(dest(vi)) be the set of edges that have one endpoint dest(vi) and another endpoint in G′. For each subtree PT(vi), a subgraph is constructed by G′⋃Live(dest(vi)). It is worth noting that the cost of the routing path, which is called the extended path, routed through node dest(vi) should be included in computing the cost of the path P(s,dest(vi)). This rerouting process is continually executed until UNREACH is empty.
The details of the farthest-first greedy (FG) algorithm are described as in Algorithm 9 .
-
Algorithm 9: Farthest-first greedy (FG).
-
Step 1. Let k = 1, . For each destination di in D, find the minimal
-
cost path P(s,di) on G1. Combine the paths to form a routing tree P. If P satisfies
-
the light-splitting constraint, then done. Otherwise perform Step 2.
-
Step 2. For each subtree PT(vi) on G1, rooted at vi, i = 1, 2, …, degree(s), find the farthest
-
destination node dest(vi), the routing path P1(s,dest(vi)) and the Edge(P1(s,dest(vi))).
-
Modify by removing Edge(P1(s,dest(vi))), i = 1, 2, …, degree(s) from and construct
-
UNREACH. While UNREACH is nonempty, perform Steps 3 and 4.
-
Step 3. Take the farthest destination in UNREACH, say v, find the minimal cost paths in the
-
set of subgraphs SG = , ⋃Live(dest(vi)), for all vi, z = 1, 2, …, k + 1}.
-
Step 4. Find the minimal cost path in the path set SG. If the path is found, assign path
-
P(s,v) to the corresponding wavelength z; subtract EdgeP(s,v)) from ; remove
-
the destination v and other destinations passed by path P(s,v) from UNREACH;
-
and update Live(dest(vi)). Otherwise, increasing k by one, if k is greater than w, will
-
return false.
Assume α = 4; consider the example shown in Figure 3. After performing Steps 1 and 2 of the farthest-first greedy algorithm, the result is shown in Figure 7(a). Because destination 3 is the farthest node in UNREACH, Step 3 tries to find the minimal cost path from s to 3. In G1 the path is s → 9 → 13 → 3 with the cost of 15. In , the extended path is 2 → 11 → 3 with the cost of 9. Similarly, in the path is s → 7 → 14 → 3 with the cost of 11 (7 + α). It is clear that the extended path c(P1(2, 3)) is the minimal cost path, thus, destination 3 is routed in the wavelength graph G2.
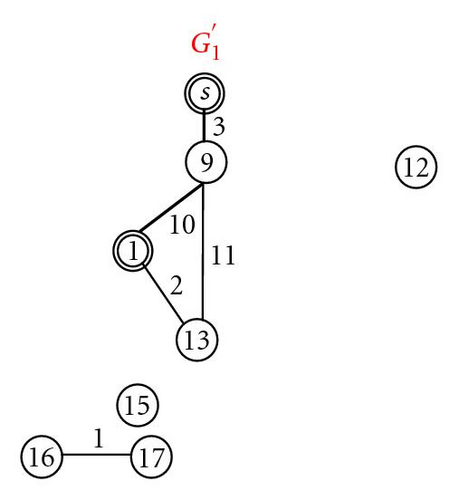
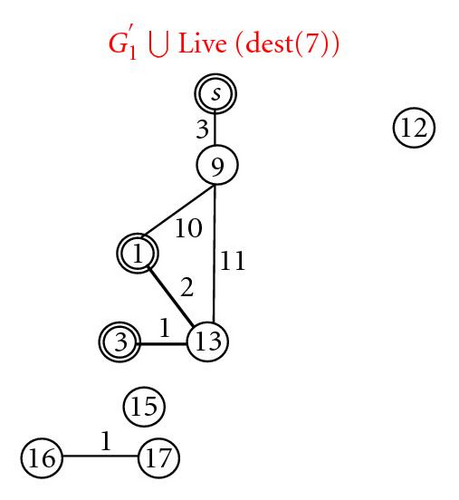
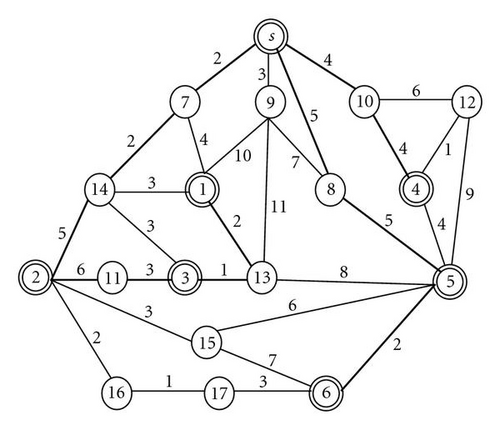
Then, to find the minimal cost routing path for destination 1, those paths on G1, G1 ⋃ Live(dest(7)), and G2 are considered. They are path P2(s,1) = s → 9 → 1 with a cost of 13, extended path P1(3, 1) = 3 → 13 → 1 with a cost of 3, and path P3(s,1) = s → 7 → 1 with a cost of 10 (6+ α). Obviously, the minimal cost path is the extended path P1(3, 1). Thus, the final result by applying the farthest-first greedy algorithm to Figure 3 is shown in Figure 7(c).
6. Experimental Results
In order to evaluate the performance of the proposed GAs, they were implemented and applied to solve problems that were randomly generated. The results of these experiments are reported below. In all the experiments, the algorithms were conducted in C++, and all the experiments were run on a personal computer (PC) with a Pentium III 1 GHZ CPU and 512 MB RAM.
6.1. Parameters
In this subsection, the effects of the various parameters of GAs are discussed. A WDM network with n = 100 nodes, m = 1208 edges, and w = 10 wavelengths was used to determine the parameters of GAs. The cost of edge is randomly selected from the set of integers {1, 2, …, 20}. The multicast request r(s,D) with |D | = 50 destinations, which are randomly selected from the set of nodes, was used in the experiments. The common parameters of GAs are the crossover probability pc = 1.0, the number of generations Ngeneration = 100, and the ratio α = 50. To determine the parameters of GAs, each GA was performed ten times and the average results are used for the comparison.
6.1.1. SGA
For the proposed SGA with heuristic initialization, the parameters of SGA are determined by performing the following experiments.
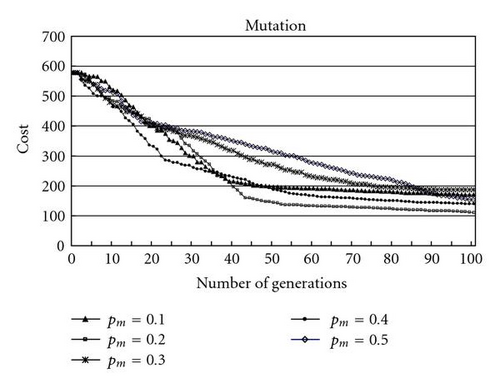
(1) Effect of the mutation probability: in Figure 8, the effect of the mutation probability on the evolution of SGA is presented. This experiment assumes pm in {0.1, 0.2, 0.3, 0.4, 0.5}. It is found that SGA leads to both faster convergence and better result when the mutation probability is equal to 0.2.
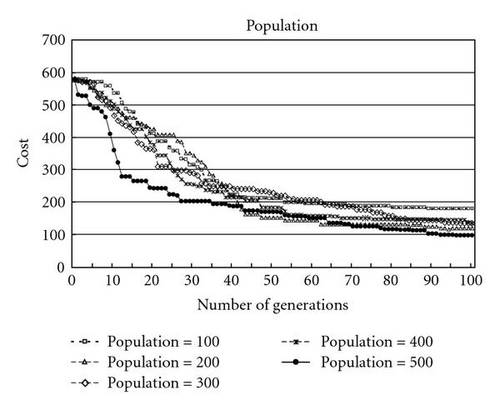
(2) Effect of the population size: in Figure 9, the effect of different number of chromosomes in the population (pop) is presented, where pop is in {100, 200, 300, 400, 500}. It is found that SGA with pop = 500 can get better results.
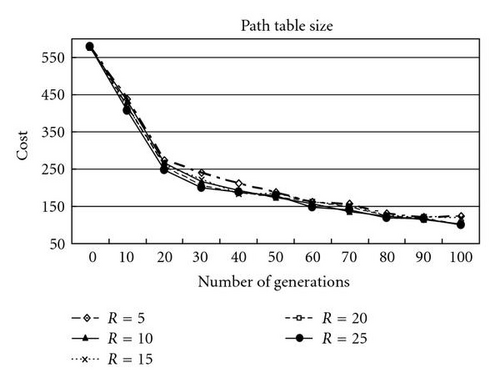
(3) Effect of the path table size: in Figure 10, the effect of different values of R (R = R1 = R2 = ⋯ = R|D|) is presented, where R is {5, 10, 15, 20, 25}. It is found that SGA with R = 25 can get better results.
6.1.2. TLGA
For the proposed TLGA with heuristic initialization, the parameters of TLGA are determined by performing the following experiments.
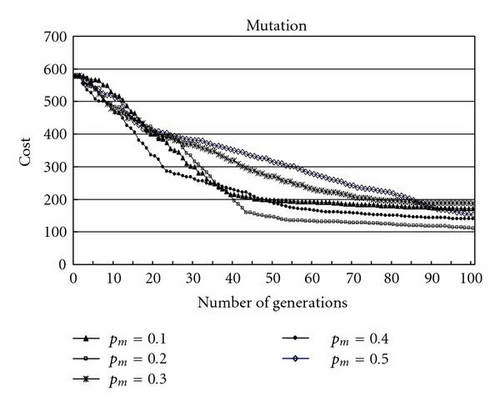
(1) Effect of the mutation probability: in Figure 11, the effect of the mutation probability on the evolution of TLGA is presented. In this experiment, pm is {0.1, 0.2, 0.3, 0.4, 0.5}. It is found that TLGA leads to both faster convergence and to better result when the mutation probability is equal to 0.2.
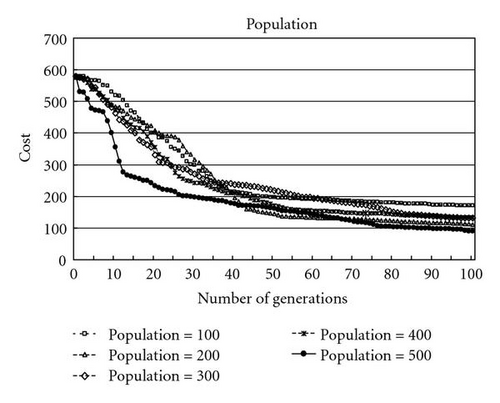
(2) Effect of the population size: in Figure 12, the effect of different number of chromosomes in population (pop) is presented, where pop is {100, 200, 300, 400, 500}. It is found that TLGA with pop = 500 can get better results.
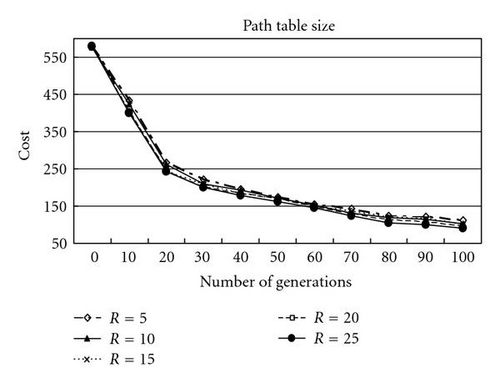
(3) Effect of the path table size: in Figure 14, the effect of different values of R (R = R1 = R2 = ⋯ = R|D|) is presented, where R is {5, 10, 15, 20, 25}. It is found that TLGA with R = 25 can get better results.
6.1.3. Discussions
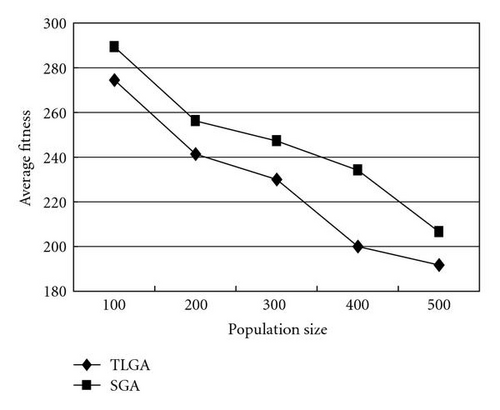
For the mutation, the purpose is to allow GAs to avoid local minima by preventing the population of chromosomes from becoming too similar to each other, thus slowing or even stopping evolution. If the mutation probability is high, the population of chromosomes may change intensely and be difficult to converge and find the optimal solution. Moreover, increasing the mutation probability will increase the running time of GAs. The experiments show that the mutation probability of both the SGA and the TLGA is set to 0.2. For the population size, in general, the larger the population size, the better the result that can be found by GAs. On the other hand, increasing the size of the population may also increase the time spent for each generation and the storage requirement. To examine the effect of the population size in details, for each experiment with Ngeneration = 100, the average fitness value is computed, where fitnessg(i) is the fitness value of the ith chromosome of the gth generation. The results are shown in Figure 13. The experiments show that both the population sizes for the SGA and the TLGA are set to 500. Moreover, in Figure 13, the average fitness value of the TLGA is better than that of the SGA. For the path table size, giving a larger path table size will allow the GA to find a better routing path and the wavelength. It may allow the GA to find a near global optimal solution. On the other hand, as the path table size increases, the time to converge is also increased. The experiments show that SGA and TLGA with the path table size set to 25 can find better results.
6.2. Comparison
In this subsection, the performance of the proposed GAs is examined and compared. For the MCMRP, the proposed algorithms were run on several randomly generated connected networks with different nodes (n is {100, 200, 300}), and with different numbers of destination nodes |D| is {10, 20, 30, 40, 50} and with different values of ratio α in {50, 100, 150}. Moreover, to examine the performance of the proposed algorithms, two heuristic algorithms are implemented and used for comparisons. They are minimal trial (MT) [9] and shortest path tree (SPT) algorithms.
The average results of SGA and TLGA and the results of FG, MT, and SPT algorithms for different values of ratio α = 50, 100, 150 are shown in Figures 15, 16, and 17, respectively. Observe the results shown in these figures, it can be found that TLGA can get the best solution. TLGA has a better performance than FG, MT, and SPT.
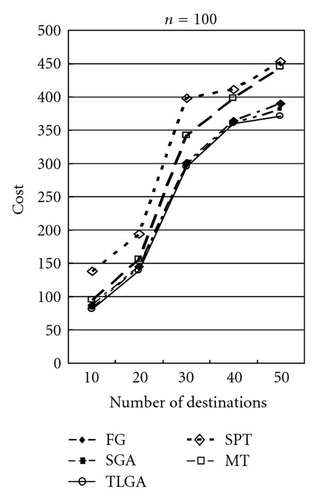
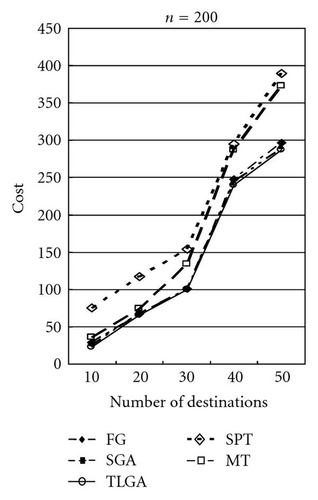
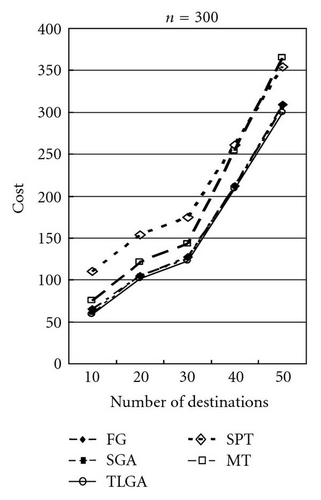
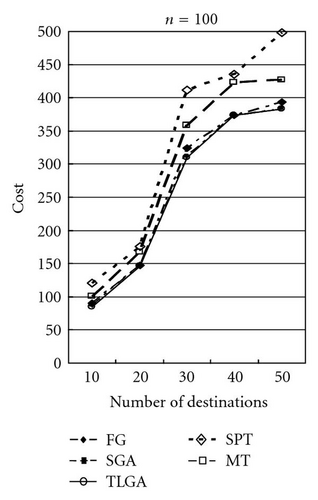
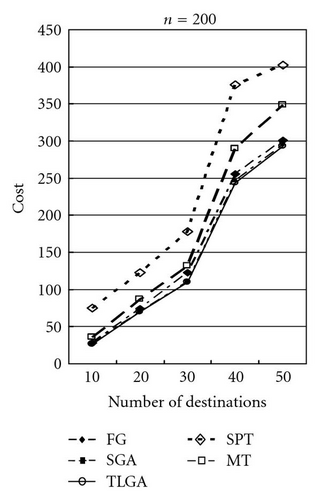
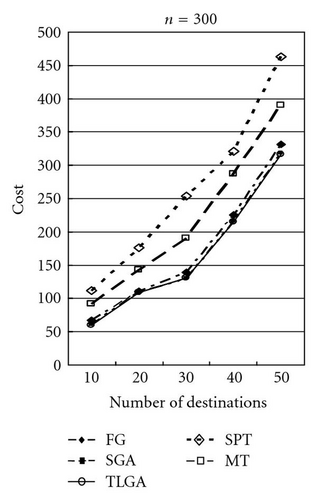
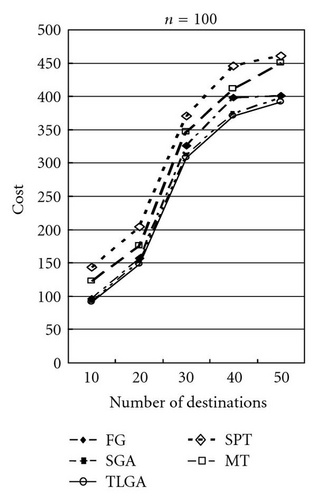
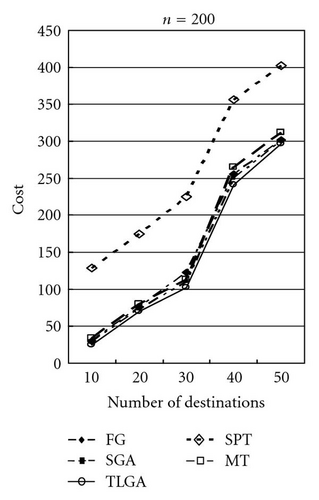
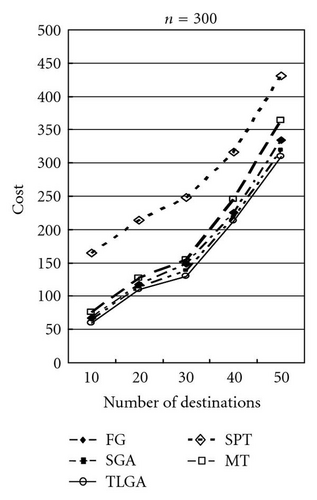
Table 1 shows the comparison in details. The average, minimal (min.), and maximal (max.) results of these GAs after running 10 times are compared. Moreover, the standard deviations (std.) of SGA and TLGA are shown. After computing the “ratio” by the formula (cost of FG/cost of TLGA × 100%) or (cost of SGA/cost of TLGA) × 100%), the farthest-first greedy (FG) algorithm gets the ratio 106.27% on average and the SGA gets a 102.45% ratio on average.
| α = 50 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FG | SGA | TLGA | SPT | MT | ||||||||
| n | |D| | FG | average | min. | max. | std. | average | min | max | std. | SPT | MT |
| 100 | 10 | 87 | 83 | 77 | 89 | 3.79 | 81 | 77 | 85 | 2.53 | 138 | 95 |
| 100 | 20 | 145 | 144 | 138 | 146 | 2.83 | 139 | 134 | 147 | 4.22 | 194 | 156 |
| 100 | 30 | 301 | 298 | 291 | 301 | 3.41 | 295 | 286 | 300 | 4.60 | 398 | 342 |
| 100 | 40 | 364 | 361 | 360 | 364 | 1.41 | 360 | 355 | 366 | 3.49 | 411 | 398 |
| 100 | 50 | 390 | 381 | 381 | 386 | 2.24 | 371 | 371 | 376 | 2.24 | 453 | 445 |
| 200 | 10 | 29 | 25 | 19 | 29 | 3.22 | 23 | 18 | 25 | 2.41 | 75 | 36 |
| 200 | 20 | 67 | 67 | 67 | 73 | 2.68 | 66 | 60 | 75 | 4.84 | 117 | 74 |
| 200 | 30 | 101 | 101 | 93 | 103 | 3.69 | 100 | 92 | 100 | 3.58 | 154 | 134 |
| 200 | 40 | 248 | 244 | 242 | 244 | 0.89 | 240 | 233 | 244 | 3.61 | 295 | 287 |
| 200 | 50 | 297 | 290 | 286 | 290 | 1.79 | 287 | 286 | 287 | 0.45 | 390 | 373 |
| 300 | 10 | 65 | 60 | 53 | 60 | 3.13 | 59 | 54 | 63 | 2.86 | 110 | 75 |
| 300 | 20 | 105 | 105 | 97 | 106 | 3.61 | 102 | 94 | 110 | 5.06 | 154 | 121 |
| 300 | 30 | 127 | 126 | 120 | 134 | 4.47 | 123 | 121 | 131 | 3.69 | 175 | 143 |
| 300 | 40 | 212 | 212 | 210 | 216 | 2.00 | 209 | 203 | 215 | 3.79 | 261 | 254 |
| 300 | 50 | 309 | 305 | 299 | 312 | 4.12 | 300 | 296 | 300 | 1.79 | 354 | 365 |
| α = 100 | ||||||||||||
| FG | SGA | TLGA | SPT | MT | ||||||||
| n | |D| | FG | average | min. | max. | std. | average | min | max | std. | SPT | MT |
| 100 | 10 | 90 | 87 | 87 | 91 | 1.79 | 85 | 79 | 94 | 4.84 | 121 | 101 |
| 100 | 20 | 147 | 147 | 145 | 151 | 2.00 | 146 | 143 | 154 | 3.82 | 176 | 167 |
| 100 | 30 | 324 | 312 | 312 | 315 | 1.34 | 310 | 306 | 316 | 3.22 | 412 | 358 |
| 100 | 40 | 374 | 374 | 372 | 381 | 3.26 | 374 | 372 | 381 | 3.26 | 435 | 423 |
| 100 | 50 | 394 | 384 | 377 | 387 | 3.41 | 383 | 381 | 387 | 2.00 | 498 | 427 |
| 200 | 10 | 28 | 28 | 24 | 32 | 2.53 | 26 | 17 | 30 | 4.40 | 75 | 36 |
| 200 | 20 | 74 | 70 | 66 | 70 | 1.79 | 70 | 69 | 72 | 1.00 | 123 | 87 |
| 200 | 30 | 123 | 110 | 103 | 114 | 3.61 | 110 | 107 | 116 | 3.00 | 178 | 132 |
| 200 | 40 | 256 | 246 | 246 | 255 | 4.02 | 244 | 241 | 247 | 1.90 | 376 | 290 |
| 200 | 50 | 301 | 295 | 289 | 300 | 3.49 | 293 | 291 | 295 | 1.26 | 402 | 349 |
| 300 | 10 | 67 | 61 | 58 | 61 | 1.34 | 60 | 56 | 63 | 2.24 | 112 | 92 |
| 300 | 20 | 111 | 110 | 109 | 114 | 1.84 | 109 | 109 | 110 | 0.45 | 176 | 143 |
| 300 | 30 | 139 | 130 | 122 | 139 | 5.39 | 131 | 124 | 134 | 3.41 | 254 | 190 |
| 300 | 40 | 225 | 216 | 208 | 224 | 5.06 | 215 | 213 | 221 | 2.83 | 321 | 287 |
| 300 | 50 | 331 | 318 | 309 | 324 | 4.84 | 316 | 312 | 324 | 4.00 | 463 | 390 |
| α = 150 | ||||||||||||
| FG | SGA | TLGA | SPT | MT | ||||||||
| n | |D| | FG | average | min. | max. | std. | average | min | max | std. | SPT | MT |
| 100 | 10 | 96 | 92 | 92 | 95 | 1.34 | 91 | 82 | 93 | 4.12 | 144 | 139 |
| 100 | 20 | 157 | 152 | 151 | 153 | 0.63 | 148 | 143 | 150 | 2.41 | 298 | 295 |
| 100 | 30 | 326 | 312 | 307 | 320 | 4.22 | 308 | 307 | 308 | 0.45 | 361 | 360 |
| 100 | 40 | 398 | 375 | 375 | 379 | 1.79 | 371 | 367 | 379 | 4.00 | 381 | 371 |
| 100 | 50 | 401 | 398 | 397 | 404 | 2.72 | 392 | 388 | 397 | 2.86 | 25 | 23 |
| 200 | 10 | 30 | 28 | 23 | 29 | 2.28 | 25 | 23 | 32 | 3.26 | 67 | 66 |
| 200 | 20 | 76 | 73 | 72 | 78 | 2.28 | 70 | 61 | 70 | 4.02 | 101 | 100 |
| 200 | 30 | 123 | 110 | 101 | 114 | 4.40 | 102 | 102 | 108 | 2.68 | 244 | 240 |
| 200 | 40 | 256 | 250 | 241 | 251 | 4.05 | 241 | 241 | 248 | 3.13 | 290 | 287 |
| 200 | 50 | 302 | 300 | 296 | 304 | 2.53 | 297 | 292 | 304 | 3.85 | 60 | 59 |
| 300 | 10 | 67 | 65 | 62 | 73 | 3.82 | 60 | 57 | 68 | 3.82 | 105 | 102 |
| 300 | 20 | 117 | 114 | 112 | 114 | 0.89 | 110 | 108 | 116 | 2.83 | 126 | 123 |
| 300 | 30 | 149 | 138 | 131 | 138 | 3.13 | 130 | 125 | 131 | 2.28 | 212 | 209 |
| 300 | 40 | 225 | 218 | 212 | 223 | 3.49 | 213 | 208 | 216 | 2.61 | 305 | 300 |
| 300 | 50 | 334 | 319 | 318 | 320 | 0.63 | 310 | 307 | 310 | 1.34 | 401 | 376 |
As mentioned above, in the TLGA, the encoding method of SGA is extended by adding an AG which represents the assigned wavelengths of the paths. Moreover, the content is modified by performing the CAA to form a feasible solution. In the CAA, three heuristic algorithms: (1) the wavelength mapping algorithm, (2) the wavelength packing algorithm, and (3) the path rerouting algorithm are called to find better wavelength assignments of the multicast tree. More crossover and mutation operators are used in the TLGA and the heuristic algorithm FG is used to generate one chromosome of the TLGA. All these improvements can help the TLGA to find better results quickly. Thus, the TLGA gets better results than the SGA and FG.
Table 2 shows the result of hypothesis statistical tests of SGA and TLGA. In this table, the difference in means and variances of results obtained by SGA and TLGA is examined. For these cases, we justify the assumptions by constructing two confidence intervals at β = 95% and 99%. First, the difference of means of the results obtained by performing the SGA and TLGA is examined. Z-distribution was used to estimate the difference between two means with two-side hypothesis “H0: the means of SGA and TLGA are the same." For confidence interval of β = 95% and 99%, the z-value should be in interval (− 1.96, 1.96) and (− 2.575, 2.575), respectively. If the z-value is within the interval, the means of SGA and TLGA are the same which accepts H0; otherwise they are different which rejects H0. Observe the results shown in Table 2, in confidence interval β = 95% for α = 50, two-fifths of the cases are rejected. For α = 100, two-fifteenths of the cases are rejected and for α = 150, all the cases are rejected. For the confidence interval β = 99% for α = 50, one-third of the cases is rejected. For α = 100, none of the cases is rejected and for α = 150, eleven-fifteenths of the cases are rejected.
| α = 50 | |||||||
|---|---|---|---|---|---|---|---|
| n | |D| | Z-value | β = 95% | β = 99% | F-value | β = 95% | β = 99% |
| 100 | 10 | 1.388 | accept H0 | accept H0 | 14.364 | reject H0 | reject H0 |
| 100 | 20 | 3.112 | reject H0 | reject H0 | 8.009 | reject H0 | reject H0 |
| 100 | 30 | 1.657 | accept H0 | accept H0 | 11.628 | reject H0 | reject H0 |
| 100 | 40 | 0.840 | accept H0 | accept H0 | 1.988 | accept H0 | accept H0 |
| 100 | 50 | 9.982 | reject H0 | reject H0 | 5.018 | reject H0 | accept H0 |
| 200 | 10 | 1.572 | accept H0 | accept H0 | 10.368 | reject H0 | reject H0 |
| 200 | 20 | 0.572 | accept H0 | accept H0 | 7.182 | reject H0 | reject H0 |
| 200 | 30 | 0.615 | accept H0 | accept H0 | 13.616 | reject H0 | reject H0 |
| 200 | 40 | 3.402 | reject H0 | reject H0 | 0.792 | accept H0 | accept H0 |
| 200 | 50 | 5.140 | reject H0 | reject H0 | 3.204 | accept H0 | accept H0 |
| 300 | 10 | 0.746 | accept H0 | accept H0 | 9.797 | reject H0 | reject H0 |
| 300 | 20 | 1.526 | accept H0 | accept H0 | 13.032 | reject H0 | reject H0 |
| 300 | 30 | 1.637 | accept H0 | accept H0 | 19.981 | reject H0 | reject H0 |
| 300 | 40 | 2.214 | reject H0 | accept H0 | 4.000 | accept H0 | accept H0 |
| 300 | 50 | 3.520 | reject H0 | reject H0 | 16.974 | reject H0 | reject H0 |
| α = 100 | |||||||
| n | |D| | Z-value | β = 95% | β = 99% | F-value | β = 95% | β = 99% |
| 100 | 10 | 1.226 | accept H0 | accept H0 | 3.204 | accept H0 | accept H0 |
| 100 | 20 | 0.733 | accept H0 | accept H0 | 4.000 | accept H0 | accept H0 |
| 100 | 30 | 1.813 | accept H0 | accept H0 | 1.796 | accept H0 | accept H0 |
| 100 | 40 | 0.000 | accept H0 | accept H0 | 10.628 | reject H0 | reject H0 |
| 100 | 50 | 0.800 | accept H0 | accept H0 | 11.628 | reject H0 | reject H0 |
| 200 | 10 | 1.246 | accept H0 | accept H0 | 6.401 | reject H0 | accept H0 |
| 200 | 20 | 0.000 | accept H0 | accept H0 | 3.204 | accept H0 | accept H0 |
| 200 | 30 | 0.000 | accept H0 | accept H0 | 13.032 | reject H0 | reject H0 |
| 200 | 40 | 1.422 | accept H0 | accept H0 | 16.160 | reject H0 | reject H0 |
| 200 | 50 | 1.705 | reject H0 | accept H0 | 12.180 | reject H0 | reject H0 |
| 200 | 10 | 1.212 | accept H0 | accept H0 | 1.796 | accept H0 | accept H0 |
| 300 | 20 | 1.669 | reject H0 | accept H0 | 3.386 | accept H0 | accept H0 |
| 300 | 30 | − 0.496 | accept H0 | accept H0 | 29.052 | reject H0 | reject H0 |
| 300 | 40 | 0.545 | accept H0 | accept H0 | 25.604 | reject H0 | reject H0 |
| 300 | 50 | 1.007 | accept H0 | accept H0 | 23.426 | reject H0 | reject H0 |
| α = 150 | |||||||
| n | |D| | Z-value | β = 95% | β = 99% | F-value | β = 95% | β = 99% |
| 100 | 10 | Ztest | reject H0 | accept H0 | 1.796 | accept H0 | accept H0 |
| 100 | 20 | 5.078 | reject H0 | reject H0 | 0.397 | accept H0 | accept H0 |
| 100 | 30 | 2.981 | reject H0 | reject H0 | 17.808 | reject H0 | reject H0 |
| 100 | 40 | 2.886 | reject H0 | reject H0 | 3.204 | accept H0 | accept H0 |
| 100 | 50 | 4.807 | reject H0 | reject H0 | 7.398 | reject H0 | reject H0 |
| 200 | 10 | 2.385 | reject H0 | accept H0 | 5.198 | reject H0 | accept H0 |
| 200 | 20 | 2.053 | reject H0 | accept H0 | 5.198 | reject H0 | reject H0 |
| 200 | 30 | 4.910 | reject H0 | reject H0 | 19.360 | accept H0 | accept H0 |
| 200 | 40 | 5.560 | reject H0 | reject H0 | 16.403 | reject H0 | reject H0 |
| 200 | 50 | 2.059 | reject H0 | accept H0 | 6.401 | accept H0 | accept H0 |
| 300 | 10 | 2.927 | reject H0 | reject H0 | 14.592 | reject H0 | reject H0 |
| 300 | 20 | 4.264 | reject H0 | reject H0 | 0.792 | accept H0 | accept H0 |
| 300 | 30 | 6.533 | reject H0 | reject H0 | 9.797 | reject H0 | reject H0 |
| 300 | 40 | 3.628 | reject H0 | reject H0 | 12.180 | reject H0 | reject H0 |
| 300 | 50 | 19.221 | reject H0 | reject H0 | 0.397 | accept H0 | accept H0 |
| Mean test | β = 95%: Z0.025 = −1.96, Z0.975 = 1.96 | β = 99%, Z0.005 = −2.575, Z0.995 = 2.575 | |||||
| Var. test | β = 95%: F0.975(9, 9) = 4.03, F0.025(9, 9) = 0.248 | β = 99%, F0.995(9, 9) = 6.541, F0.005(9, 9) = 0.153 | |||||
Second, in the difference of variances, the results obtained by performing the SGA and TLGA are examined. F-distribution was used to estimate the difference between two variances with two-side hypothesis “H0: the variances of SGA and TLGA are the same." For the confidence interval of β = 95% and 99%, the f-value with sampling size (10, 10) is interval (0.248, 4.03) and (0.153, 26.541), respectively. If the f-value is within the interval, then the variances of SGA and TLGA are the same which accepts H0; otherwise they are different which rejects H0. Observe the results shown in Table 2, in confidence interval β = 95% for α = 50, eleven-fifteenths of the cases are rejected. For α = 100, three-fifths of the cases are rejected and for α = 150, eight-fifteenths of the cases are rejected. For the confidence interval of β = 99% for α = 50, two-thirds of the cases are rejected. For α = 100, eight-fifteenths of the cases are rejected and for α = 150, two-thirds of the cases are rejected.
7. Conclusions
In this paper, the minimal cost multicast routing problem (MCMRP) on WDM networks with Tap-and-Continue (TaC) nodes is defined and studied. A new cost model which consists of the wavelength usage and communication cost is defined. The objective is to minimize the sum of the cost of used wavelengths and the communication cost of the lightforest. Specifically, the formulation for the WDM multicast routing problem is given. Because the MCMRP is NP-hard, two genetic algorithms, simple genetic algorithm (SGA) and two-level genetic algorithm (TLGA), are proposed to solve this problem.
In the proposed SGA, a path-oriented encoding chromosome is used to represent the routing paths. These routing paths are used to construct source-based light forests to represent a feasible solution to the multicast request. Moreover, to speed up the convergence of GAs, a farthest-first greedy heuristic algorithm is proposed and used to generate one of the initial chromosomes.
In the proposed TLGA, the encoding method of SGA is extended by adding an AG which represents the assigned wavelengths of the paths. Moreover, the content is modified by performing the CAA to form a feasible solution. In the CAA, three heuristic algorithms, (1) the wavelength mapping algorithm, (2) the wavelength packing algorithm, and (3) the path rerouting Algorithm, are called to find better wavelength assignments of the multicast tree. More crossover and mutation operators are used in the TLGA and the heuristic algorithm FG is used to generate one chromosome of the TLGA. All these improvements can help the TLGA to find better results quickly. Thus, the TLGA gets better results than the SGA and FG.
Acknowledgment
The author is very grateful to Associate Editor Dr. Shengxiang Yang and anonymous reviewers for their helpful suggestions and constructive comments.




