The traditional variable selection methods for survival data depend on iteration procedures, and control of this process assumes tuning parameters that are problematic and time consuming, especially if the models are complex and have a large number of risk factors. In this paper, we propose a new method based on the global sensitivity analysis (GSA) to select the most influential risk factors. This contributes to simplification of the logistic regression model by excluding the irrelevant risk factors, thus eliminating the need to fit and evaluate a large number of models. Data from medical trials are suggested as a way to test the efficiency and capability of this method and as a way to simplify the model. This leads to construction of an appropriate model. The proposed method ranks the risk factors according to their importance.

1. Introduction

Sensitivity analysis (SA) plays a central role in a variety of statistical methodologies, including classification and discrimination, calibration, comparison, and model selection [1]. SA also can be used to determine which subset of input factors (if any) accounts for most of the output variance (and in what percentage); those factors with a small percentage can be fixed to any value within their range [2]. In such usage, the focus is on determination of the important variables to simplification of the model; the original motivation for our research lay in a search for how to best arrive at such a determination. Although SA has been widely used in normal regression models to extract important input variables from a complex model so as to arrive at a reduced model with equivalent predictive power, it has limited use for selection of risk factors despite the presence of a large number of risk factors in survival regression models. The limited use of these methods to select appropriate subsets in survival regression models illustrates the desirability of development of a new method of SA-based variable selection to avoid the drawbacks of traditional methods and also simplify survival regression models by choosing the appropriate subsets of risk factors.

A considerable number of methods of variable selection have been proposed in the literature. The fundamental developments are squarely in the context of normal regression models and particularly in the context of multivariate linear regression models [3]. A comprehensive review of many variable selection methods is represented in [4]. Methods such as forward, backward, and stepwise selection and subset selection (Akaike information criterion (AIC)) and Bayesian information criterion (BIC)) are available; however none of these methods can be recommended for use in either a logistic regression model or in other survival regression models. They give incorrect estimates of the standard errors and P-values. They also can delete variables whose inclusion is critical [3]. In addition, these methods regard all the risk factors of a situation as equal, and they seek to identify the candidate subset of variables sequentially; furthermore, most of these methods focus on the main effects and ignore higher-order effects (interactions of variables).

New methods of variable selection, such as least absolute shrinkage and selection operator (LASSO) in [5], and the smoothly clipped absolute deviation (SCAD) method in [6], are at the center of attention recently in the field of survival regression models. These methods use the penalized likelihood estimation and the shrinkage regression approaches. These two approaches differ from traditional methods in their deletion of the nonsignificant covariates in the model by estimating their effects as 0. A nice feature of these methods is that they perform estimation and variable selection simultaneously, but, nevertheless, these methods suffer from some calculation and characteristics problems that are dealt with in more detail in [7, 8].

This study aims to use SA to extend and develop an effective, efficient, and time-saving variable selection method in which the best subsets are identified according to specified criteria without resorting to fitting all the possible subset regression models in the field of survival regression models. The remainder of this study is organized as follows: Section 2 gives the background of building a logistic regression model, and Section 3 deals with the proposed method. The results of implementing this method and logistic regression model are the subject of Section 4, and Section 5 consists of the discussion and conclusions.

2. Background of Constructing a Logistic Regression Model

Often the response variable in clinical data is not a numerical value but a binary one (e.g., alive or dead, diseased or not diseased). When the latter occurs, a binary logistic regression model is an appropriate method to present the relationship between the disease’s measurements and its risk factors. It is a form of regression used when the response variable (the disease measurement) is a dichotomy and the risk factors of the disease are of any type [9]. A logistic regression model neither assumes the linearity in the relationship between the risk factors and the response variable, nor does it require normally distributed variables. It also does not assume homoscedasticity, and in general has less stringent requirements than linear regression models. However, it does require that observations are independent and that the independent risk factors are linearly related to the logit of the response variable [10]. However, models involving the association between risk factors and binary response variables are found in various disciplines such as medicine, engineering, and the natural sciences. How do we model the relationship between risk factors and binary response variable? The answer to this question is the subject of the next subsections.

2.1. Constructing a Logistic Regression Model

The first step in modeling binomial data is a transformation of the probability scale from range (0, 1) to (−∞, ∞) instead of using the linear model for the response variable of the probability of success on risk factors. The logistic transformation or logit of the probability of success (π) is log {π/(1 − π)}, which is written as logit (π) and defined as the log odds of success. It is easily seen that any value of (π) in the range (0, 1) corresponds to the value of logit (π) in (−∞, +∞). Usually, binary data results from a nonlinear relationship between {π(x)} and (x), where a fixed change in (x) has less impact when {π(x)} is near (0 or 1) than when {π(x)} is near (0.5). This is illustrated in Figure 1 (see [11]).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Logit = ln (π/(1 − π)) as a function of the value of probability (π), the logit ranges from (−∞) to (+∞) as probability ranges from (0) to (1). The logit = 0 when probability = 0.5.

Thus, the appropriate link is the log odds transformation (the logit). Then if there are n binomial observations of the form π_i = y_i/n_i for i = 1, 2, …, n, where the expected value of the random variable associated with ith observation, y_i, is E(Y_i) = n_iπ_i. The logistic regression model for association of π_i on the values x_1i, x_2i, …, x_ki of k risk factors X₁, X₂, …, X_k is such that [10]

()

and the equation of success probability is

()

The linear logistic model is a member of a family of generalized linear models (GLM). The next subsection explains this model fitting process.

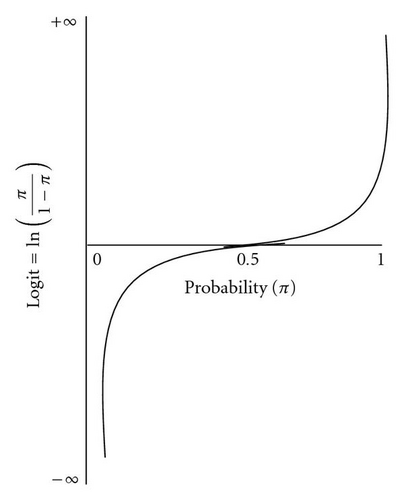
2.2. Fitting Logistic Regression Models

The mechanics of maximum likelihood (ML) estimation and model fitting for logistic regression model are a special case of GLM fitting, and then fitting the model requires estimation of the unknown parameters (β_j) of the ML function of this model using the Bernoulli ML as in the following [12]:

()

The problem now is to obtain those values

that maximize {L(β)} or its equivalent {Log L(β)} where it is as follows:

()

where

and (x_0i = 1) represent all values of (i). The derivative of this log-likelihood function with respect to the (k + 1) unknown β-parameters is given by

()

Then the likelihood equations are

()

where

is the ML estimate of {π_i}. There are two methods to solve (6) and obtain the maximum likelihood estimation of

. The one most often used is known as the Newton-Raphson method. This method begins with determination of the score matrix {U(β)} and the information matrix {I(β)} as in the following [13]:

()

Here (π^(t)) is obtained from {β^(t)} through (2), then we use {U^(t)} and {I^(t)} with the following formula

to obtain the next value (β^(t+1)) as

()

where

, this is to obtain (π^(t+1)), and so on.

2.3. Evaluating the Fitted Model

A simple model that fits adequately has the advantage of model parsimony. If a model has relatively little bias and describes reality well, it tends to provide more accurate estimates of the quantities of interest. Agresti [9] stated that “we are mistaken if we think that we have found the true model, because any model is a simplification of reality.” In light of this assertion, what then is the logic of testing the fit of a model when we know that it does not truly hold? The answer lies in the evaluation of the specific properties of this model by using criteria such as deviance, the R², the Wald Score test, the Person chi-square, and the Hosmer-Lemshow chi-square tests; for more details, see [9, 10]. Usually the first stage of construction of any model presents a large number of risk factors. Inclusion of all of them may lead to an unattractive model from a statistical viewpoint. Thus, as an important step towards an acceptable model, a decision should be made early about the proper methodology to use to select the appropriate and important risk factors. Because traditional methods of selecting variables have many limitations in their applicability to survival regression models, a new method of variables selection will be developed by using GSA to select the most influential factors in the model. This is the subject of the following section.

3. Sensitivity Analysis to Select the Most Influencing Risk Factors

There are two key problems in variable selection procedure: (i) how to select an appropriate number of risk factors from the set of risk factors, and (ii) how to improve final model performance based on the given data. So answering these questions is the objective of our proposed method by applying GSA to select the influential risk factors in the logistic regression model.

3.1. General Concept of GSA

GSA was defined in [14] as “the study of how the uncertainty in the output of a model (numerical or otherwise) can be apportioned to different sources of uncertainty in the model input.” Hence one possible way to apportion the importance of the input factors with respect to the model response is to apply GSA. In general the importance of a given risk factor X_i can be measured via the so-called sensitivity index, which is defined as the fractional contribution to the model output variance because of the uncertainty in X_i. For k risk factors, the sensitivity indices can be computed using the following decomposition formula for the total output variance V(Y) of the output Y [15]:

()

where

()

where V(Y) is the unconditional variance of output of the model (incidence of CHD), V(X_i) is the conditional variance of risk factor X_i, and V(X_i, X_j) is the variance of interaction between X_i and X_j, and so on. A first measurement of the fraction of the unconditional output variance V(Y) that is accounted for by the uncertainty in X_i, which is the first-order sensitivity index (S_i) for the factor X_i is given as

()

The second terms in (9) are known as the effect of interactions. It is a fact that the number and importance of the interaction terms usually grow (i) with the number of risk factors k, and (ii) with the range of variation of the risk factors [16]. This means that if all of the V(X_i) terms are computed, then most likely

would still be lower than the total V(Y), because the difference

is a measure of the impact of the interactions. Consequently, when

, then the model is additive (i.e., without interactions among its input factors), and thus the first order of conditional variances of (10) are all we need to decompose the model output variance. For a nonadditive model, higher-order sensitivity indices account for interaction effects among sets of input factors. However, higher-order sensitivity indices are usually not estimated directly because if the model consists of k risk factors, then the total number of indices (including the S_i′s) that should be estimated is as high as 2^k − 1. For this reason, a more compact sensitivity measurement is used; this measurement is the total effect sensitivity (S_T) index, which concentrates in one single term on all the interactions involving a given factor X_i. For example, for a model of k = 3 risk factors, the three total sensitivity indices would be [2]

()

and analogously

()

where the conditional variance in (12) expresses the total contribution to the variance of Y because of non-X_i, (i.e., to the k − 1 remaining factors), so that

includes all terms (i.e., a first order as well as interactions in (9)) that involve risk factor X_i. For a given risk factor X_i, thecoefficient of importance (IC_i) is the difference between S_Ti and S_i that reflects an important role of interactions for that risk factor in Y,

()

Explaining the interactions among risk factors helps us to improve our understanding about the model structure. Estimators for both (S_i, S_Ti) are provided by a variety of methods such as Sobol, the Fourier amplitude sensitivity test (FAST), and others; for more details, see [17].

3.2. GSA in a Logistic Regression Model

In this study, partitioning the total variance of the objective function V(Y) is the way to estimate S_i and S_Ti so as to perform a GSA. How can this model be extended to deal with a binary response variable? Although partitioning of variances is uncomplicated in models with a continuous response variable and a normal error distribution, the extension of this partitioning to models with binary responses is not simple [18]. Consequently, to extend the variance partitioning method to our binary response variable (incident of coronary heart disease (CHD)), suppose that the data is consisting of y_i, the number of people who have CHD. The actual response probability of the incidence of CHD for the ith observation π_i will have a Bernoulli distribution with a mean of p_i, where p_i is the proportion of the patients who have a disease. This response probability is therefore a random variable where E(π_i) = p_i. The variance of π_i must be equal to zero when p_i is zero or unity, and then a relationship between the unknown probability and our risk factors can be fitted. Typically a logistic regression model represents this relationship between y_i for a sample with n people who have a binomial distribution (i.e., {Y_i ~ B(n, π_i)}, i = 1, 2, …, n), and the corresponding response probability of the incidence of the disease is π_i = y_i/n for ith observation and the k risk factors X₁, X₂, …, X_k as in (4) and (5). This model assumes independence between the n observations, and then all the variations conditional on the estimates of the probabilities will be binomial with equal variance:

()

The binomial is not the only possible distribution for fitting proportion data. Other distributions exist that have greater variation (known as overdispersion) or less variation (known as underdispersion) than the binomial distribution conditional on the values of π_i′s. The simplest function for the true probability of the ith observation uses a multiplicative scale factor to determine the variance of the response as

()

where r is a scale factor that is equal to 1. If we have a binomial variation, it will be greater than 1 if there is overdispersion and less than 1 if there is underdispersion, and π_i is an unobservable random variable [19]. The advantages of the multiplicative approach are that it will allow both over- and underdispersions. The random variable Y_i is associated with the observed number of incidences of the disease for the ith unit, y_i. It will have a binomial distribution, and then the mean of Y_i, conditionalon π_i, is

()

and the conditional variance of Y_i is

()

Since π_i cannot be calculated, then the observed proportion of the disease incidence p_i has to be an estimate of π_i as

()

According to a standard result from the conditional probability theory, the unconditional expected value of a random variable Y can be obtained from the conditional expectation of Y given X using the equation

()

and the unconditional variance of Y is given by [20]

()

Applying these two results on our response variable gives

()

now

()

also

()

and so

()

in the absence of random variation in the response probability, Y_i would have a binomial distribution, B(n, p_i), and in this case when r = 1 as required, then

()

If, on the other hand, r is greater than 1, then a variation in the response probability occurs and the variance of Y_i will exceed np_i(1 − p_i), the variance under binomial sampling that leads to overdispersion. But if r is less than 1, then the variation in the response probability and the variance of Y_i will be less than np_i(1 − p_i), the variance under binomial sampling that leads to underdispersion. To use GSA to select the important covariates from the available set of covariates and construct an appropriate logistic regression model, it involves three steps.

(1) The first step is identification of the probability distribution f(x) of each covariate in the model. Usually sensitivity analysis starts from probability distribution functions (pdfs) given by the experts. This selection makes the use of the best information available of the statistical properties of the input factors. One of the methods used to obtain the pdfs starts with visualizing the observed data by examining its histogram to see if it is compatible with the shape of any distribution, as illustrated in Figure 2.

A visual approach is not always easy, accurate, or valid, especially if the sample size is small. Thus it would be better to have a more formal procedure for deciding which distribution is “best.” A number of significance tests are available for this such as the Kolmogorov-Smirnoff and chi-square tests. For more details, see [21].

(2) In the second step, the logistic regression model as in (1) and the information about the covariates obtained in step one are used to create a Monte Carlo simulation to generate the sample that will be used in the decomposition and to estimate the unconditional variance of response probability and the conditional variation for covariates as in (23) to (26).

(3) These results from step two will be used in performing GSA in the binary logistic regression model using (11), and in the result of decomposing as in (24) and (26), where the main effect indices are

()

and the total effect indices are

()

where X_−i are all X′s but X_i, and the coefficients of importance are

()

These results and the two datasets are used to test and compare the performance of the proposed GSA method as a variable selection method to identify the important risk factors obtained from these datasets with the results obtained from other existing methods of selecting variables.

4. Numerical Comparisons

The purpose of this section is to compare the performance of the proposed method with existing ones. We also use a real data example to illustrate our SA approach as a variable selection method. In the first examples in this section, we used the dataset and the results of the penalized likelihood estimate of best subset (AIC), bust subset (BIC), SCAD, and LASSO that were computed by [7] as a way to compare the performance of the proposed method with these methods.

4.1. The First Example

In this example, Fan and Li [7] applied the proposed penalized likelihood methodology to burn data collected by the General Hospital Burn Center at the University of Southern California. The dataset consists of 981 observations. The binary response variable Y is 1 for those victims who survived their burns and 0 otherwise. Risk factors are X₁ = age, X₂ = sex, X₃ = log (burn area + 1), and binary variable X₄ = oxygen (0 normal, 1 abnormal) was considered. Quadratic terms of X₁ and X₃, and all interaction terms were included. The intercept term was added, and the logistic regression model was fitted. The best subset variable selection with the AIC and the BIC was applied to this dataset. The unknown parameter λ was chosen by generalized cross-validation: it is 0.6932 and 0.0015, respectively, for the penalized likelihood estimates with the SCAD and LASSO. The constant a in the SCAD was taken as 3.7. With the selected λ, the penalized likelihood estimator was obtained at the sixth, 28th, and fifth step iterations for the penalized likelihood with the SCAD and LASSO. Table 1 contains the estimated coefficients and standard errors for the transformed data, based on the penalized likelihood estimators, and the calculation of the sensitivity indices obtained by using SimLab software to compare the performance of GSA as a variable selection method with other methods. The first five columns were calculated by [7].

Table 1. Estimated coefficients and standard errors for different variable selection methods.

Methods	MLE	Best subset AIC	Best subset BIC	SCAD	LASSO	SA S_i(S_Ti)
Factors	MLE	Best subset AIC	Best subset BIC	SCAD	LASSO	SA S_i(S_Ti)
Intercept	5.51 (0.75)	4.81 (0.45)	6.12 (0.57)	6.09 (0.29)	3.70 (0.25)	Constant
X₁	−8.8 (2.97)	−6.49 (1.75)	−12.15 (1.81)	−12.2 (.08)	0 (—)	0.487 (0.536)
X₂	2.30 (2.00)	0 (—)	0 (—)	0 (—)	0 (—)	0.014 (0.125)
X₃	−2.77 (3.43)	0 (—)	−6.93 (0.79)	−7.0 (0.21)	0 (—)	0.143 (0.218)
X₄	−1.74 (1.41)	0.30 (0.11)	−0.29 (0.11)	0 (—)	−0.28 (0.09)	0.003 (0.034)
	−0.75 (.61)	−1.04 (0.54)	0 (—)	0 (—)	−1.71 (0.24)	0.013 (0.057)
	−2.7 (2.45)	−4.55 (0.55)	0 (—)	0 (—)	−2.67 (0.22)	0.032 (0.091)
X₁X₂	0.03 (0.34)	0 (—)	0 (—)	0 (—)	0 (—)	0.014 (0.237)
X₁X₃	7.46 (2.34)	5.69 (1.29)	9.83 (1.63)	9.84 (0.14)	0.36 (0.22)	0.362 (0.502)
X₁X₄	0.24 (0.32)	0 (—)	0 (—)	0 (—)	0 (—)	0.001 (0.042)
X₂X₃	−2.15 (1.61)	0 (—)	0 (—)	0 (—)	−0.10 (0.10)	0.016 (0.075)
X₂X₄	−0.12 (0.16)	0 (—)	0 (—)	0 (—)	0 (—)	0.003 (0.047)
X₃X₄	1.23 (1.21)	0 (—)	0 (—)	0 (—)	0 (—)	0.019 (0.307)

In addition to GSA indices, Table 1 consists of the results of two traditional methods of variable selection (AIC and BIC) and two new methods (LASSO and SCAD). The traditional method, best subset procedure via minimizing the BIC scores, chooses five of 13 risk factors, whereas the SCAD chooses four risk factors. The difference between them is that the best subset keeps X₄. Neither SCAD nor the best subset variable selection (BIC) includes and in the selected subset, but both LASSO and the best subset variable selection (AIC) included them. LASSO chooses the quadratic terms of X₁ and X₃ rather than their linear terms. It also selects an interaction term X₂X₃, which may not be statistically significant. LASSO shrinks noticeably large coefficients. The last column in Table 1 shows that GSA selected the variables X₁, X₃, and X₁X₃, in addition to the intercept, which resembles the SCAD method, and differs from the other methods. According to the results in the last column of Table 1, the risk factors can be ranked according to sensitivity indices S_i and S_Ti. Age (X₁) is the first and the most influential risk factor, with a percent of contribution of 0.487, and the second most important risk factor is the interaction between X₁ and X₃, with a percentage of contribution of 0.362. The third influential risk factor is the log (area of burn + 1) (X₃) with a percentage of contribution of 0.143 as shown in Table 1. Consequently, we find that the proposed GSA variable selection method resembles SCAD in choosing the same risk factors.

4.2. The Second Example

A new dataset emerges from the original dataset prepared in [22] as a way to compare SA and the traditional method (backward elimination) as variable selection methods. Originally this study was undertaken to determine the prevalence of CHD risk factors among a population-based sample of 403 rural African-Americans in Virginia. Community-based screening evaluations included the determination of exercise and smoking habits, blood pressure, height, weight, total and high-density lipoprotein (HDL) cholesterol, and glycosylated hemoglobin, and other factors. The results of this study were presented as percentages of prevalence for most factors such as diabetes (13.6% of men, 15.6% of women), hypertension (30.9% of men, 43.1% of women), and obesity (38.7% of men, 64.7% of women), without building any models to study the relationship between CHD and its risk factors. For more details, see [8]. A new dataset was generated based on the first one as a way to calculate SA indices to extract the important risk factors for CHD from among these new factors, and then implement the logistic regression model to test the performance of the proposed method as follows.

(1)
CHD (Y) 10-year percentage risk is generated according to Framingham Point Scores. This risk is classified as 1 if the percentage of the risk is ≥20% and 0 otherwise [23].
(2)
Diabetes (debt, X₁): According to the criteria published by American College of Endocrinology (ACE) & American Association of Clinical Endocrinologists (AACE) [24] the participant has diabetes 1 if the Stabilized Glucose >140 mg/dL or Glycosylated Hemoglobin >7% or both of them more than these limits, and he has no diabetes 0 otherwise.
(3)
Total cholesterol (Chol, X₂): if a participant has total cholesterol of >200 mg/dL, he will be given a 1 and a 0 otherwise [25].
(4)
High density lipoprotein (HDL, X₃): a participant with HDL of <40 mg/dL will be given a 1 and a 0 otherwise [25].
(5)
Age (X₄): standardized values are used (X − μ)/σ.
(6)
Gender (Gan, X₅): 1 is for a male and 2 for a female.
(7)
Body mass index (BMI, X₆): values for this standard are calculated from the following equation: BMI = height/(weight)², and the participant gets 1 if BMI is >30 and a 0 otherwise [25].
(8)
Blood pressure (hypertension, Hyp, X₇): a participant has Hyp (1) if systolic blood pressure is >140 or if diastolic blood pressure is >90 or if both of them exceed these limits and 0 otherwise [25].
(9)
Waist/hip ratio (X₈), in addition to BMI, is a second factor in the determination of obesity.

This dataset was used to perform SA through the use of SimLab software and the partitioning variance methodology discussed in Section 3. An evaluation of the efficiency of the proposed method was performed by fitting all factors into logistic regression models so as to obtain comparisons of factors chosen by the proposed method with those selected by traditional variable selection method (backward elimination). SPSS software was used to get the results that follow from fitting logistic regression models.

4.2.1. The Important Risk Factors

Implementation of the GSA method for this dataset gave the results in Table 2, which shows the ranking of the risk factors in order of importance and the contribution of each one to explaining the total variance of the CHD response variable.

Table 2. Sensitivity indices and risk factors ranking.

Factors	S_i	S_Ti	IC_i	S_i (%)	Ranks
Diab	0.2018	0.22657	0.008	12	6
Chol	0.2434	0.258	0.015	14	4
HDL	0.2243	0.25424	0.03	13	5
Age	0.2636	0.28507	0.022	15	3
Gen	0.0256	0.03844	0.013	1	7
BMI	0.5161	0.56173	0.046	30	1
Hypt	0.003	0.04207	0.039	0	8
W/H	0.2706	0.29714	0.027	15	2
Sum.	1.7484	1.96326	0.2

According to the first order of sensitivity indices S_i, the BMI is the first and the most influential factor, and the waist-hip ratio ranks second. Both are components of the obesity factor. Age is the third influential factor and so on through the other factors as listed in Table 2. The total sensitivity index for a given risk factor provides a measure of the overall contribution of that risk factor to the output variance, taking into account all possible interactions with the other risk factors. The difference between the total sensitivity index and the first-order sensitivity index for a given risk factor is a measure of the contribution to the output variance of the interactions involving that factor; see (12) and (13). The second column in Table 2 shows the values of S_Ti, which gives the same rank as S_i for the risk factors. These indices point to the simple interaction between these risk factors as illustrated in the third column in the same table. Figure 3 shows the compression between the first order S_i, the total S_Ti sensitivity indices, and the interactions between risk factors.

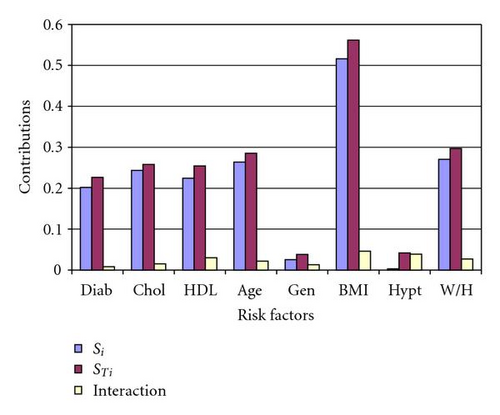
4.2.2. Implementing the Logistic Regression Model

Does the proposed method yield a reliable model? To investigate the reliability of the proposed method, we compared the results of the fitted models. Basically, when the full logistic regression model is fitted, the results are

()

These results showed the significance of the overall fit of the model according to the values of

and

in spite of the low value of Nag. R²; also showed that the individual effect for all risk factors is not significant, which means that H₀ cannot be rejected from the following null hypothesis:

()

Second, application of the logistic regression model by using those risk factors that appear in Table 2 as highly ranked by the proposed method also shows that this method ranks each risk factor according to its contribution to the incidence of the CHD response variable. The question also becomes how many variables must be selected in order to apply the logistic regression model. The possibility exists that the selection procedure may tend to underfit or overfit the model by selecting too few or too many variables. In the face of such a possibility, our objective becomes to find the model that uses the least number of variables while simultaneously explaining a reasonable percentage of variance in the dependent variable relative to the percentage explained by all the variables in the full model. Thus two models may be fitted from Table 2 to compare the results. The first logistic regression model consisted of the obesity factors (BMI, and W/H ratio), age, and total cholesterol factors that explained 74% of the total variance of the CHD response variable according to the individual effect (S_i) as in Table 2. The results of fitting this model in this manner and applying SPSS software were

()

The results in (34) showed that using these criteria for the overall fit for this model demonstrated their significance collectively and individually as risk factors that influence the incidence of CHD and raise the value of R² to 71% in comparison with the full model in (31) The second logistic regression model is fitted by adding another risk factor, HDL, to increase the percentage of explanation to 87%. The results of fitting this model as in (36) are

()

These results showed that adding the HDL risk factor does not improve the results of the first logistic regression model, but the parameter of this risk factor is not significant when we test the following hypothesis:

()

Note that the difference between the deviances of the two models is minor. Furthermore, the value of R² does not improve. Thus, according to the principle of parsimony, the first model should be considered the best model and the risk factors used to construct this model are those that are the most influential in causing CHD. Moreover, showing the different results obtained from these two models demonstrates the differences between fitting the full model with all risk factors and fitting it with only selected risk factors.

The efficiency of the proposed method of variable selection (GSA) can be measured by comparing its results as in (34) with the results gained from fitting the logistic regression model by using the backward elimination method (BEM). These results are shown in Tables 3 and 4.

Table 3. The overall fitting criteria for the BEM for a logistic regression model.

Step	−2Log L		Df	Sig.		df	Sig.	Nag. R²
6	357.813	7.268	3	0.064	8.465	8	0.389	0.30
7	359.021	6.061	2	0.048	0.055	2	0.973	0.25
8	360.189	4.892	1	0.027	—	—	—	0.20

Table 4. The estimated parameters and their significance for a logistic regression model using BEM.

Steps	Risk factors		Sig. (P)
Step 6	CHOL	0.538	0.061
	SAGE	0.151	0.271
	BMI	−0.325	0.241
	Constant	−1.711	0.000

Step 7	CHOL	0.610	0.029
	BMI	−0.300	0.276
	Constant	−1.758	0.000

Step 8	CHOL	0.605	0.030
Step 8	Constant	−1.946	0.000

Table 3 shows the overall fitting criteria required for the last three steps of a logistic regression model fitted by the use of the BEM.

Also Table 4 shows the last three steps of iteration to choose the important risk factors. These results represent the sequential elimination of the factors, which requires eight steps to rank these risk factors according to their importance; however, the proposed method does not need these iterations.

5. Conclusions

The results in Tables 1 to 4 and (31) to (36) for the two examples confirm that the proposed method is capable of distinguishing between important and unimportant risk factors. The proposed method ranked the risk factors according to their decreasing importance as shown in Tables 1 and 2. In the example in which we compared the proposed method with those methods that are typically used, we found that its performance very much resembled the SCAD method in which the same risk factors are selected. From the first example, we found that the important risk factors are age, the area of the burns, and the interaction between them. In the second example we found that the obesity factors (BMI and W/H) are the most influential risk factor on the incidence of CHD, the second risk factor is age, and the third risk factor is the total cholesterol. These play the major roles, representing approximately 74% of the incidence of CHD. Thus, they are considered the most important risk factors according to their individual percentages of contribution in the incidence of CHD as shown in Table 1. Compression between the results of the fitting of the full logistic regression model as in (31) and the chosen models as in (34) and (36) confirm the efficiency of the proposed method in its selection of the most important risk factors. Equation (34) represents the best model, according to the model evaluation criteria, because it consists of the most influential risk factors. Therefore, a medical care plan and medical interventions should comply with this ordering of these factors. Also, to further confirm these results, one of the traditional variable selection methods was used (backward elimination method), which yields different results after eight steps, but the proposed method orders the risk factors without iteration and without the need to fit multiple regression models. Finally, these results together confirm and emphasize the importance of GSA as a variable selection method.

Acknowledgment

This work was supported by USM fellowship.

References

1 Saltelli A., Chan K., and Scott E. M., Sensitivity Analysis, 2000, John Wiley & Sons, Chichester, UK.
Google Scholar
2 Saltelli A., [email protected], Ratto M., Tarantola S., and Campolongo F., Sensitivity analysis for chemical models, Chemical Reviews. (2005) 105, no. 7, 2811–2827, https://doi.org/10.1021/cr040659d.
Google Scholar
3 Khalili A. and Chen J., Variable selection in finite mixture of regression models, Journal of the American Statistical Association. (2007) 102, no. 479, 1025–1038, https://doi.org/10.1198/016214507000000590.
Google Scholar
4 Miller A. J., Subset Selection in Regression, 2002, 2nd edition, Chapman & Hall/CRC, London, UK.
Google Scholar
5 Tibshirani R., The lasso method for variable selection in the Cox model, Statistics in Medicine. (1997) 16, no. 4, 385–395, https://doi.org/10.1002/(SICI)1097-0258(19970228)16:4<385::AID-SIM380>3.0.CO;2-3.
10.1002/(SICI)1097-0258(19970228)16:4<385::AID-SIM380>3.0.CO;2-3
Web of Science® Google Scholar
6 Fan J. and [email protected], Li R., [email protected], Variable selection for Cox′s proportional hazards model and frailty model, Annals of Statistics. (2002) 30, no. 1, 74–99, https://doi.org/10.1214/aos/1015362185.
Google Scholar
7 Fan J. and Li R., Variable selection via nonconcave penalized likelihood and its oracle properties, Journal of the American Statistical Association. (2001) 96, no. 456, 1348–1360, https://doi.org/10.1198/016214501753382273.
Web of Science® Google Scholar
8 Zhang H. H. and [email protected], Lu W., [email protected], Adaptive Lasso for Cox′s proportional hazards model, Biometrika. (2007) 94, no. 3, 691–703, https://doi.org/10.1093/biomet/asm037.
Google Scholar
9 Agresti A., Categorical Data Analysis, 2002, 2nd edition, John Wiley & Sons, Hoboken, NJ, USA.
10.1002/0471249688
Google Scholar
10 Collett D., Modeling Binary Data, 2003, 2nd edition, Chapman & Hall/CRC, Boca Raton, Fla, USA.
Google Scholar
11 Cohen J., Cohen P., West S. G., and Alken L. S., Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 2003, 3rd edition, Lawrence Erlbaum Associates, Mahwah, NJ, USA.
Google Scholar
12 Cox D. R. and Snell E. J., Analysis of Binary Data, 1989, 2nd edition, Chapman & Hall/CRC, New York, NY, USA.
Google Scholar
13 Therneau T. M. and Grambsch P. M., Modeling Survival Data: Extending the Cox Model, 2000, Springer, New York, NY, USA.
Google Scholar
14 Saltelli A., K. M. Hanson and F. M. Hemez, Global sensitivity analysis: an introduction, Sensitivity Analysis of Model Output, 2005, Los Alamos National Laboratory, Los Alamos, NM, USA, 27–43.
Google Scholar
15 Saltelli A., [email protected], Tarantola S., and [email protected], Chan K. P.-S., A quantitative model-independent method for global sensitivity analysis of model output, Technometrics. (1999) 41, no. 1, 39–56, https://doi.org/10.2307/1270993.
Google Scholar
16 Saltelli A., Tarantola S., and Campolongo F., Sensitivity analysis as an ingredient of modeling, Statistical Science. (2000) 15, no. 4, 377–395, https://doi.org/10.1214/ss/1009213004.
Web of Science® Google Scholar
17 Chan K., Tarantola S., Saltelli A., and Sobol′ I. M., A. Saltelli, K. Chan, and M. Scott, Variance based methods, Sensitivity Analysis, 2000, John Wiley & Sons, New York, NY, USA, 167–197.
Google Scholar
18 Neter J., Michael H. K., Christopher J. N., and William W., Applied Linear Statistical Models, 1996, McGraw-Hill, New York, NY, USA.
Google Scholar
19 Long J. S., Regression Models for Categorical and Limited Dependent Variables, 1997, Sage, Thousand Oaks, Calif, USA.
Google Scholar
20 Saisana M., [email protected], Saltelli A., and Tarantola S., Uncertainty and sensitivity analysis techniques as tools for the quality assessment of composite indicators, Journal of the Royal Statistical Society. Series A. (2005) 168, no. 2, 307–323, https://doi.org/10.1111/j.1467-985X.2005.00350.x.
Google Scholar
21 Heiat A., Using an Excel extension for selecting the probability distribution of empirical data, Spreadsheets in Education. (2005) 2, no. 1, 95–100.
Google Scholar
22 Schorling J. B., Roach J., Siegel M. et al., A trial of church-based smoking cessation interventions for rural African Americans, Preventive Medicine. (1997) 26, no. 1, 92–101, https://doi.org/10.1006/pmed.1996.9988.
Google Scholar
23 Cleeman J. I., Grundy S. M., Becker D. et al., Expert panel on detection, evaluation, and treatment of high blood cholesterol in adults (adult treatment panel III), The Journal of the American Medical Association. (2001) 285, no. 19, 2486–2497, https://doi.org/10.1001/jama.285.19.2486.
Google Scholar
24 DiPiro J. T., Talbert R. L., Yee G. C., Matzke G. R., Wells B. G., and Posey L. M., Pharmacotherapy: A Pathophysiologic Approach, 2005, 6th edition, McGraw-Hill, New York, NY, USA.
Google Scholar
25 Koda-Kimble M. A., Young L. Y., Kradian W. A., Guglielmo B. J., Allderege B. K., and Corelli R. L., Applied Therapeutics, The Clinical Use of Drugs, 2005, 8th edition, Lippincott Williams & Wilkins, Baltimore, Md, USA.
Google Scholar

Citing Literature

All articles

Sensitivity Analysis to Select the Most Influential Risk Factors in a Logistic Regression Model

Abstract

1. Introduction

2. Background of Constructing a Logistic Regression Model