A Critical Period for Robust Curriculum-Based Deep Reinforcement Learning of Sequential Action in a Robot Arm
This article is part of the topic “Everyday Activities,” Holger Schultheis and Richard P. Cooper (Topic Editors).
Abstract
Many everyday activities are sequential in nature. That is, they can be seen as a sequence of subactions and sometimes subgoals. In the motor execution of sequential action, context effects are observed in which later subactions modulate the execution of earlier subactions (e.g., reaching for an overturned mug, people will optimize their grasp to achieve a comfortable end state). A trajectory (movement) adaptation of an often-used paradigm in the study of sequential action, the serial response time task, showed several context effects of which centering behavior is of special interest. Centering behavior refers to the tendency (or strategy) of subjects to move their arm or mouse cursor to a position equidistant to all stimuli in the absence of predictive information, thereby reducing movement time to all possible targets. In the current study, we investigated sequential action in a virtual robotic agent trained using proximal policy optimization, a state-of-the-art deep reinforcement learning algorithm. The agent was trained to reach for appearing targets, similar to a serial response time task given to humans. We found that agents were more likely to develop centering behavior similar to human subjects after curricularized learning. In our curriculum, we first rewarded agents for reaching targets before introducing a penalty for energy expenditure. When the penalty was applied with no curriculum, many agents failed to learn the task due to a lack of action space exploration, resulting in high variability of agents' performance. Our findings suggest that in virtual agents, similar to infants, early energetic exploration can promote robust later learning. This may have the same effect as infants' curiosity-based learning by which they shape their own curriculum. However, introducing new goals cannot wait too long, as there may be critical periods in development after which agents (as humans) cannot flexibly learn to incorporate new objectives. These lessons are making their way into machine learning and offer exciting new avenues for studying both human and machine learning of sequential action.
1 Introduction
Sequential action is central to our everyday lives. Indeed most of our daily activities, from driving our cars to setting the table and making coffee, can be regarded as complex sequential actions, subject to a structured hierarchy or grammar, but able to be adapted under changing circumstances (e.g., taking a detour or making espresso rather than drip coffee). The human ability to learn and perform these context-dependent sequential actions has been the subject of study for at least a century (Botvinick & Plaut, 2004; Cooper & Shallice, 2006; Lashley, 1951; Washburn, 1916). Sequential action can be represented on a symbolic level (i.e., what action should I take?), as well as on a subsymbolic, or sensorimotor level (what motor parameters do I need to use? Yamashita & Tani, 2008). Integration between the two levels of representation is required to produce smooth sequential action (e.g., Rumelhart & Norman, 1982). For example, early accounts of sequential action suggested that sequential action components could be triggered by the perception of the motor execution of the previous component (Washburn, 1916), while on the other hand there is evidence to suggest that motor planning takes place at a symbolic level initially, with subsymbolic motor parameters filled in online.
On a symbolic level, everyday action can be regarded as a sequence of subactions, sometimes with dependencies between them. For example, the action of table-setting could be divided into the subactions (1) laying placemats on the table; (2) putting plates in the middle of the placemats; (3) placing forks to the left of the plates; (4) placing knives to the right of the plates. While the order of (3) and (4) does not matter, it is clear that subaction (1) should be performed before all other subactions. It is a given that people make these inferences about dependencies during planning and execution of the actions, but how it is done is not well understood.
1.1 Anticipatory movement
Humans are able to infer structure from the statistical properties of sequences, as observed in studies of language learning, one of the most studied and storied domains of human sequential action. For example, Saffran, Aslin, & Newport (1996) showed that 8-month-old infants can use the statistical relationships between speech sounds to segment words in fluent speech, an elementary component of language acquisition. As the transition probability between phonemes of different words is lower than the transition probability between phonemes within a word, this information can be used for segmentation. As learning progresses during sequence learning, learners likely make both implicit and explicit predictions about subsequent subactions. With this information, learners can then optimize their action execution by feedforward planning, similar to context effects such as anticipatory lip rounding in speech (e.g., consider your lip position as you start pronouncing the /t/ in “tulip”; Bell-Berti & Harris, 1979) or the end-state comfort effect (if you are planning to pick up and flip an upside-down cup from a table, you usually flip your hand before grasping the cup, leaving your hand at the end of the action in a comfortable resting state; Cohen & Rosenbaum, 2004). de Kleijn, Kachergis, & Hommel (2018b) have shown these predictive effects on action execution in a serial response time (SRT) task adapted to mouse movements, in which participants must move the cursor to one of four on-screen locations, highlighted after a brief interstimulus interval (ISI) in either a random sequence or a deterministic sequence of length 10, with no instructions as to which condition they were in. Participants in the repeating sequence condition learned to predict future stimulus locations: Their mouse trajectories showed anticipatory movement toward the next stimulus during the ISI. However, in the absence of predictive information (i.e., in a random condition), participants would move their mouse cursor to a center position equidistant to all possible stimuli.
Related research has found similar anticipatory movements and suggested that such movements may be explicit: Dale, Duran, and Morehead (2012) used a trajectory SRT task with varying levels of sequence complexity and found that easier (lower complexity) sequences resulted in participants making larger predictive movements and showing more explicit knowledge of the sequence. However, a subset of participants did not make predictive movements and instead seemed to explicitly adopt a different strategy: They were observed to move the cursor to the center of the screen, equidistant from all stimuli. In particular, Dale et al. (2012) noted that “participants with low pattern awareness engaged in this form of behavior” (p. 204). Duran & Dale (2009) found further evidence of this strategy in another trajectory SRT task, concluding that the centering strategy likely helps participants compensate for lack of explicit sequence knowledge, which makes it impossible to predict the next target. Indeed, if the proximal target position is uncertain (either due to a random sequence, or to a participant's failure to learn the sequence), moving the mouse cursor to a position equidistant to all alternatives seems a rational strategy to adopt in order to guarantee minimum expected distance from the next target, and thus expected response time.
Similar results have been obtained by de Kleijn et al. (2018b), of which the results can be seen in Fig. 1. Human subjects were asked to move their mouse cursor to appearing stimuli, while not being informed of the deterministic or random nature of the sequence of appearance. While subjects in a deterministic condition proactively moved toward an anticipated stimulus during the ISI, in the random condition they moved their mouse cursor toward a position equidistant to all possible stimulus locations.
If centering behavior is indeed a strategy that is employed to compensate for lack of explicit sequence knowledge, one might expect that in a random SRT task the centering point chosen by participants could be manipulated by changing the probability distribution of the targets, with the centering point being closer to more probable stimuli. Additionally, moving stimuli would make the optimal centering position move with them, remaining equidistant to equiprobable stimuli.
1.2 The current study
Due to their embeddedness (i.e., an implementation in a simulated physical environment), virtual robots are a valuable tool for investigating models of behavior in which interaction with the environment is important (see Atkeson et al., 2000, for an extensive overview). Virtual robot paradigms have been successfully used to investigate psychological phenomena that require such embeddedness like hand–eye coordination (Kuperstein, 1988), object handling (Ito, Noda, Hoshino, & Tani, 2006), and imitation learning (Schaal, 1999). de Kleijn, Kachergis, and Hommel (2018a) investigated the behavior of feedforward neural networks evolved to perform a simple serial response task in a two-dimensional (2D) simulated environment, analogous to the mouse trajectory SRT tasks used by Dale et al. (2012) and de Kleijn et al. (2018b). The agents directly controlled the coordinates of the effector location, and their fitness was evaluated based on the total number of targets they reached, with a small penalty proportional to the total distance the effector moved (i.e., a metabolic cost). Populations of agents were trained in two different environments: one with a repeating sequence of target locations (e.g., 1–2–3–4), and the other with a random sequence. As expected, agents in the repeating sequence condition achieved superior performance, quickly reaching each target—and were even faster when given a predictive signal of where the next target would appear. Moreover, analysis of the agents' behavior revealed that those in the random condition would return to and remain at the center of the environment while waiting for the next (random) target to appear, thus minimizing their expected distance to the next target.
The present study extends this earlier work by making the environment and agent more realistic: a 3D environment with simulated physics and a double-articulated arm with actuated joints rather than having the neural controller simply output goal coordinates. Differing from our earlier work which trained agents across generations using neuroevolution, in the present work the neural controller is trained using reinforcement learning (RL), making for greater cognitive plausibility as RL algorithms learn online during an agent's lifetime by taking actions and experiencing rewards. We examine the conditions under which centering behavior emerges in this three-dimensional (3D) SRT RL task, finding that this strategy is dependent on the temporal dynamics of metabolic cost. We conclude by speculating what this research implies about human learning of sequential action.
2 Method
2.1 Implementation
For this study, we used Unity 2018.4.20f1 with the ML-Agents 0.17.0 toolkit as a physics simulator (Juliani et al., 2020). The experiment was implemented as a Unity scene consisting of an agent and targets in 3D space. Agent controllers were implemented using the TensorFlow 2.2.0 library (Abadi et al., 2015). Source code for our implementation can be found at https://github.com/rdekleijn/Sequential-Reacher.
2.2 The agent
The agent consisted of an arm with two actuators with each two degrees of freedom, with a hand functioning as a sensor that could touch the target. The agent was trained using proximal policy optimization (PPO), an on-policy deep RL algorithm (Schulman, Wolski, Dhariwal, Radford, & Klimov, 2017), a state-of-the-art RL algorithm that is widely used due to its good performance on a wide variety of tasks and its ease of tuning. Below we introduce this algorithm and its hyperparameters of interest.
2.2.1 Proximal policy optimization
The PPO algorithm collects a batch of experiences from the agent interacting with the environment. This batch is then used to generate a policy update and adjust the agent's decision-making policy. After policy update, old experiences are discarded and a new batch of experiences is collected using the revised policy and the process repeats. With each cycle, when a policy update would result in large changes, these changes are constrained and penalized. Thus, the algorithm ensures that the difference between the previous and the new policy is never too large, preventing the agent from going down an unrecoverable path of nonsensical actions.
In detail, since the optimization problem can be formalized as a sum of discounted rewards, learning a sequence of specific actions is the result of excluding other possible actions (Sutton, 1990; Sutton & Barto, 2018). Optimization is therefore not only dependent on the given reward 
but also on the set of possible actions 
chosen within a policy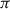 
under a given state 
, each having their own distribution. The agent starts at an initial state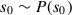 
and repeatedly samples an action 
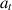from a policy 
. For each action 
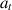, the agent receives a reward 
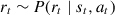, then transitions to the next state 
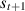with respect to the Markov decision process 
. This generates different trajectories of rewards, actions, and states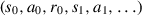 
with each trajectory having a varied spread of reward. Therefore, when sampling a batch of trajectories different gradient estimates can emerge, as trajectories can come from any region within the domain. This causes the policy distribution to move wildly over the parameter space, which can result in large differences between the original and updated policies (Mao, Venkatakrishnan, Schwarzkopf, & Alizadeh, 2018; Tucker et al., 2018). As a consequence, agents may explore a range too wide to be beneficial for learning a task and converging at a local optimum. Similarly, if too much bias is introduced as a measure to lower variance, the differences between each policy can be too small. The agent is then less likely to explore its environment, being too fixated on specific areas of the action space, either never converging or converging on a poor solution (Schulman, Moritz, Levine, Jordan, & Abbeel, 2016). In either case, the agent may not learn to perform its task well. As such, the key to a stable training procedure is to find a configuration within the parameter space which encourages the agent to find a balance between too little and too much exploration. The PPO algorithm is popular due to its ability to do this with only a few hyperparameters that govern the learning process.
The entropy regularization parameter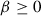 
controls the stochasticity of an agent's actions under a given policy, with larger values resulting in greater randomness of actions. Greater randomness can improve exploration by discouraging premature convergence to suboptimal deterministic policies (Mnih et al., 2016; Williams & Peng, 1991) and could be viewed as a type of curiosity. The regularization parameter 
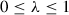used when computing the generalized advantage estimate (GAE) controls the bias-variance trade-off. The GAE measures the degree to which an action is a good or bad decision given a certain state. The parameter 
trades variance by decreasing the weights of distant advantage estimates, in favor of bias toward earlier advantage estimates. Low values correspond to relying more on the current value estimate (which can be high bias), and high values correspond to relying more on the actual rewards received in the environment, which can be high variance (Schulman et al., 2016). The acceptable divergence threshold 
constrains the possible divergence between old and new policy update to ensure that the agent does not jump into a policy that generates nonsensical actions. Small values will stabilize the training procedure, but will slow the training process.
2.3 Neural controller
- position of both arm segments (2
3 elements); - velocity of both arm segments (2
3 elements); - angular velocity of both arm segments (2
3 elements); - rotation of both actuators, represented as a quaternion (2
4 elements); - position of the hand (three elements);
- position of the goal (three elements);
- identity of the predicted next target (one-hot encoding, four elements);
- target touched (one element).
The output layer determined the torques to be applied to the actuators.
2.4 Hyperparameters
For the current study, we used default values taken from the ml-agents package (Juliani et al., 2020) for both algorithm. To examine the influence of curiosity on learning, entropy coefficients are disabled or enabled (i.e., set to 0 or the default value in the ml-agents package, respectively).
2.5 Virtual environment and design
Over the course of an episode, stimuli in one of four possible target locations—equidistant from the agent—became active and appeared in the environment. Target activation was governed by a random sequence without repeats. Once a target became active, the robotic arm was to reach for and touch the target as quickly as possible. A visualization of the environment with an active target is shown in Fig. 2.
Once the active target was touched by the effector, no targets were visible to the agent for 250 time steps. That is, the next active target appeared after an interstimulus interval (ISI) of 250 time steps. A reward with a decaying value was associated with touch of the visible target to motivate quick and accurate movement. The decaying reward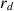 
for touching a target was 
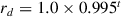, where t is the number of time steps since target onset, resetting after a new target appeared. The actual reward given to the agent was 
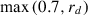. To speed up training, 20 agents were simulated in parallel in the same environment, and five simulation runs of these 20-agent environments were conducted. After 4000 time steps, each episode was ended and and a new episode started.
2.6 Learning process
In order to successfully train a reinforcement learner to sequentially reach for targets, the learner needs to be rewarded for touching a target. However, only providing positive reward when the agent touches a target can lead to the agent wildly swinging its arm around. This is one of the most simple behaviors to learn to solve the problem of sequential action: generating large random torque to each of the actuators will cause the hand of the arm to cover a large space, thereby inevitably touching the target at some point.
In the natural world, organisms are constrained by metabolic costs and placing too much stress on our actuators, and as such may be penalized for behaviors that expend excessive energy and/or apply surplus torque. To reduce the learning effort required for the robotic agent and improve credit assignment, we implemented curriculum learning as a method to guide agent training (Bengio, Louradour, Collobert, & Weston, 2009; Elman, 1993). Curriculum learning is commonly used to help an agent learn a complex task and is implemented by designing a training process that begins with the agent learning a simpler concept and then progressing to more complex, related concepts (Goodfellow, Bengio, & Courville, 2016). That is, earlier tasks or lessons are commonly made easier by guiding the agent, training the agent on simpler action–reward observations that can be used to bootstrap later learning. This basic strategy is widely known to accelerate progress in animal training within behavioral sciences (Skinner, 1958), where it is referred to as shaping. It is a method by which successive approximations of a target behavior are reinforced. By increasing or boosting the immediate reward, it is possible to encourage or discourage certain actions, the goal being to shape the reward so that intermediate actions are encouraged or discouraged.
We used curriculum learning to divide the simulation in two lessons. In the first lesson, the agent was given a decaying reward with an initial value of 1.0 for touching the target, as described above. No penalty was imposed for movement, in order to encourage the agent to explore the action space. After some delay the second lesson commenced, with the only change being an imposed penalty of −0.001 
the absolute distance of hand displacement in each time step. In the current study, we used delay values of 0 (immediate onset of second lesson), 400K, 800K, and 2M time steps. Thus, the agent was penalized for making inefficient or extraneous movements, encouraging optimized reaching to the target.
3 Results
We first examine the cumulative reward achieved by agents in each condition, before turning to characteristics of the agents' movements, including response times, distance traveled, and distance from the target. We generally focus our analyses on the time steps late in training (episodes 5–6 million), when performance has stabilized. All reported t-statistics are based on Welch's two-sample t-tests due to unequal distributions between conditions.
3.1 Cumulative reward
Fig. 3 shows the cumulative reward per episode across time steps. The curriculum learners with lesson two onset at time step 400K and 800K outperform learners with onset 0 and 2M, ts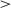 
2.44, ps 
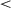.026. Overall, learners with very early (0) or very late (2M) onset performed worse than learners with intermediate (400K or 800K) onset. Also, these groups of learners show much larger variance, suggesting less stable training.
To test whether the variability in performance of these conditions differs, we compared standard deviations (SD) of cumulative reward from 100 split-half resamples, again examining time steps at the end of training (5–6 million). That is, for each condition, we randomly split the sample 100 times and calculated the SD of each split-half, resulting in 200 SDs per condition, which we then compared with t-tests. These comparisons confirmed that the 0-onset curriculum resulted in higher variability (mean resampled SD = 0.30) than either the 400K-onset (mean SD = 0.06; t(396) = 522.94, p 
.001) or the 800K-onset curriculum (mean SD = 0.04; t(331) = 679.05, p 
.001). The 800K-onset resulted in significantly lower variability in cumulative reward than the 400K-onset (t(346) = 75.42, p 
.001).
Fig. 4 shows that the condition with onset 0 resulted in two separate behavioral strategies, with a group of agents that spent a lot of time close to the optimal position, but remaining relatively still. Whereas the very best learners with onset 0 outperformed the 400K and 800K condition with scores as high as 0.720, as seen in the figure, the group remaining still received a mean cumulative reward of −0.019 and consists of both 0-onset and 2M-onset agents.
Overall, we see that having the curriculum onset during a Goldilocks period—not too early, and not too late—resulted in higher, less-variable performance: agents need some time to explore a large part of the action space and learn how to reach the rewarding targets, but need to learn not to make extraneous movements (through a penalty) before too long. While the very best agents may have come from the condition with onset 0, it is clear that avoiding early or late onsets leads to more stable training, with a higher probability of consistently developing a successful policy.
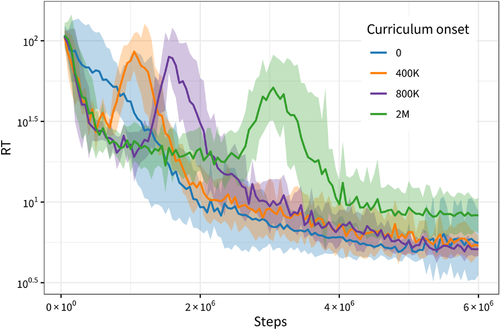
3.2 Response times
Fig. 5 shows response times (RTs) for different onsets of the second lesson. For all onset values, RTs decrease with training, indicating that agents succeed in learning to touch the targets. Examining the variability of agents' RTs in the final million episodes by comparing the SD of resampled splits of the data shows that 0-onset agents (mean resampled SD = 5.12) had significantly more variability than either 400K-onset agents (SD = 1.28; t(215) = 73.52, p 
.001) or 800K-onset agents (SD = 0.67; t(200) = 86.80, p 
.001). The 800K-onset agents also showed significantly less variability than the 400K-onset agents (t(232) = 56.89, p 
.001), suggesting that more time for initial unpenalized exploration results in more consistent response times post-curriculum. However, a too late onset seems to lead to slower RTs, as the 2M-onset learners are slower (M = 8.50) than the 400K (M = 5.39) and 800K (M = 5.12) learners, ts 
3.51, ps 
.007.
3.3 Movement characteristics
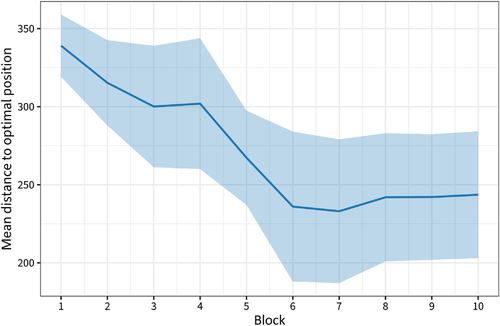
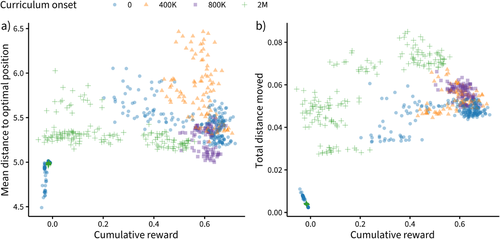
3.3.1 Distance to optimal position
Fig. 6a shows the mean distance to the optimal position, equidistant to all possible target locations. After training, both the 0-onset condition (M = 5.28) and the 800K-onset (M = 5.26) showed smaller distances to the optimal position than the 400K condition (M = 5.79), ts 
13.38, ps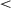 
.001, with no difference between the 0-onset and 800K-onset condition, t = 0.761, p = .447.
We examined the variability of agents' distance to the optimal position in the final million episodes by comparing the SD of 100 resampled splits of the data and found that 0-onset agents (mean resampled SD = 0.30) had significantly less variability than 400K-onset agents (SD = 0.34; t(312) = 28.83, p 
.001), while 800K-onset agents showed significantly less variability (SD = 0.14) than either 0-onset agents (t(334)= 189 , p 
.001) or 400K-onset agents (t(246) = 148.19, p 
.001).
3.3.2 Total distance moved
Fig. 6b shows the mean absolute distance moved per time step for different curriculum onsets. For all conditions except 0-onset, movement initially increased as the learner started exploring the action space. The onset of the second curriculum lesson induced a strong decrease of extraneous movement. The learners with onset 0 showed a smaller total distance moved (M = 0.034) than the curriculum learners with onset 400K (M = 0.053), t(16.82) = 3.19, p = .005.
Examining the variability of agents' total distance moved in the final million episodes by comparing the SD of resampled splits of the data shows that 0-onset agents (mean resampled SD = 0.02) had significantly more variability than either 400K-onset agents (SD = 0.005; t(359) = 414.1, p 
.001) or 800K-onset agents (SD = 0.004; t(331) = 679.05, p 
.001). The 800K-onset agents also showed significantly less variability than the 400K-onset agents, t(359) = 54.68, p 
.001, suggesting that more time for initial unpenalized exploration results in more consistent amounts of total distance moved after training.
The optimization strategy of PPO with curriculum learning seems similar to our earlier findings (de Kleijn et al., 2018b) in which humans optimize sequential reaching behavior, which was also found by Dale et al. (2012) and Duran & Dale (2009). PPO with curriculum learning, but not without curriculum learning, shows a similar optimization. As the sequence in the current study is randomly determined, an optimal strategy is to move to a position equidistant to all possible stimuli as is visible in Fig. 6b. In the case of PPO, the training starts with an initial phase in which the action space is explored. This is obviously not necessary with adult humans, as most are well aware of the available action space using a computer mouse.
4 Discussion
The present study investigated the learning of a simple time-pressured sequential reaching task in a 3D environment with simulated physics and a double-articulated arm with actuated joints, expecting to find that deep RL agents would learn to recenter their effector during the ISI in order to minimize the expected distance to the next target. However, we found that centering behavior—which is characterized by relatively little overall movement combined with a small average distance to the optimal position and high reward—most visibly emerged for agents for which the curriculum onset was neither early nor late. In other words, there seems to be a critical period for curriculum onset that leads to best performance. Critical periods in human development—where new skills are easy to acquire only within a specific time window, not earlier or later—have been hypothesized and investigated in a variety of domains (for a review, see Bornstein, 2014). In this curriculum, agents were first rewarded for reaching targets, and only later given a penalty for extraneous movement. Without a movement penalty, agents tended to learn a strategy of swinging their arm wildly to touch any target that might appear. If the movement penalty was included at the beginning of training, agents tended to fail to explore the action space enough to learn to reach the targets consistently, although a few lucky agents managed to escape this regime. If the movement penalty was introduced too late, agents became too set in their ways and failed to adjust their behavior for the new penalty. Only when the movement penalty was introduced after the agents had a brief “childhood” of unpenalized exploration, and before they had fully optimized goal reaching in this state, did they consistently learn to reach the target without making extraneous movements.
What does this tell us about human action learning, and what does it tell us about learning and executing everyday action? First, it is notable that the curriculum-trained deep RL agents—more cognitively plausible and in a more physically realistic simulator than the neural agents in de Kleijn et al. (2018a)—ultimately arrive at the same centering behavior observed in adults in unpredictable trajectory serial response tasks (Dale et al., 2012; de Kleijn et al., 2018b). Second, on the surface, there seems to be some relation between this staged learning and the motor babbling observed in young infants, in whom random motor movements appear to be intrinsically motivated, and which result in exploration of the action space (Baranes & Oudeyer, 2013). Motor babbling has been hypothesized to be a necessary component of developing goal-directed behavior (Lee, 2011), and more generally it has been observed that infants show more exploratory behavior than older people (Gopnik et al., 2017). This shift away from exploratory behavior may result from a variety of factors, from the need to optimize movements due to increasing time pressure as we age, or from degradation of joints and actuators, to changing intrinsic valuation of new exploratory actions versus already-learned goals.
While in the present study we implemented a change in the training goal at an arbitrary time point, it is worth noting the possibility that agents could be put in charge of shaping their own curriculum, as infants are hypothesized to be to a large extent (Smith, Jayaraman, Clerkin, & Yu, 2018). Also, it remains to be seen what the effect of gradual versus sudden reward changes is on the learning process, as is often used in curriculum learning. Finally, it should be noted that in our earlier research on evolving neural controllers, curriculum-based learning was likely unnecessary due to the lower dimensionality of the action and effector spaces: the greater complexity and realism of the 3D environment may more accurately represent the learning problem that infants initially face.
This work represents only the first exploratory steps toward a full understanding of humans as learners of complex sequential action. As such, many questions remain unanswered.
For example, additional curriculum steps are needed in order for the deep RL agents to become sensitive to predictive information? It has been found that until 9 months of age, infants fail to show the anticipatory grasp adjustments that adults show as they reach for objects (Rosenbaum, 1991). One explanation could be that the cognitive effort required to perform the reaching movement at all prevents optimization from taking place. Only when the reaching movement has been well-trained does cognitive capacity become available to optimize movement. The current study suggests that premature optimization can indeed interfere with later performance. The relationship between symbolic prediction and subsymbolic optimization has been the subject of ample studies (for an overview, see de Kleijn, Kachergis, & Hommel, 2014). At the highest level, discrete actions (e.g., “pour coffee into a mug” or in the current study “move to target 2”) can be learned and predicted. However, in the current study, no true prediction can occur due to the uniformly random target probabilities. Indeed, it is exactly this lack of predictability that gives rise to our described results. In a deterministic task, for example, Nissen and Bullemer's original SRT in a trajectory paradigm (de Kleijn et al., 2018b), the next target could be predicted perfectly, resulting in predictive movement toward the target. Future studies could integrate the symbolic prediction process and the resulting subsymbolic motor optimization process.
Aside from the curriculum needed to learn the optimal centering strategy in situations where the next target's location is uncertain, what behaviors are learned when the target sequence become predictable, either deterministically or probabilistically? Earlier research has shown that the manipulation of target probability, by making one target more likely to appear than others, leads to a shift in resting location away from the center toward the more probable target. The PPO algorithm used would be expected to show similar behavior, as the received reward is a function of the distance of the target to the position of the arm at target onset by means of reward decay. Of course, everyday action is characterized by non-uniform transition probabilities between actions, most notably between and within subactions. Future research could elaborate on how agents decide their resting location in different temporal positions of a sequence in a hierarchical task, as target probabilities can (and in real life, will) change when approaching subtask boundaries, a phenomenon also involved in word segmentation during language learning, where within-word syllables have higher transition probabilities than between-word syllables.
If there are high-level goals such as setting a table, in which the order of some steps does not matter (e.g., placing the plates vs. the silverware), do agents show the flexibility that people show, or do they need to be given demonstrations in order to generalize appropriately? It has been argued (e.g., Cooper & Shallice, 2006) that goals play a role here, although this has not been the subject of the current study. In the current study, this could fundamentally be learned through the used reward function. However, it seems unlikely that humans learn this temporal independence through observation or reward, as infants are not often exposed to their caregivers pouring the coffee without getting a mug first, let alone try it themselves. A better explanation would be through the use of a world model, discussed next.
Is intrinsic motivation for exploration combined with a rich repertoire of goals sufficient to create agents that self-curricularize to achieve more complex goals and higher rewards, or does the environment also need to change? Researchers have recently explored training agents via self-play (e.g., Lee, Kim, Choi, & Lee, 2018) as one way of generating steadily more sophisticated situations (self-curricularized) and resulting behaviors. Other approaches have built agents that implement not only an action selection model but also a world model, which makes predictions about the effects of the agent's actions on the world (as perceived by the world model), supplying an objective (predicted vs. actual outcomes) on which different forms of curiosity can be tested (e.g., Haber, Mrowca, Wang, Fei-Fei, & Yamins, 2018). Although these questions remain unanswered so far, we believe that virtual robot environments hold promise to help study these topics, providing valuable data for both machine learning researchers and cognitive scientists.
