Spatial prediction of poverty in Gauteng province (South Africa) in-between Censuses using land use datasets
Abstract
To realize the first sustainable development goal of ending “poverty in all its forms everywhere,” local governments in South Africa need to implement informed targeted policy interventions based on up-to-date data and sound analytics. Statistics South Africa (Stats SA) Censuses reveal the socioeconomic circumstances of people living in South Africa but are only conducted every 10 years. As a result, most analytical studies done in-between Censuses rely on outdated socioeconomic data. This study demonstrates how poverty levels in one of the provinces of South Africa, Gauteng, can be predicted when up-to-date Census datasets are not available. The spatial lag model is used to explain the relationship between the South African Multidimensional Poverty Index (SAMPI) and statistically significant variables extracted from land use datasets (i.e., land areas classified as built-up, informal, residential, township, and non-urban), and to ultimately predict the levels of poverty. Out-of-sample predicted poverty levels obtained based on the spatial lag model correlate with the actual levels of poverty thereby reflecting known spatial patterns of the levels of poverty in Gauteng province.
1 INTRODUCTION
Poverty remains a socioeconomic challenge that continues to plague many countries in the developing world. The dire consequences of poverty have triggered concerted global efforts to eradicate it. The first United Nations Sustainable Development Goal of ending “poverty in all its forms everywhere” is a clear example of the world's commitment to addressing poverty. However, such global efforts can only materialize through regional, country-wide, and local initiatives and targeted policy interventions. In South Africa, more than half (50%) of the population lived in poverty in 2015 (Stats SA, 2017a). The hard lockdown restrictions due to COVID-19 further contributed to an increasing unemployment rate that South Africa continues to grapple with to date. The outcomes of a national longitudinal household survey conducted by the National Income Dynamics Study (NIDS) in 2020, estimated a substantial increase in poverty for individuals who had lost their jobs (Jain et al., 2020). In a country where there is a multitude of needs and interests competing for few resources, the South African government's efforts toward alleviating poverty need to be guided by evidence-based policies for targeted interventions. Hence, a need for reliable socioeconomic data and statistics to support and promote informed and evidence-based policy formulation.
Statistics South Africa (Stats SA) Censuses reveal the socioeconomic circumstances of people living in South Africa but are only conducted every decade. Logistical considerations and high operational costs are among the reasons that contribute to Censuses being conducted only once every 10 years. Although community surveys are conducted in-between Censuses, the output datasets of such surveys are representative at larger scales of data aggregation (e.g., at the municipal and provincial levels only). In contrast, policy makers in government implement policies and programs geared toward poverty alleviation based on administrative boundaries such as the ward (a unit of data aggregation lower than the municipality). For example, in Gauteng province, 50 wards named “fifty priority wards” were selected for targeted poverty alleviation policies as part of the “service delivery war room” program initiated by the provincial government in 2012 (Wray & Storie, 2012). In the absence of up-to-date socioeconomic data, such as those provided by Stats SA, it becomes a challenge to formulate evidence-based policies that can appropriately inform the implementation of programs to address current poverty issues at a granular level of administrative boundaries such as the ward. For example, the South African Multidimensional Poverty Index (SAMPI), which is employed as a multidimensional approach to measuring poverty in South Africa at the ward level, was constructed based on Census data collected in 2011 (Stats SA, 2014).
Traditional ways of collecting data (e.g., Census surveys) for assessing socioeconomic outcomes such as poverty are costly. Data collected from satellite imagery can be used as a passive and less expensive means for analyzing socioeconomic circumstances and predicting poverty when national Censuses or other demographics are outdated, not available, or not accessible (Jean et al., 2016). One of the early direct applications of remotely sensed imagery in the social science domain is the work by Hall et al. (2001) who used land cover and GIS to identify pockets of urban poverty in Argentina. Back then (i.e., in the 90s), the temporal and spatial resolutions of remotely sensed images were not as high as they are today.
Satellite imagery is increasingly available at higher spatial and temporal resolutions and its use as a proxy for estimating or predicting economic activities and ultimately poverty is expanding (Xu et al., 2021). For example, poverty has been predicted based on the relationship between the intensity of nighttime light (visible on satellite imagery) and a measure of poverty computed from socioeconomic variables (Jean et al., 2016; Okaidat et al., 2021; Perez et al., 2017; Xie et al., 2016; Xu et al., 2021; Yeh et al., 2020). This confirmed the assumption that a greater intensity of light at night in an area is associated with lower levels of poverty. Researchers also confirmed that the physical environment represented through human settlements, land use, land cover, etc., in which people live, reflects their respective socioeconomic circumstances (Duque et al., 2015; Jean et al., 2016; Perez et al., 2017; Xie et al., 2016). An interesting example is the one by Peng et al. (2023) who proposed a set of composite slum spectral indices for mapping slums in Mumbai, India. While employing remotely sensed images to predict poverty, some studies have also explicitly acknowledged the spatial heterogeneity of features on the landscape. These include Li et al. (2023) who proposed a “point-to-region co-learning” framework that considers the characteristics of neighbouring features to predict low-income areas in Kenya. Pettersson et al. (2023) employed publicly available satellite imagery to develop an algorithm that considers the geographical and temporal characteristics of features to predict poverty in selected countries in Africa (including South Africa). Alongside socioeconomic, demographic, and other relevant spatial and non-spatial data, Akinyemi (2010) mentioned land cover as a common dataset for measuring and assessing poverty. These studies inspired this investigation into the use of satellite imagery for estimating and predicting poverty in South Africa.
While regional and country-level analyses (e.g., Jean et al., 2016; Okaidat et al., 2021; Perez et al., 2017; Xie et al., 2016) are very relevant for continental or global initiatives such as those led by the World Bank and other international organizations (e.g., USAID), transferability of the methods employed for modeling and/or predicting poverty within individual countries at a granular level of data aggregation poses a challenge. For example, Pettersson et al. (2023) extended Yeh et al. (2020)'s algorithm to devise a model capable of learning from geographical and temporal features. However, Pettersson et al. (2023)'s algorithm exhibited lower performance for South Africa due to fewer collected samples.
A specific mention of the lack of suitability of nighttime light in the context of South Africa needs to be highlighted. Figure 1 shows the yearly average nighttime light intensity across South Africa. Looking at the entire country, it is mostly characterized by low nighttime light intensities, except for a few urban areas. Typically, nighttime light mirrors the urban footprint, regardless of the varied socioeconomic circumstances of the population. In other words, nighttime light does not always discriminate between poor and rich areas, making its use inefficient in predicting poverty in the context of South Africa. Hence, with minimal spatial variation of nighttime light in both urban and non-urban areas (refer to Figure 1), it becomes a challenge to obtain reliable models that can describe the relationship between the intensity of light at night and poverty measured by the SAMPI. Given these reasons, nighttime light was not considered as a potential predictor of poverty in the analyses performed in this study.
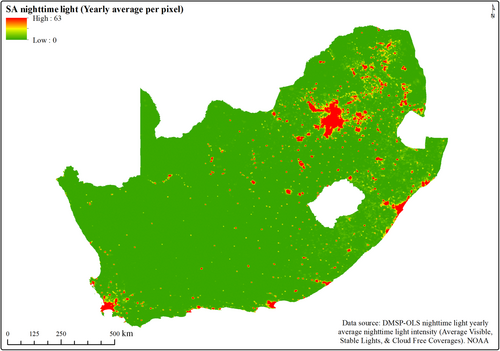
Furthermore, in the context of developing countries (e.g., South Africa), limitations such as the low resolution of nighttime light imagery and the high monetary cost involved in the acquisition of high-resolution day-time imagery, make it a challenge to implement or replicate country-level studies, such as the ones conducted by Jean et al. (2016), and Xie et al. (2016), at a finer granularity. Although Perez et al. (2017) and Yeh et al. (2020) have proposed the use of freely available day-time imagery (e.g., Landsat images), the interpretability of their results impairs the adoption of such studies for policy formulation and implementation.
The complexity of artificial intelligence (AI) and machine learning algorithms lies in the difficulties of fully interpreting the deep learning algorithms developed to adequately address specific challenges in predictive analytics. For example, Barbierato and Gatti (2024) highlight the difficulties in understanding how complex and multilayered neural network models arrive at a particular decision based on a combination of multiple factors. Machine learning algorithms consume information, in our case properties of remotely sensed imagery such as reflectance, that is less interpretable in the context of describing the drivers of poverty. This study therefore employs a national land cover dataset that has already been classified into intuitive land use classes. The aim is to model the relationship between the built-environment variables extracted from the South African national land cover datasets and the SAMPI at the ward level, with Gauteng province as an example. The analysis is performed at a granular level by using the ward as the spatial unit of data aggregation.
Several studies have employed (non-spatial) regression models in the prediction of poverty using satellite imagery (e.g., Pan & Hu, 2018; Xu et al., 2021; Yong et al., 2022). However, they ignored misspecifications that might occur due to induced spatial autocorrelation observed in data aggregated at a spatial unit, for example, county, ward, or municipality. When employed on spatially aggregated data, linear regression models fail to address a model misspecification manifesting itself in spatially autocorrelated residuals. This results in the violation of the Gauss–Markov assumption of linear regression: independence of the error terms (Griffith & Paelinck, 2011). In their identification of predictors of child poverty in the United States, Voss et al. (2006) used spatial regression models to explicitly highlight the deficiencies of failing to incorporate spatial effects in the modeling process when ordinary least squares regression models are used. Hence, this study incorporates spatial dependence in the analysis by employing a spatial regression model. Akbar et al. (2022) also employed spatial regression models to explain poverty, but their independent variables were extracted from a field-based survey of rural infrastructure in Pakistan. Similarly, David et al. (2018) based their spatial regression modeling exercise on the 2011 Stats SA Census data when explaining potential causes of poverty patterns among the 234 municipalities in South Africa. Neither of these mentioned studies made use of satellite imagery. A few exceptions include Pokhriyal and Jacques (2017) who modified the kernel function of their Gaussian process regression model to include the spatial distances between centroids of polygons when predicting poverty, based on variables extracted from remotely sensed imagery and other relevant socioeconomic and environmental datasets. However, the spatial lag model was suitable for explaining and ultimately predicting poverty in this study.
Hence, this study makes the case for a spatial regression model to explain and predict poverty based on covariates extracted from freely available land use datasets in the context of Gauteng province. Furthermore, this study proposes a suitably fitted spatial lag model to perform an out-of-sample prediction of poverty using variables extracted from land use datasets.
- Addressing the challenges of having to rely on outdated Census data to determine the levels of poverty in the province of Gauteng, South Africa. Hence, this study proposes an approach for predicting or estimating poverty when up-to-date Census datasets are not available. This approach can easily be replicated in other provinces of South Africa and other parts of the world with similar socioeconomic conditions as Gauteng province.
- Highlighting existing shortcomings of current studies (e.g., Pan & Hu, 2018; Xu et al., 2021; Yong et al., 2022) that have employed regression models that ignore spatial dependence in their respective formulation when predicting or explaining poverty using remotely sensed data (e.g. land cover). This is done in order to propose the use of a spatial regression model that incorporates spatial dependence in its functional form.
In spatial regression analysis, spatial prediction can be performed in- or out-of-sample (Goulard et al., 2017). In the case of in-sample predictions, values for the independent variables and the dependent variable are known a priori, while with out-of-sample predictions, known values of the independent variables are used to predict unknown values of the dependent variable based on a model that was constructed based on known values of the independent variables and the dependent variable. Most studies we have reviewed from the literature focussed on in-sample predictions (e.g., Akbar et al., 2022; David et al., 2018; Kamenetsky et al., 2019), which limits the predictions to data that are known to the model. In this study, we also conducted an out-of-sample prediction analysis, which is essential for predicting poverty when up-to-date Census datasets are not available. To the best of our knowledge, this is the first study that employs a spatial regression model using built-environment variables derived from satellite imagery to predict poverty in South Africa. Compared with other methods, this is less complex to implement and explain, and also more cost-efficient. The remainder of this article is structured as follows: Section 2 describes the study area, presents the datasets that were used, and explains how poverty estimation and prediction was done. Results are presented and discussed in Section 3, with concluding remarks in Section 4.
2 STUDY AREA, DATA, AND METHOD
2.1 Study area
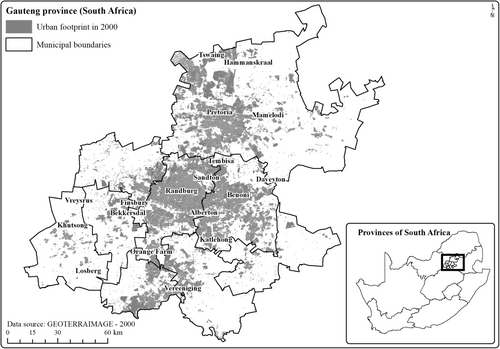
As the economic hub of South Africa with its 34% share of the country's total GDP (Stats SA, 2017b), Gauteng is regarded as a place of socioeconomic opportunities. This makes Gauteng a milieu of constant in-migration which puts pressure on the availability, efficiency, and quality of the province's service infrastructure. For these reasons, Gauteng was selected as the study area of choice for studying poverty in South Africa. Future work could expand poverty estimates and predictions to other provinces. Figure 2 illustrates the geographic location of Gauteng province in South Africa, with its urban footprint in the year 2000, and municipal boundaries. The government implements poverty alleviation policies based on the ward, an administrative boundary at a level lower than the municipality (Wray & Storie, 2012). The analysis performed in this study was based on 508 wards in Gauteng province, as per the administrative boundaries of South Africa demarcated in 2011 (MDB, 2023). However, since 2016, there are 529 wards in Gauteng province (MDB, 2023). Nevertheless, the 508 wards were considered because the computed SAMPI dataset is available based on the 2011 ward demarcated boundaries.
2.2 Data description
2.2.1 The South African Multidimensional Poverty Index (SAMPI)
SAMPI is a multidimensional index of poverty based on Census data collected in 2001 and 2011 in South Africa. It is a linear combination of socioeconomic variables, constructed by following the “Alkire-Foster” methodology (Alkire & Foster, 2011). The flexibility of the “Alkire-Foster” methodology enabled the adjustment of indicators and the inclusion of an additional dimension (i.e. economic activity) in the construction of the SAMPI (Stats SA, 2014). Table 1 provides the list of indicators, dimensions, and deprivation cutoffs considered in the construction of the SAMPI. Dimensions are weighted equally (1/4 per dimension). Similarly, there is an equal share of the weight assigned to a dimension among all of its indicators.
| Dimension | Indicator | Weight | Deprivation cut-offs |
|---|---|---|---|
| Health | Child mortality | 1/4 (25%) | If any child under the age of 5 has died in the past 12 months |
| Education | Years of schooling | 1/8 (0.125%) | If no household member aged 15 or older has completed 5 years of schooling |
| School attendance | 1/8 (0.125%) | If any school-aged child (aged 7 to 15) is out of school | |
| Standard of living | Fuel for lighting | 1/28 (0.036%) | If a household is using paraffin/candles/nothing/other |
| Fuel for heating | 1/28 (0.036%) | If a household is using paraffin/wood/coal/dung/other/none | |
| Fuel for cooking | 1/28 (0.036%) | If a household is using paraffin/wood/coal/dung/other/none | |
| Waster access | 1/28 (0.036%) | If no piped water in a dwelling or on a stand | |
| Sanitation type | 1/28 (0.036%) | If not a flush toilet | |
| Dwelling type | 1/28 (0.036%) | If an informal shack/traditional dwelling/caravan/tent/other | |
| Asset ownership | 1/28 (0.036%) | If a household does not own more than one radio, television, telephone, or refrigerator and does not own a car | |
| Economic activity | Unemployment | 1/4 (0.125%) | If all adults (aged 15–64) in the household are unemployed |
A household is defined as being multidimensionally poor if a third or more of its indicators satisfy the 11 indicators' deprivation cut-offs. The proportion of multidimensionally poor households within a given ward constitutes the headcount or prevalence of poverty. The intensity (or acuteness or depth) of poverty is the average percentage of deprivations (i.e., the indicators that satisfy deprivation cut-offs) experienced by multidimensionally poor households within a given ward. The SAMPI is then obtained by computing the product of the intensity of poverty and the headcount. A full report on the SAMPI can be obtained from StatsSA's website (Stats SA, 2014).
2.2.2 Land use
This study employs two sets of land use data: the 2000 and 2013–2014 land use datasets. The 2000 land use dataset is based on Landsat images collected in 2000, 2001, and 2002 (GEOTERRAIMAGE—2014) (GCRO, 2024). The 2013–2014 land use dataset is a subset of the 2013–2014 South African National Land Cover (SANLC) dataset, which is made available freely and openly by the Department of Forestry, Fisheries and the Environment (DFFE) in South Africa (DFFE, 2024). The 2013–2014 SANLC dataset is based on the 2013 and 2014 Landsat images. The 12 land use classes listed in Table 2 were considered in the analysis performed in this study. Land use classes 1–11 are collectively classified as urban land cover. The proportion of a ward area covered by each of the 12 land use classes was hypothesized as a potential explanatory variable of the SAMPI.
| Land use class (ward area proportion) | Description | |
|---|---|---|
| 1 | Commercial | Includes commercial, offices, government, health facilities, train stations, churches, may include residential flats, etc. |
| 2 | Industrial | Industrial, power stations, etc. |
| 3 | Residential | Formal residential housing, townhouses, hostels complexes, flats, etc. |
| 4 | Township | Townships and RDP housing |
| 5 | Informal | Informal residential housing |
| 6 | Smallholding | Smallholdings and small farms |
| 7 | Village | Traditional villages |
| 8 | Sport and golf | Sports fields and golf courses, exclude school sports fields |
| 9 | School and sport grounds | School buildings and school sports grounds |
| 10 | Built-up | Any areas of which the classification is unknown, runways/airports and associated buildings, holiday chalets, cemeteries, etc. |
| 11 | Mine buildings | Mine buildings |
| 12 | Non-urban | Includes: bare (non-vegetated) land, erosion, mines water permanent, mines water seasonal, mines (bare and semi-bare), plantation, cultivated land, low shrubland, shrubland fynbos, grassland, woodland/open bush, thicket/dense bush, indigenous forest, wetlands, water permanent and water seasonal |
2.3 Data preparation
The analysis distinguishes between two sets of data as presented in Table 3 with their corresponding variables. These two datasets have been aggregated at the ward level. In 2011, there were 508 wards in Gauteng but only 497 wards were considered for the analysis. Eleven wards were excluded from the analysis because of missing indicators of poverty or extremely low levels of poverty (i.e., negligible values of the SAMPI).
| Dependent variable | Dataset 1 | Dataset 2 |
|---|---|---|
| Year: 2001 | Year:2011 | |
| South African Multidimensional Poverty Index (2001) | South African Multidimensional Poverty Index (2011) | |
| SAMPI 2001 | SAMPI 2011 | |
| Independent variables/covariates | Land use class (ward area proportion) based on 2000 Landsat Images | Land use class (ward area proportion) based on 2013/2014 Landsat Images |
| Commercial | Commercial | |
| Industrial | Industrial | |
| Residential | Residential | |
| Townships | Townships | |
| Informal | Informal | |
| Smallholdings | Smallholdings | |
| Villages | Villages | |
| Golf courses and sports ground | Golf courses and sports ground | |
| Schools (and sports ground) | Schools (and sports ground) | |
| Mines | Mines | |
| Built-up | Built-up | |
| Non-urban | Non-urban |
The first set of data (i.e. “Dataset 1”) is composed of the 2001 SAMPI as the dependent variable for each ward, and 12 covariates extracted as land use classes from the 2000 land use data. Being a land use class, each covariate is quantified as the proportion of land area it covers in each of the 497 wards. The same description applies to “Dataset 2” with the exception that the dependent variable is the 2011 SAMPI for each ward, and the covariates have been extracted from the 2013/2014 land use data.
2.4 Methodology and approach
The methodological approach adopted in this study consists of three main analytical processes, namely, model selection, model training, and prediction. As presented in Table 3, two sets of data, namely, “Dataset 1” and “Dataset 2” were considered for the analysis. The first dataset (i.e., “Dataset 1”) was used for selecting and training the appropriate model (i.e., the spatial lag model) which was subsequently employed to perform both in-sample and out-of-sample prediction of poverty. The in-sample prediction process used selected covariates from “Dataset 1,” while the “out-of-sample” prediction process was based on corresponding selected variables extracted from “Dataset 2.” Hence, the model selection and training process was only based on variables extracted from “Dataset 1”.
2.4.1 Model selection
The model selection process was guided by an exploratory spatial data analysis (ESDA) which is essential for discovering spatial autocorrelation and spatial heterogeneity in the data. More importantly, in the context of regression analysis, an ESDA serves the purpose of identifying possible misspecifications in the statistical models considered for the analysis (Chi & Zhu, 2008). At first, the dependent variable (i.e., “SAMPI 2001” from the first dataset, i.e., “Dataset 1”) was transformed to closely conform to the assumption of normality. In particular, the choice of the Box-Cox transformation was motivated by the need to adhere to the Gauss–Markov assumptions of linear regression analysis (Box & Cox, 1964).
To obtain a parsimonious regression model that also eliminates multicollinearity, a stepwise regression analysis was performed. This resulted in the reduction of the original set of 12 variables to a set of five statistically significant variables, namely, “Informal,” “Non-urban,” “Residential,” “Built-up,” and “Townships” which were free of any multicollinearity problem. Even though the residuals of the reduced multiple regression model were normally distributed after the Box-Cox transformation of the dependent variable (i.e. “SAMPI 2001”), it became clear that a spatial regression model would be appropriate since the residuals exhibited statistically significant patterns of spatial autocorrelation.
The outcome of the ESDA and detailed scrutiny of the baseline ordinary least squares (OLS) model led to the selection of the spatial lag model as the most appropriate for this study. This decision was based on the results of the Lagrange multiplier tests as prescribed by Anselin (1988, 2005). Hence, this study employs a spatial regression model that incorporates a spatially lagged dependent variable as one of its covariates.
The spatial lag model assumes a global spillover effect due to the interaction among agents, regions, or processes in space (LeSage, 2014). In spatial regression analysis, a spillover occurs when changes in an independent explanatory variable in a given region result in changes in the dependent variable in neighboring regions (Golgher & Voss, 2016). Such changes could be restricted locally within a neighborhood (i.e., local spillover effect) or they could propagate to an entire study area (i.e., global spillover). The spatial lag model is used to model phenomena that may result in a global spillover. In this study, we used the spatial lag model for modeling poverty because the results of an ESDA, namely, the local indicator of spatial association (LISA), revealed clusters of poverty localized in specific neighborhoods in Gauteng (see Figure 3). The results of LISA have been further confirmed by the empirical results of the Lagrange multiplier tests on the residuals of the baseline OLS regression model which suggest that a spatial lag term should be incorporated in the specification of the spatial regression model.
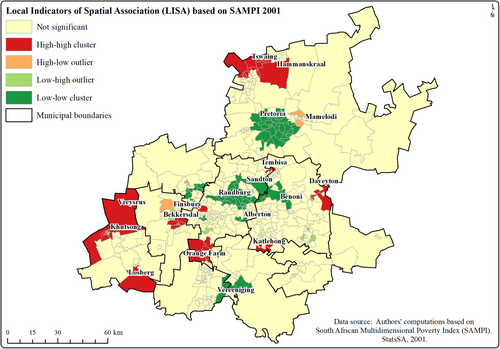
Our approach is further motivated by Golgher and Voss (2016) who argued that a well-defined theoretical model should inform the choice for an empirical spatial model. Theory suggests that poor households may be constrained to specific neighborhoods due to shared socioeconomic conditions such as limited housing stocks and/or offerings or scarce employment opportunities. Voss et al. (2006) refer to these types of socioeconomic constraints as a grouping of forces that may be responsible for the observed patterns of spatial autocorrelation in the dependent variable (i.e., poverty). Hence, our approach is grounded on both theoretical and empirical foundations. Furthermore, in comparison to the black box of machine learning methods, the results from a statistical model such as a spatial lag model can be explained, which facilitates adoption by policymakers and the public in general.
When the values ρ and Θ are not different from zero, the SEM is obtained. The SEM is appropriate when the spatial dependence in the dependent variable is not substantive. However, the significant pattern of spatial autocorrelation observed in the error term is a nuisance that the SEM addresses. The spatially lagged X (SLX) model is obtained when the values of ρ and λ are not different from zero. Unlike the other spatial regression models which require the method of maximum likelihood to estimate the model parameters, the parameters of the SLX can be estimated based on the OLS method. The SDM is obtained when the value of λ is not different from zero. The SDM is appropriate when spatial dependence is substantive in both the dependent and independent variables. Conversely, when spatial dependence is not substantive in the dependent variable with the value of ρ = 0, the SDEM is obtained. Lastly, when Θ = 0, the Kelejian-Prucha model is obtained. The “in-sample” and “out-of-sample” predictions of these models were compared with those of the spatial lag model.
2.4.2 Model training and prediction
As already mentioned at the beginning of Section 2.4.1., the spatial lag model was trained based on the 2001 SAMPI as the dependent variable, and the independent variables were extracted from the 2000 land use dataset (i.e., “Dataset 1”) as described in Table 3. The trained spatial lag model was used to perform in-sample and out-of-sample predictions. The out-of-sample prediction of poverty (i.e., predictions of poverty in 2011) was based on the covariates extracted from the 2013–2014 version of the land use dataset (i.e., “Dataset 2”). Laurent and Margaretic (2021) also performed a similar analysis but considered polygons with missing data as suitable candidates for out-of-sample spatial prediction of unemployment based on a selection of relevant independent socioeconomic variables in France.
Equation (4) is derived from the convenient rearrangement of the spatial lag model (see Equation (2)) to have all the known parameters and variables on the right-hand side while the unknown variable to be predicted (i.e., the dependent variable term) is kept on the left-hand side.
It should be noted that land use datasets produced from land cover datasets strictly obtained in 2001 and 2011 were not readily available at the time this study was conducted. Hence, the explanatory variables represent the best possible approximation of land use classes in 2001 and 2011, respectively. This limitation should be addressed in future work, for example, by producing land cover/use datasets for the missing years to fill in the gaps of the authoritative “South African National Land-Cover Datasets” made freely and publicly available by the Department of Forestry, Fisheries and the Environment in South Africa (DFFE, 2024).
3 RESULTS AND DISCUSSION
3.1 Exploratory spatial data analysis (ESDA)
Table 4 provides values of the Pearson correlation coefficient between the dependent variable (i.e., SAMPI in 2001 and 2011) and each of the hypothesized explanatory variables for the respective year. The directions of the positive or negative relationship between the SAMPI and each of the hypothesized explanatory variables appear as expected. The variable that represents land use classified as “Informal” has a higher correlation coefficient value with the SAMPI in 2001 and 2011 (0.434 and 0.37 respectively) compared with the remaining explanatory variables mentioned in Table 4. There is a change in the strength of the correlation between “Informal” land use and poverty from 0.434 in 2001 to 0.37 in 2011. Such a decrease could be attributed to some of the policy reforms adopted by the South African government right after the dawn of democracy in 1994. One such policy is the housing program of the reconstruction and development plan (RDP) which promoted the construction of millions of formal houses for the previously disadvantaged population in South Africa (Harrison & Todes, 2015). Subsequent related initiatives include the Informal Settlement Upgrading Program which was adopted in 2004 (Huchzermeyer, 2009). Also, as expected, the relationship between poverty and Golf courses and sports grounds, commercial land, built-up areas, and residential areas is negative, suggesting that such areas are associated with low poverty levels.
| Land use class (ward area proportion) | SAMPI 2001 | p-value (at 5% level of significance) | SAMPI 2011 | p-value (at 5% level of significance) |
|---|---|---|---|---|
| Informal | 0.434 | 0.00 | 0.37 | 0.00 |
| Non-urban | 0.274 | 0.00 | 0.336 | 0.00 |
| Villages | 0.057 | 0.208 | 0.031 | 0.489 |
| Townships | 0.149 | 0.00 | 0.003 | 0.953 |
| Mines | −0.074 | 0.099 | 0.126 | 0.005 |
| Smallholdings | −0.064 | 0.153 | 0.067 | 0.138 |
| Industrial | −0.074 | 0.099 | −0.065 | 0.148 |
| Golf courses and sports grounds | −0.289 | 0.00 | −0.261 | 0.00 |
| Commercial | −0.264 | 0.00 | −0.263 | 0.00 |
| Schools (and sports ground) | −0.124 | 0.006 | −0.192 | 0.00 |
| Built-up | −0.249 | 0.00 | −0.251 | 0.00 |
| Residential | −0.624 | 0.00 | −0.518 | 0.00 |
The descriptive statistics of the hypothesized explanatory variables are provided in Tables 5 and 6. The levels of poverty decreased from 2001 to 2011, as can be seen from the mean of the SAMPI per ward decreasing from 0.47 in 2001 to 0.02 in 2011.
| Land use class (ward area proportion) | N | Mean | SD | Min | q.25% | q.50% | q.75% | Max |
|---|---|---|---|---|---|---|---|---|
| SAMPI 2001 | 508 | 0.047 | 0.053 | 0 | 0.006 | 0.03 | 0.073 | 0.29 |
| Commercial | 508 | 0.037 | 0.06 | 0 | 0.004 | 0.018 | 0.048 | 0.576 |
| Industrial | 508 | 0.017 | 0.048 | 0 | 0 | 0 | 0.007 | 0.431 |
| Residential | 508 | 0.149 | 0.208 | 0 | 0 | 0.033 | 0.215 | 0.761 |
| Townships | 508 | 0.16 | 0.243 | 0 | 0 | 0.003 | 0.295 | 0.883 |
| Informal | 508 | 0.055 | 0.146 | 0 | 0 | 0 | 0.022 | 0.92 |
| Smallholdings | 508 | 0.034 | 0.094 | 0 | 0 | 0 | 0.005 | 0.711 |
| Villages | 508 | 0.006 | 0.044 | 0 | 0 | 0 | 0 | 0.667 |
| Golf courses and sports ground | 508 | 0.011 | 0.026 | 0 | 0 | 0 | 0.009 | 0.243 |
| Schools (and sports ground) | 508 | 0.036 | 0.039 | 0 | 0.006 | 0.02 | 0.054 | 0.194 |
| Mines | 508 | 0 | 0 | 0 | 0 | 0 | 0 | 0.001 |
| Built-up | 508 | 0.034 | 0.057 | 0 | 0.008 | 0.02 | 0.037 | 0.594 |
| Non-urban | 508 | 0.461 | 0.282 | 0 | 0.221 | 0.394 | 0.722 | 0.999 |
| Land use class (ward area proportion) | N | Mean | SD | Min | q.25% | q.50% | q.75% | Max |
|---|---|---|---|---|---|---|---|---|
| SAMPI 2011 | 508 | 0.02 | 0.029 | 0 | 0.003 | 0.009 | 0.026 | 0.22 |
| Commercial | 508 | 0.038 | 0.061 | 0 | 0.005 | 0.019 | 0.048 | 0.587 |
| Industrial | 508 | 0.018 | 0.049 | 0 | 0 | 0 | 0.007 | 0.445 |
| Residential | 508 | 0.154 | 0.212 | 0 | 0 | 0.035 | 0.236 | 0.779 |
| Townships | 508 | 0.171 | 0.247 | 0 | 0 | 0.007 | 0.331 | 0.891 |
| Informal | 508 | 0.059 | 0.15 | 0 | 0 | 0.001 | 0.03 | 0.938 |
| Smallholdings | 508 | 0.031 | 0.085 | 0 | 0 | 0 | 0.006 | 0.691 |
| Villages | 508 | 0.007 | 0.047 | 0 | 0 | 0 | 0 | 0.686 |
| Golf courses and sports ground | 508 | 0.012 | 0.025 | 0 | 0 | 0 | 0.01 | 0.187 |
| Schools (and sports ground) | 508 | 0.036 | 0.039 | 0 | 0.006 | 0.022 | 0.054 | 0.193 |
| Mines | 508 | 0.011 | 0.032 | 0 | 0 | 0 | 0.005 | 0.24 |
| Built-up | 508 | 0.046 | 0.062 | 0 | 0.014 | 0.032 | 0.054 | 0.521 |
| Non-urban | 508 | 0.429 | 0.276 | 0 | 0.198 | 0.369 | 0.671 | 0.996 |
The 12 hypothesized explanatory variables contained in “Dataset 1” as presented in Table 3 were included in an initial/baseline OLS regression model (i.e., the training model). However, the dependent variable (i.e., SAMPI 2001) was subjected to a Box-Cox transformation to closely conform to the assumptions of normality, linearity, absence of multicollinearity, and normality and independence of the residuals which are necessary for the application of the Gauss–Markov theorem. The results of the baseline OLS regression model as illustrated in Table 7 suggest a very poor fit with regression coefficients having p-values greater than the significance level (0.05). The multicollinearity number was also extremely high (i.e., 37459.59). Although this initial OLS model had normally distributed residuals, they were however not independent. The residuals were spatially autocorrelated (Moran's I = 0.22 and p-value <0.05), implying that OLS regression is not suitable and that a spatial regression model should be considered. Although the adjusted coefficient of determination was above 0.5 (i.e., 0.53), the obtained regression model could not be relied upon given the spatial autocorrelation patterns displayed by its residuals and the extremely high condition number suggesting a substantial occurrence of multicollinearity.
| Dependent variable: SAMPI 2001: South African multidimensional poverty index 2001 | ||
|---|---|---|
| Independent variables | Coefficients/values | p-value |
| Commercial | −106.4 | 0.729 |
| Industrial | −105.3 | 0.732 |
| Residential | −107.1 | 0.727 |
| Townships | −105.5 | 0.731 |
| Informal | −104.0 | 0.735 |
| Smallholdings | −106.1 | 0.730 |
| Villages | −105.6 | 0.731 |
| Golf courses and sports ground | −107.5 | 0.726 |
| Schools (and sports ground) | −105.9 | 0.730 |
| Mines | −605.7 | 0.423 |
| Built-up | −106.8 | 0.728 |
| Non-urban | −105.4 | 0.731 |
| (Intercept) | 103.3 | 0.737 |
| Adj. R2 | 0.53 | |
| AIC (Akaike Information Criterion) | 649.7 | |
| Log-likelihood | −310.85 | |
To obtain a parsimonious model that is also free from multicollinearity, the initial OLS regression model was subjected to a stepwise (forward, backward, and bi-directional) regression analysis, and five explanatory variables (i.e., “Built-up,” “Informal,” “Residential,” “Townships,” and “Non-urban”) emerged as being statistically significant (refer to Table 8). The selection criteria were based on the Akaike Information Criterion (AIC) values and the level of significance. The threshold for the level of significance of any variable to enter into the model was set to 0.01, and 0.05 was set for remaining in the model. The main purpose of performing a stepwise regression analysis was to obtain a parsimonious model that has the same or superior performance results than the initial OLS model with the 12 originally hypothesized explanatory variables. Based on the AIC, the parsimonious OLS regression model with only five independent variables appears to display the best performance results compared with the initial OLS regression model with 12 explanatory variables. After running an OLS regression analysis based on the reduced number of explanatory variables, the residuals of the obtained regression model were still spatially autocorrelated. This suggests that the residuals could contain some information that cannot be explained by the regression model in its current form.
| Dependent variable: SAMPI 2001: South African multidimensional poverty index 2001 | ||
|---|---|---|
| Independent variables/statistics | Coefficients/values | p-value |
| Built-up | −1.05 | 0.021 |
| Informal | 1.97 | 0.00 |
| Non-urban | 0.71 | 0.00 |
| Residential | −1.16 | 0.00 |
| Townships | 0.49 | 0.009 |
| (Intercept) | −2.83 | 0.00 |
| Adj. R2 | 0.53 | |
| AIC (Akaike Information Criterion) | 642 | |
| Log-likelihood | −315 | |
| Diagnostics for spatial dependence | ||
| Moran's I (on residuals) | 0.23 | 0.00 |
| Lagrange multiplier (lag) | 85.7 | 0.00 |
| Robust LM (lag) | 17.82 | 0.00 |
| Lagrange multiplier (error) | 71.18 | 0.00 |
| Robust LM (error) | 3.33 | 0.068 |
3.2 Results of the spatial regression models
Although the spatial lag model proved to be suitable for the analysis performed in this study, the results of other spatial regression models have also been discussed. This is done to highlight the superiority of the spatial lag model, and also conform with common practices as been observed in other similar studies that have discussed spatial regression models (see Akbar et al., 2022; Voss et al., 2006). The spatial lag model performed relatively well in terms of the model fit measures such as the AIC (565.31) and log-likelihood value (−274.67) compared with the other spatial regression models considered in this study (see Table 10). Its lag coefficient was statistically significant confirming the results of the robust Lagrange multiplier (lag) test that suggested the inclusion of a spatially lagged dependent variable as one of the covariates in the model (see Table 9). All the covariates had their respective signs as expected. Hence, the direction of the relationship between “SAMPI 2001” and each of the covariates was encapsulated in the spatial lag model as anticipated. To correct the misspecification of the baseline model, the residuals of the spatial lag model exhibited a pattern of complete spatial randomness (Moran's I for residuals was 0.02 with a p-value >0.05). Lastly, all the covariates in the spatial lag model were statistically significant except for the “Built-up” and “Townships” variables. Section 3.3 provides a detailed contextual discussion of the results of the spatial lag model and possible implications.
| WARD_ID | Old predictions | New predictions | Difference |
|---|---|---|---|
| 79700026 | 0.170 | 0.037 | 0.133 |
| 79700096 | 0.111 | 0.095 | 0.016 |
| 79700065 | 0.076 | 0.064 | 0.012 |
| 79700067 | 0.066 | 0.059 | 0.008 |
| 79700025 | 0.056 | 0.051 | 0.005 |
| 79700066 | 0.045 | 0.042 | 0.003 |
| 79700068 | 0.067 | 0.066 | 0.002 |
| 79700069 | 0.049 | 0.047 | 0.002 |
A possible candidate model that also accounts for spatial dependence in a misspecified OLS (linear) regression model is the SEM (Elhorst, 2010). The results of SEM based on the five significant covariates appear to be superior compared with its OLS regression counterpart (see Table 10). Furthermore, the residuals of the SEM model are not spatially autocorrelated (Moran's I = −0.01 and p-value >0.05. Although the spatially lagged X model (SLX) performed better than the baseline OLS regression model, its residuals were spatially autocorrelated. Furthermore, the SLX performed poorly in terms of the model fit results such as the AIC and the log-likelihood value compared with the SEM (see Table 10). The SDEM performed better than the baseline OLS model, SEM, and SLX; and its residuals display patterns of complete spatial randomness. The SDM and the SDEM had similar performance results. However, the spatially lagged covariates for both the SDM and the SDEM were not statistically significant except for the “Informal” variable which was statistically significant in the SDEM. This suggests that the inclusion of spatially lagged covariates did not substantially improve the SDEM or the SDM to the extent of outperforming the spatial lag model. In terms of the model fit measures (e.g., AIC and log-likelihood values) for both in-sample and out-of-sample predictions), the difference between the three models (spatial lag model, SDM, and SDEM) is marginal. Lastly, the Kelejian-Prucha (SAC) model and the MANSKI model were not further considered since they produced contrasting results within their respective specifications. The SAC model produced two lag coefficients: the lag coefficient for the spatially lagged dependent variable was statistically significant (ρ = 0.4*, see Table 10), while the one for the spatially lagged error term was not significant (λ = 0.11, see Table 10). The opposite was true for the MANSKI model since the lag coefficient for the spatially lagged dependent variable was not statistically significant (ρ = −0.29, see Table 10), while the one for the spatially lagged error term was statistically significant (λ = 0.67*, see Table 10). This suggests that the inclusion of a spatially lagged error term in the SAC model did not contribute to the extent of outperforming the spatial lag model. Along the same vein, the inclusion of the spatially lagged dependent variable as one of the covariates in the MANSKI model did not contribute to the extent of outperforming the spatial lag model.
| Variables/performance measure | OLS model estimates | SEM estimates | SLX model estimates | Spatial lag model estimates | SDM estimates | SDEM estimates | Kelejian-Prucha (SAC) model estimates | Manski model estimates |
|---|---|---|---|---|---|---|---|---|
| Intercept | −2.825* | −2.81* | −2.596* | −1.561* | −1.38* | −2.85* | −1.726* | −3.792* |
| Built-up | −1.052* | −0.402 | −0.335 | −0.450 | −0.034 | −0.174 | −0.442 | −0.262 |
| Informal | 1.971* | 1.614* | 1.433* | 1.335* | 1.295* | 1.351* | 1.397* | 1.448* |
| Non-urban | 0.706* | 0.672* | 0.56* | 0.498* | 0.54* | 0.548* | 0.542* | 0.589* |
| Residential | −1.16* | −1.031* | −1.00* | −0.887* | −0.972* | −0.989* | −0.913* | −0.984* |
| Townships | 0.488* | 0.442* | 0.267 | 0.240 | 0.239 | 0.245 | 0.278 | 0.282 |
| Lag_Built-up | −1.998 | −1.314 | −1.795 | −1.901 | ||||
| Lag_Informal | 0.884 | −0.02 | 1.194* | 1.91* | ||||
| Lag_Non-urban | −0.085 | −0.23 | 0.258 | 0.601 | ||||
| Lag_Residential | −0.597 | 0.155 | −0.312 | −0.525 | ||||
| Lag_Townships | −0.001 | −0.068 | 0.260 | 0.48 | ||||
| Lag coefficient (for the dependent variable and/or the error term) | λ = 0.52* | ρ = 0.46* | ρ = 0.48* | λ = 0.49* | ρ = 0.4*; λ = 0.11 | ρ = −0.29; λ = 0.67* | ||
| Residual standard error (SE) | 0.46 | 0.42 | 0.45 | 0.41 | 0.41 | 0.41 | 0.41 | 0.39 |
| R2 (Coefficient of determination) | 0.53 | – | 0.55 | – | – | – | – | – |
| Log-likelihood | −314.98 | −282.05 | −303.23 | −274.67 | −272.12 | −270.33 | −274.24 | 269.33 |
| AIC | 643.95 | 580.1 | 630.46 | 565.31 | 570.24 | 566.66 | 566.47 | 566.66 |
| Moran's I p-value (residuals) | 0.229* (p-value = 0.00) | −0.01 (p-value = 0.62) | 0.24* (p-value = 0.00) | 0.02 (p-value = 0.25) | 0.002 (p-value = 0.44) | −0.007 ((p-value = 0.57) | −0.002 (p-value = 0.5) | 0.003 (p-value = 0.43) |
| In-sample predictions: performance measures (SAMPI 2001) | ||||||||
| MAE | 0.36 | 0.38 | 0.36 | 0.36 | 0.36 | 0.36 | – | – |
| RMSE | 0.46 | 0.46 | 0.45 | 0.45 | 0.45 | 0.45 | – | – |
| MAPE | 0.16 | 0.16 | 0.15 | 0.16 | 0.15 | 0.15 | ||
| sMAPE | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | 0.15 | ||
| r (Pearson's correlation coefficient) | 0.73 | 0.73 | 0.75 | 0.74 | 0.74 | 0.75 | – | – |
| r 2 | 0.54 | 0.53 | 0.56 | 0.56 | 0.55 | 0.56 | ||
| Out-of-sample predictions: performance measures (SAMPI 2011) | ||||||||
| MAE | 0.47 | 0.47 | 0.46 | 0.47 | 0.47 | 0.47 | – | – |
| RMSE | 0.57 | 0.56 | 0.56 | 0.57 | 0.57 | 0.57 | – | – |
| MAPE | 0.17 | 0.16 | 0.16 | 0.17 | 0.16 | 0.17 | ||
| sMAPE | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | 0.18 | ||
| r (Pearson's correlation coefficient) | 0.63 | 0.63 | 0.63 | 0.63 | 0.63 | 0.64 | – | – |
| r 2 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | 0.40 | ||
| Difference in model performance between in-sample and out-of-sample predictions | ||||||||
| MAE | 0.11 | 0.09 | 0.1 | 0.11 | 0.11 | 0.11 | ||
| RMSE | 0.11 | 0.1 | 0.11 | 0.12 | 0.12 | 0.12 | ||
| MAPE | 0.01 | 0 | 0.01 | 0.01 | 0.01 | 0.02 | ||
| sMAPE | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | 0.03 | ||
- Note: r, Pearson's correlation coefficient between predicted and actual values of SAMPI.
- * Significant variable/parameter (level of significance: 0.05).
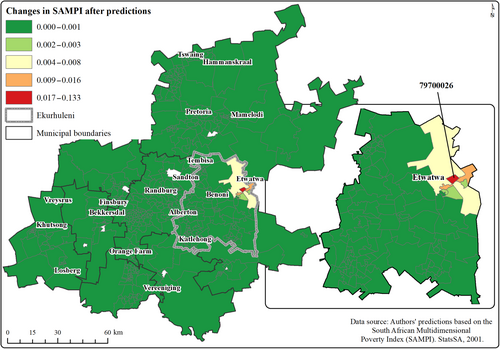
Besides the statistical results which favor the spatial lag model over other spatial regression models tested in this study, theoretical considerations have also guided our choices as already explained in the methodology section (i.e., Section 2.4). Given the patterns of spatial autocorrelation displayed by the levels of poverty across space by wards in the province of Gauteng (see Figure 3), we hypothesize that exogenous variables should have considerable influence on the dependent variable at the local level even though such an impact can propagate to all the wards in the entire study area given the global effect of the spatial lag model. As an illustration, the map in Figure 4 presents changes in poverty levels after altering the value of informal land area from 0.63 to 0 km2 in ward 79700026 in the municipality of Ekurhuleni, while keeping the remaining covariates constant. Although changes in ward 79700026 cascaded to all the other wards in the study area, immediate neighbors of ward 79700026 experienced positive changes in poverty reduction. In other words, wards that share a boundary with ward 79700026 witnessed a noticeable decrease in the levels of poverty (i.e., spillover effect) while ward 79700026 itself experienced the highest positive change because of the direct effect (see Table 9).
To assess the quality of the predictions made by the computed spatial regression models, the mean absolute error (MAE), root mean square error (RMSE), mean absolute percentage error (MAPE), and symmetric mean absolute percentage error (sMAPE) were computed in two ways. In the first instance, the measures of model performance (i.e., MAE, RMSE, MAPE, and sMAPE) were calculated based on the results of in-sample predictions. In the second instance, the same measures of model performance were calculated based on the results of out-of-sample predictions. The idea was to assess the performance of the spatial lag model based on the dataset it had not seen yet. In general, the values of MAE, RMSE, MAPE, and sMAPE were relatively low for both in-sample and out-of-sample predictions of the SAMPI. This suggests that for both in-sample and out-of-sample predictions, on average, the predicted values of the SAMPI are not far away from the actual observed values (see Table 10).
The MAE, RMSE, MAPE, and sMAPE form part of a family of measures that evaluate the performance of models based on the average discrepancy between the predicted and actual values (Chicco et al., 2021). The lower the discrepancy, the better the performance of a given model. Although there is a lack of consensus in terms of which value of these measures indicates the best-performing model, in general, values closer to zero point to reliable predictions.
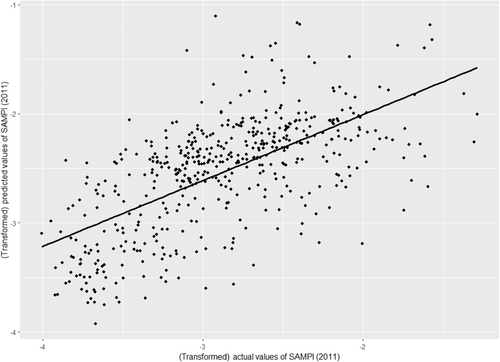
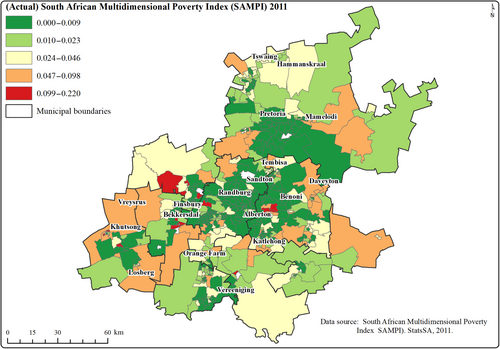
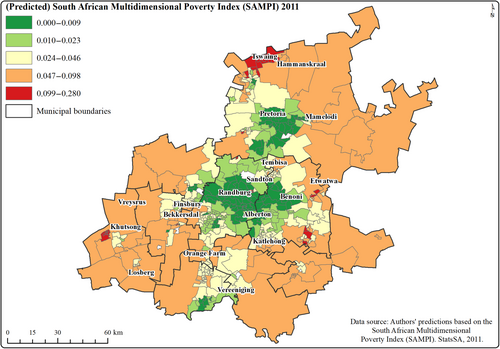
The Pearson's correlation coefficient r and its corresponding square r2 are used to evaluate the linear relationship between the predicted and actual values. Higher values of r or r2 indicate better-performing models (see Pettersson et al., 2023). The models' results for in-sample predictions exhibited relatively high Pearson's correlation coefficient r values that ranged between 0.73 and 0.75, and a moderate value of squared r2 values that ranged between 0.53 and 0.56 (see Table 10). The spatial lag model had an r value of 0.74 and a r2 value of 0.56. All the models exhibited the same value of r and r2 for the out-of-sample predictions. However, the results of the Lagrange multiplier (LM) tests as prescribed by Anselin (2005) indicated the suitability of the spatial lag model. The positive relationship pattern displayed by the scatter plot (see Figure 5) confirmed the strong linear relationship between the actual and predicted values of the 2011 SAMPI (i.e., out-of-sample) based on the spatial lag model. Hence, the overall results of the analysis suggest that the constructed spatial lag model is capable of performing relatively well on new datasets. Furthermore, the mapping of the out-of-sample predicted values of the SAMPI reproduced known spatial patterns of poverty in Gauteng province (see Figures 6 and 7). In other words, the spatial lag model predicted high poverty levels in wards with actual high levels of poverty. Similarly, low levels of poverty predictions were also observed in wards with actual low poverty levels.
3.3 Discussion
The following paragraphs present a contextual discussion of the outcomes of the spatial regression models obtained from applying the method and sequence of analyses explained in Section 2.4. A summary of the results in the form of direct, indirect, and total effects, describing the spatial interactions among the 497 wards is presented in Table 11. The interpretation of these spatial interactions has been guided by LeSage and Pace (2009)'s recommendations. An individual direct effect can be interpreted as the change in the SAMPI (i.e. poverty) at a given ward due to a change in an explanatory variable at the same ward. The average direct effect across all the 497 wards for the SAMPI due to a unit change in each of the five explanatory variables (i.e., covariates) respectively, is presented in Table 11 under the “Direct effect” column. The indirect or spillover effect can be interpreted as a change in the SAMPI in a ward due to a change in an explanatory variable at another ward. The average indirect effect across all the 497 wards is presented in Table 11 under the “Indirect effect” column. The average total effect is the sum of the average direct and indirect effects. As can be seen (in Table 11), except for “Built-up” and “Townships,” the coefficients illustrating the direct effect of each of the explanatory variables on the dependent variable are statistically significant (i.e., p-value <0.05), and they have their respective signs as expected. That is, a positive sign for the “Informal,” and “Non-urban” variables, and a negative sign for the “Residential” variable. This suggests that an increase in land areas classified as “Informal” or “Non-urban” in a given ward would result in a direct increase in the levels of poverty in that ward. Conversely, an increase in land areas classified as “Residential” in the same ward would result in a direct decrease in the levels of poverty in that ward. The spillover (or indirect) effect on the SAMPI that arises from changes in terms of the land area classified as “Informal” or “Non-urban” is positive and statistically significant. This suggests that an increase in terms of the land area classified as “Informal” or “Non-urban” in a given ward would translate into an increase in the levels of poverty in its surrounding wards.
| Explanatory variable | Direct effect | Indirect effect | Total effect |
|---|---|---|---|
| Impact measures (SLAG) | |||
| Built-up | −0.47 | −0.36 | −0.83 |
| Informal | 1.4 | 1.07 | 2.47 |
| Non-urban | 0.52 | 0.40 | 0.92 |
| Residential | −0.93 | −0.71 | −1.64 |
| Townships | 0.25 | 0.19 | 0.44 |
| Simulated p-values | |||
| Built-up | 0.25 | 0.26 | 0.25 |
| Informal | 0.00 | 0.00 | 0.00 |
| Non-urban | 0.002 | 0.003 | 0.001 |
| Residential | 0.00 | 0.00 | 0.00 |
| Townships | 0.134 | 0.143 | 0.134 |
Given that the “Residential” variable has a negative indirect effect, it means that an increase in terms of the land area classified as “Residential” in a given ward would translate into a decrease in the levels of poverty in its surrounding wards. The impact of such spillover effects would propagate to the entire study area since the spatial lag has been employed. The spillover effects for land areas classified as “Built-up” and “Townships” are not statistically significant (i.e., p > 0.05). Furthermore, their total effects are also not statistically significant.
The spatial mapping of land areas classified as informal and townships corroborate the outcome of the spatial regression models, given that they are mostly located in poor neighborhoods at the fringes of the different municipalities, far from the centers of major economic activity (refer to Figure 8). In the context of South Africa, townships are land areas that were segregated and reserved for the Black, Indian, and Colored population groups during the apartheid era. Due to the legacy of these segregationist policies, coupled with today's poor municipal infrastructure and service delivery, these neighborhoods are the most affected by poverty. To this day, issues and challenges related to adequate formal housing provisions, access to clean water and energy, and access to proper sanitation and health care are still prominent in such areas. These neighborhoods include Soweto and Alexandra in the City of Johannesburg Metropolitan Municipality, Atteridgeville, Mamelodi, and Soshanguve in the City of Tshwane Metropolitan Municipality and Katlehong, Kwa-Thema, and Tembisa in the City of Ekurhuleni Metropolitan Municipality. See the map in Figure 8.
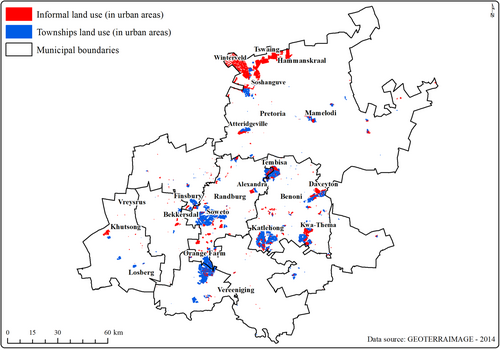
Given the legacy of segregationist policies that characterized South Africa pre-1994, Gauteng province is just a microcosm that reflects the urban morphology of the country. The typical typology of cities in most provinces is characterized by a single (or few at the most) small centers of economic activity, surrounded by other areas (i.e. land use classes). Most of the wealthy and middle-income earners live in neighborhoods that are close to the economic centers where the built infrastructure is reasonably well maintained and service delivery is efficient. Most of the poor population, who also constitute the majority of the population in South Africa, reside in settlements that are far from job opportunities in centers of economic activity. Hence, it is very likely that the modeling approach adopted in this study to explain and predict poverty patterns using a spatial lag model is transferable to other provinces of South Africa. Further research could explore how transferable this approach would be in other cities across the globe with a similar urban morphology and/or history of segregationist policies.
Lastly, a worthwhile contribution of this study is demonstrated in the simulation exercise depicted in Figure 4. Figure 4 illustrates the spatial interaction among the wards when the land area classified as ‘Informal’ in one of the wards (i.e. ward 79700026) decreased from 0.63 to 0 km2, resulting in a remarkable reduction in the levels of poverty in that particular ward (i.e. direct effect), also in the surrounding wards (i.e., spillover effect). The intensity of the spillover effect was negligible beyond the wards that were not directly connected to ward 79700026. This simulation exercise which can be useful for policy formulation and monitoring is feasible based on a spatial regression model (i.e., the spatial lag model). A simulation based on other covariates can easily be performed as well.
4 CONCLUSION AND POLICY IMPLICATIONS
This study employs the spatial lag model to explain the relationship between the SAMPI and statistically significant variables derived from land use datasets. The spatial lag model is also used to predict the levels of poverty in the absence of up-to-date socioeconomic data collected by Stats SA during Censuses. All in all, the model predictions reflect the spatial distribution of the levels of poverty across the province. The results of the modeling exercise, coupled with the poverty maps produced, can be used to inform government policies for targeting poverty alleviation initiatives in specific neighborhoods. The five variables that have been identified as statistically significant drivers of poverty in the province are related to informal settlements, areas that have been classified as townships, non-urban areas, built-up, and residential areas. The results reveal that wards with high proportions of informal settlements, townships, and non-urban areas tend to be associated with higher levels of poverty. This highlights the importance of implementing existing policies such as the National Development Plan (NDP) that seeks to support the construction of formal houses, infrastructure development, and the improvement and maintenance of existing infrastructure in poverty-stricken areas (National Planning Commission, n.d.). This study also confirms the importance of the “Breaking New Ground (BNG)” policy which promotes the upgrading of informal settlements to improve the quality of life of residents (Department of Human Settlements, 2004). This study demonstrates that informal settlements contribute to rising levels of poverty, not only in a given ward but also in its immediate surrounding wards. Finally, concerning townships which have been identified as being among the drivers of poverty in the province, this analysis confirms the importance of the Gauteng provincial government's program, referred to as the “Gauteng township economy revitalization strategy”, seeking to support entrepreneurial initiatives in areas classified as townships (Gauteng Province, n.d.).
Besides revealing and predicting the spatial patterns of poverty, this study illustrates a spatial interaction scenario where plausible explanatory variables can be manipulated to monitor their effects on the resulting levels of poverty in space. More importantly, the analytical method employed in this article can be used as a tool for continuously monitoring and evaluating the effectiveness of the government's policies and programs aimed at alleviating poverty. Besides Gauteng, the findings and recommendations of this study can be applied to other provinces in South Africa. Its applicability to cities in other countries or regions with a segregationist history should be explored.
ACKNOWLEDGMENTS
The authors would like to thank Mr Werner Charles Ruch (Director: Research and Product Development at Stats SA) for sharing the 2001 and 2011 South African Multidimensional Poverty Index (SAMPI) data. The authors also thank the anonymous Reviewers for their insightful comments and suggestions.
CONFLICT OF INTEREST STATEMENT
The authors declare that they have no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
The South African Multidimensional Poverty Index (SAMPI) data that support the findings of this study are available from the corresponding author upon reasonable request. However, the South African Land-Cover datasets can be downloaded from the Department of Forestry, Fisheries and the Environment (Republic of South Africa)'s website: https://egis.environment.gov.za/sa_national_land_cover_datasets.




