Geography of voter turnout in Slovak local elections (1994–2018): The effects of size and contagion on local electoral participation
Abstract
The main goal of this article is to analyze spatial disparities in local electoral participation in Slovakia between 1994 and 2018 on a very detailed spatial structure of all (almost 3000) municipalities. To achieve this goal, methods of global and local spatial autocorrelation and spatial regression are used. Municipality-level analysis, then, provides three main results. First, cartographic presentations provide spatial evidence of highly stable patterns of electoral participation in Slovak municipalities. In the long term, there was no substantial inter-electoral change in the clustering of voter turnout in the different municipalities, except for an overall significant decline in the homogeneity of the clusters with low or high electoral turnout. Second, while there was some positive spatial autocorrelation of turnout between a concrete municipality and its surroundings, suggesting the existence of a contagion effect, this effect was not too strong and quickly waned with growing distance. Third, as especially the local elections in 2018 suggested that local political environment has its own dynamics that are increasingly independent of municipality size, a more detailed analysis of the local political context combining both quantitative and qualitative techniques should be a priority in the future.
1 INTRODUCTION
Electoral behavior is one of the central areas of political science research. This claim is especially true for the national level of governance (elections to national parliaments, or their lower chambers in particular), while our understanding of subnational patterns of voting is fragmented and incomplete, with especially local elections and voting being relatively underexplored (Gendźwiłł & Steyvers, 2021). Most authors thus paid particular attention to the so-called first-order elections (Blais & Dobrzynska, 1998; Franklin, 2004; Kostadinova, 2003; Linek & Petrúšek, 2016), and only a much smaller number of studies focused on subnational levels of government (Bolgherini et al., 2024; Cancela & Geys, 2016; Frandsen, 2002; Kouba et al., 2021; van Houwelingen, 2017).
This article uses a spatial econometric approach to fill the conspicuous knowledge gap with respect to aggregate-level single-country studies of turnout in local elections (e.g., Breux et al., 2017; Dubois & Leprince, 2017; Fukumoto & Horiuchi, 2016; Hajnal & Lewis, 2003; Rallings & Thrasher, 2005). We aim to analyze electoral participation in Slovakia on a very detailed spatial structure and an extensive yearly time series (1994–2018). To achieve the main goal—to examine the spatial dimension of the disparities in voter turnout in local elections at the level of all (almost 3000) Slovak municipalities—the methods of global and local spatial autocorrelation and spatial regression are used. Another reason to choose this topic is that although some studies have analyzed voter turnout in Slovak local elections (Klimovský, 2022; Klimovský & Žúborová, 2011; Kostelecký & Krivý, 2015; Mikuš & Gurňák, 2014), a comprehensive spatial analysis of local turnout in Slovakia is still missing.
In this context, for instance, Plešivčák et al. (2016) claimed that a long-term and systematic geographic study of electoral participation was missing in Slovakia (as of 2016), even if findings about spatiotemporal differentiation of (non)participation suggest the importance of knowing the context and reasons of that differentiation in various types of elections. Similarly, Kostelecký and Krivý (2015) stated that existing research paid only limited attention to the vertical dimension of the spatial differentiation of electoral behavior, that is, to different election results between municipality size categories or between urban and rural areas. Moreover, most of the spatial analyses conducted thus far (focusing exclusively on parliamentary elections) have focused on higher levels of aggregation—the district level (e.g., Kevický, 2020a; Kostelecký, 2001; Madleňák, 2012; Madleňák & Pink, 2012; Mikuš, 2014), providing a somewhat distorted view of reality as important intra-regional differences may be obscured in analysis at the district or regional levels of aggregation.
Although the above critique by Plešivčák et al. was followed by a few works providing detailed spatial analysis of voter turnout at the municipal level of aggregation (Kevický, 2020b; Kevický & Daněk, 2020), those again were limited exclusively to parliamentary elections. More importantly, the statement about the under-exploration of subnational patterns of voter turnout is also true for studies from other areas across the world, in which geographical approaches to local turnout are relatively rare (e.g., Bolgherini et al., 2024; Mansley & Demšar, 2015; Maškarinec, 2022); most studies are concerned with presidential or parliamentary elections and performed at larger-scale aggregations (e.g., Darmofal, 2006; Fiorino et al., 2021; Manoel et al., 2022; Tam Cho & Rudolph, 2008).
We focus on the local elections rather than general elections given the growing importance of the local tier in the multilevel governance of many contemporary democracies (Loughlin et al., 2012). The patterns and dynamics of local voting can be considered as a missing link in the study of multilevel elections (Bolgherini et al., 2021; Gendźwiłł & Steyvers, 2021), and local democracy plays a very important role in local communities' effective daily functioning (Mansley & Demšar, 2015). At the same time, a subnational comparative method offers several advantages: (1) increasing the number of observations and thus mitigating the limitation of a small-N research design to enable more meaningful and controlled comparisons; (2) strengthening the capacity to accurately code cases and thus make valid causal inferences; and (3) better handling the spatially uneven nature of major political processes (Snyder, 2001).
The relevance of studying Slovak local elections to scientists as well as the general public, then, is based on several reasons. First, spatial analysis of local turnout addresses the above-mentioned research gap, namely the lack of works using geographical approaches to analyzing local turnout at a lower scale of aggregation. Second, Slovakia is a highly suitable case for answering the question of whether there is some form of spatiotemporal (in)stability of voter turnout between elections as it belongs to the very small group of European countries with extremely fragmented settlement (municipality) structures (Jüptner & Klimovský, 2022), resisting the ongoing world-wide trend to merge municipalities (Tavares, 2018).1
The extremely fragmented settlement structure of Slovakia thus, on the one hand, entails more demanding data collection and processing but, on the other hand, it offers a considerably higher number of observations than studies in countries with much more concentrated municipality structures, enabling us to put research questions to more reliable tests. At the same time, the methodological advantages of going local are particularly important in spatial econometric analysis because precisely the choice of spatial research techniques is strongly determined by the preferred scale of aggregation. It is indeed the municipality level that provides suitable conditions for applying local analysis methods because at higher levels of aggregation (district, regional, etc.), the methods become devoid of their local nature and highly imprecise results tend to be obtained.
However, the aim of this article goes beyond presenting the possibilities offered by maps, or geospatial analytical methods, for exploring the spatial interaction effects of voter turnout patterns between Slovak municipalities. The main ambition (research question) of the article is to show to what extent a given (low/high) level of voter turnout in a municipality in one election shifts (partly in the form of a contagion effect) into surrounding municipalities in the following elections. Precisely this question can be answered using suitable spatial data analysis techniques that help us not only identify transformations of the clustering patterns of voter turnout in local elections. At the same time, spatial autocorrelation or spatial regression models can show us whether there does exist some level of spatial autocorrelation of voter turnout between a concrete municipality and its surroundings, suggesting the existence of a contagion effect, because processes of spatial diffusion and contagion are frequently manifested as spatial dependence within quantitative data (Shin & Agnew, 2002). Here, autocorrelated geographic patterns in data are especially typical of those patterns where contagion or diffusion effects were at play (Tam Cho, 2003).
Furthermore, when analyzing the possible effects of contextual factors, it is necessary to differentiate between contagious diffusion, typical for adjoining units and hierarchical diffusion, which spreads broadly through commonly shared influences (Cohen & Tita, 1999). While contagious diffusion depends on direct contact and is the classic way of the spreading of a given phenomenon over a large territorial area, hierarchical diffusion, in contrast, does not require direct contact and instead occurs through spontaneous innovation or imitation. Here, the spread of a given phenomenon is mediated by broad cultural influences affecting the entire population (or a subgroup), which may exhibit a high level of spatial diffusion.2 Contagious diffusion can be further divided into relocation diffusion, where the observed phenomenon (turnout in our case) leaves the point of origin (municipality in our case) and spreads outward (i.e., to surrounding municipalities), and expansion diffusion, where the centre or place of origin continues to experience high incidence rates of the diffusing phenomenon (see Cohen & Tita, 1999, pp. 453–455).
In our study of electoral turnout, we expect the contribution of diffusion processes to be driven especially by the expansion type of diffusion, which at local level can reflect information networks, neighborhood effects, various sociodemographic, economic or socio-cultural factors, or political interactions and exchanges (Shin & Agnew, 2007). In contrast to studies that examine only individual actors outside of the context in which they reside, there is considerable evidence that contextual factors are also at play (Tam Cho, 2003).
Precisely these outer contextual bounds bring to the foreground the necessity to deal with socioeconomic characteristics of “places” and the spatial relations between them (i.e., the structural/aggregate level of explanation), instead of the purely individual level of explanation of political behavior, here different levels of voter turnout. It is necessary to study structure as differences between places based on factors such as municipality size, urbanization level, education, occupational structure, unemployment, religious or ethnicity structure, and so on.
Indeed, while existing studies of aggregate local turnout (below) find several factors influencing the level of subnational electoral participation, more empirical tests are needed to verify the possible influence of the proximity of municipalities with various levels of turnout on the amount of turnout in a concrete municipality, especially ones using spatial (geographical) approaches at a fine-grained level of aggregation.3
Finally, it is necessary to mention some limitations of the research, such as potential biases in our data. Among the disadvantages of using aggregate spatial data is primarily the ecological fallacy problem, that is, the risk of making erroneous inferences about unobserved behavior of individuals in a population based on observed behavior of the population as a whole (Robinson, 1950)4 but also spatial autocorrelation, that is, the fact that for spatial data, as opposed to nonspatial data, variable values cannot be considered mutually independent (Fortin & Dale, 2009).5
Nevertheless, the so-called ecological fallacy problem arises out of adopting a research perspective based on aggregate data. While such data cannot help us fully understand the reasons behind people's individual behavior, they are useful for even highly detailed analyses of regional (local) differentiation because the aggregate values have been calculated from data for sufficiently large population samples. This eliminates the risks associated with individual data collection, which are often ignored (e.g., sampling error and sampling procedure). At the same time, there are no sample survey data at the level of all Slovak municipalities to provide a detailed picture of the relationships between turnout levels and individual voters' characteristics. Nevertheless, we deem it necessary to emphasize that our findings do not pertain to individual people; instead, the unit of observation is represented by communities of people living in a given territory (municipalities).
2 LITERATURE REVIEW
Concerning previous research on turnout in Slovak elections, some authors show that whereas oscillations and instability were characteristic of the spatial distribution of electoral turnout in the 1990s, the (district-level) distribution of voter support in parliamentary elections stabilized after 2000 (Gyárfášová & Krivý, 2013; Kevický, 2020a). More specifically, Madleňák (2012) identified five types of districts with a general trend of decreasing voter turnout in Eastern Slovakian districts and, in contrast, a growing trend in the capital city of Bratislava and its surroundings. Similarly, Kevický (2020a) found consistently low participation mainly in the districts of eastern and southern Slovakia, together with parts of north-western Slovakia, while consistently high electoral participation existed mainly in the northern regions of Žilina and Trenčín, and since the 2002 elections also in Bratislava. More importantly, Kevický and Daněk (2020) municipal-level analysis showed that geographical differences in turnout deepened over time, with above-average turnout found especially in western and central Slovakia (as well as Bratislava and surroundings and central Slovakia in the elections of 2010–2016), below-average turnout found especially in northern borderland districts and in eastern Slovakia, and also an accelerating decrease found in southern Slovakia since 2010 (see Kevický, 2020b; Kevický & Daněk, 2020).
Most of the analyses, then, agree that turnout in Slovakian parliamentary elections is mostly determined by socioeconomic factors, as better economic situation, higher social-economic status, or higher educational-level increase turnout in Slovak regions and municipalities (see Gyárfášová & Krivý, 2013; Kevický, 2020b; Rybář et al., 2017). Furthermore, an analysis of the relationship between voter turnout and municipality size found the highest average levels of voter turnout in the smallest municipalities and the largest cities. Moreover, for the first time since the Slovak transition to democracy in 1990, the average turnout in the 2020 parliamentary elections was higher in largest cities than in the smallest municipalities (see Kevický, 2020b). Similarly, Gyárfášová and Krivý (2013) confirmed the previous statement about a consistently high turnout in small municipalities, together with a steadily increasing turnout in the largest cities.
Finally, Kostelecký and Krivý's (2015) analysis of urban–rural differences in voter turnout in both parliamentary and local elections between 1998 and 2010 concluded that in contrast to parliamentary elections, the relationship between municipality size and local turnout is linear, thus the larger a municipality, the lower the turnout, with turnout in the smallest municipalities still being more than double that in the largest cities. In contrast, Klimovský (2022) argued that although local turnout in the largest cities and district capitals is usually below the average (and thus partially depends on the population size of the municipalities), there is no clear negative correlation between voter turnout and population size.
There are relatively few spatial analyses of local elections in general and none in the case of Slovakia. One minor exception is a recent study of Bolgherini et al. (2024) which showed that local turnout is higher in small and rural Slovak municipalities than in large urban ones and that there is no distinctive local turnout clustering (as shown by basic cartographic analysis)—although this analysis is limited to the 2018 local election. Moving on to other studies, Sloboda and Černěnko (2022) examined the spatial aspect of competitiveness in Slovak local (mayoral) elections and found no visible spatial pattern of competitiveness across Slovakia's territory. Similarly, Plešivčák et al. (2022) analyzed the issue of legitimacy regarding the powers of Slovak mayors and election results and found a mosaic-like pattern of distribution of legitimacy across the country's municipalities. An important role was played especially by local population size (the categorical variable of municipality size) and generally by Slovakia's settlement structure, that is, the spatial concentration of smaller and larger settlements (see Plešivčák et al., 2022, pp. 235–237).
Finally, to mention some previous studies of aggregate local turnout in other countries than Slovakia, they found several factors influencing the level of electoral participation. Above all, most studies agreed on municipal size as the key explanatory variable of local turnout (Dahl & Tufte, 1973; Denters et al., 2014; Górecki & Gendźwiłł, 2021; Kouba & Lysek, 2023; van Houwelingen, 2017), confirming the so-called “decline-of-community” model (Verba & Nie, 1972, p. 270) or the “Lovely Lilliput” thesis (Denters et al., 2014, p. 17). For instance, Cancela and Geys's (2016) meta-analysis of national and subnational elections (covering 185 studies published between 2002 and 2015) showed that turnout in subnational elections is primarily affected by size and composition of the geographical unit, concurrent elections and the electoral system, whereas campaign expenditures, election closeness and registration requirements have higher explanatory power in national elections.
Similarly, Gendźwiłł and Kjær's (2021) analysis of horizontal variation in the national–local turnout gap (covering 12 European countries and 14,666 municipalities) confirmed a strong and consistent positive correlation with size, as the gap between turnout levels in local versus national elections increases in larger municipalities. Furthermore, van Houwelingen (2017) confirmed the negative effect of population size on local political participation, but this relationship appeared to be non-linear, as the negative size effect on turnout was stronger for small municipalities (with a population of 20,000 or less) than for larger municipalities (that have more than 100,000 citizens).
Bolgherini et al. (2024), then, confirmed the stronger negative effects of size and urbanization on local turnout (as well as their mutual independence), but the important finding of their comparative study was not only that urbanization matters more but also that urbanization and size matter more in Eastern than Western countries, with almost zero effects of size in Western European municipalities.6 In contrast, Kouba et al. (2021) cross-national time-series comparative analysis of local turnout (covering 97 democratic countries across the globe) found that compulsory voting, concurrent first-order elections, and autonomy of local elected authorities drive turnout in local elections, while in contrast to many previous studies, no effect of size was found.
3 MATERIALS AND METHODS
In this article, we analyze data on electoral participation in Slovak local elections on an extended time series from 1994 to 2018. We use the data for all 2927 Slovak municipalities, as former analyses of the socio-spatial differentiation of Slovakia's historic settlement regions (Klobučník & Slavík, 2013), various aspects of local politics (Plešivčák et al., 2022; Sloboda & Černěnko, 2022), or voter turnout in parliamentary elections (Kevický, 2020b; Kevický & Suchánek, 2023) suggested the need to work at the lowest scale possible, since analysis at higher levels of aggregation (regions, districts, etc.) may obscure substantial intra-regional differences, whereas similar spatial disparities can be expected in the case of local voter turnout as well. In this article, voter turnout is defined as a share of registered voters in a given municipality. Data on voter turnout are available from the Slovak Statistical Office election server.
We use several spatial techniques to study spatial effects and analyze the dynamics of voter turnout in Slovak municipalities. Our exploration of the spatial structure of voter turnout begins with the formal detection of spatial autocorrelation using Moran's I statistic (Cliff & Ord, 1981). The way Moran's I is calculated is much like the Pearson correlation coefficient, and the same applies to interpreting the values of Moran's I. The values Moran's I range between −1 and +1. The value of −1 indicates perfect negative autocorrelation, +1 indicates perfect positive autocorrelation and 0 indicates a random pattern of spatial clustering in the data.7 More specifically, in terms of turnout, when a municipality with high turnout neighbors municipalities with similarly high turnout (or when there are neighboring municipalities with low levels of turnout), there is a positive spatial autocorrelation or spatial clustering (with Moran's I approaching +1). Conversely, when municipalities with low turnout levels are surrounded by municipalities with high turnout levels (or vice versa), there is a negative spatial autocorrelation, which helps us identify spatial outliers (with Moran's I approaching −1). Finally, near-zero Moran's I values indicate absent spatial autocorrelation, that is, spatial independence or no identifiable pattern of spatial distribution of municipalities with high or low levels of turnout, respectively (Fotheringham et al., 2002).
However, Moran's I is an overall measure of linear association, whose single value is valid for the entire study area. In other words, it indicates the mean value of a set of possibly substantial spatial differences. In analyzing spatial data, it is highly unlikely for the resulting statistical indicator to apply to all parts of the study area, as one can expect substantial regional (local) differences affecting not only the resulting values of certain indicators but also, more importantly, the level of determination of various phenomena and processes.8
For this reason, Moran's I can serve as a suitable tool for identifying whether turnout in a given country exhibits any form of spatial clustering of municipalities. On the other hand, it cannot determine where exactly to find any substantial clusters of municipalities with consistently low turnout (i.e., limited citizens' active involvement in the political process), which may represent areas with symptoms of a crisis of democracy or citizens' discontent with the way democracy works.
Since the aim of this article is to identify potentially different patterns of turnout in local elections within larger units and their transformation between elections, a local indicator of spatial association—LISA (Anselin, 1995) is used to obtain a more detailed insight into the ways voter turnout is clustered throughout Slovak territory. The LISA indicators are calculated for each unit (municipality), and statistically significant values can be mapped or categorized (by spatial autocorrelation type) into four groups, each represented by one quadrant of the Moran diagram (Figure 1). This helps us identify municipalities with positive or negative spatial dependence—high values of turnout in a municipality accompanied by similarly high turnout in surrounding municipalities (hot spots) or, in contrast, a low-value municipality surrounded by other municipalities with similarly low turnout (cold spots)—or spatial outliers with high turnout values surrounded by low turnout values and vice versa (see Anselin, 1995). We present the patterns of voter turnout in Slovak municipalities in four classes of clusters: high–high (H–H), low–low (L–L), high–low (H–L), and low–high (L–H).
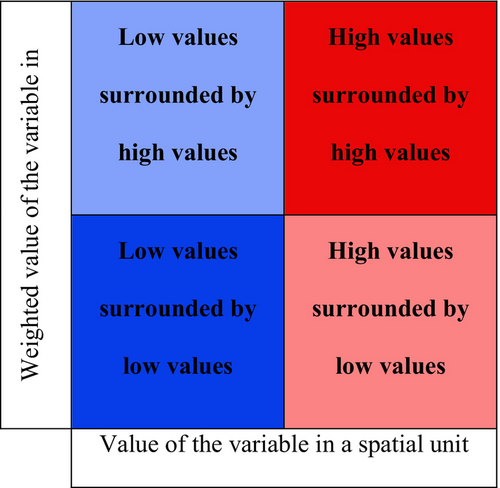
We use both univariate and bivariate LISA indicators. While univariate LISA indicators can show the clustering of local turnout in one election, and thus provide a more static view, the advantage of bivariate LISA indicators is in allowing us to compare how local turnout transformed between pairs of elections. Given the spatial nature of geographical data (i.e., spatial autocorrelation and spatial dependence), a map presentation of bivariate LISA indicators can reveal whether the spatial patterns indicate hidden (underlying) processes and actors shaping them and modifying them in time (Fortin & Dale, 2009). Thus, it can illustrate how the process of (in)stability and variability of turnout in local elections is geographically determined when gradual or abrupt interelectoral changes of turnout are observed in a territory (Shin & Agnew, 2007).
When comparing the maps of univariate and bivariate LISA indicators, and similar forms of clustering may indicate spatiotemporal stability (i.e., no diffusion effect); and conversely, highly contrasting patterns (spatiotemporal instability) may indicate the emergence of a contagious diffusion effect for turnout between neighboring municipalities. More specifically, in the case of bivariate correlation, we present maps of so-called outward diffusion indicating the ways voter turnout in a given unit in elections t shifts towards voter turnout in surrounding units in elections t + 1 (Anselin, 2005). In this respect, bivariate LISA extends the previous cross-sectional method (i.e., univariate LISA) to cover the dynamics of change in spatial dependencies over time (Cohen & Tita, 1999).
However, as the local Moran's I statistic is useful, especially for descriptive analysis of the given phenomenon, and our aim is also to demonstrate a possible contagion effect on local turnout, we use a spatial econometric strategy that helps us integrate spatial interaction in a regression model, the so-called spatial lag model. The spatial lag model incorporates the dependent variable's (local turnout in our case) spatial effects directly, as an additional independent variable (Anselin, 2002), and the new variable (turnout [W] variable) indicates the level of spatial autocorrelation of the variable (local turnout) between a given spatial unit (municipality) and its surroundings (neighboring municipalities).
As suggested by some authors (Tam Cho & Rudolph, 2008; Wing & Walker, 2010), spatial lag models are most appropriate when the spatial patterning is a function of neighboring observations. The reason why the spatial lag model is the most consistent with contagion theories and diffusion processes is that it can show that the amount of a neighbor's contribution (of turnout in surrounding municipalities) is not an artefact of observed and unobserved independent variables but actually affects turnout in the given municipality—that local political behavior is somehow driven by the neighbors (Tam Cho, 2003).
Besides the local turnout [W] variable, we use some other factors that may matter for electoral participation as shown above. First, we include municipality size (logarithm of the number of inhabitants) as most studies confirmed its decisive effect on voter turnout.9 Second, we use turnout in previous elections—previous turnout variable—as we expect that the degree of turnout in a specific local election will reproduce at a similar level (low or high) in the following election. However, as the previous turnout variable could be an endogenous predictor of the percentage of voters who cast a vote in following elections (i.e., the dependent variable), we control for the effect of this independent variable including its lagged version, too. As we expect citizens to be more likely to go to the polls where their fellow citizens more often go to the polls in the long-term perspective, we include the non-lagged version of the previous turnout (previous turnout (t – 1) variable), as well as its versions lagged by one (previous turnout (t – 2) variable) and two election cycles (previous turnout (t – 3) variable); one election cycle spans 4 years. Finally, we use two control variables which previous studies showed as important predictors of turnout in Slovakia. Socioeconomic status is expressed as unemployment (proportion of the unemployed population), while stratification is measured by the primary education variable (proportion of people with primary education).
4 EMPIRICAL ANALYSIS
The analysis of local electoral participation in Slovak municipalities shows considerable stability of electoral behavior. After an initial higher civic mobilization in the context of the country's democratic transition in 1990, when turnout in local elections reached 63.75% (compared to 95.39% in parliamentary elections), the first local elections after the splitting of Czechoslovakia (31 December 1992) saw a decline of voter turnout by 11 percentage points (52.42%). Local turnout last exceeded the 50% threshold in 1998 (53.95%) and in the following five elections, it stabilized around the average level of 48.77%, with oscillations of ±1 percentage point (Table 1).
| Year | Turnout | Moran's I | Local Moran's I (number of municipalities) | |||
|---|---|---|---|---|---|---|
| H–H | L–L | L–H | H–L | |||
| 1994 | 52.42 | 0.144 | 519 | 306 | 154 | 153 |
| 1998 | 53.95 | 0.205 | 605 | 357 | 140 | 164 |
| 2002 | 49.51 | 0.176 | 555 | 347 | 170 | 163 |
| 2006 | 47.65 | 0.132 | 409 | 251 | 133 | 134 |
| 2010 | 49.69 | 0.113 | 384 | 229 | 132 | 108 |
| 2014 | 48.34 | 0.101 | 372 | 229 | 152 | 129 |
| 2018 | 48.67 | 0.067 | 283 | 185 | 148 | 111 |
- Source: Slovak Statistical Office; own calculation.
Furthermore, the analysis of the distribution of turnout using spatial correlation based on global Moran's I for the same period yielded a positive global Moran's I value for every election year. This suggested that areas with a similar density (high or low) were clustered. However, while there was a rise in the value of global Moran's I between 1994 and 1998, the following local elections witnessed a decrease in turnout clustering.
The subsequent LISA analysis of electoral participation showed that among the areas that were correlated, most featured the H–H pattern (between 9.7% and 20.7%, with a mean value of 15.3%), followed by the L–L pattern (between 6.3% and 12.2%, with a mean value of 9.3%), the L–H pattern (between 4.5% and 5.8%, with a mean value of 5.0%) and the H–L pattern (between 3.8% and 5.6%, with a mean value of 4.7%). However, while the share of voters participating in local elections only showed a slight decrease of <4 percentage points between the local elections of 1994 and 2018, the share of municipalities in both categories (H–H and L–L) shows a persistent (with several minor exception) decline of almost 14 percentage points between 1994 and 2018, with a maximum of 43.3% in 1994 compared to 24.8% in 2018.
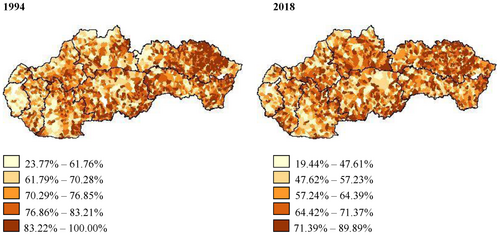
To analyze the change in Moran's I over time, bivariate Moran's I was calculated, as bivariate spatial autocorrelation can help to quantify the assumption of spatiotemporal (in)stability of voter turnout in the long term (Table 2). Here again, we can see an initial (very minor) rise of clustering in subsequent elections, with the highest value of bivariate Moran's I between the elections of 1998 and 2002, followed by a continued decline of the level of inter-electoral clustering of turnout, with the lowest value between the elections of 2014 and 2018. However, when we compared the value of bivariate spatial autocorrelation in the entire time period observed, the differences were not very large (with the exception of the considerably low value of bivariate clustering between the elections of 2014 and 2018), suggesting that the spatial patterns of electoral participation in local elections have been relatively stable over time. This is also illustrated by a comparison of basic electoral maps of the territorial distribution of voter turnout between 1994 and 2018 (Appendix A).
| 1998 | 2002 | 2006 | 2010 | 2014 | 2018 | |
|---|---|---|---|---|---|---|
| 1994 | 0.163 | 0.147 | 0.110 | 0.110 | 0.107 | 0.071 |
| 1998 | 0.169 | 0.128 | 0.131 | 0.135 | 0.096 | |
| 2002 | 0.139 | 0.130 | 0.125 | 0.087 | ||
| 2006 | 0.112 | 0.108 | 0.078 | |||
| 2010 | 0.104 | 0.071 | ||||
| 2014 | 0.074 |
- Source: Slovak Statistical Office; own calculation.
To illustrate the overall stability of the spatial patterns of turnout in Slovak local elections, we compared spatial clustering in the local elections of 1998 (the highest level of the local Moran's I statistic) with the local elections of 2018 (the lowest level of the local Moran's I statistic); the remaining spatial patterns do offer a similar picture. In accordance with the low values of Moran's I, the values of local Moran's I, too, indicate rather lower levels of spatial clustering between positive or negative values of electoral participation; at best, there were 32.9% of municipalities with positive (1998) or 11.4% of municipalities with negative autocorrelation (2002), respectively. The LISA cluster maps (Figure 2), then, visualize the areas with significant spatial clustering of municipalities with above-average (below-average) values of turnout in their local elections as high–high (low–low) clusters, whereas municipalities that differ in their level of turnout from their neighborhood are high–low or low–high spatial outliers.
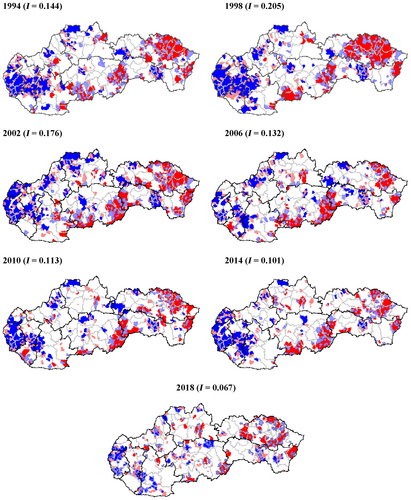
On one hand, the results of the LISA analysis show the divergent character of the spatial autocorrelation of local turnout across the Slovak territory. On the other hand, the maps for individual election years do not indicate any substantial change or transformation in inter-municipal turnout between elections, with the exception of a generally decreasing level of turnout clustering in Slovak local elections. This conclusion suggests a high stability of turnout between election years, which is nevertheless consistent with the Pearson correlation coefficient values (Table 3) indicating the inter-electoral stability (uniformity) of the spatial patterns of local electoral participation, although there is once again a steady decline of inter-municipal stability of local turnout.
| 1998 | 2002 | 2006 | 2010 | 2014 | 2018 | |
|---|---|---|---|---|---|---|
| 1994 | 0.620 | 0.483 | 0.388 | 0.365 | 0.334 | 0.271 |
| 1998 | 0.643 | 0.534 | 0.479 | 0.466 | 0.364 | |
| 2002 | 0.567 | 0.495 | 0.481 | 0.364 | ||
| 2006 | 0.516 | 0.452 | 0.365 | |||
| 2010 | 0.491 | 0.405 | ||||
| 2014 | 0.452 |
- Source: Slovak Statistical Office; own calculation.
Generally, in 1998, municipalities with high levels of local turnout were concentrated especially in the extensive area covering large parts of the eastern Slovakian Prešov Region, with the exception of its eastern and especially western parts. In contrast, other parts of the country saw only sporadic occurrences of the H–H pattern, with some minor exceptions of municipalities on the border of two regions: the southern part of the Banská Bystrica Region and the easternmost part of the Košice Region.
In contrast to the H–H pattern, the clustering of the L–L pattern was much less common in Slovakian municipalities (the number of municipalities with the H–H pattern was two to three times higher in the different elections), but its territorial distribution was again limited to a few selected regions of Slovakia. Here, too, several extensive areas can be identified where Slovak citizens exhibit rather low willingness to participate in local elections. The first such area covers large parts of the country's western borderland, including a sizable section of the Bratislava Region (with the capital city of Bratislava), from which the area of low turnout (the L–L pattern) extends eastwards to the neighboring Trnava Region (although it encompasses only municipalities located in the Region's central districts) and a cluster of several municipalities along the Nitra Region's border with the Trnava Region (both regional capitals, Trnava and Nitra, are also included in the area of low turnout). In other parts of Slovakia's territory, larger clusters of low-turnout municipalities are sparse; these typically include other regional capitals and their immediate surroundings—Košice, Trenčín, Banská Bystrica (in contrast, Žilina and Prešov are two regional capitals not surrounded by contiguous areas of low turnout)—or other large cities (e.g., Poprad in the Prešov Region).
The following four local elections (2002, 2006, 2010, and 2014) witnessed a considerable decline in Moran's I values, which resulted in the long-term decline of local turnout clustering, although the main patterns of turnout clustering across the Slovak territory remained visible in their basic outlines. Thus, the municipalities with large clusters of the H–H pattern remained concentrated in the Prešov Region, although the size of the initial contiguous area of high local turnout was reduced to several smaller units. Similarly, the relatively contiguous area of high turnout along the Ukrainian border (in the eastern Košice Region) was preserved. Other than that, there were no larger clusters of municipalities with a large share of citizens using their right to vote in local elections.
Furthermore, the decline of clustering was visible to a similar extent in the case of the L–L pattern. The relatively large area of neighboring low-turnout municipalities that used to cover almost the entire western Bratislava Region and parts of the Trnava and Nitra Regions was reduced to a few smaller clusters. More importantly, whereas relatively large clusters of low-turnout municipalities formed around almost all regional capitals in 1998 (except Žilina and Prešov), in 2018 this was only the case for the country's two largest cities, the capital city of Bratislava and Košice in the east.
Furthermore, just as the results of bivariate Moran's I have consistently identified rather low levels of global spatial clustering of electoral participation between local elections, so does its spatial representation in the form of bivariate local clusters (Figure 3) show only a minor occurrence of regionalisation of municipalities with low or high levels of turnout lasting (or shifting) between elections. More importantly, the identified clusters of bivariate local indicators of spatial autocorrelation are largely identical to the maps of univariate LISA indicators for the different municipal elections presented above. A comparison of selected election years at the beginning and end of the observed time period but also temporally distant pairs of elections, confirms a high level of spatiotemporal stability of electoral participation in the different municipalities—despite their, once again, significantly decreasing number.
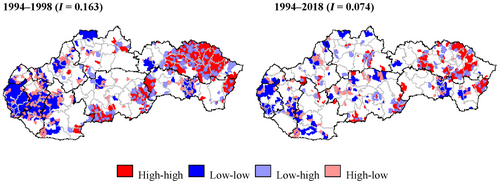
Table 4 presents results from the spatial regression models estimating effects on electoral participation in Slovak local elections. A basic comparison of the regression models indicates very similar amounts of total variance explained (between 35% and 39%), with the exception of the last local elections (27%, an 8% decrease in the explained variance of the model between the 2014 and 2018 elections). Furthermore, the effect of most variables in all models was consistent with theoretical assumptions (with changing direction of effects only in some minor cases and especially for variables with weak effects), and very similar effects of independent variables were observed across local elections.
| 2006 | 2010 | 2014 | 2018 | |
|---|---|---|---|---|
| Constant | 15.753 (3.115)*** | 20.731 (3.312)*** | 24.628 (3.273)*** | 14.703 (3.357)*** |
| Turnout (W) | 0.178 (0.035)*** | 0.105 (0.038)** | 0.089 (0.039)* | 0.148 (0.042)*** |
| Municipality size (log) | −2.042 (0.422)*** | −1.794 (0.425)*** | −2.487 (0.411)*** | −0.638 (0.430) |
| Primary education | 0.019 (0.038) | 0.058 (0.038) | 0.079 (0.037)* | −0.039 (0.040) |
| Unemployment | 0.066 (0.045) | 0.075 (0.045) | −0.036 (0.044) | −0.069 (0.048) |
| Previous turnout (t − 1) | 0.335 (0.020)*** | 0.275 (0.018)*** | 0.257 (0.018)*** | 0.299 (0.020)*** |
| Previous turnout (t − 2) | 0.238 (0.022)*** | 0.168 (0.021)*** | 0.139 (0.019)*** | 0.188 (0.020)*** |
| Previous turnout (t − 3) | 0.018 (0.016) | 0.153 (0.020)*** | 0.191 (0.020)*** | 0.121 (0.019)*** |
| Log-likelihood | −11,121.6 | −11,132.3 | −11,093.3 | −11,331.6 |
| AIC | 22,259.2 | 22,280.7 | 22,202.5 | 22,679.1 |
| BIC | 22,307.1 | 22,328.5 | 22,250.4 | 22,727.0 |
| N | 2927 | 2927 | 2927 | 2927 |
| R 2 | 0.388 | 0.358 | 0.346 | 0.267 |
- Note: Unstandardised regression coefficients, standard errors in parentheses.
- Source: Slovak Statistical Office; own calculation.
- * p < 0.001;
- ** p < 0.01;
- *** p < 0.05.
In the first step of the analysis, the new turnout [W] variable in the spatial lag model indicates the effect of autocorrelation on variance of the dependent variable. The effect varied in time, but while there was a moderate decline of the effect on the dependent variable of spatial autocorrelation of voter turnout between a given municipality and its surroundings between the elections of 2006 and 2014, the last local elections brought the effect of the variable back to almost the same level as in 2006. However, in all local elections since 2006, growing autocorrelation had a positive effect on turnout: a unit (1%) growth of spatial autocorrelation between a municipality and its surroundings was accompanied by a turnout growth between 0.09% (the local elections of 2014) and 0.18% (the local elections of 2006), with a mean value of 0.13% for all elections studied. In substantive terms, this evidence of a slightly positive effect of spatial autocorrelation on local turnout levels in a given municipality suggests that a low turnout rate as well as a high turnout rate is partly driven by the contagion effect, that is, by factors common to both the unit in question and its surroundings (as positive autocorrelation identifies both areas where high-level turnout in one unit is accompanied by high levels in neighboring units and areas where low turnout in one unit is associated with low levels in neighboring places). However, as this effect is only moderate, in contrast to the high levels of inter-electoral stability (uniformity) of turnout in individual municipalities, we can hypothesize that idiosyncratic factors (specific to the municipality in question and different across municipalities) are very important for explaining local-level electoral participation.
The Slovakian case, too, confirmed municipal size as a very strong (or key) explanatory variable of local turnout. However, its strongly negative effect varied to a relatively large extent. More importantly, while the elections between 2006 and 2014 saw a strong decline of turnout with growing municipality size (although the negative size effect first exhibited some decline and then a strong growth), a much more substantial transformation was observed in the 2018 local elections. On one hand, the negative size effect on local electoral participation was preserved; on the other hand, it decreased to almost one-fourth of the 2014 level (and to almost one-third of the 2010 level). Thus, the 2018 elections suggested a large weakening of the effect of Slovakia's settlement structure on electoral participation, which is a starting point for a more detailed investigation as to why this heterogeneity exists and what kind of social processes it relates to.
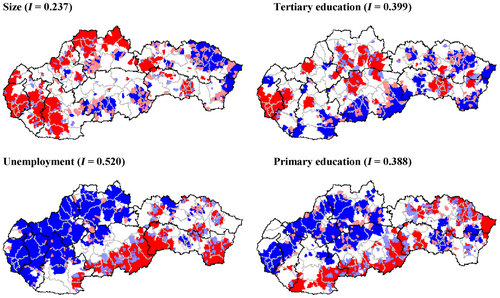
A brief attempt to visualize the transformation of the relationship between size and local turnout (Figure 4) again demonstrates that in the year 1998 (at the highest level of clustering of high/low-turnout municipalities), there were relatively large clusters of municipalities where a larger local population was associated with low turnout in local elections (especially municipalities in western Slovakia's Bratislava, Trnava and Nitra Regions) or, conversely, small municipality size was associated with high turnout (especially a large cluster of municipalities in eastern Prešov Region plus several minor clusters in the Banská Bystrica and Košice Regions).
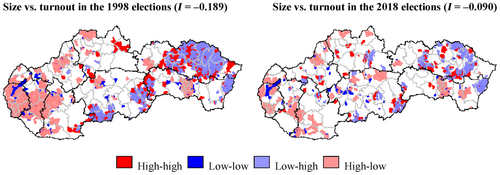
So, although our results show that the claim of higher turnout in smaller municipalities was generally valid, the map showing the clustering of municipalities according to their size, as well as the cluster maps for other independent variables (Appendix B), show a relatively large number of municipalities deviating from this pattern, especially in the case of larger municipalities. Furthermore, in addition to the results of regression analysis, also the values of bivariate Moran's I (Table 5) identified a significant drop of the global spatial clustering between size and voter turnout in the 2018 elections (to half the levels of the first three local elections). More importantly, the gradually decreasing effect of size on local turnout was confirmed not only by the above-mentioned regression coefficients in spatial lag model but also by Pearson correlation coefficient values (Table 5). The initial rise of the negative association between size and local turnout, which approximated as much as −0.5 in the 1998/2002 pair of elections, was followed by a gradual decrease, which culminated in 2018 when the negative relationship between local population and voter turnout slumped to the level of weak correlation (−0.264).
| 1994 | 1998 | 2002 | 2006 | 2010 | 2014 | 2018 | |
|---|---|---|---|---|---|---|---|
| Bivariate Moran's I | −0.167 | −0.189 | −0.172 | −0.139 | −0.125 | −0.130 | −0.090 |
| Pearson correlation | −0.404 | −0.496 | −0.489 | −0.403 | −0.374 | −0.381 | −0.264 |
- Source: Slovak Statistical Office; own calculation.
This development also has its spatial representation in the form of bivariate local clusters, as the LISA cluster map for 2018 only shows minor occurrences of any form of spatial clustering (i.e., spatial dependence) between size and local turnout compared to practically all previous elections (not documented) in which the patterns of bivariate LISA cluster maps were very similar to the year 1998 (Figure 4).
Other interesting results relate to the question of whether the degree of turnout in a specific local election reproduces at a similar level in the following local elections. However, as previous turnout would be an endogenous predictor of the percentage turnout in the following elections, we controlled for the effect of electoral participation, including its lagged versions. Overall, our data confirmed the assumption that the historical level of local political (electoral) participation affects the degree to which voters are willing to participate in the local electoral race in the future. In all regression models, turnout in previous elections relatively strongly influenced turnout in following elections.
Furthermore, the positive effect of turnout in previous elections was relatively constant across all models, and more importantly, even if the previous turnout percentage is lagged (regardless of whether by one or two terms, that is, practically 8 or 12 years), it is still (with one exception) significant in the positive direction. This confirms the importance of local context. We found a decreasing effect of previous turnout in local elections (with growing time since the election), possibly a sign of a gradual change in the electorate (although more in-depth investigation would be required to prove this). In spite of that, the persistent significant positive effect of the variable shows that exposure to a local political culture characterized by higher or, in contrast, lower voter turnout levels generally plays an important role in the reproduction of that political culture, one which encourages (or fails to encourage) voters to cast their ballots to influence the workings of the local political process in their community. On the other hand, as presented above, also the stability of turnout in local elections between election years (Table 3) has a tendency to decrease from the level of substantial to very strong correlation (above 0.6 in the elections of 1998 and 2002) to medium size to substantial correlation (under 0.5 in the elections of 2014 and 2018).
Finally, concerning the control variables, the effect of both variables was very weak and, with one exception, not statistically significant. At the same time, their effect was not constant between elections, and in many cases influenced local turnout in the opposite way than shown by previous results of Slovak parliamentary elections. In almost all elections, then, a higher proportion of voters with primary education in a municipality made a positive contribution to local turnout,10 while the effect of unemployment was rather mixed: rising unemployment was connected to higher interest among voters to participate in some local elections, while other elections saw the opposite effect.
5 DISCUSSION AND CONCLUSION
The main goal of the article was to examine long-term development trends in spatial distribution of electoral participation in Slovak local elections. Although our analysis is limited to a single country, we believe that the results are interesting for a general audience as well, as the extremely fragmented settlement structure of Slovakia provides a highly suitable context for applying spatial econometric techniques of aggregate-data analysis. An analysis of spatial distribution of local electoral participation using the methods of spatial autocorrelation and spatial regression was practically applied to examine the small-scale level of all almost 3000 Slovak municipalities for seven local elections between the years 1994 and 2018, and the mapping of local turnout resulted in several main conclusions.
The analysis of electoral participation distribution using global Moran's I showed that the spatial pattern of voter turnout in Slovak municipalities proved to be relatively highly stable. At the same time, both the univariate LISA cluster maps (depicting the spatial clustering of and spatial deviations from local turnout in a single election) and the bivariate LISA cluster maps (that help us analyze the spatiotemporal (in)stability of local turnout between elections) demonstrated that in spite of the disparate character of the spatial autocorrelation of local turnout across the Slovak territory, there is no substantial inter-electoral change of the clustering of turnout in the different municipalities, except for an overall significant decline of the homogeneity of the clusters identified. This suggests a high level of spatiotemporal stability of voter turnout between local elections in the different municipalities, whether they were places of higher or lower participation of citizens in their local politics.
Furthermore, our analysis rather supports Klimovský's (2022) claim that although electoral participation tends to be higher in smaller municipalities, this relationship is not entirely linear. Indeed, the regression results, as well as the values of the Pearson correlation coefficient, show that the relationship between size and turnout significantly weakened in the 2018 local elections. This, along with a simultaneous decline of the regression model's explanatory power, suggests that a gradual partial decoupling might be underway between the settlement structure (local population size as a scale or categorical variable) and the level of voter turnout in local elections. We can hypothesize that the above-mentioned continuing decline of turnout clustering was caused by, among other things, the slight but long-term approximation of turnout levels between the smallest municipalities and major cities observed elsewhere (see Kostelecký & Krivý, 2015, pp. 400–402).
Although the rise of local turnout in largest cities falls short of the level reached in the parliamentary elections of 2020, where voter turnout in the largest cities did exceed the smallest municipalities (Kevický, 2020b), and the assumed trend of rising local turnout does not apply to all large cities, many of the largest Slovak cities witnessed a significant rise of turnout in the 2018 local elections. The assumed trend of rising local turnout does not apply to all large cities: for instance, in the capital city of Bratislava, local turnout grew from 33.79% in 2014 to 40.67% in 2018, while the country's second largest city, Košice, exhibited an almost constant level of local turnout (34.45% compared to 35.71%).11 In contrast, a significant increase in voter turnout was recorded by many municipalities over 20,000 inhabitants.12
Worth mentioning is one of the reasons for voters' rising interest in local elections in many larger cities, namely their demand for a new type of politics and a generational change, which boosted the success of independent (often progressive) candidates in mayoral elections, for instance in the capital city of Bratislava or in Nitra (see Horváth & Machyniak, 2018, pp. 80–83; Kováčová, 2019, pp. 157–162). This was also connected to the increased use of social media in the election campaign, especially by independent candidates in large cities. However, a clear explanation of the substantial decline of the size effect on local turnout in 2018 would require simultaneous analysis of individual data to shed light on the changing motivations of voters in Slovak municipalities. As such data is unfortunately not available at the chosen level of aggregation, the question remains a challenge for future research.
Last but not least, while we found some positive spatial autocorrelation of turnout between a given municipality and its surroundings, suggesting the existence of a contagion effect, this effect was not too strong. More importantly, as shown by the LISA maps, this effect quickly waned with growing distance. The fact that we have found only limited presence of local turnout diffusion between neighboring municipalities thus suggests that in the Slovak case, we could not confirm the existence of expansion diffusion, which is based (depends) on direct contact and the spreading of given phenomenon (experiences of higher or lower electoral participation in local political cultures) over a large (surrounding) territorial area. Furthermore, as our analysis also showed that there is no clear relationship between the clustering of voter turnout and municipality size in Slovakia, we did not find sufficient support for hierarchical diffusion, which does not require direct contact but is mediated by broad cultural influences that vary between municipality size categories, with substantial spatial diffusion within each category.
Therefore, one of the central conclusions of our research is that voter turnout attained in a municipality in a specific election (namely as far back as in the early 1990s in many municipalities) reproduces at a similar level in the following election in the same municipality and its close vicinity, rather than diffusing to more remote surrounding municipalities in the form of a contagion effect, future research should seek to identify the main reasons why in some parts of the Slovak territory the effect of size, that is, that of the country's extremely fragmented settlement structure, contradicts the pattern of higher turnout in smaller municipalities.
Precisely such geographic comparison at the lowest level of aggregation is a good demonstration of how that approximation is reflected in the spatial dimension, too. The empirical findings based on geospatial techniques thus may also have their substantial local policy implications as our results suggest that the levels of citizens' political participation in local political decision-making processes are largely endogenous phenomena. This is evidenced by the results of spatial regression (spatial lag models) because, regardless of whether the previous turnout variable was lagged by one or two terms, its permanently positive effect (although decreasing with growing time since the previous election) suggested that a political culture characterized by higher civic (electoral) participation or, in contrast, higher electoral abstention has a tendency to reproduce in time.
Furthermore, as we mentioned the endogenous character of local turnout in Slovakia, we can hypothesize that local political processes in individual municipalities are driven by idiosyncratic factors (specific to the individual municipality), which seem highly important for explaining local-level electoral participation. A high degree of randomness in patterns of local turnout, then, could be, at least partly, attributed to the diverse nature of municipalities in Slovakia, together with the country's generally very fragmented settlement structure. Here, future research should answer the question whether the scope the diffusion effect in turnout is dependent on the specific settlement structure in Slovakia, because as we mentioned above, in the case of descriptive representation of women, the contagion effect was typical rather of countries with more concentrated settlement structures (Nordic countries) than ones with more fragmented structures (Spain, Czechia).
Finally, as especially the local elections in 2018 suggested that the local political environment has its own dynamics increasingly independent of municipality size and this environment has a tremendous power to strengthen or erode local turnout, a more detailed analysis of the effect size of internal/external factors on patterns of local electoral participation remains a challenge for future research, where an analysis of local political context combining both quantitative and qualitative techniques should be a priority. Another reason is that although our spatial-econometric methods (LISA indicators, or spatial lag model) can find some presence of diffusion or contagion processes, the evidence of these processes is indirect because the spatial regression models cannot identify a specific (causal) mechanism producing the spatial effects (Tam Cho, 2003). In this context, the discovery of spatial effects can provide orientation for future research. This research will require working with individual data and placing more detailed emphasis on uncovering the causal mechanisms behind differences in the determinants of local turnout in individual municipalities, or the determinants which produce diffusion in some places, compared to other places without the presence of this phenomenon.
ACKNOWLEDGMENT
This study was prepared under a grant project supported by the Czech Science Foundation, Grant No. 24-10612S, “Local-level democratic performance and quality of government in Central and Eastern Europe at time of multiple crises and democratic backsliding”. Open access publishing facilitated by Univerzita Jana Evangelisty Purkyne v Usti nad Labem, as part of the Wiley - CzechELib agreement.
CONFLICT OF INTEREST STATEMENT
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Endnotes
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in Štatistický úrad SR at https://slovak.statistics.sk.