Review of Income and Wealth
Volume 71, Issue 1 e12688
ORIGINAL ARTICLE
Open Access

Poverty convergence clubs

Ángel S. Marrero, 

Ángel S. Marrero

CEDESOG, Universidad de La Laguna

Search for more papers by this author
Gustavo A. Marrero, 

Corresponding Author

Gustavo A. Marrero

CEDESOG, Universidad de La Laguna

Departamento de Economía and CEDESOG, Universidad de La Laguna

Correspondence to: Gustavo A. Marrero, Departamento de Economía and CEDESOG, Universidad de La Laguna, San Cristóbal de La Laguna, Spain ([email protected])

Search for more papers by this author
Luis Servén, 

Luis Servén

CEMFI and Bank of Spain

Search for more papers by this author
First published: 14 March 2024
https://doi.org/10.1111/roiw.12688
Citations: 2

The authors acknowledge helpful comments by two anonymous referees and the editor, and the financial support from the Ministerio de Economía y Competitividad (Spain) under the project PID2022-137352NB-C44.

Abstract

Global eradication of extreme poverty requires absolute convergence of poverty rates worldwide towards zero. Empirical analysis of poverty data for 100 emerging and developing countries over four decades reveals that such a goal is likely to remain elusive. Rather than absolute convergence, we find club convergence: countries' long-run poverty rates cluster into several distinct clubs, whose number depends on the specific poverty dimension considered. Only the lowest-poverty club exhibits poverty rates approaching zero by the end of the sample. In contrast, the highest-poverty club, which accounts for nearly half the world's poor, evokes a poverty trap: its average poverty barely budged over the entire period examined. Overall, income—its initial level and, especially, its growth rate—matters more than inequality for shaping countries' club membership, particularly for the highest-poverty club. Nevertheless, inequality plays a substantive role for membership in the intermediate-poverty clubs, which achieved the greatest poverty reduction.

1 Introduction

The first of the Sustainable Development Goals (SDGs) is the global eradication of extreme poverty by 2030. To achieve it, poverty across developing countries should converge to zero by such date. However, despite the considerable progress made at global poverty reduction over the last two decades, there is still a long way to go: in 2019, people living below the poverty line of US$2.15 (in 2017 PPP dollars) still represent 8.4 percent of the world population (648 million people). Moreover, poverty rates display considerable variation between and within world regions (World Bank, 2022). This prompts the question whether poverty is in fact converging towards zero across the world.

In this paper, we provide an empirical assessment of poverty convergence across a large sample of emerging and developing countries. Using poverty data from PovcalNet, we consider three different dimensions of absolute poverty (Ferreira et al., 2016): the scale of poverty (as captured by the headcount rate, the poverty measure at the heart of the SDGs), poverty intensity (as measured by the poverty gap), and poverty severity (as measured by the squared poverty gap and the Watts index). For each of these poverty dimensions, our framework allows for four possible scenarios: divergence, absolute convergence, conditional convergence, and club convergence (Johnson & Papageorgiou, 2020).

This paper is, as far as we are aware, the first to perform formal tests of the hypothesis of club convergence in absolute poverty. Conceptually, a poverty convergence club is a set of countries whose poverty rates may differ over an extended period, but converge to one another in the long-run (Galor, 1996). While traditional empirical techniques (borrowed from the empirical growth literature) may be useful to disentangle poverty divergence from absolute or conditional convergence, they are not appropriate to differentiate these situations from club convergence (Durlauf & Johnson, 1995; Islam, 2003). Instead, we use the panel clustering testing approach of Phillips and Sul (2007, 2009). Building on a nonlinear factor model with time-varying loadings, it can be used to test a variety of hypotheses on the series dynamics, including divergence, club convergence, and both absolute and conditional convergence, without the need of specific assumptions regarding the order of integration of the series.

Using data for a sample of 100 emerging and developing countries over 1981–2019, we unambiguously reject the hypotheses of absolute and conditional convergence. Instead, we find strong evidence of club convergence: four clubs for the scale of poverty (as captured by the headcount), and two or three clubs for poverty intensity and severity. For all poverty measures considered, the average poverty rate of the highest-poverty club remains virtually unchanged at very high levels (e.g., between 50 percent and 60 percent for headcount poverty) over the four decades. Out of the 614 million poor in our sample countries in the final year of analysis, 259 million (i.e., almost half) live in countries belonging to the highest-poverty club of headcount poverty, whose lack of progress at poverty reduction over the sample period effectively makes it akin to a poverty trap (Azariadis & Stachurski, 2005; Bowles et al., 2006).

At the other end, for all poverty measures examined, the average poverty rate of the lowest-poverty club follows a downward trend, approaching zero by the end of the sample. Intermediate-poverty clubs diverge from the highest-poverty club since the mid-1990s, and show the largest poverty reduction of all clubs over the entire sample.

We find that geography matters for club membership, but it is far from being the only factor at play. For example, Sub-Saharan African countries account for most of the membership in the highest-poverty club, but almost half of all Sub-Saharan African countries belong to other clubs with lower average poverty levels. Moreover, outside the highest-poverty club, membership is geographically quite diverse. The country ordering defined by the poverty clubs does not amount to a mere partition of the country sample into contiguous subsets according to countries' poverty rates at the end of the period of analysis. Likewise, the club-based ordering is also different from those derived from conventional country classifications based on per capita income, such as the World Bank income classification.

In the second part of the paper, we characterize the effect of income and inequality on countries' likelihood of belonging to a particular club. In line with the existing literature (see references in Section 2), we assume that these two variables summarize the fundamental factors driving poverty dynamics (and hence club formation). Since our dependent variable, club membership, is an ordinal discrete variable, we estimate an ordered response model (Greene & Hensher, 2010; McKelvey & Zavoina, 1975) that relates club membership to per capita income and inequality (as captured by the Gini index). We further distinguish between the initial values of the forcing variables and their changes over the sample period, since the formation of clubs may depend on both dimensions.

Using this approach, we can assess the respective roles of initial income and inequality, as well as their changes over time, for countries' poverty club membership. This allows us to address two important questions. First, to what extent is membership just driven by countries' initial conditions, as opposed to their subsequent performance? Second, what is the overall contribution of inequality, as opposed to income, to club membership? Furthermore, we can also assess if the answers to these questions are the same for all clubs, or if they are different for high- and low-poverty clubs.

For this purpose, we estimate a general model including all four explanatory variables (initial conditions and changes in both income and inequality), as well as two restricted models—one including only initial conditions, and another including only income variables—and compare their ability to correctly predict countries' poverty club membership.

For all four poverty measures considered and the entire sample, we find that the biggest contributors to the formation of poverty clubs are initial income and its change over time, while inequality plays a secondary role in shaping poverty club membership. However, closer examination of our results yields additional insights, which apply to all the poverty measures considered. First, the lowest-poverty clubs are dominated by countries that started from favorable initial conditions in terms of income and/or inequality. Second, country membership in the highest-poverty clubs is very well predicted by initial income and its growth rate, while inequality does not play a major role. Lastly, initial conditions have contributed relatively little to countries' membership in intermediate-poverty clubs. The inequality dimension matters more for membership in these clubs than it does for membership in the highest-poverty clubs.

The rest of the paper is structured as follows. In Section 2, we explain our contribution to the literature. In Section 3, we provide an overview of the poverty data used and conduct a classical convergence analysis. In Section 4, we describe the implementation of our club convergence methodology and the main empirical results for the alternative poverty measures considered. In Section 5, we estimate an ordered response model to analyze the relation between club membership and the two main drivers of poverty: income and inequality. Finally, Section 6 presents the main conclusions.

2 Contribution to the Literature

Our paper is embedded in an extensive literature on convergence (recently surveyed by Johnson & Papageorgiou, 2020; Kremer et al., 2021) and on the multidirectional links among poverty, growth and inequality (recently surveyed by Cerra et al., 2021; Marrero & Servén, 2022). Three strands of that literature are especially relevant in our context, namely those respectively concerned with poverty convergence; the formation of convergence clubs; and the contribution of income and inequality to poverty.

Few papers have analyzed the issue of poverty convergence. Moreover, they reach conflicting conclusions. Using PovcalNet data, Ravallion (2012) finds no evidence of convergence among a set of 90 developing countries. However, Sala-i-Martín (2006) reaches the opposite conclusion using data from the World Income Inequality Database (WIID), although he cautions of a certain degree of divergence in some Sub-Saharan African countries (Pinkovskiy & Sala-i-Martin, 2013). More recently, Ouyang et al. (2019) have revisited the issue of poverty convergence using an extended version of Ravallion's data. For their full country sample, they find no evidence of convergence. However, they do find convergence among Sub-Saharan African countries. Overall, poverty convergence remains an open question. We contribute to this literature by bringing the club convergence perspective and offering formal tests of club convergence in absolute poverty.

In turn, research on the formation of convergence clubs derives from the literature on multiple equilibria (Abramovitz, 1986; Baumol, 1986), and the convergence club approach has been applied mainly to individual income or to country-level GDP per capita (Bartkowska & Riedl, 2012; Phillips & Sul, 2009; Quah, 1996). This paper applies this approach to poverty. Importantly, the existence of income convergence clubs does not automatically imply the existence of poverty convergence clubs. The reason is that poverty depends on both mean income and inequality (Bourguignon, 2003). Countries converging to the same income club but following sufficiently different inequality paths could converge to different poverty clubs. Thus, to assess the existence of poverty convergence clubs it is necessary to apply the club convergence approach to poverty itself rather than income, and this is our contribution to the literature on this front.

Another strand of the literature explores the links between income growth and inequality, on the one hand, and poverty, on the other. The bulk of this literature focuses on the poverty-reducing effect of growth and the factors that shape it (Bourguignon, 2003; Dollar et al., 2016; Dollar & Kraay, 2002; Kraay, 2006; Ravallion, 2004). Empirically, there is broad agreement that growth reduces poverty, hence fostering aggregate growth is pro-poor (see also Bergstrom, 2020; Bluhm et al., 2018; Ferreira et al., 2010). In contrast, the contribution of changes in inequality to poverty reduction has generally been found to be much smaller, which probably explains why the literature on the impact of inequality on poverty is more limited, although there are several relevant exceptions, such as Ravallion (2005), Kalwij and Verschoor (2007) or Fosu (2017). More recently, Bergstrom (2020) or Lakner et al. (2022) find evidence supporting the relevant role of declining inequality for poverty reduction. To this literature we contribute by assessing the respective contributions of income and inequality to shaping countries' membership in the different poverty convergence clubs, and examining how those contributions may vary across clubs.

3 Absolute Poverty Dynamics Around the World

We consider the following family of additive poverty measures, denoted by P $$ P $$ (Sen, 1976; Watts, 1968):
P ( z ) = ∫ 0 P 0 Ω [ y ( q ) ; z ] dq , $$ P(z)={\int}_0^{P0}\Omega \left[y(q);z\right]\mathrm{dq}, $$ (1)
where z $$ z $$ is the poverty line, y ( q ) $$ y(q) $$ denotes the income of the qth $$ qth $$ percentile of the income distribution at time t $$ t $$ (the time sub-index is omitted to save notation) and P0  = F ( z ) $$ =F(z) $$ , with F ( · ) $$ F\left(\cdotp \right) $$ the cumulative distribution of income, is the headcount poverty rate. For Ω ( y ( q ) ; z ) = ( z − y ( q ) / z ) θ $$ \varOmega \left(y(q);z\right)={\left(z-y(q)/z\right)}^{\theta } $$ , we obtain the Foster–Greer–Thorbecke class of poverty measures (Foster et al., 1984), which includes the headcount (letting θ = 0 $$ \theta =0 $$ ) P0, the poverty gap ( θ = 1 $$ \theta =1 $$ ), henceforth denoted P1, and the squared poverty gap ( θ = 2 $$ \theta =2 $$ ), denoted P2. For Ω ( y ( q ) ; z ) = ln [ z / y ( q ) ] $$ \varOmega \left(y(q);z\right)=\ln \left[z/y(q)\right] $$ , we obtain the Watts index, denoted W.

Each of these measures provides information on a different dimension of absolute poverty. P0 captures the scale of poverty, that is, the proportion of the population with income below the poverty line z $$ z $$ . It does not change in response to changes in the income distribution below the poverty line, that is, when a very poor individual becomes less poor or when a poor individual becomes even poorer. In turn, P1 provides a measure of poverty intensity, as it shows the (average) shortfall of the income of the poor relative to the poverty line. P2 and W capture the severity of poverty. P2 weighs the income gap of each household by the size of the gap itself, hence increases in the resources of the poorest individuals reduce overall poverty by more than do changes in the resources of less-poor individuals. Finally, W places a bigger weight than P2 on very low incomes, and a lower weight on the incomes of less-poor individuals.

Time-series data on these poverty measures are taken from PovcalNet, using a poverty line of US$2.15 per individual per day at 2017 PPP, which replaces the earlier threshold of US$1.90 per individual per day at 2011 PPP (Ferreira et al., 2016). PovcalNet's poverty estimates are constructed from household surveys. In countries where survey data are not available on an annual basis, growth rates from national accounts are used to project consumption or income forward and backward, obtaining interpolated data.

From the initial set of 166 countries, we retain only those whose surveys report poverty information at the national level, and drop those with solely rural or urban coverage. To keep the focus on poverty, we also disregard rich countries, since their absolute poverty levels are zero or very close to zero for all measures and years in the sample. Lastly, we drop countries with less than two surveys during the period and those with incomplete time series. Thus, our final sample consists of 100 emerging and developing countries over the period 1981–2019 (see Appendix A for details).

Table 1 reports descriptive statistics for the four poverty measures in 1981 and 2019, as well as their annual change over the period. Figure 1 shows the time path of their respective cross-sectional averages as well as the 25 and 75th percentiles. Several facts common to all four poverty measures are worth noting.

TABLE 1. Absolute Poverty: Descriptive Statistics
Headcount (P0) Poverty gap (P1) Squared poverty gap (P2) Watts (W)
Descriptive statistic 1981 2019 Annual p.p. change 1981 2019 Annual p.p. change 1981 2019 Annual p.p. change 1981 2019 Annual p.p. change
Mean 35.89 16.70 −0.52 16.09 5.98 −0.28 9.50 3.00 −0.18 26.60 8.74 −0.49
sd 29.09 20.60 −0.23 16.29 8.99 −0.20 11.19 5.13 −0.16 31.20 14.20 −0.46
p25 7.67 1.03 −0.20 2.23 0.26 −0.05 0.92 0.09 −0.02 2.97 0.30 −0.07
p50 29.05 6.80 −0.55 9.80 1.90 −0.22 5.34 0.63 −0.14 13.14 2.40 −0.30
p75 61.66 24.87 −1.01 26.66 8.04 −0.50 15.23 3.32 −0.31 42.98 10.92 −0.83
  • Notes: The table reports descriptive statistics (mean, standard deviation and percentiles) for the four poverty measures at the beginning and the end of the sample period). p25 denotes the 25th percentile, p50 the median and p75 the 75th percentile. Poverty measures are expressed in %, and annual changes in percentage points (p.p.).
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Absolute poverty trends. Note: The figures show the time path of the cross-sectional average and 25th and 75th percentiles of each poverty measure for the sample of 100 emerging and developing countries over the period 1981–2019.

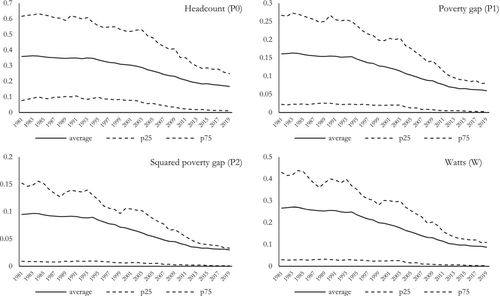
First, their respective cross-country averages follow similar trends. Between 1981 and 1993, average P0 remained relatively stable at around 35 percent, while the averages of the other poverty measures show a very slight decline, with P1, P2 and W hovering around 15 percent, 9 percent and 25 percent, respectively. However, between 1993 and 2019 the averages of all four measures exhibit a substantial reduction. Average P0 falls from 35 percent in 1993 to 17 percent in 2019, which amounts to a reduction of 0.7 percentage points (p.p.) per year. Over the same period, average P1, P2 and W similarly decline by 0.36, 0.23 and 0.61 p.p. per year, respectively. Second, the sample distributions of the four poverty measures are skewed to the right, as median poverty is in all cases much lower than average poverty. The third fact is the reduction in the between-country dispersion of absolute poverty over the sample period. All four poverty measures exhibit much lower standard deviation in 2019 than in 1981 (see Table 1). The time path of their 25–75th percentiles (Figure 1) reveals that dispersion decreases markedly after 1993. Moreover, the decline is more intense for poverty intensity (P1) and poverty severity (P2 and W) than for the poverty headcount.

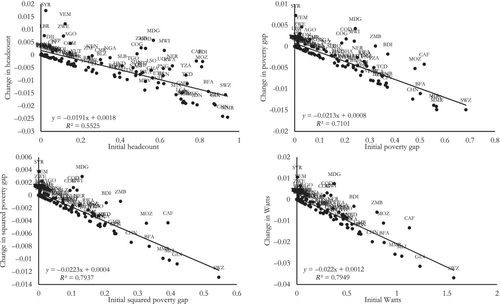
As a preliminary exploration of poverty convergence, Figure 2 shows the relationship between the annual change in poverty (in p.p.) between 1981 and 2019 and its initial level (in 1981) for the four poverty measures considered (i.e., absolute β-convergence graphs). The four scatter plots exhibit negative slopes, so that, on average, countries with higher initial poverty tended to reduce their poverty rate by more than did countries with lower initial poverty. Globally, absolute poverty is not diverging. However, cross-sectional regressions of poverty changes on initial poverty do not discriminate between absolute convergence and other types of convergence (Durlauf & Johnson, 1995; Quah, 1993, 1996).

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Absolute poverty. Beta convergence. Note: The figures show, for the sample of 100 emerging and developing countries, standard β-convergence graphs for the different poverty measures, that is, the relationship between the annual change in poverty (in p.p.) between 1981 and 2019 and its initial level (in 1981).

A more informative graphical tool is the distribution of poverty indices over time, which is useful for visualizing long-term trends in poverty across countries and detecting potential accumulation points suggestive of club convergence (Pittau et al., 2010; Quah, 1997). For the four poverty measures considered, Figure 3 shows these distributions for the beginning (1981), the middle (2000) and the end of the sample period (2019).

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Poverty distributions at initial, middle and final period. Note: The figures show the cross-country distribution of each poverty measure at the beginning (1981), middle (2000), and end (2019) of the sample period.

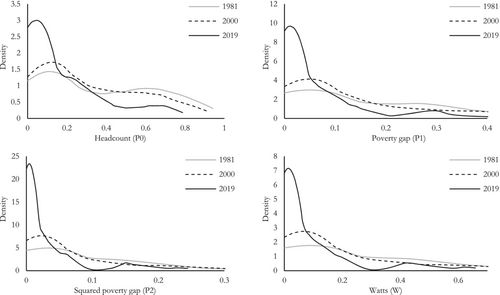
In all cases, there is a steady decline in the mean of the distribution, so that in 2019 it is about half of its 1981 value. Moreover, all distributions show a thinning in the middle and are at least bimodal or, to use the term coined by Quah (1997), twin-peaked, with one mode corresponding to low poverty levels and the other to high poverty levels. For example, for the headcount, one peak is located between 0 and 0.15 and another between 0.6 and 0.7, depending on the year.

As the figure shows, the global mode is the lower-poverty one. Moreover, its density has increased over the years. In 2019, there are many more countries around the low-poverty mode than in 1981 or 2000. In fact, the distributions in 1981 and in 2000 resemble each other more closely than they resemble the 2019 distribution. While poverty shows a downward trend over the entire sample period, the gap between the high- and low-poverty modes has widened. For example, for the headcount poverty rate, it was about 50 p.p. in 1981 and 2000, while it is about 65 p.p. in 2019.

Multimodal cross-country distributions may reflect the existence of convergence clubs, with each mode corresponding to a convergence club. However, multimodality is neither necessary nor sufficient for convergence clubs to exist (Pittau et al., 2010). A rigorous assessment of poverty convergence requires empirical tools better suited to deal with such settings. This is the task undertaken in the next section.

4 Poverty Convergence Clubs: Empirical Results

In this Section we describe the implementation of the Phillip and Sul (2007) club convergence method and the main empirical results for the alternative poverty measures considered. To save space, technical details are relegated to several appendices.

4.1 Implementation

Implementation of the Philips and Sul (henceforth P-S) approach (described in detail in Appendix B) requires a balanced panel dataset, and we use interpolated annual data from PovcalNet on the different measures of poverty over the 1981–2019 period. The P-S approach focuses on the long-term component of the variable of interest. Prior to its empirical implementation, it is necessary to purge the data of cyclical components and short-term noise through a suitable form of smoothing. For this purpose, P-S specifically suggest using the Hodrick and Prescott (1997) filter (HP), because it is well-suited to short time series, it does not require prior specification of the nature of the time series trends, and the only input it needs is the value of the smoothing parameter. In their application to annual data, P-S use the HP filter with a smoothing parameter of 400, which probably leads to excess smoothing. Indeed, the seminal paper of Hodrick and Prescott (1997) uses a smoothing parameter of 100.

Ravn and Uhlig (2002) propose a general rule for selecting the smoothing parameter under different data frequencies. In our baseline specification, we follow Ravn and Uhlig's rule and set the smoothing parameter at 6.25. This amounts to a cautious choice that applies minimal filtering to the original series. Nevertheless, because the choice of smoothing parameter may affect the empirical results obtained with the P-S approach (Tomal, 2023), we perform additional experiments with smoothing parameter values of 100 and 400. They show that the qualitative results regarding the number of clubs and club membership remain largely unchanged (see Appendix C).

4.2 Results

We first test the null hypothesis of absolute convergence for the four poverty measures considered by estimating Philips and Sul's so-called log-t regression (Equation (B4) in Appendix B). Detailed results for the parameters and statistics of this regression (omitted here to save space) are shown in Table B1 in Appendix B. In all cases, we unambiguously reject both absolute and conditional convergence for the full sample—in spite of the appearance of absolute convergence that a naïve look at Figure 2 might suggest.

Second, we use the clustering algorithm described in P-S to differentiate between global divergence and club convergence. The procedure reveals club convergence: four clubs for the headcount poverty rate, three for poverty gap and Watts, and two for the squared poverty gap. The detailed list of countries belonging to each club is shown in Table 2, with clubs arranged in descending order of long-run poverty—that is, Club 1 is the club with the highest long-run levels of poverty.

TABLE 2. Poverty Club Membership
Headcount (P0)
1 Belize, Burkina Faso, Burundi, Central African Republic, Comoros, Congo, Dem. Rep., Congo, Rep., Djibouti, Eswatini, Kenya, Lesotho, Madagascar, Malawi, Mozambique, Niger, Papua New Guinea, Rwanda, Syrian Arab Republic, Tanzania, Uganda, Yemen, Rep., Zambia, Zimbabwe
2 Angola, Benin, Cameroon, Chad, Ghana, Haiti, Liberia, Nigeria, Sao Tome and Principe, Solomon Islands, South Africa, Sudan
3 Bangladesh, Botswana, Cote d'Ivoire, Ethiopia, Gambia, The, Guatemala, Guinea, Honduras, India, Mali, Namibia, Senegal, Vanuatu
4 Algeria, Bhutan, Bolivia, Brazil, Bulgaria, Cabo Verde, Chile, China, Colombia, Costa Rica, Dominican Republic, Ecuador, Egypt, Arab Rep., El Salvador, Fiji, Gabon, Indonesia, Iran, Islamic Rep., Iraq, Jamaica, Kiribati, Korea, Rep., Lao PDR, Malaysia, Maldives, Mauritania, Mauritius, Mexico, Mongolia, Morocco, Myanmar, Nepal, Nicaragua, Pakistan, Panama, Paraguay, Peru, Philippines, Poland, Romania, Seychelles, Sri Lanka, St. Lucia, Thailand, Tonga, Trinidad and Tobago, Tunisia, Turkiye, Uruguay, Vietnam
Poverty gap (P1)
1 Belize, Benin, Burundi, Central African Republic, Congo, Dem. Rep., Congo, Rep., Cote d'Ivoire, Djibouti, Guinea-Bissau, Madagascar, Malawi, Mozambique, Syrian Arab Republic, Togo, Yemen, Rep., Zambia, Zimbabwe
2 Angola, Burkina Faso, Cameroon, Chad, Comoros, Eswatini, Ghana, Haiti, Honduras, Kenya, Lesotho, Liberia, Niger, Nigeria, Papua New Guinea, Rwanda, Sao Tome and Principe, Solomon Islands, South Africa, Sudan, Tanzania, Uganda, Vanuatu
3 Algeria, Bangladesh, Bhutan, Bolivia, Botswana, Brazil, Bulgaria, Cabo Verde, Chile, China, Colombia, Costa Rica, Dominican Republic, Ecuador, Egypt, Arab Rep., El Salvador, Ethiopia, Fiji, Gabon, Gambia, The, Guatemala, Guinea, India, Indonesia, Iran, Islamic Rep., Iraq, Jamaica, Kiribati, Korea, Rep., Lao PDR, Malaysia, Maldives, Mali, Mauritania, Mauritius, Mexico, Mongolia, Morocco, Myanmar, Namibia, Nepal, Nicaragua, Pakistan, Panama, Paraguay, Peru, Philippines, Poland, Romania, Senegal, Seychelles, Sri Lanka, St. Lucia, Thailand, Tonga, Trinidad and Tobago, Tunisia, Turkiye, Uruguay, Vietnam
Squared poverty gap (P2)
1 Belize, Benin, Burundi, Central African Republic, Comoros, Congo, Dem. Rep., Congo, Rep., Cote d'Ivoire, Djibouti, Guinea-Bissau, Kenya, Madagascar, Malawi, Mozambique, Sao Tome and Principe, Syrian Arab Republic, Togo, Yemen, Rep., Zambia, Zimbabwe
2 Algeria, Angola, Bangladesh, Bhutan, Bolivia, Botswana, Brazil, Bulgaria, Burkina Faso, Cabo Verde, Cameroon, Chad, Chile, China, Colombia, Costa Rica, Dominican Republic, Ecuador, Egypt, Arab Rep., El Salvador, Eswatini, Ethiopia, Fiji, Gabon, Gambia, The, Ghana, Guatemala, Guinea, Haiti, Honduras, India, Indonesia, Iran, Islamic Rep., Iraq, Jamaica, Kiribati, Korea, Rep., Lao PDR, Lesotho, Liberia, Malaysia, Maldives, Mali, Mauritania, Mauritius, Mexico, Mongolia, Morocco, Myanmar, Namibia, Nepal, Nicaragua, Niger, Nigeria, Pakistan, Panama, Papua New Guinea, Paraguay, Peru, Philippines, Poland, Romania, Rwanda, Senegal, Seychelles, Solomon Islands, South Africa, Sri Lanka, St. Lucia, Sudan, Tanzania, Thailand, Tonga, Trinidad and Tobago, Tunisia, Turkiye, Uganda, Uruguay, Vanuatu, Vietnam
Watts (W)
1 Belize, Benin, Burundi, Central African Republic, Comoros, Congo, Dem. Rep., Congo, Rep., Cote d'Ivoire, Djibouti, Guinea-Bissau, Kenya, Madagascar, Malawi, Mozambique, Syrian Arab Republic, Togo, Yemen, Rep., Zambia, Zimbabwe
2 Angola, Botswana, Burkina Faso, Cameroon, Chad, Eswatini, Ethiopia, Ghana, Haiti, Honduras, Lesotho, Liberia, Niger, Nigeria, Papua New Guinea, Rwanda, Sao Tome and Principe, Solomon Islands, South Africa, Sudan, Tanzania, Uganda, Vanuatu
3 Algeria, Bangladesh, Bhutan, Bolivia, Brazil, Bulgaria, Cabo Verde, Chile, China, Colombia, Costa Rica, Dominican Republic, Ecuador, Egypt, Arab Rep., El Salvador, Fiji, Gabon, Gambia, The, Guatemala, Guinea, India, Indonesia, Iran, Islamic Rep., Iraq, Jamaica, Kiribati, Korea, Rep., Lao PDR, Malaysia, Maldives, Mali, Mauritania, Mauritius, Mexico, Mongolia, Morocco, Myanmar, Namibia, Nepal, Nicaragua, Pakistan, Panama, Paraguay, Peru, Philippines, Poland, Romania, Senegal, Seychelles, Sri Lanka, St. Lucia, Thailand, Tonga, Trinidad and Tobago, Tunisia, Turkiye, Uruguay, Vietnam
  • Notes: The table shows the list of countries belonging to each of the estimated poverty clubs under each poverty measure. Countries in bold belong to the highest-poverty club under all poverty measures. Countries underlined belong to the lowest-poverty club under all poverty measures.

These results are consistent with the poverty distributions shown in Figure 3. For P0, the two accumulation points seen in the distribution correspond mostly to countries in Club 4, for the low-poverty mode, and to Clubs 1, 2, and 3 for the high-poverty mode. The flatness of the distribution around the high-poverty mode seems to conceal the existence of multiple clubs, which is revealed by the P-S approach. A similar situation occurs for P1 and W, while for P2 the P-S approach confirms the visual bi-modal distribution shown in Figure 3.

For each poverty measure, Table 3 summarizes the main characteristics for the full sample and each club: the number of countries and the average levels of poverty at the beginning and end of the period, along with its annual change. For P0, P1, P2 and W, the average levels of poverty in 2019 are 46.9 percent, 20 percent, 9.8 percent and 28.7 percent in the highest-poverty clubs, and 1.8 percent, 0.9 percent, 1.3 percent and 1 percent in the lowest-poverty clubs, respectively.

TABLE 3. Absolute Poverty: Convergence Clubs
Absolute poverty rate (average)
Measure Club Number of countries 1981 2019 Annual p.p. change
Headcount (P0) Club1 23 51.06 46.9 −0.11
Club2 12 37.13 24.79 −0.32
Club3 13 52.06 12.06 −1.05
Club4 50 23.92 1.77 −0.58
Divergent units 2
Full sample 100 35.89 16.70 −0.52
Poverty gap (P1) Club1 17 20.24 20.05 0.00
Club2 23 20.47 8.83 −0.31
Club3 60 13.24 0.89 −0.32
Full sample 100 16.09 5.98 −0.28
Squared poverty gap (P2) Club1 20 10.81 9.75 −0.03
Club2 80 9.17 1.32 −0.21
Full sample 100 9.50 3.00 −0.18
Watts (W) Club1 19 32.73 28.69 −0.11
Club2 23 36.55 11.84 −0.65
Club3 58 20.65 0.98 −0.52
Full sample 100 26.60 8.74 −0.49
  • Notes: For each poverty club under each poverty measure, the third column shows the number of member countries and the last three columns report the average poverty rates (expressed in %) at the beginning and the end of the sample period, along with its annual change in p.p.

Figure 4 shows the time path of the cross-sectional mean (with its 90% confidence interval) for each poverty measure and club. For the highest-poverty club (Club 1 in all measures), average poverty shows little change between the beginning and the end of the sample period—it remains at high levels throughout. For the lowest-poverty club (Club 4 for P0, Club 2 for P2 and Club 3 for P1 and W), the trend is also similar for all poverty measures: average poverty shows a slight but persistent reduction throughout the period to reach an average of almost zero in 2019.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Absolute poverty trends by convergence club. Note: The figures show the time path of the cross-sectional average of each poverty measure and year, and for each poverty club between 1981 and 2019, along with the 90% confidence intervals.

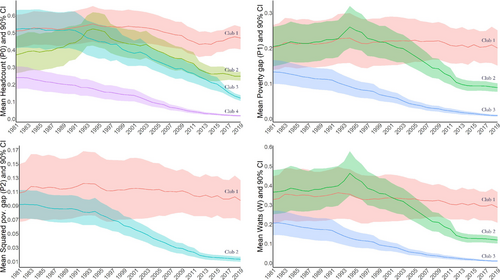
Intermediate clubs (Clubs 2 and 3 for P0 and Club 2 for P1 and W) show the largest extent of poverty reduction over the sample period. For headcount poverty, the comparison between Clubs 2 and 3 is interesting. Their poverty levels approach each other until becoming virtually identical by the mid-1990s. Thereafter, however, headcount poverty declines sharply among Club 3 countries, even approaching the levels of Club 4, while it undergoes a more modest reduction among Club 2 countries.

More broadly, the club composition provides a mixed perspective on the progress with global poverty eradication. Only the countries belonging to the lowest-poverty club appear to be converging to near-zero poverty. Table 3 shows that, depending on the poverty measure under consideration, they roughly represent between 50 percent and 80 percent of the country sample. In turn, countries in the intermediate-poverty clubs are making progress towards reduced, but not zero, long-run poverty rates. At the other end, however, countries belonging to the highest-poverty club have seen little poverty reduction in the last 40 years, which suggests that they may be caught in a poverty trap.

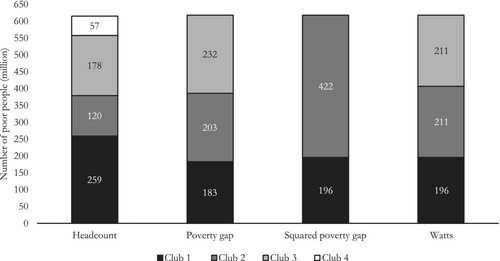
The distribution of the world's poor across clubs at the end of the sample period allows a more precise view on the prospects for global poverty eradication. We can compute it by summing the number of poor across each club's member countries in 2019. Figure 5 shows the distribution that results for each of the poverty measures considered. The total number of poor in our sample in 2019 equals 614 million. Out of that total, 259 million (42 percent) live in countries “trapped” in Club 1 of headcount poverty. At the other end, only 57 million live in countries approaching complete poverty eradication (i.e., belonging to Club 4 of headcount poverty). Moreover, Figure 5 also shows that, of those 259 million trapped in a high-poverty equilibrium, about 71 percent (183 million) appear to be trapped also in a path of persistently high poverty intensity (as implied by their allocation to Club 1 of the poverty gap), and about 76 percent (196 million) are stuck in persistently high poverty severity as well (as implied by their allocation to Club 1 of the squared poverty gap and the Watts index). Overall, the conclusion is that global poverty eradication is likely to remain elusive on current trends.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Total number of poor in 2019, by poverty club. Notes: The figure shows how the world's poor were allocated in 2019 across poverty clubs. For each country, we multiply its headcount poverty rate by its 2019 population. The totals by club are calculated summing the number of poor over the countries belonging to each club under the corresponding poverty measure.

To conclude this section, we should emphasize that the poverty clubs we identify differ from conventional groupings based on countries' geographic location or their observed levels of poverty or per capita income.

Geographic location does matter for club membership, especially for the highest-poverty club, but it is far from being the only factor at play (see Table A2 in Appendix A). For instance, while countries in Sub-Saharan Africa account for most of the membership in Club 1 (i.e., 78 percent, 76 percent, 80 percent and 79 percent of the member countries for P0, P1, P2 and W, respectively), around 25 percent of the region's countries belong to clubs with lower poverty levels. Moreover, membership in all the other clubs is geographically quite diverse: intermediate clubs comprise countries from Sub-Saharan Africa, Latin America and the Caribbean, East Asia and Pacific and South Asia, while lower-poverty clubs include countries from all regions.

Similarly, we show in Figure 6 that the poverty clubs we find do not reflect a mere partition of the country sample into contiguous subsets according to countries' poverty rates at the end of the period of analysis. Nor do the country groups defined by the poverty clubs match the groups derived from conventional classifications based on countries' per capita income, such as the World Bank income classification as of 2019 (see Figure 6). While there is a good deal of commonality between both classifications, it is far from a perfect match, which confirms that the club-based clustering provides independent information relative to that provided by the income-based clustering.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Poverty clubs, world bank's income groups and poverty levels in 2019. Notes: In the figures, the vertical axis measures the 2019 poverty rate of each country, with countries grouped by poverty club along the horizontal axis. The symbols (square, circle and triangle) denote the classification of each country according to the World Bank income classification for 2019: high and upper-middle income (combined in the figure into a single group), lower-middle income, and low income.

These comparisons serve to underscore the fact that the clubs are defined by countries' (estimated) long-run poverty rates, themselves driven by poverty trends over the sample period, and not only by the levels of poverty or income at any particular moment of the sample. Thus, the club-based clustering provides independent information relative to that provided by standard income-based or current poverty-based clustering.

5 Poverty Club Membership, Income and Inequality

What drives the formation of poverty clubs, and countries' membership in them? In principle one could think of a host of possible fundamental factors. However, from (1), poverty can be seen to be a function of mean per capita income and a suitable measure of inequality. Thus, whatever those fundamental factors happen to be, their influence on the formation of poverty clubs must be primarily channeled through mean income and inequality.

Generally, the empirical literature (Bourguignon, 2003; Chen & Ravallion, 2010; Ferreira, 2012; Kraay, 2006 or Dollar & Kraay, 2002, among many others) that has sought to quantify the respective contributions of income and inequality to poverty employs a linear (or log-linear) specification, such as:
P it = α i + γ log y ‾ it + φ G it + v it , $$ {P}_{\mathrm{it}}={\alpha}_i+\gamma \log {\overline{y}}_{\mathrm{it}}+\varphi {G}_{\mathrm{it}}+{v}_{\mathrm{it}}, $$ (2)
where y ‾ it $$ {\overline{y}}_{\mathrm{it}} $$ is mean per capita income and inequality ( G it $$ {G}_{\mathrm{it}} $$ ) is typically measured by the Gini index. Equation (2) can be derived from the analytical framework summarized in Appendix D.

Based on this framework, we can quantify the respective roles of income and inequality in determining the club membership of each country. For both variables, we distinguish between their initial conditions and their changes along the transition, since they may have different effects on the formation of poverty clubs.

5.1 An Ordered Response Model of Poverty Club Membership

To get a quantitative assessment of the respective roles of income and inequality for poverty club formation, we estimate an empirical model of poverty club membership. Membership is an ordinal discrete variable which takes values from 1 up to the maximum number of clubs, which varies across poverty measures. Thus, we estimate an ordered logit model relating club membership (as obtained from the P-S's clustering approach) to initial conditions and changes in mean income and the Gini index. In practical terms, (see Appendix D for more details), we estimate:
P i * = β 1 log y i t 0 + φ 1 G i t 0 + β 2 ∆ logy i + φ 2 ∆ G i + ε i , $$ {P}_i^{\ast }={\beta}_1\log {y}_{\mathrm{i}{\mathrm{t}}_0}+{\varphi}_1{G}_{\mathrm{i}{\mathrm{t}}_0}+{\beta}_2\Delta {\mathrm{logy}}_{\mathrm{i}}+{\varphi}_2\Delta {G}_i+{\varepsilon}_i, $$ (3)
where P i * $$ {P}_i^{\ast } $$ is an unobserved latent variable, which represents the steady-state level of poverty; y t 0 $$ {y}_{t_0} $$ and G t 0 $$ {G}_{t_0} $$ respectively denote the initial values of mean income and the Gini index, and ∆ log y i $$ \Delta \log {y}_i $$ and ∆ G i $$ \Delta {G}_i $$ are their changes over the sample period.

This framework allows us to address two issues of interest. First, how big is the role of initial conditions relative to that of transitory factors (as captured by the changes over time in income and the Gini index) in determining club membership? This is of interest from a policy perspective—while initial conditions are given, there may be ample scope for policy interventions affecting the transition.

Second, how big is the role of inequality in determining poverty club membership? The empirical literature referenced in Section 2 generally concludes that observed poverty trends are largely driven by changes in mean income, with inequality playing a relatively minor role. Our empirical setting allows us to verify if the same conclusion applies to the formation of poverty clubs, and whether the conclusion varies across clubs and/or poverty measures.

To assess both of these issues, we compare the results from estimating the full model (3) with those from two suitably restricted models, the first one including only initial conditions and the second only income variables:
P i * = β 11 log y i t 0 + φ 11 G i t 0 + v i , $$ {P}_i^{\ast }={\beta}_{11}\log {y}_{\mathrm{i}{\mathrm{t}}_0}+{\varphi}_{11}{G}_{\mathrm{i}{\mathrm{t}}_0}+{v}_i, $$ (4)
P i * = β 12 log y i t 0 + β 22 ∆ logy i + w i . $$ {P}_i^{\ast }={\beta}_{12}\log {y}_{\mathrm{i}{\mathrm{t}}_0}+{\beta}_{22}\Delta {\mathrm{logy}}_i+{w}_i. $$ (5)

The larger the difference between the explanatory powers of models (3) and (4), the more relevant is the role of income and Gini index changes, given initial conditions, in shaping countries' poverty club membership. Likewise, the larger the difference between the explanatory powers of models (3) and (5), the more relevant is the role of the initial Gini index and its subsequent changes, given income.

5.2 Preliminary Evidence

We use mean per capita income expressed in US dollars per day (PPP-adjusted) as a measure of income, and the Gini index as a measure of inequality, both extracted from PovcalNet. Table 4 shows, for each club and poverty measure, the average levels of income and inequality for the initial and final year of the sample period, as well as their annual growth (annual change in the case of the Gini index) (see Table A2 in Appendix A for the full details on income and inequality by country). PovcalNet provides interpolated information on mean income (thus, we have data for 1981 and 2019 in all cases), but it does not provide interpolated information on the Gini index and other inequality measures. When 1981 and/or 2019 data on the Gini index are not available, we use the value from the survey closest to the missing year.

Table 4. Income and Inequality: Descriptive Statistics by Club
Income 1981 Income 2019 Gini (circa 1981) Gini (circa 2019) Annual income growth (%) Annual Gini change (p.p)
Poverty measure Poverty club Mean sd Mean sd Mean sd Mean sd Mean sd Mean sd
Headcount (P0) Club 1 3.96 2.50 3.79 1.64 48.30 10.00 45.07 6.43 0.17 1.80 −0.17 0.50
Club 2 5.36 3.65 5.27 2.25 43.15 9.32 41.94 8.36 0.30 1.56 −0.22 0.63
Club 3 4.07 2.85 6.75 2.47 47.74 10.91 40.09 9.07 1.75 1.43 −0.36 0.29
Club 4 8.29 5.42 16.38 8.62 41.34 9.01 38.43 6.65 2.12 1.72 −0.22 0.59
Poverty gap (P1) Club 1 4.58 2.68 3.66 1.72 46.63 10.08 44.10 7.54 −0.42 1.41 −0.10 0.51
Club 2 4.59 3.20 5.15 2.11 46.26 9.58 42.82 7.08 0.71 1.64 −0.28 0.51
Club 3 7.44 5.37 14.76 8.73 42.42 9.66 38.75 7.19 2.14 1.61 −0.24 0.55
Squared poverty gap (P2) Club 1 4.97 2.69 3.95 1.77 46.91 10.35 43.83 7.00 −0.46 1.31 −0.15 0.55
Club 2 6.63 5.10 12.34 8.71 43.30 9.60 39.79 7.46 1.83 1.70 −0.25 0.53
Watts (W) Club 1 4.93 2.76 3.86 1.77 47.69 10.02 43.99 7.16 −0.48 1.34 −0.18 0.54
Club 2 4.18 3.03 5.26 2.27 45.63 9.19 42.92 7.58 0.96 1.59 −0.22 0.47
Club 3 7.59 5.40 15.03 8.74 42.18 9.69 38.56 7.03 2.15 1.63 −0.24 0.56
Full sample 6.30 4.76 10.66 8.51 44.02 9.81 40.60 7.51 1.38 1.87 −0.23 0.53
  • Notes: The table shows, for each poverty club under each poverty measure, the average levels of income (expressed in 2017 PPP-adjusted USD per day) and the Gini index (in %) at the beginning and end of the sample period, along with their annual growth (annual change in p.p. for the Gini index) over the sample period.

A preliminary inspection of Table 4 suggests that club formation is related to both the initial levels and dynamics of income and inequality. In most cases (but not all), the lower-(higher) poverty clubs exhibit higher (lower) initial average income levels. In turn, they invariably exhibit higher (lower) average income growth and, therefore, a higher (lower) average level of income at the end of the period. Across all poverty measures, average income growth is almost zero or negative for the highest-poverty club (Club 1), while it reaches around 2 percent per year for the lowest-poverty club (Club 4 for P0, Club 2 for P2 and Club 3 for the other measures).

The lower-(higher) poverty clubs also start from lower (higher) initial inequality levels. In contrast, the annual change in average inequality does not seem to vary across clubs in the same systematic way as income growth does. However, it is worth noting that the levels of inequality have decreased during the sample period across all clubs and for all poverty measures, although the reduction appears more marked for the intermediate clubs. This faster inequality decline may have been a relevant contributor to the relatively fast decline of the average poverty rate of Club 2 shown in Figure 4 for the cases of P1 and W, and Clubs 2 and 3 of P0.

5.3 Estimation Results of the Ordered Logit Model

Table 5 reports the parameter estimates of Equations (3-5) for headcount poverty and for the other poverty measures, respectively. In general, all coefficients are significant and carry the expected signs. The positive signs of the coefficients on initial income and income growth indicate that the probability of belonging to lower-poverty clubs increases with both dimensions of income. The negative signs of the coefficients on the initial level of inequality and its change over time indicate the opposite, in line with most of the existing literature.

TABLE 5. Ordered Logit Model Estimation Results. Headcount, Poverty Gap, Squared Poverty Gap and Watts
Headcount (P0) Poverty gap (P1) Squared poverty gap (P2) Watts (W)
Full model Rest. model Rest. model Full model Rest. model Rest. model Full model Rest. model Rest. model Full model Rest. model Rest. model
Variable (only initial cond.) (only income) (only initial cond.) (only income) (only initial cond.) (only income) (only initial cond.) (only income)
Initial income (log) 0.09 0.01 0.05 0.05 0.01 0.04 0.03 0.00 0.03 0.05 0.01 0.04
(0.02) (0.00) (0.01) (0.01) (0.00) (0.01) (0.01) (0.00) (0.01) (0.01) (0.00) (0.01)
Annual income growth 3.72 2.02 2.65 2.14 1.84 1.86 2.74 2.07
(0.65) (0.32) (0.47) (0.37) (0.43) (0.44) (0.48) (0.35)
Initial Gini index −0.31 −0.07 −0.16 −0.05 −0.10 −0.04 −0.19 −0.06
(0.06) (0.02) (0.04) (0.02) (0.05) (0.03) (0.05) (0.02)
Annual Gini index change −3.77 −2.36 −1.31 −2.04
(1.01) (0.86) (0.96) (0.84)
μ 1 $$ {\mu}_1 $$ 0.33 −2.74 6.65 −0.28 −2.78 5.11 −0.55 −2.79 3.78 −1.09 −2.97 4.98
(1.71) (1.01) (1.20) (1.75) (1.04) (1.18) (2.32) (1.29) (1.38) (1.76) (1.05) (1.11)
μ 2 $$ {\mu}_2 $$ 2.64 −2.06 8.06 3.40 −1.51 7.96 2.49 −1.73 7.70
(1.78) (1.00) (1.30) (1.86) (1.01) (1.43) (1.83) (1.01) (1.36)
μ 3 $$ {\mu}_3 $$ 5.59 −1.39 9.65
(1.91) (0.99) (1.47)
N 98 98 98 100 100 100 100 100 100 100 100 100
Pseudo-R2 0.66 0.11 0.46 0.60 0.06 0.50 0.53 0.03 0.49 0.61 0.06 0.48
  • Notes: The table shows the estimated results of the ordered logit models in Equations (3-5) for the headcount, poverty gap, squared poverty gap and the Watts index. The full model includes initial income, initial Gini index, average income growth and average Gini change. The first restricted model includes only initial income and the initial Gini index, and the second includes only initial income and its average growth rate. Standard errors in parentheses.
  • *** p < 0.01;
  • ** p < 0.05;
  • * p < 0.1.

To provide a metric for the point estimates, we can recover the odds ratio for each variable by taking the exponential of its estimated coefficient. We provide an illustration of the odds ratios using the full model estimates for the case of headcount poverty (first column of Table 5). For instance, a 1 percent increase in initial income (e.g., raising it from 10 to 10.10 dollars per day), holding the rest of the variables constant, raises the odds of belonging to the lowest-poverty club (Club 4) relative to the rest (Clubs 2, 3 and 4) by 9% ( e 0.09 = 1.09 $$ {e}^{0.09}=1.09 $$ ). Similarly, the odds of belonging to the highest-poverty club (Club 1) decrease by 31 percent when the growth rate of income increases 0.1 p.p. per year ( 1 − 1 / e 3.72 · 0.1 = 0.31 $$ 1-1/{e}^{3.72\cdotp 0.1}=0.31 $$ ). Over the 39-year sample period (i.e., between 1981 and 2019), this is equivalent to an income growth of 3.9 percent, which should be compared with the average growth rate of the entire sample ( 1.38 · 39 = 54 percent $$ 1.38\cdotp 39=54\ \mathrm{percent} $$ , see Table 4). This simple quantitative exercise shows the importance of income growth for escaping extreme poverty (i.e., moving from a higher-poverty club to a lower-poverty club).

As for the Gini index, the odds of belonging to the highest-poverty club, relative to the rest, decrease by 27 percent when the initial Gini index decreases 1 p.p. ( 1 − e − 0.31 = 0.27 $$ 1-{e}^{-0.31}=0.27 $$ ). Likewise, the odds decrease 31 percent following an annual reduction of 0.1 p.p. in the Gini index ( 1 − e − 3.77 10 = 0.31 $$ 1-{e}^{-\frac{3.77}{10}}=0.31 $$ ). Such annual reduction would entail a drop in the Gini index of 3.9 p.p. over the 39-year sample period, which is a significant but not infeasible amount.

Table 5 also reports McFadden's pseudo-R2, which summarizes the overall explanatory power of each model. For the full model (3), the values are quite high, regardless of the poverty measure considered (0.66 for P0, 0.60 for P1 and W, and above 0.50 for P2). Hence, income and inequality, taken together, do an excellent job at explaining poverty club membership.

Comparing these pseudo-R2 with those obtained from the restricted models, we obtain a first idea about the relevance of each channel and dimension in placing each country in its corresponding club. The first restricted model (4), which includes initial conditions only, yields a pseudo-R2 below 0.11 for all poverty measures, far below the values obtained with the full model. The second restricted model (5), which includes income variables only, yields a pseudo-R2 of about 0.50 for all poverty measures, closer to, but still below, those from the full model, with the gap being particularly large for P0. These simple comparisons suggest that, first, income and inequality changes contribute more than initial conditions to explaining club membership; second, income explains more than inequality; third, the contribution of inequality (relative to that of income) seems to be larger for P0 than for the other poverty measures.

A more direct way of assessing the contribution of the individual variables to the model's overall explanatory power is through the use of dominance statistics. The dominance statistics of the individual regressors add up to the pseudo-R2 value (Budescu, 1993; Grömping, 2007).

Table 6 reports the dominance statistics of the full model (3) for each of the four poverty measures. The table shows that initial income and, especially, annual income growth, are consistently the most dominant factors. For P0, initial income almost plays the leading role, while for the other poverty measures income growth is clearly the most dominant factor.

TABLE 6. Dominance Statistics of the Full Model
Variable Headcount (P0) Poverty gap (P1) Squared poverty gap (P2) Watts (W)
Initial income (log) 0.26 0.19 0.09 0.19
Annual income growth 0.28 0.35 0.40 0.34
Initial Gini index 0.09 0.05 0.03 0.06
Gini index change 0.02 0.02 0.02 0.01
Pseudo-R2 0.66 0.60 0.53 0.61
  • Notes: The table reports the dominance statistics of the full model in Equation (3), including initial income, initial Gini index, average income growth and average Gini change. The dominance statistics quantify the respective contribution of each variable to McFadden's pseudo-R2.

In contrast, the contributions of initial inequality and its change over time are much smaller. Like with income, their magnitude is roughly constant across poverty measures: contrary to what occurs with income, initial inequality contributes more to the overall fit, while the change in inequality plays a more modest role.

If we do not use interpolated income data, so that we exclusively have income and inequality data extracted from surveys closest to the beginning (1981) and end of the period (2019), the results do not change substantially. The role of income growth diminishes, while the role of inequality remains unchanged.

5.4 Predicting Club Membership

The preceding discussion focused on the ability of the empirical models (3)–(5) to explain overall club formation, as well as on the contributions of income and inequality, their initial conditions and subsequent changes, to that explanatory power. However, this may still yield an incomplete picture, in that the models' explanatory ability, and the roles of the different variables, are likely to vary, perhaps widely, across clubs.

To address this question, we use a prediction exercise. Specifically, we analyze the ability of the empirical specifications (3)–(5) to correctly predict countries' membership in the different clubs, and assess the respective roles of income and inequality, as well as their initial conditions and performance over time, in shaping the accuracy of such predictions.

Hence, we use the estimates of the ordered logit models (3)–(5) to compute, for each country and poverty measure, the probability of belonging to each club, given the country's characteristics (i.e., initial levels of income and Gini index, and their changes). Next, we take the highest of these club-specific probabilities as indicating the country's club membership predicted by the model. We compare these predictions with actual club membership, as derived from the P-S clustering procedure (Table 3). For each poverty measure, we compute the number and percentage of countries whose club membership is correctly/incorrectly predicted—thus building so-called confusion matrices (Ting, 2011). In this way, we can also identify the specific countries for which the restricted and the full-model predictions differ.

The main objective of this exercise is to provide insights on how the roles of the different variables shaping club membership vary across clubs. Thus, we break down by club the prediction accuracy analysis. For each estimated model, Table 7 shows the number and percentage of countries whose club membership is correctly/incorrectly predicted (i.e., the confusion matrices by club). The rows correspond to actual membership, and the columns to model predictions. The main diagonal shows the successes in the prediction of each model for each club, while the cells outside the main diagonal represent failed predictions. The percentages add up to 100 for each row.

TABLE 7. Confusion Matrices by Club. Headcount, Poverty Gap, Squared Poverty Gap and Watts
Full model vs Actual membership
Full model
Actual membership Club 1 Club 2 Club 3 Club 4 Total
Headcount (P0) Club 1 83% (19) 9% (2) 9% (2) 0% (0) 100% (23)
Club 2 25% (3) 33% (4) 42% (5) 0% (0) 100% (12)
Club 3 0% (0) 38% (5) 46% (6) 15% (2) 100% (13)
Club 4 0% (0) 0% (0) 2% (1) 98% (49) 100% (50)
Poverty gap (P1) Club 1 65% (11) 29% (5) 6% (1) 100% (17)
Club 2 17% (4) 70% (16) 13% (3) 100% (23)
Club 3 0% (0) 3% (2) 97% (58) 100% (60)
Squared poverty gap (P2) Club 1 65% (13) 35% (7) 100% (20)
Club 2 4% (3) 96% (77) 100% (80)
Watts (W) Club 1 63% (12) 37% (7) 0% (0) 100% (19)
Club 2 22% (5) 65% (15) 13% (3) 100% (23)
Club 3 0% (0) 3% (2) 97% (56) 100% (58)
Restricted model (only initial conditions) vs Actual membership
Initial conditions only
Actual membership Club 1 Club 2 Club 3 Club 4 Total
Headcount (P0) Club 1 48% (11) 0% (0) 0% (0) 52% (12) 100% (23)
Club 2 17% (2) 0% (0) 0% (0) 83% (10) 100% (12)
Club 3 54% (7) 0% (0) 0% (0) 46% (6) 100% (13)
Club 4 8% (4) 0% (0) 0% (0) 92% (46) 100% (50)
Poverty gap (P1) Club 1 18% (3) 0% (0) 82% (14) 100% (17)
Club 2 4% (1) 0% (0) 96% (22) 100% (23)
Club 3 3% (2) 0% (0) 97% (58) 100% (60)
Squared poverty gap (P2) Club 1 0% (0) 100% (20) 100% (20)
Club 2 0% (0) 100% (80) 100% (80)
Watts (W) Club 1 21% (4) 0% (0) 79% (15) 100% (19)
Club 2 9% (2) 0% (0) 91% (21) 100% (23)
Club 3 5% (3) 0% (0) 95% (55) 100% (58)
Restricted model (only income) vs Actual membership
Income only
Actual membership Club 1 Club 2 Club 3 Club 4 Total
Headcount (P0) Club 1 78% (18) 4% (1) 9% (2) 9% (2) 100% (23)
Club 2 58% (7) 17% (2) 17% (2) 8% (1) 100% (12)
Club 3 8% (1) 23% (3) 38% (5) 31% (4) 100% (13)
Club 4 0% (0) 0% (0) 6% (3) 94% (47) 100% (50)
Poverty gap (P1) Club 1 59% (10) 35% (6) 6% (1) 100% (17)
Club 2 13% (3) 65% (15) 22% (5) 100% (23)
Club 3 0% (0) 7% (4) 93% (56) 100% (60)
Squared poverty gap (P2) Club 1 65% (13) 35% (7) 100% (20)
Club 2 5% (4) 95% (76) 100% (80)
Watts (W) Club 1 63% (12) 32% (6) 5% (1) 100% (19)
Club 2 17% (4) 57% (13) 26% (6) 100% (23)
Club 3 0% (0) 5% (3) 95% (55) 100% (58)
  • Notes: The table reports the predictive performance for each club of the ordered logit models in Equations (3-5) for the headcount, poverty gap, squared poverty gap and the Watts index. The full model includes initial income, initial Gini index, average income growth and average Gini change. The first restricted model includes only initial income and the initial Gini index, and the second includes only initial income and its average growth rate. The predictive performance is expressed as the percentage and number (in parentheses) of countries correctly predicted that is, those for which the club membership predicted by the model under consideration matches their actual club membership as obtained using Phillip and Sul's (2007) method. The rows correspond to actual membership, and the columns to model predictions. The main diagonal (in bold) shows the successful predictions of each model for each club, while the cells outside the main diagonal represent failed predictions. The percentages add up to 100 for each row.

In addition, in Table E1 in Appendix E we show the predictive accuracy of each model over the full country sample, given by the sum of the main diagonals of Table 7. When performing this exercise, we obtain the same conclusions as in the preceding subsection: income plays a bigger role than inequality, and income growth matters more than initial income, while initial inequality plays a bigger role than its changes over time.

When examining Table 7, we can extract three main conclusions. First, membership in the lowest-poverty club is well predicted by all models. In all cases, the percentage of successful predictions exceeds 90 percent (i.e., the lowest percentage is 92 percent for the full and initial conditions-only models for P0). Interestingly, the model featuring initial conditions only does nearly as well (even better, in the case of P2) in this regard as the full model. Thus, initial (favorable) income and inequality conditions suffice to predict with a high degree of accuracy which countries will wind up in a low-poverty club.

Second, membership in the highest-poverty club (Club 1 in all cases) is fairly well predicted by the income-only model. This is particularly the case for headcount poverty (for which the membership predictions of the income-only model are correct in 78 percent of the cases) and less so for the rest of poverty measures (around 60 percent successful predictions). This suggests that inequality has played only a modest role for countries winding up in the highest-poverty club. However, this does not mean that inequality is invariably unimportant for predicting membership in the highest-poverty club.

In contrast, initial conditions play a secondary role when explaining countries' membership in the highest-poverty club. For P0, the initial conditions-only model correctly predicts 48 percent of the Club 1 membership, while for the other poverty measures, the success rate at predicting membership in this club is 21 percent or less. Indeed, several countries actually belonging to Club 1 under P0, which enjoyed relatively favorable initial conditions, are predicted by the initial conditions-only specification to wind up in Clubs 3 or 4, while the full model correctly places them in Club 1. Closer inspection reveals that these countries experienced large increases in the Gini index and decreases in their income levels between 1981 and 2019.

Third, the various models generally have a harder time at predicting membership in intermediate-poverty clubs in P0, P1 and W. The initial conditions-only model does especially poorly in this regard, as its predictions of membership in these clubs are all incorrect. The conclusion is that initial conditions have been of relatively little consequence for countries belonging to intermediate-poverty clubs.

The income-only model does better at predicting intermediate-club membership—but the success rate of its predictions is in all cases below that of the full model. This underperformance is especially visible for P0, where the success rate of the income-only model at predicting membership in Club 2 is 16 p.p. lower than that of the full model. From this we can conclude that the inequality dimension plays a more substantive role in determining membership in intermediate-poverty clubs. This stands in contrast with membership in the highest-poverty clubs, for which inequality has played a limited role over the time sample considered, as we saw above.

6 Conclusions

In this paper we have analyzed the dynamics of different dimensions of poverty using a large cross-country panel dataset comprising 100 emerging and developing countries over almost four decades. Importantly, our framework allows not only for standard forms of poverty convergence across countries—absolute and conditional convergence—but also for club convergence, which has not been explored in the existing literature.

Using a panel clustering approach, we unambiguously reject absolute and conditional convergence. Instead, we find strong evidence of poverty convergence clubs: different groups of countries are converging to different long-run poverty levels. This applies to all the poverty measures we explore.

The implication is that, to the dismay of the development community, the goal of global poverty eradication—which would require worldwide convergence of absolute poverty towards zero—may be at risk: between one-third and two-thirds of the countries in our sample (depending on the poverty measure under consideration) do not appear to be on the path towards zero poverty. Some of these countries—those that wound up in the highest-poverty clubs identified by our analysis—have seen their poverty rates remain at very high levels during the entire period of analysis. Other countries—those in intermediate-poverty clubs—have achieved a substantial reduction in their poverty rates, but remain far from the zero-poverty goal. Only for the countries clustered into the lowest-poverty club that we identify do we find clear evidence that poverty is converging towards zero. This heterogeneity is consistent with the literature that, in general, has found no evidence of poverty convergence.

Convergence clubs are associated with the existence of multiple long-run poverty equilibria. Countries' long-run poverty rate depends not only on fundamental factors, but also on their initial conditions (i.e., their initial levels of income and inequality). In contrast, under absolute or conditional convergence, initial conditions are irrelevant in the long run. Indeed, we find that initial conditions predict with a high degree of accuracy which countries end up belonging to a low-poverty club. Most of them start our period of analysis with a relatively favorable position (i.e., high income, and/or low inequality, and thus low poverty). In contrast, initial conditions play a secondary role in explaining countries' membership in the highest-poverty clubs, and are even less relevant for predicting the membership of intermediate-poverty clubs.

The paper also yields insights on the roles of income and inequality (measured by the Gini index) in the formation of poverty clubs. Overall, we find that income is the greatest driving force, in line with the existing literature. This is particularly true for the highest-poverty clubs, whose member countries experienced relatively low-income growth and/or started from low-income levels, and thus converge to a high-poverty equilibrium. In contrast, for countries belonging to intermediate-poverty clubs, income still plays the dominant role, but inequality also matters for their club membership.

In summary, our results do not prompt optimism about the rapid eradication of global poverty. Many countries—certainly those trapped in the highest-poverty clubs, but possibly also many of those belonging to the intermediate-poverty clubs—appear to be falling behind.

While our framework has abstracted from policy levers, it naturally prompts the question of whether, and how, policies to achieve long-run poverty reduction should vary across poverty clubs. For example, one could conjecture that, for countries stuck in the highest-poverty clubs—whose formation appears to be driven primarily by income rather than inequality—raising income growth should be the top priority to exit the poverty trap. Yet this does not necessarily imply that the secondary role of inequality found in the sample for the poorest countries must persist also in the future. Even very poor countries might be able to deploy redistributive policies—such as targeted expenditures or tax reforms—more actively in the future than done over the sample period, thus enhancing the contribution of inequality to the trends in their poverty rates. Likewise, for countries converging towards lower-poverty equilibrium levels, such as those in the intermediate poverty clubs, a faster and more effective reduction of poverty could be achieved with inequality improvements complementing income growth.

  • 1 Between 1990 and 2019, the average headcount poverty rate fell from 65.8% to 1.1% in East Asia and the Pacific, from 16.7% to 4.3% in Latin America and the Caribbean, and from 49.7% to 8.5% in South Asia. In sub-Saharan Africa, the poverty rate fell by almost 19 percentage points between 1990 and 2019, but 35.1% of the region's population (some 421 million people) still live below the $2.15 poverty line. There are also large differences between countries within each region. In South Asia, for example, the headcount poverty rate fell from around 41% to 7% in Bangladesh and from around 13% to almost zero in Sri Lanka between 1990 and 2019. The contrast is even starker in sub-Saharan Africa: In Zambia, the headcount poverty rate rose from about 56% to 61%, while in Namibia it fell from about 54% to 17% over the same period.
  • 2 An alternative method for analyzing club convergence is the use of mixture models (Battisti & Parmeter, 2013; Owen et al., 2009; Pittau et al., 2010), based on the “distribution dynamics” approach pioneered by Quah (1997). It yields estimates of the probability that each country's observations are drawn from a particular distribution in the mixture, offering a natural metric for assigning countries to specific clubs. The method requires the identification of multiple mixture components, an examination of the parameters associated with those components, and an assessment of the mobility of countries over time, as outlined by Pittau et al. (2016).
  • 3 In general, poverty dynamics (just like the dynamics of income or inequality) is governed by a set of economic fundamentals, such as technology, fiscal policy, trade openness or market structure (Johnson & Papageorgiou, 2020). The key difference between club convergence and other forms of convergence, such as absolute and conditional convergence, is that initial conditions also play a role in the dynamic process. Thus, differences in initial conditions can become permanent: countries experiencing similar shocks to economic fundamentals (captured by changes in income and inequality) along the transition path may converge to different long run poverty rates if their initial conditions (captured by initial income and inequality levels) are sufficiently different.
  • 4 Ouyang et al. (2019) attempt to tackle the possibility of club convergence through some simple tests of region-wise poverty convergence. However, those tests are not informative about club convergence in general, except in the particular case in which club membership is known a priori and driven exclusively by geographic factors.
  • 5 The existence of poverty convergence clubs is explained by non-linearities in the relationship between poverty and its main driving forces, namely income and inequality. Van der Weide and Milanovic (2018) and Marrero et al. (2021) show that there is also a non-linear relation between the latter two variables: inequality has different effects on the income prospects of different parts of the distribution (i.e., negative for the poor and positive or insignificant for the rich).
  • 6 Under lognormality, W has also a useful interpretation as the time to exit poverty—that is, the number of years it would take for a poor household to grow out of poverty given a hypothetical, steady growth of annual income (or consumption). It can be shown that the exit time is exactly given W divided by the rate of growth of the income of the poor.
  • 7 Poverty estimates are homogenized using PPP exchange rates for household consumption from the 2017 International Comparison Program.
  • 8 For those reasons, we drop Guyana, Lebanon, Marshall Islands, Micronesia, Nauru, Samoa, South Sudan, Suriname, Timor Leste, Tuvalu and Venezuela, as well as the former Yugoslavia and Soviet Union countries, as in Ravallion (2012), since these latter countries display atypical behavior due to their transition from socialist to market economies.
  • 9 PovcalNet also provides information for 2020 and 2021, but at present only for a few countries.
  • 10 In some cases, another mode is also observed for intermediate values of the poverty rate. This is the case of the headcount poverty rate in 2019, which exhibits another mode at around 0.20.
  • 11 According to the Ravn and Uhlig rule, the value of the smoothing parameter is obtained multiplying the value of the smoothing parameter of the HP filter conventionally used to detrend quarterly time series ( λ = 1600 ) $$ \left(\lambda =1600\right) $$ by the inverse of the fourth power of the frequency of observation as compared to quarterly data ( α ) $$ \left(\alpha \right) $$ : 1 α 4 λ $$ \frac{1}{\alpha^4}\lambda $$ . In our case, for annual data, α = 4 $$ \alpha =4 $$ , thus the smoothing parameter is 1 4 4 1600 = 6.25 $$ \frac{1}{4^4}1600=6.25 $$ .
  • 12 A few countries featuring medium or high poverty rates at the end of the sample period do change their club membership when the value of the smoothing parameter changes. This is not a weakness of the method, but rather an expected occurrence, as these countries are likely to be close to more than one steady state, unlike countries that are unambiguously converging to a lower or higher poverty level.
  • 13 For instance, within Club 2 we find countries such as Chad and Ghana, which reduced their headcount poverty rates by around 36 p.p. between 1996 and 2019, but their poverty rates in the final year are still far from zero. However, within Club 3 there are countries that start in 1981 with poverty levels similar to those observed in countries of Clubs 1 and 2 and, after 39 years, managed to bring them close to zero. This is the case, for example, of Senegal and India. In addition, for the poverty gap and the Watts index, countries belonging to Club 2 exhibit a peculiar behavior: the club's average poverty trajectory crosses that of Club 1 in 1999, at a level of P1 and W around 25% and 35%, respectively. This is because several countries from Club 2 in both measures (i.e., Burkina Faso & Eswatini) started in 1981 with very high levels of P1 and W and managed to reduce them sharply by 2019. In contrast, other countries from Club 1 (i.e., Madagascar and Malawi) started with smaller levels of P1 and W but failed to reduce them by the end of the sample period.
  • 14 We calculate the number of poor in each country multiplying its 2019 headcount poverty rate by its total population in the same year. Both magnitudes are shown in Table A1 in Appendix A.
  • 15 These observations are based on the fact that, as Table 2 shows, all countries belonging to Club 1 under P1, P2 and Watts also belong to Club 1 of headcount poverty. The only exceptions are Benin, Cote d'Ivoire and Sao Tome and Principe. However, their combined total number of poor in 2019 is just 5 million, which is immaterial for the calculations in the text.
  • 16 If that were the case, every country in Club 1, for example, would exhibit higher poverty in 2019 than every country in Club 2, and the same would apply to Club 2 versus Club 3, and so on. Figure 6 clearly shows that this is not the case: there is considerable overlap between the ranges of 2019 poverty rates of the various clubs, even between those of the highest- and lowest- poverty clubs.
  • 17 We should caution that estimation of the ordered logit model implicitly assumes that the club classification obtained from the Phillips and Sul clustering procedure is exact, as do other papers using this strategy (Bartkowska & Riedl, 2012; Belloc & Molina, 2023; Cavallaro & Villani, 2022, among others). To the extent that it is not, our results will tend to overstate the precision of the logit estimates. There is no simple way to correct for this, as it would essentially require modeling the sampling error of the P-S procedure. Still, to the extent that our main result—that is, the dominant role of income vis-à-vis inequality in shaping long-run poverty trends in the sample—is fully consistent with the findings of earlier literature employing very different techniques, we are confident that our estimates of the respective contributions of income and inequality should not be too far off their true values.
  • 18 The illustration in the text assumes changes of arbitrary magnitude in the values of the variables. Alternatively, we could have organized the discussion around 1-standard deviation changes of the variables. However, this would have resulted in unrealistically large changes when applied to the initial income conditions.
  • 19 McFadden's pseudo-R2 is defined as 1 − log L full / log L null $$ 1-\left[\log \left({L}_{\mathrm{full}}\right)/\log \left({L}_{\mathrm{null}}\right)\right] $$ , where [ log L full $$ \Big[\log \left({L}_{\mathrm{full}}\right) $$ is the log likelihood of the estimated model and log L null $$ \log \left({L}_{\mathrm{null}}\right) $$ is the log likelihood of the model without covariates and only a set of intercepts. It captures the performance improvement of the estimated specification relative to the null model. Values close to 1 indicate a high predictive ability. However, pseudo-R2 are typically lower than their OLS counterparts (see, e.g., Smith & McKenna, 2013). According to McFadden, “its values tend to be considerably lower than those of the R2 index and should not be judged by the standards for a good fit in OLS. For example, values of 0.2 to 0.4 represent an excellent fit” (McFadden, 1977).
  • 20 Dominance statistics are based on the estimation of 2 K − 1 $$ {2}^K-1 $$ models including all possible combinations of K $$ K $$ independent variables. The dominance statistic of each independent variable is a weighted average of its marginal contribution to the pseudo-R2 in the models in which the variable is included (Luchman, 2013).
  • 21 Two relevant examples for P0 are those of Burkina Faso and Eswatini, which the full-model prediction correctly places in Club 1, while the income-only model does not. The likely reason is that both countries exhibit initial inequality and/or inequality changes well above the sample medians.
  • 22 Examples are Republic of Congo, Syria and Zimbabwe.
  • 23 There are multiple examples of countries that the initial conditions-only model places in a high-poverty club, while the prediction of the full model correctly locates them in a lower-poverty intermediate club. This is the case, for example, of Botswana, Gambia, Guatemala, Honduras and Senegal. Under P0, all these countries belong in Club 3, but the initial conditions-only model places them in Club 1. The common thread is that, in spite of relatively adverse initial conditions, these countries were able to improve their position over time through sustained increases in income levels and, in most cases, reductions (or small increases) in inequality.
  • 24 The predictive power of the estimated models declines when we use income and inequality data derived exclusively from surveys. This is particularly reflected in the reduced ability of income and inequality to correctly predict countries' membership in intermediate clubs.
  • 25 Ignoring the inequality dimension makes the income-only model incur in systematic prediction errors regarding the club membership of intermediate-club countries. Some countries with very large initial levels and/or worsening inequality are optimistically predicted to belong to the lowest-poverty club (some examples under P0 are Guatemala, Honduras, Namibia and South Africa). The opposite happens to countries with low initial levels and/or improving inequality, which are pessimistically allocated to higher-poverty clubs (e.g., Solomon Islands and Sudan). In contrast, the full model, inclusive of inequality, predicts club membership correctly in these cases.

The full text of this article hosted at iucr.org is unavailable due to technical difficulties.