Heterogeneity in soil water and light environments and dispersal limitation: what facilitates tree species coexistence in a temperate forest?
Abstract
In the present study, we analysed the habitat association of tree species in an old-growth temperate forest across all life stages to test theories on the coexistence of tree species in forest communities. An inventory for trees was implemented at a 6-ha plot in Ogawa Forest Reserve for adults, juveniles, saplings and seedlings. Volumetric soil water content (SMC) and light levels were measured in 10-m grids. Relationships between the actual number of stems and environmental variables were determined for 35 major tree species, and the spatial correlations within and among species were analysed. The light level had no statistically significant effect on distribution of saplings and seedlings of any species. In contrast, most species had specific optimal values along the SMC gradient. The optimal values were almost identical in earlier life stages, but were more variable in later life stages among species. However, no effective niche partitioning among the species was apparent even at the adult stage. Furthermore, results of spatial analyses suggest that dispersal limitation was not sufficient to mitigate competition between species. This might result from well-scattered seed distribution via wind and bird dispersal, as well as conspecific density-dependent mortality of seeds and seedlings. Thus, both niche partitioning and dispersal limitation appeared less important for facilitating coexistence of species within this forest than expected in tropical forests. The tree species assembly in this temperate forest might be controlled through a neutral process at the spatial scale tested in this study.
Introduction
How do multiple tree species coexist in a forest community? This is one of the major issues in ecological studies of forests. Recently, there has been debate from different perspectives: niche assembly (habitat association) versus stochastic processes, such as dispersal limitation. The former emphasises heterogeneity in abiotic and biotic environments, which enable niche segregation among species along gradients of multiple environmental variables (Rüger et al. 2009; Brown et al. 2013); until now, many studies have presented data that support this hypothesis. For example, some species have biased distribution under a specific topography or soil condition, suggesting mitigation of competition with other species (Comita & Engelbrecht 2009; Vieilledent et al. 2010; Chuyong et al. 2011; Metz 2012; Baldeck et al. 2013; Brown et al. 2013). In addition to soil-related factors, light availability makes an important contribution to species composition in the early life stages (Abe et al. 1995; Webb & Peart 2000; Rüger et al. 2009).
In contrast to the niche assembly perspective, the stochastic perspective has recently been highlighted (Hubbell 2001; Rosindell et al. 2011). This theory places less emphasis on environmental heterogeneity and related niche partitioning and suggests that a stochastic process, such as seed dispersal limitation, can explain the local species assembly pattern. From this perspective, some studies, based on data obtained from large-scale forest plots, argue about the limited role of local habitat specialisation and instead emphasise dispersal limitation in the organisation of forest communities (Seidler & Plotkin 2006; Lin et al. 2011; Shen et al. 2013).
Recent studies have suggested that these two hypotheses are not mutually exclusive (Li et al. 2009; Lin et al. 2011). When testing these hypotheses, it should be noted that the importance of environmental heterogeneity might vary between life stages (de Toledo et al. 2011; Metz 2012). Comita et al. (2007) suggested that individuals in the adult tree stage more often have significant distributional correlations with specific soil moisture conditions. Hu et al. (2012) further argued that the distribution of small trees is likely to be explained by dispersal limitation, whereas the distribution of adult trees is more likely to be determined by the environment. These studies postulate that the associations of mature trees with specific habitat conditions can be formed during the early life stages via differentiated growth and mortality between species (Metz 2012).
However, there are some concerns about these previous studies. First, the soil conditions were categorised in most cases on the basis of apparent topography or soil classification types (Gunatilleke et al. 2006; Comita et al. 2007; Chuyong et al. 2011; de Toledo et al. 2011; Metz 2012); however, soil conditions vary continuously rather than discretely in a spatial context (Baldeck et al. 2013). Thus, simplifying soil conditions by categorisation would reduce information related to soil environmental variation, and this may lower the robustness of any statistical analysis (Itoh et al. 2010). Second, analyses of tree distributions have often used inventory data from the well-established stages. The environmental regulation of specific distributions could change ontogenetically (as reviewed above); therefore, studies of the spatial configurations of trees should also consider younger life stages (Comita et al. 2007; Metz 2012; Ota et al. 2012; Oki et al. 2013). Third, previous studies were mostly conducted in tropical forests and rarely in temperate forests. Temperate forests comprise less species than tropical forests; therefore, the former forests should provide good samples for validating the generality of theories developed for tropical forests. Some previous studies suggest that the species assemblies of temperate forests may be niche-determined rather than chance-determined (Nakashizuka 2001; Myers et al. 2013). More recently, however, it has been suggested that niche partitioning in terms of habitat associations among species is not apparent, even in temperate forests (Shibata et al. 2010). Hence, dispersal limitation may also play an important role in temperate forests in shaping the diversity and spatial patterns of tree species.
The present study analysed the species distribution pattern in a temperate forest through various life stages, from seedlings to mature adults, to assess the importance of habitat associations and dispersal limitations. First, tree species distribution was analysed with respect to soil and light conditions during the ontogenetic life stages. The number of stems in each species during each life stage was modelled using an equation that included environmental factors as continuous explanatory variables and that considered spatial autocorrelation. The model parameters were estimated using a Bayesian framework, which tested whether each species had a specific niche space along environmental gradients, possibly resulting in the avoidance of interspecific competition. Second, intraspecific spatial correlations among life stages and interspecific spatial correlations in each life stage were analysed to assess the effect of dispersal limitation on mitigating the overall interspecific competition. Based on the results of these analyses, the following questions were addressed: (i) do tree species have different optimal distributions relative to soil and light conditions; (ii) do specific tree distributions change relative to environmental variables through ontogenetic life stages; (iii) are seedlings distributed more frequently in the vicinity of conspecific adult trees; (iv) are tree species distributed exclusively with each other in any life stage; and (v) what are the roles of niche assembly and dispersal limitation in the context of coexistence of tree species within a temperate forest?
Material and Methods
Study site
The present study was conducted in the Ogawa Forest Reserve (OFR), which is an old-growth deciduous hilly forest. OFR is located in the southern part of the Abukuma Mountains, Ibaraki Prefecture, central Japan (36°56′ N, 140°35′ E, 610 m a.s.l.). The mean monthly temperature is 10.7 °C, with highest monthly mean of 22.6 °C in August and lowest −0.9 °C in February. Annual precipitation is approximately 1910 mm, and highest in August and September and lowest in December and January, while the maximum snow depth often reaches 50 cm (Mizoguchi et al. 2002).
Within the 6-ha permanent plot (300 × 200 m; Fig. 1), which was established in 1987 in OFR (Masaki et al. 1992), there were 61 tree species with >15-cm DBH, i.e. 49 tall tree species and 12 shrub species. Fagaceae, Betulaceae and Acer were the dominant taxa in this forest. More detailed information on the tree species composition in OFR is available in Masaki et al. (1992) and Masaki (2002).
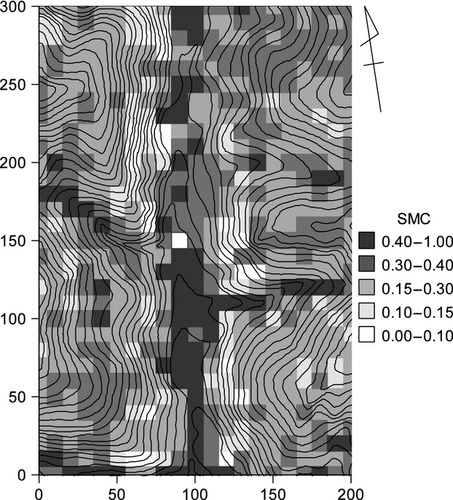
The elevational difference within the plot was 50 m. A small stream ran from north to south through the middle of the plot. The typical soil types were Andic Haplumbrepts and other types (e.g. Andic Dystrochrepts) (Yoshinaga et al. 2002); further information on topography and soil types can be found in Yoshinaga et al. (2002). In a preliminary study (M. Takahashi et al., unpublished research), where soil samples were obtained at depths of 5–15 cm at 17 locations representing these soil types in the plot, soil nitrogen content did not vary significantly among soil types (anova P = 0.1), while the liquid phase varied significantly among soil types (anova P = 0.04). Liquid phase values showed a significant correlation with depth of 50 cm (r = 0.75, P < 0.01). Based on these preliminary results, we assumed that the volumetric soil water content at a depth of 15 cm could be used as a representative variable for soil conditions potentially affecting the tree species distribution (Kozlowski et al. 1991; Palmiotto et al. 2004; Engelbrecht et al. 2007).
Field methods
Tree inventory
We categorised four tree life stages: mature adult, immature juvenile, sapling and seedling. For stems >15 cm GBH (girth at breast height), reproductive trees were defined as adults and non-reproductive trees were defined as juveniles. The specific threshold between adults and juveniles was set at 0.3 × specific maximum girth within the plot, based on results presented in Shibata & Tanaka (2002) and their unpublished results. For smaller stems, those taller than 30 cm were defined as saplings, while those <30-cm high and >1 year old were defined as seedlings. The inventory was conducted for each of the stages with the sampling designs described below.
The 6-ha plot was demarcated into 600 cells using 10-m grids and further divided visually into sub-cells of 5 × 5 m (2400 sub-cells in total). Within each sub-cell, stems of juvenile and adult trees were identified in May 2005. Saplings of tree species were identified in a quadrat of 2 × 2 m placed at each of the grids (651 quadrats and 2604 m2 in total) in May 2004. In 2006, a sub-quadrat (1 × 1 m) was placed within each of the 2 × 2-m quadrats (651 m2 in total) and seedlings of the tree species were identified. During these inventories, approximately 7400 stems were identified in total across the life stages (1141 adults, 3180 juveniles, 1761 saplings and 1324 seedlings).
Environmental variables
The volumetric water content was measured as an index of the soil moisture content (SMC) in autumn 2006 using an electronic sensor (HydroSense; Campbell Scientific Inc., UT, USA) 3 days after the last rainfall. The values at five points randomly selected within each quadrat at a depth of 15 cm from the soil surface were measured and averaged (Fig. 1). The number of days during May–September (153 days) in recent years (i.e. 2011–2013) when rainfall did not occur in the previous 3 days ranged from 94–107 days, suggesting that SMC data of this study represented 60–70% of the overall SMC in a growing season (based on data collected by the Japan Meteorological Agency at a site 4 km apart).
The light conditions were measured in summer 2006. We took hemispherical photographs using a digital camera (COOLPIX 5000, Nikon, Tokyo, Japan) with a fish-eye lens (FC-E8, Nikon) at 1 m above the ground surface at the centre of each quadrat. The relative photon flux density in each quadrat was estimated from the images using CanopOn (version 2.01), which was developed by A. Takenaka (http://takenaka-akio.org/etc/canopon2/).
In the following analyses, four subcells around a grid were merged (and redefined as a subplot) and the environmental variables obtained at the grid were assigned to stems in the corresponding subplot. A variable measured on the border of the 6-ha plot was assigned to one and two sub-cells (also redefined as a subplot of smaller area) at the corner and edge, respectively (i.e. areas of these subplots were smaller).
Analyses
Species with more than five adult trees were used in the present study (35 species; Table 1). We use a hierarchical Bayesian framework to model the relationship between the number of stems and an environmental variable.
| taxon | adult | juvenile | sapling | seedling | recruitment |
|---|---|---|---|---|---|
| Betulaceae | |||||
| Betula grossa | 22 | 11 | – | – | low |
| Ostrya japonica | 30 | 31 | – | 6 | |
| Carpinus cordata | 47 | 498 | 42 | 9 | |
| Carpinus japonica | 15 | 30 | – | – | low |
| Carpinus tschonoskii | 38 | 54 | 5 | 10 | |
| Carpinus laxiflora | 57 | 411 | 13 | 49 | |
| Fagaceae | |||||
| Fagus crenata | 39 | 110 | 474 | 24 | |
| Fagus japonica | 150 | 475 | 126 | 69 | |
| Quercus crispula | 14 | 23 | – | 34 | |
| Quercus serrata | 132 | 149 | – | 239 | |
| Castanea crenata | 41 | 13 | – | – | low |
| Magnoliaceae | |||||
| Magnolia obovata | 5 | 10 | – | – | low |
| Hamamelidaceae | |||||
| Hamamelis japonica | 18 | 14 | 28 | – | |
| Rosaceae | |||||
| Prunus buergeriana | 5 | – | – | – | low |
| Prunus grayana | 5 | 21 | 112 | 19 | |
| Prunus verecunda | 26 | 36 | – | 8 | |
| Sorbus japonica | 15 | 25 | 12 | 14 | |
| Malus tschonoskii | 5 | – | – | – | low |
| Sapindaceae | |||||
| Acer amoenum | 26 | 536 | 166 | 145 | |
| Acer sieboldianum | 10 | 72 | 33 | 8 | |
| Acer tenuifolium | 13 | 104 | 89 | 65 | |
| Acer rufinerve | 33 | 22 | 31 | 170 | |
| Acer mono | 23 | 143 | 92 | 105 | |
| Acer nikoense | 8 | 23 | – | – | low |
| Acer cissifolium | 8 | 14 | 5 | – | |
| Sabiaceae | |||||
| Meliosma myriantha | 12 | 105 | 58 | – | |
| Aquifoliaceae | |||||
| Ilex macropoda | 11 | 40 | 45 | 10 | |
| Cornaceae | |||||
| Swida controversa | 59 | 63 | 18 | 18 | |
| Benthamidia japonica | 10 | 55 | 15 | – | |
| Araliaceae | |||||
| Acanthopanax sciadophylloides | 6 | 21 | 72 | 51 | |
| Kalopanax pictus | 11 | 5 | – | 18 | |
| Clethraceae | |||||
| Clethra barbinervis | 38 | 87 | 40 | 61 | |
| Styracaceae | |||||
| Styrax japonica | 15 | 20 | 75 | 8 | |
| Styrax obassia | 148 | 343 | 21 | 28 | |
| Oleaceae | |||||
| Fraxinus lanuginosa | 20 | 49 | 90 | 77 | |
Specific distribution throughout the environment
 (1)
(1)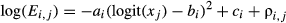 (2)
(2)where ai, bi and ci represent species-specific parameters; xj is the value of an environmental variable (SMC or light level) that ranges from 0 to 1; and ρi,j is the spatial random effect on the j-th subplot [or (sub)quadrat]. The variable xj was logit-transformed in the model to ensure that it ranged from −∞ to ∞. The parameter ai is the degree of specialisation of the i-th species on the focal environmental variable. If ai is 0, this function is flat, suggesting that this species is distributed independently of the values of the variable for this environment (i.e. generalist). However, if ai is positive, this function is unimodal, suggesting that the number of stems of this species is higher at a certain range of this environmental gradient (i.e. specialist). If ai is negative, the shape of the curve is concave and the number of stems of this species tends to be distributed in extreme environmental conditions. When ai is positive, the parameter bi represents the location of the peak of the convex curve, which is the optimal environment for the i-th species. The parameter ci is the height of the curve, which roughly reflects the specific population size.
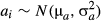 (3)
(3)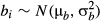 (4)
(4) (5)
(5)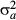 , 1/
, 1/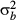 and 1/
and 1/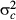 . Spatial random effects were modelled as an intrinsic Gaussian conditional autoregressive (CAR) effect (Latimer et al. 2006). For the j-th subplot [or (sub)quadrat], the CAR effect has a normal distribution with a mean ρ of its neighbours and variance:
. Spatial random effects were modelled as an intrinsic Gaussian conditional autoregressive (CAR) effect (Latimer et al. 2006). For the j-th subplot [or (sub)quadrat], the CAR effect has a normal distribution with a mean ρ of its neighbours and variance:
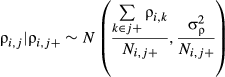 (6)
(6)where j+ denotes the set of neighbours and Nj+ is the number of neighbouring subplots [or (sub)quadrats] (with smaller values at the edge or the corner of the 6-ha plot). The number of adjacent subplots [or (sub)quadrats] that needed to be encompassed as the neighbourhood was defined on the basis of the spatial scale of distributional aggregation in each life stage (see below and Results). The conditional variance 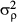 is a hyper-parameter. A gamma distribution with shape parameter = 0.001 and scale parameter = 0.001 was also used as a non-informative prior of 1/
is a hyper-parameter. A gamma distribution with shape parameter = 0.001 and scale parameter = 0.001 was also used as a non-informative prior of 1/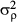 .
.
The posterior distributions of the parameters were separately obtained for each life stage and for each of light (only for seedling and sapling stages) and SMC level using a Markov chain Monte Carlo (MCMC) method with OpenBUGS (Lunn et al. 2009). Three chains were initialised with different values of these parameters. The convergence of MCMC was assessed visually, with reference to Gelman and Rubin's convergence diagnostics (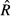 ) smaller than 1.1 (Gelman et al. 2004). The number of iterations required for convergence varied from 80,000 to 220,000, depending on the life stages and environmental variables. We used 20,000 additional iterations and thinned the chains every two steps to obtain a posterior sample size of 10,000, which yielded the posterior distributions. When the credible interval of parameter ai encompassed 0, the i-th species was assumed to be generalist in that specific life stage. For species with less stems, the estimated values (a, b, c) might converge on values of the hyper-parameters (μa, μb, μc). To confirm this, the estimated values of the parameters were plotted against the specific sample sizes.
) smaller than 1.1 (Gelman et al. 2004). The number of iterations required for convergence varied from 80,000 to 220,000, depending on the life stages and environmental variables. We used 20,000 additional iterations and thinned the chains every two steps to obtain a posterior sample size of 10,000, which yielded the posterior distributions. When the credible interval of parameter ai encompassed 0, the i-th species was assumed to be generalist in that specific life stage. For species with less stems, the estimated values (a, b, c) might converge on values of the hyper-parameters (μa, μb, μc). To confirm this, the estimated values of the parameters were plotted against the specific sample sizes.
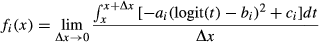 (7)
(7)We solved this equation numerically. A random number, k, was uniformly generated between 0 and 1, the expected number of stems (E) in environment k was calculated, and the number of stems (N) was randomly obtained using a Poisson distribution, where E is the mean. If the value of N was 3, for example, we obtained the vector {k, k, k}. This procedure was repeated until the total length of the vectors reached 100,000 and f(x) was assessed as the probability density.
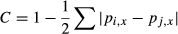 (8)
(8)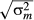 ) of logit(C) for a community m (e.g. 595 values of C for 35 species) were compared among adult, juvenile, sapling and seedling stages and Random and Uniform communities, which were estimated using a Bayesian framework as follows:
) of logit(C) for a community m (e.g. 595 values of C for 35 species) were compared among adult, juvenile, sapling and seedling stages and Random and Uniform communities, which were estimated using a Bayesian framework as follows:
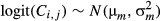 (9)
(9)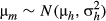 (10)
(10)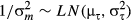 (11)
(11)where, μh, μτ,  and
and 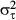 are hyper-parameters. Non-informative priors for the first two parameters were a normal distribution with mean = 0 and variance = 1000, and the inverses of the last two parameters was a gamma distribution with shape parameter = 0.001 and scale parameter = 0.001. Estimation with MCMC was undertaken in the same way as described earlier, with 9000 iterations, discarding the first 1000 steps as a burn-in.
are hyper-parameters. Non-informative priors for the first two parameters were a normal distribution with mean = 0 and variance = 1000, and the inverses of the last two parameters was a gamma distribution with shape parameter = 0.001 and scale parameter = 0.001. Estimation with MCMC was undertaken in the same way as described earlier, with 9000 iterations, discarding the first 1000 steps as a burn-in.
Spatial analyses
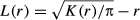 (12)
(12)A negative value of L(r) indicated regular distribution and a positive value indicated aggregated pattern at scale r. First, adult and juvenile trees were randomly distributed within the sub-cells to which they belonged. For saplings and seedlings, the trees with the same number as the (sub)quadrat to which they belonged were randomly distributed within the corresponding subplot. These distributions were used as the observed distribution. Second, a random distribution of trees within the 6-ha that had the same number as each life stage was generated. This random distribution was generated 20,000 times and used to estimate the expected range (i.e. 95% confidence envelope) of L(r), and the spatial scale of aggregation was evaluated on the basis of a comparison with the observed L(r).
To evaluate specific seed dispersal limitation, the univariate L(r) was expanded to a bivariate function L12(r) (Lan et al. 2009), and the spatial correlations between the adult and seedling (or sapling) stages were tested by comparing observed and expected values of L12(r). In this test, a random distribution was generated 20,000 times by torus translation. Similarly, the interspecific spatial correlations were tested in each stage for all of the species pairs. The number of pairs was 595, 528, 253 and 276 for the adult, juvenile, sapling and seedling stages, respectively (Table 2).
| stage | number of pairs | interspecific spatial correlation | ||
|---|---|---|---|---|
| positive | not significant | negative | ||
| adult | 595 | 86 (14.5%) | 405 (68.1%) | 104 (17.5%) |
| juvenile | 528 | 149 (28.2%) | 236 (44.7%) | 143 (27.1%) |
| sapling | 253 | 65 (25.7%) | 121 (47.8%) | 67 (26.5%) |
| seedling | 276 | 102 (37.0%) | 127 (46.0%) | 47 (17.0%) |
All the calculations for L and L12 were implemented for the range of r from 0 to 30 m at every 0.5-m interval. If multiple r-values existed, whereby the observed Ls were more than the 95% confidence envelope and these values were not continuous, we adopted the minimum value as the spatial scale of aggregation.
Results
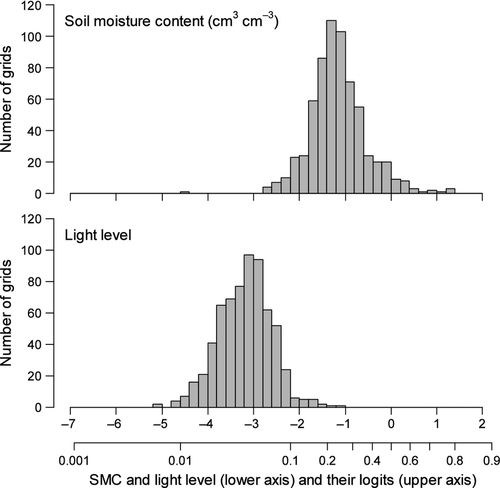
The SMC values ranged from 0.05 to 0.8 (cm3 cm−3), which corresponded to −2.9 to 1.4 (mean = −1.16) after logit transformation (Fig. 2, upper). The light level ranged 0.005 to 0.25, which corresponded to −5.3 to −1.1 (mean = −3.18; Fig. 2, lower). Among the 35 species tested, two, 12 and 11 species had less than five stems in the juvenile, sapling and seedling stages, respectively (Table 1). Seven species were low-recruitment species, with less than five saplings and seedlings according to the sampling method used in the present study.
Analysis based on L(r) showed that over 60% of the species had aggregated distributions during any life stage, and the scales of spatial aggregation for the aggregated species were estimated as 10.7 ± 6.3 m, 7.6 ± 6.5 m, 5.0 ± 3.5 m and 6.2 ± 7.7 m for the adult, juvenile, sapling and seedling stages, respectively. Based on these results, the nearest neighbouring subplots [or (sub)quadrats] (i.e. a distance of 10 m) were used to simplify evaluation of the spatial autocorrelation in the following analyses of any species.
Analysis based on the light level as an environmental variable did not detect any significant bias of the parameter a from 0 in either the seedling or sapling stage (data not shown). Thus, the distributions of seedlings and saplings of the species tested were not significantly affected by the spatial heterogeneity of light conditions in this forest; therefore only the SMC results were considered in the following analyses. The estimated values of parameters a, b and c with respect to SMC are shown in Fig. 3 and summarised in Appendices S1–4. For parameter a (Fig. 3, top), all the species had significant positive values in the adult stage (ca. 0.3–0.5), with the exception of Acer mono (ca. 0.2), which had a credible interval that encompassed 0. In the juvenile stage, all species other than Kalopanax pictus (<0.2) had significant positive values (ca. 0.2–0.3). Saplings and juveniles had similar values, and seedlings tended to have the highest values in comparison with other stages. The values of species with smaller sample sizes did not tend to converge.
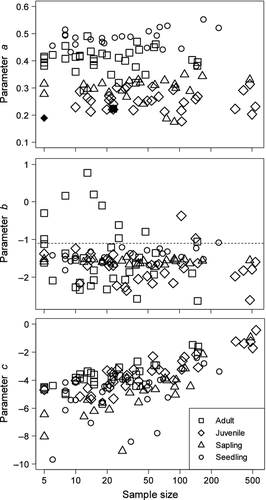
For parameter b (Fig. 3, middle), most species had values around −1.5 (which corresponded to SMC ≈ 0.2 cm3 cm−3) in the seedling and sapling stages. In the juvenile stage, some species tended to have smaller values that ranged from −2 to −1 (SMC 0.1–0.3), and values in the adult stage tended to have a wider range than those in the preceding stages, i.e. from −2.5 to 0.7 (SMC 0.1–0.7). The values of species with smaller sample sizes did not tend to converge.
For parameter c, the estimated values tended to be higher with increasing sample sizes, irrespective of the life stage, as expected (Fig. 3, bottom).
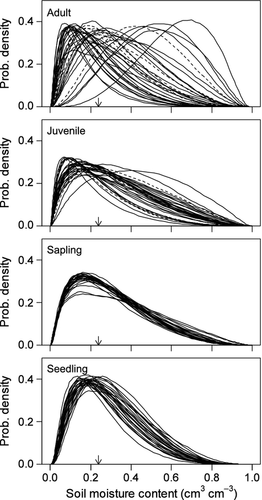
The probability densities in terms of SMC are shown in Fig. 4. In the seedling stage, most species had similar functions and a narrower distribution range than at other stages in terms of SMC. The range distribution in the sapling stage was larger than that in the seedling stage. The differentiation of optimal values between species appeared to begin in the juvenile stage, and this tendency was more conspicuous in the adult stage. Low-recruitment species did not show a consistent tendency of a biased distribution toward wetter or drier conditions.
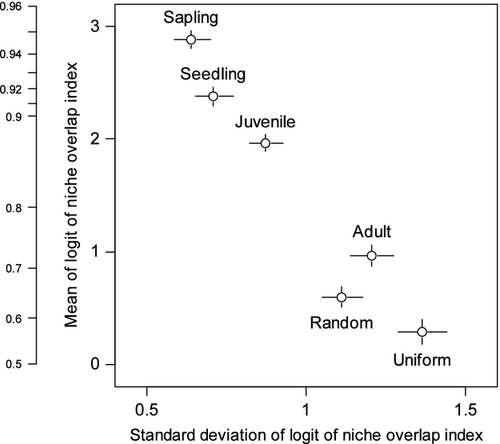
The niche overlap index for the adult stage was significantly smaller than for younger stages, but significantly larger than the Random and the Uniform communities in terms of credible intervals of the posterior of the mean (Fig. 5). The niche overlap index at the juvenile stage was intermediate between the adult and other stages, but was relatively closer to the sapling and seedling stages. Among the six communities tested, the Uniform community showed minimum values of niche overlap.
The intraspecific spatial correlations between adults and seedlings were not significant for 24 species at any spatial scale and were significant only for three species (Fagus crenata, Quercus crispula and Quercus serrata) beyond a spatial scale of 16.0 ± 9.5 m. In the sapling stage, correlations were not significant for 23 species and significant for Fagus crenata and Acer tenuifolium beyond the spatial scale of 20.0 m and 22.5 m, respectively. For adult–juvenile relationships, about half of the species (16 species) showed significantly positive spatial correlation beyond the spatial scale of 8.3 ± 5.5 m, and the other 17 species did not show significant correlations (data not shown).
Among the pairs of different species, no more than 30% had significant negative spatial correlations at specific spatial scales in any of the life history stages (Table 2).
Discussion
The results of the present study in a temperate forest are in accordance with previous findings from tropical forests in some respects. Comita et al. (2007) suggested that individuals in the adult tree stage have more frequent significant distributional correlations with soil moisture conditions. Hu et al. (2012) also argued that the distributions of adult trees are more likely to be determined by the environment than those of younger trees. This study also postulated that the association of mature trees with specific habitat conditions could be formed ontogenetically, probably via differentiated growth and mortality between life stages, as in tropical forests (Metz 2012). However, whether niche partitioning along environmental gradients contributes to coexistence of species in this forest is unclear. Furthermore, the role of dispersal limitation also appeared to be less significant.
Does habitat association maintain species diversity?
Based on results of the present study, the answer to the question “Do tree species have different optimal values for their distributions relative to the soil and light conditions?” is yes with respect to SMC but no with respect to light. With the exception of Acer mono in the adult stage and Kalopanax pictus in the juvenile stage, all the species had significantly positive values for parameter a with respect to SMC, suggesting that their distribution patterns had unimodal curves along the SMC gradient and that each species had an optimal value on this gradient.
Based on estimated values of b, the optimal SMC tended to be more variable among species in later life stages, while interspecific competition was not completely relaxed at every stage, as shown by mean values of the niche overlap indices, which were significantly larger than expected for a random assembly. In a previous study (Masaki et al. 1992), habitat segregation among species was suggested on the basis of visual assessments of specific distribution within the plot. However, the quantitative soil condition data collected in this study showed that habitat was partitioned less effectively than could be randomly assumed. Furthermore, the forest studied did not include an extremely wet or dry habitat (e.g. swampy habitat; Harms et al. 2001) and did not experience dry summer each year (as in seasonal evergreen tropical forests; Baltzer et al. 2008). Considering that SMC mostly ranged between 0.1 and 0.5 in the plot (Fig. 2, upper), and that most of the species distribution overlapped within this range (Fig. 4), efficient niche segregation along the SMC gradient was difficult. Although Palmiotto et al. (2004) reported specific different responses to soil conditions on the basis of an experimental study, their experiment used extreme soil conditions to elucidate the specific differences more clearly. Heterogeneity in soil conditions at the landscape scale, where extreme soil conditions are found, may be sufficient to determine tree distributions (Laurance et al. 2010). However, at the local scale, spatial variations in soil conditions may not fully explain the species assemblies.
No effective niche segregation with respect to the light environment was detected in the seedling and sapling stages. Another previous study in OFR suggested that saplings of some tree species were present at a higher density under canopy gaps than in other areas (Abe et al. 1995). However, this result depended on intensive sampling efforts under the gaps. In this forest, sites with abundant light (e.g. light level >0.1) were very rare (Fig. 2), which probably explained the failure to detect light effects on seedling and sapling distributions. Under the current conditions, the community of seedlings and saplings should be mainly composed of more shade-tolerant species. Several species that had few seedling and sapling populations, such as Betula grossa and Castanea crenata, are expected to decrease in the future (Masaki et al. 1992). The majority of the other species are considered to be less gap-dependent in the study forest (Abe et al. 1995); therefore, current spatial variation in the light environment is not considered to be critical for the coexistence of tree species. If an exceptionally large and intense disturbance occurs in future, we may be able to detect niche segregation in terms of the light environment in seedling and sapling stages.
Thus, we postulate that the coexistence of tree species within this old-growth forest might not be substantially facilitated by niche segregation in terms of both the soil and the light environments.
Do tree distributions change with the life stages?
Initially, we expected that seedlings of any species would be distributed as habitat generalists because the seeds of most species in this forest were widely dispersed, having a highly scattered distribution (Masaki et al. 1994; Nakashizuka et al. 1995; Shibata & Nakashizuka 1995; Tanaka et al. 1997). However, distribution of seedlings was concentrated within a specific range in the soil moisture environment, just as habitat specialists. Seedlings are often vulnerable to extreme soil water availability conditions (Comita & Engelbrecht 2009). This may explain why early stages of the trees in this forest had distribution modes at modest conditions in terms of SMC.
In contrast, the tree specific habitat diverged with the life stage: nine changed to wetter and 15 did to drier habitats from the seedling to adult stages (Appendix S1, S4). Changes of distribution to wetter habitats with life stage has been found in many previous studies (Gunatilleke et al. 2006; Comita et al. 2007; Chuyong et al. 2011), suggesting that a preference for wetter habitats in later stages may be common among tree species in both tropical and temperate forests. However, one should also consider that ontogenetic physiological development of desiccation tolerance over life stages (Ishida et al. 2005) could enable the majority of species to change habitat to drier areas in the adult stage.
Metz (2012) concluded that species become more niche-partitioned in later life stages because of specific differential mortality in different habitats. We consider the change of habitat with life stage in this forest could be explained by similar mechanisms, and this can be tested in future by monitoring the growth and survival of younger trees.
Are species exclusively distributed in space?
Hu et al. (2012) found that species distribution was determined by dispersal limitation in the younger stages. However, no evidence of effective dispersal limitation was found in the present study. The seedlings and saplings of most species had independent distributions relative to their conspecific adults, except for a few species with large seeds. Juveniles displayed a positive spatial correlation with conspecific adult trees for about half of the species studied, but these correlations between older-stage trees were likely to result not from dispersal limitation, but rather from changes in habitats preferred by conspecific adult trees. In addition, most species had spatially nonexclusive distributions compared with others (>80% of species pairs) in any life stage. Thus, dispersal limitation did not appear to facilitate the coexistence of multiple species within this forest community, according to statistical analysis.
There are several possible reasons for the absence of effects of dispersal limitation in this study. First, this may be a consequence of the seed dispersal patterns in this forest. Approximately half of the species in this forest were found to have winged seeds (i.e. Betulaceae, Acer and Fraxinus), which resulted in a highly scattered seed distribution (Nakashizuka et al. 1995; Shibata & Nakashizuka 1995; Tanaka et al. 1997). Bird-dispersed seeds also had a very scattered distribution in this forest (Masaki et al. 1994) compared with the patterns modelled in tropical forests (Schupp et al. 2002). In addition, even the acorns of Quercus have been reported to be well scattered in this forest via secondary dispersal through rodents (Iida 1996). Thus, dispersal limitation may be less likely in this forest than expected in tropical forests.
Second, density-dependent mortality is also causal. Previously, Masaki & Nakashizuka (2002) and Shibata et al. (2010) analysed the current-year seedling mortality and showed that most species experienced highest mortality during the year immediately after germination, which was positively and negatively correlated with the conspecific seedling density and distance from the nearest conspecific mature tree, respectively. This mechanism may result in no contagious distribution of >1-year-old seedlings around conspecific mature trees.
Thus, dispersal limitation may only play a restricted role in this temperate forest in regulating species assembly. Most species could potentially reach a vacant site after the death of a mature tree via effective seed dispersal. Furthermore, many species in this forest exhibit synchronised seed production over the years, irrespective of taxon (Shibata et al. 2002). This means that every species has an equivalent opportunity to be recruited to a site wherever and whenever it becomes vacant.
How is tree species diversity maintained?
Why was difference in habitats not clear in the present study? We offer three possible explanations to this question. First, interspecific niche differentiation may have been detected if other environmental variables had they been included in the analysis. The spatial variation in resources other than SMC, such as nitrogen (although it is spatially less variable than SMC in this forest) and phosphorus, could affect the species distribution patterns (John et al. 2007). Effects of these other factors need to be tested in future studies.
Second, the temporal oscillation in environmental conditions may have effects on habitat association. The adult trees of low-recruitment species may be the legacy of past disturbances in this forest (Masaki et al. 1992). At present, this old-growth forest has a low proportion of light gaps (Fig. 2, lower). The current light regime is unlikely to be beneficial for recruitment of light-demanding species. However, if an intensive and large-scale disturbance occurs in this forest, the spatial heterogeneity in light conditions will be sufficient to affect recruitment patterns of tree species. The roles of spatiotemporal dynamics in coexistence of tree species need to be tested on the basis of long-term monitoring studies.
Third, spatial scales should be considered (Wang et al. 2012). Most previous studies in tropical or subtropical forests were conducted in larger-scale inventory plots (e.g. 50 ha), and these studies often categorised habitats into several types (each ca. 10–20 ha) on the basis of analyses (Gunatilleke et al. 2006; Comita et al. 2007; Chuyong et al. 2011). However, these studies did not consider the species assembly rules within each category, which is similar to the present study in terms of spatial scale. We consider it likely that species assembly could be regulated through a neutral process at the local scale (<10–20 ha), whereas partitioning of the environment would be detected among guilds of species at larger scales (Pearse et al. 2013).
To conclude, we propose two hypotheses for further studies. First, as also suggested in tropical forests, species assemblies could be controlled through a neutral process in temperate forests where the habitats of species appear to be identical rather than well partitioned in terms of SMC. Second, seed dispersal limitation might not play a substantial role in shaping local species assemblies in temperate forests because of more scattered seed distribution than in tropical forests. More comparative studies of temperate forests are required to establish a general and convincing theory regarding the mechanism that maintains tree species diversity in forest communities worldwide (Shen et al. 2013).
Acknowledgements
We thank Dr. T. Nakashizuka, Dr. T. Nagaike, and Dr. T. Tanaka for helpful support throughout this study. We also thank Dr. N. Miyashita for critical suggestions on statistical modelling, and Dr. A. Itoh for useful comments on an earlier version of the manuscript. We would like to thank Enago (www.enago.jp) for the English language review. This study was partly funded by the Technology Development Fund (S-9) of the Ministry of the Environment, Japan. Part of the data used in the present study was derived from the Forest Dynamics Database provided by the Forestry and Forest Products Research Institute and from the Monitoring Sites 1000 Project launched by the Ministry of the Environment, Japan. The meteorological data of the Japan Meteorological Agency was obtained from the Agriculture, Forestry and Fisheries Research Council, Japan.