Prospect theory and public service outcomes: Examining risk preferences in relation to public sector reforms
Abstract
Prospect theory has been widely acknowledged in the social sciences as a frame for understanding how people deal with uncertainty. Yet, little is known about whether key expectations from prospect theory also hold in a public service setting. In this article, I draw on prospect theory to examine under what conditions citizens prefer uncertain – but potentially advantageous – reforms to reforms with more certain outcomes. A population-based survey experiment with the participation of 1,395 Danish citizens and two consecutive experiments with 1,680 US MTurkers produced a consistent pattern across contexts: citizens to a large extent prefer certain to risky reforms and are more willing to take risks if reforms are associated with gains rather than losses. The latter finding is in opposition to expectations and suggests that the particularities of the public sector should be taken into account when applying insights from prospect theory to this sector.
1 INTRODUCTION
Uncertainty about the effects of public initiatives and reforms is a fundamental condition in politics and the public sector. Multi-dimensional outcomes produced by several actors with sometimes competing interests and complex and ever-changing scope conditions contribute to this fundamental uncertainty. Yet, uncertainty is arguably a variable condition. Sometimes, the effects of initiatives and reforms are relatively given; other times, they are highly uncertain and may be both positive and negative. The variation in the certainty with which outcomes will occur is relevant to a range of questions of importance to politics and the organization of the public sector. These are questions such as how and under what conditions citizens prefer a given reform proposal to competing proposals, how policy-makers can build support for reforms of the public sector, how citizens prioritize between different kinds of outcomes, and whether they to a larger extent are willing to accept risky reforms to achieve some outcomes than others (e.g. Boeri et al. 2002; O'Donnell and Tinios 2003; Rattsø and Sørensen 2004; Boeri and Tabellini 2002).
In this article, I draw on prospect theory (Kahneman and Tversky 1979; Tversky and Kahneman 1992) to examine under what conditions citizens prefer risky – but potentially advantageous – reforms to reforms with more certain outcomes. Specifically, I draw on the insight from prospect theory that citizens are prone to a number of psychological biases leading them to prefer certain outcomes to risky outcomes (risk aversion) and to have a stronger preference for avoiding losses than for acquiring gains. In doing so, the article contributes to extant research by examining the relevance of key expectations from prospect theory in a public sector setting. Several studies draw on insights from prospect theory without considering in greater detail the relevance of prospect theory to a public sector setting (e.g. Vis and Van Kersbergen 2007; Dull 2009; Moynihan and Lavertu 2012; Bewan and Wilson 2013; Nielsen and Moynihan 2017). However, the public sector differs in important respects from the scenarios originally covered by prospect theory. Important in this respect, some studies suggest that the presence and strength of the biases depend on the context that the outcomes relate to (e.g. Hershey and Schoemaker 1980; Leclerc et al. 1995).
Moreover, the article suggests an empirical design to examine under what conditions citizens prefer reforms with uncertain outcomes to reforms with certain outcomes. Specifically, the hypotheses are tested in a randomized between-subjects population-based survey experiment with 1,395 responses from a representative sample of Danish citizens and two experiments with 1,680 US MTurkers. In all experiments, respondents were asked to choose between two reforms of public services; one with a known outcome and one with a probabilistic outcome. I experimentally manipulate whether the reform is expected to lead to gains or losses in various outcomes.
In the next section, I present prospect theory with a particular emphasis on four common characteristics of human decision-making identified in this framework: risk aversion, asymmetry of risk aversion in gain and loss domains (also known as the reflection effect), loss aversion, and probability weighting. I then discuss the application of prospect theory to public sector outcomes. This is followed by a presentation, discussion, and analysis of my experiments. The analysis produces a consistent pattern across contexts: citizens to a large extent prefer certain to probabilistic reforms and are more willing to take risks if reforms are associated with gains rather than losses. The latter finding is in outright opposition to the expectation that people are loss averse, and the article therefore concludes by discussing what can explain this deviation from what has sometimes been described as an effect that, by behavioural standards, is ‘exceptionally large and reliable’ (Lerner and Keltner 2001, p. 148) as well as a discussion of the limitations of the current study and guidelines for future research on the topic.
2 PROSPECT THEORY AND DECISION-MAKING BIASES
Acknowledging that expected utility theory – a core element in rational choice theory – and hence of relevance to both public administration and political science – continually failed empirically, Kahneman and Tversky (1979) developed prospect theory as a descriptively more correct theory of decision-making under risk. Risk is here understood as the probability that an event takes place times the impact of the event (Vis 2011). Central to prospect theory is the idea that people are prone to a range of decision-making biases that affect their preferences and behaviour. Prospect theory does not attempt to explain why such biases occur but is rather a description of biases that are found to affect decision-making in behavioural experiments. With its background in economics, prospect theory is particularly concerned with examining under what conditions people prefer to take risky decisions to potentially achieve a better economic outcome than if a more safe choice is made. However, prospect theory has also been applied widely beyond economic decisions. Insights from prospect theory have been used to explain, for instance, the choice between political candidates and how to vote in political referendums (Quattrone and Tversky 1988), why people take part in collective action (Fanis 2004), the effects of governance models on performance (Bewan and Wilson 2013), election administrators’ preferences for e-voting technology (Moynihan and Lavertu 2012), strategies pursued by managers in change situations (Jawahar and McLaughlin 2001), why political leaders pursue risky reforms (Vis and Van Kersbergen 2007), and whether politicians are more concerned about either policy or votes (i.e. basing their decisions mostly on one of these dimensions) when making decisions (Linde and Vis 2017).
One important bias is the so-called certainty effect. This refers to the tendency that people have to ‘overweight outcomes that are considered certain, relative to outcomes which are merely probable’ (Kahneman and Tversky 1979, p. 265). Thus, Kahneman and Tversky (1979) demonstrate in a series of experiments that their respondents are considerably more likely to choose certain rather than probable outcomes even if the expected utility of the probable outcome is higher. This suggests that people are generally risk averse. Risk aversion furthermore tends to increase when more is at stake (Gomez 2008). The concept of risk aversion is closely related to the concept of loss aversion. According to prospect theory, individuals are loss averse, meaning that ‘losses hurt more than equal gains please’ (McDermott 2004, p. 298; see also Camerer 2005). Losses typically have more than twice as strong an impact on individuals than gains (Akalis 2008; Vis 2011, p. 335), meaning that people generally have a biased preference for the status quo over change (Quattrone and Tversky 1988; Akalis 2008) because the ‘disadvantages of leaving it [the status quo] loom larger than advantages’ (Kahneman et al. 2000, p. 163).
Furthermore, the risk willingness of an individual is asymmetric. Individuals are more likely to accept risks when they face losses (i.e. are in a domain of losses) than when they face gains (i.e. are in a domain of gains) (Kahneman and Tversky 1979, p. 268; Schoemaker 1993, p. 52). This is well illustrated by the classical and widely cited Asian Disease Experiment (Tversky and Kahneman 1981). In this within-subject design, in which two equivalent frames in terms of expected utility are compared, participants are first asked to imagine that the US is preparing for the outbreak of an unusual Asian disease that is expected to kill 600 people. Two different programmes to combat the disease are proposed (A and B). Under the gain frame, participants read that the exact scientific estimates of the consequences are as follows: ‘If Programme A is adopted, 200 people will be saved. If Programme B is adopted, there is a one-third probability that 600 people will be saved and a two-thirds probability that no one will be saved’. Under the loss frame, participants are told that ‘If Programme C is adopted, 400 people will die. If Programme D is adopted, there is a one-third probability that nobody will die and a two-thirds probability that 600 people will die’. Although a preference for the certain ‘risk-averse’ option (Programme A under the gain frame) should lead someone to prefer the equivalent option under the loss frame (Programme C), the norm is for people to select A under gain frames and D under loss frames. Across investigations, an average of 70–80 per cent of respondents become risk seeking (i.e. choose the gamble) when the above choices are framed as losses and become risk averse (i.e. choose the certain outcome) when identical choices are framed as gains (Lerner and Keltner 2001, p. 148).
In the original experiment of Tversky and Kahneman (1981), an almost complete reversal of preferences took place as 72 per cent preferred the certain outcome in the gains domain, whereas 78 per cent preferred the risky outcome in the loss domain (Wallin et al. 2016). The logic is also generally found in cases that are quite different from the Asian Disease Experiment. For instance, Bazerman (2001) describes a plant closure problem where managers are considerably more likely to choose a certain option when they are presented with a positively framed version of the problem, whereas a majority selects the risky option when they are presented with a negatively framed version of the same problem. In sum, sure gains are generally sought, while sure losses are avoided by means of risk-taking.
The asymmetry of risk aversion is related to a fourth type of bias identified in prospect theory: probability weighting (Schoemaker 1993, pp. 52f.). Probability weighting is the idea that probabilities are generally underweighted,1 and hence, the effect of an outcome's probability on an option's perceived value is nonlinear (Linde and Vis 2017, p. 104). This in turn means that people have a tendency to act as if something is less likely to occur than it actually is. Because of the underweighting of probabilities, people tend to assign too little weight to the potential gains from engaging in a potentially risky but beneficial reform. Similarly, they also tend to assign too little weight to potentially detrimental effects, which explains why they are more likely to accept risk to avoid losses than they are to accept risk to achieve additional gains.
3 APPLYING PROSPECT THEORY TO PUBLIC SECTOR OUTCOMES
Risk aversion hypothesis: On average, citizens prefer certain to risky reform outcomes.
Asymmetry hypothesis: On average, citizens to a greater extent prefer certain reform outcomes when they are in a gain domain (i.e. when reform outcomes are positive) than when they are in a loss domain (i.e. when reform outcomes are negative).
On the other hand, the marketing literature on loss aversion is open to the idea that central predictions from prospect theory are moderated by contextual factors (e.g. Ariely et al. 2005; Novemsky and Kahneman 2005). This suggests that the particularities of the public sector should be acknowledged. Importantly, public sector reform outcomes in several respects differ from the outcomes used in economic studies and there is indeed some evidence that the type of outcome at stake may be important to the presence of the patterns suggested by prospect theory. For instance, Linde and Vis (2017) find no evidence of the asymmetry in risk preferences in gain and loss domains when they present politicians with scenarios focusing on either vote outcomes or economic outcomes. There are different ways in which characteristics of outcomes may moderate the predictions from prospect theory.
First, in many cases, reform outcomes arguably have a less direct and personal impact on citizens than the monetary gains and losses often studied in economics. Consider, for instance, reorganizations of local police forces or fire-fighting services. Such reorganizations may have an impact on the efficiency of the services but are unlikely to affect the daily lives of most citizens. In this sense, many public sector reform outcomes are collective in nature. Based on previous findings in the literature that risk aversion tends to increase when more is at stake (Gomez 2008), we should expect people to be relatively less risk averse in relation to collective outcomes from public sector reforms than in relation to personal outcomes. The less direct and personal implications of reform outcomes are also important because people are likely to be less strongly emotionally attached to such outcomes. From an affective perspective, emotional attachment is likely to increase the feeling of loss when an item or a good is given away and hence to increase asymmetry of risk preferences (Ariely et al. 2005, p. 136; Aggarwal and Zhang 2006). Hence, from this perspective, less strong asymmetric patterns are to be expected for reform outcomes that people feel less emotionally attached to.
Second, Leclerc et al. (1995) find that people are more risk averse with respect to decisions involving losses than in decisions involving gains in time. This is in contrast to the prospect-theoretical expectation that people will be more risk seeking in loss domains. They suggest non-fungibility of time as an explanation of the discrepancy between decisions involving time and decisions involving money. Because time is less substitutable than money, planning is more important, and hence, risk has to be avoided in loss domains in particular. Similarly, public sector outcomes such as equity and efficiency are non-fungible for single individuals. Even if some money is saved by implementing a reform, the money saved will not be available for the single individual. Hence, the non-fungibility of many public sector outcomes suggests a reversed asymmetric pattern according to which people will be relatively more risk seeking in gain than in loss domains.
4 DATA AND DESIGN
To test the hypotheses, I need data that allow me to compare risk preferences in gain and loss domains. Comparable data satisfying this precondition are unlikely to exist. I therefore rely on data from survey experiments. Importantly, randomized survey experiments allow me to manipulate the independent variable (gains and losses from reforms) and to identify causal impacts of the experimental treatments used. While survey experiments promise high internal validity, findings from such designs may be criticized for being artificial, and they may only to a limited extent generalize beyond the experimental setting (Munck and Verkuilen 2005, p. 389). In this study, the concern about low external validity was dealt with by using a sample that is representative of the Danish population at large on a number of background characteristics and by means of two replication studies (including extensions).
5 EXPERIMENT 1: METHOD
The sample in experiment 1 consists of 1,395 Danish citizens participating in an online panel administered by the survey company Userneeds. Data were gathered in June 2014. While the panel resembles the working-age population at large on characteristics such as gender, age, and education, the sample may differ from the population at large on unmeasured attitudinal and behavioural aspects. However, as shown in table A1 in the appendix, one key aspect of the sample is that it is both very diverse in terms of socio-demographic composition and in terms of characteristics such as the respondents’ ability to interpret numerical information. Moreover, including measured characteristics in the analysis does not alter the experimental findings.2 This reduces the concern that potential skewness in the sample limits the external validity.
The experiment is based on a case that I expected respondents could easily relate to: the case of school mergers. The organization of public schools is a highly debated topic in Denmark. From 2007 to 2015, the number of public schools dropped from 1,604 to 1,197 (Ministry of Social Affairs and the Interior 2016). It has several times been suggested that school mergers are likely to have both economic consequences (typically because of economies of scale) and service quality consequences in the sense that large and small schools may differ in their ability to teach pupils the curriculum (Blom-Hansen 2004; Bækgaard 2010; Houlberg et al. 2016). I exploit this fact in the experimental design by focusing on both economic and service quality consequences.
I use an experimental design inspired by the Asian Disease Experiment even though it is more complex and differs in important respects. The experiment uses between-subjects random assignment of respondents to six different experimental arms. Key characteristics of the experimental arms are presented in table 1, while the full survey questions are presented in table 2. All respondents – regardless of which experimental arm they were in – were presented with the same introductory text and had to choose their preferred reform among two possible options; one reform with certain economic and service quality outcomes (‘the baseline reform’) and another reform in which either the economic or the service quality outcome is probabilistic (‘the risky reform’).
| T1 | T2 | T3 | T4 | T5 | T6 | |
|---|---|---|---|---|---|---|
| Framing of economic outcomes of reforms | Economic gains | Economic gains | Economic losses | Economic losses | Economic gains | Economic gains |
| Framing of service quality outcomes of reforms | Service losses | Service losses | Service gains | Service gains | Service gains | Service gains |
| Uncertainty about | service outcomes | economic outcomes | service outcomes | economic outcomes | service outcomes | economic outcomes |
| T1 | T2 | T3 | T4 | T5 | T6 |
|---|---|---|---|---|---|
| Imagine that two reforms are proposed in your home municipality. Both reforms entail that a number of schools are closed and replaced with larger schools. However, the reforms have different consequences: | |||||
| a. If reform A is chosen, municipal school expenditures will drop by 10 per cent, and the percentage of pupils passing the final exam will drop from 90 to 88 per cent. | a. If reform A is chosen, municipal school expenditures will drop by 10 per cent, and the percentage of pupils passing the final exam will drop from 90 to 88 per cent. | a. If reform A is chosen, municipal school expenditures will increase by 10 per cent, and the percentage of pupils passing the final exam will increase from 90 to 92 per cent. | a. If reform A is chosen, municipal school expenditures will increase by 10 per cent, and the percentage of pupils passing the final exam will increase from 90 to 92 per cent. | a. If reform A is chosen, municipal school expenditures will drop by 10 per cent, and the percentage of pupils passing the final exam will increase from 90 to 92 per cent. | a. If reform A is chosen, municipal school expenditures will drop by 10 per cent, and the percentage of pupils passing the final exam will increase from 90 to 92 per cent. |
| b. If reform B is chosen, municipal school expenditures will drop by 10 per cent. There is furthermore a likelihood of one-third that the percentage of pupils passing the final exam will drop from 90 to 84 per cent and a likelihood of two-thirds that the percentage will remain unchanged. | b. If reform B is chosen, the percentage of pupils passing the final exam will drop from 90 to 88 per cent. There is furthermore a likelihood of one-third that municipal school expenditures will drop by 30 per cent and a likelihood of two-thirds that expenditures will remain unchanged. | b. If reform B is chosen, municipal school expenditures will increase by 10 per cent. There is furthermore a likelihood of one-third that the percentage of pupils passing the final exam will increase from 90 to 96 per cent and a likelihood of two-thirds that the percentage will remain unchanged. | b. If reform B is chosen, the percentage of pupils passing the final exam will increase from 90 to 92 per cent. There is furthermore a likelihood of one-third that municipal school expenditures will increase by 30 per cent and a likelihood of two-thirds that expenditures will remain unchanged. | b. If reform B is chosen, municipal school expenditures will drop by 10 per cent. There is furthermore a likelihood of one-third that the percentage of pupils passing the final exam will increase from 90 to 96 per cent and a likelihood of two-thirds that the percentage will remain unchanged. | b. If reform B is chosen, the percentage of pupils passing the final exam will increase from 90 to 92 per cent. There is furthermore a likelihood of one-third that municipal school expenditures will drop by 30 per cent and a likelihood of two-thirds that expenditures will remain unchanged. |
| Which of the reforms would you prefer? [response options: Reform A; Reform B]. | |||||
As outcomes, I focus on two potential implications of school consolidation: changes in municipal school expenditures (the economic outcome) and in pass rates at the final exam (the service quality outcome). For the risky reforms, the probabilistic outcome is likely to occur with a probability of two-thirds and to an even stronger extent than in the baseline reform. However, according to the experimental vignette, there is also a one-third chance that the outcome will remain at the same level as hitherto. Hence, the design makes it possible to estimate whether and under what conditions respondents prefer a reform with certain outcomes to a reform with a similar expected utility, where one of the outcomes is very likely to occur but may also not occur at all.
One important challenge in experiments comparing the impact of various outcomes is how to make the outcomes comparable. Consider, for instance, T1 in table 1. In this treatment, the respondents are presented with a scenario with economic gains and service quality deterioration. However, the two outcomes are not measured on the same scale, as the economic reduction in the baseline reform is 10 per cent, while the decline of the service quality is a drop of 2 percentage points in the share of pupils passing their final exam. The difference in scales was used deliberately to make the vignette scenario appear realistic, which would not be the case had the scales been similar. The difference, however, comes at a cost as changes in economic outcomes are likely to appear more dramatic than changes in service quality outcomes, meaning that we should expect relatively stronger reactions on economy than services than if the changes in the two outcomes had been presented on the same scale.
In all experimental arms, the expected utility of the two reforms that the respondents were presented with was similar, and hence, the only difference between the two reforms is whether both outcomes are presented as certain or one of the outcomes is presented as being probabilistic. The dependent variable is thus dichotomous with ‘0’ meaning that the baseline reform is preferred, and ‘1’ that the risky reform is preferred. Another similarity between all experimental arms is that at least one of the two outcomes is positive.3
However, the experimental arms differ on two dimensions, meaning that a 3 × 2 factorial design is used. On the one dimension, the arms differ on whether (a) both outcomes are positive (that is, both economic gains and service quality gains are expected); (b) the economic outcome is positive while the service quality outcome is negative; and (c) the service quality outcome is positive while the economic outcome is negative. On the other dimension, the arms differ on whether it is the economic or the service quality outcome that is presented as probabilistic in one of the reforms. The design thus makes it possible to examine the hypotheses by making a number of pairwise comparisons. For instance, the impact of whether there is uncertainty on either the service outcome or the economic outcome can be analysed by comparing responses to T1, T3, and T5 to those of T2, T4, and T6. Similarly, the impact of respondents being presented with either economic gains or losses on their preferences for a risky reform can be analysed by comparing the responses to T3 and T4 to those of T5 and T6. Logistic regressions (see table A2 in the appendix) comparing the composition of each of the groups to that of the others show that there are only a few significant differences between the groups, and hence, the analysis is conducted without including control variables.
6 EXPERIMENT 1: RESULTS
The risk aversion hypothesis claims that citizens on average are more likely to prefer certain to risky reform outcomes. The hypothesis is examined by means of a one sample t-test in which it is analysed whether the share of respondents reporting that they prefer certain reform outcomes is significantly different from a situation in which citizens on average are indifferent between certain and risky outcomes (equivalent to the dependent variable taking the value 0.5). With 58.9 per cent of the respondents preferring the certain to the risky reform, the experimental findings lend support to the hypothesis (t = 6.773; p < 0.01 in a two-tailed test).
The asymmetry hypothesis deals with the expectation that people are more willing to choose a risky reform if they are in a loss domain. This hypothesis is examined using three different t-tests. First, I test whether the likelihood of preferring risky outcomes is significantly different between loss and gain domains in general. Second, I conduct similar tests on two subsamples. In the one subsample, I compare service gains and losses, and in the other, I compare economic gains and losses. Table 3 shows the results. Contrary to the expectation, the analysis in all specifications shows that citizens are significantly more inclined to choose the risky reform if the reform is associated with gains. This tendency is particularly pronounced for economic losses and gains where the likelihood of choosing the risky reform is more than 9 percentage points higher in the gain than in the loss treatments, but it also comes out significant at the 0.1 level in the comparison of losses and gains in terms of service quality. One possible interpretation of the findings is that the economic outcome is a more salient reference for the respondents than service quality. However, since, the numbers linked to economic and service quality changes are not similar, such a conclusion should be made with caution.
| All respondents | Service losses and gains only | Economic losses and gains only | |
|---|---|---|---|
| (T1, T2, T3, and T4 compared to T5 and T6) | (T1 and T2 are compared to T5 and T6) | (T3 and T4 are compared to T5 and T6) | |
| Loss domains | 0.386 | 0.402 | 0.369 |
| Gain domains | 0.461 | 0.461 | 0.461 |
| Difference | −0.076*** | −0.059* | −0.092*** |
| N | 1,395 | 924 | 935 |
- Entries are the share of respondents preferring the risky to the certain reform.
- * p < 0.1;
- **p < 0.05;
- *** p < 0.01. Two-tailed t-tests.
7 EXPERIMENTS 2 AND 3: METHOD
In the first experiment, in contrast to expectations, respondents turned out to be more risk seeking in gain domains than in loss domains. One aim of experiments 2 and 3 is to replicate this result in another context. Another aim is to extend the experimental design in order to explore scope conditions of the results in experiment 1. Experiments 2 and 3 were both placed in the same online survey, which used responses from 1,680 US Amazon MTurkers.4 The survey used a fixed order of questions, and hence, experiment 2 was placed right before experiment 3 in all versions of the survey. Respondents were randomly assigned to treatments in both experiments. In addition to experiments 2 and 3, the respondents were asked to describe why they responded as they did in experiment 3 right after this experiment. Responses to this question are included in the discussion of the results.
Finally, the survey contained a replication of the Asian Disease Experiment in a between-subjects version at the end of the survey. Results from this experiment are solely used to test whether the respondents in the study behave as the ones in Tversky and Kahneman's study when presented with the original Asian Disease framework. The results indeed suggest that this is the case, with 57.8 per cent of the respondents preferring the risky option in the loss domain and only 19.7 per cent preferring the risky option in the gain domain. Data were gathered in September 2016. MTurk respondents are not representative of the population at large in terms of their demographic background. In the current case, the sample primarily consists of young white Caucasians (see table A3 in the appendix). Yet, previous research reveals considerable similarity between many treatment effects obtained from population-based and MTurk studies (Mullinix et al. 2015).
Experiments 2 and 3 are based on the same logic. Both experiments replicate parts of experiment 1 while simultaneously allowing for extensions. As for the replication, experiment 2 reuses major parts of T4 and T6 from experiment 1, meaning that variation between gains and losses is experimentally manipulated in the same way as in experiment 1. Furthermore, two extensions are included in the design. It is well known that the size of the change in outcome is likely to matter with people being more risk averse when more is at stake (Gomez 2008, p. 56). I therefore experimentally manipulate whether the economic changes are relatively large (10 per cent in the baseline reform/30 per cent in the risky reform) as in experiment 1 or relatively small (3 per cent in the baseline reform/9 per cent in the risky reform).
Furthermore, construal level theory (Liberman and Trope 1998; Trope and Liberman 2003) suggests that the psychological distance deriving from, for instance, social distance (Does the decision have consequences for me or for others?), spatial distance (Will the decision have consequences nearby or elsewhere?), and temporal distance (Will the decision have immediate consequences or consequences later in the future?) matters to risk-taking. Construal level theory predicts more risk-averse behaviour in cases with low psychological distance and that the difference in risk-seeking between gain and loss domains is lower in such cases (Trautman and Van de Kuilen 2012, p. 256). As in the literature on construal level theory, I manipulate the psychological distance by emphasizing aspects of social, spatial, and temporal distance (e.g. Fujita et al. 2006; Trautman and Van de Kuilen 2012).
The experiment hence uses a 2 × 2 × 2 factorial design with variation in domain (gain or loss), size of the change in outcome (relatively large or small), and construal level (high or low). Experiment 3 uses the same treatments and with similar numbers but instead focuses on reorganization of local police forces in order to explore whether the results travel to another kind of service as well. Table 4 presents the experimental treatments.
| Experiment 2 | Experiment 3 |
|---|---|
|
Imagine that two reforms are proposed in (an American school district/your local school district).1 Both reforms entail that a number of schools are replaced with larger schools, and they will therefore (have consequences/have immediate consequences)1 for the costs of running the schools and hence for the tax rates of the (citizens living in the school district/citizens living in the school district, including you).1 However, the two reforms have different consequences: If reform A is chosen, district school expenditures will (increase by/drop by)2 (10/3)3 per cent, and the percentage of pupils passing the final exam will increase from 90 to 92 per cent. If reform B is chosen, the percentage of pupils passing the final exam will increase from 90 to 92 per cent. There is furthermore a likelihood of one-third that district school expenditures will (increase by/drop by)2 (30/9)3 per cent and a likelihood of two-thirds that expenditures will remain unchanged. Which of the reforms would you prefer? |
Imagine now that two reorganizations of the local police force are proposed in (an American town/the town where you live).1 The two reorganizations are expected to have consequences for the efficiency of the local police force. Both are expected to reduce the costs of running the local police force significantly and to affect the crime rate in (the precinct/your neighbourhood).1 However, the proposed reorganizations have different consequences for the crime rate: If reorganization A is chosen, arrests of burglars will (rise/decrease)2 by (10/3)3 per cent. If reorganization B is chosen, there is a one-third probability that arrests of burglars will (rise/decrease)2 by (30/9)3 per cent and a two-thirds probability that the arrest rate will remain unchanged. Which of the reorganizations would you prefer? |
- 1 Treatments aimed at causing variation in construal level. Sentences before the forward slash = relatively high psychological distance, whereas sentences after the slash = relatively low psychological distance.
- 2 Treatments aimed at varying gains and loss domains. Increasing expenditures (experiment 2) and a decrease in the arrest rate (experiment 3) are here understood as loss domains.
- 3 Treatments aimed at varying the size of the change.
Logistic regressions comparing the composition of each of the experimental groups to that of the others indicate that the treatments in both experiments are generally balanced, yet with some imbalances in terms of the race composition of some of the treatments (see table A4 in the appendix). Robustness checks of all analyses were therefore conducted with control variables included. This does not alter the experimental findings.
8 EXPERIMENTS 2 AND 3: RESULTS
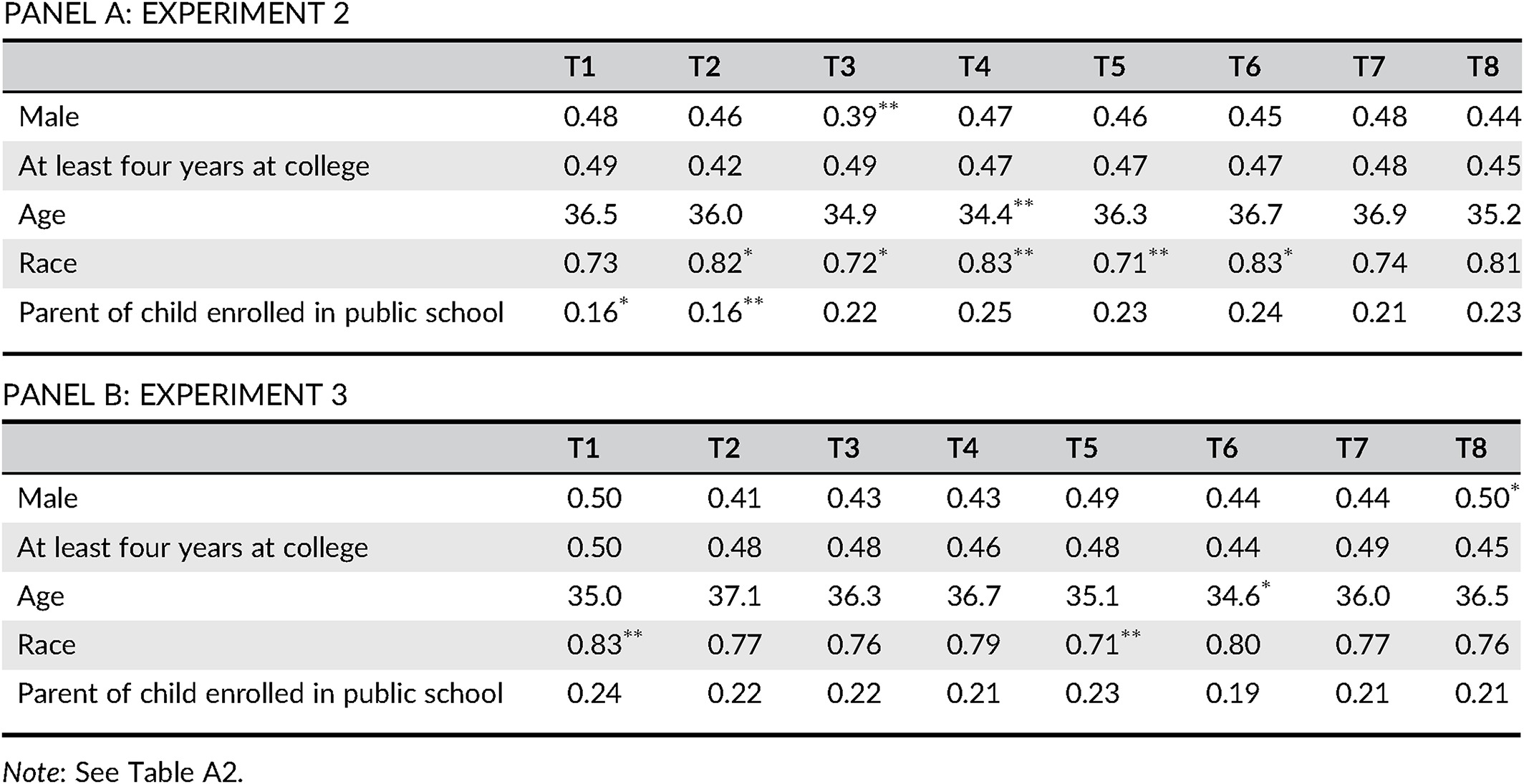
The results strongly support the risk aversion hypothesis since 64.9 per cent in experiment 2 (t = 12.774; p < 0.01; two-tailed t-test) and 68.1 per cent (t = 15.848; p < 0.01; two-tailed t-test) in experiment 3 prefer the certain to the risky option. Results presented by treatment are reported in figures 1 and 2, while significance tests appear in table A5 in the appendix. The preference for certain reform outcomes persists across all treatments, although to a varying extent. Looking first at the results from experiment 2, which are presented in figure 1, it appears that the preference for risky reforms is considerably higher in gain domains and for small outcome changes. In both cases, the effects of these treatments are highly statistically significant. The psychological distance treatment, on the other hand, has no independent impact, but the logistic regression analysis in the appendix shows an interaction between psychological distance and the domain treatment, with larger psychological distance having a positive impact on preferences for risky reforms – but only in gain domains.5
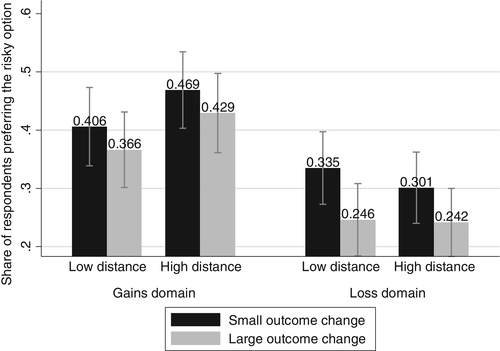
The results from experiment 3 (presented in figure 2) show a picture that is generally consistent with experiment 2. Most notably, the preference for risky reforms is again considerably and significantly higher in gain domains, although the effect is less pronounced than in experiment 2. Small outcome changes also tend to have a positive impact on the preference for risky reforms. The effect of this treatment is, however, not significant. Finally, psychological distance does not have a statistically significant impact in experiment 3. Since manipulation checks (Baekgaard et al. 2015, p. 334) were not conducted in any of the experiments, I cannot be certain that the insignificant treatments got through to the respondents. I therefore cannot exclude the possibility that stronger manipulations would have created significant effects even though the manipulation on, for instance, psychological distance was designed to maximize treatment power by emphasizing the construal level several times.
In sum, a consistent pattern emerges across experiments 1, 2, and 3, where certain reforms are preferred to risky but potentially advantageous reforms and where risky reforms, in contrast to the theoretical expectation, are to a greater extent preferred in gain than in loss domains. The question remains why this pattern of more risk-seeking preferences in gain domains is found here. While it is difficult to give a definite answer to this question, the open-ended question that followed immediately after experiment 3 may provide some hints about the reason. A majority of respondents provide answers that are useless in this context because they refer to personality (‘I am not the kind of person who likes to gamble’). However, some respondents provide more useful answers about their thoughts. Several respondents emphasize certainty as an important value in relation to projects in the public sector. For instance, one respondent writes that ‘Government should not be making policy based on chance. They should pursue certainty, not gamble with the safety of the public’, while another states that ‘I like a strong measure of certainty when deciding a major social project that involves the lives of citizens. I think taking a risk is rather awful for the people.’
Based on the responses, a possible explanation of the larger risk willingness in gain domains also emerges. Several respondents who received the loss domain treatment state that it would simply be too risky to choose the risky reform in the loss domain: ‘Reorganization B was too risky for this kind of issue’ and ‘Burglary is a pretty serious issue and it seemed too risky that arrests will go down as much as 30 per cent’. On the other hand, respondents who received the gain domain treatment tend to see risk-taking as an acceptable behaviour that may lead to even better outcomes and with nothing lost if it does not work: ‘It is a big percentage in which the arrest of burglars will rise compared to reorganization A. If it does not work, it will remain the same as it was so no harm done. So I'd rather take a risk in trying to make it a lot better than just raising it by 10 per cent which is not much.’
It should be mentioned that it is difficult to come up with a useful quantitative measure of the extent to which these lines of thought are general phenomena, and hence, the interpretation based on the respondents’ statements should be made with some caution. What they do seem to suggest, however, is that norms and logics particular to the public sector may be at play, where certainty is seen as a prime value in relation to public sector projects, but where making uncertain decisions is acceptable for some if this is not at risk of changing the status quo in a negative direction.
9 CONCLUSION
Prospect theory has a prominent status in the social sciences. The biases described by prospect theory are widely applied and studied across various disciplines including public administration to the extent that they appear to sometimes be considered universal phenomena. However, the public sector differs in important respects from the scenarios that respondents are presented with in most studies on prospect theoretical biases. It is therefore a critical question to public administration studies drawing on prospect theory whether central predictions from this framework travel to the public sector context as well.
Based on an experimental design with the participation of Danish citizens, I find evidence supporting the expectation that people are generally risk averse in the sense that, on average, they prefer certain to risky reform outcomes. The level of risk aversion identified here is somewhat higher than the level of risk aversion in the classical Asian Disease experiment (47 per cent preferred the certain option in the Asian Disease experiment (Tversky and Kahneman 1981, p. 453) as compared to 58.9–68.1 per cent in my experiments). Moreover, studying the asymmetry of risk preferences in gain and loss domains, I surprisingly find evidence in outright opposition to the expectation of prospect theory. In my experiment, people are more likely to gamble with reform gains than losses. Both findings are successfully replicated in two experiments with participation of American MTurkers.
The explanation for this deviation from prospect theory may have to do with the character of the outcomes that the respondents were presented with. Compared to purely financial outcomes, outcomes in this experiment are non-fungible and, compared to the Asian Disease experiment outcomes, they are arguably associated with less strong emotional reactions. Moreover, qualitative evidence suggests that norms and logics particular to the public sector may be at play, where certainty is considered an important value in relation to public sector projects, but where making uncertain decisions is acceptable if this is not at risk of changing the status quo in a negative direction. It is a task for future research to uncover the causes of this asymmetric pattern.
Some limitations of the study should be acknowledged. First, there is no status quo option in the experimental scenarios used. This limits the comparability with real-world policy decisions where status quo will often be one of the options. Examining status quo bias in relation to public sector reforms by including a status quo option in the experimental vignettes seems a relevant next step for future research. Second, even though survey experiments with random assignment to different treatments were used, internal validity might still be a concern when comparing different outcomes (economic and service quality outcomes). In the current experiments, outcomes were deliberately presented on different scales in order to make the experiment appear as realistic as possible. However, one important implication of this design is that we cannot know whether differences in preferences for different outcomes are true or based on the difference in scales. Neither does the design allow for an examination of whether the findings are peculiar to the public sector as such.
Future research could address these shortcomings by manipulating the degree of publicness of organizations and outcomes by, for instance, analysing reorganizations in comparable public and private organizations. Relatedly, future research may benefit from designing studies that allow for competitive theory testing between prospect theory and other known explanations of risk behaviour such as the priority heuristic (Brandstätter et al. 2006) in order to attain stronger evidence of the explanatory power of various theoretical perspectives in the domain of public services. Another useful extension would be to address the concept validity in the study. Gain and loss domains are surprisingly ambiguous concepts in the literature. Usually, they are manipulated by letting the evaluative polarity of words (whether people are saved or dead in the Asian Disease experiment and whether outcomes increase or drop in my experiments) determine a reference point, which in turn defines whether the domain is one of gains or losses. Such a manipulation is, however, at best, indirect, and calls into question whether findings reflect differences between gain and loss domains or rather the valence of the words used (Wallin et al. 2016). A useful extension would therefore be to study whether the findings can be reproduced if gains and losses are manipulated differently than in the current experiments, for instance, by explicitly stating whether reform attempts are undertaken to avoid losses or increase gains.
In addition to testing central expectations of prospect theory in a setting with different outcomes, the present study also has implications for literature on public policy and administration. For instance, the findings might help explain why risky reforms are sometimes supported by the public and other times not (Boeri et al. 2002; O'Donnell and Tinios 2003; Boeri and Tabellini 2012). The findings also question whether the combination of blame avoidance and asymmetric risk preferences is indeed what makes it worthwhile for politicians to sometimes pursue risky reforms, as suggested by, for instance, Vis and Van Kersbergen (2007). From a more practical perspective, an important implication for policy-makers is that risky reforms are likely to face opposition. Moreover, when building popular support for a given reform proposal, policy-makers should be aware that the support for risky reforms depends on for which outcomes risk is high and whether the risk is taken either to increase gains or to avoid losses.
APPENDIX
| Mean | SD | Min | Max | N | |
|---|---|---|---|---|---|
| Male (dummy) | 0.477 | 0.500 | 0 | 1 | 1,309 |
| University degree (dummy) | 0.552 | 0.497 | 0 | 1 | 1,309 |
| Age (years) | 45.624 | 13.815 | 18 | 67 | 1,309 |
| Parent of child enrolled in public school (dummy) | 0.215 | 0.411 | 0 | 1 | 1,379 |
| Ability to interpret numerical information1 | 4.720 | 2.235 | 0 | 8 | 1,309 |
- 1 Measured by the abbreviated numeracy scale (see Weller et al. 2013).
| T1 | T2 | T3 | T4 | T5 | T6 | |
|---|---|---|---|---|---|---|
| Male | 0.488 | 0.451 | 0.465 | 0.483 | 0.526* | 0.449 |
| Age | 44.517 | 45.686 | 44.939 | 46.190 | 46.623 | 45.749 |
| University degree (dummy) | 0.570 | 0.544 | 0.613** | 0.545 | 0.531 | 0.507* |
| Parent of child enrolled in public school | 0.230 | 0.210 | 0.165** | 0.234 | 0.238 | 0.220 |
| Numerical ability | 4.802 | 4.726 | 4.791 | 4.464 | 4.671 | 4.870 |
- Note: Entries are means.
- * p < 0.1;
- ** p < 0.05;
- ***p < 0.01.
- Differences in respondent characteristics were tested by analysing the difference between each treatment and all other treatments combined in multivariate logistic regressions.
| Mean | SD | Min | Max | N | |
|---|---|---|---|---|---|
| Male (dummy) | 0.455 | 0.498 | 0 | 1 | 1,680 |
| At least four years at college (dummy) | 0.473 | 0.499 | 0 | 1 | 1,680 |
| Age (years) | 35.771 | 11.278 | 18 | 75 | 1,677 |
| Race (white Caucasian = 1) | 0.773 | 0.449 | 0 | 1 | 1,680 |
| Parent of child enrolled in public school (dummy) | 0.215 | 0.418 | 0 | 1 | 1,680 |
| Experiment 2 | Experiment 3 | |||
|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | |
| Loss domain | −0.608 (0.104)** | −0.334 (0.176)* | −0.182 (0.105)* | −0.234 (0.181) |
| Large change in outcome | −0.259 (0.104)* | −0.196 (0.176) | −0.097 (0.105) | −0.232 (0.177) |
| High psychological distance | 0.096 (0.104) | 0.229 (0.172) | −0.120 (0.105) | −0.284 (0.178) |
| Loss domain × Large change | −0.203 (0.210) | 0.026 (0.211) | ||
| Loss domain × High distance | −0.356 (0.209)* | 0.252 (0.211) | ||
| Large change × High distance | 0.063 (0.208) | 0.090 (0.211) | ||
| N | 1,680 | 1,680 | 1,675 | 1,675 |
| McFadden's R2 | 0.019 | 0.021 | 0.003 | 0.003 |
- Note: Entries are logistic regression coefficients. Robust standard errors in parentheses. Intercept included in regression but not shown in the presentation.
- * p < 0.1;
- ** p < 0.05;
- ***p < 0.01.