Multilocus approaches for the measurement of selection on correlated genetic loci
Abstract
The study of ecological speciation is inherently linked to the study of selection. Methods for estimating phenotypic selection within a generation based on associations between trait values and fitness (e.g. survival) of individuals are established. These methods attempt to disentangle selection acting directly on a trait from indirect selection caused by correlations with other traits via multivariate statistical approaches (i.e. inference of selection gradients). The estimation of selection on genotypic or genomic variation could also benefit from disentangling direct and indirect selection on genetic loci. However, achieving this goal is difficult with genomic data because the number of potentially correlated genetic loci (p) is very large relative to the number of individuals sampled (n). In other words, the number of model parameters exceeds the number of observations (p ≫ n). We present simulations examining the utility of whole-genome regression approaches (i.e. Bayesian sparse linear mixed models) for quantifying direct selection in cases where p ≫ n. Such models have been used for genome-wide association mapping and are common in artificial breeding. Our results show they hold promise for studies of natural selection in the wild and thus of ecological speciation. But we also demonstrate important limitations to the approach and discuss study designs required for more robust inferences.
Introduction
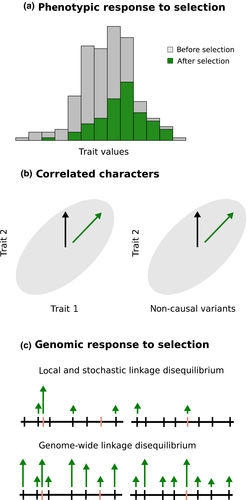
Natural selection is the mechanism of adaptation and often drives speciation (Schluter 2001; Schluter & Conte 2009; Gompert et al. 2012; Nosil 2012). Consequently, many attempts have been made to measure phenotypic selection in the wild, with the earliest studies occurring in the late 1800s (Bumpus 1899; Endler 1986; Kingsolver et al. 2001; Siepielski et al. 2013). Phenotypic selection can be quantified from changes in the distribution of trait values in a population within a generation (due to mortality), or from the association between trait values and quantitative measures of fitness components (e.g. seed set, weight, etc.; Lande & Arnold 1983; Shaw et al. 2008). However, correlations among characters complicate measures of selection, as direct selection on one character induces indirect selection on correlated characters (Table 1 , Fig. 1). Consequently, the total selection experienced by a trait can include direct selection on that character and the indirect effects of selection on any correlated characters (Kingsolver et al. 2001). Lande & Arnold (1983) showed that direct and indirect selection can be disentangled using multiple regression. Specifically, partial regression coefficients obtained from regressing fitness on a set of characters are estimates of the direct selection on each trait (these coefficients define the average gradient of the relative fitness surface). Although many modifications and refinements of this approach have been made (e.g. Schluter 1988; Rausher 1992; Geyer et al. 2007; Reynolds et al. 2016), these changes have not altered the conceptual basis of the approach.
| Term | Definition |
|---|---|
| Direct selection | Selection on a genetic locus resulting from its effect on fitness |
| Indirect selection | Selection on a genetic locus caused by LD with directly selected genotypes at other loci |
| Total selection | Combined effects direct and indirect selection on a genetic locus |
| Linkage disequilibrium (LD) | Statistical correlations between genotypes at different loci (physical linkage can facilitate LD but is not required for it) |
| Selection coefficient (s) | Measure of the strength of selection (direct or total), often expressed as the difference in expected fitness between alternative homozygotes |
| Polygenic modelling | Methods for connecting phenotypes to genotypes that consider many loci at once and do not rely on binary classifications of loci as associated or un-associated with phenotype |
| PVE | Proportion of the phenotypic variation explained by the genetic data, which should approach the narrow-sense heritability of the trait (fitness) as the genome becomes saturated with genetic markers |
| PGE | The proportion of the PVE explained by loci with measurable effects on a trait (fitness); the remainder of the PVE comprises loci with near infinitesimal effects |
| n-γ | Number of genetic markers with measurable effects on the phenotype (fitness) |
| PIP | Posterior inclusion probability, that is the posterior probability that a genetic marker is under direct selection (or is in high LD with an un-sequenced locus under direct selection) |
| HPDI | Highest posterior density interval, that is the interval that contains the most probable parameter values such that every value in the interval is more probable than any value not in the interval |
More recently, attempts have been made to measure selection on genetic loci or genomes based on short-term (e.g. within-generation) changes in allele frequencies (e.g. Barrett et al. 2008; Anderson et al. 2013; Pespeni et al. 2013; Anderson et al. 2014; Gompert et al. 2014; Egan et al. 2015; Thurman & Barrett 2016). The premise of these studies is that phenotypic selection within a generation alters the distribution of trait values and that this results in a within-generation shift in allele frequencies at the causal loci affecting these traits (direct selection) and other genetic variants in linkage disequilibrium (LD) with them (indirect selection; Fig. 1). The extent to which phenotypic selection is transmitted down to the genetic-level depends on the heritability of the selected traits and patterns of LD. In stark contrast to our understanding of phenotypic selection, relatively little is known about individual episodes of selection on genetic loci, particularly under natural or semi-natural conditions (Barrett & Hoekstra 2011; Thurman & Barrett 2016). This is relevant, as measuring selection at the genetic-level could help resolve key questions about the maintenance of molecular variation in populations (e.g. Gillespie 1991; Hahn 2008; Huang et al. 2014) and the causes of ecological specialization (e.g. Agrawal et al. 2010; Anderson et al. 2013; Gompert et al. 2015; Gompert & Messina 2016). Quantifying selection in the wild is also important for understanding speciation, as reproductive isolation often evolves as a direct consequence of divergent selection and local adaptation (e.g. Jiggins et al. 2001; Nosil et al. 2002; Lowry & Willis 2010; Ording et al. 2010). Indeed, divergent selection is a form of reproductive isolation when it causes immigrant or hybrid inviability (Wu 2001; Nosil et al. 2005). Moreover, direct or indirect selection on genetic loci and genomes can cause DNA sequence divergence that pleiotropically results in reproductive incompatibilities (e.g. Swanson & Vacquier 2002; Tang & Presgraves, 2009). Finally, the likelihood of speciation with gene flow and the persistence of distinct species upon secondary contact depend critically on the genome-wide consequences of selection (Barton & Bengtsson 1986; Barton & De Cara 2009; Feder et al. 2012; Flaxman et al. 2013; Feder et al. 2014; Flaxman et al. 2014; Yeaman 2015).
Distinguishing between the direct and indirect effects of episodes of selection on allele frequency change is a notable challenge for genomic studies. Under most conditions, the number of correlated genetic loci will greatly outnumber the number of individuals studied (genome scans typically consider tens of thousands to millions of nucleotide variants and many fewer individuals). Thus, traditional statistical methods, such as the multiple regression approach proposed by Lande & Arnold (1983) for phenotypic selection, cannot be used to obtain estimates of direct selection on each locus (such methods require the number of observations, n, to exceed the number of model parameters, p). In other words, parsing direct and indirect selection on phenotypic and genomic variation present the same conceptual issue, but different analytical tools are needed for the latter because p ≫ n.
We show that this problem can be approached using sparse linear mixed models that were developed for genome-wide association (GWA) mapping of polygenic traits and genomic prediction (Meuwissen et al. 2001; Ober et al. 2012; Habier et al. 2013; Zhou et al. 2013). The potential utility of GWA methods is unsurprising, as measuring episodes of selection on genetic loci is a special case of trait mapping. However, the conditions and study designs under which these methods will be most useful for inferring selection require further quantification, which we provide here. We focus on a specific model, the Bayesian sparse linear mixed model (BSLMM) introduced by Zhou et al. (2013), but related models and methods exist and will likely yield similar broad conclusions (e.g. Erbe et al. 2012). The method we focus on uses Bayesian variable selection, model averaging and shrinkage inducing priors to extend the Lande & Arnold (1983) multiple regression approach to cases where the number of characters (i.e. loci) exceeds the number of observations.
Herein, we demonstrate the utility and limitations of BSLMMs for studying selection by applying this method to a series of simulated data sets. We show that BSLMMs can be used to detect direct selection when fitness has a simple genetic basis. Additionally, we show that BSLMMs can generate quantitative summaries of selection across the genome, such as estimates of the additive genetic variation for fitness, under a wider variety of conditions. Whereas the quantitative summaries could also be obtained using traditional quantitative genetic breeding designs, such methods are not practical for many nonmodel organisms. Thus, approaches such as those considered here could help extend the direct study of selection to a broader range of organisms, an important goal if we are to achieve general understanding of ecological speciation.
Methods
Theoretical background and statistical models
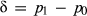 , where
, where 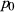 and
and 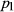 are the population allele frequencies before and after selection, respectively (here we assume viability selection). While selection differentials are intuitive in phenotypic studies, selection coefficients are more useful for quantifying total selection on genotypes and are more directly related to population genetic models. Assume genotypes
are the population allele frequencies before and after selection, respectively (here we assume viability selection). While selection differentials are intuitive in phenotypic studies, selection coefficients are more useful for quantifying total selection on genotypes and are more directly related to population genetic models. Assume genotypes 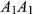 ,
, 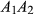 and
and 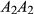 have relative expected fitnesses of
have relative expected fitnesses of 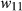 ,
, 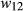 and
and 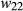 , respectively (here marginal fitnesses are defined based on the fitness effects of the genotypes and patterns of LD with other causal variants). The selection coefficient s is then defined based on the difference in the marginal fitnesses of alternative homozygotes, such that,
, respectively (here marginal fitnesses are defined based on the fitness effects of the genotypes and patterns of LD with other causal variants). The selection coefficient s is then defined based on the difference in the marginal fitnesses of alternative homozygotes, such that,  ,
, 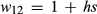 and
and 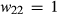 (here h denotes the heterozygote effect, that is the fitness of the heterozygote relative to the difference between the two homozygotes; Gillespie 2004). Under this formulation,
(here h denotes the heterozygote effect, that is the fitness of the heterozygote relative to the difference between the two homozygotes; Gillespie 2004). Under this formulation,
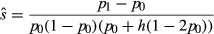 (1)
(1)Thus, selection coefficients represent a particular standardization of the selection differential based on genetic variation, and one that differs from the standardization used in phenotypic studies (in phenotypic studies selection differentials are standardized by the phenotypic variance; Lynch & Walsh 1998).
In an infinite population, Eqn. 1 could be used to calculate s exactly. However, stochastic processes (e.g. random mortality) in finite populations compound allele frequency changes due to drift and selection, making statistical inference of s necessary and adding uncertainty to estimates of selection. Thus, it is necessary to account for the possible contribution of drift to observed changes in allele frequencies. We present simple simulations in the online supplemental material (OSM) to illustrate this point, namely that genetic drift can cause substantial changes in allele frequency that can be misinterpreted as evidence of selection (distinguishing drift from selection is also an issue for phenotypic studies, although this is often not discussed).
Given this consideration, maximum-likelihood or Bayesian methods can be used to obtain interval estimates of s from genetic data under an appropriate stochastic model that allows drift and selection to contribute to allele frequency change (e.g. Wright-Fisher or Moran models with selection; Ewens 2004). Additionally, randomization or simulation-based methods can be used to test the null hypothesis that s = 0 for a particular locus, as was done by Gompert et al. (2014) in their null model 1, or to test the global null hypothesis that s = 0 for all genetic loci (i.e. that selection did not affect any of the genetic loci). This can be done by comparing the number of loci with significant evidence of selection to the number expected by chance under the global null (Gompert et al. 2014). Note, however, that the failure to reject null models of locus-specific or genome-wide drift is not evidence for the absence of selection, and thus, this does not mean that s = 0 (most genetic loci will exhibit at least very low levels of LD with some causal variants in any finite population, and thus, the vast majority of cases where these null models cannot be rejected will represent type II errors; Gompert 2016). We discuss these issues in more detail in the OSM (see ‘Total Selection’).
These concerns related to parsing the contributions of drift and selection apply to inference of direct selection as well, but methods for estimating direct selection must additionally account for correlations among genotypes at different loci. Lande & Arnold (1983) proposed using multiple regression to solve the problem of trait correlations in phenotypic studies. Their approach works well as long as correlations among variables are not too strong and the number of observations (individuals) exceeds the number of traits (i.e. for p < n). Their approach still generally assumes that all relevant traits have been measured, which would be equivalent to assuming all causal variants have been assayed in genomic studies (the latter will rarely be true; we discuss the implications of this below). Using their approach, partial regression coefficients provide measures of direct selection (Lande & Arnold 1983). More specifically, for bi-allelic loci with genotypes coded as 0, 1 or 2 copies of an allele, a partial regression coefficient, β, equals 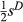 , where
, where 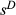 is defined similarly to s but only includes direct selection on the genotype (here we assume perfect additivity, that is h = 0.5). When a relatively small number of genes or genomic regions are of interest, studies can be designed so that the number of individuals exceeds the number of genetic loci, and thus, standard multiple regression approaches could be used to estimate
is defined similarly to s but only includes direct selection on the genotype (here we assume perfect additivity, that is h = 0.5). When a relatively small number of genes or genomic regions are of interest, studies can be designed so that the number of individuals exceeds the number of genetic loci, and thus, standard multiple regression approaches could be used to estimate 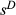 (e.g. the major effect gene Eda in sticklebacks; Rennison et al. 2015). However, this will rarely be true for larger population genomic data sets (in such cases p ≫ n).
(e.g. the major effect gene Eda in sticklebacks; Rennison et al. 2015). However, this will rarely be true for larger population genomic data sets (in such cases p ≫ n).
Bayesian sparse linear mixed models can be applied even when p > n by adopting shrinkage or sparsity-inducing priors, which pull parameter estimates back towards zero (e.g. Bernardo et al. 2003; Pérez et al. 2010; Guan & Stephens 2011). This class of methods includes polygenic models and whole-genome regression approaches that have been successfully applied in genome-wide association studies (GWASs) and for genomic prediction and genomic selection in plant and animal breeding (e.g. Meuwissen et al. 2001; Goddard & Hayes 2007; Heffner et al. 2008; Hayes et al. 2009; Resende et al. 2012; Zhou et al. 2013; Thomasen et al. 2014). Inference of direct selection can be approached in the same manner as mapping a phenotypic trait but with fitness or some component of fitness as the phenotype. Thus, all of the lessons we have learned from decades of GWASs, such as the need for large sample sizes, apply here (e.g. Visscher et al. 2012). We advance this existing knowledge by focusing on conditions most relevant for detecting selection, that is, cases where the phenotype (fitness) has a low to moderate heritability and diffuse genetic architecture, and by considering genome-level summaries and locus-specific measures of selection.
Here, we focus on and describe one such model, the BSLMM proposed by Zhou et al. (2013), which is part of the gemma software package. We show how BSLMMs can be used to estimate direct selection when numerous (tens or hundreds of thousands) genetic loci have been sequenced, while also providing higher-level summaries of the genetic architecture of fitness, such as the number of loci with measurable effects on fitness. The latter information is extracted from a few key parameters in the model (caveats and limitations of these parameters are discussed below).
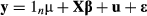 (2)
(2)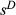 (direct selection) that account for uncertainty in whether
(direct selection) that account for uncertainty in whether  (we refer to these estimates as
(we refer to these estimates as 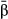 , whereas estimates that assume
, whereas estimates that assume 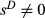 are denoted
are denoted 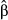 ). Depending on the nature and sparsity of the genetic data, some, most or all of the causal variants may not be sequenced, particularly with reduced representation sequencing methods (e.g. GBS, RADseq, exome sequencing, etc.; Tiffin & Ross-Ibarra 2014). However, direct selection on the causal variants can still potentially be accounted for through LD with other variants (Fig. 2). Here, we are really using indirect selection on a locus linked to the (un-sequenced) causal variant as a proxy for direct selection on the missing causal variant. Nonetheless, this can be conceptualized as an estimate of direct selection in the sense that the effects of other (i.e. correlated and sequenced) genetic loci have been accounted for (i.e. the only indirect effects are those coming from missing loci). This issue is conceptually similar to the issue of inference of direct selection on phenotypes when not all phenotypes have been measured (Lande & Arnold 1983).
). Depending on the nature and sparsity of the genetic data, some, most or all of the causal variants may not be sequenced, particularly with reduced representation sequencing methods (e.g. GBS, RADseq, exome sequencing, etc.; Tiffin & Ross-Ibarra 2014). However, direct selection on the causal variants can still potentially be accounted for through LD with other variants (Fig. 2). Here, we are really using indirect selection on a locus linked to the (un-sequenced) causal variant as a proxy for direct selection on the missing causal variant. Nonetheless, this can be conceptualized as an estimate of direct selection in the sense that the effects of other (i.e. correlated and sequenced) genetic loci have been accounted for (i.e. the only indirect effects are those coming from missing loci). This issue is conceptually similar to the issue of inference of direct selection on phenotypes when not all phenotypes have been measured (Lande & Arnold 1983).
When fitness is determined by a large number of loci with very small or near infinitesimal effects, the contribution of this genetic variation to fitness might not be captured by the vector or partial regression coefficients, β. However, even in this case, genetic variation for fitness (and thus the full contribution of direct selection to variation in realized fitness) can be inferred using information from the overall genetic similarity among individuals. In Eqn. 2, this is accounted for by the vector u, which denotes each individual's deviation from the mean expected fitness based on their complete multilocus genotype. More specifically, a multivariate normal prior is placed on u with a variance–covariance matrix that is proportional to the genetic similarity or kinship matrix, which is calculated from the data and treated as a constant in the model; u is then inferred from the data given this prior.
Thus, similar to classic quantitative genetic approaches, the model includes overall relatedness as a potential predictor of similarity in fitness (Lynch & Walsh 1998). In contrast to quantitative genetic approaches, controlled crosses with specific breeding designs are not required, and thus, BSLMMs can be used in systems were controlled crosses are not practical or ethical. Nonetheless, breeding designs will affect the structure of the kinship matrix and amount of LD in the population, and patterns of relatedness can affect the efficacy of the method (see our results below). Thus, different experimental designs might be preferable for specific research questions (we discuss this point in detail below). The kinship matrix also serves to control for population structure and can often do so more effectively than including population structure covariates (Zhao et al. 2007; Kang et al. 2008).
The hierarchical nature of the model provides a means to estimate parameters that summarize direct selection across the genome (Guan & Stephens 2011; Zhou et al. 2013). These include the proportion of variation in fitness explained by all of the genetic data (PVE) through  and u (PVE should approach narrow-sense heritability with sufficient genetic sampling), the proportion of the PVE explained by genetic loci with measurable effects (via the
and u (PVE should approach narrow-sense heritability with sufficient genetic sampling), the proportion of the PVE explained by genetic loci with measurable effects (via the  ), which is denoted PGE, and the number of genetic variants with measurable effects on fitness (denoted n-γ). These metrics incorporate uncertainty in the specific genetic variants under selection, meaning that accurate estimates of these parameters should be possible even if the specific targets of direct selection cannot be localized. This is important, as these parameters alone can provide important information about genetic variation for fitness. Moreover, in some systems, such as hybrid zones, variation in fitness reflects components of reproductive isolation (e.g. hybrid inviability) making these measures relevant for studies of speciation.
), which is denoted PGE, and the number of genetic variants with measurable effects on fitness (denoted n-γ). These metrics incorporate uncertainty in the specific genetic variants under selection, meaning that accurate estimates of these parameters should be possible even if the specific targets of direct selection cannot be localized. This is important, as these parameters alone can provide important information about genetic variation for fitness. Moreover, in some systems, such as hybrid zones, variation in fitness reflects components of reproductive isolation (e.g. hybrid inviability) making these measures relevant for studies of speciation.
However, inference of these parameters is affected by the extent to which causal variants are effectively tagged by LD with sequenced variants, such that PVE and n-γ will only approach the true heritability and number of causal variants if all or most causal variants are in LD with sequenced variants. This will of course depend on the sparsity of the genetic data, general patterns of LD and the extent to which causal variants and sequenced variants have similar allele frequencies (Visscher et al. 2012). More generally, the performance of BSLMMs for detecting selection will depend on numerous factors that can usefully be explored with simulated data (as in this study).
Simulations of fitness data
We generated and analysed data sets to assess the potential and limits of BSLMMs to quantify direct selection under different sampling designs and with different genetic architectures. The performance of this method has been evaluated in the context of genomic prediction and inference of PVE (Zhou et al. 2013). Our goal here was to also evaluate performance in terms of partial regression coefficients (i.e. measures of direct selection on individual genotypes in our current formulation) and to examine performance under conditions that are more relevant for studies of genome-wide selection in the wild, namely low to moderate heritability and diffuse genetic architectures for fitness (Mousseau & Roff 1987; Kruuk et al. 2000; Hoffmann et al. 2016). We also considered sample sizes that, while reasonably large, are more realistic for studies of natural populations (compared to sample sizes that might be obtainable for studies of human disease).
Fitness data sets were simulated under a variety of conditions and analysed using the BSLMM implemented in gemma. We considered accuracy of inference with respect to individual estimates of 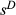 and summaries of the genetic basis of variation in fitness (e.g. PVE). We used previously generated genotyping-by-sequencing (GBS) genotype data as the starting point for simulations of fitness values. That is, we assigned selection coefficients to GBS genotypes and used these to compute the expected fitness for each individual based on the GBS data. This approach was used because it captures realistic patterns of genetic variation and linkage disequilibrium. We did not make inferences about selection in these specific species or populations (i.e. the fitness values were assigned by us in the aforementioned simulation context). Although we used GBS data, BSLMM could be used with whole-genome sequences, or even data sets that include a mixture of SNPs and structural variants. Our primary genetic data set included 592 Timema cristinae stick insects collected from a single population with genotypes for 246 258 SNPs (mean minor allele frequency = 0.09). A full description of these data can be found in Comeault et al. (2015). We first considered a quantitative metric of fitness (e.g. adult weight, longevity, seed set, flower number, etc.).
and summaries of the genetic basis of variation in fitness (e.g. PVE). We used previously generated genotyping-by-sequencing (GBS) genotype data as the starting point for simulations of fitness values. That is, we assigned selection coefficients to GBS genotypes and used these to compute the expected fitness for each individual based on the GBS data. This approach was used because it captures realistic patterns of genetic variation and linkage disequilibrium. We did not make inferences about selection in these specific species or populations (i.e. the fitness values were assigned by us in the aforementioned simulation context). Although we used GBS data, BSLMM could be used with whole-genome sequences, or even data sets that include a mixture of SNPs and structural variants. Our primary genetic data set included 592 Timema cristinae stick insects collected from a single population with genotypes for 246 258 SNPs (mean minor allele frequency = 0.09). A full description of these data can be found in Comeault et al. (2015). We first considered a quantitative metric of fitness (e.g. adult weight, longevity, seed set, flower number, etc.).
We initially simulated 50 replicate data sets with a narrow-sense heritability of fitness (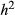 ) of 0.3 or 0.05 and with 10, 100 or 1000 causal variants (we use L to denote the number of causal variants). We sampled the fitness effect of each causal variant from a standard normal distribution and assumed that the causal variants affected fitness additively with incomplete dominance (h=0.5). Causal variants were chosen randomly from the set of genotyped SNPs and used to calculate expected fitness values. We then analysed each data set with and without the causal variants included as potential covariates in the model. We did this because many causal variants will not be sequenced with partial genome sequencing approaches (Tiffin & Ross-Ibarra 2014), such as GBS, but can still potentially be accounted for through LD with other variants. As mentioned previously, when causal variants are missing from the data set, we are really measuring indirect selection on a linked locus as a proxy for direct selection on the missing causal variant.
) of 0.3 or 0.05 and with 10, 100 or 1000 causal variants (we use L to denote the number of causal variants). We sampled the fitness effect of each causal variant from a standard normal distribution and assumed that the causal variants affected fitness additively with incomplete dominance (h=0.5). Causal variants were chosen randomly from the set of genotyped SNPs and used to calculate expected fitness values. We then analysed each data set with and without the causal variants included as potential covariates in the model. We did this because many causal variants will not be sequenced with partial genome sequencing approaches (Tiffin & Ross-Ibarra 2014), such as GBS, but can still potentially be accounted for through LD with other variants. As mentioned previously, when causal variants are missing from the data set, we are really measuring indirect selection on a linked locus as a proxy for direct selection on the missing causal variant.
Additional simulations were conducted to further test how different conditions influence the efficacy of this method. First, the simulations described above were repeated using a binary metric of fitness, such as survival. We converted each individual's quantitative score into a binary score by assuming that 50% of individuals with the highest quantitative score had a viability of 1, whereas the rest of the individuals had a viability of 0. Another set of simulations assessed the performance improvement through increased sample size (i.e. larger n). We sampled 2500 individuals from the set of genotyped individuals with replacement and then simulated phenotypic data as described above for the initial set of simulations, but without the 1000 causal variants treatment. Genotypes (i.e. individuals) were replicated to obtain this sample size; this alters the structure of the kinship matrix and could affect performance independent of sample size. To test the effect of replicating genotypes (vs. increasing sample sizes), we generated another series of data sets where we randomly chose 148 of the 592 individuals and replicated them each four times (with N kept constant at 592). This also allowed us to evaluate the benefits and costs of more structured experimental designs (e.g. experiments involving full or half-sib families or even clones).
We simulated a final series of fitness data sets using GBS data from Rhagoletis pomonella (Dryad doi:10.5061/dryad.mb2tj). These data were described by Egan et al. (2015). Whereas this was a smaller data set (149 individuals and 33 723 SNPs), it is of interest because inversion polymorphisms result in large blocks of elevated LD, and more generally, LD is higher in R. pomonella (e.g. significant LD often extends beyond 10 cM) than in T. cristinae [e.g. average LD between SNPs ranges from 0.007 (SNPs < 100 bp apart) to 0.004 (SNPs > 100 bp apart); Feder et al. 2003; Gompert et al. 2014; Egan et al. 2015]. Thus, it allowed us to ask whether increased LD offset the negative effect of a smaller sample size (for simplicity, we focus on the effect on PVE and n-γ). To this end, we replicated genotypes in a subset of simulations to obtain the same sample size as we had for the T. cristinae data (N = 592 individuals). Note that higher levels of LD generally make it easier to tag causal variants, but more difficult to localize them (see, e.g. Rieseberg & Buerkle 2002), and that LD should in general improve estimates of PVE as this only requires tagging causal variants. As with the initial set of simulations, we generated replicate data sets with 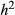 equal to 0.3 or 0.05 and 10, 100 or 1000 causal variants (we only considered a quantitative metric of fitness, and only 10 or 100 causal variants for the simulations with 592 individuals).
equal to 0.3 or 0.05 and 10, 100 or 1000 causal variants (we only considered a quantitative metric of fitness, and only 10 or 100 causal variants for the simulations with 592 individuals).
Analyses of the simulated data
We fit a BSLMM for each data set using gemma with two replicate MCMC runs, each with a 1 million iteration burnin, 2 million sampling iterations and a thinning interval of 100. Kinship matrixes were calculated as 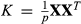 , where X is the matrix of genotypic data and p is the number of loci.
, where X is the matrix of genotypic data and p is the number of loci.
We quantified the evidence of direct selection on individual SNPs based on posterior inclusion probabilities, model-averaged estimates of selection (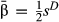 ) and point estimates of β assuming β ≠ 0 (denoted
) and point estimates of β assuming β ≠ 0 (denoted 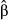 ). Both estimates of selection coefficients account for correlations among genotypes at different loci. We then assessed performance based on the correlation between true and inferred selection coefficients and the normalized root-mean-square error (RMSE; normalized by the range of β). SNP effects were only considered for data sets that included the causal variants to make comparisons with true results readily interpretable.
). Both estimates of selection coefficients account for correlations among genotypes at different loci. We then assessed performance based on the correlation between true and inferred selection coefficients and the normalized root-mean-square error (RMSE; normalized by the range of β). SNP effects were only considered for data sets that included the causal variants to make comparisons with true results readily interpretable.
We summarized posterior distributions for genetic architecture parameters (we focused mostly on PVE and n-γ, but also present estimates of PGE) based on the posterior mode and the 90% highest posterior density interval (HPDI), as calculated with the R package coda. The accuracy and precision of these parameter estimates were then quantified based on the RMSE and 90% HPDI coverage, where the latter is the proportion of the time that the true parameter value was included in the 90% HPDIs. Thus, lower RMSE and higher 90% HPDI coverage equate to greater accuracy and precision of the BSLMM approach for inferring our parameters of interest.
Results
Estimating direct selection
Under most conditions, partial regression coefficients (i.e. measures of direct selection or 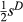 ) were only weakly correlated with their true values (Fig. 3), such that distribution of true vs. estimated effect sizes differed (Fig. 4). A notable exception occurred when fitness had a high heritability (
) were only weakly correlated with their true values (Fig. 3), such that distribution of true vs. estimated effect sizes differed (Fig. 4). A notable exception occurred when fitness had a high heritability ( ) and was determined by a modest number of variants (L = 10). Under these conditions, estimates of selection (
) and was determined by a modest number of variants (L = 10). Under these conditions, estimates of selection (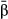 ) were highly correlated with their true values (mean r = 0.73, SD = 0.16) and the inferred and true effect size distributions were similar (Fig. 4c). Correlations between true and estimated effects were also higher when only causal variants were considered (Fig. 3), or when the sample size was increased to 2500 (Fig. S1, Supporting information). In contrast, replicating genotypes (without increasing N) caused a decrease in correlations between true and inferred measures of selection (Fig. S2, Supporting information).
) were highly correlated with their true values (mean r = 0.73, SD = 0.16) and the inferred and true effect size distributions were similar (Fig. 4c). Correlations between true and estimated effects were also higher when only causal variants were considered (Fig. 3), or when the sample size was increased to 2500 (Fig. S1, Supporting information). In contrast, replicating genotypes (without increasing N) caused a decrease in correlations between true and inferred measures of selection (Fig. S2, Supporting information).
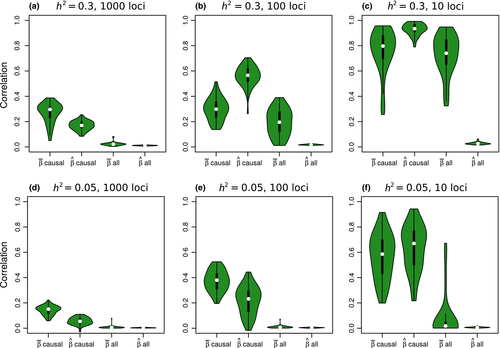
 = narrow-sense heritability and L = number of causal variants) are shown in each panel. Correlations for different combinations of
= narrow-sense heritability and L = number of causal variants) are shown in each panel. Correlations for different combinations of  and L are shown in different panels. Correlations were calculated for model-average (
and L are shown in different panels. Correlations were calculated for model-average (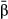 ) and raw (
) and raw (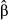 ) estimates of direct selection and were calculated based on all SNPs or only the causal variants. [Colour figure can be viewed at wileyonlinelibrary.com]
) estimates of direct selection and were calculated based on all SNPs or only the causal variants. [Colour figure can be viewed at wileyonlinelibrary.com]
 = narrow-sense heritability and L = number of causal variants) are shown in each panel (50 replicate data sets per conditions). One-to-one diagonal lines are included for reference. Effect size distributions for each simulated data set were obtained by averaging distributions over ten random draws from the posterior distribution of the gemma model parameters γ and β. [Colour figure can be viewed at wileyonlinelibrary.com]
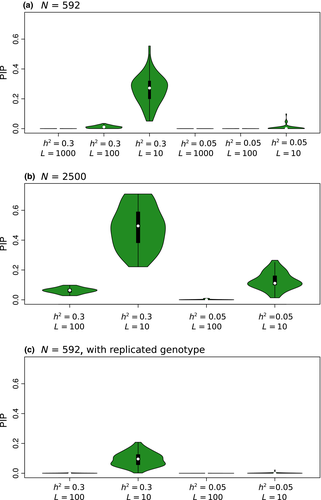
= narrow-sense heritability and L = number of causal variants) are shown in each panel (50 replicate data sets per conditions). One-to-one diagonal lines are included for reference. Effect size distributions for each simulated data set were obtained by averaging distributions over ten random draws from the posterior distribution of the gemma model parameters γ and β. [Colour figure can be viewed at wileyonlinelibrary.com]The mean posterior inclusion probability (PIP) for causal variants was relatively high for  and L = 10 (0.26, SD = 0.10), but was near-zero for more diffuse genetic architectures or when
and L = 10 (0.26, SD = 0.10), but was near-zero for more diffuse genetic architectures or when  was low (Fig. 5a). Average PIPs for causal variants nearly doubled when the sample size was increased from 592 to 2500 individuals (0.48 for
was low (Fig. 5a). Average PIPs for causal variants nearly doubled when the sample size was increased from 592 to 2500 individuals (0.48 for 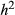 = 0.3 and L = 10, and 0.13 for
= 0.3 and L = 10, and 0.13 for 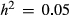 and L = 10; Fig. 5b), but decreased notably when genotypes were replicated without increasing N (Fig. 5c). The accuracy of estimates of direct selection was also affected by the genetic architecture of fitness and the estimator used. For example, estimates of partial regression coefficients were the least accurate (i.e. had the greatest RMSE) when data sets were simulated with diffuse genetic architectures or when point estimates of selection (
and L = 10; Fig. 5b), but decreased notably when genotypes were replicated without increasing N (Fig. 5c). The accuracy of estimates of direct selection was also affected by the genetic architecture of fitness and the estimator used. For example, estimates of partial regression coefficients were the least accurate (i.e. had the greatest RMSE) when data sets were simulated with diffuse genetic architectures or when point estimates of selection (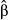 ) were used rather than model-averaged estimates (
) were used rather than model-averaged estimates (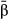 ; Fig. S3, Supporting information). As with other metrics, increasing sample size to 2500 resulted in a decline in normalized RMSE (Fig. S4, Supporting information), but using replicated genotypes while keeping the sample size at 592 increased normalized RMSE (Fig. S5, Supporting information).
; Fig. S3, Supporting information). As with other metrics, increasing sample size to 2500 resulted in a decline in normalized RMSE (Fig. S4, Supporting information), but using replicated genotypes while keeping the sample size at 592 increased normalized RMSE (Fig. S5, Supporting information).
 = narrow-sense heritability and L = number of causal variants). [Colour figure can be viewed at wileyonlinelibrary.com]
= narrow-sense heritability and L = number of causal variants). [Colour figure can be viewed at wileyonlinelibrary.com]Quantitative estimation of genetic variation for fitness
Even with moderately large sample sizes (e.g. 100s of individuals), considerable uncertainty was observed for estimates of the proportion of variation in fitness explained by the genetic data (PVE) and the number of causal variants with measurable effects (n-γ; e.g. Figs S6, S7, S8, Supporting information). Despite this overall lack of precision, posterior point estimates of PVE were reasonably accurate (e.g. for the T. cristinae data with N = 592, RMSE varied from 0.06 to 0.23; Table 2, Fig. 6). The accuracy of point estimates increased with sample size and replication of individual genotypes, with much lower RMSE (and higher 90% HPDI coverage) for N = 2500 or N = 592 with replicates than N = 592 with unique genotypes (0.01 to 0.02 for N = 2500 compared to 0.09 to 0.19 for similar conditions with N = 592; Table 2, Fig. S9, Supporting information).
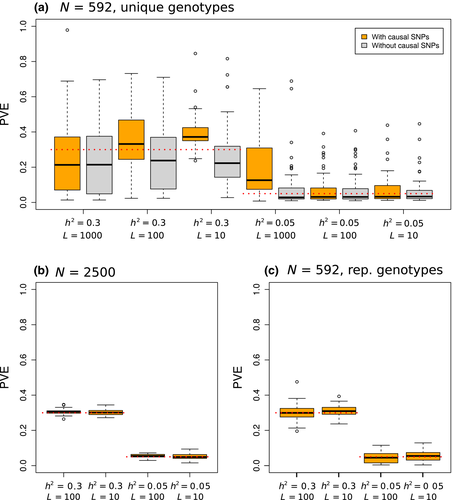
 = narrow-sense heritability, L = number of causal variants, N = number of individuals). [Colour figure can be viewed at wileyonlinelibrary.com]
= narrow-sense heritability, L = number of causal variants, N = number of individuals). [Colour figure can be viewed at wileyonlinelibrary.com]
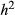
|
No. loci | Metric | Causal | N | PVE | No. SNPs | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Estimate | RMSE | 90% cov. | Estimate | RMSE | 90% cov. | |||||
| 0.3 | 1000 | Quantitative | True | 592 | 0.26 | 0.20 | 0.92 | 8.7 | 991.7 | 0.00 |
| 0.3 | 100 | Quantitative | True | 592 | 0.34 | 0.19 | 0.86 | 18.3 | 85.6 | 0.84 |
| 0.3 | 10 | Quantitative | True | 592 | 0.39 | 0.14 | 0.80 | 7.3 | 5.6 | 0.88 |
| 0.05 | 1000 | Quantitative | True | 592 | 0.09 | 0.14 | 0.96 | 3.5 | 996.5 | 0.00 |
| 0.05 | 100 | Quantitative | True | 592 | 0.08 | 0.09 | 0.98 | 3.6 | 96.4 | 0.82 |
| 0.05 | 10 | Quantitative | True | 592 | 0.07 | 0.09 | 0.94 | 3.5 | 6.6 | 1.00 |
| 0.3 | 1000 | Binary | True | 592 | 0.12 | 0.23 | 0.72 | 8.8 | 991.8 | 0.00 |
| 0.3 | 100 | Binary | True | 592 | 0.16 | 0.18 | 0.84 | 4.6 | 95.4 | 0.74 |
| 0.3 | 10 | Binary | True | 592 | 0.26 | 0.15 | 0.90 | 6.0 | 7.0 | 0.94 |
| 0.05 | 1000 | Binary | True | 592 | 0.05 | 0.06 | 1.00 | 3.8 | 996.2 | 0.00 |
| 0.05 | 100 | Binary | True | 592 | 0.05 | 0.07 | 0.96 | 3.6 | 96.4 | 0.83 |
| 0.05 | 10 | Binary | True | 592 | 0.07 | 0.10 | 0.96 | 4.1 | 6.1 | 1.00 |
| 0.3 | 100 | Quantitative | True | 2500 | 0.30 | 0.02 | 0.90 | 63.2 | 45.3 | 0.62 |
| 0.3 | 10 | Quantitative | True | 2500 | 0.31 | 0.02 | 0.90 | 7.2 | 3.7 | 0.78 |
| 0.05 | 100 | Quantitative | True | 2500 | 0.05 | 0.02 | 0.80 | 9.1 | 99.1 | 0.68 |
| 0.05 | 10 | Quantitative | True | 2500 | 0.05 | 0.01 | 0.94 | 3.9 | 6.8 | 0.84 |
| 0.3 | 100 | Quantitative | True | 592 |
0.31 | 0.03 | 0.96 | 4.8 | 99.5 | 0.74 |
| 0.3 | 10 | Quantitative | True | 592 |
0.30 | 0.05 | 0.84 | 4.3 | 6.1 | 0.74 |
| 0.05 | 100 | Quantitative | True | 592 |
0.05 | 0.03 | 0.92 | 3.3 | 96.7 | 0.66 |
| 0.05 | 10 | Quantitative | True | 592 |
0.04 | 0.03 | 0.88 | 3.0 | 7.1 | 1.00 |
| 0.3 | 1000 | Quantitative | False | 592 | 0.24 | 0.19 | 0.88 | 4.2 | 995.8 | 0.00 |
| 0.3 | 100 | Quantitative | False | 592 | 0.25 | 0.19 | 0.94 | 5.2 | 94.9 | 0.92 |
| 0.3 | 10 | Quantitative | False | 592 | 0.26 | 0.19 | 0.92 | 3.8 | 6.4 | 0.98 |
| 0.05 | 1000 | Quantitative | False | 592 | 0.08 | 0.14 | 0.96 | 3.6 | 996.5 | 0.00 |
| 0.05 | 100 | Quantitative | False | 592 | 0.08 | 0.10 | 0.98 | 3.8 | 96.4 | 0.82 |
| 0.05 | 10 | Quantitative | False | 592 | 0.07 | 0.09 | 0.96 | 3.5 | 6.4 | 1.00 |
-
Results are shown for data sets generated from the T. cristinae genetic data; see (Table S1, Supporting information) for results from the R. pomonella data. Average metrics across replicates are reported with and without causal variants included in the analysis. ‘estimate’ denotes the point estimate of the parameter (posterior mode), ‘RMSE’ is the root-mean-square error, and ‘90% cov.’ gives the proportion of times the true parameter value was included in the 90% HPDIs. ‘no. loci’ gives the actual number of causal variants (L), whereas ‘no. SNPs’ refers to the number of causal variants inferred from the model. ‘N’ is the sample size (N) and
 denotes cases where genotypes were replicated (see the main text for details).
denotes cases where genotypes were replicated (see the main text for details).
The proportion of variation in fitness explained by the genetic data was often lower for binary fitness metrics than for quantitative fitness metrics, although this did not have a consistent effect on accuracy (i.e. in some cases, this gave better estimates as results for the quantitative metric were upwardly biased; Table 2; Fig. S10a, Supporting information). Simulations based on the R. pomonella data gave more variable and less accurate estimates of PVE than did those from T. cristinae, particularly with  and L = 100 or 1000 (Table S1; Fig. S10b, Supporting information). However, results based on the R. pomonella data were similar to T. cristinae when we replicated genotypes to obtain the same sample sizes, suggesting that the poorer performance with the R. pomonella data was due to low sample sizes rather than high LD (Table S1; Fig. S10, Supporting information). In total, 90% HPDIs for PVE generally included the true parameter value (the worst performance was observed for binary metrics; Table 2).
and L = 100 or 1000 (Table S1; Fig. S10b, Supporting information). However, results based on the R. pomonella data were similar to T. cristinae when we replicated genotypes to obtain the same sample sizes, suggesting that the poorer performance with the R. pomonella data was due to low sample sizes rather than high LD (Table S1; Fig. S10, Supporting information). In total, 90% HPDIs for PVE generally included the true parameter value (the worst performance was observed for binary metrics; Table 2).
Estimation of the number of casual variants
Performance was notably poorer in terms of estimating the number of causal variants (i.e. for inference of n-γ compared to PVE), but these results were also more difficult to interpret (Table 2, S1, Supporting information). Specifically, we seldom found evidence for greater than 10 variants with measurable effects on fitness, regardless of conditions (the greatest exception was for the case of 100 causal variants with  and N = 2500; Table 2). Thus, estimates of n-γ were mostly (but not entirely) independent of simulation conditions (i.e. of the true parameter values). However, because the magnitude of fitness effects varied among causal variation (which were normally distributed) and many had very small effects (this is particularly true for the case where 1000 variants explained only 5% of the variation in fitness), not all of these variants necessarily had ‘measurable’ effects on fitness and many were likely subsumed in the polygenic term (i.e. via their contribution to overall genetic similarity captured by the kinship matrix).
and N = 2500; Table 2). Thus, estimates of n-γ were mostly (but not entirely) independent of simulation conditions (i.e. of the true parameter values). However, because the magnitude of fitness effects varied among causal variation (which were normally distributed) and many had very small effects (this is particularly true for the case where 1000 variants explained only 5% of the variation in fitness), not all of these variants necessarily had ‘measurable’ effects on fitness and many were likely subsumed in the polygenic term (i.e. via their contribution to overall genetic similarity captured by the kinship matrix).
This interpretation is consistent with the fact that our estimates of PVE were fairly accurate, and that the proportion of the PVE that was attributable to loci with measurable, rather than infinitesimal effects (PGE in gemma) decreased with the number of causal variants. For example, mean estimates of PGE based on the Timema data with  were 0.79, 0.41 and 0.03 for simulations with L = 10, 100 and 1000, respectively. Also in support of this, SNP posterior inclusion probabilities (PIPs), which measure the probability a locus has a measurable effect on fitness and are the basis for estimates of the number of causal variants (n-γ), were positively correlated with effect sizes. Average correlations (Pearson's r values) between PIPs and effect sizes for these same data sets were 0.61 (L = 10), 0.27 (L = 100) and 0.05 (L = 1000).
were 0.79, 0.41 and 0.03 for simulations with L = 10, 100 and 1000, respectively. Also in support of this, SNP posterior inclusion probabilities (PIPs), which measure the probability a locus has a measurable effect on fitness and are the basis for estimates of the number of causal variants (n-γ), were positively correlated with effect sizes. Average correlations (Pearson's r values) between PIPs and effect sizes for these same data sets were 0.61 (L = 10), 0.27 (L = 100) and 0.05 (L = 1000).
Discussion
Estimating direct selection
We found that BSLMMs could provide useful information about individual bouts of direct selection on genetic loci under at least some conditions, but that important and sometimes strong limitations exist. For example, we showed that reasonably accurate estimates of selection coefficients could be obtained when sample sizes were large (N = 2500), the genetic architecture of fitness was relatively concentrated (L = 10) and fitness was more heritable ( ). With that said, even very large sample sizes gave poor estimates of direct selection when fitness had a diffuse genetic architecture (e.g.
). With that said, even very large sample sizes gave poor estimates of direct selection when fitness had a diffuse genetic architecture (e.g. 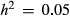 and L = 1000). Thus, when heritability is low or fitness is highly polygenic, it might not be practical or even possible to obtain large enough samples for accurate estimates of direct selection on individual loci. These results are consistent with the general finding from GWASs over the past few decades that large sample sizes are often required but not always sufficient to map phenotypes for complex or quantitative traits onto genotypes (Manolio et al. 2009; Visscher et al. 2012).
and L = 1000). Thus, when heritability is low or fitness is highly polygenic, it might not be practical or even possible to obtain large enough samples for accurate estimates of direct selection on individual loci. These results are consistent with the general finding from GWASs over the past few decades that large sample sizes are often required but not always sufficient to map phenotypes for complex or quantitative traits onto genotypes (Manolio et al. 2009; Visscher et al. 2012).
Replicating genotypes (while holding N constant) actually degraded performance with respect to estimating direct selection. We suspect this occurred because fewer independent data points were available to isolate the effects of individual loci on fitness. With this in mind, our results suggest that experiments designed to detect direct selection on individual genes should maximize sample sizes without necessarily attempting to include multiple individuals from the same family or replicate clones (when this is an option). In some systems, it might be possible to obtain larger total sample sizes by studying multiple experimental populations in a block design (as in Gompert et al. 2014), perhaps at the expense of sample sizes within populations or blocks. Moreover, such replicated block designs could provide additional information about the consistency of selection across space or genomic backgrounds. In the end, the large experiments required to accurately measure direct selection on genes might benefit from (or even require) multi-investigator collaborative efforts on the same scale as those currently used to map human diseases (e.g. N > 100 000 as in IL6R Genetics Consortium Emerging Risk Factors Collaboration 2012).
In addition to study design, we found that the estimator used to infer selection coefficients mattered. In particular, we obtained more accurate estimates of direct selection (lower RMSE and a higher correlation with the true values) with model-averaged coefficients (i.e. 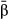 ) than with those that assumed a nonzero effect (i.e.
) than with those that assumed a nonzero effect (i.e. 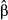 ). A notable exception occurred for concentrated genetic architectures when only considering causal variants. Here,
). A notable exception occurred for concentrated genetic architectures when only considering causal variants. Here, 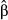 consistently outperformed
consistently outperformed 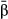 with respect to RMSE and the correlation with the true parameter value. But, because causal variants will rarely be known a priori, we still recommend using model-averaged regression coefficients to estimate direct selection on genetic loci.
with respect to RMSE and the correlation with the true parameter value. But, because causal variants will rarely be known a priori, we still recommend using model-averaged regression coefficients to estimate direct selection on genetic loci.
Quantifying genetic variation for fitness
Some key questions about selection can be addressed directly from statistical summaries of direct selection at the genome-level (e.g. via the model parameters PVE, PGE and n-γ). When the heritability of fitness is low or fitness is highly polygenic, focusing on these questions and parameters might be the most productive way forward (Rockman 2012). For example, estimates of PVE can be converted into measures of additive genetic variation for fitness and these could be productively compared across environments, populations or fitness components. In turn, these measures are of interest for studies of speciation as genetic variation for fitness determines the evolutionary response to selection and thereby affects the possibility for colonization of new habitats. Whereas such information could also be obtained using traditional quantitative genetic breeding designs (Falconer & Mackay 1996), these methods are not practical for many nonmodel organisms.
We found that fairly accurate estimates of PVE could be obtained under a wider variety of conditions than estimates of direct selection on genes. The accuracy of PVE point estimates was determined mostly by sample size (bigger was of course better) and whether or not genotypes were replicated. Specifically and in contrast to the results for estimating selection coefficients (see above), replication of genotypes increased the accuracy of PVE estimates, likely by both increasing LD and increasing the explanatory power of overall genetic similarity. Thus, when possible, studies designed to estimate PVE should include replicate clones or inbred lines. Note, however, that this will come at the cost of decreasing one's ability to parse individual genotypic effects (compared to an analysis of the same number of unrelated individuals). When clones are not available, other structured designs, such as studies of siblings or hybrids, should have a similar albeit less pronounced effect. Because structured designs increase LD and thereby make it easier to tag a greater proportion of causal variants with fewer sequenced loci, they could be particularly appropriate when generating GBS data.
Unfortunately, n-γ was routinely underestimated, particularly when L was large, although performance did improve with N = 2500. This however does not necessarily reflect a failure of the method, as the effects of many causal variants were simply subsumed in the polygenic term when the number of causal variants was large. As such, these smaller effect causal variants did not contribute to estimates n-γ. Nonetheless, based on our results, estimates of n-γ should be interpreted with extreme caution.
Additional considerations and future directions
Further refinements and extensions of BSLMMs have the potential to increase the utility of these models for studying direct selection. For example, current BSLMMs do not account for dominance or epistasis, which are central to many theories of speciation (e.g. Orr 1995; Turelli & Orr 2000; Gavrilets 2004; Orr 2005). Dominance can readily be incorporated into whole-genome regression models, such as BSLMMs, and the same is true in principle for epistasis but the number of genotype combinations present a daunting, but not insurmountable, computational challenge (Zhang & Liu 2007; Jiang et al. 2009; Wang et al. 2010; Ritchie , 2011, 2015). Our understanding of speciation would benefit from measures of selection that explicitly incorporate genotype–environment interactions or that tie selection to trait genetics. Genotype–environment interactions for fitness are central to ecological speciation and have been tested for in many studies, but often by post hoc comparisons rather than formal inference within a model (e.g. Gompert et al. 2014). With that said, adding additional model parameters for genotype–environment interactions or epistasis will further increase the sample size required for accurate inferences. Thus, trade-offs exist between extending the realism of models and obtaining reliable estimates of parameters with limited sample sizes. Notably, methods now exist that take trait architectures into account when testing for selection based on spatial patterns of genetic variation (Berg & Coop 2014). Similar approaches could be used to powerfully connect fitness to phenotype and genotype in short-term studies of selection, and doing so should not entail a cost (unlike adding epistasis) as this would decrease the number of free parameters in the model. Such an integrative framework has the potential to truly advance our understanding of the causes and dynamics of speciation in nature.
Beyond methodological refinements, progress in understanding selection's role in speciation can be made by combining information from studies of direct selection with genome scans of natural populations or even long-term evolve and resequence experiments. Population genomic methods (e.g. 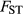 outlier analyses and tests for allele frequency–environment correlations; Beaumont & Balding 2004; Foll & Gaggiotti 2008; Coop et al. 2010; Günther & Coop 2013) gain power to detect selection by compounding the evolutionary consequences of selection over many generations (Lewontin & Krakauer 1973). However, such approaches rarely provide actual estimates of selection (Thurman & Barrett 2016), do not parse direct vs. indirect selection and can be confounded by demographic processes (Excoffier et al. 2009). In contrast, short-term studies of direct selection can employ experimental designs where demography is known precisely and where processes other than selection and drift (e.g. gene flow, mutation and recombination) are eliminated (e.g. Gompert et al. 2014). Consistency of patterns between these types of studies would implicate direct selection as a key driver of divergence and suggest selection has acted in a consistent manner through time. Conversely, a lack of consistency could suggest methodological shortcomings, indicate a greater role for other evolutionary processes (such as drift and linked selection) or show that selection or LD varies through time. Such temporal variation in selection has been detected in phenotypic and genetic studies (Barrett et al. 2008; Siepielski et al. 2009; Anderson et al. 2014; Bergland et al. 2014; Thurman & Barrett 2016), but has rarely been incorporated into models of speciation.
outlier analyses and tests for allele frequency–environment correlations; Beaumont & Balding 2004; Foll & Gaggiotti 2008; Coop et al. 2010; Günther & Coop 2013) gain power to detect selection by compounding the evolutionary consequences of selection over many generations (Lewontin & Krakauer 1973). However, such approaches rarely provide actual estimates of selection (Thurman & Barrett 2016), do not parse direct vs. indirect selection and can be confounded by demographic processes (Excoffier et al. 2009). In contrast, short-term studies of direct selection can employ experimental designs where demography is known precisely and where processes other than selection and drift (e.g. gene flow, mutation and recombination) are eliminated (e.g. Gompert et al. 2014). Consistency of patterns between these types of studies would implicate direct selection as a key driver of divergence and suggest selection has acted in a consistent manner through time. Conversely, a lack of consistency could suggest methodological shortcomings, indicate a greater role for other evolutionary processes (such as drift and linked selection) or show that selection or LD varies through time. Such temporal variation in selection has been detected in phenotypic and genetic studies (Barrett et al. 2008; Siepielski et al. 2009; Anderson et al. 2014; Bergland et al. 2014; Thurman & Barrett 2016), but has rarely been incorporated into models of speciation.
Evolve and resequence experiments provide a powerful means to measure selection by compounding information over many generations (e.g. Cooper et al. 2003; Blount et al. 2008; Burke, et al. 2010, 2014; Long et al. 2015; Gompert & Messina 2016), and could be used to distinguish between direct and indirect selection (using, e.g. ‘driver’ ‘passenger’ models as in Illingworth & Mustonen 2011). However, such studies have been mostly restricted to organisms with short generation times that can be maintained in the laboratory (e.g. viruses, bacteria, yeast and Drosophila), and laboratory conditions may fail to capture the complexity of nature. In contrast, experiments that measure one or several bouts of selection within a generation can be conducted with a greater diversity of organisms under natural or semi-natural conditions. Indeed, hundreds or even thousands of such within-generation estimates of phenotypic selection have increased our awareness of how variable selection can be across traits, time periods and populations, and refinement of this awareness continues (Kingsolver et al. 2001; Siepielski et al. 2009). It will thus be important to recognize when multigeneration experiments are needed (e.g. to measure the effect size distribution of mutations fixed during a bout of adaptation), vs. when replicated within-generation experiments might be more productive (e.g. to contrast directions of selection on genotypes across a suite of environments or to distinguish between mechanisms by eliminating mutation, recombination). When possible, short-term measures of selection should be compared to results from longer-term evolve and resequence experiments on the same species to determine whether the former can be extrapolated to predict evolutionary trajectories over greater timescales (which are clearly relevant for speciation).
Alternative approaches
Some questions in speciation can only be addressed by disentangling direct and indirect selection. For example, measures of direct selection are most relevant for identifying the specific genes or alleles that cause reproductive isolation. Nonetheless and despite our focus on direct selection in this manuscript, there are cases where the combined effects of direct and indirect selection (i.e. total selection) are of interest and thus where the ‘problem’ of correlated genetic loci disappears.
First, the expected genomic response to an episode of selection (i.e. genome wide changes in genotype and gamete frequencies) is dictated by total selection, not direct selection alone. This means that evolutionary change from one generation to the next is best predicted from total selection. With that said, longer-term predictions will only be valid if LD is maintained through time, for example by tight physical linkage or by selection and gene flow as can occur in hybrid zones (Barton & Hewitt 1985). Otherwise, patterns of LD will change via recombination and changes in allele or haplotype frequencies.
Second, several important evolutionary phenomena depend on the total selection experienced by genetic loci each generation (i.e. direct selection and LD with causal variants), including genetic hitchhiking (Maynard-Smith & Haigh 1974), genome-wide congealing during speciation with gene flow (Flaxman, et al. 2013, 2014) and the reduction in effective gene flow across a hybrid zone (i.e. the barrier to gene flow; Barton 1983; Barton & Bengtsson 1986; Gavrilets 2004; Barton & De Cara 2009). Thus, under a range of conditions, whether populations can speciate with gene flow or remain distinct upon secondary contact depends on the total selection (specifically total selection in the context of divergent selection or selection against hybrids) rather than only direct selection on causal variants (Barton 1983; Flaxman et al. 2014). In conclusion, total selection matters because it is not always just individual genes that respond to selection, but potentially sets of genes or genomes (Lewontin 1974), and thus measures of total selection provide key information about evolutionary processes in general, and speciation in particular.
Acknowledgements
We would like to thank and S. Xu, P. Schluter and S. Rogers for organizing this special issue, and four anonymous reviewers for comments that improved this manuscript. ZG was funded by the US National Science Foundation (NSF DEB #1638768), and PN was supported by the Royal Society of London via a University Research Fellowship. Computing, storage and other resources from the Division of Research Computing in the Office of Research and Graduate Studies at Utah State University and the Center for High-Performance Computing at the University of Utah are gratefully acknowledged.
References
Z.G. generated and analysed the simulated data sets. All authors wrote and revised the manuscript.
Data accessibility
Simulated data sets and perl and R scripts used to simulate and analyse these data have been archived at the DRYAD data repository (doi:10.5061/dryad.ns47q).




