A new probabilistic approach to estimating marine gastropod densities from baited traps
Funding information
This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors. The article writing by JCG was supported by the “Laboratoire d'Excellence” LabexMER (ANR-10-LABX-19) and co-funded by a grant from the French government under the programme “Investissements d'Avenir”.
Abstract
A new probabilistic approach is proposed to assess muricid species population abundances at scales relevant to both Ancient and Modern coastal fisheries. Motivated by the long-term goal of reconstructing the dynamics of exploited murex populations during Antiquity, the objective was to estimate the population density of the banded dye-murex, Hexaplex trunculus (Linnaeus, 1758) from successive captures with baited traps, using a method similar to the technique employed in the Mediterranean purple dye industry. The stochastic model developed simulates cumulative captures while accounting for high variability. It was calibrated with data acquired during a field trapping experiment (Crete Island, Greece). Traps’ catchability and Effective Area of Attraction (EAA) were estimated using the individual speed and behavioural response towards bait from laboratory experiments. Average density of H. trunculus was estimated as 2.2 ± 1.4 SE individuals per square metre, with no significant differences between seagrass and rocky habitats. The clearing time of successive capture experiments averaged 84 ± 6 SE hr. Clearing ca. 0.4 ha of subtidal area would be necessary to produce ca. 1.0 g of pure Tyrian purple pigment. The method described is generalizable to making population abundance estimates for similar groups, such as whelks, in modern fisheries.
1 PROBLEM
There is a general lack of information about the impact of earlier economic activities on coastal invertebrate populations. Long time series reconstructing trends in ancient population dynamics are rare in marine historical ecology (e.g., Edwards, Beaugrand, Hays, Koslow, & Richardson, 2010). This has led researchers to mine data from traditional and non-traditional historical ecology sources (McClenachan, Ferretti, & Baum, 2012; de Vooys & van der Meer, 1998). The problem of “trusting” these latter sources cannot be overlooked, and qualifying these data has become a central challenge for application in other disciplines like zooarchaeology (Wolverton, 2013). Data validation issues therefore must be addressed through experimentation, comparative reconstruction and re-analysis of their original historical contexts (Taylor, 2013).
During Antiquity, Hexaplex trunculus was exploited intensively (ca. from 4000 until about 1350 BP), along with Bolinus brandaris and Stramonita haemastoma as a source for the famous “Royal” or “Tyrian” purple dyes throughout the Mediterranean basin (Cardon, 2003; Forstenpointner, Quatember, Galik, Weissengruber, & Konecny, 2007; Oliver, 2015). Dye production from “murex” species, once believed to be exclusive to Mediterranean cultures, has been traced in archaeological sites all over the world (Cardon, 2003; Giner, 2009; Haubrichs, 2004). The dye, produced from precursor molecules present in the gastropod's hypobranchial gland (Cooksey, 2001), was time-consuming and labour intensive to collect, making this pigment a valuable trade commodity (Burke, 1999; Giner, 2009; Ruscillo, 2005).
While information about the dye chemistry and the related economy are numerous, very little concerns the species’ population ecology. In particular, it remains unexplained how an industry which required such high numbers of individual organisms (a widely-cited estimate is 1.4 g of pigment from 12,000 individuals; Friedländer, 1909) could have exploited for so long a species assumed to exist in relatively low average densities and distributed according to high aggregation patterns. Early writers like Aristotle (Historia Animalium) and Pliny the Elder (Historiae Naturalis) wrote knowledgeably on biological and ecological features of gastropods used, including their life history traits, behaviour, seasonality and preferred habitats. They also described how individuals were harvested and processed afterwards. In contrast, they did not address any population issues.
The unknown population dynamics at exploitation sites is a critical missing link for understanding of this dyestuff's industrial past. To reconstruct trends, species population sizes and density distributions are fundamental information (Pielou, 1977), yet with rare exceptions, they cannot be measured exhaustively. This is a long-standing difficulty in ecology, particularly for marine environments. Many exploited marine animal populations are estimated based on methods developed for fisheries (Serchuk, 1978). However, these are of little help for historical ecology as to fulfil modern stock management objectives, abundance estimates have been considered unnecessary (Gulland, 1969), and instead, relative measures, like the Catch Per Unit of Effort, have prevailed (Caddy & Mahon, 1995; Eddy, Coll, Fulton, & Lotze, 2015; Petrere, Giacomini, & De Marco, 2010; Valentinsson, Sjödin, Jonsson, Nilsson, & Wheatley, 1999). In addition, today, population studies of these gastropods remain scarce (e.g., Elhasni, Vasconcelos, Ghorbel, & Jarboui, 2013; Mutlu & Ergev, 2008; Vasconcelos, Carvalho, Castro, & Gaspar, 2008), even as they are still exploited as a food resource and after having been harvested for millennia (Alvarez, Godino, Balbo, & Madella, 2011; Klein & Steele, 2013).
To reconstruct past dynamics of muricid populations, estimates are needed of population densities from “depletion” sampling techniques analogous to the harvest techniques used in the past and for which a validation method can be inferred. This article develops such a statistical method by characterizing the fishing process in shallow coastal environments for both ancient (Nielsen-Bekker, 2009) and modern contexts (Vasconcelos et al., 2008). Only the banded dye-murex, Hexaplex trunculus (Linnaeus, 1758), was targeted because it appears more common at archaeological sites (Oliver, 2015). Hexaplex trunculus colonize all Mediterranean coasts extending as far north as the Gallican coast and south to Morocco (Bañón, Rolán, & García-Tasende, 2008; Vasconcelos et al., 2008). At present, it is considered a minor commercial species (Sawyer, Zuschin, Riedel, & Stachowitsch, 2009; Vasconcelos et al., 2008) and is still harvested with artisanal methods (Peharda & Morton, 2006; Vasconcelos et al., 2008) remarkably similar to those described by Aristotle and Pliny the Elder.
2 MATERIALS AND METHODS
The conceptualization of the statistical technique is based on a depletion method where individuals are removed from the targeted population at each sampling (Serchuk, 1978). The design combines analytical calculations, numerical simulations and data assimilation from behavioural and field experiments (Figure 1a) using sets of baited traps (Figure 1b) installed in the shallow, coastal study area near the Heraklion Marine Research Center (HCMR) on Crete Island (Greece; Figure 1c). Crete was chosen for the field testing because it was one of the earliest centres of Mediterranean purple dye production (Stieglitz, 1994) and the H. trunculus coastal population abundance is unknown. All animals removed were handled as little as possible, with recovery periods to minimize stress.
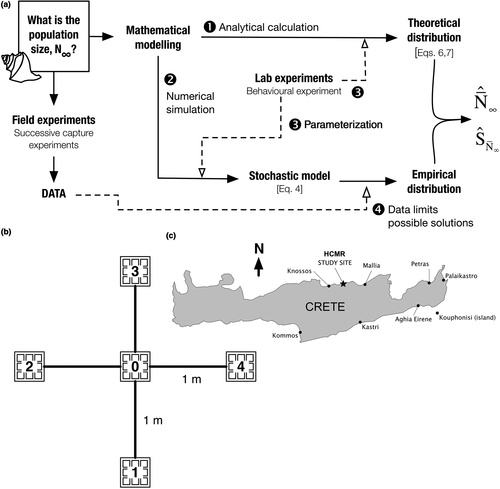
2.1 Successive capture experiments
The experimental method used baited “wallet-line” traps (Vasconcelos et al., 2008). Two different habitats were investigated in July 2013: a rocky substrate consisting of both loose boulders and exposed bedrock, and a seagrass (Posidonia oceanica (Linnaeus) Delile, 1813) meadow. Water depths were <5 m.
Each “wallet” is constructed from rigid plastic netting (mesh size 1.5 × 1.5 cm) and had a finished surface area equal to 225 cm2 (15 cm on a side). An installation consisted of five “wallets” total, arranged as a squared cross (Figure 1b): one trap at the centre (trap 0) with additional traps attached at the extremity of four, one-metre long branches. This arrangement differs from the 100 m long lines described in Vasconcelos et al. (2008) and is better suited to making observations on a single substrate patch. Each wallet-trap was baited with squid and sardine flesh and ballasted to prevent any movement during a capture experiment. Traps were installed on each substrate by diving. Throughout the remainder of the presentation, “trap” will refer to individual “wallet-traps.”
Traps retrieved after preliminary overnight tests were completely emptied of their bait, suggesting that the experimental time was too long relative to the size of the traps and the bait attractiveness for consumers in the attraction area. Thus, the duration was shortened to between 3 and 4 hr (Table 1), which also permitted complete cycles of installation and removal within daylight hours on multiple sites. Each trap was collected and placed separately in a labelled plastic bag and transported to the laboratory where H. trunculus individuals could be identified, counted and measured (longest length from siphon canal to apex in mm). Three series of two successive capture experiments were performed in sea grass meadows and two series of three successive captures on the rocky substrate. Wallet-traps are not exclusive for H. trunculus (Vasconcelos et al., 2008); any other secondary consumers caught were identified.
| Experiment | Duration, (hr) | Trap 0 - C | Trap 1 - S | Trap 2 - W | Trap 3 - N | Trap 4 - E | Total (ind/experiment) |
|---|---|---|---|---|---|---|---|
| SG - A1 | 3.50 | 0 | 0 | 5 | 0 | 1 | 6 |
| SG - A2 | 3.50 | 0 | 1 | 0 | 0 | 0 | 1 |
| SG - B1 | 3.50 | 1 | 1 | 1 | 0 | 0 | 3 |
| SG - B2 | 3.40 | 0 | 1 | 0 | 1 | 1 | 3 |
| SG - C1 | 3.50 | 0 | 3 | 1 | 4 | 2 | 10 |
| SG - C2 | 3.25 | 0 | 0 | 0 | 0 | 2 | 2 |
| RK - A1 | 3.25 | 2 | 0 | 0 | 1 | 3 | 6 |
| RK - A2 | 3.40 | 2 | 7 | 5 | 0 | 0 | 14 |
| RK - A3 | 3.70 | 1 | 3 | 1 | 1 | 1 | 7 |
| RK - B1 | 3.15 | 0 | 0 | 0 | 2 | 0 | 2 |
| RK - B2 | 3.10 | 0 | 0 | 0 | 0 | 0 | 0 |
| RK - B3 | 3.50 | 1 | 1 | 2 | 0 | 1 | 5 |
3 THEORY AND CALCULATIONS
3.1 Concepts underpinning fluctuating captures
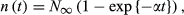 (1)
(1)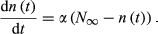 (2)
(2)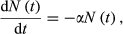 (3)
(3)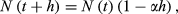 (4)
(4)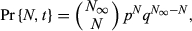 (5)
(5)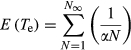 (6)
(6)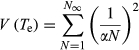 (7)
(7)3.2 Estimating the asymptotic value of abundance of the targeted subpopulation (N∞)
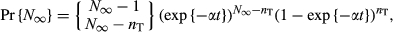 (8)
(8)3.3 Behavioural experiments to estimate α and the effective area of attraction
Ten organisms collected on the traps, then depurated for 72 hr, were placed individually in experimental, flat-bottomed tanks, and their movements were observed and photographed (every 30 s) over a period of 10 min. For each individual, the total distance (in cm) covered and the direction followed (in radial degrees) were recorded at time intervals of 30 s. Four replicates were performed for each individual (twice without food and twice with food) placed at the centre of the container. The average speed (in m/hr) was calculated from the total distance travelled by each individual during the observation period.
Speed and direction were introduced into a correlated random walk simulation model (Renshaw & Henderson, 1981) to explore the behaviour of the organisms within the trap configuration. To define the dimensions of the Effective Area of Attraction (EAA) around each wallet-trap installation, simulations were performed for 100 virtual snails placed randomly in a 4 × 4 m2 area at the centre of which was placed the trap installation, and then running 500 iterations for a maximum of 3 hr or until the virtual snail was trapped. The number of times that a virtual snail falls in one of the five traps was counted to determine the probability that one individual will be captured as a function of the distance to the closest centre of one of the five traps. The effective area of attraction was then determined from the largest radius from a centre of the closest trap for which the probability that an individual can be caught is strictly greater than zero. To estimate α, 500 individuals were withdrawn randomly in the EAA and each individual snail realized one independent movement for the duration of the experiment according to the rules (i.e., speed and direction) determined by the observed behaviour of the organisms. The catchability rate α (in hr−1) was determined as the proportion of individuals reaching a particular trap per unit of time. This procedure was repeated 500 times to permit calculation of the frequency distribution.
All calculations and simulations were performed with SciLab (version 5.5.2; Scilab Enterprises, 2012).
4 RESULTS
4.1 Capture experiments
Results for all of the successive capture experiments from the field site are given in Table 1. The average numbers of individuals captured were 8 in seagrass (SG), and 17 on the rocky (RK) substrates, during an average immersion time of 3.4 hr. Captures for three of the five experiments (SG B; RK A, RK B) do not show any decreasing trend. There was no difference in average between the rocky substrate and seagrass meadow. The variability appears slightly higher on the rocky substrate than the seagrass meadow and had a smaller number of replicates due to high wind conditions during the field experiment. There is no difference related to the position of the individual traps, neither for the centre nor for a specific axis (26 individuals on the North–South axis and 26 individuals on the East–West axis, not counting the central trap). Although, the traps were not size selective; individuals with a large range of sizes were trapped (distribution not shown), very small individuals (0.7–0.8 cm) were found within the traps, while larger ones (the largest captured was 5.2 cm long) fed on the bait from the outside. Other species were attracted to, or captured by the traps: fish (including Thalassoma pavo, Scorpaena sp., Muraena helena) were visually identified in the area when recovering the traps, and other gastropods (including Nassarius unifasciatus), crustaceans (crabs, including Xantho poressa), brittle stars and polychaetes (Hermodice carunculata) were found in, or on, the traps after recovery. By-catch populations were not quantified in this study.
4.2 Effective area of attraction and catchability rate
Both measures of the EAA value and catchability rate were made on members of the population being studied. During the behaviour experiments, movements of individuals are not oriented in one particular direction, neither with, nor without bait. The percentage of immobility was high, 63% and 52% of the time, with and without bait, respectively. Average speed estimates were performed for moving individuals only (0.92 ± 0.75 SD m/hr and 1.16 ± 1.10 SD m/hr, with and without bait, respectively). Given the measurements’ precision, 1.00 m/hr was used to estimate the trap depletion area with the correlated random walk numerical simulations (Figure 2a).
From the behaviour experiment, the probability table of the correlated random walk model was defined first by a probability of performing a movement or not (i.e., the animal remains in same position). Movement to adjacent cells is simulated by selecting among seven possible directions, without allowing backtracking movements. No specific attraction for traps was simulated, as no specific orientation was detected by the behaviour experiment. The direction followed was chosen from a Gaussian distribution centred on the last direction followed. This implies that individuals avoid making frequent, sharp changes in direction never observed in the experiments. Speed was fixed as a constant with the exception that organisms can stop moving any time along their individual tracks.
Under these conditions, the maximum significant average radius of attraction around each trap was estimated as 135 cm. This value was used to determine the Effective Area of Attraction (EAA; defines the total benthic surface sampled by each set of five traps). The EAA was estimated at 15 m² for the trap configuration and takes into account the overlap of the five separate EAAs. The average value of α (the catchability rate, or the rate at which we expect to catch a snail on one of the five traps) was equal to 0.047 hr−1 (Figure 2b), with a standard error (as an estimate of the uncertainty) equal to 0.010 hr−1. The statistical distribution appeared to be Gaussian (Figure 2b; Chi squared test with a significance level of 0.05).
4.3 Density estimates and expected time of extinction for successive captures
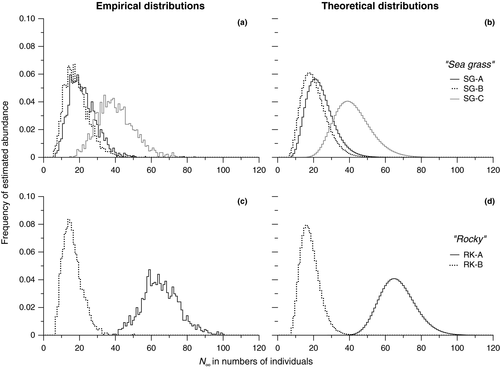
Results of the density estimates are presented in Table 2. Estimated abundances in the EEA fluctuated from 23 ± 8 (SE) and 42 ± 11 (SE) individuals in the seagrass meadows (SG), and 17 ± 6 (SE) and 68 ± 11 (SE) individuals on the rocky substrate (RK), yielding overall average densities of between 2 (SG) and 3 (RK) individuals per square metre. Both empirical and theoretical probability distributions are remarkably consistent for all experimental conditions (Figure 3). The overlap between the five separate EAAs complicated the density estimate. Here, it is assumed to not modify the density estimate significantly because of the very low numbers and the sharp decrease in the probability to be trapped from the centre of a trap to the edge of the corresponding EAA.
| Substrate | Mean abundance, nb ind | SE, nb ind | Mean density, nb ind/m² | SE, nb ind/m² | Mean extinction time (Te), hr | SE, hr |
|---|---|---|---|---|---|---|
| SG A | 22.9 | 8.0 | 1.5 | 0.53 | 78.9 | 26.9 |
| SG B | 19.7 | 7.6 | 1.3 | 0.51 | 75.6 | 26.9 |
| SG C | 42.1 | 11.0 | 2.8 | 0.73 | 91.9 | 27.1 |
| RK A | 68.1 | 10.8 | 4.5 | 0.72 | 102 | 27.2 |
| RK B | 17.1 | 5.6 | 1.1 | 0.37 | 72.7 | 26.8 |
An expected time of extinction (Te) for successive captures was calculated from the density estimates using the stochastic model. The depletion estimated by the model should be complete in all cases between 73 hr (for the lowest abundance estimate) and 102 hr (for the higher abundance estimate), with a near constant standard error estimate of about 30 hr (Table 2). Because the process is identical for all five cases, there is a trivial increase in the extinction time with respect to the abundance estimates.
5 DISCUSSION
Passive, baited traps are common fishing gear in benthic coastal fisheries. Techniques using baiting experiments are very different from other depletion methods based on trawling and dredging where the population decreases as the scraped surface increases (Hennen, Jacobson, & Tang, 2012). The theoretical development expands on earlier ideas about depletion methods and benthic population estimates (Eggers, Rickard, Chapman, & Whitney, 1982; Gros & Santarelli, 1986; Hennen et al., 2012; Valentinsson et al., 1999). Existing quantitative descriptions of how baited trap methods work have focused on characterizations of the CPUE index and estimates of areas of attraction (Eggers et al., 1982; Gros & Santarelli, 1986). Serchuk (1978) stated that the size of the initial population can be estimated with a depletion method by establishing the relationships either between CPUE and cumulative effort or between CPUE and cumulative catch. However, establishing a relationship between a population size and other variables used in fisheries (i.e., “selectivity,” “catchability” and “effort”) remains problematic (Eggers et al., 1982; Harley, Myers, & Dunn, 2001; Kideys, 1993; Petrere et al., 2010). Indeed, to estimate a population size, successive catches should be performed in the same area until the average catches (per unit of effort) decline in trend for the targeted species (Hennen et al., 2012; Leslie & Davis, 1939; Rago, Weinberg, & Weidman, 2006; Serchuk, 1978). This necessity can create absurd situations like that described in (Valentinsson et al., 1999) where repeated trapping reduces a population to the point that it cannot recover and is a challenge when targeted populations are small.
These difficulties with this particular fishery method inspired us to propose to estimate Murex population density, not with a deterministic model, but with a stochastic one (Equation 4) calculating a “probable” abundance (N∞) within a calculated “area of attraction.” Catchability (α) was expressed as a normalized rate (in units of time−1), hence is a constant, different from the catchability given in both Rago et al. (2006) and Hennen et al. (2012). Both these studies rely on linking fishing performance and properties of the targeted population. The stochastic nature of the process in this method permitted to cope with high variabilities in successive catches, masking the depletion trend; this property concords with observations of the “frequent occurrence of very dissimilar fishing yields between adjacent lines” (Vasconcelos et al., 2008: 296).
5.1 Distributions
The estimates reported in Table 2 are, to our knowledge, the first modern population density estimates for H. trunculus on Crete Island (average for both substrates was 2.2 ± SE 1.4 ind/m2). These values compare favourably with other published data from Mediterranean sites, such as 5 ind/m2 on a sand bottom of <10 m depth (Mutlu & Ergev, 2008) and about 6 ind/m2 as estimated from the data in Vasconcelos et al. (2008). However, the year-long study conducted by Vasconcelos et al. (2008) indicates strong seasonal variations can be expected.
In addition, “fishermen,” as Eggers et al. (1982: 451) pointed out, “target the placement of gear in areas that traditionally yield the highest catches.” This principle suggests that estimates of targeted species abundances based on CPUE would be biased. In our case, this problem would be attenuated because H. trunculus has been described as a ubiquitous species present on soft (Poppe & Goto, 1991; Vasconcelos et al., 2008), hard (Rilov, Benayahu, & Gasith, 2004) and mixed substrates (Peharda & Morton, 2006) with a homogeneous macroscale distribution estimated (Sawyer et al., 2009). In contrast, their spatial distribution has been presented as strongly structured by food resources: within an oyster bed local densities as high as 120 ind/m2 have been reported (values cited in Peharda and Morton (2006) and in Sawyer et al. (2009) citing Zavodnik and Simunović, 1997).
5.2 Bait attraction and activity patterns
In contrast with other studies, periods of inactivity are permitted in our model, which accounts for the relatively small EAA value. For example, Gros and Santarelli (1986) estimated an EAA of 372 m2 for baited pots used to fish Buccinum species, assuming constant activity, despite the numerous statements about inactivity for gastropods, such as: Buccinum undatum and Busycon carica “may spend a large proportion of its time quiescent” (Kideys, 1993: 44); Nucella lapillus moved <20 cm during a 12-hr foraging period (Hughes & Drewett, 1985); and H. trunculus individuals colonizing mussel beds were found to be immobile for 7.3 hr (out of 22.9 hr) on average (Sawyer et al., 2009).
In addition, the amount of time spent feeding for H. trunculus is unknown. Laboratory observations indicate individuals can survive starvation periods of up to 6 months (Sawyer et al., 2009). This is consistent with descriptions in ancient sources that “purples” (assumed to be H. trunculus and B. brandaris) may be held for many weeks before pigment was extracted (Pliny the Elder [1601 edition]: Book IX, Ch. 36).
In our study, a correlated random walk model was used to simulate the crawl path of the individual snails, implying that the attractiveness of the bait was low. This behavioural response in static water conditions has been noted earlier (Nickell & Moore, 1992) and may constitute a limitation of our study. In addition, behaviour was studied for individuals isolated from each other; however, group foraging is reported for this species (Peharda & Morton, 2006) suggesting some kind of communication between individuals which may subvert our assumption of randomness. The laboratory experiments used a small amount of sand on the bottom of the tank to permit the passage of the snail and after each experiment the sand was mixed and partially replaced to minimize any potential effect from a mucus trail which could have created a confused signal for the next animal. Therefore, our model parameterization could be improved by incorporating in situ observations from new miniaturized tracking devices deployable on individuals (Brownscombe et al., 2015; Lyons, Pope, Kostka, & Houghton, 2012; Mooney et al., 2015).
5.3 Feeding preferences and immersion time
Predatory and scavenging behaviours have been exploited in traditional fisheries for harvesting this species. Their diet includes sponges, tube worms, a variety of bivalves, limpets, barnacles, tunicates, other gastropods, fish carrion and even conspecifics (Peharda & Morton, 2006; Pliny the Elder, 1601; Rilov et al., 2004; Sawyer et al., 2009; and Spight, Birkeland, & Lyons, 1974). Several reports mention live bivalves being used by fishermen to collect H. trunculus (Morton, Peharda, & Harper, 2007; Pliny the Elder, 1601; and Vasconcelos et al., 2008). However, dead bait was used because live bait can increase trap immersion time. Vasconcelos et al. (2008) used live bait with a trapping time of 24–36 hr because live prey is less accessible. Muricidae attacks live mollusc prey by drilling or chipping the shell, a process lasting from 12 hr to up to 7 days (Peharda & Morton, 2006 and Sawyer et al., 2009). While longer immersion times may increase the number of individuals caught, it also increases risk of their predation on the traps (Vasconcelos et al., 2008) and some of their known predators (moray eels, Sparidae) were observed in the vicinity of the traps during experiments.
5.4 Determining baselines and reconstructing ancient practice
Depletion experiments for estimating population sizes of benthic scavengers with low densities are more practical and reliable than direct observation and point sampling (Rago et al., 2006) because they exploit the behavioural patterns of a targeted organism. For example, surveys of the macrobenthos on Crete using typical bottom sampling techniques (transects, box corers and grab samples) did not detect the presence of H. trunculus, or other muricid species (Karakassis & Eleitheriou, 1997; Koulouri, Dounas, Arvanitidis, Koutsoubas, & Eleftheriou, 2006; Tselepides, Papadopoulou, Podaras, Plaiti, & Koutsoubas, 2000). None of these methods were designed to sample low density populations, so an absence of muricids was not surprising. In the subtidal zone, the wallet-trap method is well-suited to cost-effective systematic sampling campaigns or monitoring programmes, regardless of the nature of the substrates.
The method described here constitutes a starting point to study the impact of earlier activities of dye production on coastal populations of Muricidae, in general. Crete is an interesting location to make these observations because it is geographically distant from other coasts, and therefore, natural Muricidae populations are assumed to be relatively isolated from other populations. It then becomes possible to test if they were subject to overfishing during the intense period of dye production. It was suggested by Columella (Res Rustica, Liber VIII,16,7) that a form of aquaculture may have been put in place to sustain the development of the dye industry, however, this remains hypothetical. First estimates suggest that, for producing 1.0 g of purple dye, it is necessary to clear out the population on ca. 0.40 ha of subtidal shore. Using the linear arrangement of traps described in Vasconcelos et al. (2008), a line of about 50 traps spaced at 3.0 m, it can be estimated that the deployment of about 20 lines would be necessary to obtain the required number of individuals for a total fishing time effort of about 4 days based on the average clearing time estimate. This represents a very small fraction of the total available surface around Crete Island and a minor fishing effort, believed to be entirely compatible with the period during which dye industry flourished.
6 CONCLUSIONS
This study presents a new statistical method to calculate marine gastropod population densities and clearing time, associated with their uncertainty estimates. The method is designed to estimate a population density from baited pot fishing techniques that were employed during Antiquity for harvesting Muricidae (Ruscillo, 2005) or that are currently used in whelk (Buccinum undatum) fisheries. This information is largely absent from the ecological literature due to the prevalence of CPUE estimates or practical difficulties in observing the organisms in their habitat.
In this case, calculations based on preliminary estimates suggest that the effort to obtain a sufficient amount of raw dye product (which seemed disproportionate initially) is not as high as has been previously suggested in the archaeological literature. However, we caution that we are still far from concluding that the impact of harvesting large numbers of gastropods in fisheries is negligible. A more ambitious historical ecology study should be carried out to make precise estimates of fishing pressure and to model the dynamic of the population, including harvests for the pigment precursor according to economic demand. This, in combination with a large-scale trapping study, would provide a complete view of the system of purple dye production organized throughout the Mediterranean some 4,000 years ago (Burke, 1999; Ruscillo, 2005; Stieglitz, 1994; and Watrous, 1998).
ACKNOWLEDGEMENTS
We are very grateful to Prof. Margarida Castro of the University of Algarve for having introduced us to the “wallet-traps” and for providing the initial materials. We also thank the HCMR in Heraklion, Crete, especially Dr. Christos Arvanitidis for having hosted and supported our field and laboratory experiments during the EMBC Summer School 2013 session. This study was part of the European EMBC+ Master of Science programme.
COMPETING INTERESTS
The Authors have no competing interests to declare.




