Species distribution, ecology, abundance, body size and phylogeny originate interrelated rarity patterns at regional scale
Abstract
The most pervasive macroecological patterns concern (1) the frequency distribution of range size, (2) the relationship between range size and species abundance and (3) the effect of body size on range size. We investigated these patterns at a regional scale using the tenebrionid beetles of Latium (Central Italy). For this, we calculated geographical range size (no. of 10-km square cells), ecological tolerance (no. of phytoclimatic units) and abundance (no. of sampled individuals) using a large database containing 3561 georeferenced records for 84 native species. For each species, we also calculated body mass and its ‘phylogenetic diversity’ on the basis of cladistic relationships. Frequency distribution of range size followed a log-normal distribution as found in many other animal groups. However, a log-normal distribution accommodated well the frequency distribution of ecological tolerance, a so far unexplored issue. Range size was correlated with abundance and ecological tolerance, thus supporting the hypothesis that a positive correlation between distribution and abundance is a reflection of interspecific differences in ecological specialization. Larger species tended to have larger ranges and broader ecological tolerance. However, contrary to what known in most vertebrates, not only small-sized, but also many medium-to-large-sized species exhibited great variability in their range size, probably because tenebrionids are not so strictly influenced by body size constraints (e.g. home ranges) as vertebrates. Moreover, in contrast to other animals, tenebrionid body size does not influence species abundances, probably because these detritivorous animals are not strongly regulated by competition. Finally, contrary to the assumption that rare species should be mainly found among lineages that split from basal nodes, rarity of a tenebrionid species was not influenced by the phylogenetic position of its tribe. However, lineages that split from more basal nodes had lower variability in terms of species geographical distribution, ecological tolerance and abundance, which suggests that lineages that split from more basal nodes are not only morphologically conservative but also tend to have an ecological ‘inertia’.
Introduction
Species rarity has strongly attracted the interest of macroecologists especially in the last 20 years (Lomolino et al. 2010). Rarity is often considered an indication of species extinction risk (Davies et al. 2000), and many studies have attempted to use rarity measures for conservation purposes (e.g. Arita et al. 1990; Kattan 1992; Manne and Pimm 2001; Isaac et al. 2009), especially when it is difficult to obtain other kinds of data for estimating species extinction risk (Fattorini 2008, 2010a,b, 2011; Fattorini et al. 2012). Large-scale studies on species rarity have led to the identification of some recurrent macroecological patterns: (1) the frequency distribution of range size, (2) the relationship between range size and species abundance and (3) the effect of body size on range size. The first pattern consists in the virtually ubiquitous highly right skewed distribution of range size: most species have small ranges and few are widespread (see Lomolino et al. 2010 for examples, and Gaston 1990 for exceptions). The second pattern is that widespread species tend to be more abundant than localized ones (Gaston 1990). The third pattern assumes that body mass influences range size. This is a much more controversial pattern: theoretical argumentations suggest that larger species should have larger ranges, which is a commonly observed pattern, but theoretical reasons exist for a reverse pattern, which is also frequently found (Gaston 1990).
These patterns have been mainly interpreted as a result of ecological processes. A plethora of hypotheses have been proposed to explain why most species are geographically, ecologically and numerically rare, why species abundance influence other forms of rarity (especially range size), and why body size should affect geographical, ecological or population rarity. Most researches have been conducted on vertebrates, especially birds and mammals (Cotgreave and Pagel 1997; Yu and Dobson 2000; Harcourt et al. 2005; Blackburn et al. 1998; but see Strona et al. 2012 for global fishes and Lomolino et al. 2010 for extensive reviews), whereas invertebrates, and in particular insects, have been less investigated (see Morse et al. 1988; Gaston 1990; Ulrich 2001 and Dennis et al. 2012 as examples). Thus, macroecological analyses on insects would be particularly useful to understanding how really ubiquitous are these patterns across taxa and to obtain further insights about the underlying mechanisms.
Although the role of phylogeny as a driving factor of macroecological patterns has recently came into focus (Harcourt et al. 2005), phylogenetic relationships are usually treated more as a ‘problem’ that should be controlled for (Felsenstein 1985; Strona et al. 2012) than a possible source of rarity in itself (Vane-Wrigth et al. 1991; Posadas et al. 2001). Thus, the role of phylogenetic history as a driver of rarity is largely unexplored, although Cotgreave and Pagel (1997) argued that rare species are typically found among lineages that split from basal nodes.
In this paper, we investigated the aforementioned three basic patterns, and their possible relationships with phylogeny, at a regional scale using the tenebrionid beetles (Coleoptera Tenebrionidae) from Latium (Central Italy). Latium is placed in the centre of the Mediterranean hot spot of biodiversity (Myers et al. 2000; Cox and Underwood 2011) and hosts about half of all tenebrionid species recorded in mainland Italy (S. Fattorini, unpublished data). Thanks to a long history of entomological research in Latium, we were able to assembly a very large set of data, which allowed us to investigate simultaneously three aspects of rarity (by range, ecology and population abundance). As far as we know, this is the first study of a regional scale analysis that integrates multiple rarity measures and phylogeny to elucidate macroecological patterns in an insect family.
Materials and methods
Data sources
We assembled a database including 3561 tenebrionid records from Latium. Here, the word ‘record’ refers to a unique combination of species, place, year and source, but may involve from one to several hundreds of specimens. In total, the database included data for 84 native species and 25 349 specimens directly examined, plus literature data for 1394 specimens. Data spanned from 1860 to 2011 and originated from museum and private collections (25 collections, herein simply referred as ‘museum’ collections), publications (334 scrutinized references, published from 1875 to 2010; list available from the corresponding author upon request) and unpublished species lists (see 5). The database included the following entries: species name, sample site, latitude, longitude, altitude, phytoclimatic unit, date, collector(s), number of specimens (for a few literature records for which this datum was not available, it was set to 1), museum collection and reference(s).
Sample sites were geo-referenced (latitude and longitude decimal degrees) with the maximum precision allowed by the original datum. Then, each point record was assigned to a 10 × 10 km grid cell using the UTM system.
When available from the label data of museum specimens or explicitly given in literature records, elevation data were included in the database as recorded by the collector (probably using a barometric altimeter or topographical maps). When elevation was not reported among label data or not given in literature records, it was retrieved by overlapping point records with topographical maps at the best available resolution.
Tenebrionids include certain cosmopolitan species, such as Alphitophagus bifasciatus, Gnathocerus cornutus, Latheticus oryzae, Tribolium castaneum, Tribolium confusum, Tenebrio molitor, Tenebrio obscurus and Alphitobius diaperinus, which are associated with stored food. Entomologists rarely collect these species because they are common pests. Therefore, they were not considered in the analysis.
Species rarity
To fulfil Hartley and Kunin's (2003) recommendations of considering different aspects of rarity, species rarity was assessed here using a multidimensional characterization that takes into account: (1) geographical distribution (wide/narrow distribution), (2) habitat specificity (broad/restricted habitat specificity) and (3) abundance (abundant/scarce population) (see Rabinowitz 1981). Such a multidimensional characterization of species rarity has been previously applied to bryophytes (Gabriel et al. 2011), vertebrates (e.g. Kattan 1992; Manne and Pimm 2001; Isaac et al. 2009) and arthropods (e.g. Fattorini 2008, 2010a,b, 2011; Fattorini et al. 2012).
Geographical rarity
As a measure of geographical rarity, we used the number of 10 × 10 km UTM cells occupied by a species, as commonly used in insect rarity studies (see, for example, papers presented in Reemer et al. 2003).
Ecological rarity
Ecological rarity was evaluated as ‘habitat specificity’ (Hughes et al. 2000) by assessing species distribution across the 15 main phytoclimatic units (PHY) occurring in Latium and defined on the basis of climatic indices and vegetational settings (Blasi 1994). The assumption is that the larger the number of phytoclimatic units occupied by a species, the wider the species ecological tolerance. As a related, alternative measure, we calculated for each species a Shannon H’ index (Devictor et al. 2010) using species abundances across phytoclimatic units (HPHY). Decreasing HPHY values indicate increasing habitat specificity of the species.
Because a number of environmental (notably climatic) parameters vary with altitude, we have also used measures of elevational range to express ecological rarity. For this, we have first divided the study area into 24 elevational belts of 100 m (0–100 m, 101–200 m, 201–300 m, etc.). Then, we have calculated for each species the number of occupied belts (ELE), assuming that a smaller elevational range reflects higher ecological specialization. As a related, alternative measure, we calculated for each species a Shannon H’ index using species abundances across the elevation belts (HELE). Finally, as a combined measure of species ecological specialization (HTOT), we summed (Hanski 1978) values of HPHY and HELE. Because the five measures PHY, HPHY, ELE, HELE and TOT were highly intercorrelated (Spearman rank correlation coefficients: 0.644 < rs < 0.944; p < 0.000001, n = 84), we decided to use only PHY, which is the simplest and most intuitive to interpret. Because PHY increases with decreasing habitat specificity – as intended here – we will refer it as ‘ecological tolerance’.
Species abundance
Number of specimens collected for each species was considered a measure of local rarity (ABU), assuming contactability as a proxy for population size (cf. Strayer 1999). To assess whether the number of collected specimens is a good measure of population size, we performed a correlation analysis with data obtained from pitfall traps. Pitfall traps are a widely used method to obtain standardized quantitative data for ground dwelling insects (Samways et al. 2010). From the database used in this paper, we could recover data from pitfall traps for 17 tenebrionid species. Then, we correlated abundance data obtained only from pitfall traps with total number of collected specimens excluding those obtained by pitfall traps (rs = 0.623, p = 0.008, n = 17; a correlation between data from only pitfall traps and total number of collected specimens, including those coming from pitfall traps, was obviously even stronger: rs = 0.922, p < 0.0001). Correlation between these two measures indicates that using total number of specimens is a good measure for population size, at least analogous to what can be obtained by standardized techniques.
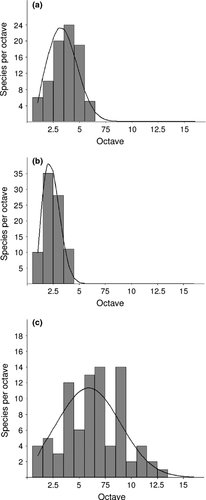
The frequency distribution of the three forms of rarity was contrasted with a log-normal distribution. Many studies found that frequency distribution of range size tends to follow a log-normal distribution (see, for example, Gaston 1990). The log-normal distribution seems also fit many species abundance distributions, although this issue is controversial (see Williamson and Gaston 2005; Hayek and Buzas 2010). We do not know previous studies that fitted frequency distribution of ecological rarity. To test whether frequency distributions of all the aforementioned rarity measures followed log-normal distributions, we used the software past (Hammer et al. 2001), which implements the algorithm reported in Krebs (1989). The octaves referred to power-of-2 abundance classes. Correlations between rarity forms were tested using Spearman rank correlation coefficients. Here, as in other analyses presented in this paper, probability levels might be affected by phylogenetic pseudo-replication, that is, inflation of sample size using taxa that are similar by common descent and yet are counted as data points. However, individual genera are considered to be relatively free of phylogenetic constraints for these sorts of analyses (Harvey and Pagel 1991). Because in our data set, most species were represented by only one genus, we think that this makes it negligible the impact of pseudo-replication on correlation analyses.
Body mass
There is a large amount of literature about the relationship between body mass and geographical range and species abundance (reviewed in Lomolino et al. 2010). We investigated these patterns using the macroecological approaches of Gotelli and Entsminger (2001). For this, body mass is plotted against species ranges, and the scatterplot is divided into lines that should represent evolutionary/ecological constraints. A first line divides the graph diagonally, thus creating two triangles. To assess whether one triangle is unusually ‘empty’ (or unusually ‘rich’), the observed frequency distribution is compared with that obtained by a null model through a series of simulations. Analogously, boundary lines are traced at the four corners of the scatterplot, and a null-model distribution is used to test whether a certain corner host fewer (or more) points than expected by chance. The null-model distribution can be also used to construct a simulated regression line, which can be then used to evaluate whether the observed regression coefficient is significantly higher (or lower) than expected. We used these approaches also to investigate the relationship between ecological tolerance and body mass, which seems a so far unexplored issue.
Because relationships of body mass with range, as well as with abundance and ecological tolerance, were adequately linearized by logarithmic transformations (see Lomolino et al. 2010), we always used log10-transformed data. Values of body mass were log (x + 1) transformed to avoid negative values.
The null hypothesis of no relationship between body mass and rarity measures (geographical range size, abundance or ecological tolerance) was assessed by boundary tests using variance as a dispersion index. Simulated random matrices were built by reshuffling 1000 times the observed values of each pair of variables analysed with a similar number of data points as in the original data set. The observed variance was then compared with the distribution of variances obtained from the simulated data sets. We used the right triangle for a general shape test and then tested separately each corner as defined by symmetric boundaries. These analyses were accomplished using the Macroecology module of the ecosim 7 software (Gotelli and Entsminger 2001) with the ‘data defined’ algorithm (Gotelli and Entsminger 2001).
Beetle biomass was estimated from linear measurements (Radtke and Williamson 2005; Ulrich 2007; Ulrich and Fiera 2010) using the equation M = 0.0197L3.408 (Fattorini 2009), where L is mean body length and M the mean weight (body mass). This equation was obtained from weight and length measures of many Mediterranean tenebrionids and had a very good fit (R2 = 0.912). Mean species weight of the species involved in this study was calculated using arithmetic mean L (mm) of available data on minimum and maximum body length. Minimum and maximum body length values were prevalently obtained from Aliquò et al. (2006) and a few other additional resources.
We also used mean body length to assess whether smaller species are under-represented in collections as a possible result of collectors’ bias towards larger species. For this, we calculated the number of sampled individuals for body length classes (<5 mm, 5–10 mm, 15–20 mm, etc.). We found that the smallest dimensional class (<5 mm) was the most abundant, which indicates that small species are not under-sampled (see Fig. S1).
Phylogenetic rarity
We used two phylogenetic indices to express taxon phylogenetic ‘position’ based on taxon relationships (Vane-Wrigth et al. 1991; Posadas et al. 2001). There is no comprehensive and universally accepted phylogeny of Tenebrionidae. Thus, we have constructed a supertree combining cladistic results for different tenebrionid lineages presented in Doyen and Tschinkel (1982: for the overall topology, resolved for most tenebrionid lineages), Doyen (1993: for tribes within the subfamily Pimeliinae) and Fattorini (2002: for re-allocation of certain pimeliine tribes). This allowed the reconstruction of a general, fully resolved cladogram for all tenebrionid tribes involved in the present study (Fig. S2). Alphitobini and Triboliini were aggregated with Ulomini because current cladistic reconstruction seems to not support a status of independent tribes (Doyen and Tschinkel 1982). Current information also indicates that the tribes used in tenebrionid taxonomy are monophyletic units. For example, the evolutionary lineages found by Doyen and Tschinkel (1982) and Doyen (1993) largely fit traditional tribes. Also, morphological analyses of the mouthparts of Pimeliinae based on comparison of several genera within major tribes revealed that there is minimal variation among genera belonging to the same tribe, whereas between-tribe differences are very strong (S. Fattorini and A. Di Giulio, unpublished data). Thus, tribes appear a suitable systematic level for our analyses.
Because we did not have within-tribe phylogenies, all species belonging to the same tribe received the same phylogenetic score. To measure the amount of information contained in cladograms based on values of taxonomic distinctiveness between taxa, we used the index I, which assigns equal values to sister taxa. To calculate I, a value of 1 is assigned to each terminal taxon that belongs to a pair of terminal sister taxa. The taxon that constitutes the sister group of this pair receives a value of 2 (equal to the sum of its sister group), and so on for each taxon in the cladogram. I scores increase with the basal position of the node from which the taxon arose, whereas taxa at the end of intense bifurcation processes receive low scores. According to Posadas et al. (2001), this index tends to produce results affected by the overweighting of lineages that split from more basal nodes. Thus, as a second measure, we used the index W, which is calculated as the number of phylogenetically informative statements that can be made for each taxon. First, an index i is used to express the number of phylogenetic steps involved in the diversification pattern of each taxon. This index is calculated as the number of groups (nodes) to which each taxon belongs. Then, the basic phylogenetic weight Q is calculated for each terminal taxon as Qj = Σi/ij, where j is each specified taxon (tribe). Individual Q values reflect the proportion of the total diversity of the group contributed by each taxon. W scores are obtained for each Q value as W = Qj/Qmin. In spite of the fact that W index gives the highest values to lineages that split from the most basal nodes, it does not overweight these taxa (Posadas et al. 2001). Lower values indicate higher cladistic ‘isolation’, whereas species at the end of an intense process of diversification will receive higher scores. Although these indices express ‘cladistic’ relationships, we will refer to them as indices of phylogenetic rarity for simplicity.
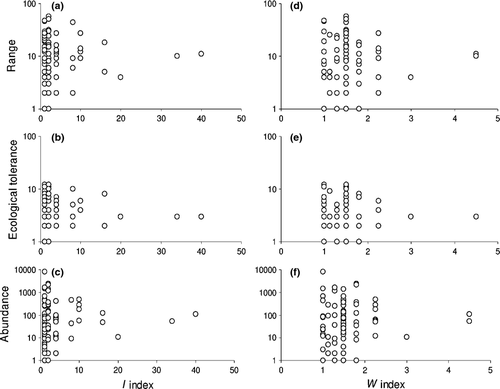
Most tribes were represented by more than one species in the study area. This allowed us to calculate, for each tribe, mean values (and standard deviations with respect to the overall means) of species geographical range, ecological tolerance and abundance. Mean values were considered a measure of tribal average rarity for each rarity dimension, whereas standard deviations were used as a measure of variability of rarity scores. Then, we correlated values of phylogenetic scores (as expressed by the two indices I and W described above) of each tribe with mean and standard deviations of geographical range, ecological tolerance and abundance.
In addition, we calculated, for each rarity dimension, the number of rare species for each phylogenetic score. For this, we calculated for each dimension the median values of species’ scores and considered as rare for a given dimension those species that had scores below the median value (see Kattan 1992). Then, for each rarity measure, we calculated correlations between the percentage of rare species for a certain phylogenetic score and the phylogenetic score, to test whether the percentage of rare species increased or decreased with phylogenetic scores. Because of the low number of data points in these analyses, we always used Spearman non-parametric correlation tests, with alpha set at 0.05. Analyses were conducted using statistica 6.0 (StatSoft, Tulsa, OK, USA). Values of range size (no. of UTM cells), ecological tolerance (no. of phytoclimatic units), abundance (no. of individuals), body mass, I index and W index are given in Table S1.
Results
Frequency distribution of species ranges were close to a log-normal distribution (Fig. 1a, χ2 = 3.883; p = 0.4221). Similarly, we found that values of ecological rarity (tolerance) followed a log-normal distribution (Fig. 1b, χ2 = 0.4916; p = 0.7821). By contrast, species abundance distribution deviated significantly from the log-normal curve (Fig. 1c, χ2 = 0.8271; p = 0.03267).
Species abundance was strictly correlated with geographical range (rs = 0.830, p < 0.0001) and rather strongly with ecological tolerance (rs = 0.620, p < 0.0001). A strong correlation was also found between geographical range and ecological tolerance (rs = 0.874, p < 0.0001).
Although the relationship between range size and body mass was week (y = 0.5816x + 0.8692, R2 = 0.1065; Fig. 2a), the regression slope was significantly greater than the simulated slope of 0.0008 (p = 0.010). The observed variance was 30.75, whereas the average of variance of the 1000 simulated data sets was only 7.170. The tail probability for observed variance is 0.037. These results suggest that the points are not randomly distributed in the two-dimensional space: some corners have too many points and others have too few than expected from a random distribution. A ‘shape number of points’ analysis indicates that 45 data points fell within the left triangle shape. This does not differ significantly from the average of the simulated values (51.04; p = 0.993). By contrast, 60 points fell in the right triangle, compared with an average of only 54.30 points for the simulated data sets (p = 0.014). This indicates that data points were unusually concentrated in this triangle. The boundary number of points and the boundary sum of squares tests indicate that the upper right-hand corner of the space is not unusually empty, although there are only six observations in that region of the space (number of points p = 0.960; sum of squares p = 0.618). This is an expected result, because there are few species with large geographical range and few species with large body mass. Similarly, in the upper left-hand corner, there were not fewer species than expected by chance even though only one specie fell in this space (number of points p = 0.093; sum of squares p = 0.570). By contrast, the lower right-hand corner contained only eight species (instead of 13.36 expected by chance) and resulted significantly ‘empty’ (number of points p = 0.015; sum of squares p < 0.0001). Finally, the lower left-hand corner had more species (19) than expected (11.79; number of points p = 0.001; but sum of squares p = 0.414). Thus, the observed points tend to be concentrated near the origin.
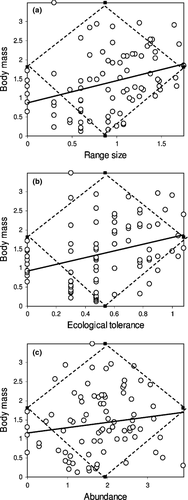
The relationship between ecological tolerance and body mass was week (y = 0.884x + 0.9216, R2 = 0.105; Fig. 2b), yet the regression slope was significantly greater than the simulated slope of 0.0001 (p = 0.001). The observed variance was 54.75, whereas the average of variance of the 1000 simulated data sets was only 19.81. The tail probability for observed variance was 0.004. These results suggest that the points are not randomly distributed in the two-dimensional space. The ‘shape number of points’ analysis indicates that 45 data points fell within the left triangle shape. This was significantly lower than the average of the simulated values (52.208; p = 0.002). By contrast, 59 points fell in the right triangle, compared with an average of 51.93 points for the simulated data sets (p = 0.002). Thus, there is a concentration of points in this triangle. The boundary number of points and the boundary sum of squares tests indicate that numbers of species points in both upper corners were not significantly different from those predicted by the null model (results not shown). The lower right-hand corner had less species (7) than expected (12.40; number of points p = 0.01; sum of squares p < 0.0001). By contrast, the lower left-hand corner had more species (24) than expected by chance (12.61; number of points p < 0.00001; but sum of squares p = 0.567). Thus, there is a tendency of points to concentrate near the origin.
Finally, the relationship between abundance and body mass was positive (y = 0.1387x + 1.151, R2 = 0.0225; Fig. 2c), but the regression slope was not significantly greater than the simulated slope of 0.00 (p = 0.080). The observed variance was 19.08, whereas the average of variance of the 1000 simulated data sets was only 7.247. The tail probability for observed variance was 0.123. These results suggest that the points are randomly distributed in the two-dimensional space. Fifty-four data points fell within the left triangle shape. This does not differ significantly from the average of the simulated values (58.145; p = 0.967). Similarly, 46 points fell in the right triangle, compared with an average of 48.99 points for the simulated data sets (p = 0.151). The boundary number of points and the boundary sum of squares tests indicate that numbers of species points were not significantly different from those predicted by the null model in all corners (results not shown), except the lower left-hand corner, which had more species (21) than expected (13.58; number of points p = 0.002; but sum of squares p = 0.429). Thus, the overall pattern is quite random, with a slight tendency of points to concentrate near the origin.
Inspection of scatterplots of rarity values against phylogenetic scores (Fig. 3) suggests that, for all rarity measures, point dispersal tends to decrease at increasing phylogenetic scores. However, it can be also realized that the number of species highly decreases at increasing phylogenetic scores. So, variation in point dispersal might appear decreasing only by chance. Moreover, there is a conspicuous tendency of rarity values of species with high phylogenetic scores to be nearer to the means of all the species. To further investigate this pattern, we calculated mean and standard deviations of each rarity measure for each tribe and correlated these values with tribe phylogenetic scores. We found significant negative correlation between the index I and standard deviations of all three rarity measures (population: rs = −0.932, p = 0.0002; geography: rs = −0.831, p = 0.0056; ecology: rs = −0.746, p = 0.0210). Similar results were obtained with W (population: rs = −0.667, p = 0.071; geography: rs = −0.881, p = 0.0039; ecology: rs = −0.802, p = 0.0165). No significant correlation was obtained for mean values (results not shown). Similarly, no significant correlation was found between number of rare species in each rarity dimension and phylogenetic scores (results not shown).
Discussion
In many animal groups, the frequency distribution pattern of range size is highly right skewed, with most species having small ranges and relatively few having large ones (Jones et al. 2002; Gaston 2003; Lomolino et al. 2010; Strona et al. 2012). However, which mathematical function best describes this general pattern is unclear and, most probably, different organisms have different frequency distributions (Gaston 1990). In some instances, a lognormal distribution has been shown to provide a good fit (e.g. Rapoport 1982; Anderson 1984), and our study also indicates that the frequency distribution of range sizes (measured as no. of 10 km squares occupied) of tenebrionid beetles at regional scale is close to a log-normal distribution. We also found that ecological tolerance followed a log-normal distribution. In community ecology, a log-normal distribution of species abundances is expected when a number of unrelated factors govern the way species accumulate (May 1975). The same might be true in a macroecological perspective, with range size and ecological tolerance following a log-normal distribution when the studied species are an assemblage of multiple communities. However, we found that tenebrionid abundances did not follow a log-normal distribution. This might be a reflection of the composite nature of our data set, which includes an entire regional fauna and hence multiple communities, possibly with different species abundance distributions. Another possible explanation is that common species might be under-represented in collections if collectors tend to collect more likely uncommon species. However, this is unlikely because tenebrionids are not considered particularly attractive by collectors and are largely collected as by-product of generalized collecting activities performed by entomologists mostly interested in other groups.
Brown (1984) suggested that a positive correlation between distribution and abundance may be a reflection of interspecific differences in ecological specialization. According to Hanski et al. (1993), the underlying mechanism is that species able to exploit a wide range of resources become both widespread and locally abundant, whereas ecological specialists have both a restricted distribution and a low abundance (see also Gaston and Lawton 1990). We found that ecological tolerance correlated positively with both species abundance and geographical range, thus supporting this interpretation.
We found that larger species tend to have, on average, larger ranges and broader ecological tolerance. A positive correlation between body size and range size has been previously observed at large scale for several animal taxa (Gaston and Blackburn 1996). However, contrary to previous findings (Gaston and Blackburn 1996; Jones et al. 2002), the spatial relationship between log(range size) and log(body size) found in tenebrionids is not strictly triangular, because not only small-sized, but also many medium-to-large-sized species exhibit great variability in their range size (see Fig. 2a). The triangular relationship found in many organisms (see Lomolino et al. 2010 for a review) has been interpreted as a result of three constraints: (1) species cannot be smaller than a certain values; (2) species cannot exceed the overall available area; and (3) species with larger body size tend to be rarer and hence the lower right corner of the graph will contain less points. The presence of a number of species in the upper right corner not smaller than expected by a random distribution suggests that tenebionids do not conform to the general rule. A possible explanation lies in the fact that most tenebrionids are small insects and even the most widely distributed ones occupy only a small fraction of total available area, which makes constraints less effective in conditioning the triangular pattern. It is also difficult to explain why larger species tend to occupy larger areas. Several explanations have been proposed for this patterns, most of which based on the assumption that larger species have larger home ranges (see Gaston 1990), which may holds for many vertebrates, but not for tenebrionids. Species that can maintain peak rates of population increase over larger area are likely to have larger geographical populations. The greater vulnerability of smaller species to density-independent perturbations might reduce the area over which they are able to maintain such rates and thus increase their likelihood of having smaller ranges (Gaston 1990). This hypothesis may be appropriate for tenebrionids and is at least in part corroborated by the positive correlation of body size with the number of exploited habitats. In general, we can assume that if larger species have a broader ecological tolerance, they increase their probability of surviving to density-independent perturbations. This is supported by the fact that although most species have small body size and low ecological tolerance, species with large body size and broad ecological tolerance are also common (upper left triangle in Fig. 2b).
In contrast to many researches reporting a negative correlation between body size and abundance (e.g. Cotgreave 1993; Gaston 1994; Blackburn and Gaston 1997, 1999), tenebrionid body size seems to not influence species abundances. In fact, a strong association between body size and many aspects of the biology of the species, including population abundance, has been reported especially for mammals and birds (e.g. Calder 1983a,b; Peters 1983; Schmidt-Nielsen 1984; Harcourt et al. 2005) and can be associated with competition. Competition among closely related species may drive differences in body size, because if closely related sympatric species diverge in their body size, this reduces competition. For example, related, sympatric vertebrates often differ in body size by a factor of about 1.3, producing a graded size series among related species (Eadie et al. 1987; Lewin 1987). Moreover, if a key resource, like food, is very limited, larger species, which require more food, will have small populations. This cannot be valid for insects, such as tenebrionids, that feed on detritus, usually an abundant resource. Because food is abundant and competition is low, several similar-sized species can coexist in a single community, and sometimes in very high numbers.
According to Cotgreave and Pagel (1997), rare species should be mainly found among lineages that split from basal nodes. In general, we found that rarity of a tenebrionid species was not influenced by the phylogenetic position of its tribe. However, we found that lineages with higher phylogenetic scores (i.e. which split from the most basal nodes of the cladogram) tend to have lower variability in terms of species geographical distribution, ecological tolerance and abundance and to show values nearer to the means of all the species. In other words, our data suggest a trend towards an increase in within-tribe variability for species range, ecological tolerance and abundance for tribes that are in a more derived position within the cladistic reconstruction. This suggests that lineages that split from basal nodes are not only conservative for morphological characteristics (like those evaluated in the cladistic analyses used to construct the tenebrionid cladogram used here), but tend to have also an ecological ‘inertia’, whereas derivative lineages tend to produce species which are morphological similar, but ecologically more varied.
We are aware of the many limits of our study, involving (1) the cladistic reconstruction, (2) the measures of body size, (3) the use of museum data to estimate rarity measures and (4) the low number of species with high phylogenetic scores, which makes it difficult to establish how the reduced variability observed at higher phylogenetic scores is a reflection of chance. However, we feel that our analytical approach was rather robust. Although the cladistic reconstruction was obviously incomplete (and inclusion of other tribes would change the topology, thus affecting phylogenetic scores), we used rank-based analyses, and we believe that it is improbable that the addiction of further terminal taxa would change the overall ranking from very basal to most derived tribes. Measures of body size were derived from body length. Although this is an indirect way, it is considered a safe procedure and again the use of non-parametric analyses should minimize the influence of slightly incorrect measures. Finally, the data used in this study were obtained from non-standardized methods. However, the very large sampling effort made through more than a century by hundreds of collectors interested in different insect groups and who used any kind of collecting method (hand searching, pitfall traps, aerial traps, soil examination, etc.) ensure that these data collectively form a ‘random’ sampling, not affected by biases due to collector preferences for certain biotopes, sites or species. Therefore, we feel that our results depict a true state of affairs, but further research is needed to assess how generalized they are among taxonomic groups and regions.
Acknowledgements
We thank all amateur entomologists who allowed us to examine their personal collections: R. Antonelli, A. Cotta's heirs, E. Migliaccio, P. Maltzeff, R. Pace, U. Pessolano and G. Di Giulio. P. Leo kindly provided us with unpublished data. We are also grateful to A. Vigna Taglianti (Sapienza University of Roma), C. Manicastri (Zoological Museum of Rome) and G. Carpaneto (Roma Tre University) for allowing us to examine the collections in their care. Full details about collections are available from the authors upon request. R. Lo Monaco helped us to collect body length measures. We are grateful to two anonymous referees for their comments on a previous version of this paper.




