We study a two-stage contest between two players who differ in ability, with a prize awarded in the second stage. In the first stage, players compete, and the winner enjoys a reduced effort cost in the second stage. The second-stage contest is simultaneous, while the first-stage contest can be simultaneous or sequential. We investigate how a sequential first stage affects the catching-up and discouragement effects between players. Additionally, we explore the optimal first-stage timing structure of contest designers with different objectives, that is, maximizing effort in the second stage, total effort across both stages, or the winner's total effort. Interestingly, a designer focused on maximizing second-stage effort prefers a simultaneous first-stage contest, contrary to the conventional intuition that the stronger player should lead.

1 Introduction

There are plenty of situations in which individuals or groups of individuals compete with each other, exerting costly efforts to win a prize. These efforts might include monetary expenditures or time spent, while the prize awarded might include monopoly rents, sports awards, or even fame. Beginning from the seminal works of Krueger (1974) and Tullock (1980), who studied rent-seeking, these competitions have been widely studied by economists, spawning the contest theory literature.1

While most of the early research focuses on single-stage contests (Hillman and Riley 1989; Baye et al. 1993), there are cases in which contests take place in more than one stage. In these contests, the efforts submitted in the first stage affect the efforts and, therefore, the outcomes of the subsequent stages. Harris and Vickers (1987) were the first to study a multi-stage race, in which the player who makes a specific number of advances is the winner of the game. Konrad and Kovenock (2009) extends this study by adding intermediate prizes awarded to the winner of each round.2

This paper examines a two-stage contest with two players competing to win a single, non-divisible prize. The two players are ex ante asymmetric, meaning that one of them has an ex ante effort cost advantage. In the first stage, there is no award, but the two players compete to gain an advantage in the second stage. At the beginning of the second stage, the first-stage winner and loser have been determined, and the former obtains an advantage expressed as an effort cost lower than that of her opponent. Then, with the second-stage effort costs allocated according to the outcome of the first stage, the two players compete again to win the final prize.

An environment in which a two-stage contest with a win advantage can be applied is an election-lobbying game. Consider a pre-election period with two lobbies, each supporting a different candidate. To help its favorite candidate win the election, each lobby exerts effort, for example, campaign contributions, endorsements, and media campaigns, to persuade the constituency to vote for this candidate. Once the election winner takes office, the lobby that supported her earlier—probably being politically aligned with her—will typically be more efficient in influencing policy than the lobby that supported the opponent.3 Similar win advantages appear in procurement contests, where firms first invest in research activities before submitting final bids. The firm making a greater initial investment may gain a cost advantage when developing the final proposal. Likewise, in sports tournaments with multiple matches between the same opponents, winning an early game often provides psychological momentum or tactical insights for subsequent matches.

While previous work has analyzed similar settings with simultaneous moves in the first stage (Clark et al. 2012), our paper contributes by investigating how a sequential timing of first-stage efforts might change the strategic dynamics. A sequential contest arises when one of the two players observes the opponent's level of effort before making her own.4 What distinguishes this study from the existing ones is that we do not examine a sequential contest independently but embody it in the first stage of a two-stage contest.

The sequential timing aspect is particularly relevant in the contexts mentioned above. In lobbying, an interest group might begin its campaign early, allowing other groups to observe and respond accordingly. In procurement, firms often strategically announce preliminary investments through press releases, and then the competitors react to these commitments. Lastly, in sports, coaches frequently implement early strategies that force opponents to react by adjusting their game plans.

We demonstrate that different first-stage move orders by the two players might significantly impact the players' strategies, leading to some interesting results regarding optimal contest design. When the strong player acts as a leader in the first stage, the discouragement effect is amplified compared to a simultaneous first stage, reducing the weak player's effort in both stages. Conversely, when the weak player acts as a leader in the first stage, the catching-up effect is enhanced, increasing the weak player's effort. These timing effects create different competitive dynamics that carry over to the second stage, affecting the players' effort levels and participation decisions.

Next, we consider a contest designer with three possible objectives: maximizing second-stage effort, total effort, or the winner's expected effort. In the first case, consider a lobbying contest where interest groups may compete through multiple rounds of influence activities. A contest designer representing the politician being lobbied might be mainly concerned with maximizing the quality of policy proposals in the final round, rather than preliminary positioning efforts. In the second case, consider an organizer of a series of sports events. Such an organizer might want the highest possible effort from all the players in all the games. Finally, in the last case, consider a procurement contest where the contracting agency might care most about the quality of the winning proposal, which will be implemented (Serena 2017a).

Our analysis reveals several interesting findings. A contest designer focusing on the second-stage effort strictly prefers a simultaneous first-stage contest. Similarly, a contest designer who maximizes either total or the winner's effort might prefer a simultaneous first-stage contest under specific conditions. These results challenge the intuition that sequential contests with the strong player leading would generally generate more competitive effort.

While Clark et al. (2012) also examine dynamic contests with a win advantage, the primary contribution of this study is the analysis of sequential timing in the first stage and how the sequence of first-stage moves might affect strategic behavior. The introduction of sequential timing provides new insights into how the catching-up effect and discouragement effect operate in dynamic contests. By allowing for different move orders, we can analyze how being a leader or follower interacts with ex ante asymmetry to generate some results not observed in a simultaneous setting.

This paper is also related to Clark and Nilssen (2013), which examines learning by doing in a dynamic contest.5 However, one of the assumptions in that study is that the greater the effort exerted by a player in the first stage, the lower her effort cost in the second stage. In our model, a player must win in the first stage to enjoy a lower effort cost in the second stage, regardless of her exerted effort. Another study close to ours is Beviá and Corchón (2013), which also considers a two-period contest in which the second-stage asymmetry between the players depends on the outcome of the first stage. However, in that study, each player's ability in the second period depends on the share of the prize earned in the first period.

The remainder of the paper is organized as follows. In Section 2, we present an overview of the model. Section 3 includes the analysis of the first-stage and second-stage contests. In Section 4, we discuss the contest designer's optimal first-stage timing of efforts. Finally, Section 5 concludes the paper. The proofs are relegated to Appendix A.

2 Overview of the Model

Consider a two-stage contest with two players competing for a prize, normalized to 1, awarded in the second stage. In the first stage, both players exert effort to gain an advantage in the second stage. Their cost functions are linear, but one of the two players, Player 1, has a lower effort cost than her opponent. We will sometimes refer to this player as the strong player and her opponent, Player 2, as the weak player. Submitting efforts ${x}_{1}$ and ${x}_{2}$ , respectively, Player 1's cost function is then ${c}_{1}({x}_{1})=a{x}_{1}$ , where $0\lt a\le 1$ , and Player 2's cost function is ${c}_{2}({x}_{2})={x}_{2}$ . We observe that Player 1's advantage is captured by her lower effort cost, $a\le 1$ .6

At the beginning of the second stage, the winner of the first stage has been determined. Now, player $i$ exerts effort ${y}_{i,w}$ if she has won in the first stage and ${y}_{i,l}$ if not. Player $i$ 's cost is $c\lt 1$ if she has won in the first stage and is equal to 1 if not. Thus, we could say that the award the two players compete for in the first stage is a lower effort cost in the second stage.

Using the lottery contest success function proposed by Tullock (1980) and axiomatized by Skaperdas (1996) and Clark and Riis (1998), we assume that each player's probability of winning at either stage is equal to the ratio of this player's effort to the sum of efforts. Thus, generally, when player

i

makes effort

{e}_{i},i=1,2

, her probability of winning is

{q}_{i}({e}_{1},{e}_{2})=\left\{\begin{array}{ll}\displaystyle \frac{{e}_{i}}{{e}_{1}+{e}_{2}}, & \,\text{if}\,\,\max \{{e}_{1},{e}_{2}\}\gt 0\\ \displaystyle \frac{1}{2}, & \,\text{otherwise}\,.\end{array}\right.

3 Equilibrium Analysis

In this section, we use backward induction to determine the subgame perfect Nash equilibrium of the game. Thus, we start analyzing the second stage and proceed with the first one.

3.1 Second Stage

The winner and loser of the first stage, Player

w

and Player

l

, respectively, have already been determined in the second stage.7 If Player

i

won in the first stage, her payoff function is

{\pi }_{i,w}={p}_{i,w}-ac{y}_{i,w},\begin{array}{ll}a\lt 1 & \,\text{if}\,\,i=1,\\ a=1 & \,\text{if}\,\,i=2\end{array}

where

{y}_{i,w}

and

{y}_{j,l}

are player

i

(winner) and

j

's (loser) efforts, respectively;

{p}_{i,w}=\frac{{y}_{i,w}}{{y}_{i,w}+{y}_{j,l}}

is the probability that player

i

wins the prize, i.e., her effort over the sum of efforts, and the parameter

a

represents Player 1's ex ante advantage carried over to the second stage. If Player

i

lost in the first stage, her payoff function is

{\pi }_{i,l}={p}_{i,l}-a{y}_{i,l},\begin{array}{ll}a\lt 1 & \,\text{if}\,\,i=1,\\ a=1 & \,\text{if}\,\,i=2\end{array}

where

{p}_{i,l}=\frac{{y}_{i,l}}{{y}_{i,l}+{y}_{j,w}}

In equilibrium, Player 1 chooses effort ${y}_{1,w}^{* }=\frac{1}{{(ac+1)}^{2}}$ or ${y}_{1,l}^{* }=\frac{c}{{(c+a)}^{2}}$ and Player 2 chooses effort ${y}_{2,w}^{* }=\frac{a}{{(c+a)}^{2}}$ or ${y}_{2,l}^{* }=\frac{ac}{{(ac+1)}^{2}}$ . The second-stage equilibrium payoffs are ${\pi }_{1,w}^{* }=\frac{1}{{(ac+1)}^{2}}$ or ${\pi }_{1,l}^{* }=\frac{{c}^{2}}{{(c+a)}^{2}}$ for Player 1 and ${\pi }_{2,w}^{* }=\frac{{a}^{2}}{{(c+a)}^{2}}$ or ${\pi }_{2,l}^{* }=\frac{{a}^{2}{c}^{2}}{{(ac+1)}^{2}}$ for Player 2.

3.2 First Stage

In the first stage, there are three possible cases: (i) players move simultaneously, (ii) Player 1 is the leader and Player 2 the follower, and (iii) Player 2 is the leader and Player 1 the follower. We discuss each case separately.

3.2.1 Simultaneous Contest

Let us begin with the case of a simultaneous first-stage contest. Each player chooses her effort,

{x}_{i},i=1,2

, without knowing her opponent's choice. Recall that Player 1 has an ex ante advantage captured by her lower effort cost,

a\in (0,1]

, while Player 2's effort cost equals 1. Player

i

's expected payoff is the sum of the probability of winning in the first stage and, therefore, earning payoff

{\pi }_{i,w}

in the second stage, plus the probability of losing in the first stage and, therefore, earning payoff

{\pi }_{i,l}

in the second stage, minus the first-stage expenditure.8 Thus, player

i

's expected payoff can be expressed as

{\mathbb{E}}[{\pi }_{i}]=\frac{{x}_{i}}{{x}_{1}+{x}_{2}}{\pi }_{i,w}^{* }+\left(1-\frac{{x}_{i}}{{x}_{1}+{x}_{2}}\right){\pi }_{i,l}^{* }-a{x}_{i},\begin{array}{ll}a\lt 1 & \,\text{if}\,\,i=1,\\ a=1 & \,\text{if}\,\,i=2.\end{array}

(1)

The two players choose the level of effort that maximizes their expected payoffs. Maximization of Equation (1) provides the equilibrium first-stage efforts. The corresponding equilibrium expected payoffs are included in Appendix C.

Lemma 1.When Players 1 and 2 move simultaneously in the first stage, the equilibrium efforts are

\begin{array}{rcl}{x}_{1,S}^{* } & = & \displaystyle \frac{{a}^{2}(1-{c}^{2})({c}^{2}+2ac+1){[c(2+ac)+a]}^{2}}{{(1+a)}^{2}{(c+a)}^{2}{(ac+1)}^{2}{\{c[ac-2(1-a)a+2]+a\}}^{2}},\\ {x}_{2,S}^{* } & = & \displaystyle \frac{{a}^{4}(1-{c}^{2}){({c}^{2}+2ac+1)}^{2}[c(2+ac)+a]}{{(1+a)}^{2}{(c+a)}^{2}{(ac+1)}^{2}{\{c[ac-2(1-a)a+2]+a\}}^{2}}.\end{array}

Comparative statics analysis shows that $\frac{\partial {x}_{1,S}^{* }}{\partial c}\lt 0$ and $\frac{\partial {x}_{2,S}^{* }}{\partial c}\lt 0$ , implying that as the second-stage advantage increases, the players become less motivated to win in the first stage and, therefore, have the incentive to decrease their first-stage efforts. Now, as $a$ varies, we find that $\frac{\partial {x}_{2,S}^{* }}{\partial a}\gt 0$ , which means that Player 2 reduces her first-stage effort as her opponent's ex ante advantage increases. Regarding Player 1, her response to an increase in $a$ is ambiguous. Particularly, $\frac{\partial {x}_{1,S}^{* }}{\partial a}\lt 0$ if $a$ is sufficiently high or if both $a$ and $c$ are sufficiently low. Intuitively, if Player 1 is sufficiently strong and the second-stage advantage at stake is substantial, she decreases her effort the weaker she becomes. Nevertheless, $\frac{\partial {x}_{1,S}^{* }}{\partial a}\gt 0$ for low $a$ and high $c$ , implying that if Player 1's ex ante advantage is sufficiently high and the second-stage advantage low, she may decrease her first-stage effort the stronger she becomes as a response to the reduced effort by her opponent.

The results of the simultaneous first-stage contest demonstrate the tension between the discouragement and catching-up effect identified by Clark et al. (2012). The discouragement effect is observed in $\frac{\partial {x}_{2,S}^{* }}{\partial a}\gt 0$ , where we notice that the weak player reduces effort as the strong player's advantage increases, i.e., as $a$ becomes lower. At the same time, the catching-up effect appears through the weak player's incentive to win the first stage and secure a lower cost for the second stage, partially offsetting her ex ante disadvantage. This is evident in how both players respond to changes in the second-stage advantage.Particularly, $\frac{\partial {x}_{1,S}^{* }}{\partial c}\lt 0$ and $\frac{\partial {x}_{2,S}^{* }}{\partial c}\lt 0$ indicate that both players increase their first-stage effort as the second-stage advantage becomes greater, i.e., as $c$ becomes lower. The weak player sees the potential to “catch up” through winning the first stage, while the strong player aims to maintain her advantageous position. This simultaneous case serves as the benchmark against which we will examine how sequential timing in the first stage amplifies or moderates these effects. As we will see in the following sections, the balance between discouragement and catching-up changes significantly when players move sequentially instead of simultaneously.

3.2.2 Player 1 [2] Acts as a Leader [Follower]

In the first case of a sequential first-stage contest, we assume that Player 1 acts as a leader in the first stage, and Player 2 makes her move after having observed that effort. Thus, Player 2's optimization problem is given by Equation (1) for

i=2

. Regarding Player 1, when she has to decide how much effort to exert, she considers Player 2's reaction function. Thus, her optimization problem is

\mathop{\max }\limits_{{x}_{1}\ge 0}\left\{\frac{{x}_{1}}{{x}_{1}+{x}_{2}^{* }({x}_{1})}{\pi }_{1,w}^{* }+\frac{{x}_{2}^{* }({x}_{1})}{{x}_{1}+{x}_{2}^{* }({x}_{1})}{\pi }_{1,l}^{* }-a{x}_{1}\right\}.

(2)

Maximization of Equation (2) provides the result in Lemma 2.

Lemma 2.When in the first stage Player 1 [2] acts as a leader [follower], the equilibrium efforts are

({x}_{1,12},{x}_{2,12})=\left\{\begin{array}{cc}\left({x}_{1,12}^{* },{x}_{2,12}^{* }\right)\, & \,\text{if}\,\,\left(\frac{1}{2}\lt a\le \frac{\sqrt{2}}{2}\,\,\text{and}\,\,c\lt {c}^{^{\prime} }\right)\,\,\text{or}\,\,\left(a\gt \frac{\sqrt{2}}{2},\forall c\right)\\ \left({x}_{1,12}^{* * },0\right)\, & \,\text{if}\,\,a\le \frac{1}{2},\forall c\end{array},\right.

where

\begin{array}{rcl}{x}_{1,12}^{* } & = & \displaystyle \frac{(1-{c}^{2}){(a{c}^{2}+a+2c)}^{2}}{4{a}^{2}{(c+a)}^{2}{(ac+1)}^{2}({c}^{2}+2ac+1)},\\ {x}_{2,12}^{* } & = & \displaystyle \frac{(1-{c}^{2})(a{c}^{2}+a+2c)\left[2-\displaystyle \frac{a{c}^{2}+a+2c}{{a}^{2}({c}^{2}+2ac+1)}\right]}{4{(c+a)}^{2}{(ac+1)}^{2}},\\ {x}_{1,12}^{* * } & = & \displaystyle \frac{{a}^{2}(1-{c}^{2})({c}^{2}+2ac+1)}{{[a{c}^{2}+({a}^{2}+1)c+a]}^{2}},\\ {c}^{^{\prime} } & = & \displaystyle \frac{1-2{a}^{3}-\sqrt{1-{a}^{2}[4{a}^{2}(1-{a}^{2})+1]}}{a(2a-1)}.\end{array}

The comparative static results indicate that $\frac{\partial {x}_{2,12}^{* }}{\partial c}\lt 0$ and $\frac{\partial {x}_{2,12}^{* }}{\partial a}\gt 0$ , implying a straightforward behavior by Player 2. As the second-stage advantage increases, Player 2 intensifies her effort in the first stage. In contrast, as her opponent's ex ante advantage becomes stronger in the first stage, Player 2 moderates her effort. Regarding Player 1, her behavior while the advantages vary is more complicated. Specifically, the sign of $\frac{\partial {x}_{1,12}^{* }}{\partial c}$ depends on the level of $a$ . Figure 1 illustrates Player 1's first-stage effort as a function of the second-stage advantage for different levels of $a$ . We observe that for moderate levels of ex ante asymmetry, Player 1's first-stage effort is increasing in $c$ for a high second-stage advantage (low $c$ ) and decreasing in $c$ for a lower second-stage advantage (high $c$ ). On the other hand, for lower levels of ex ante asymmetry, i.e., a greater $a$ , Player 1's first-stage effort decreases in the second-stage advantage. Regarding Player 1's behavior as her ex ante advantage varies, it can be shown that $\frac{\partial {x}_{1,12}^{* }}{\partial a}\lt 0$ and $\frac{\partial {x}_{1,12}^{* * }}{\partial a}\gt 0$ . If Player 1's ex ante advantage is sufficiently low, she increases her effort as her advantage goes up. However, if her advantage is already significant, as this advantage decreases, the greater the effort she has to exert to induce her opponent not to participate in the contest.9

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Player 1's (leader) first-stage effort for (a) $a\in \left(\frac{1}{2},\frac{\sqrt{2}}{2}\right]$ and (b) $a\in \left(\frac{\sqrt{2}}{2},1\right]$ .

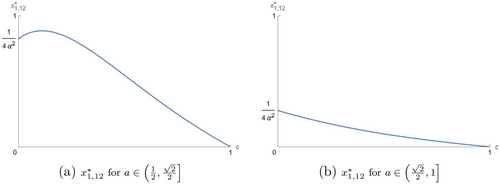
3.2.3 Player 2 [1] Acts as a Leader [Follower]

In the second possible sequential contest, Player 2 moves first, and Player 1 follows after observing Player 2's effort. Following a similar process, we find the two players' equilibrium efforts, which we summarize in the following.

Lemma 3.When Player 2 [1] acts as a leader [follower] in the first stage, the equilibrium efforts are

{x}_{2,21}^{* }=\frac{{a}^{4}(1-{c}^{2}){({c}^{2}+2ac+1)}^{2}}{4{(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+2c+a)}

and

{x}_{1,21}^{* }=\frac{{a}^{2}(1-{c}^{2})({c}^{2}+2ac+1)[(2-a)a{c}^{2}+2(2-{a}^{3})c+(2-a)a]}{4{(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+2c+a)}.

We observe in Lemma 3 that, when Player 2 acts as a leader in the first stage, Player 1 never stays inactive. We can also show that $\frac{\partial {x}_{2,21}^{* }}{\partial c}\lt 0,\frac{\partial {x}_{1,12}^{* }}{\partial c}\lt 0$ , and $\frac{\partial {x}_{2,21}^{* }}{\partial a}\gt 0$ , i.e., both players reduce their effort as the second-stage advantage becomes lower. Player 2 decreases her effort as her opponent's ex ante advantage becomes greater. However, $\frac{\partial {x}_{1,21}^{* }}{\partial a}$ might be positive or negative depending on the level of the second-stage advantage. Figure 2 illustrates how Player 1's equilibrium effort varies as her ex ante advantage changes for different levels of second-stage advantage.

Comparison of the efforts in all three possible contests yields our first main result.

Proposition 1.

i.
When the strong player acts as a leader in the first stage, the discouragement effect is amplified compared to a simultaneous first stage, reducing the weak player's first-stage and expected second-stage effort.
ii.
When the weak player acts as a leader in the first stage, the catching-up effect is enhanced compared to a simultaneous first stage, increasing the weak player's first-stage and expected second-stage effort.

The above result demonstrates how the timing of moves changes the competitive dynamics through two mechanisms. When the strong player moves first, the decrease in the weak player's effort represents an increased discouragement effect. The strong player's first-mover advantage allows her to make an effort that further reduces the weak player's incentive to compete, increasing asymmetry beyond the ex ante one. Conversely, when the weak player moves first, her increased effort depicts an enhanced catching-up effect. This first-mover advantage partially offsets her ex ante disadvantage, allowing her to establish a stronger competitive position than in a simultaneous contest.

4 Optimal First-Stage Timing

We now study the game from the perspective of a contest designer by investigating the optimal sequence of moves in the first stage. Following the discussion in the Introduction, we consider a contest designer with three possible objectives: maximizing second-stage, total, and winner's effort. We discuss the three cases separately.

4.1 Second-Stage Effort Maximizer

The contest designer who is concerned about the second-stage effort maximizes

{Y}_{k}=\frac{{x}_{1,k}}{{x}_{1,k}+{x}_{2,k}}({y}_{1,w}+{y}_{2,l})+\frac{{x}_{2,k}}{{x}_{1,k}+{x}_{2,k}}({y}_{2,w}+{y}_{1,l}),

where

k\in \{S,12,21\}

depending on the order of moves in the first stage. The first [second] term in the sum is the probability that Player 1 [2] wins in the first stage times the corresponding effort in the second stage.

4.2 Total Effort Maximizer

The contest designer's objective is to maximize total effort, i.e., the sum of first and second-stage efforts. It is straightforward that she maximizes

{\mathrm{TE}}_{k}={x}_{1,k}+{x}_{2,k}+{Y}_{k},

where

{Y}_{k}

is the second-stage expected effort.

4.3 Winner's Effort Maximizer

In the last case, we investigate the problem of a contest designer concerned about the winner's expected effort. Thus, she maximizes

W{E}_{k}=\frac{{x}_{1,k}}{{x}_{1,k}+{x}_{2,k}}({p}_{1,w}{y}_{1,w}+{p}_{2,l}{y}_{2,l})+\frac{{x}_{2,k}}{{x}_{1,k}+{x}_{2,k}}({p}_{2,w}{y}_{2,w}+{p}_{1,l}{y}_{1,l}).

(3)

The first [second] term of the sum represents the expected second-stage winner's effort, conditional on Player 1 [2] winning in the first stage.

The following result summarizes the contest designer's expected payoffs for each possible objective discussed above and every sequence of players' first-stage moves.

Proposition 2.

i.
For a contest designer who maximizes second-stage effort, the optimal first-stage contest is simultaneous.
ii.
For a contest designer who maximizes total effort, the optimal first-stage contest is:
- –
  For $a\gt \frac{1}{2}$ , sequential with the strong player leading
- –
  For $\frac{\sqrt{5}}{5}\lt a\le \frac{1}{2}$ and $c$ sufficiently low, or for $a\le \frac{\sqrt{5}}{5}$ and any $c$ , simultaneous
- –
  Otherwise, sequential with the strong player leading and the weak player not participating
iii.
For a contest designer who maximizes the winner's effort, the optimal first-stage contest is:
- –
  For $a\gt \frac{1}{2}$ ,
  - *
    When $c$ is sufficiently low, sequential with the strong player leading
  - *
    When $c$ is sufficiently high, simultaneous
- –
  For $a\le \frac{1}{2}$ ,
  - *
    When $c$ and $a$ are sufficiently low, or when $c$ is sufficiently high, simultaneous
  - *
    Otherwise, sequential with the strong player leading and the weak player not participating

Proposition 2 provides several interesting insights about how the timing structure in the first stage affects a contest designer's payoff. Probably the most striking is that for a contest designer who maximizes second-stage effort, a simultaneous first-stage contest is optimal. This finding challenges the intuition that letting a strong player lead would generate the greatest competition. By moving first, the strong player strategically exerts an effort that discourages the weak player, creating an asymmetry that carries over to the second stage. This asymmetry reduces the second-stage competition. In contrast, a simultaneous first-stage contest makes the second stage less asymmetric and, thus, more competitive.

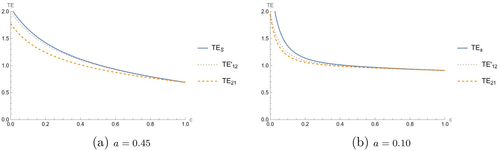
For a total effort maximizer, the optimal first-stage contest depends on the degree of ex ante asymmetry between the two players and the second-stage advantage. When ex ante asymmetry is moderate ( $a\gt 1\unicode{x02215}2$ ), a sequential contest with the strong player leading generates the highest total effort. The strong player's high effort induces the weak player to respond accordingly, generating a total effort greater than in the case of a simultaneous first stage. However, with a high ex ante asymmetry ( $a\le 1\unicode{x02215}2$ ), when $a$ is sufficiently close to 1/2 and the second-stage advantage is low, a simultaneous contest becomes optimal as it ensures balanced participation from both players. When asymmetry is even higher ( $a\le \sqrt{5}\unicode{x02215}5$ ), a simultaneous first-stage contest is preferred for any level of second-stage advantage. Surprisingly, for specific parameter values between these ranges, a first-stage contest where the weak player does not participate is optimal, as in such a case, the strong player must exert a substantial effort to preempt the weak player. This can be verified in Figure 3, where we can observe that the total expected effort when Player 1 preempts Player 2, $T{E}_{12}^{^{\prime} }$ , can be greater than $T{E}_{21}$ .

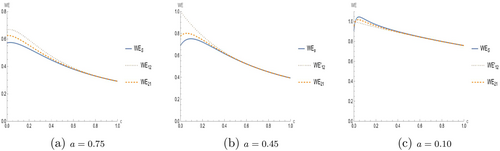
Finally, for a winner's effort maximizer, when the ex ante asymmetry is moderate and the second-stage advantage is low, a sequential first-stage contest with the strong player leading is optimal as it increases the probability that the stronger player wins in the first stage, and exerts a high effort in the second. However, with a more substantial second-stage advantage, a simultaneous first-stage contest becomes optimal as it prevents excessive discouragement and maintains a more symmetric competition, which increases the winner's expected effort. In Figure 4, we observe how the winner's expected effort varies for different levels of ex ante asymmetry in the three timing structures.

5 Conclusion

In this paper, we studied a two-stage contest with two ex ante asymmetric players competing in the first stage to gain an advantage, which increases their probability of winning a final prize in the second stage. While moving simultaneously in the second stage, we let the two players move sequentially in the first stage and analyzed all the first-stage contests that might arise.

Our analysis demonstrates how sequential timing alters the strategic dynamics between players. When the strong player acts as a leader in the first stage, the discouragement effect is amplified compared to a simultaneous first stage, reducing the weak player's effort in both stages. Conversely, when the weak player acts as a leader, the catching-up effect is enhanced, increasing the weak player's effort in both stages. These timing effects create significantly different competitive dynamics that carry through to the second stage.

We then investigated the contest designer's problem by considering three objectives: maximizing second-stage effort, total effort, and the winner's effort. Our analysis revealed some interesting insights for contest design. The timing structure significantly affects how the catching-up and discouragement effects operate, with different designer types preferring different move orders in the first stage. Probably most surprisingly, a contest designer who maximizes second-stage effort strictly prefers a simultaneous first-stage contest. On the other hand, a designer who maximizes total or winner's effort finds simultaneous contests optimal under specific parameter conditions. These findings highlight the complex interaction between ex ante asymmetry, win advantage, and timing structure in a dynamic contest. A natural extension would be introducing asymmetric information about players' abilities and how it affects the timing structure. This task is left for future research.

Acknowledgments

I am grateful to the Editor, Rabah Amir, an Associate Editor, and two anonymous referees for their insightful comments and constructive suggestions. I also thank Alexander Matros, David Rietzke, and Orestis Troumpounis for valuable discussions. Part of this research was conducted during a research visit to the University of Illinois Urbana-Champaign, whose hospitality is much appreciated. Open access funding provided by Universitat Innsbruck/KEMÖ.

Endnotes

1 For some surveys on the contests literature, see Konrad (2009) and Beviá and Corchón (2024).

2 Some other related studies are Klumpp and Polborn (2006), Fu and Lu (2012), Krumer (2013), Gelder (2014), and Hinnosaar (2024).

3 Protopappas (2022) considers a similar lobbying-election game with endogenous lobbying prices.

4 For studies in sequential contests, see Dixit (1987); Linster (1993); Leininger (1993); Morgan (2003); Serena (2017b); and Protopappas (2023).

5 There are also other studies considering that winning in previous stages gives you an advantage in the following stages, for example, Baik and Lee (2000); Konrad (2002); Kovenock and Roberson (2009); Clark and Nilssen (2018), and Arve and Chiappinelli (2021).

6 We use non-strict inequality to include also the symmetric case

a=1

, where the two players' costs are equal.

7 The second stage of the contest has already been analyzed in previous studies (see, e.g., Clark et al. (2012)).

8 This is a special case of Clark et al. (2012), who consider an additional prize for the winner of the first stage.

9 The combination of sequentiality and asymmetry makes the analysis of

\frac{\partial {x}_{1,12}^{* }}{\partial c}

and

\frac{\partial {x}_{1,21}^{* }}{\partial a}

highly complicated. For these cases, we provide graphical results illustrated in Figures 1 and 2.

10 See Appendix B for the exact levels of the efforts.

Appendix A: Proofs

Proof of Lemma 1.The FOC of Equation (1) for Player $i$ is

\frac{\partial {\mathbb{E}}[{\pi }_{i}]}{\partial {x}_{i}}=\frac{\left[\frac{1}{{(ac+1)}^{2}}-\frac{{c}^{2}}{{(c+a)}^{2}}\right]{x}_{d}}{{({x}_{a}+{x}_{d})}^{2}}-a=0,\begin{array}{ll}a\lt 1 & \,\text{if}\,\,i=1,\\ a=1 & \,\text{if}\,\,i=2,\end{array}\,j=1,2,j\ne i,

and the SOC for a maximum is

\frac{{\partial }^{2}{\mathbb{E}}[{\pi }_{i}]}{\partial {x}_{i}^{2}}=-\frac{2\left[\frac{1}{{(ac+1)}^{2}}-\frac{{c}^{2}}{{(c+a)}^{2}}\right]{x}_{2}}{{({x}_{1}+{x}_{2})}^{3}}\lt 0,i,j\in \{1,2\},j\ne i,

which is satisfied as

\frac{1}{{(ac+1)}^{2}}-\frac{{c}^{2}}{{(c+a)}^{2}}\gt 0,\forall c,a

The solution of the system of reaction functions from the FOC gives us the results in Lemma 1. $\square$

Proof of Lemma 2.From (1), Player 2's (follower) reaction function is

{x}_{2}^{* }({x}_{1})=\left\{\begin{array}{ll}\displaystyle \frac{\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}-{(c+a)}^{2}{(ac+1)}^{2}{x}_{1}}{{(c+a)}^{2}{(ac+1)}^{2}}, & \,\text{if}\,\,{x}_{1}\lt {\bar{x}}_{1}\\ 0 & \,\text{otherwise}\,.\end{array}\right.

(A1)

where

{\bar{x}}_{1}=\frac{{a}^{2}(1-{c}^{2})(2ac+{c}^{2}+1)}{{({a}^{2}c+a{c}^{2}+c+a)}^{2}}

From Equation (2), we have that Player 1's (leader) expected payoff is

{\mathbb{E}}[{\pi }_{1,12}]=\left\{\begin{array}{ll}\displaystyle \frac{{c}^{2}}{{(c+a)}^{2}}-\displaystyle \frac{a{x}_{1}[\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}-a(1-{c}^{4})+2{c}^{3}-2c]}{\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}}, & \text{if}\,{x}_{1}\lt {\bar{x}}_{1}\\ \displaystyle \frac{1}{{(ac+1)}^{2}}-a{x}_{1}, & \text{otherwise}.\end{array}\right.

(A2)

The FOC for ${x}_{1}\lt {\bar{x}}_{1}$ is

\frac{a[-2(\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}+{c}^{3}-c)-a{c}^{4}+a]}{2\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}}=0

and the SOC is

-\frac{a(1-{c}^{2})(a{c}^{2}+a+2c)}{4{x}_{1}\sqrt{{a}^{2}(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(2ac+{c}^{2}+1){x}_{1}}}\lt 0,

which is true for all

c\in (0,1)

Solving the FOC for ${x}_{1}$ , we find that Player 1 chooses effort ${x}_{1,12}^{* }$ , and from Equation (A1), we discover that Player 2 responds by choosing ${x}_{2,12}^{* }$ . For ${x}_{1}\ge {\bar{x}}_{1}$ , Player 1's expected payoff is decreasing in effort and, thus, maximized when ${x}_{1,1{2}^{* * }}={\bar{x}}_{1}$ , implying zero effort for Player 2. Finally, ${x}_{1,12}^{* }\lt {\bar{x}}_{1}$ if $\frac{1}{2}\lt a\le \frac{\sqrt{2}}{2}$ and $c\lt {c}^{^{\prime} }$ , or only if $\frac{\sqrt{2}}{2}\lt a\lt 1$ . $\square$

Proof of Lemma 3.Player 1's (follower) reaction function is

{x}_{1}^{* }({x}_{2})=\left\{\begin{array}{ll}\displaystyle \frac{\sqrt{-\left(({c}^{2}-1)(a{c}^{2}+a+2c){({a}^{2}c+a{c}^{2}+c+a)}^{2}{x}_{2}\right)}-{({a}^{2}c+a{c}^{2}+c+a)}^{2}{x}_{2}}{{({a}^{2}c+a{c}^{2}+c+a)}^{2}}, & \,\text{if}\,\,{x}_{2}\lt \displaystyle \frac{a+2c-a{c}^{4}-2{c}^{3}}{{(c+a)}^{2}{(ac+1)}^{2}}\\ 0, & \,\text{otherwise}\,.\end{array}\right.

Player 2's (leader) expected payoff is

{\mathbb{E}}[{\pi }_{2,21}]=\left\{\begin{array}{ll}{x}_{2}\left[\displaystyle \frac{{a}^{2}(1-{c}^{2})(2ac+{c}^{2}+1)}{\sqrt{(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+a+2c){x}_{2}}}-1\right]+\displaystyle \frac{{a}^{2}{c}^{2}}{{(ac+1)}^{2}}, & \,\text{if}\,\,{x}_{2}\lt \displaystyle \frac{a+2c-a{c}^{4}-2{c}^{3}}{{(c+a)}^{2}{(ac+1)}^{2}}\\ \displaystyle \frac{{a}^{2}}{{(c+a)}^{2}}-{x}_{2}, & \,\text{otherwise}\,.\end{array}\right.

The FOC for ${x}_{2}\lt \frac{a+2c-a{c}^{4}-2{c}^{3}}{{(c+a)}^{2}{(ac+1)}^{2}}$ is

\frac{{a}^{2}(1-{c}^{2})(2ac+{c}^{2}+1)}{2\sqrt{(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+a+2c){x}_{2}}}-1=0,

and the SOC is

-\frac{{a}^{2}(1-{c}^{2})(2ac+{c}^{2}+1)}{4{x}_{2}\sqrt{(1-c)(1+c){(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+a+2c){x}_{2}}}\lt 0,

which is satisfied for all

c\in (0,1)

Solving the FOC, we find that Player 2 makes effort ${x}_{2,21}^{* }$ . We can also verify that ${x}_{2,21}^{* }\lt \frac{a+2c-a{c}^{4}-2{c}^{3}}{{(c+a)}^{2}{(ac+1)}^{2}}$ for all $c$ and $a$ , which means that Player 1 always participates in the contest, making effort ${x}_{1,21}^{* }$ . $\square$

Proof of Proposition 1.

i.
When the strong player acts as a leader, we compare the equilibrium efforts from Lemmas 1 and 2. We can show numerically that ${x}_{2,12}^{* }\lt {x}_{2,S}^{* }$ for all $a\in (0,1]$ and $c\in (0,1)$ . For $a\le \frac{1}{2}$ , Lemma 2 shows that ${x}_{2,12}^{* }=0$ . For the second-stage effects, comparing ${p}_{1,12}=\frac{{x}_{1,12}^{* }}{{x}_{1,12}^{* }+{x}_{2,12}^{* }}$ with ${p}_{1,S}=\frac{{x}_{1,S}^{* }}{{x}_{1,S}^{* }+{x}_{2,S}^{* }}$ , numerical verification confirms that ${p}_{1,12}\gt {p}_{1,S}$ . Player 2's expected second-stage efforts with a sequential and simultaneous first stage are $E[{y}_{2,12}]={p}_{1,12}{y}_{2,l}+(1-{p}_{1,12}){y}_{2,w}$ and $E[{y}_{2,S}]={p}_{1,S}{y}_{2,l}+(1-{p}_{1,S}){y}_{2,w}$ , respectively. Subtracting the second from the first equation, we obtain that $E[{y}_{2,12}]-E[{y}_{2,S}]=({p}_{1,12}-{p}_{1,S})({y}_{2,l}-{y}_{2,w})$ . As ${y}_{2,l}\lt {y}_{2,w}$ and ${p}_{1,12}\gt {p}_{1,S}$ , it follows that $({p}_{1,12}-{p}_{1,S})({y}_{2,l}-{y}_{2,w})\lt 0$ , which implies $E[{y}_{2,12}]\lt E[{y}_{2,S}]$ .
ii.
When the weak player acts as a leader, we compare the equilibrium efforts from Lemmas 1 and 3. Following a process similar to before, we get ${x}_{2,21}^{* }\gt {x}_{2,S}^{* }$ and ${p}_{2,21}\gt {p}_{2,S}$ for all $a\in (0,1]$ and $c\in (0,1)$ . Player 2's expected second-stage efforts are $E[{y}_{2,21}]={p}_{2,21}{y}_{2,w}+(1-{p}_{2,21}){y}_{2,l}$ and $E[{y}_{2,S}]={p}_{2,S}{y}_{2,w}+(1-{p}_{2,S}){y}_{2,l}$ . The difference of these two gives $E[{y}_{2,21}]-E[{y}_{2,S}]=({p}_{2,21}-{p}_{2,S})({y}_{2,w}-{y}_{2,l})$ . As ${y}_{2,w}\gt {y}_{2,l}$ and ${p}_{2,21}\gt {p}_{2,S}$ , it follows that $({p}_{2,21}-{p}_{2,S})({y}_{2,w}-{y}_{2,l})\gt 0$ , which implies $E[{y}_{2,21}]\gt E[{y}_{2,S}]$ .

\square

Proof of Proposition 2.In the following, we present in detail the way we calculate the efforts each type of contest designer maximizes. The proofs of the inequalities in the proposition are tedious and, therefore, omitted.

i.
The expected second-stage effort if players move simultaneously in the first stage is given by ${Y}_{S}^{* }$ .10 If in the first stage Player 1 is the leader [follower], the expected second-stage effort is given by ${Y}_{12}^{* }$ [ ${Y}_{21}^{* }$ ]. If in the first stage Player 1 is the leader and Player 2 does not enter the contest, the expected second-stage effort is given by ${Y}_{12}^{* * }={y}_{1,w}^{* }+{y}_{2,l}^{* }=\frac{1}{ac+1}$ . It is tedious to show that ${Y}_{S}^{* }\gt {Y}_{12}^{* }\gt {Y}_{21}^{* }$ for $a\gt \frac{1}{2}$ , and ${Y}_{S}^{* }\gt {Y}_{12}^{* * }\gt {Y}_{21}^{* }$ for $a\le \frac{1}{2}$ .
ii.
It is straightforward to find the sum of the first and second-stage efforts. In the case of only Player 1 participating in the first-stage contest, the total effort is $T{E}_{12}^{* * }={x}_{1,1{2}^{* * }}+{y}_{1,w}^{* }+{y}_{2,l}^{* }=\frac{{a}^{2}}{{(c+a)}^{2}}+\frac{ac(1-ac)+1}{{(ac+1)}^{2}}$ .
iii.
The winner's expected effort is given by Equation (3). In the case of only Player 1 participating in the first-stage contest and, therefore, winning the second-stage advantage with certainty, the winner's expected effort is $W{E}_{12}^{* * }={p}_{1,w}{y}_{1,w}+{p}_{2,l}{y}_{2,l}=\frac{{a}^{2}{c}^{2}+1}{{(ac+1)}^{3}}$ .

Appendix B: Expected Payoffs

B.1 Simultaneous First Stage

\begin{array}{rcl} & & {\mathbb{E}}\left[{\pi }_{1,S}^{* }\right]=\displaystyle \frac{\begin{array}{r}4{a}^{8}{c}^{6}+4{a}^{7}{c}^{5}({c}^{2}+3)+{a}^{6}{c}^{4}({c}^{4}+4{c}^{3}+10{c}^{2}+4c+13)\\ +2{a}^{5}{c}^{3}({c}^{5}+{c}^{4}+10{c}^{3}+4{c}^{2}+5c+3)+{a}^{4}(8{c}^{7}+{c}^{6}+32{c}^{5}+3{c}^{4}+8{c}^{3}+3{c}^{2}+1)+\\ 2{a}^{3}c(5{c}^{5}+{c}^{4}+10{c}^{3}+4{c}^{2}+c+3)\\ +{a}^{2}{c}^{2}({c}^{4}+4{c}^{3}+10{c}^{2}+4c+13)+4a{c}^{3}({c}^{2}+3)+4{c}^{4}\end{array}}{{(a+1)}^{2}{(c+a)}^{2}{(ac+1)}^{2}{[2{a}^{2}c+a{(1-c)}^{2}+2c]}^{2}}\\ & & {\mathbb{E}}\left[{\pi }_{2,S}^{* }\right]=\displaystyle \frac{\begin{array}{r}{a}^{4}(2ac+{c}^{2}+1)[4{a}^{5}{c}^{3}+6{a}^{4}({c}^{4}+{c}^{2})+2{a}^{3}c(2{c}^{4}+{c}^{3}+2{c}^{2}+c+2)\\ +{a}^{2}({c}^{6}+4{c}^{5}+{c}^{4}+8{c}^{3}+{c}^{2}+1)+2a{c}^{4}({c}^{2}+5)+4{c}^{5}]\end{array}}{{(a+1)}^{2}{(c+a)}^{2}{(ac+1)}^{2}{[2{a}^{2}c+a{(1-c)}^{2}+2c]}^{2}}\end{array}

B.2 Player 1 [2] Acts as a Leader [Follower]

\begin{array}{ccc} & & {\mathbb{E}}\left[{\pi }_{1,12}^{* }\right]=\frac{\displaystyle \begin{array}{c}8{a}^{4}{c}^{5}+4{a}^{3}(5+{c}^{2}){c}^{4}-{a}^{2}({c}^{6}-8{c}^{5}+{c}^{4}-16{c}^{3}-{c}^{2}-1)-4a({c}^{4}-{c}^{3}-c-1)c\\ +4(1-{c}^{2}){c}^{2}\end{array}}{4a{(c+a)}^{2}{(ac+1)}^{2}({c}^{2}+2ac+1)}\\ & & {\mathbb{E}}\left[{\pi }_{1,12}^{* * }\right]=\frac{{c}^{2}+2ac-2{a}^{4}c(1-{c}^{2})-{a}^{3}(1-{c}^{4})+{a}^{2}}{{(c+a)}^{2}{(ac+1)}^{2}}\\ & & {\mathbb{E}}\left[{\pi }_{2,12}^{* }\right]=\frac{\displaystyle \begin{array}{c}8{a}^{7}{c}^{3}+4{a}^{6}{c}^{2}(5+{c}^{2})+8{a}^{5}c(2+{c}^{2})+4{a}^{4}(2{c}^{5}+{c}^{2}-2c+1)\\ +4{a}^{3}({c}^{6}+5{c}^{4}-5{c}^{2}-1)-{a}^{2}({c}^{6}-8{c}^{5}+{c}^{4}-{c}^{2}+8c-1)\\ +4ac(1-{c}^{4})+4{c}^{2}(1-{c}^{2})\end{array}}{4{a}^{2}{(c+a)}^{2}{(ac+1)}^{2}({c}^{2}+2ac+1)}\end{array}.

B.3 Player 2 [1] Acts as a Leader [Follower]

\begin{array}{ccc} & & {\mathbb{E}}\left[{\pi }_{2,21}^{* }\right]=\frac{\displaystyle \begin{array}{c}{a}^{2}[4{a}^{4}(1-{c}^{2}){c}^{2}-4{a}^{3}({c}^{4}-{c}^{3}-c-1)c-{a}^{2}({c}^{6}-8{c}^{5}+{c}^{4}-16{c}^{3}-{c}^{2}-1)\\ +4a({c}^{2}+5){c}^{4}+8{c}^{5}]\end{array}}{4{(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+2c+ac)}\\ & & {\mathbb{E}}\left[{\pi }_{1,21}^{* }\right]=\frac{\displaystyle \begin{array}{c}{a}^{2}[4{a}^{4}(1-{c}^{2}){c}^{2}-4{a}^{3}({c}^{4}-{c}^{3}-c-1)c-{a}^{2}({c}^{6}-8{c}^{5}+{c}^{4}-16{c}^{3}-{c}^{2}-1)\\ +4a({c}^{2}+5){c}^{4}+8{c}^{5}]\end{array}}{4{(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+2c+a)}\end{array}.

Appendix C: Expected Efforts

C.1 Second-Stage Expected Effort

\begin{array}{ccc} & & {Y}_{S}^{* }=\frac{2{a}^{4}{c}^{2}+{a}^{3}c({c}^{2}+3)+2{a}^{2}({c}^{2}+1)+ac({c}^{2}+3)+2{c}^{2}}{(a+1)(c+a)(ac+1)(2{a}^{2}c+a{(1-c)}^{2}+2c)}\\ & & {Y}_{12}^{* }=\frac{4{a}^{4}{c}^{2}+2{a}^{3}c({c}^{2}+3)-{a}^{2}({c}^{3}-3{c}^{2}+c-3)+a{(c-1)}^{3}+2(c-1)c}{2{a}^{2}(a+c)(ac+1)(2ac+{c}^{2}+1)}\\ & & {Y}_{12}^{* * }=\frac{1}{ac+1}\\ & & {Y}_{21}^{* }=\frac{2{a}^{4}(c-1)c-{a}^{3}{(1-c)}^{3}-{a}^{2}({c}^{3}-3{c}^{2}+c-3)+2ac({c}^{2}+3)+4{c}^{2}}{2(c+a)(ac+1)(a{c}^{2}+2c+a)}\end{array}.

C.2 Total Expected Effort

\begin{array}{ccc} & & {\mathrm{TE}}_{S}^{* }=\frac{\displaystyle \begin{array}{c}2{a}^{6}{c}^{3}+{a}^{5}{c}^{2}(3{c}^{2}+5)+{a}^{4}(-{c}^{5}+8{c}^{3}+7c)-{a}^{3}({c}^{6}+{c}^{4}-15{c}^{2}-3)\\ +{a}^{2}(-{c}^{5}+8{c}^{3}+7c)+a{c}^{2}(3{c}^{2}+5)+2{c}^{3}\end{array}}{(a+1){(c+a)}^{2}{(ac+1)}^{2}[2{a}^{2}c+2c+a{(1-c)}^{2}]}\\ & & {\mathrm{TE}}_{12}^{* }=\frac{\displaystyle \begin{array}{c}4{a}^{6}{c}^{3}+2{a}^{5}{c}^{2}(3{c}^{2}+5)-{a}^{4}c({c}^{3}-15{c}^{2}+c-11)\\ -{a}^{3}({c}^{6}+{c}^{5}-{c}^{4}+5{c}^{3}-20{c}^{2}+2c-4)-{a}^{2}({c}^{5}+4{c}^{4}-9{c}^{3}+7{c}^{2}-8c+1)\\ +ac(3{c}^{3}-5{c}^{2}+5c-3)+2(c-1){c}^{2}\end{array}}{2{a}^{2}{(c+a)}^{2}{(ac+1)}^{2}({c}^{2}+2ac+1)}\\ & & T{E}_{12}^{* * }=\frac{{a}^{2}}{{(c+a)}^{2}}+\frac{ac(1-ac)+1}{{(ac+1)}^{2}}\\ & & {\mathrm{TE}}_{21}^{* }=\frac{\displaystyle \begin{array}{c}{a}^{5}c(3{c}^{3}-5{c}^{2}+5c-3)-2{a}^{6}(1-c){c}^{2}-{a}^{4}({c}^{5}+4{c}^{4}-9{c}^{3}+7{c}^{2}-8c+1)\\ -{a}^{3}({c}^{6}+{c}^{5}-{c}^{4}+5{c}^{3}-20{c}^{2}+2c-4)-{a}^{2}c({c}^{3}-15{c}^{2}+c-11)\\ +2a{c}^{2}(3{c}^{2}+5)+4{c}^{3}\end{array}}{2{(c+a)}^{2}{(ac+1)}^{2}(a{c}^{2}+2c+a)}\end{array}.

C.3 Winner's Expected Effort

\begin{array}{ccc} & & {\mathrm{WE}}_{S}^{* }=\frac{\displaystyle \begin{array}{c}2{a}^{7}{c}^{4}+{a}^{6}{c}^{3}({c}^{2}+5)+5{a}^{5}({c}^{4}+{c}^{2})+{a}^{4}(3{c}^{5}+10{c}^{3}+c)\\ +{a}^{3}({c}^{6}+7{c}^{4}+5{c}^{2}+1)+{a}^{2}c(2{c}^{4}+3{c}^{2}+5)\\ +a{c}^{2}({c}^{2}+5)+2{c}^{3}\end{array}}{(a+1){(a+c)}^{2}{(ac+1)}^{3}(2{a}^{2}c+a{(1-c)}^{2}+2c)}\\ & & {\mathrm{WE}}_{12}^{* }=\frac{\displaystyle \begin{array}{c}4{a}^{7}{c}^{4}+2{a}^{6}{c}^{3}({c}^{2}+5)-{a}^{5}{c}^{2}({c}^{3}-9{c}^{2}+c-9)+2{a}^{4}c(2{c}^{4}-2{c}^{3}+8{c}^{2}-c+1)\\ +{a}^{3}({c}^{6}-{c}^{5}+9{c}^{4}-6{c}^{3}+9{c}^{2}-c+1)+2{a}^{2}c({c}^{4}-2{c}^{3}+2{c}^{2}-2c+3)\\ +ac({c}^{3}-5{c}^{2}+5c-1)+2(c-1){c}^{2}\end{array}}{2{a}^{2}{(c+a)}^{2}{(ac+1)}^{3}({c}^{2}+2ac+1)}\\ & & W{E}_{12}^{* * }=\frac{{a}^{2}{c}^{2}+1}{{(ac+1)}^{3}}\\ & & {\mathrm{WE}}_{21}^{* }=\frac{\displaystyle \begin{array}{c}2{a}^{7}(c-1){c}^{3}+{a}^{6}{c}^{2}({c}^{3}-5{c}^{2}+5c-1)-2{a}^{5}c(2{c}^{4}-3{c}^{3}+{c}^{2}-3c+1)\\ -{a}^{4}({c}^{6}-5{c}^{5}+{c}^{4}-14{c}^{3}+5{c}^{2}-c+1)+2{a}^{3}({c}^{6}+6{c}^{4}-2{c}^{3}+3{c}^{2}-c+1)\\ +{a}^{2}c(4{c}^{4}-{c}^{3}+5{c}^{2}-c+9)+2a{c}^{2}({c}^{2}+5)+4{c}^{3}\end{array}}{2{(c+a)}^{2}{(ac+1)}^{3}(a{c}^{2}+2c+a)}\end{array}

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

Arve, M., and O. Chiappinelli. 2021. “The Role of Budget Constraints in Sequential Elimination Tournaments.” Scandinavian Journal of Economics 123, no. 4: 1059–1087.
10.1111/sjoe.12440
Web of Science® Google Scholar
Baik, K. H., and S. Lee. 2000. “Two-Stage Rent-Seeking Contests With Carryovers.” Public Choice 103, no. 3–4: 285–296.
10.1023/A:1005003713923
Web of Science® Google Scholar
Baye, M. R., D. Kovenock, and C. G. de Vries. 1993. “Rigging the Lobbying Process: An Application of the All-Pay Auction.” American Economic Review 83, no. 1: 289–294.
Web of Science® Google Scholar
Beviá, C., and L. Corchón. 2024. Contests: Theory and Applications. Cambridge University Press.
10.1017/9781009504409
Google Scholar
Beviá, C., and L. C. Corchón. 2013. “Endogenous Strength in Conflicts.” International Journal of Industrial Organization 31, no. 3: 297–306.
10.1016/j.ijindorg.2012.09.002
Web of Science® Google Scholar
Clark, D. J., and T. Nilssen. 2013. “Learning by Doing in Contests.” Public Choice 156, no. 1–2: 329–343.
10.1007/s11127-011-9905-9
Web of Science® Google Scholar
Clark, D. J., and T. Nilssen. 2018. “Keep on Fighting: The Dynamics of Head Starts in All-Pay Auctions.” Games and Economic Behavior 110: 258–272.
10.1016/j.geb.2018.05.005
Web of Science® Google Scholar
Clark, D. J., T. Nilssen, and J. Y. Sand. 2012. Motivating Over Time: Dynamic Win Effects in Sequential Contests.
Google Scholar
Clark, D. J., and C. Riis. 1998. “Contest Success Functions: An Extension.” Economic Theory 11: 201–204.
10.1007/s001990050184
Web of Science® Google Scholar
Dixit, A. 1987. “Strategic Behavior in Contests.” American Economic Review 77: 891–898.
Web of Science® Google Scholar
Fu, Q., and J. Lu. 2012. “The Optimal Multi-Stage Contest.” Economic Theory 51, no. 2: 351–382.
10.1007/s00199-009-0463-z
Web of Science® Google Scholar
Gelder, A. 2014. “From Custer to Thermopylae: Last Stand Behavior in Multi-Stage Contests.” Games and Economic Behavior 87: 442–466.
10.1016/j.geb.2014.06.003
Web of Science® Google Scholar
Harris, C., and J. Vickers. 1987. “Racing With Uncertainty.” Review of Economic Studies 54, no. 1: 1–21.
10.2307/2297442
Web of Science® Google Scholar
Hillman, A. L., and J. G. Riley. 1989. “Politically Contestable Rents and Transfers.” Economics & Politics I, no. I: 17–39.
10.1111/j.1468-0343.1989.tb00003.x
Google Scholar
Hinnosaar, T. 2024. “Optimal Sequential Contests.” Theoretical Economics 19: 207–244.
10.3982/TE5536
Web of Science® Google Scholar
Klumpp, T., and M. K. Polborn. 2006. “Primaries and the New Hampshire Effect.” Journal of Public Economics 8, no. 90: 1073–1114.
10.1016/j.jpubeco.2005.08.009
Google Scholar
Konrad, K. A. 2002. “Investment in the Absence of Property Rights; the Role of Incumbency Advantages.” European Economic Review 46, no. 8: 1521–1537.
10.1016/S0014-2921(01)00201-X
Web of Science® Google Scholar
Konrad, K. A. 2009. Strategy and Dynamics in Contests. Oxford University Press.
10.1093/oso/9780199549597.001.0001
Google Scholar
Konrad, K. A., and D. Kovenock. 2009. “Multi-Battle Contests.” Games and Economic Behavior 66, no. 1: 256–274.
10.1016/j.geb.2008.05.002
Web of Science® Google Scholar
Kovenock, D., and B. Roberson. 2009. “Is the 50-State Strategy Optimal?” Journal of Theoretical Politics 21, no. 2: 213–236.
10.1177/0951629808100764
Google Scholar
Krueger, A. O. 1974. “The Political Economy Seeking of the Society.” American Economic Review 64, no. 3: 291–303.
Google Scholar
Krumer, A. 2013. “Best-of-Two Contests With Psychological Effects.” Theory and Decision 75, no. 1: 85–100.
10.1007/s11238-012-9313-8
Web of Science® Google Scholar
Leininger, W. 1993. “More Efficient Rent-Seeking: A Münchhausen Solution.” Public Choice 75: 43–62.
10.1007/BF01053880
Web of Science® Google Scholar
Linster, B. G. 1993. “Stackelberg Rent-Seeking.” Public Choice 77, no. 2: 307–321.
10.1007/BF01047872
Web of Science® Google Scholar
Morgan, J. 2003. “Sequential Contests.” Public Choice 116, no. 1–2: 1–18.
10.1023/A:1024252514806
Web of Science® Google Scholar
Protopappas, K. 2022. “Optimal Lobbying Pricing.” Social Choice and Welfare 59, no. 1: 37–61.
10.1007/s00355-021-01383-2
Web of Science® Google Scholar
Protopappas, K. 2023. “Manipulation of Moves in Sequential Contests.” Social Choice and Welfare 61, no. 3: 511–535.
10.1007/s00355-023-01461-7
Web of Science® Google Scholar
Serena, M. 2017a. “Quality Contests.” European Journal of Political Economy 46: 15–25.
10.1016/j.ejpoleco.2016.10.008
Web of Science® Google Scholar
Serena, M. 2017b. “Sequential Contests Revisited.” Public Choice 173, no. 1–2: 131–144.
10.1007/s11127-017-0467-3
Web of Science® Google Scholar
Skaperdas, S. 1996. “Contest Success Functions.” Economic Theory 7, no. 2: 283–290.
10.1007/BF01213906
Web of Science® Google Scholar
Tullock, G. 1980. “ Efficient Rent Seeking.” In Toward a Theory of Rent-Seeking Society, edited by J. Buchannan, R. Tollison, and G. Tullock, 97–112. Texas A&M University Presss.
Google Scholar

Volume27, Issue3

June 2025

e70041

Optimal Timing in Competition for Advantage: A Two-Stage Contest

ABSTRACT

1 Introduction

2 Overview of the Model