The literature has produced mixed findings on the relationship between industry agglomeration and firm-level productivity where it concerns the self-selection of productive firms into locations characterized by different levels of industry agglomeration. We argue that the nature of this self-selection crucially depends on whether incumbent and entrant firms compete on the same market. Adverse selection of less productive firms into a location only dominates if knowledge spillovers in agglomerated locations are harmful to productive entrants: when the entrant and local incumbents target the same (domestic) product market and the entrant risks losing market share and profits. We find evidence for this notion in analysis of location decisions for new plants at the fine-grained geographical level in Japan by firms with known productivity records in the industry (multi-plant firms). We conclude that sorting processes do occur, but that the nature of these processes can only be uncovered in analysis that considers competition on product markets and accurate measures of firm heterogeneity in productivity.

1 Introduction

Extant literature on industrial agglomeration and productivity has produced mixed findings. On the one hand, studies have observed that the geographic agglomeration of firms is associated with higher productivity (e.g., Rosenthal and Strange 2020; Melo, Graham, and Noland 2009; Combes et al. 2012; Lavoratori and Castellani 2021; Andersson, Larsson, and Wernberg 2019). This has been attributed to the presence of Marshallian agglomeration externalities providing productivity advantages due to geographical clustering: the provision of specialized (labor) inputs and business services, and increased knowledge spillovers and local demand. These possible externalities generally motivate firms to choose locations where similar establishments are clustered, an intuition that has been supported by formal economic models (Krugman 1991; David and Rosenbloom 1990) and empirical studies (Belderbos, Olffen, and Zou 2011; Head, Ries, and Swenson 1994; Alcácer and Delgado 2016; Alcácer and Chung 2007; Frenken, Cefis, and Stam 2015; Belderbos, Kazimierczak, and Goedhuys 2022b).

The relationship between productivity and industrial agglomeration has also been suggested to be driven by a ‘selection’ effect associated with heightened competition within clusters. Collocation of firms in local markets can lead to tougher competition on input and output markets, forcing the exit of weaker firms with lower productivity (Melitz and Ottaviano 2008; Syverson 2004). As this implies that productive firms are more likely to benefit from, and survive, in locations with industry agglomeration than their less productive counterparts, it suggests that another reason for a positive relationship between agglomeration and productivity is that the more productive firms self-select into high-density locations (“positive sorting”).

However, the positive sorting conjecture has received little support in empirical testing, with research finding predominantly insignificant relationships (Faberman and Freedman 2016; Combes et al. 2012). Studies on (foreign) market entry in contrast have even concluded that larger and more research and development (R&D)-intensive firms are less, rather than more, responsive to locational agglomeration than smaller, less R&D-intensive firms (Myles Shaver and Flyer 2000; Belderbos and Carree 2002; Alcácer and Chung 2007; Mariotti, Mosconi, and Piscitello 2019). Hence, these studies observe “adverse selection” of “weaker” firms into agglomerated regions—although they were not able to use accurate firm performance measures in terms of productivity. Adverse selection may occur if productive firms with the most innovative technologies and organizational and process skills contribute more to local knowledge spillovers than less productive firms. This provides collocated firms of lower productivity with the opportunity to learn and increase their market share if they can mimic product designs and organizational approaches or acquire knowledge through employee mobility from the productive firms. As productive firms have an incentive to avoid strengthening local firms in this manner, they avoid locations with pronounced industry agglomeration. This leads to a negative relationship between productivity and agglomeration, in a process of adverse selection.

In this paper, we ague that the contrasting findings on the relationship between productivity at entry and agglomeration can be reconciled by considering the role of product market competition. The sorting effects of industry agglomeration depend on whether entrant and incumbent firms compete in the same product and geographic market. If firms are direct rivals in the same market, knowledge spillovers strengthening rivals have a direct negative effect on a productive firms’ market share and profit. Hence, although productive firms should be attracted to locations providing agglomeration benefits, the presence of incumbents competing in the same product market is likely to discourage productivity leaders to collocate due to the asymmetry in knowledge spillovers that disadvantages productivity leaders much more than productivity laggards. In the absence of product market competition, however, spillovers emanating from newly established plants of productive firms are les harmful for a productive firm's market share and profitability, and the positive influence of agglomeration dominates.

We uncover the nature of sorting effects by examining plant location decisions (during the period 2002–2008) by Japanese multi-plant firms at the fine-grained locational level. We improve on prior studies by taking a fine-grained approach accurately measuring the relevant productivity of entrants, the fine-grained geographical nature of knowledge spillovers, and the nature of product market competition. By focusing on multi-plant firms, we can accurately identify (adverse) selection effects by relating location decisions to entrant firms’ relevant ex ante productivity, as measured by the performance of their existing plants in the industry of entry. By taking a fine-grained geographical approach, distinguishing the 1805 regions that represent the lowest administrative unit in Japan in the observation period, we focus on the geographically proximate locational context in which non-market mediated knowledge spillovers tend to occur (Rosenthal and Strange 2020). We measure product market competition in a precise manner, by not only focusing on 4-digit industries—which is considered a relevant delineation of product markets (Bloom, Schankerman, and Van Reenen 2013)—but by also distinguishing between exporting and non-exporting firms. While entrants selling in the same 4-digit domestic market will be competing directly in a narrowly defined industry with local incumbents, exporting firms can be active in a variety of (geographic) end markets and hence are less likely to be direct market competitors.

We estimate conditional and mixed (random coefficients) logit models of location choice by entrant firms controlling for the positive influence of Marshallian agglomeration externalities (Glaeser and Kerr 2009; Alcácer and Chung 2013), which is important to separate and identify sorting effects. We control for intra-firm collocation advantages (e.g., Alcácer and Delgado 2016), local urbanization economies (Jacobs 1969; Beaudry and Schiffauerova 2009), purchasing power (e.g., Lavoratori and Castellani 2021; Rosenthal and Strange 2020), and local land rental costs (e.g., Puga 2010). We observe the most pronounced adverse selection effects for productive domestic market-oriented entrants facing incumbents with the same domestic market orientation, targeting the same product markets. In contrast, when entrants and local incumbents are less likely to compete in the same markets—if entrants target export markets and incumbents target the domestic market—positive agglomeration effects dominate.

Our study contributes to the literature on agglomeration and productivity by demonstrating that negative sorting processes do occur, but that they can only be uncovered in a more fine-grained analysis that considers accurate measures of firm heterogeneity and the nature of product market competition. Adverse selection is not a general feature of entry into agglomerated regions, but occurs if entrants and incumbents compete in the same product and geographic markets. This also provide an important nuance to the literature on (foreign) entry.

2 Background: Prior Literature on Agglomeration, Entry, and Productivity

Extant literature has proposed different theoretical influences shaping the relationship between industry agglomeration and productivity. The predominant explanation is the notion of Marshallian agglomeration externalities, which contends that firms can enjoy positive externalities stemming from geographical industry clustering, leading to productivity benefits. These externalities can occur on the input side, as increased demand for inputs and labor stimulates the provision of specialized (labor) inputs and specialized business services. Externalities may also occur through locally bounded spillovers of technological and organizational knowledge within the cluster, and on the demand side, as collocation of firms lowers search costs for customers and thus heightens local industry demand (e.g., Rosenthal and Strange 2020). This intuition has also been supported by formal economic models predicting clustering related to increasing returns (Krugman 1991; David and Rosenbloom 1990).

A second influence shaping the relationship between agglomeration and productivity that has been put forward is a “selection” effect associated with heightened competition within clusters. On the one hand, collocation of firms in local markets can lead to tougher competition on input and output markets, forcing the exit of weaker firms with lower productivity and leading to a “positive sorting” process through which more productive firms enter and remain in agglomerated areas (Melitz and Ottaviano 2008; Syverson 2004). Productive firms may also benefit more directly from agglomeration, for instance because hiring more specialized, productive workers provides relatively large productivity benefits to firms that operate more efficiently (Combes et al. 2012), or because efficient firms benefit more from the presence of specialized suppliers (Baldwin and Okubo 2006).

On the other hand, a stream of literature focusing on firm heterogeneity and asymmetric knowledge spillovers has argued that there may instead be negative sorting or “adverse selection” effects occurring in agglomerated areas. The explanation for this pattern relates to the role of knowledge spillovers in local industry agglomeration. Productive firms with the most innovative technologies and organizational and process skills contribute more to local knowledge spillovers than less productive firms. This provides the collocated less productive firms with the opportunity to learn and increase their market share if they can mimic product designs and organizational approaches or acquire knowledge through employee mobility. Evidence on the effects of plant openings and closures on local productivity has confirmed that such local learning from leading firms can be substantial (Greenstone, Hornbeck, and Moretti 2010). Productive firms thus have an incentive to avoid such spillovers to guard their market share and profits, and hence may seek to avoid locations with pronounced industry agglomeration. This suggests that the more productive firms, are less, rather than more, likely to self-select into industry clusters. Adverse selection rather than positive sorting occurs - due to asymmetry in knowledge spillovers between market rivals.

Finally, while Marshallian agglomeration economics emphasize the benefits of regional clustering of industries and hence specialization, another stream of literature has posited that it is the diversity of industries in the region that provide benefits (Jacobs 1969; Beaudry and Schiffauerova 2009; Lavoratori and Castellani 2021; Andersson, Larsson, and Wernberg 2019). A greater variety of industries within a region can foster knowledge externalities through greater opportunities to share and recombine ideas. Such potential benefits, which have also been coined “urbanization economies,” are seen to play in the wider geographic areas and particularly in the context of cities.

Several research traditions have sought to uncover empirical evidence on the relationship between agglomeration and productivity. Research relating local productivity to industry agglomeration has generally observed that agglomeration is associated with productivity benefits (e.g., Rosenthal and Strange 2020; Melo, Graham, and Noland 2009; Combes et al. 2012; Lavoratori and Castellani 2021; Andersson, Larsson, and Wernberg 2019), while it has proven difficult to disentangle Marshallian agglomeration economics from urbanization economics (Beaudry and Schiffauerova 2009). A related literature has aimed to identify the mechanisms underlying Marshallian externalities, by measuring the degree to which the specialized nature of local labor, supplier and buyer industries, and knowledge spillovers provides benefits to a focal industry (Alcácer and Chung 2013; Glaeser and Kerr 2009) and generally confirmed the positive role of such agglomeration externalities.

A research stream on locational choices of firms has found support for the notion that externalities motivate firms to choose locations where similar establishments are clustered (e.g., Belderbos, Olffen, and Zou 2011; Head, Ries, and Swenson 1994; Alcácer and Delgado 2016; Alcácer and Chung 2007; Frenken, Cefis, and Stam 2015; Belderbos, Kazimierczak, and Goedhuys 2022b). Studies examining the relationship between industry agglomeration and the formation of new firms have likewise observed a positive association between the two (e.g., Rosenthal and Strange 2003; Glaeser and Kerr 2009). Less support has been found for the notion of positive sorting of such entrants: Faberman and Freedman (2016) find no evidence of positive sorting for U.S. establishments in metropolitan areas, while Combes et al. (2012) likewise fail to find evidence of selection of higher productivity firms in France. Another research stream focusing on (foreign) market entry in the context of knowledge asymmetries has, by and large, concluded that larger and more research and development (R&D)-intensive firms are less, rather than more, responsive to locational agglomeration than smaller, less R&D-intensive firms (Myles Shaver and Flyer 2000; Belderbos and Carree 2002; Alcácer and Chung 2007; Mariotti, Mosconi, and Piscitello 2019). In general, the extant literature on sorting has not yet been able to provide clear answers on the nature of the relationship between agglomeration and sorting. Our paper contributes by providing such answers by conducting a fine-grained analysis examining ex-ante productivity levels of entrant firms and the level of product market competition in detail.

2.1 Our Paper

We conclude that the notion of Marshallian externalities received broad support, while there are inconclusive results on the nature of sorting processes. We argue that the nature of sorting depends on firms’ ex ante productivity and the precise nature of product market competition. Sorting effects of agglomeration depend on whether entrant and incumbent firms compete in the same product and geographic market. If firms are direct rivals in the same market, knowledge spillovers strengthening the rival have a direct effect on firms’ market shares and profits. Hence, although productive firms should be attracted to locations providing agglomeration benefits, the presence of incumbents competing in the same product market is likely to discourage productivity leaders to collocate due to the asymmetry in knowledge spillovers that will disadvantage leaders much more than laggards. If on the other hand productive firms do not face such direct threats to market share and profits, adverse selection effects will play a lesser role.

Prior empirical studies have not generally been able to provide a meticulous testing framework. Identifying the nature of the sorting process requires (1) accurate measurement of ex-ante productivity of the entrant firms; (2) accurate measurement of the relevant product markets on which entrants and incumbents are competing; (3) fine grained locational analysis to uncover the influence of knowledge spillovers; (4) controlling for Marshallian externalities and urbanization economies. Our empirical strategy explained in the next section is designed to meet these requirements.

3 Empirical Strategy, Data, Variables, and Method

3.1 Empirical Strategy

We examine the plant location decisions of Japanese multi-plant firms at the fine-grained location level of municipalities and wards in Japan that represent the lowest administrative regional units in the country. We identify market competition by not only focusing on industry agglomeration and entry into 4-digit industries—which is considered a relevant delineation of product markets (Bloom, Schankerman, and Van Reenen 2013)¹, but by also distinguishing between exporting and non-exporting entrant firms and incumbents. While entrants selling in the domestic market will be competing directly in a narrowly defined industry with local incumbents if incumbents also target the domestic market, exporting firms are more likely to be active in a variety of (geographic) end markets and hence are less likely to face direct market competition from incumbents. We therefor distinguish between exporting firms and pure domestic market-oriented firms—both on the incumbent side and on the entrant side—to examine the role or product market rivalry in the same geographic market. Direct product market rivalry occurs if both the incumbents and the entrants are (1) active in the same 4-digit industry (2) sell on the domestic market.

To identify positive or negative sorting we require a measure of firm productivity before entry, and a productivity measure that should be relevant for the focal product market where the firm faces knowledge spillovers. We obtain an accurate measure of productivity by focusing the analysis of entry on multi-plant firms, for which we can observe productivity levels in the focal industry by examining their existing plants. We control for Marshallian externalities by including measures of the industrial structure of the local region, i.e. the specialization of the local region in supplier and buyer industries, industries with a related knowledge base, and industries using similar types of labor as the focal industry. After controlling for measures of Marshallian externalities, the effect of focal industry agglomeration represents the response of firms to product market competition and within-industry knowledge spillovers: the focus of our sorting analysis. Positive or negative sorting (adverse selection) is inferred by the interaction term between 4-digit industry agglomeration and entrant firm productivity.

To account for the possibility that productive firms may benefit more from particular Marshallian externalities than less productive firms Combes et al. 2012; Baldwin and Okubo 2006), we also allow the effects of the variables measuring these externalities to vary due to the productivity of the entrant. Finally, we include a measure of urbanization economics (industry diversity) to capture possible positive influences on entry of regional diversity.

3.2 Data

We draw on the Census of Manufacturers in Japan to identify new and existing plant establishments. We retrieved data for new entries and the productivity and exports of manufacturing plants (of incumbents as well as entrants) for the period 2001–2008. The reason for focusing on this period is as follows. First, shipment data for Japanese plans in the census distinguishing between exports and domestic shipments—an important distinction in our research—are available only from 2001 onward. Second, we end our observation period in 2008, since the shock of the global financial turmoil and recession in 2008 may cause a structural break complicating the analysis.² Since we require 1 year of data to measures lagged export status and productivity, the period during which we analyze the location of new plant entries is 2002–2008.

To identify whether adverse selection occurs, we need reliable data on heterogeneity in firm productivity and have to conduct several rounds of screening. We cannot use plants’ productivity after entry, as this is likely to be endogenous to agglomeration effects, but we can use information on productivity of existing plants of the entrant firm in the same industry. This implies that we focus analysis on new entries by multi-plant firms, for which we can establish firm level productivity in the industry before entry.

We are interested in entry decisions regarding locations that are new to the investing firm (in a particular industry). In existing locations, the establishment of new plants will not be very different from the expansion of existing plants, so that considerations with respect to external agglomeration effects or knowledge spillover are less likely to be relevant. We therefore focus on the location choice for new plants in locations in which a firm has no existing plant in the industry. In other words, we exclude new entries if firms already have a plant in the same industry in the same location. We retain new entries if the existing establishment of the firm in the location is in a different industry or if it fulfils headquarters operations.

To ensure that our productivity measure is accurate, we only focus on new establishments where we have observations of the productivity level for at least two plants belonging to the same firm and industry This helps to avoid that our measure of productivity is “contaminated” by idiosyncratic locational characteristics affecting the productivity level of a single sister plant. If a multi-plant firm has higher productivity levels across locations, this likely reflects superior capabilities, technologies, and knowledge that can be transferred across plants, and that are potentially put at risk of spillovers when the firm establishes a new plant in the vicinity of rival firms. We observe 883 new manufacturing plant establishments in new to the firm locations by 749 firms with a least two existing plants in the same industry as the new plant during 2002–2008. This is our sample for analysis.³ We distinguish entries by firms that have export operations (their existing plants export) and entries by firms that do not export from their existing plants.

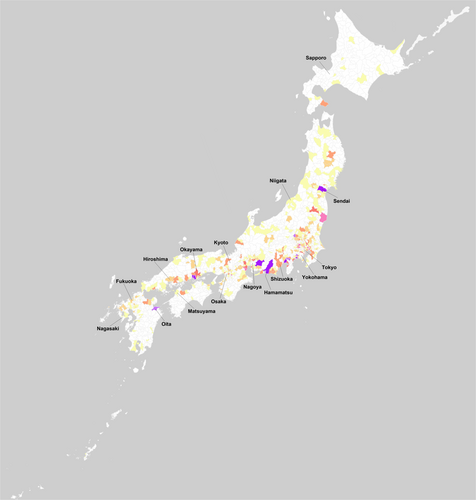
We use the most detailed regional demarcation available in Japan, namely, municipalities and wards.⁴ This is the lowest administrative level in Japan, and there are 1788 regions (“locations” in our analysis) in total at this level during the observation period.⁵ The 23 wards of Tokyo, for instance, are separate administrative units with their own councils and administration, while the rest of the Tokyo metropolitan area consists of a further 39 administrative regions. The average population of a region/location is 72,000. This demarcation is generally more-fine grained than the NUTS-3 regions in Europe or Metropolitan Statistical Areas in the United States. The regional demarcation is illustrated in Figure 1 below.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Regions in Japan receiving new manufacturing entries by the sample firms. Note: Number of entries ordered by darkness of color, with regions in purple receiving the largest number of entries (more than 20) and regions in yellow receiving 1–2 entries.

While the (theoretical) maximum number of locations firms can choose from is 1788, we conservatively take the choice set for a particular 4-digit industry as smaller and consisting only of locations for which there is evidence that there is a realistic chance that they are a potential destination for new plant establishments. Specifically, we include locations in the choice set if we observe at least one existing or new establishment in the industry in that location. Omitting region-industry combinations without any establishments or plant entries keeps the models convergent and computationally feasible, whilst including locations with no realistic chance of receiving investments runs the risk of violating the independence of irrelevant alternatives assumption (see below) characterizing conditional logit models (McFadden 1974; McFadden and Train 2000).

Table 1 provide details on the locational choice set and the entries per industry. We aggregated the statistics to the level of 45 industry groups for exposition. There is a good spread of entries across the spectrum of industry groups. The largest numbers of entries are recorded in the food industry and the motor vehicle parts industries. On average, the choice set for entries in a 4-digit industry consists of 403 regions. Our restriction of the choice sets to those regions that have hosted or attracted at least one establishment in the industry leads to variation in choice sets across industries. Choice sets range from five regions for highly spatially concentrated industries with few establishments (flour manufacturing within the flour and grain milling industry) to 1054 regions for geographically distributed industries (food manufacturing not classified elsewhere within the miscellaneous foods industry). Multiplying the number of entries with the number of locations in the choice set for the 4-digit industry give the number of observations in the locational choice models.

Table 1. New plant entries and number of locations in the choice set per industry group.

				Choice set: # locations per 4-digit industry
	# 4-Digit industries	# Entries	# Firms	# Obs	Mean	SD	Median	Min	Max
Livestock products	3	39	25	12087	312	94	298	198	476
Seafood products	4	9	9	3184	354	189	479	110	526
Flour and grain mill products	2	5	5	731	146	79	180	5	186
Miscellaneous foods and related products	14	101	83	70278	693	335	926	27	1054
Prepared animal foods and organic fertilizers	1	10	8	1231	123	3	122	119	127
Beverages	4	12	12	2174	181	134	176	27	316
Textile products	9	19	15	5159	281	172	275	68	674
Lumber and wood products	3	8	8	2117	265	117	323	21	351
Furniture and fixtures	2	2	2	1292	646	8	646	640	652
Pulp, paper, and coated and glazed paper	3	21	11	775	37	12	31	22	67
Paper products	4	33	30	10440	316	83	343	35	374
Printing	3	43	40	30400	704	291	829	154	912
Rubber products	2	5	5	1472	294	156	354	17	379
Chemical fertilizers	1	2	2	91	46	2	46	44	47
Basic inorganic chemicals	2	9	8	966	107	2	107	104	110
Organic chemicals	4	5	5	187	37	40	12	7	97
Miscellaneous chemical products	5	18	17	1655	92	59	117	20	186
Pharmaceutical products	3	19	14	1787	94	58	129	10	142
Petroleum products	2	5	3	82	16	14	11	8	41
Coal products	2	9	6	890	99	75	55	46	209
Glass and its products	4	19	19	2201	116	39	130	16	138
Cement and its products	3	43	35	17240	401	130	404	135	627
Miscellaneous ceramic, stone and clay products	5	9	9	696	77	102	43	28	346
Miscellaneous iron and steel	9	40	35	8001	200	128	170	9	380
Smelting and refining of non-ferrous metals	3	4	4	200	50	18	57	23	63
Non-ferrous metal products	4	7	7	926	132	31	141	70	158
Fabricated constructional metal products	3	26	23	21117	812	88	802	709	994
Miscellaneous fabricated metal products	13	45	37	9058	201	111	120	40	481
General industry machinery	4	12	12	2965	247	91	292	80	312
Special industry machinery	5	22	21	6306	287	92	262	157	412
Miscellaneous machinery	5	14	14	6722	480	254	605	15	681
Office and service industry machines	2	5	5	1023	205	60	164	156	272
Electrical distribution and industrial apparatus	4	28	25	11,260	404	107	437	176	580
Household electric appliances	1	4	1	1468	367	—	367	367	367
Electronic data processing machines	1	2	2	749	375	19	375	361	388
Communication equipment	2	3	3	505	168	45	194	116	195
Electronic (measuring) equipment	1	3	3	558	186	3	188	182	188
Semiconductor devices and integrated circuits	2	17	13	1249	73	11	78	43	80
Electronic parts	6	27	24	11473	417	246	372	16	703
Miscellaneous electrical machinery equipment	3	6	4	1291	215	95	269	42	274
Motor vehicles	1	1	1	69	69	—	69	69	69
Motor vehicle parts and accessories	1	104	81	82614	793	49	834	733	844
Other transportation equipment	3	4	3	377	94	30	98	61	120
Precision machinery & equipment	5	8	8	848	106	39	114	58	162
Plastic products	8	53	49	21081	398	197	366	6	627
Miscellaneous manufacturing industries	3	3	3	557	186	128	159	73	325
All	174	883	749	357552	403	303	344	5	1054

Note: Choice sets are locations for which a least one plant is observed in the 4-digit industry.
***p < 0.01, **p < 0.05, *p < 0.10.

Figure 1 illustrate the regions in Japan and the frequency of manufacturing entries by the sample firms, with darker colors representing greater frequency. The entries exhibit a substantial regional spread, in particular across the main island (Honshu). Due to the high congestion costs and space limitations, new manufacturing are typically not that abundant in the Tokyo area. Higher numbers of entries are found around the northern city of Sendai, near Hamamatsu and Nagoya (the home of an automobile cluster around Toyota) in the center, and near Okayama and Oita further south.

3.3 Productivity (TFP)

Plant-level TFP is measured using the index number method, based on data available from the Japan Industrial Productivity Database (Fukao et al. 2007; Belderbos et al. 2013; RIETI 2018). An advantage of the index number method is that it allows for heterogeneity in the production technology of individual firms, while other methods controlling for the endogeneity of inputs (e.g., Olley and Pakes 1996; Levinsohn and Petrin 2003) assume an identical production technology among firms within an industry (Van Biesebroeck 2007; Aw, Chen, and Roberts 2001).⁶ The index-based method has a long history (e.g., Caves, Christensen, and Diewert 1982; Jorgenson and Griliches 1967) and its flexibility in use across settings has made it the productivity measure of choice for international productivity comparisons such as the KLEMS project (Van Ark, O'Mahony, and Timmer 2008; Bontadini et al. 2023). The productivity index captures the TFP of a plant relative to a representative firm in the industry in a base year and uses gross output-based measures.⁷ The relative measurement is well suited for our purpose, as we are interested in relative measures of productivity in an industry rather than absolute measures.

We investigate what position plants occupy in the distribution of productivity levels across plants in the same 4-digit industry in Japan during the year before entry. We calculate, on a yearly basis, the TFP premium as the log of the difference between the output weighted average TFP in the firm's existing plants and the mean level of TPF in the industry (using plant output as weights). Leading firms (those with TFP above the mean) have positive values for the TFP premium, while lagging firms (those with TFP below the mean) have negative values for the TFP premium.

Our calculations indicate that multi-location plant firms are more productive than single-location plant firms, with firms with existing plants in one or more locations enjoying a TFP premium of 0.063 compared with the industry average. Our focus on multi-plant firms most likely raises the bar for finding adverse selection related to heterogeneity in productivity, since we effectively focus on firms in the top of the distribution, diminishing the variation in productivity.

3.4 Industry Agglomeration and Marshallian Externalities

To disentangle agglomeration mechanisms from the agglomeration effects related to spillovers to rivals, we employ the specification of Alcácer and Chung (2013) and Glaeser and Kerr (2009). We distinguish the effect of the volume of agglomeration in an industry and location from the specialization of the location in other industries that can provide agglomeration advantages through Marshallian mechanisms: supplier linkages, buyer linkages, labor pooling, or knowledge spillovers from related industries. The logic is that agglomeration is associated with a specialized industry structure in a region that provides advantages for new entries. With the Marshallian externalities due to industry structure in a region controlled for, the volume of agglomeration in the focal industry in a region is representative of the influence of competition and knowledge spillovers in the product market.

Industry agglomeration is measured as output in the industry at the 4-digit level in the region relative to the industry-year average across regions. We follow previous literature by using industry output as a size related count of establishments, given that this allows to better account for scale effects compared with an establishment count (Arzaghi and Henderson 2008; Martin, Mayer, and Mayneris 2011, Lavoratori and Castellani 2021). Specifically, we measure industry agglomeration as:

Industry a {gglomeration}_{klt} = \frac{Y_{klt}}{\sum_{l = 1}^{L} Y_{klt} / L},

where subscript

k

denotes the 4-digit industry,

l

represents the location,

t

stands for time, and

Y_{klt}

is the output of industry

k

in location

l

at time

t

. L is is the total number of locations in the choice set. We distinguish industry agglomeration between exporting and non-exporting plants by calculating the output of plants that export, and plants that do not export, respectively.

We follow Glaeser and Kerr (2009) and Alcácer and Chung (2013) in constructing regional specialization variables to measure agglomeration externalities. We use the term “fit” to indicate that the specialization of a region in terms of the structure of local industries fits the supply, demand, labor, and/or knowledge needs of the industry in question (Alcácer and Chung 2013). Supplier (buyer) fit measures the locations’ relative specialization in related supplier (buyer) industries. To determine a location's specialization, we yearly input-output tables provided by the JIP database. Formally, we measure buyer fit for industry i in location l as follows:

{Buyerfit}_{klt} = [\sum_{k} outpu t_{i \to k} \times \frac{Y_{klt}}{Y_{kt}}] \times {[\frac{Y_{lt}}{Y_{t}}]}^{- 1} .

The subscripts $i, k$ denote industries, $l$ is the location, $t$ denotes time, $Y_{klt}$ is the output of industry $k$ in location $l$ at time $t$ , $outpu t_{i \to k}$ is the share of industry $i$ 's output that i sells to industry $k .$ $Y_{kt} = \sum_{l} Y_{klt}$ , $Y_{lt} = \sum_{k} Y_{klt}$ , and $Y_{t} = \sum_{k} \sum_{l} Y_{klt}$ . The measure multiplies the output share of industry k with the output share of that industry in the region in question. The smaller the deviations of the two across industries, the stronger the ‘fit’ between the local industry structure and the buyer profile of industry i. As suggested by Glaeser and Kerr (2009), the expressions are multiplied by the inverse sum of the ratio of the location's output over national output to ensure independence of industry size.

Following Glaeser and Kerr (2009) and Alcácer and Chung (2013), the measure of supplier fit is a variation on this. The supplier fit variable compares the share of a region in the national output of industry

k

with the share of industry

k

in the input needs of industry i:

{Supplier}_{klt} = - \sum_{k} (|inpu t_{i \leftarrow k} - \frac{Y_{klt}}{Y_{lt}}|) .

We measure labor fit for industry i in location l as:

{Laborfit}_{klt} = - \sum_{o} |L_{io} - \frac{{\hat{E}}_{olt}}{{\hat{E}}_{lt}}|,

where ο indexes occupations,

L_{io}

is the percentage of industry

i

's employment in occupation

o

, which is obtained from the 2005 Population Census, and

{\hat{E}}_{olt}

represents employment in occupation

o

in location

l

at time

t

, which is obtained from the Census of Manufacture. Hence, labor fit increases if the region is specialized in those industries that share similar occupations as industry i. In that case, the occupation use of the industry is aligned with the actual distribution of employment across occupations in the region.

The knowledge fit variable represents spillovers from other industries—as opposed to within-industry spillovers—associated with local agglomeration. To measure the importance of knowledge spillovers across industries, we make use of cross-industry patent citations to identify industries that are most likely to provide relevant knowledge to industry i. Specifically, we measure knowledge fit as follows:

{Knowledgefit}_{klt} = [\sum_{k} {citations}_{i \leftarrow k} \times \frac{P_{klt}}{P_{kt}}] \times {[\frac{P_{lt}}{P_{t}}]}^{- 1} .

Where ${citations}_{i \leftarrow k}$ is the share of backward citations that patents in industry $i$ make to industry $k$ , $P_{klt}$ is the stock of patents generated by firms in industry $k$ in location $l$ at time $t$ , while $P_{kt} = \sum_{l} P_{klt}$ , $P_{lt} = \sum_{k} P_{klt}$ , and $P_{t} = \sum_{k} \sum_{l} P_{klt}$ . Patent citation and patent stock data are obtained from the IIP Patent Database compiled by the Institute of Intellectual Property based on Japan Patent Office data. If there are multiple citations (from within the same or from different industries), each citation counts in the calculation of the inter-industry knowledge flow weights based on citation shares. The knowledge fit variable takes a higher value if the region is specialized in patenting in those domains that are more often cited by firms in the industry.

Finally, our analysis includes a variable measuring the potential beneficial effects of urbanization at a broader geographic level of geography (e.g., Lavoratori and Castellani 2021; Rosenthal and Strange 2020; Martin, Mayer, and Mayneris 2011; Andersson, Larsson, and Wernberg 2019; Beaudry and Schiffauerova 2009). We follow prior work (e.g., Lavoratori and Castellani 2021) by measuring urbanization advantages as the diversity of industrial activity in the broader region. In the context of Japan, such broader regions are defined as economic areas, of which there are 843 (Asahi Newspaper Corporation 2010). We include the Blau index of industry diversity (e.g., Beaudry and Schiffauerova 2009) which is one minus the Herfindahl index of the concentration of manufacturing output across industries.

3.5 Control Variables

We include a range of control variables in the location choice models. First, since we measure agglomeration using output, the measure may mask different types of regional industry structures in terms of the distribution of output among existing plants. For instance, output may be concentrated among one or two large plants, or it may be evenly distributed across many plants. If a large plant dominates, there may be fewer spillovers than if output is more or less evenly distributed across plants, and entrants may be discouraged if they fear the competition of the dominant firm (Alcácer and Chung 2013). Opportunities to benefit from spillovers may be reduced if there is a strong concentration of activities in one or a few firms (Cantwell and Mudambi 2011; Belderbos and Somers 2015). We therefore include the Herfindahl Hirschman (HHI) Index (e.g., Martin er al. 2011)—the sum of the market shares of individual plants in the region and industry—as an indicator of concentration.

While the buyer fit variable captures demand-side agglomeration benefits, a limitation is that it is based on input-output tables and only captures the presence of industrial buyers in the region and hence does not capture the demand from consumers for final goods. Therefore, to control for variation in the purchasing power of end consumers in a region, we include taxable income per capita. Income per capita is available at the economic area level (Asahi Newspaper Corporation 2010).

Our analysis also controls for congestion effects (Rosenthal and Strange 2020), by including a measure of land prices. We obtain information on land prices from Toyo Keizai Inc (2013).8 Finally, we control for “internal agglomeration” or collocation effects due to other establishments of the firm. We include a dummy variable for the presence of other plants of the firm in a different industry (including firm's headquarters operations). In addition, we include two variables capturing the distance of the region to the firm's headquarters (in cases in which headquarters are located in a different region), and the distance to the nearest other plant of the firm, respectively.

3.6 Method

The location choice literature (e.g. Alcácer and Chung 2007, 2013; Head, Ries, and Swenson 1994; Head and Mayer 2004; Du, Belderbos, and Somers 2022; Belderbos, Olffen, and Zou 2011) has primarily used the conditional logit model (McFadden 1974) to analyze the locational determinants of investments. The conditional logit model can be derived from a profit maximization framework under suitable assumptions concerning the distribution of the error term. McFadden (1974) proposed modeling expected utility in terms of the characteristics of choices, rather than the characteristics of agents making the decision. In the context of location choices by firms for new plant establishments, firm characteristics do not vary by location and as such cannot affect the location choice. The value of such firm characteristics would be identical across choices such that they would drop out of the equation. If locational characteristics are firm-specific (such as the presence of a headquarters facility in the region), or if the influence of locational characteristics is moderated by firm characteristic (such as the moderating effect of firm TFP on the influence of industry agglomeration), firm characteristics do play a role.

We illustrate this with a formal representation of the conditional logit model. Suppose investing firm f makes a location decision D_f among L alternatives. Let U_fl be the expected utility of the l-th choice for the firm. U_fl is an independent random variable with a systematic component x_fl’β, where x_fl represents a vector of characteristics of the l-th choice for firm f. The expected utility of firm f's location choice can be modeled in terms of the observable attributes of the choice and an unobservable error term:

U_{fl} = x_{fl} β + ε_{fl} .

McFadden (1974) showed that if the error terms

ε_{fl}

are independent and identically distributed with Type I extreme-value distribution, the probability that firm f chooses to invest in location l is given by the following formula:

Pr (D_{f} = l) = \frac{exp (x_{fl} β + ε_{fl})}{\sum_{l = 1}^{L} exp (x_{fl} β + ε_{fl})} .

This conditional logit model can be estimated with maximum likelihood. It is important to note that the conditional logit model assumes independence of irrelevant alternatives (IIA). The IIA property states that for any two alternatives, the ratio of probabilities is independent of the characteristics of any other alternative in the choice set. This characteristic also implies the absence of correlations between error terms across alternatives. At the detailed regional level of analysis, the likelihood of spatial correlation is high, as regional boundaries do not necessarily demarcate the border of agglomeration externalities.⁹ One solution to this is to estimate random coefficient mixed logit models (McFadden and Train 2000) that relax the IIA assumption by allowing coefficients to vary. We do so in a supplementary analysis, allowing all coefficients to have a random parameter with a normal distribution. A second approach, which we also employ, is to examine distance-weighted variables measured across (neighboring) regions. In such models, industry agglomeration becomes the sum of the output of all industry establishments in a particular region and other (neighboring) regions weighted by the geographic distance between regions, with weights taken as 3/2r (where r represents distance).¹⁰ We extend the reach of the agglomeration variables to 5 and 10 km from the region's core.

We test for adverse selection or positive sorting by including the interaction term of the 4-digit industry agglomeration measure and the TFP premium variable. That is, we add a term of the form $x_{f} \times x_{fl} β$ , where $x_{f}$ is TFP and $x_{fl}$ is industry agglomeration. We also interact the TFP premium variable with the agglomeration mechanism (specialization) variables to allow for heterogeneity in agglomeration benefits among firms. Subsequently, we examine location decisions separately for entrants with, and without, an export orientation, and for different kinds of agglomeration (exporting incumbents vs. non-exporting incumbents). We expect that adverse selection occurs primarily of incumbents and entrants are direct competitors: they are active in the same 4-digit industry and they target the same (domestic) market.

3.7 Descriptive Statistics

Table 2 shows the descriptives and correlations of the variables. Continuous variables, except for the agglomeration fit variables (which can take negative values), are expressed in natural logarithm. Table 3 provides some prima facie evidence of potential adverse selection. Panel I shows the average industry output agglomeration values for regions chosen by entrants, distinguishing between agglomerations of exporting and non-exporting plants. The table compares the agglomeration levels between leading TFP firms (firms with TFP above the median of entrants in the industry) and lagging TFP firms (firm with TFP below the median). We observe a clear pattern, with agglomeration levels higher for laggards (1.693) than for leaders (0.881). This difference is statistically significant (p < 0.05). A similar pattern is observed for non-exporter agglomeration (1.588 vs. 0.758, p < 0.05). In contrast, for exporter agglomeration, there is no such difference (0.657 vs. 0.669, p = 0.96). Distinguishing between exporting and non-exporting firm entries, Panel II shows that for non-exporting firms, similar patterns are observed, with the differences between TPF leaders and laggards are even more significant. On the other hand, Panel III, for exporting firm entries, shows that while agglomeration levels in all cases are lower for TFP leaders, the differences with TPF laggards are not significant. Even in the case of exporter agglomeration, where competitive considerations are most likely to play a role for exporting entrants, the difference does not reach conventional significance levels (p = 0.051). We conclude that the descriptive evidence is in line with our conjecture that TFP leaders are less likely to locate in agglomerated areas, in particular if they face local rivals there that compete on the same product and geographic market.

Table 2. Descriptive statistics and correlations.

		Mean	SD	[1]	[2]	[3]	[4]	[5]	[6]	[7]	[8]	[9]	[10]	[11]	[12]	[13]	[14]	[15]	[16]	[17]
[1]	Entry	0.002	0.050	1.000
[2]	TFP premium (ln)	0.057	0.228	0.001	1.000
[3]	Industry agglomeration (ln)	0.000	4.510	0.014	0.000	1.000
[4]	Non-exporter industry agglomeration (ln)	0.000	4.493	0.012	0.000	0.974	1.000
[5]	Exporter industry agglomeration (ln)	0.000	3.531	0.009	0.000	0.267	0.151	1.000
[6]	Buyer industry fit	24.410	66.617	0.005	−0.002	0.136	0.123	0.170	1.000
[7]	Supplier industry fit	−27.504	35.365	0.016	−0.015	−0.016	−0.020	0.040	−0.166	1.000
[8]	Knowledge fit	1.787	8.136	0.006	−0.011	0.036	0.033	0.026	0.038	0.053	1.000
[9]	Labor fit	−1.214	0.236	0.009	−0.025	0.211	0.198	0.179	0.261	−0.259	0.029	1.000
[10]	HHI	0.487	0.371	−0.006	−0.003	0.437	0.414	−0.021	−0.017	−0.021	0.018	−0.011	1.000
[11]	HQ of the firm	0.000	0.021	0.070	0.004	0.011	0.011	0.011	0.007	0.006	0.001	0.001	−0.005	1.000
[12]	Firm plant other industry	0.001	0.032	0.032	0.012	0.016	0.017	0.009	0.008	0.003	0.001	0.011	−0.002	0.093	1.000
[13]	Min. distance from firm's other plant (	5.178	1.141	−0.040	−0.035	−0.093	−0.092	−0.052	0.007	−0.024	0.032	−0.002	0.014	−0.026	−0.032	1.000
[14]	Distance from firm's HQ	5.541	1.065	−0.046	−0.034	−0.104	−0.102	−0.056	0.001	0.051	0.045	−0.059	0.017	−0.166	−0.040	0.688	1.000
[15]	Land price	−0.465	0.957	0.007	0.030	0.200	0.199	0.081	−0.022	−0.029	−0.046	0.002	−0.024	0.035	0.016	−0.248	−0.320	1.000
[16]	Industry diversity	0.778	0.247	0.006	0.015	0.129	0.130	0.016	−0.069	−0.074	0.034	−0.074	0.270	0.005	0.004	−0.032	−0.053	0.267	1.000
[17]	Income per capita	7.157	0.217	0.011	0.020	0.157	0.154	0.090	−0.001	−0.031	−0.078	0.074	−0.050	0.029	0.014	−0.342	−0.421	0.684	0.033	1.000

Note: All variables except dummy variables and fit measures are in natural logarithm.

Table 3. Differences in agglomeration levels of entry locations: TFP leaders versus TFP laggards.

I. All firms’ entries	All	Laggards (less than median)	Leaders (above median)	p value difference
Agglomeration	1.287	1.693	0.881	0.028**
Non-exporter agglomeration	1.172	1.588	0.758	0.024**
Exporter agglomeration	0.663	0.657	0.669	0.967
# Entries	883	441	442
II. Non-exporter entries	All	Laggards (less than median)	Leaders (above median)	p value difference
Agglomeration	1.132	1.628	0.579	0.008***
Non-exporter agglomeration	1.050	1.512	0.535	0.013**
Exporter agglomeration	0.565	0.444	0.699	0.373
# Entries	747	394	353
III. Exporter entries	All	Laggards (less than median)	Leaders (above median)	p value difference
Agglomeration	2.135	2.241	2.079	0.876
Non-exporter agglomeration	1.846	2.224	1.646	0.585
Exporter agglomeration	1.205	2.443	0.551	0.051*
# Entries	136	47	89

Note: ***p < 0.01, **p < 0.05, *p < 0.10. Agglomeration is the difference from the industry average.

4 Empirical Results

The results of the conditional logit models of location choice for new plants are presented in Table 4. Model 1 includes the agglomeration and control variables, Model 2 adds the interaction of agglomeration and TFP of the investing firm, while Model 3 also includes the interactions of TFP and the agglomeration mechanism (“fit”) variables. Models 4 and 5 distinguish between exporting and non-exporting entrant firms. Model 5 also separates the influences of exporting and non-exporting incumbent agglomeration in the region.

Table 4. Conditional logit estimates of the location choice for new plant entries.

				Model 4		Model 5
	Model 1	Model 2	Model 3	Non-exporters	Exporters	Non-exporters	Exporters
Industry agglomeration	0.0853***	0.0888***	0.0902***	0.0907***	0.0708***
	[0.00945]	[0.00968]	[0.00972]	[0.0105]	[0.0264]
TFP premium * Industry agglomeration		−0.0535*	−0.0655**	−0.107***	0.176*
		[0.0285]	[0.0296]	[0.0317]	[0.0905]
Non-exporter industry agglomeration						0.0785***	0.0433*
						[0.0103]	[0.0242]
TFP premium * Non-exporter industry agglomeration						−0.104***	0.1150
						[0.0316]	[0.0832]
Exporter industry agglomeration						0.0180	0.0320
						[0.0111]	[0.0195]
TFP premium * Exporter industry agglomeration						−0.0124	−0.0457
						[0.0398]	[0.0807]
Buyer industry fit	0.0829**	0.0815**	0.0858**	0.0781**	0.273**	0.0794**	0.276**
	[0.0352]	[0.0352]	[0.0355]	[0.0393]	[0.115]	[0.0391]	[0.116]
Supplier industry fit	0.272	0.276	0.406*	0.394*	−0.0833	0.3810	−0.1240
	[0.204]	[0.204]	[0.210]	[0.234]	[0.515]	[0.234]	[0.517]
Knowledge fit	0.000182	0.000201	−0.0002	0.000871	−0.04330	0.0009	−0.0440
	[0.00255]	[0.00257]	[0.00290]	[0.00262]	[0.0314]	[0.00260]	[0.0315]
Labor fit	0.374	0.377	0.2180	0.075	1.232*	0.1130	1.207*
	[0.240]	[0.240]	[0.253]	[0.279]	[0.663]	[0.279]	[0.673]
TFP premium * Buyer industry fit			−0.0249	0.0211	-0.684	0.0202	−0.5960
			[0.207]	[0.224]	[0.724]	[0.223]	[0.698]
TFP premium * Supplier industry fit			−2.086**	−2.766**	1.473	−2.771**	1.4780
			[0.955]	[1.075]	[2.232]	[1.076]	[2.211]
TFP premium * Knowledge fit			−0.0099	−0.00706	−0.0556	−0.0071	−0.0443
			[0.0103]	[0.0106]	[0.180]	[0.0105]	[0.180]
TFP premium * Labor fit			1.865**	2.339**	−1.355	2.316**	−0.7340
			[0.900]	[0.978]	[2.637]	[0.978]	[2.602]
HHI	−1.091***	−1.091***	−1.093***	−1.149***	−0.830***	−1.032***	−0.535*
	[0.120]	[0.120]	[0.120]	[0.132]	[0.304]	[0.129]	[0.282]
HQ of the firm	1.405***	1.431***	1.423***	1.690***	−1.469	1.716***	−1.4470
	[0.353]	[0.354]	[0.354]	[0.373]	[1.472]	[0.372]	[1.463]
Firm plant other industry	1.677***	1.675***	1.637***	1.633***	1.962***	1.625***	1.994***
	[0.296]	[0.297]	[0.298]	[0.352]	[0.556]	[0.352]	[0.558]
Min. distance from firm's other plant	−0.583***	−0.584***	−0.585***	−0.618***	−0.360***	−0.619***	−0.367***
	[0.0353]	[0.0353]	[0.0353]	[0.0377]	[0.103]	[0.0377]	[0.102]
Distance from firm's HQ	−0.228***	−0.227***	−0.227***	−0.209***	−0.383***	−0.206***	−0.381***
	[0.0317]	[0.0317]	[0.0316]	[0.0337]	[0.0976]	[0.0336]	[0.0971]
Land price	−0.429***	−0.428***	−0.431***	−0.438***	−0.418***	−0.426***	−0.390**
	[0.0573]	[0.0573]	[0.0574]	[0.0622]	[0.155]	[0.0620]	[0.153]
Industry diversity	0.913***	0.915***	0.928***	0.952***	0.920**	0.910***	0.832*
	[0.172]	[0.172]	[0.173]	[0.187]	[0.451]	[0.188]	[0.457]
Income per capita	0.455*	0.453*	0.437*	0.482*	−0.0617	0.462*	−0.1070
	[0.253]	[0.253]	[0.252]	[0.273]	[0.702]	[0.272]	[0.699]
Wald Chi-square	978.0***	981.4***	989.3***	1020.8***		1002.3***
logLikelihood	−4438.7	−4437.0	−4433.1	−4417.3		−4426.5
Locational choice-set (average)	402.6	402.6	402.6	402.6		402.6
Number of entries	883	883	883	883		883
Observations	357,552	357552	357552	357552		357552

Note: ***p < 0.01, **p < 0.05, *p < 0.10. Standard errors in brackets.

The results show that entry probabilities are positively related to industry agglomeration, buyer fit, supplier fit (Models 3 and 4), labor fit (for exporters in Model 5), industry diversity, and income per capita. Prior activities in the region by the firm (headquarters or other plants) also increase entry choice probabilities, while industry concentration, land prices, and distance to other establishments of the firm exert negative influences. Knowledge spillover fit has no significant association with entry, perhaps because spillovers are more important within a particular focal industry rather than across different industries and because the influence of such spillovers is also partially picked up by supplier and buyer industry specialization in the region.

While the coefficients of the conditional logit model cannot be interpreted as marginal effects, the coefficients in exponentiated form represent the change in the odds (the probability ratio) that a firm chooses one particular region instead of another region. To facilitate comparison across variables, we calculate the odds ratio effects due to a standard deviation change in the variables. The coefficient (β = 0.0853) for industry agglomeration implies that a standard deviation change in agglomeration increases the odds that a region is chosen by 46 percent. This compares with an implied increase in the odds due to a standard deviation change in the land price of 39 percent, and an increase in the odds due to a standard deviation increase in income per capita by 10 percent, for instance.

The estimated influence of industry agglomeration in Model 1 conceals substantial variation in the role of agglomeration across the investing firms. The TFP premium in interaction with industry agglomeration brings this out and represents the sorting effect. The negative and marginally significant coefficient (β = −0.0535) in Model 2 suggests that, overall, there is weak adverse selection: productivity leaders are less attracted to industry agglomeration than productivity laggards. The interaction coefficient becomes more strongly negative and strongly statistically significant in Model 3 (β = −0.0655), in which also the agglomeration mechanisms are included in interaction with the TFP premium. Model 3 also shows that more productive firms are relatively more attracted to regions with a better labor fit, but less attracted to regions with a better supplier fit. The latter finding contradicts Baldwin and Okubo's (2006) hypothesis that more productive firms may benefit more from agglomeration because such firms benefit more from the presence of specialized suppliers. A possible explanation is that for leading firms supply industry specialization in a region is less important because they tend to procure inputs from preferred suppliers located further away (Todo, Matous, and Inoue 2016).

When we distinguish exporters and non-exporters in Model 4, we find that a negative interaction effect is observed only for non-exporters (β = −0.107). In contrast, for exporting firms, a larger TFP premium is associated with a marginally significant positive response to industry agglomeration (β = 0.176). In Model 5, we further consider the evidence on sorting by examining non-exporting firms’ response to the agglomeration of competing non-exporting incumbent plants. The results show that while non-exporter agglomeration attracts non-exporting firms’ plants (β = 0.0785), it also is non-exporter agglomeration that generates the negative selection effect of firms in terms of their TFP premium (β = −0.104). This provides further evidence that negative sorting occurs when firms focus on the same geographic product market. Meanwhile, for exporting firms, we find a marginally significant effect of non-exporter agglomeration (β = 0.0433), but there is no evidence of adverse selection. We posit that this is due to that fact that exporters and non-exporters target different geographic markets, reducing direct market rivalry. Exporter agglomeration exerts no significant influence on entry, which may be related to the much lower exporter plant density—with the average of non-exporter agglomeration more than 10 times greater (see Table 3).

The significantly negative interaction between the TFP premium and industry agglomeration suggests that the effects of agglomeration on the odds of location choice differ across firms. How important are these differences? Based on the estimated coefficients it can be calculated that the odds effects of industry agglomeration for non-exporting entrants is linearly declining and ranges from a large 154 percent for firms with the lowest TFP to a statistically insignificant minus 8 percent for the leading TPF firms in the industry. Using the estimates for the interaction term of the TFP premium and non-exporting plant agglomeration in Model 5 shows that non-exporting plant agglomeration raises the odds of location choice for non-exporting entrant firms by 137 percent for TFP laggards with the lowest TFP but reduces it by 11 percent for TFP leaders with the highest TFP. These results point to a very substantial negative sorting effect based on investing firms’ TFP levels: laggards, not leaders, are attracted to agglomerated regions.

4.1 Supplementary Analyses

We conducted a range of supplementary analyses for the specification in Model 5 to examine the robustness of our findings. The results are reported in Table 5. First, we estimated random coefficient mixed logit models that allow for general patterns of investor heterogeneity and correlated error terms across regions. Unlike conditional logit models, mixed logit models do not rely on the assumption of the independence of irrelevant alternatives. The results are consistent with those reported in Table 4. This is in line with our observation that while there is spatial correlation between entry decisions, Moran's test (Kondo 2018) generally rejected the hypothesis of spatial correlation of error terms of the models that we estimate. The estimated interaction effect between non-exporter agglomeration and the productivity premium is substantially larger than in Table 4 (β = −0.193) but has a higher standard error and is marginally significant.

Table 5. Supplementary analysis.

	Mixed logit		5 km geo scope		10 km geo scope		Fixed effects		(Non)exporting plants
	Exporting firms	Non-exporting firms	Exporting firms	Non-exporting firms	Exporting firms	Non-exporting firms	Exporting firms	Non-exporting firms	Exporting plants	Non-exporting plants
Exporting Industry agglomeration	0.021	−0.006	0.0343*	0.015	0.012	−0.005	0.002	−0.002	0.0428*	0.015
	[0.0241]	[0.0300]	[0.0189]	[0.0107]	[0.0182]	[0.00968]	[0.0208]	[0.0122]	[0.0221]	[0.0107]
TFP premium * exporting Industry agglomeration	−0.083	−0.045	−0.017	0.014	0.025	−0.003	−0.042	−0.030	−0.018	−0.012
	[0.111]	[0.0505]	[0.0747]	[0.0370]	[0.0665]	[0.0346]	[0.0830]	[0.0421]	[0.0829]	[0.0394]
Non-exporting industry agglomeration	0.256***	0.237***	0.0441*	0.0688***	0.030	0.0526***	0.036	0.0470***	0.026	0.0820***
	[0.0808]	[0.0288]	[0.0242]	[0.0103]	[0.0254]	[0.0106]	[0.0253]	[0.0117]	[0.0270]	[0.0102]
TFP premium * non-exporting Industry agglomeration	0.252	−0.193*	0.095	−0.0998***	0.151	−0.0781**	0.067	−0.0898***	0.074	−0.0960***
	[0.312]	[0.114]	[0.0826]	[0.0312]	[0.0942]	[0.0332]	[0.0813]	[0.0314]	[0.0940]	[0.0313]
Buyer industry fit	0.182	0.054	0.285**	0.100***	0.204	0.0989**	0.217	0.141**	0.087	0.055
	[0.190]	[0.0509]	[0.127]	[0.0387]	[0.131]	[0.0415]	[0.136]	[0.0614]	[0.139]	[0.0412]
Supplier industry fit	−0.769	−0.031	0.230	0.398*	1.096*	0.657**	0.978*	1.290***	0.079	0.412*
	[0.710]	[0.266]	[0.550]	[0.237]	[0.648]	[0.281]	[0.537]	[0.275]	[0.600]	[0.228]
Knowledge fit	−0.043	−0.005	−0.043	0.001	−0.056	0.002	0.000	0.003	0.029	0.001
	[0.0398]	[0.00680]	[0.0325]	[0.00252]	[0.0384]	[0.00262]	[0.0410]	[0.00326]	[0.0410]	[0.00261]
Labor fit	0.483	−0.187	0.036	−0.014	0.076	−0.010	0.778	0.087	1.434*	0.154
	[0.804]	[0.313]	[0.0744]	[0.0221]	[0.0717]	[0.0222]	[0.743]	[0.343]	[0.760]	[0.276]
TFP premium * Buyer industry fit	−1.288	−0.002	−0.394	0.086	0.263	0.052	−0.409	−0.139	0.968	−0.235
	[1.211]	[0.287]	[0.698]	[0.214]	[0.804]	[0.239]	[0.765]	[0.341]	[0.951]	[0.240]
TFP premium * Supplier industry fit	−0.001	−2.067	0.496	−1.908*	−0.716	−2.658**	0.290	−2.379**	2.220	−2.799***
	[3.221]	[1.264]	[2.318]	[1.108]	[2.715]	[1.273]	[2.189]	[1.092]	[2.497]	[1.047]
TFP premium * Knowledge fit	0.096	−0.012	−0.087	−0.005	−0.057	−0.009	−0.016	−0.002	−0.470	−0.007
	[0.165]	[0.0125]	[0.201]	[0.0103]	[0.225]	[0.0145]	[0.160]	[0.0165]	[0.301]	[0.0107]
TFP premium * Labor fit	0.364	1.060	−0.037	0.084	−0.266	0.075	0.635	2.802**	−4.819	3.009***
	[3.677]	[1.263]	[0.292]	[0.0701]	[0.404]	[0.0724]	[2.806]	[1.269]	[2.988]	[0.953]
HHI	0.840**	0.855***	−0.491*	−0.924***	−0.328	−0.728***	−0.517*	−0.827***	0.013	−1.093***
	[0.377]	[0.123]	[0.278]	[0.124]	[0.262]	[0.114]	[0.302]	[0.145]	[0.326]	[0.126]
HQ of the firm	−4.903	2.015***	−1.218	1.777***	−1.091	1.838***	−3.034	1.151***	−0.668	1.627***
	[4.060]	[0.672]	[1.456]	[0.371]	[1.434]	[0.371]	[1.962]	[0.435]	[1.352]	[0.366]
Firm plant other industry	−1.224	−2.732	2.065***	1.716***	2.071***	1.752***	1.565**	1.481***	3.029***	1.390***
	[5.032]	[2.368]	[0.559]	[0.353]	[0.559]	[0.355]	[0.621]	[0.385]	[0.607]	[0.341]
Min. distance from firm's other plant	−0.243	−0.583***	−0.370***	−0.617***	−0.355***	−0.616***	−0.399***	−0.623***	−0.276**	−0.628***
	[0.166]	[0.0535]	[0.102]	[0.0376]	[0.102]	[0.0376]	[0.109]	[0.0427]	[0.120]	[0.0370]
Distance from firm's HQ	−0.538***	−0.209***	−0.374***	−0.205***	−0.360***	−0.202***	−0.582***	−0.352***	−0.386***	−0.211***
	[0.146]	[0.0447]	[0.0968]	[0.0335]	[0.0966]	[0.0334]	[0.112]	[0.0421]	[0.109]	[0.0330]
Land price	−0.438**	−0.348***	−0.410***	−0.438***	−0.368**	−0.406***	−0.022	−0.153	−0.269	−0.441***
	[0.185]	[0.0662]	[0.153]	[0.0624]	[0.154]	[0.0629]	[0.596]	[0.572]	[0.187]	[0.0605]
Industry diversity	1.109	0.514**	0.710	0.868***	0.651	0.798***	0.710	0.906	0.119	1.008***
	[0.759]	[0.208]	[0.445]	[0.188]	[0.444]	[0.187]	[1.225]	[1.123]	[0.511]	[0.187]
Income per capita	0.042	0.506*	0.017	0.483*	−0.042	0.442	3.524	4.508*	−0.978	0.559**
	[0.813]	[0.295]	[0.680]	[0.270]	[0.672]	[0.271]	[2.568]	[2.427]	[0.817]	[0.266]
Wald Chi-square	−8567.8***		964.6***		936.2***		1449.1***		1027.9***
logLikelihood	−4283.9		−4445.4		−4459.6		−3582.1		−4413.8
Locational choice-set (average)	402.6		402.6		402.6		181.8		402.6
Number of entries	883		883		883		883		883
Observations	357552		357552		357552		161312		357552

Note: ***p < 0.01, **p < 0.05, *p < 0.10. Standard errors in brackets.

Second, we broadened the geographic scope of agglomeration to allow for more varied spatial decay effects (e.g., Puga 2010; Cainelli and Ganau 2018; Verstraten, Verweij, and Zwaneveld 2018). Specifically, we recalculated agglomeration by adding industry output of adjacent regions that are within a 5- or 10-km radius of the center of the region of investment, after weighting the industry output in those adjacent regions by the inverse of distance. The results indicate that adverse selection patterns weaken with distance, with the coefficient on the interaction effect taking a smaller but consistently negative value (β = −0.099 and β = −0.078, respectively). This is in line with earlier findings on the proximate effects of knowledge spillovers (Jofre-Monseny, Marín-López, and Viladecans-Marsal 2011; Rosenthal and Strange 2020; Andersson, Larsson, and Wernberg 2019; Lavoratori and Castellani 2021). We also conducted alternative empirical tests by adding spatial lags for the agglomeration variables 5 and 10 km distant adjacent regions. The spatially lagged agglomeration variables had a negative sign. This is consistent with the notion that agglomeration benefits occur in a spatially constrained manner, and that higher agglomeration levels in adjacent regions may bring such regions in closer competition with the region of interest, reducing entry probabilities. The interaction terms of the spatially lagged agglomeration term and entrant firm TFP were not significant, and the findings on selection were unchanged. The results suggest that the agglomeration and sorting effects are confined tot he fine grained regional level.

Third, we estimated models with regional fixed effects. While fixed effects control further for idiosyncratic locational factors that could encourage or discourages new plant investments in a region, a drawback is that the inclusion of fixed effects implies that regions that did not attract any entries during the period of investigation have to be omitted from the analysis, since the absence of entries is fully explained by the fixed effect. This leads to a sample selection and attrition effect, reducing the mean choice set to 182 (down from 403), and more than halving the number of observations. Nevertheless, the results regarding the influence of agglomeration and its interaction with TFP are consistent with those in Table 4, with the negative coefficient on the interaction term of the TFP premium and non-exporter agglomeration for non-exporters being only slightly smaller (in absolute value).

Fourth, instead of distinguishing exporting firms from non-exporting firms, we distinguished exporting entries (plants) from non-exporting entries. Although the exporting decision for new plants will be taken simultaneously with the entry location decision and is partly endogenous, we do expect and find patterns consistent with the results in Table 4. We find adverse selection only for non-exporting new plants, and the coefficient estimate is of a similar size (β = −0.082) as that in Table 4.¹¹

5 Conclusion

The literature has produced ambiguous findings concerning the salience and direction of the sorting process on entry in response to industry agglomeration. We posit that this is related to the variety of sorting influences at play. On the one hand, productive firms may be more likely to survive heightened product market competition. On the other hand, productive firms face greater risks of knowledge dissipation to collocated rival firms and contribute more than they receive in terms of knowledge spillovers from plants in close proximity. Our study sought to provide more insights into these relationships by relating entry location choices to a clear indicator of ex ante productivity of entrants, examining entries by multi-plant firms for which existing productivity levels can be accurately observed, and by distinguishing the influence of industry agglomeration of direct market rivals—domestic market oriented firms in the same 4-digit industry—from the influence of industry agglomeration of firms that are not directly competing in the same end market (exporters).

Results of conditional logit models of the location choice for new manufacturing entries in Japan at the detailed geographic level provide strong support for the notion of adverse selection of manufacturing entries related to the risk of knowledge dissipation. If existing establishments and high productivity entrants share the same (domestic) market, knowledge dissipation concerns are salient, as knowledge spillover-induced increases in competitiveness of incumbent rivals are likely to directly affect the market share and profitability of a firm choosing a location for its plant. Industry agglomeration reduces, rather than increases, the likelihood of entry for the most productive firms. If entrants and incumbents are less likely to share the same end markets—i.e. entrants target export markets—positive agglomeration and sorting effects dominate. We conclude that sorting processes on entry do occur, but that these can only be uncovered in a detailed analysis—as in this study—that takes ex ante measures of firm heterogeneity and the nature of product markets into account.

Our findings also have relevance for policy makers. They suggest that regional administrators seeking to attract investments may be able to entice leading firms to invest in their region even in the absence of a strong regional industry cluster. Adverse selection generally leads to a greater spread among locations for a given industry, as leading firms tend to choose regions with fewer rivals. This provides opportunities for regions without existing establishment density. At the same time, agglomerations can and will attract entrants if there is sufficient diversity in the industry cluster: the cluster does not only consist of firms focusing on the same (domestic) market but also contains firms focusing on a variety of export markets, and firms in related industries that serve as buyers or suppliers. With such diversity, cluster policies aiming for a concentration of industrial activity in a region can still attract new investments by leaders. This is an important nuance to the notion of smart specialization (Balland et al. 2019; Belderbos, Benoit, and Derudder 2022a) recommending regions to choose their growth paths based on existing strengths.

Our research is not without limitations. Future research may also address some of these limitations of our research, for instance by including wage costs in addition to land costs (Verstraten, Verweij, and Zwaneveld 2018), and by examining spatial clusters of establishments rather than regions with administrative boundaries (Puga 2010). Sensitivity regarding alternative measures of TPF calculation (e.g., Ackerberg, Caves, and Frazer 2015 and Gandhi, Navarro, and Rivers 2020) should also be examined—although perhaps the TFP rankings that we use to identify adverse selection are less likely to change.

Perhaps more important, our findings relate to the context of the Japanese manufacturing sector. Given the dearth of studies on entry and agglomeration in Japan, with most prior research focused on the United States and Europe, this is a welcome contribution to the literature. On the other hand, perhaps the problem of collocation and knowledge spilllovers is a degree stronger in Japan given the relatively lack of new locations for manufacturing plants in the country due to Japan's geography with 70% of land mountainous and/or covered by dense forests. Future research should aim to conduce fine grained studies relating agglomeration to (entrant) productivity for other countries.

Our paper contributes to an expanding strand of research that examines agglomeration effects at the fine-grained spatial level to uncover heterogeneous influences of agglomeration (Jofre-Monseny, Marín-López, and Viladecans-Marsal 2011; Andersson, Larsson, and Wernberg 2019; Lavoratori and Castellani 2021; Cainelli and Ganau 2018; Verstraten, Verweij, and Zwaneveld 2018). Our study shows that adverse selection is only significant if entrant firms face local rivals competing on the same product and geographic market. We suggest that in addition to focusing on fine-grained spatial levels, future research should provide ample consideration to the nature of product market competition to better understand the complex relationship between establishment density and productivity through sorting effects, competition, and agglomeration externalities.

Acknowledgments

This paper is the result of a joint research project of the National Institute of Science and Technology Policy (NISTEP) and the Research Institute for Economy, Trade and Industry (RIETI). René Belderbos gratefully acknowledges support from NISTEP and RIETI. The authors thank Jun Zenibayashi for able research assistance and an anonymous reviewer and the editor Edward Coulson for their constructive comments on earlier drafts.

Conflicts of Interest

The authors declare no conflicts of interest.

Endnotes

1 Bloom, Schankerman and Van Reenen (2013) suggest that R&D spillovers have profoundly different effects if they occur between market rivals.

2 Unfortunately, we were unable to gain access to the data for later years to examine this in detail.

3 In auxiliary analysis, we confirmed that the multi-plant firms are not typically located in agglomerated areas, such that they face sufficient variation in their choice set for new regions for new plant establishments.

4 These are called ‘shikuchouson’ (市区町村).

5 We used the official 1788 regions as of 2008 and use those delineations for the entire period 2000–2008. If regions merged during this period, we manually adjusted the regional demarcation in the earlier years. This ensures a consistent location set during our observation period.

6 Disadvantages are the assumption of constant returns to scale, and the required aggregation of inputs using weights, which may increase sensitivity to measurement errors.

7 See Fukao et al. (2007) for a detailed account of the TPF measure.

8 We also experimented with a regional wage premium variable, using estimated regional wage premiums from the Mincer-type wage function by Kawaguchi and Kambayashi (2009). The wage premium data are available only for 1 year, however, and are strongly correlated with the land price variable. Joint inclusion left the wage variable insignificant.

9 Jofre-Monseny, Marín-López and Viladecans-Marsal (2011) and Rosenthal and Strange (2020) observed that knowledge spillover considerations only play a role in entry decisions at a fine-grained, highly localized level. Similar observations are made by Andersson, Larsson and Wernberg (2019) and Lavoratori and Castellani (2021).

10 This follows Head and Mayer (2004). The weight assumes that demand is equally distributed in a circle of radius r.

11 We also ran the regressions omitting 28 industries, 176 entries, and 89,685 observations representing livestock, food, and drinks industries, as it is conceivable idiosyncratic local effects such as local taste or local supply conditions may affect location choices. The results were again similar to—but not stronger than—those in Table 4.

Open Research

Data Availability Statement

The micro data are drawn from government sources and cannot be disclosed under the research agreement with the government of Japan.

References

Ackerberg, D. A., K. Caves, and G. Frazer. 2015. “Identification Properties of Recent Production Function Estimators.” Econometrica 83, no. 6: 2411–2451.
10.3982/ECTA13408
Web of Science® Google Scholar
Alcácer, J., and W. Chung. 2007. “Location Strategies and Knowledge Spillovers.” Management Science 53, no. 5: 760–776.
10.1287/mnsc.1060.0637
Web of Science® Google Scholar
Alcácer, J., and W. Chung. 2013. “Location Strategies for Agglomeration Economies.” Strategic Management Journal 35, no. 12: 1749–1761.
10.1002/smj.2186
Google Scholar
Alcácer, J., and M. Delgado. 2016. “Spatial Organization of Firms and Location Choices Through the Value Chain.” Management Science 62, no. 11: 3213–3234.
10.1287/mnsc.2015.2308
Web of Science® Google Scholar
Andersson, M., J. P. Larsson, and J. Wernberg. 2019. “The Economic Microgeography of Diversity and Specialization Externalities: Firm-level Evidence From Swedish Cities.” Research Policy 48, no. 6: 1385–1398.
10.1016/j.respol.2019.02.003
Web of Science® Google Scholar
Van Ark, B., M. O'Mahony, and M. P. Timmer. 2008. “The Productivity Gap Between Europe and the United States: Trends and Causes.” Journal of Economic Perspectives 22, no. 1: 25–44.
10.1257/jep.22.1.25
Web of Science® Google Scholar
Arzaghi, M., and J. V. Henderson. 2008. “Networking Off Madison Avenue.” Review of Economic Studies 75, no. 4: 1011–1038.
10.1111/j.1467-937X.2008.00499.x
Web of Science® Google Scholar
Asahi Newspaper Corporation. 2010. Todofuken Betsu Minryoku Sokutei Shiryoshu (National Capacities Database). Tokyo: Asahi Shinbunsha.
Google Scholar
Aw, B. Y., X. Chen, and M. J. Roberts. 2001. “Firm-Level Evidence on Productivity Differentials and Turnover in Taiwanese Manufacturing.” Journal of Development Economics 66: 51–86.
10.1016/S0304-3878(01)00155-9
Web of Science® Google Scholar
Baldwin, R. E., and T. Okubo. 2006. “Heterogeneous Firms, Agglomeration and Economic Geography: Spatial Selection and Sorting.” Journal of Economic Geography 6, no. 3: 323–346.
10.1093/jeg/lbi020
Web of Science® Google Scholar
Balland, P. A., R. Boschma, J. Crespo, and D. L. Rigby. 2019. “Smart Specialization Policy in the European Union: Relatedness, Knowledge Complexity and Regional Diversification.” Regional Studies 53, no. 9: 1252–1268.
10.1080/00343404.2018.1437900
Web of Science® Google Scholar
Beaudry, C., and A. Schiffauerova. 2009. “Who's Right, Marshall or Jacobs? The Localization Versus Urbanization Debate.” Research Policy 38, no. 2: 318–337.
10.1016/j.respol.2008.11.010
Web of Science® Google Scholar
Belderbos, R., F. Benoit, and B. Derudder. 2022a. “World City Innovation and Service Networks and Economic Growth.” Papers in Regional Science 101, no. 4: 979–1000.
10.1111/pirs.12687
Web of Science® Google Scholar
Belderbos, R., and M. Carree. 2002. “The Location of Japanese Investments in China: Agglomeration Effects, Keiretsu, and Firm Heterogeneity.” Journal of the Japanese and International Economies 16: 194–211.
10.1006/jjie.2001.0491
Web of Science® Google Scholar
Belderbos, R., K. Fukao, K. Ito, and W. Letterie. 2013. “Global Fixed Capital Investment by Multinational Firms.” Economica 80, no. 318: 274–299.
10.1111/ecca.12014
Web of Science® Google Scholar
Belderbos, R., M. Kazimierczak, and M. Goedhuys. 2022b. “Trademarks, Patents, and the Appropriation Strategies of Incumbents: The Scope of New Firm Formation in European Regions.” Regional Studies 56, no. 2: 210–226.
10.1080/00343404.2021.1947486
Web of Science® Google Scholar
Belderbos, R., W. V. Olffen, and J. Zou. 2011. “Generic and Specific Social Learning Mechanisms in Foreign Entry Location Choice.” Strategic Management Journal 32, no. 12: 1309–1330.
10.1002/smj.938
Web of Science® Google Scholar
Belderbos, R., and D. Somers. 2015. “Do Technology Leaders Deter Inward R&D Investments? Evidence From Regional R&D Location Decisions in Europe?” Regional Studies 49, no. 11: 1805–1821.
10.1080/00343404.2015.1018881
Web of Science® Google Scholar
Van Biesebroeck, J. 2007. “Robustness of Productivity Estimates.” The Journal of Industrial Economics 55, no. 3: 529–569.
10.1111/j.1467-6451.2007.00322.x
Web of Science® Google Scholar
Bloom, N., M. Schankerman, and J. Van Reenen. 2013. “Identifying Technology Spillovers and Product Market Rivalry.” Econometrica 81, no. 4: 1347–1393.
10.3982/ECTA9466
Web of Science® Google Scholar
Bontadini, F., C. Corrado, J. Haskel, M. Iommi, and C. Jona-Lasinio, 2023. EUKLEMS & INTANProd: Industry Productivity Accounts With Intangibles Sources of Growth and Productivity Trends: Methods and Main Measurement Challenges, LUISS Lab of European Economics. https://euklems-intanprod-llee.luiss.it.
Google Scholar
Cainelli, G., and R. Ganau. 2018. “Distance-Based Agglomeration Externalities and Neighbouring Firms’ Characteristics.” Regional Studies 52, no. 7: 922–933.
10.1080/00343404.2017.1360482
Web of Science® Google Scholar
Cantwell, J. A., and R. Mudambi. 2011. “Physical Attraction and the Geography of Knowledge Sourcing in Multinational Enterprises.” Global Strategy Journal 1, no. 3–4: 206–232.
10.1002/gsj.24
Web of Science® Google Scholar
Caves, D. W., L. R. Christensen, and W. E. Diewert. 1982. “The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity.” Econometrica 50, no. 6: 1393–1414.
10.2307/1913388
Web of Science® Google Scholar
Combes, P.-P., G. Duranton, L. Gobillon, D. Puga, and S. Roux. 2012. “The Productivity Advantages of Large Cities: Distinguishing Agglomeration From Firm Selection.” Econometrica 80, no. 6: 2543–2594.
10.3982/ECTA8442
Web of Science® Google Scholar
David, P. A., and J. L. Rosenbloom. 1990. “Marshallian Factor Market Externalities and the Dynamics of Industrial Localization.” Journal of Urban Economics 28, no. 3: 349–370.
10.1016/0094-1190(90)90033-J
Web of Science® Google Scholar
Du, H. S., R. Belderbos, and D. Somers. 2022. “Research Versus Development: Global Cities and the Location of MNCs’ Cross-Border R&D Investments.” Regional Studies 56, no. 12: 2001–2018.
10.1080/00343404.2022.2033198
Web of Science® Google Scholar
Faberman, R. J., and M. Freedman. 2016. “The Urban Density Premium Across Establishments.” Journal of Urban Economics 93: 71–84.
10.1016/j.jue.2016.03.006
Web of Science® Google Scholar
Frenken, K., E. Cefis, and E. Stam. 2015. “Industrial Dynamics and Clusters: A Survey.” Regional Studies 49, no. 1: 10–27.
10.1080/00343404.2014.904505
Web of Science® Google Scholar
Fukao, K., S. Hamagata, T. Inui, et al. 2007. Estimation Procedure and TFP Analysis of the JIP Database 2006 (revised), RIETI Discussion Paper No. 07-E-003. https://www.rieti.go.jp/jp/publications/summary/07010003.html.
Google Scholar
Gandhi, A., S. Navarro, and D. A. Rivers. 2020. “On the Identification of Gross Output Production Functions.” Journal of Political Economy 128, no. 8: 2973–3016.
10.1086/707736
Web of Science® Google Scholar
Glaeser, E. L., and W. R. Kerr. 2009. “Local Industrial Conditions and Entrepreneurship: How Much of the Spatial Distribution Can We Explain?” Journal of Economics & Management Strategy 18, no. 3: 623–663.
10.1111/j.1530-9134.2009.00225.x
Web of Science® Google Scholar
Greenstone, M., R. Hornbeck, and E. Moretti. 2010. “Identifying Agglomeration Spillovers: Evidence From Winners and Losers of Large Plant Openings.” Journal of Political Economy 118, no. 3: 536–598.
10.1086/653714
Web of Science® Google Scholar
Head, K., and T. Mayer. 2004. “Market Potential and the Location of Japanese Investment in the European Union.” Review of Economics and Statistics 86, no. 4: 959–972.
10.1162/0034653043125257
Web of Science® Google Scholar
Head, K., J. Ries, and D. Swenson. 1994. “Agglomeration Benefits and Location Choice: Evidence From Japanese Manufacturing Investments in the United States.” Journal of International Economics 38, no. 3/4: 223–247.
Google Scholar
Jacobs, J. 1969. The Economies of Cities. New York: Random House.
Google Scholar
Jofre-Monseny, J., R. Marín-López, and E. Viladecans-Marsal. 2011. “The Mechanisms of Agglomeration: Evidence From the Effect of Inter-Industry Relations on the Location of New Firms.” Journal of Urban Economics 70, no. 2–3: 61–74.
10.1016/j.jue.2011.05.002
Web of Science® Google Scholar
Jorgenson, D. W., and Z. Griliches. 1967. “The Explanation of Productivity Change.” The Review of Economic Studies 34, no. 99: 249–283.
10.2307/2296675
Google Scholar
Kawaguchi, D., and R. Kambayashi. 2009. “ Tokei no Setsugo Data no Sakusei to Riyo: Kogyo Tokei Chosa to Chingin Kozo Kihon Chosa no Rei [Compilation and Use of Merged Micro-Data of Government Surveys: The Case of the Census of Manufactures and the Basic Survey on Wage Structure].” In Ohyo Mikuro Keiryo Keizai-gaku [Applied Micro-Econometrics], edited by Yukinobu Kitamura. Tokyo, Japan: Nihon Hyoron-sha.
Google Scholar
Kondo, K. (2018). Testing for Global Spatial Autocorrelation in Stata.Research Institute of Economy, Trade, and Industry.
Google Scholar
Krugman, P. 1991. “Increasing Returns and Economic Geography.” Journal of Political Economy 99, no. 3: 483–499.
10.1086/261763
Web of Science® Google Scholar
Lavoratori, K., and D. Castellani. 2021. “Too Close for Comfort? Microgeography of Agglomeration Economies in the United Kingdom.” Journal of Regional Science 61, no. 5: 1002–1028.
10.1111/jors.12531
Web of Science® Google Scholar
Levinsohn, J., and A. Petrin. 2003. “Estimating Production Functions Using Inputs to Control for Unobservables.” Review of Economic Studies 70, no. 2: 317–341.
10.1111/1467-937X.00246
Web of Science® Google Scholar
Mariotti, S., R. Mosconi, and L. Piscitello. 2019. “Location and Survival of MNEs’ Subsidiaries: Agglomeration and Heterogeneity of Firms.” Strategic Management Journal 40, no. 13: 2242–2270.
10.1002/smj.3081
Web of Science® Google Scholar
Martin, P., T. Mayer, and F. Mayneris. 2011. “Spatial Concentration and Plant-Level Productivity in France.” Journal of Urban Economics 69, no. 2: 182–195.
10.1016/j.jue.2010.09.002
Web of Science® Google Scholar
McFadden, D. 1974. “ Conditional Logit Analysis of Qualitative Choice Behavior.” In Frontiers in Econometrics, edited by P. Zarembka, 105–142. New York: Academic Press.
Google Scholar
McFadden, D., and K. Train. 2000. “Mixed MNL Models for Discrete Response.” Journal of Applied Econometrics 15, no. 5: 447–470.
10.1002/1099-1255(200009/10)15:5<447::AID-JAE570>3.0.CO;2-1
Web of Science® Google Scholar
Melitz, M. J., and G. I. P. Ottaviano. 2008. “Market Size, Trade and Productivity.” Review of Economic Studies 75, no. 1: 295–316.
10.1111/j.1467-937X.2007.00463.x
Web of Science® Google Scholar
Melo, P. C., D. J. Graham, and R. B. Noland. 2009. “A Meta-Analysis of Estimates of Urban Agglomeration Economies.” Regional Science and Urban Economics 39, no. 3: 332–342.
10.1016/j.regsciurbeco.2008.12.002
Web of Science® Google Scholar
Myles Shaver, J., and F. Flyer. 2000. “Agglomeration Economies, Firm Heterogeneity, and Foreign Direct Investment in the United States.” Strategic Management Journal 21, no. 12: 1175–1193.
10.1002/1097-0266(200012)21:12<1175::AID-SMJ139>3.0.CO;2-Q
Google Scholar
Olley, G. S., and A. Pakes. 1996. “The Dynamics of Productivity in the Telecommunications Equipment Industry.” Econometrica 64: 1263–1297.
10.2307/2171831
Web of Science® Google Scholar
Puga, D. 2010. “The Magnitude and Causes of Agglomeration Economies.” Journal of Regional Science 50, no. 1: 203–219.
10.1111/j.1467-9787.2009.00657.x
Web of Science® Google Scholar
RIETI., 2018. Japan Industrial Productivity Database 2018, Research Institute of Economics, Trade and Industry. Tokyo. https://www.rieti.go.jp/en/database/JIP2018/index.html#01.
Google Scholar
Rosenthal, S. S., and W. C. Strange. 2003. “Geography, Industrial Organization, and Agglomeration.” Review of Economics and Statistics 85: 377–393.
10.1162/003465303765299882
Web of Science® Google Scholar
Rosenthal, S. S., and W. C. Strange. 2020. “How Close Is Close? The Spatial Reach of Agglomeration Economies.” Journal of Economic Perspectives 34, no. 3: 27–49.
10.1257/jep.34.3.27
Web of Science® Google Scholar
Syverson, C. 2004. “Market Structure and Productivity: A Concrete Example.” Journal of Political Economy 112, no. 6: 1181–1222.
10.1086/424743
Web of Science® Google Scholar
Todo, Y., P. Matous, and H. Inoue. 2016. “The Strength of Long Ties and the Weakness of Strong Ties: Knowledge Diffusion Through Supply Chain Networks.” Research Policy 45, no. 9: 1890–1906.
10.1016/j.respol.2016.06.008
Web of Science® Google Scholar
Toyo Keizai Inc. 2013. Chiiki Keizai deta CD-ROM (Regional Economy Data CD-ROM). Tokyo: Toyo Keizai Inc.
Google Scholar
Verstraten, P., G. Verweij, and P. J. Zwaneveld. 2018. “Complexities in the Spatial Scope of Agglomeration Economies.” Journal of Regional Science 59, no. 1: 1–27.
Web of Science® Google Scholar

Citing Literature

Volume65, Issue3

June 2025

Pages 698-717

Does Industry Agglomeration Attract Productive Firms? The Role of Product Markets in Adverse Selection

ABSTRACT

1 Introduction