Income Inequality and National Strategy for Inner Areas: Does Location Matter?
ABSTRACT
This paper examines the relationship between income inequality and municipalities classified as “inner areas” according to the classification proposed by the National Strategy for Inner Areas (NSIA) from 2012 to 2018. This classification categorizes municipalities into different groups based on their distance from essential service provision centers. By adopting a multilevel approach along with Beta Generalized Linear Mixed Models, we obtain two major results. First, inner areas show a lower income concentration index than non-inner municipalities. Ultra-peripheral municipalities manifest the greatest difference. Second, our findings show that location matters. While the sign is negative in southern and northern Italy, we find the opposite result in the central regions, where the ultra-peripheral municipalities show higher income inequality compared to non-inner areas.
1 Introduction
This paper explores the territorial aspect of income inequality by analyzing the role of “inner areas” on income inequality in Italian municipalities from 2012 to 2018. The issue is of great interest within the broader international debate on ever-increasing territorial inequalities (Martin 2021). Divergences and gaps in income appear not only within the traditional north/south dichotomy, but also between city centers and suburbs, and notably between cities and inner areas. The economic crisis triggered by the COVID-19 pandemic has further exacerbated the issues of income distribution and economic inequalities at the heart of this larger political debate, both at the national and the community level (European Commission 2022).
Recent contributions have provided extensive empirical evidence on income inequalities between and within countries, and have shed light on potential contributing factors (Furceri and Ostry 2019; Hortas-Rico and Rios 2019; Moser and Schnetzer 2017; Ostry, Berg, and Kothari 2021). It is clear that territorial characteristics are crucial when analyzing economic disparities (De Renzis, Faggian, and Urso 2022; Viesti 2021) and when proposing local solutions to reduce them.
In addition, empirical analyses often focus only on certain determinants of income distribution while neglecting others. Indeed, many studies tend to take a broad-strokes view by using data that covers the entire national territory, thus overlooking relevant local characteristics that are fundamental for explaining income inequalities (Atkinson and Brandolini 2009; Förster and Tóth 2015; Furceri and Ostry 2019; Nolan, Richiardi, and Valenzuela 2019; Viesti 2021). To the best of our knowledge, the role of inner area municipalities – seen as potential drivers of income distribution, particularly for ultra-peripheral zones – has thus far been neglected in the literature. Only Gallo and Pagliacci (2020) and Mastronardi and Cavallo (2020) have addressed this issue at the municipal level by examining the relationship between territorial factors and income inequality vis-à-vis the inner area classifications. Notably, these two contributions offer opposing results, thus justifying a deeper investigation of the issue.
To identify inner areas, we refer to the classification of municipalities as defined by the National Strategy for Inner Areas (NSIA), which was developed by Italy's Department for Economic Development and Cohesion. The program was launched in 2012 and promoted territorial policies within the 2014–2020 and 2021–27 programming period. Accordingly, inner areas are defined as Italian territorial areas that are considerably far from essential services such as education, health, and railway services (see Barca, Casavola, and Lucatelli 2014; Carlucci, Guerrizio, and Lucatelli 2012). From a spatial perspective, these territorial peripheries may present certain impediments and, as a result, may negatively influence their residents' quality of life and social inclusion. These challenges reflect the ‘slow burn’ process of depopulation, aging, and reduced services, reinforcing marginalization (Compagnucci and Morettini 2020). At the same time, their remoteness may offer value from an environmental standpoint, which can be exploited for economic purposes.
Another critical element of the previous literature is the methodological approach, which often fails to capture the characteristics of the outcome variable most commonly used in the literature, namely the income concentration index or Gini index used as a measure of inequality. Although the Gini index comprises the continuous interval (0,1), several contributions present empirical analyses involving Gaussian linear models. To account for the nature of the dependent variables in the Gini index, we use Beta Generalized Linear Mixed Models (Beta GLMMs) – which are suitable for longitudinal and multilevel structure data – to overcome statistical issues inherent in the employment of Gaussian regression models in this context. Hence, by exploiting the panel nature of our data, the extensive timespan under analysis allows us to observe the evolving characteristics of each local government in terms of opportunities and economic trends. This longer timespan differentiates our work from the previous studies, which use only cross-sectional data. Finally, to capture the multilevel geographical nature of the data (the municipalities in our study are located in 20 different Italian regions), we employ a two-level nested estimation method in which the municipalities are stratified by region. We assume that random variations from the overall mean of the Gini index are due to regional heterogeneity; in other words, each Italian region registers a different intercept.
With these considerations in mind, our paper aims to fill any remaining gaps in the previous studies. Our main contributions are fourfold. First, we explore income distribution at the municipal level by employing the inner area designation and using a panel data approach. Most notably, we incorporate diverse municipal-level data from multiple sources, ensuring greater heterogeneity and avoiding sole reliance on fiscal declarations from the Ministry of Economy and Finance. Second, we investigate whether the role of inner areas in the result of the Gini index mean differs across Italian geographical macro-regions. Third, we use the reparametrized Beta distribution to fit the observed values of the Gini index and to estimate the precision parameter, which enables us to verify whether inner areas located in different macro-regions have higher/lower variability in income concentration compared to non-inner areas. Fourth, our study pioneers the joint use of a multilevel approach and Beta models. This approach takes into consideration the geographic interconnections of municipalities within each region while also accounting for the nature of our dependent variable (Gini index) ranging between 0 and 1.
The main results of our econometric analysis suggest territorial differences between inner and non-inner areas. In both northern and southern Italy, the inner areas show lower inequality when compared to non-inner area municipalities. In the central regions of the country, we estimate a positive impact for ultra-peripheral areas on the income inequality index. Lastly, our findings demonstrate territorial differences in the variability of income concentration. In contrast to non-inner areas, inner-area municipalities present a lower dispersion of income inequality. Our analysis of the spatial distribution of income has uncovered notable patterns of income disparity. This result confirms that tailored interventions to address regional challenges such as rural infrastructure and urban overcrowding require targeted actions to foster inclusive growth and well-being among residents (Viesti 2021; De Renzis, Faggian, and Urso 2022).
The remainder of the text is organized as follows. The following section offers a review of the literature. Section 3 and 4 provide details on the NSIA classification system and our empirical strategy, respectively. Section 5 illustrates the data and descriptive statistics we employ, while Section 6 discuss the results obtained. Section 7 presents our conclusions.
2 Literature Review
The mechanisms underlying the formation of regional socioeconomic inequalities and their resulting impact have always been topics of great interest from both a theoretical and an empirical perspective (Storper 2018; Fratesi and Perucca 2019; Iammarino, Rodriguez-Pose, and Storper 2019). In particular, two strands of literature examine the impact of several determinants on income inequality. The first considers macroeconomic determinants, while the second analyses income concentration at a micro level (e.g., municipalities, provinces, regions).1 Our study falls within the second category of literature.
The empirical literature considers diverse groups of determinants to account for the theoretical aspects of income distribution. More specifically, demographic and gender factors represent two essential drivers for income inequality. A commonly adopted approach in empirical contributions is the evaluation of demographic phenomena using the share of the inactive population (persons under the age of 15 and persons over the age of 65) in the total population (Burtless 2009). However, the contributions that consider the effects of gender on income distribution are very recent and continue to leave many aspects unexplored (Dang and Viet Nguyen 2021). Furthermore, the explanatory components relating to education and training levels deserve particular attention when studying income distribution (Gregorio and Lee 2002; Bergh and Fink 2008; Abdullah, Doucouliagos, and Manning 2015). Finally, some studies also account for other fundamental variables and indicators that may potentially influence economic inequalities, such as local development indicators (Rajan and Zingales 2003; Law, Tan, and Azman-Saini 2014; Acciari and Mocetti 2013; Furceri and Ostry 2019; Ostry, Berg, and Kothari 2021), technological improvements (Dao et al. 2017), internationalization (Helpman 2017; Furceri, Loungani, and Zdzienicka 2018).
As an example of the second strand of literature on income inequalities at a subnational level, Förster, Jesuit and Smeeding (2005) study income inequality in four Central and Eastern European countries (the Czech Republic, Hungary, Poland, and Russia) by comparing the Gini index and other income concentration indicators at both the regional and national level. Interestingly, this paper shows that national-level investigations have contributed significantly to the understanding of income distribution, while regional analyses capture intra-country variance in terms of inequality. The study by Glaeser, Resseger, and Tobio (2009) further disaggregates the geographic level of income inequality investigation in its measurement of the Gini index across American metropolitan areas.
In recent decades, empirical studies on income inequality have noted profound geographical differences, particularly in Italy, which contains the highest levels of inequality above the European average.2 Studies have highlighted that, in reality, the average level of the Gini index hides a strong heterogeneity between geographic macro areas of the country, between regions and between Italian provinces. Acciari and Mocetti (2013) used data on tax returns from the Ministry of Economy and Finance (MEF) to show that in 2011, the Gini index in southern Italy was three percentage points higher than that related to the central and northern regions. However, the authors did not feel that this gap completely explains the heterogeneity of inequality at the territorial level. The territorial differentials within the two geographical macro areas are wide. In this vein, Mauro, Biggeri, and Maggino (2018) provided a set of statistical methods suitable for measuring and comparing family income inequality between different regions of Italy and within each area to assess the degree to which these factors contribute to overall inequality at the national level.
According to more recent economic literature (e.g., Gallo and Pagliacci 2020; Viesti 2021), it is crucial to consider spatial aspects when studying differences in income inequalities between administrative units (regions, provinces, and cities) and the effect of city centers and suburbs as defined by the NSIA. The latter represents direct action to support sustainable territorial competitiveness, and to oppose, in the medium term, the demographic decline that characterizes Italy's inner areas.
In this regard, Gallo and Pagliacci (2020) assessed the impact of rural and remote areas on income inequality using data on Italian municipalities in 2015. They found that peripheral and ultra-peripheral regions had a positive effect on the Gini index with respect to cities classified as poles. Gallo and Pagliacci (2020) did not differentiate between inner and non-inner areas in terms of impact, but rather between the five subcategories (inter-municipality pole, belt, intermediate, peripheral, and ultra-peripheral areas), with only the category of “pole” representing the classification of non-inner areas. Indeed, while their regressions included five dummies to identify the subcategories mentioned above, they defined the hubs/poles as the control group.
Finally, by using data from Italian cities in 2015, Mastronardi and Cavallo (2020) used a binary variable to test the differences between poles and the other categories of municipalities. Their findings are in line with the idea that urban centers present greater income inequalities than do inner areas, as the characterizing social and economic context allows for more job opportunities, especially in tertiary industries, as well as higher income levels.
The mixed results from the previous literature have encouraged our further investigation of the role of inner areas in the broader analysis of income inequality. In light of the existing literature, we study the effect of inner areas on inequality in comparison to “center” categories (i.e., poles, inter-poles, and outlying cities) by utilizing the territorial localization of these municipalities.
3 National Strategy for Inner Areas
The NSIA classification, introduced in regional policies during the 2014–2020 programming period, was first launched in 2012 by the Italian government and promoted by the Department for Economic Development and Cohesion.3 The central aim of this strategy is to bolster the nation's socioeconomic status by generating employment opportunities, promoting social integration, and tackling the issues surrounding territorial population decline (Barca, Casavola, and Lucatelli 2014).
The NSIA classification identifies certain territories as peripheral in terms of their access to essential services. This lack of access can impact their residents' quality of life, economic potential, and level of social inclusion. Inner areas, as defined by the NSIA classification, are characterized by a substantial distance from essential services such as education, health, and mobility. However, they often possess significant environmental and cultural resources, including water resources, agricultural systems, natural and human landscapes, as well as archeological assets, small museums, and historic settlements. These areas are highly diverse due to the dynamics of natural systems and anthropogenic processes.
A polycentric understanding of the Italian territory as characterized by networks or clusters of municipalities (centers offering services) forms the basis for identifying inner areas. The methodology involves several steps: first, the identification of individual urban poles (hubs) capable of providing essential services. This approach also considers cases where multiple contiguous municipalities together form a network system that offers essential services, thus constituting an inter-municipal pole or hub. The remaining municipalities are then categorized into four zones based on their distance from the nearest hub: outlying areas (up to 20 min), intermediate areas (between 20 and 40 min), peripheral areas (between 40 and 75 min), and ultra-peripheral areas (more than 75 min). The latter three zones collectively constitute the “inner areas” (Barca, Casavola, and Lucatelli 2014). Consequently, two main classes of municipalities emerge: the center, which comprises poles, inter-municipal poles, and outlying areas; and the inner area, consisting of intermediate, peripheral, and ultra-peripheral municipalities.4
Table 1 presents the number and percentage of municipalities based on the NSIA classification. In 2018, 48.56% of Italian municipalities were categorized as centers, while 51.44% fell under the classification of inner areas. Considering the individual NSIA categories, the majority of municipalities within centers are classified as outlying municipalities (90%). Within the inner areas, the majority of municipalities are intermediate, followed by peripheral and ultra-peripheral municipalities. Overall, outlying areas, intermediate areas, and peripheral areas are the most common classifications nationwide. In terms of macro-regions, the north has more centers (61%), while the south has more inner areas (71%). Focusing on inner areas disaggregation, outlying zones represent the higher proportion of municipalities in all macro-regions. Northern and central Italy has a higher proportion of municipalities in intermediate areas, whereas the south has more peripheral areas.
| NSIA classification | Number Municipalities in 2018 | % on the total number of Municipalities in 2018 | NSIA classes | Number Municipalities in 2018 | % Municipalities in NSIA classification in 2018 | % on the total number of Municipalities in 2018 |
|---|---|---|---|---|---|---|
| ITALY | ||||||
| A—poles | 216 | 0.0563 | 0.0273 | |||
| Centers | 3837 | 0.4856 | B—inter-municipality poles | 121 | 0.0315 | 0.0153 |
| C—outlying areas | 3500 | 0.9122 | 0.4429 | |||
| D—intermediate areas | 2292 | 0.5638 | 0.2901 | |||
| Inner Areas | 4065 | 0.5144 | E—peripheral areas | 1479 | 0.3638 | 0.1872 |
| F—ultra-peripheral areas | 294 | 0.0723 | 0.0372 | |||
| Total | 7902 | 7902 | ||||
| NORTH | ||||||
| A—poles | 106 | 0.0394 | 0.0242 | |||
| Centers | 2693 | 0.6146 | B—inter-municipality poles | 53 | 0.0197 | 0.0121 |
| C—outlying areas | 2534 | 0.9410 | 0.5783 | |||
| D—intermediate areas | 1119 | 0.6625 | 0.2554 | |||
| Inner Areas | 1689 | 0.3854 | E—peripheral areas | 511 | 0.3025 | 0.1166 |
| F—ultra-peripheral areas | 59 | 0.0349 | 0.0135 | |||
| Total | 4382 | 4382 | ||||
| % on the total number of Municipalities in Italy | 0.5500 | |||||
| CENTER | ||||||
| A—poles | 46 | 0.1141 | 0.0474 | |||
| Centers | 403 | 0.4155 | B—inter-municipality poles | 25 | 0.0620 | 0.0258 |
| C—outlying areas | 332 | 0.8238 | 0.3423 | |||
| D—intermediate areas | 399 | 0.7037 | 0.4113 | |||
| Inner Areas | 567 | 0.5845 | E—peripheral areas | 165 | 0.2910 | 0.1701 |
| F—ultra-peripheral areas | 3 | 0.0053 | 0.0031 | |||
| Total | 970 | 970 | ||||
| % on the total number of Municipalities in Italy | 0.1200 | |||||
| SOUTH AND ISLANDS | ||||||
| A—poles | 64 | 0.0864 | 0.0251 | |||
| Centers | 741 | 0.2906 | B—inter-municipality poles | 43 | 0.0580 | 0.0169 |
| C—outlying areas | 634 | 0.8556 | 0.2486 | |||
| D—intermediate areas | 774 | 0.4279 | 0.3035 | |||
| Inner Areas | 1809 | 0.7094 | E—peripheral areas | 803 | 0.4439 | 0.3149 |
| F—ultra-peripheral areas | 232 | 0.1282 | 0.0910 | |||
| Total | 2550 | 2550 | ||||
| % on the total number of Municipalities in Italy | 0.3200 | |||||
- Source: Authors’ elaboration.
4 Empirical Strategy
4.1 Methodology in a Nutshell
In this section, we provide a specification of the model we use to indicate the measure of economic inequality (in our case, the Gini index) with a set of predictors, taking into account both the hierarchical structure and panel nature of the available data.
The main indicator for evaluating income inequality is the Gini coefficient. This numerical measure examines typical deviations in income distribution, ranging from 0 (representing perfect equality) to 1 (representing perfect inequality). Renowned for its favorable characteristics, the Gini coefficient showcases mean independence, population size independence, and symmetry (Coccorese and Dell'Anno 2022).
The challenge of computing the Gini index for data grouped into income classes, such as income or tax statistics grouped for confidentiality, is a persistent concern in empirical research (Abounoori and McCloughan 2003). Previous studies have emphasized the downward bias introduced by grouping income into limited classes. To address this issue, researchers have proposed two main approaches. The first involves fitting parametric functions to average incomes within each group, which would align with the properties of a theoretical Lorenz curve. This method, favored by applied researchers, utilizes estimated parameters to calculate the Gini coefficient. The second approach establishes nonparametric bounds on the Gini index, thus avoiding assumptions about the shape of the Lorenz curve but requiring information on the lower and upper limits of each group. This approach illustrates scenarios of uniformity as well as maximum inequality within the groups. Both approaches contribute to overcoming the challenge of Gini index computation in grouped data analysis (Van Ourti and Clarke 2011).
Given that the Gini index can be considered a continuous random variable in the interval , one of the possible distributions used to interpret this variable with limited support is the Beta distribution. Considering the nature of our data, we adopted an extended version of the Beta regression model, often called the Beta Mixed Model or Generalized Beta Model with Mixed Effects (Beta GLMM).5 This model accounts for random effects in a classical Beta regression model, thus resolving the problem of dependence within clusters. In studies that collect repeated measures on each subject or cluster subjects into groups, observations associated with the same statistical unit are usually correlated, implying a violation of the assumptions associated with regression models (Bonat, Ribeiro, and Zeviani 2015). Consequently, this class of models is suitable for analyzing longitudinal and multilevel, hierarchically-structured data.
4.2 Model Specification
We highlight that the linear predictor includes the key variable of our analysis, INNER AREA, which is a dummy variable taking the value one if the municipal has the characteristic of an inner area with respect to the centers; SOUTH and CENTER dummies control for the Italian regional gap; the interaction term between INNER AREA and SOUTH/CENTER test the changing effect of INNER AREA on income inequality across Italian macro areas.
In additional columns, we report the estimations of full models in which we include the vectors of control variables not considered in the main model. These estimations act as robustness checks to account for relevant contextual features at municipal and regional levels.
First, according to Kuznets's influential hypothesis (Kuznets 1955; Rajan and Zingales 2003), we test whether income inequality follows an Inverse-U shape by controlling for the level of economic growth measured on the regional basis by inserting the variable REGIONAL GDP PER CAPITA and its square in the model. Second, in line with literature investigating the determinants of income inequality at the national level, we consider different groups of determinants (Furceri and Ostry 2019; Nolan, Richiardi, and Valenzuela 2019). Specifically, we include TAX REVENUE and a set of variables capturing mayoral characteristics (MAYOR AGE, MAYOR BACHELOR, MAYOR FEMALE) to account for the institutional context, as institutions such as municipal governance significantly influence income distribution (Stiglitz 2012; Acemoglu and Robinson 2020; Zhang, Zhou, and Fan 2020). The preferences of local administrators shape redistribution efforts and, consequently, impact income inequality. Mayors may address local income inequality through financial and social support programs (Einstein and Glick 2018; Nitschke and Roesel 2023). Moreover, as a proxy of gender (GENDER) – an important determinant of income inequality as seen in the previous literature (e.g., among others, Dang and Viet Nguyen 2021) – we have introduced into the model an index defined as the ratio between the share of female employees and the municipality's population. The variable EDUCATION includes a control for the level of education in each municipality, namely the share of permanent employees holding the minimum of a bachelor's degree. The pivotal role of education in income inequality is widely recognized (see Abdullah, Doucouliagos, and Manning 2015), as it enables upward mobility and informed decision-making, potentially reducing income gaps (World Bank 2002). At the same time, employers who favor highly educated individuals can also exacerbate inequality and widen wage disparities. Overall, higher education levels tend to equalize income distribution, but disparities in educational achievement can heighten income inequality (Thorbecke and Charumilind 2002; Rodríguez-Pose and Tselios 2009).
We also utilize a proxy for innovation to account for the effect of technological improvements. More specifically, we include the dummy UNIVERSITY, which is equal to one if a university is located within the municipality and 0 if not. The hypothesis that the presence of a university positively contributes to knowledge spillover is well documented in the literature (Bonaccorsi et al. 2014; Muhamad et al. 2022; Rukanyangira and Oidu 2021).
We also include some sociodemographic characteristics such as SENIOR INDEX and MERGED MUNICIPALITY. These control variables allow us to account for the redistributive effects of pensions among an older population as well as the merger of municipalities in the period under consideration. Finally, TIME TREND captures the effect of time on the Gini index.
The descriptive statistics shown in Table 2 influenced the choice of determinants for dispersion models, as they evidence the fact that the variation ranges of the Gini index signal strong variability. Likewise, Table 3 shows that our key regressors affect the variability of the inequality measure (e.g. inner area categories and geographic localization).
| Year | Mean | StdD | CV | Min | Max |
|---|---|---|---|---|---|
| 2012 | 0.3776 | 0.0392 | 0.1037 | 0.2525 | 0.6281 |
| 2013 | 0.3765 | 0.0399 | 0.1061 | 0.224 | 0.752 |
| 2014 | 0.3769 | 0.0405 | 0.1074 | 0.2095 | 0.6319 |
| 2015 | 0.3804 | 0.0403 | 0.1059 | 0.1604 | 0.6749 |
| 2016 | 0.3794 | 0.0403 | 0.1062 | 0.2073 | 0.5992 |
| 2017 | 0.383 | 0.0404 | 0.1055 | 0.2285 | 0.7031 |
| 2018 | 0.3842 | 0.0412 | 0.1072 | 0.2376 | 0.758 |
- Source: Authors’ elaboration. The source of data for the Gini index computation is the Ministry of Economy and Finance website.
| NSIA classification | Mean | Minimum | Maximum | Coefficient of variation | NSIA classes | Mean | Minimum | Maximum | Coefficient of variation |
|---|---|---|---|---|---|---|---|---|---|
| ITALY | |||||||||
| A—poles | 0.4203 | 0.3534 | 0.5392 | 0.0687 | |||||
| Centers | 0.3849 | 0.2376 | 0.6317 | 0.1047 | B—inter-municipality poles | 0.3971 | 0.3279 | 0.4831 | 0.0828 |
| C—outlying areas | 0.3823 | 0.2376 | 0.6317 | 0.1048 | |||||
| D—intermediate areas | 0.3839 | 0.2486 | 0.758 | 0.1109 | |||||
| Inner Areas | 0.3836 | 0.2384 | 0.758 | 0.1094 | E—peripheral areas | 0.3845 | 0.2438 | 0.5708 | 0.1074 |
| F—ultra-peripheral areas | 0.3766 | 0.2384 | 0.4947 | 0.1061 | |||||
| Total | 0.3842 | 0.2376 | 0.758 | 0.1072 | 0.3842 | 0.2376 | 0.758 | 0.1072 | |
| NORTH | |||||||||
| A—poles | 0.415 | 0.3534 | 0.5392 | 0.0754 | |||||
| Centers | 0.3773 | 0.2376 | 0.6317 | 0.1099 | B—inter-municipality poles | 0.3802 | 0.3279 | 0.4831 | 0.0864 |
| C—outlying areas | 0.3757 | 0.2376 | 0.6317 | 0.1098 | |||||
| D—intermediate areas | 0.3738 | 0.2486 | 0.7372 | 0.1282 | |||||
| Inner Areas | 0.3736 | 0.2384 | 0.7372 | 0.1302 | E—peripheral areas | 0.3727 | 0.2438 | 0.5708 | 0.1336 |
| F—ultra-peripheral areas | 0.3764 | 0.2384 | 0.4947 | 0.1415 | |||||
| Total | 0.3759 | 0.2376 | 0.7372 | 0.1181 | 0.3759 | 0.2376 | 0.7372 | 0.1181 | |
| CENTER | |||||||||
| A—poles | 0.4116 | 0.3621 | 0.4877 | 0.0593 | |||||
| Centers | 0.3863 | 0.3043 | 0.582 | 0.0809 | B—inter-municipality poles | 0.3923 | 0.3537 | 0.4602 | 0.0758 |
| C—outlying areas | 0.3823 | 0.3043 | 0.582 | 0.0799 | |||||
| D—intermediate areas | 0.3835 | 0.2748 | 0.758 | 0.1048 | |||||
| Inner Areas | 0.3831 | 0.2748 | 0.758 | 0.1009 | E—peripheral areas | 0.3818 | 0.2937 | 0.4977 | 0.0899 |
| F—ultra-peripheral areas | 0.4028 | 0.3664 | 0.4729 | 0.1507 | |||||
| Total | 0.3844 | 0.2748 | 0.758 | 0.0931 | 0.3844 | 0.2748 | 0.758 | 0.0931 | |
| SOUTH AND ISLANDS | |||||||||
| A—poles | 0.4354 | 0.3744 | 0.488 | 0.049 | |||||
| Centers | 0.4117 | 0.2955 | 0.498 | 0.0648 | B—inter-municipality poles | 0.4209 | 0.3834 | 0.4647 | 0.0407 |
| C—outlying areas | 0.4087 | 0.2955 | 0.498 | 0.0646 | |||||
| D—intermediate areas | 0.3988 | 0.2647 | 0.5255 | 0.073 | |||||
| Inner Areas | 0.3931 | 0.2647 | 0.5403 | 0.0841 | E—peripheral areas | 0.3925 | 0.297 | 0.5403 | 0.0872 |
| F—ultra-peripheral areas | 0.3763 | 0.2678 | 0.4622 | 0.0947 | |||||
| Total | 0.3985 | 0.2647 | 0.5403 | 0.0815 | 0.3985 | 0.2647 | 0.5403 | 0.0815 | |
- Source: Authors' elaboration.
Moreover, we replicated the analysis with a greater degree of disaggregation by substituting our main variable – INNER AREA – with INTERMEDIATE, PERIPHERAL, and ULTRA-PERIPHERAL. It is worth noting that in our analysis, both the INNER AREA dummy and the NSIA classes INTERMEDIATE, PERIPHERAL, and ULTRA-PERIPHERAL are defined in such a way as to carry out the comparison with all categories comprising centers (e.g., poles, inter-poles, outlying cities).
5 Data and Descriptive Statistics
5.1 Data and Sample
We accessed several sources to retrieve our data. We drew fiscal declarations by municipality for 2012–2018 from the website of the Ministry of Economy and Finance (MEF – Department of Finance).8 The latter provides information on the income and stock of taxpayers across consistent income brackets and for each municipality. This data is derived from tax returns spanning the period under consideration. The uniformity of income intervals is maintained over time and across municipalities to ensure comparability. We calculated the Gini index using municipality-specific tabulated data on declared gross income, which is classified into seven income intervals. Specifically, the income intervals are (in thousands of euros): (i) 0–10,000; (ii) 10,000–15,000; (iii) 15,000–26,000; (iv) 26,000–55,000; (v) 55,000–75,000; (vi) 75,000–120,000; and (vii) greater than 120,000.9
Tax returns for each municipality comprise all sources of income including labor, pensions, property, self-employment, and business income. Property income is calculated based on cadastral rent and encompasses all forms of property income including land as well as owned and rented residential and commercial buildings. In other words, registration of a previously unregistered building is reflected in the tax base as imputed rent (Rubolino 2023).
We gathered information on Italian inner areas, as classified by the National Strategy for Inner Areas (NSIA), from the website of the National Agency for Territorial Cohesion.10
Data on personnel indicators, demographic characteristics and other local features of the municipalities were obtained from the Italian National Institute of Statistics (ISTAT).11 We also consulted the Bureau van Dijk's Aida PA to retrieve financial data on local public authorities.12 Lastly, we gathered information on municipal administrators from the website of the Italian Ministry of the Interior.13
5.2 Descriptive Statistics
Table 2 reports the descriptive statistics referring to our dependent variable, the Gini index, for each year included in the analysed period. Figure 1 displays the trend of the Gini index for Italy and the three macro-areas of the north, center, and south. Even if the trends are quite similar and slightly increasing with a peak in 2015, the presence of differences among areas is evident. The southern regions show the highest concentration while northern Italy demonstrates the lowest values of the Gini index.
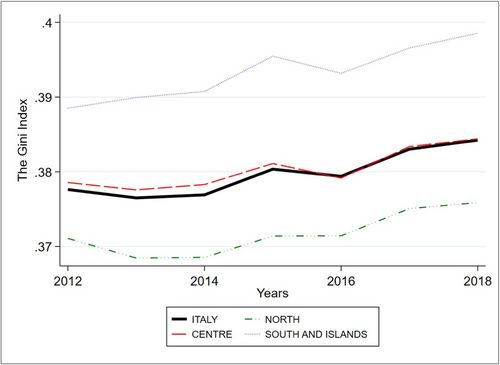
Table 3 presents the Gini coefficient for 2018 categorized by NSIA classifications in Italy.14 The national average Gini index is approximately 0.38, with southern Italy recording the highest average at 0.39 and the north exhibiting the lowest value at 0.37. Central regions display an average Gini index of 0.38. It is notable that both nationally and within the three macro areas, inner areas generally have lower average Gini index values compared to non-inner areas. Upon further analysis, cities classified as poles consistently show higher Gini coefficients. Ultra-peripheral, peripheral, and intermediate areas in the north demonstrate lower Gini coefficients, as do ultra-peripheral municipalities in southern regions. Conversely, in the central region, poles and ultra-peripheral municipalities report the highest Gini index values. The data in Table 3 reveal significant variability in the Gini index, with ranges and coefficients of variation consistently higher in inner areas compared to centers. These descriptive measures suggest the presence of heteroskedasticity in the dependent variable, prompting the adoption of a dispersion model that utilizes Beta regression for further investigation.
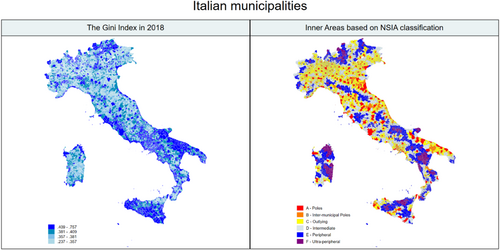
Figure 2 shows maps of the Gini index for Italian municipalities in 2018 alongside the inner area classification. The figure reveals a gap between the northern and southern regions in terms of income distribution and inner area classification. Northern municipalities, which are mostly classified as centers, exhibit lower levels of income concentration compared to those in southern regions, which consist mainly of inner municipalities with higher income inequality. In central Italy, where the Apennines define the presence of inner areas,15 most Gini index figures fall within the low to medium range except for those areas surrounding the capital city of Rome, where intermediate and peripheral municipalities exhibit higher income inequality.
Lastly, while Table 4 offers a description and main summary statistics of the variables employed in the econometric analysis, Table 5 shows the correlation matrix between them.
| Variable | Description | Mean/Relative frequency | Std. Dev. | Min | Max | Obs | Source |
|---|---|---|---|---|---|---|---|
| INNER AREA | Dummy = 1 if the municipal has the characteristic of an internal area (D + E + F) | 0.5172 | 0.4997 | 0 | 1 | 7902*7 | IACT |
| INTERMEDIATE | Dummy = 1 if the municipal has the characteristic of an intermediate area (D) | 0.2908 | 0.4542 | 0 | 1 | 7902*7 | IACT |
| PERIPHERAL | Dummy = 1 if the municipal has the characteristic of an peripheral area (E) | 0.1873 | 0.3902 | 0 | 1 | 7902*7 | IACT |
| ULTRA-PERIPHERAL | Dummy = 1 if the municipal has the characteristic of an ultra-peripheral area (F) | 0.0391 | 0.1938 | 0 | 1 | 7902*7 | IACT |
| SOUTH | Dummy = 1 if the municipality is located in the South Italy and islands | 0.3227 | 0.4675 | 0 | 1 | 7902*7 | |
| CENTER | Dummy = 1 if the municipality is located in the Center Italy | 0.1228 | 0.3282 | 0 | 1 | 7902*7 | |
| REGIONAL GDP PER CAPITA | The gross domestic product per capita at the regional level | 14.6369 | 25.3302 | 0.0096 | 757.171 | 53,706 | MEF |
| TAX REVENUE | The ratio between tax revenue and total tax revenue | 0.6262 | 0.1887 | 0 | 0.97 | 53,706 | AIDA |
| (tax revenue + income from contributions and current transfers + non-tax revenue) | PA | ||||||
| MAYOR AGE | The age of the municipality's mayor | 52.2092 | 10.5161 | 20 | 96 | 53,706 | DAIT |
| MAYOR BACHELOR | Dummy = 1 if the municipality's mayor has a bachelor degree or a grater education level | 0.4914 | 0.4999 | 0 | 1 | 53,706 | DAIT |
| MAYOR FEMALE | Dummy = 1 if the municipality's mayor is female | 0.1321 | 0.3386 | 0 | 1 | 53,706 | DAIT |
| Gender | The ratio between female employees (permanent and executives) and permanent employees staff; the variable is standardized by considering the municipality's population | 0.0416 | 0.1098 | 0 | 3.5714 | 53,706 | ISTAT |
| EDUCATION | The ratio between permanent employees/managerial staff with at least a bachelor degree and permanent employees/managerial staff | 0.1853 | 0.1496 | 0 | 1 | 53,706 | ISTAT |
| UNIVERSITY | Dummy = 1 if a university is located in the municipality | 0.0073 | 0.0849 | 0 | 1 | 53,706 | MIUR |
| SENIOR INDEX | The ratio between inhabitants >= 65 and inhabitants <= 14 | 2 | 1.5771 | 0.2734 | 56 | 53,525 | ISTAT |
| MERGED MUNICIPALITY | Dummy = 1 if the municipality has been merged between 2012 and 2018 | 0 | 0.1089 | 0 | 1 | 53,525 | ISTAT |
- Source: Authors’ elaboration. 7902*7 stands for 7902 Italian municipalities observed for 7 years. IACT stands for Italian Agency for Territorial Cohesion (NSIA archive). MEF stands for Ministry of Economy and Finance. AIDA PA, held by Bureau van Dijk, contains economic and financial information on Italian Public Authorities. DAIT stands for Dipartimento per gli Affari Interni e Territoriali of the Italian Ministry of the Interior. MIUR stands for Ministry of Education, University and Research. ISTAT stands for Italian National Institute of Statistics.
| Regional GDP Per Capita | Tax Revenue | Mayor Age | Mayor Bachelor | Mayor Female | Gender | Education | University | Senior Index | Merged Municipality | |
|---|---|---|---|---|---|---|---|---|---|---|
| REGIONAL GDP PER CAPITA | 1 | |||||||||
| TAX REVENUE | 0.0999 | 1 | ||||||||
| MAYOR AGE | 0.0227 | 0.0395 | 1 | |||||||
| MAYOR BACHELOR | −0.1618 | 0.0149 | −0.1561 | 1 | ||||||
| MAYOR FEMALE | 0.0992 | 0.0298 | −0.0683 | 0.0667 | 1 | |||||
| GENDER | 0.0839 | −0.1047 | 0.0222 | −0.11 | 0.0079 | 1 | ||||
| EDUCATION | 0.0024 | 0.0079 | −0.0229 | 0.0506 | 0.0297 | −0.074 | 1 | |||
| UNIVERSITY | −0.0146 | −0.0047 | 0.011 | 0.0502 | −0.0081 | −0.0314 | 0.0307 | 1 | ||
| SENIOR INDEX | −0.057 | −0.0952 | 0.0512 | −0.0567 | −0.0148 | 0.2867 | −0.0954 | −0.0124 | 1 | |
| MERGED MUNICIPALITY | 0.0756 | −0.0448 | −0.0083 | −0.0063 | −0.004 | −0.0157 | −0.0056 | −0.0094 | −0.0064 | 1 |
- For a description of the variables, see Table 4.
6 Estimation Results
Given the nature of our outcome variable and the data clustered by municipality, we estimate a Beta regression multilevel model with random effects. We insert a random group intercept into the model, which defines groups by the regions containing the municipalities included in our empirical analysis. We estimate both the equations for the mean and for precision parameter.16 First, we present our findings for the aggregated data regarding inner area municipalities, and then we provide results when the dummy INNER AREA is disaggregated in intermediate, peripheral and ultra-peripheral municipalities.
6.1 Estimations for the Beta Regression: The Role of Inner Areas
Table 6 reports estimates of different specifications for the mean and the dispersion model. In particular, the first block refers to the equations in mean. Based on the discussion of evidence on aggregated inner areas, the different specifications displayed in the table vary according to the progressive inclusion of the covariates.
| No control variables | Adding control variables | ||||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
| CONDITIONAL MEAN MODEL | |||||
| INNER AREA | −0.0452*** | −0.0451*** | −0.0281*** | −0.0079*** | −0.0023 |
| (0.0014) | (0.0014) | (0.0022) | (0.0023) | (0.0023) | |
| SOUTH | 0.0951*** | 0.0951*** | 0.1123*** | 0.1413*** | 0.1398*** |
| (0.0228) | (0.0228) | (0.0221) | (0.0274) | (0.0264) | |
| CENTER | 0.0230 | 0.0230 | 0.0275 | 0.0156 | 0.0185 |
| (0.0279) | (0.0279) | (0.0271) | (0.0278) | (0.0266) | |
| INNER AREA*SOUTH | −0.0325*** | −0.0326*** | −0.0311*** | ||
| (0.0030) | (0.0030) | (0.0030) | |||
| INNER AREA*CENTER | −0.0125*** | −0.0156*** | −0.0156*** | ||
| (0.0042) | (0.0041) | (0.0041) | |||
| REGIONAL GDP PER CAPITA | 0.0093** | 0.0090** | |||
| (0.0041) | (0.0041) | ||||
| REGIONAL GDP PER CAPITA 2 | −1.124e-04* | −1.099e-04* | |||
| (6.67e-05) | (6.673e-05) | ||||
| TAX REVENUE | 0.1092*** | 0.0989*** | |||
| (0.0048) | (0.0048) | ||||
| MAYOR AGE | 0.0005*** | 0.0006*** | |||
| (0.0001) | (0.0001) | ||||
| MAYOR BACHELOR | 0.0162*** | 0.0159*** | |||
| (0.0013) | (0.0013) | ||||
| MAYOR FEMALE | −0.0163*** | −0.0164*** | |||
| (0.0020) | (0.0020) | ||||
| GENDER | −0.1893*** | −0.1530*** | |||
| (0.0080) | (0.0081) | ||||
| EDUCATION | 0.0672*** | 0.0610*** | |||
| (0.0046) | (0.0046) | ||||
| UNIVERSITY | 0.1554*** | 0.1574*** | |||
| (0.0061) | (0.0061) | ||||
| SENIOR INDEX | −0.0095*** | ||||
| (0.0005) | |||||
| MERGED MUNICIPALITY | −0.0128** | ||||
| (0.0065) | |||||
| TIME TREND | 0.0056*** | 0.0056*** | 0.0045*** | 0.0051*** | |
| (0.0003) | (0.0003) | (0.0004) | (0.0004) | ||
| INTERCEPT | −0.4978*** | −0.5202*** | −0.5267*** | −0.8102*** | −0.7872*** |
| (0.0161) | (0.0162) | (0.0157) | (0.0695) | (0.0687) | |
| DISPERSION MODEL | |||||
| INNER AREA | −0.3572*** | −0.3595*** | −0.2725*** | −0.2659*** | −0.2571*** |
| (0.0129) | (0.0129) | (0.0166) | (0.0169) | (0.0169) | |
| SOUTH | 0.8379*** | 0.8474*** | 1.0452*** | 1.0414*** | 1.0436*** |
| (0.0142) | (0.0141) | (0.0224) | (0.0231) | (0.0231) | |
| CENTER | 0.57969*** | 0.5811*** | 0.5788*** | 0.6517*** | 0.6479*** |
| (0.0191) | (0.0191) | (0.0286) | (0.0291) | (0.0291) | |
| INNER AREA*SOUTH | −0.3095** | −0.2885*** | −0.2742*** | ||
| (0.0290) | (0.0297) | (0.0297) | |||
| INNER AREA*CENTER | −0.0269 | −0.0801** | −0.0598 | ||
| (0.0388) | (0.03937) | (0.03939) | |||
| Intercept | 5.0200*** | 5.0233*** | 4.9916*** | 5.0303*** | 5.0273*** |
| (0.0093) | (0.0093) | (0.0103) | (0.0105) | (0.0105) | |
| AIC | −209,644 | −209,955 | −210,181 | −206,590 | −206,915 |
| Log Likelihood | 104,831 | 104,987 | 105,104 | 103,318 | 103,482 |
| Num. Obs. | 55,314 | 55,314 | 55,314 | 53,706 | 53,700 |
| Num. Groups: Region | 20 | 20 | 20 | 20 | 20 |
| Var: Region (Intercept) | 0.0021 | 0.0021 | 0.0019 | 0.0019 | 0.0018 |
- The dependent variable is the Gini Index. Results are not expressed as marginal effects. The standard errors are reported in parentheses.
- *** p < 0.01;
- ** p < 0.05;
- * p < 0.1.
In Columns 1 and 2, we find strong evidence that income inequality in inner areas is smaller than in non-inner areas. For both models, the estimated parameters of INNER AREA are negative and strongly significant (−0.045). However, the following comments refer to the estimations shown in Column 3 of Table 6, which reports the results of the best specification from a statistical perspective; indeed, it produces the lowest AIC value.17 In this model, we exploit the territorial dimension of the Gini index by including the interaction between INNER AREA and the geographic location of the municipalities. We find that municipalities classified as inner areas have lower income inequality compared to non-inner areas, across all geographic localizations. However, the magnitude of these effects shows enough divergence to justify a more detailed inspection of the phenomenon. We shed light on this subject by analyzing potential factors influencing differences in inequality between southern, central, and northern regions among inner area municipalities.
In northern Italy, we find a clear difference between inner areas and non-inner areas. Indeed, the estimated coefficient associated with INNER AREA should be interpreted only for the control group for the geographical location, which is NORTH. The estimated parameter is equal to −0.028 (as reported in Column 3), meaning that the inner municipalities register a lower inequality index. Observing INNER AREA*SOUTH, we find notable differences between inner and non-inner areas in the southern regions as well. In these regions, the odds of the average concentration being an inner area is about 6% lower than the odds ratio for non-inner areas located in southern Italy [exp(−0.02808–0.03250) = exp(−0.06058) = 0.9412; 0.9412–1 = −0.06].18 Moreover, when considering the interaction INNER AREA*CENTER, the odds of the average concentration being an inner area is about 4% lower than the odds ratio for non-inner areas in the central regions of the country.19 Essentially, increased job opportunities in the centers do not always translate into dignified living conditions for the population, given the high levels of income inequality.
These findings further explore the initial investigation in Acciari and Mocetti (2013), which also provides a map of income inequality across different regions. Indeed, while Acciari and Mocetti (2013) find the existence of regional disparities in Italy, our study goes much deeper by investigating the influential role of inner-area versus non-inner area municipalities within these regions. Our results are also in line with Mastronardi and Cavallo (2020) who, by estimating linear regression models, find a higher Gini index for hub municipalities when compared to income concentration in inner areas. In this case, as well, we move beyond the previous authors' findings by verifying the relationship between inner areas and income inequality in the various geographical regions, as discussed above.
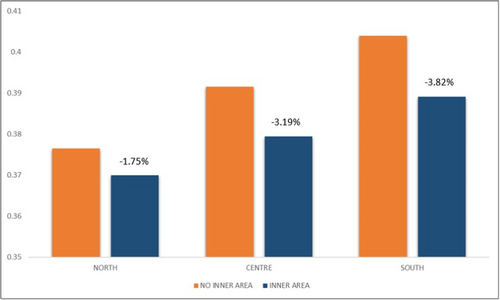
To better explain the economic impact of inner area status for municipalities located in different regions of the country, Figure 3 reports the marginal effects and the relative percentage change between non-inner and inner areas, referring to Model 3 of Table 6. Here we find that location matters. Indeed, the impact of inner area status differs by macro-region. In the north of the country, inner areas register a 1.75% lower Gini index as compared to non-inner areas.20 The reduction is even greater for central regions in Italy, where the marginal effect is equal to −3.19%. Finally, inner area status in southern Italy decreases the Gini index by the highest percentage (−3.82%).
Our investigation provides further contributions with respect to the previous literature in terms of the modeling of its dispersion model, reported in the second block of Table 6, which highlights significant differences in the variability of the Gini index between the different geographic regions. In particular, according to Column 3 of Table 6, there is an increase in the variability of income inequality for inner areas in all Italian macro-regions. The negative sign of INNER AREA signifies a reduction in the estimation of the precision parameter and, therefore, an increase in the variability of the Gini index. By contrast, when the dummy INNER AREA is equal to 0, an increase in the estimation of the precision parameter associated with SOUTH and CENTER suggests a lower variability of income inequality in pole municipalities.
6.2 The Role of Controlling Variables
From an economic standpoint, several factors can influence income concentration. Taking this fact into account, Columns 4 and 5 of Table 6 offer robustness checks of the results for our key variables with the addition of a set of control variables.
First of all, we estimate a concave quadratic relationship between higher regional income per capita and the logit of income inequality. Indeed, the signs of the estimated coefficients are negative for the quadratic terms and positive linear terms of REGIONAL GDP PER CAPITA. This result implies that the link between income inequality and regional GDP per capita displays an inverse U-shaped pattern over the period under scrutiny. However, the quadratic component of GDP is weakly significant, and thus we cannot draw firm conclusions regarding Kuznets's and Piketty's theories.
Interestingly, as also highlighted in the previous literature (Furceri and Ostry 2019), we found a puzzling scenario when considering institutional factors. The inclusion of these controls at a municipal level represents a strong contribution to the previous literature on income inequality. Indeed, this group of variables accounts for the institutional context of the local governments under consideration in our analysis. Specifically, we find that higher tax revenues translate to higher income disparities (the sign of TAX REVENUE is positive). The investigation by Asawasakulkrai (2022) studies the effect of tax revenues on income inequality at the national level (measured through the Gini index). Even if the broader scope of observation differs from our more targeted analysis at a municipal level, the underlying result is the same: a higher degree of tax revenue does not necessarily result in a reduction of income inequality. Iosifidi and Mylonidis (2017) also find a positive relationship between tax revenue and income inequality; they suggest that the government's reliance on personal income taxation results in more of a burden than a support for the average income earner, leading to a higher level of income inequality.
The same sign is estimated for the variables MAYOR AGE and MAYOR BACHELOR, which capture details about the municipality's political context. Our evidence shows that municipalities governed by elderly mayors and/or those with a bachelor's degree or higher register an increased level of Gini index. The first result may be due to career concerns, whereby younger politicians behave more strategically in response to electoral incentives (Alesina, Cassidy, and Troiano 2019), thus leading them to prioritize the well-being of their constituents more often than older mayors might do. Conversely, we find that when the mayor of the municipality is female, income is distributed more equally (the sign of MAYOR FEMALE is negative, meaning a reduction of Gini). The recent study of Ermini, Santolini, and Ciommi (2023) confirms this interesting result, demonstrating that greater representation of women in municipal, executive, and council leadership has significant associations with improved municipal well-being.
In the same line of reasoning, we found a strong negative impact of the share of female employees on income inequality (GENDER). One possible explanation of this evidence theorizes a negative association between gender equality and income inequality through various channels (Gonzales et al. 2015). First, gender gaps in wage and labor force participation rates directly contribute to income inequality, leading to inequality in earnings between men and women. Thus, as women increase their access to the labor market, they effectuate a rise in household income and a decline in poverty and, thus, in income inequality. Gender inequality in education also yields economic inefficiency, as restricting women from educational achievements limits the supply of skilled workers, leading to lower employment and wage levels which are primary causes of income inequality. Finally, gender gap inequalities limit women's participation in productive employment and better-suited jobs, reducing the value of output and the potential economic growth dividend, thereby influencing income distribution (Baloch et al. 2018).
Our results also suggest that income inequality increases along with education levels, which we demonstrate with the variable EDUCATION. This correlation is well documented in the literature. A larger share of highly educated workers in a given municipality may signal a larger earnings differential between highly educated and less educated workers, thus leading to higher income inequalities (Rodríguez-Pose and Tselios 2009; Shahabadi, Nemati, and Hosseinidoust 2018).
When we refer to the inverse effect of UNIVERSITY, which accounts for the presence of a university within the municipality, we can say it is a proxy for the presence of knowledge spillover in that municipality (Bonaccorsi et al. 2014; Muhamad et al. 2022; Rukanyangira and Oidu 2021). The estimated positive coefficient indicates that the presence of a university in the municipality exacerbates inequalities in the distribution of income. To the extent that the knowledge spillover favors those with higher skills and widens the “skills gap” through the proliferation of technological developments, it adversely affects the distribution of income by reducing the demand for lower-skill jobs and increasing the premium for higher-skill employment (Acciari and Mocetti 2013; Dabla-Norris et al. 2015; Furceri and Ostry 2019). Lastly, in terms of sociodemographic characteristics, the senior index has a negative impact on the Gini index, suggesting that income distribution appears more balanced where the population contains a higher number of elderly residents. As Mastronardi and Cavallo (2020) have argued, in municipalities with a higher number of elderly residents, the distribution of income is more balanced because of the equalizing effects of the pension system. This result is also in line with Acciari and Mocetti (2013), who estimate a significant negative coefficient associated with the presence of a higher share of retired people within the population.
Similarly, income inequality is lower in merged municipalities than in non-merged ones. The idea that the consolidation of municipalities results in administrative efficiency and the well-being of residents is controversial (Goto 2023). Our finding can be explained in terms of gains obtained by merged governments, such as (i) reorganization of institutional structures in the territory and (ii) an increase in the quality and variety of services offered in the new municipal aggregation (Aiello, Mercuri, and Bonanno 2017). With a higher probability, both these aspects can foster equal opportunities among residents (and, thus, lower income inequalities) compared to non-merged municipalities.
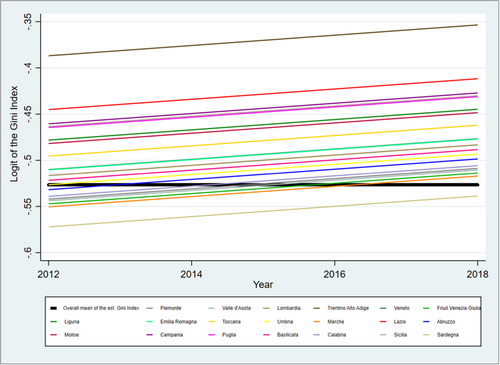
Finally, we estimate a positive coefficient for the TIME TREND, signaling a slightly positive trend in the Gini index over time (the estimated coefficient is equal to 0.005). Figure 4 shows the link between the Gini index and the time trend for all 20 regions. The slopes of the functions are the same because we do not assume a random slope in the multilevel specification of our models. However, based on the graphs, we can capture differences in terms of a shift in the inequality index among the various regions. The red line represents the overall estimated mean of the Gini index ().
6.3 Further Analysis: Inner Area Disaggregation
After disaggregating inner areas, we find that the AIC statistics reported in Table 7 show that the best specification is Model 3, from which it emerges that the importance of inner areas in terms of income inequality is heterogeneous. The variables of interest are INTERMEDIATE, PERIPHERAL, and ULTRA-PERIPHERAL. According to Column 3, we observe a noteworthy difference from our earlier results. In northern Italy, we find strong differences between all inner area subcategories (intermediate, peripheral, and ultra-peripheral municipalities) and centers. The odds ratios for classification as intermediate, peripheral and ultra-peripheral are approximately 2, 4% and 5% lower than the odds ratio for non-inner areas.21
| No control variables | Adding control variables | ||||
|---|---|---|---|---|---|
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |
| Conditional Mean Model | |||||
| INTERMEDIATE | −0.0337*** | −0.0337*** | −0.0209*** | −0.0060** | −0. 0033 |
| (0.0015) | (0.0015) | (0.0025) | (0.0025) | (0.0025) | |
| PERIPHERAL | −0.0574*** | −0.0574*** | −0.0418*** | −0.0131*** | −0.0046 |
| (0.0019) | (0.0018) | (0.0036) | (0.0037) | (0.0037) | |
| ULTRAPERIPHERAL | −0.0945*** | −0.0940*** | −0.0530*** | −0.0184* | −0.0022 |
| (0.0040) | (0.0040) | (0.0096) | (0.0102) | (0.0104) | |
| SOUTH | 0.1026*** | 0.1027*** | 0.1156*** | 0.1369*** | 0.1430*** |
| (0.0228) | (0.0228) | (0.0222) | (0.0273) | (0.0306) | |
| CENTER | 0.0215 | 0.0215 | 0.0278 | −0.0037 | 0.0101 |
| (0.0279) | (0.0279) | (0.0272) | (0.0287) | (0.0325) | |
| INTERMEDIATE*SOUTH | −0.0219*** | −0.0209*** | −0.0202*** | ||
| (0.0033) | (0.0033) | (0.0033) | |||
| PERIPHERAL*SOUTH | −0.0271*** | −0.0346*** | −0.0357*** | ||
| (0.0043) | (0.0044) | (0.0044) | |||
| ULTRAPERIPHERAL*SOUTH | −0.0562*** | −0.0681*** | −0.0710*** | ||
| (0.0106) | (0.0112) | (0.0112) | |||
| INTERMEDIATE*CENTER | −0.0194*** | −0.0197*** | −0.0201*** | ||
| (0.0046) | (0.0045) | (0.0045) | |||
| PERIPHERAL*CENTER | −0.0049 | −0.0119** | −0.0116* | ||
| (0.0061) | (0.0060) | (0.0060) | |||
| ULTRAPERIPHERAL*CENTER | 0.1386*** | 0.1172*** | 0.0985*** | ||
| (0.0296) | (0.0285) | (0.0281) | |||
| REGIONAL GDP PER CAPITA | 0.0080** | 0.0083** | |||
| (0.0041) | (0.0041) | ||||
| REGIONAL GDP PER CAPITA 2 | −9.61e-05 | −1.10e-04* | |||
| (6.61e-05) | (6.63e-05) | ||||
| TAX REVENUE | 0.1019*** | 0.0933*** | |||
| (0.0048) | (0.0048) | ||||
| MAYOR AGE | 0.0005*** | 0.0006*** | |||
| (0.0001) | (0.0001) | ||||
| MAYOR BACHELOR | 0.0162*** | 0.0161*** | |||
| (0.0013) | (0.0013) | ||||
| MAYOR FEMALE | −0.0159*** | −0.0153*** | |||
| (0.0019) | (0.0019) | ||||
| GENDER | −0.1901*** | −0.1570*** | |||
| (0.0081) | (0.0082) | ||||
| EDUCATION | 0.0647*** | 0.0584*** | |||
| (0.0046) | (0.0046) | ||||
| UNIVERSITY | 0.1540*** | 0.1551*** | |||
| (0.0061) | (0.0061) | ||||
| SENIOR INDEX | −0.0084*** | ||||
| (0.0005) | |||||
| MERGED MUNICIPALITY | −0.0109*** | ||||
| (0.0065) | |||||
| TIME TREND | 0.0056*** | 0.0056*** | 0.0047*** | 0.0052*** | |
| (0.0003) | (0.0003) | (0.0004) | (0.0004) | ||
| Intercept | −0.4989*** | −0.5215*** | −0.5270*** | −0.7780*** | −0.7725*** |
| (0.0161) | (0.0162) | (0.0157) | (0.0685) | (0.0698) | |
| DISPERSION MODEL | |||||
| INTERMEDIATE | −0.2584*** | −0.2596*** | −0.2410*** | −0.2262*** | −0.2274*** |
| (0.0145) | (0.0145) | (0.0191) | (0.0193) | (0.0193) | |
| PERIPHERAL | −0.4231*** | −0.4227*** | −0.3229*** | −0.3287*** | −0.3015*** |
| (0.0175) | (0.0175) | (0.0257) | (0.0263) | (0.0262) | |
| ULTRA-PERIPHERAL | −0.8306*** | −0.0845** | −0.3231*** | −0.4052*** | −0.4234*** |
| (0.0330) | (0.0330) | (0.0670) | (0.0699) | (0.0703) | |
| SOUTH | 0.9238*** | 0.9348*** | 1.0504*** | 1.0499*** | 1.0447*** |
| (0.0145) | (0.0145) | (0.0224) | (0.0233) | (0.0231) | |
| CENTER | 0.5590*** | 0.5606*** | 0.5785*** | 0.6375*** | 0.641*** |
| (0.0191) | (0.0191) | (0.0287) | (0.0293) | (0.0291) | |
| INTERMEDIATE*SOUTH | −0.0770** | −0.0536+ | −0.0488+ | ||
| (0.0336) | (0.0343) | (0.0344) | |||
| PERIPHERAL*SOUTH | −0.2766*** | −0.2666 | −0.2711*** | ||
| (0.0378) | (0.0386) | (0.0386) | |||
| ULTRA-PERIPHERAL*SOUTH | −0.6991*** | −0.5849*** | −0.5163*** | ||
| (0.0780) | (0.0811) | (0.0817) | |||
| INTERMEDIATE*CENTER | −0.0684 | −0.1151*** | −0.1093* | ||
| (0.0425) | (0.0432) | (0.0430) | |||
| PERIPHERAL*CENTER | 0.0927* | 0.0691 | 0.0763 | ||
| (0.0558) | (0.0566) | (0.0565) | |||
| ULTRA-PERIPHERAL*CENTER | −0.3884* | −0.2723* | −0.2231 | ||
| (0.2316) | (0.2259) | (0.2243) | |||
| Intercept | 5.0098*** | 5.0128*** | 4.992*** | 5.0302*** | 5.0293*** |
| (0.0094) | (0.0094) | (0.0104) | (0.0105) | (0.0105) | |
| AIC | −210,364 | −210,688 | −210,928 | −207,224 | −207,456 |
| Log Likelihood | 105,195 | 105,358 | 105,490 | 103,647 | 103,765 |
| Num. Obs. | 55,314 | 55,314 | 55,314 | 53,706 | 53,700 |
| Num. Groups: Region | 20 | 20 | 20 | 20 | 20 |
| Var: Region (Intercept) | 0.0021 | 0.0021 | 0.0019 | 0.0019 | 0.0027 |
- The dependent variable is the Gini Index. Results are not expressed as marginal effects. The standard errors are reported in parentheses.
- *** p < 0.01;
- ** p < 0.05;
- * p < 0.1;
- +p < 0.15.
In southern and central Italy, we also find noticeable differences between inner areas and center zones. Beginning with the interaction between SOUTH and INTERMEDIATE, we estimate a negative parameter, meaning that the odds ratio of the average concentration for intermediate municipalities in southern Italy is about 4% lower than the odds ratio of the average concentration of non-inner areas.22 With regard to the interaction PERIPHERAL*SOUTH, the odds ratio of the average concentration for PERIPHERAL is about 6.7% lower than the odds ratio of the average concentration for centers.23 The coefficient of the interaction between SOUTH and ULTRA-PERIPHERAL implies that the odds ratio of the average concentration for ULTRA-PERIPHERAL is about 10% lower than the odds ratio of the average concentration for non-inner area classification.24
As for the gap between inner and non-inner areas in the central regions, we estimated that the odds ratios of the average concentration for INTERMEDIATE and PERIPHERAL are respectively about 4% and 4.6% lower than the odds ratio of the average concentration for center zones.25 By contrast, when we look at the interaction ULTRA-PERIPHERAL*CENTER, the estimated coefficient is positive (0.139). This implies that the odds ratio of the average concentration for ULTRA-PERIPHERAL municipalities in the central regions of the country is about 9% greater than the odds ratio of the average concentration for non-inner areas.26 In light of these findings, along with those regarding inner areas, we note that while there is an abundance of job opportunities in centers, the opportunities do not consistently translate into satisfactory living standards across the population, thus contributing to notable levels of income inequality.
These results demonstrate the crucial importance of further disaggregating the NSIA classifications. After implementing a stronger disaggregation, we found evidence of a clear heterogeneity in terms of income inequality. Ultra-peripheral areas manifest the greatest difference in income disparities with respect to non-inner areas, and they do so in a heterogeneous manner. Ultra-peripheral municipalities that are more than 75 minutes away from a center show a lower income concentration than other types of municipalities in the north and south of the country, while in the same subcategory of inner areas located in the central regions, we estimated a higher Gini index than non-inner areas. Thus, it seems that ultra-peripheral areas propel the disparity between inner and non-inner areas in terms of income inequality. Our findings also demonstrate a high amount of heterogeneity for the southern and northern regions of the country: in ultra-peripheral areas with less access to essential services, the reduction of income inequalities is likely due to greater flexibility and a propensity to seize the opportunities offered by government programs. Thus, it seems that additional economic policy efforts should be implemented to promote socioeconomic inclusion in more remote country areas. Our findings are confirmed even when we change the model specification by including control variables (e.g., socioeconomic and demographic characteristics as well as time trends).
Our results stand in contrast of those reported in Gallo and Pagliacci (2020); indeed, they demonstrate marginally positive effects for the three inner subcategories compared to only one category defined in the macro-group of centers, e.g., poles. Additionally, the prior study claims that in Italy, inner areas “clearly do not matter” (Gallo and Pagliacci 2020, p. 217). Our evidence contradicts this notion and, conversely, offers an opportunity to analyze the advantages of suburbs (Viesti 2020) and to encourage economic policies that favor socioeconomic promotion in these areas. Finally, our findings are in line with De Renzis, Faggian and Urso (2022), who find that inner areas are more adaptable to the prolonged challenges associated with peripheral conditions.
In the dispersion model results reported in the second block of Table 7 (Column 3), intermediate, peripheral and ultra-peripheral municipalities show lower precision coefficients, implying an increased variability in terms of income concentration. The same categories of municipalities in southern and central Italy elicited similar findings, with the exception of peripheral municipalities in central region.
In sum, our findings demonstrate territorial differences in the variability of income concentration, and inner-area municipalities present a lower dispersion of income inequality compared to non-inner areas.
Figure 5 illustrates our calculations of the marginal effect of non-inner areas (control group) and the three subcategories of the inner areas (intermediate, peripheral or ultra-peripheral) on income concentration. These marginal effects refer to Column 3 of Table 7.
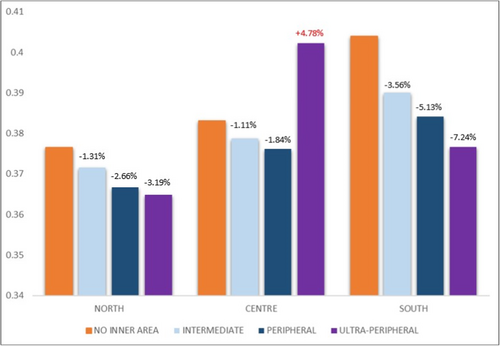
In northern Italy, all municipalities comprising the three subcategories of inner areas demonstrate reduced inequality with respect to non-inner areas. Ultra-peripheral municipalities register a high difference with respect to poles (-3.19%). In the south, intermediate areas show a decrease of income inequality by 3.56% over that of the poles. The reduction is more evident for peripheral and ultra-peripheral municipalities, which register a diminishing income concentration index of about 5.1% and 7.2%, respectively. Even in this case, the overall reduction associated with inner areas in the south (Column 3 of Table 6) is mainly driven by the results obtained for ultra-peripheral municipalities (Column 3 of Table 7).
The results for the central regions of the country are puzzling. Income inequality is slightly decreased in intermediate or peripheral municipalities, while the Gini index appears to increase in ultra-peripheral municipalities compared to non-inner areas by about 5 percentage points. To better explain our findings for central Italy, we refer to Figure 1 (Section 3.2). One explanation may involve structural and infrastructural factors. As the map shows, the territorial formation and the distribution of central inland areas are largely determined by the presence of the Apennine mountain range and by the clustering of most inner areas within Lazio, and more particularly around Rome (De Renzis, Faggian, and Urso 2022). Even if the number of inner areas classified as ultra-peripheral municipalities is very low, the estimated coefficient of the interaction term ULTRA-PERIPHERAL*CENTER (Column 3 of Table 7) is positive and statistically significant. In other words, the morphological characteristics of the central region reduce access to essential services, as the Apennines obstruct connections between the poles and the inland areas and, as a consequence, inner area municipalities show greater income inequalities as compared to those in the north and south.
7 Concluding Remarks
This paper has empirically investigated the relationship between the NSIA classification of inner areas and income inequality within Italian municipalities during the period 2012–2018. Our study considers the broader rural-urban divide as well as the subcategories of inner areas, and it adopts a GLMM multilevel approach with Beta distribution and random intercept at the regional level. Using these approaches, we offer evidence that inner-area municipalities play a crucial role in income inequality based on the geographical distribution. Our findings show notable differences within the three macro-regions of Italy. In examining these dynamics in northern and southern Italy, our study reveals that ultra-peripheral areas account for a majority of the gap between inner and non-inner areas in terms of income inequality. In the areas furthest away from essential services, the reduction in income inequalities appears more pronounced, likely due to greater adaptability and propensity to take advantage of government programs and opportunities. Notwithstanding, in central regions income inequality rises in ultra-peripheral areas with respect to the poles. Findings suggest that challenging geographic features and the clustering of municipalities in one region lead to infrastructure limits that, in turn, may exacerbate income disparities. Finally, our findings offer insights into the variability of income concentration, from which territorial differences also emerge. In particular, municipalities in inner areas present a higher dispersion of income inequality in contrast to those in non-inner areas.
The results suggest that location matters in our analysis of these socioeconomic factors. In particular, our evidence shows that empirical analyses at a greater degree of disaggregation are crucial to reveal granular differences between Italian macro areas and to corroborate heterogeneity in income inequality when considering inner areas. This conclusion is relevant for the crafting of economic policies at both the local and the supranational. In this regard, the United Nations' Sustainable Development Goals program created as part of its 2030 Agenda recognizes that inequalities hinder a country's long-term development, generating violence, disease and environmental degradation. Indeed, one of the program's specific goals aims to reduce inequalities and disparities in terms of opportunities, income and power. In this framework, our study affirms the necessity of implementing strategies to reduce income disparities and aligns with the UN's 2030 Agenda.
Acknowledgments
Open access publishing facilitated by Universita della Calabria, as part of the Wiley - CRUI-CARE agreement.
Conflicts of Interest
The authors declare no conflicts of interest.
Endnotes
Appendix: Methodological Approach
This Appendix reports statistical details on the approach used for our empirical analysis.
The estimation of the regression coefficients can be obtained by maximizing the following likelihood function with respect to and : .
Considering the nature of our data, we adopted an extended version of the Beta regression model, indicated in the literature with the term Beta Mixed Model or Generalized Beta Model with Mixed Effects (Beta GLMM).27
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




