Activity–composition relations for the calculation of partial melting equilibria in metabasic rocks
Abstract
A set of thermodynamic models is presented that, for the first time, allows partial melting equilibria to be calculated for metabasic rocks. The models consist of new activity–composition relations combined with end-member thermodynamic properties from the Holland & Powell dataset, version 6. They allow for forward modelling in the system Na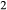 O–CaO–K
O–CaO–K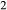 O–FeO–MgO–Al
O–FeO–MgO–Al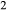 O
O –SiO
–SiO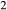 –H
–H O–TiO
O–TiO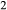 –Fe
–Fe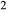 O
O . In particular, new activity–composition relations are presented for silicate melt of broadly trondhjemitic–tonalitic composition, and for augitic clinopyroxene with Si–Al mixing on the tetrahedral sites, while existing activity–composition relations for hornblende are extended to include K
. In particular, new activity–composition relations are presented for silicate melt of broadly trondhjemitic–tonalitic composition, and for augitic clinopyroxene with Si–Al mixing on the tetrahedral sites, while existing activity–composition relations for hornblende are extended to include K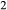 O and TiO
O and TiO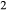 . Calibration of the activity–composition relations was carried out with the aim of reproducing major experimental phase-in/phase-out boundaries that define the amphibolite–granulite transition, across a range of bulk compositions, at ≤13 kbar.
. Calibration of the activity–composition relations was carried out with the aim of reproducing major experimental phase-in/phase-out boundaries that define the amphibolite–granulite transition, across a range of bulk compositions, at ≤13 kbar.
Introduction
The introduction in recent decades of forward modelling via calculated phase diagrams (e.g. Powell & Holland, 1988; Powell et al., 1998) represents a major development in metamorphic petrology. Suitable phase diagrams, commonly known as pseudosections, map the equilibrium phase assemblages subject to constraints of bulk composition, usually in pressure–temperature (P–T), temperature–bulk composition (T–X) or pressure–bulk composition (P–X) space. To produce such diagrams, the thermodynamics of each of the phases involved must be described by a model. A model consists of one or more end-members, with thermodynamic properties typically taken from an internally consistent thermodynamic dataset. For multiple-end-member phases, such as solid solutions, the end-member properties must be combined with activity–composition (a–x) relations describing the thermodynamics of mixing of the end-members.
End-member thermodynamic datasets in current use include those of Holland & Powell (2011), Berman (1988), Gottschalk (1996) and Chatterjee et al. (1998). The development of model a–x relations for minerals and melts has a long history, with much early work having the purpose of generating thermodynamically based thermometers and barometers (e.g. Wood & Banno, 1973; Stormer, 1975; Thompson, 1976; Newton & Haselton, 1981). Model a–x relations are almost inevitably under-constrained by the available data, and so, when the aim is to calculate phase diagrams, it is sensible to select a–x relations for the various phases that have been parameterized to work together as a set. In this way, deficiencies in the thermodynamic model for one phase may compensate for those in the model for another phase, producing appropriate stable assemblages overall. Widely used sets of a–x relations include those developed for the modelling of metapelitic or ultramafic rocks based on the Holland & Powell (1998, 2011) datasets (e.g. White et al., 2007, 2014; Klemme et al., 2009; Chu & Ague, 2013; Holland et al., 2013), and those incorporated into the MELTS software and its extensions pMELTS, pHMELTS and rhyolite-MELTS, for modelling of partial melting equilibria in ultramafic and felsic systems (Ghiorso & Sack, 1995; Ghiorso et al., 2002; Asimow et al., 2004; Smith & Asimow, 2005; Gualda et al., 2012).
Until now, no set of a–x relations has been available for the modelling of partial melting equilibria in metabasic rocks. The current MELTS, pMELTS and rhyolite-MELTS models are not intended to calculate equilibria between melt and amphibole or biotite. A–x relations by, for example, Coggon & Holland (2002), Diener et al. (2007), Green et al. (2007), Diener & Powell (2012), founded on the superceded Holland & Powell (1998) dataset, allow modelling of subsolidus metabasic rocks up to amphibolite and eclogite facies. However, there is no corresponding model for the melt phase; the metapelite melt model of Holland & Powell (2001) and White et al. (2007, 2014) is not parameterized for any but peraluminous, K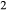 O-rich, CaO-poor felsic melt compositions. Moreover, the a–x relations for several key solid phases are not appropriate for use at granulite facies temperatures: the hornblende model of Diener et al. (2007) omits K
O-rich, CaO-poor felsic melt compositions. Moreover, the a–x relations for several key solid phases are not appropriate for use at granulite facies temperatures: the hornblende model of Diener et al. (2007) omits K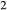 O and TiO
O and TiO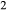 , while the clinopyroxene model of Green et al. (2007) does not allow for Al on the tetrahedral site, or for Mg or Fe
, while the clinopyroxene model of Green et al. (2007) does not allow for Al on the tetrahedral site, or for Mg or Fe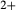 on the M2-site.
on the M2-site.
Our new work fills these gaps. In this paper, we provide a–x relations for broadly tonalitic–trondjhemitic silicate melt, high-temperature augitic clinopyroxene, and K-,Ti-bearing hornblende, representing revision and substantial extension of previous models. Other phases that are required for the modelling also appear in metapelitic equilibria, and we have taken the relevant a–x relations from the set of White et al. (2014). The two sets of a–x relations therefore overlap. As a set, the thermodynamic models for metabasite melting equilibria are formally calibrated to 13 kbar, and should be used at higher pressures only with sceptical assessment of the results. The 13 kbar limit was imposed due to the lack of a thermodynamic model for aqueous fluid containing a significant proportion of dissolved silicate material, and was inferred from experimental and modelling work on the solubility of silicate minerals (Manning, 1994; Gerya et al., 2005; Manning, 2007; Newton & Manning, 2008; Dolejš & Manning, 2010; Hunt & Manning, 2012).
This paper presents the development and calibration of the new a–x relations, while in a companion paper (Palin et al., 2016b, this issue), we examine their application to forward modelling in a range of basic to intermediate bulk compositions. Calibration of the a–x relations ultimately made use of experiments in natural systems, modelled in the system Na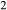 O–CaO–K
O–CaO–K O–FeO–MgO–Al
O–FeO–MgO–Al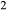 O
O –SiO
–SiO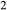 –H
–H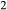 O–TiO
O–TiO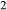 –Fe
–Fe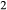 O
O (NCKFMASHTO). A large body of experimental work has explored phase relations in partially molten metabasic rocks, frequently seeking to determine the origins of tonalite–trondhjemite–granodiorite (TTG) magmas (e.g. Beard & Lofgren, 1991; Rapp et al., 1991; Rushmer, 1991; Sen & Dunn, 1994; Wolf & Wyllie, 1994; Patiño Douce & Beard, 1995; Rapp & Watson, 1995; Skjerlie & Patiño Douce, 1995; Springer & Seck, 1997; López & Castro, 2001; Skjerlie & Patiño Douce, 2002; Foley et al., 2003; Auzanneau et al., 2006; Qian & Hermann, 2013; Zhang et al., 2013; Ziaja et al., 2014). During the calibration process, for a subset of the experimental studies, forward calculations of phase relations at the experimental bulk compositions were compared with the observations. The primary goal was to reproduce major phase-in/phase-out boundaries, which, it is hoped, ensures that the behaviour of the models will be broadly realistic in the forward-modelling context for which they are intended.
(NCKFMASHTO). A large body of experimental work has explored phase relations in partially molten metabasic rocks, frequently seeking to determine the origins of tonalite–trondhjemite–granodiorite (TTG) magmas (e.g. Beard & Lofgren, 1991; Rapp et al., 1991; Rushmer, 1991; Sen & Dunn, 1994; Wolf & Wyllie, 1994; Patiño Douce & Beard, 1995; Rapp & Watson, 1995; Skjerlie & Patiño Douce, 1995; Springer & Seck, 1997; López & Castro, 2001; Skjerlie & Patiño Douce, 2002; Foley et al., 2003; Auzanneau et al., 2006; Qian & Hermann, 2013; Zhang et al., 2013; Ziaja et al., 2014). During the calibration process, for a subset of the experimental studies, forward calculations of phase relations at the experimental bulk compositions were compared with the observations. The primary goal was to reproduce major phase-in/phase-out boundaries, which, it is hoped, ensures that the behaviour of the models will be broadly realistic in the forward-modelling context for which they are intended.
General Notes on the Thermodynamic Models
The set of a–x relations presented here will be referred to as the ‘metabasite set’. It is suitable for use with versions 6.2 or 6.3 of the Holland & Powell (2011) dataset (ds62, ds63), created on 6 February 2012 and 15 January 2015 respectively. The figures in this paper were calculated with version 6.2. The update to version 6.3 includes a key refinement to the thermodynamics of the H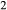 O end-member in the melt, and is expected to give slightly more realistic results at the wet solidus. In other respects, differences between calculations with ds62 and ds63 are believed to be insignificant. The a–x relations should not, however, be expected to give meaningful output with the older, widely used version 5.5 (ds55) of the dataset (Holland & Powell, 1998); indeed ds55 lacks one of the necessary melt end-members. Full descriptions of the a–x relations of the metabasite set appear in the Appendix, along with a guide to downloading the files necessary for using them via the software thermocalc (Powell & Holland, 1988). Calculations in this paper were carried out with thermocalc, version tc340i.
O end-member in the melt, and is expected to give slightly more realistic results at the wet solidus. In other respects, differences between calculations with ds62 and ds63 are believed to be insignificant. The a–x relations should not, however, be expected to give meaningful output with the older, widely used version 5.5 (ds55) of the dataset (Holland & Powell, 1998); indeed ds55 lacks one of the necessary melt end-members. Full descriptions of the a–x relations of the metabasite set appear in the Appendix, along with a guide to downloading the files necessary for using them via the software thermocalc (Powell & Holland, 1988). Calculations in this paper were carried out with thermocalc, version tc340i.
This paper will refer to two existing groups of a–x relations used for calculations on metapelitic rocks. The first, the metapelite ‘ds55-set’, was published by White et al. (2007) for use with version 5.5 of the Holland & Powell dataset (created 22 November 2003), and has since been slightly modified. The second, the metapelite ‘ds6-set’, was a major revision of the same models for version 6.1 of the dataset (created 13 November 2011), by White et al. (2014).
Abbreviations for the names of end-members are consistent with the Holland & Powell dataset, and are either explained in the text or defined in the Appendix. End-members that are treated as pure phases are quartz (q), albite (ab), sphene (sph), rutile (ru) and lawsonite (law). The following solution phases appear in the text and figures: actinolite (act), glaucophane (gl), hornblende (hb), orthopyroxene (opx), garnet (g), plagioclase (pl,  , and pli,
, and pli, 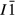 , the latter used for comparison with experiments where
, the latter used for comparison with experiments where 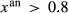 ), potassium feldspar (ksp), biotite (bi), muscovite (mu), chlorite (chl), silicate melt (L), epidote (ep), ilmenite (ilm), magnetite (mt) and olivine (ol). Additionally five clinopyroxene (cpx) phases are referred to, represented with two different sets of a–x relations. Augitic clinopyroxene (aug) and pigeonite (pig) are considered to have the general formula [Ca, Na, Mg, Fe2+]M2 [Mg, Fe
), potassium feldspar (ksp), biotite (bi), muscovite (mu), chlorite (chl), silicate melt (L), epidote (ep), ilmenite (ilm), magnetite (mt) and olivine (ol). Additionally five clinopyroxene (cpx) phases are referred to, represented with two different sets of a–x relations. Augitic clinopyroxene (aug) and pigeonite (pig) are considered to have the general formula [Ca, Na, Mg, Fe2+]M2 [Mg, Fe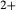 , Al, Fe3+]M1 [Si, Al]
, Al, Fe3+]M1 [Si, Al]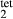 , while diopside (di), jadeite (jd) and omphacite (o) have the general formula [Ca, Na]
, while diopside (di), jadeite (jd) and omphacite (o) have the general formula [Ca, Na]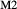 [Mg, Fe
[Mg, Fe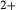 , Al, Fe3+]M2 Si
, Al, Fe3+]M2 Si , with omphacite forming via order–disorder on the M sites.
, with omphacite forming via order–disorder on the M sites.
Among these phases, the a–x relations for metabasite melt (L), augitic clinopyroxene (aug and pig) and clinoamphibole (hb, gl and act) are newly calibrated to address partial melting of metabasitic rocks. Of the clinoamphiboles, only hornblende is normally relevant to supersolidus amphibolite–granulite facies conditions, but the new amphibole a–x model is also appropriate for actinolite and glaucophane at lower temperatures. The remaining a–x models in the metabasite set, for the phases garnet, orthopyroxene, feldspar, spinel–magnetite and ilmenite, were taken from the metapelite ds6-set.
Additionally, the existing a–x model for the potentially ordered sodic–calcic pyroxenes jd, di and o (from Green et al., 2007, for use with ds55), has been updated for use with ds6 of the Holland & Powell dataset (Holland & Powell, 2011). This model, the ‘omphacite’ model, remains the appropriate clinopyroxene model to use under subsolidus conditions where co-existing clinopyroxenes might occur. It should not be used in calculations that also involve the augitic clinopyroxene model.
Form of the a–x relations
Like the metapelite ds55- and ds6-sets, the a–x relations developed in this paper are macroscopic regular solution models, in which non-ideal enthalpic interactions are present between pairs of end-members, expressed as interaction energies 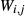 . The mixing-on-sites approach is adopted, in order to give an approximately correct form for the ideal entropy of mixing. The regular solution paradigm is modified by allowing the
. The mixing-on-sites approach is adopted, in order to give an approximately correct form for the ideal entropy of mixing. The regular solution paradigm is modified by allowing the 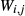 in principle to be linear functions of pressure and temperature, although in practice it is almost never possible to resolve these two dependencies, and the
in principle to be linear functions of pressure and temperature, although in practice it is almost never possible to resolve these two dependencies, and the 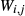 are usually treated as constant or functions of pressure only. The formulation is discussed extensively by Powell & Holland (1993) and Holland & Powell (1996a, b), under the name ‘symmetric formalism’. A further modification, the asymmetric formalism (Holland & Powell, 2003), introduced asymmetry in the manner of van Laar (1906) via ‘volume’ parameters,
are usually treated as constant or functions of pressure only. The formulation is discussed extensively by Powell & Holland (1993) and Holland & Powell (1996a, b), under the name ‘symmetric formalism’. A further modification, the asymmetric formalism (Holland & Powell, 2003), introduced asymmetry in the manner of van Laar (1906) via ‘volume’ parameters, 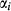 , associated with each end-member i.
, associated with each end-member i.
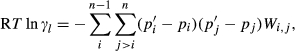 (1)
(1)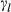 is the non-ideal activity coefficient of end-member ℓ, T is the temperature, R is the gas constant,
is the non-ideal activity coefficient of end-member ℓ, T is the temperature, R is the gas constant,  is the proportion of end-member k in the phase,
is the proportion of end-member k in the phase, 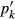 is the value of
is the value of 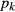 in end-member ℓ, such that
in end-member ℓ, such that 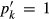 where k = ℓ and
where k = ℓ and 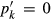 where k≠ℓ, and the n end-members in the phase form an independent set. In the asymmetric formalism, the non-ideal contributions are written
where k≠ℓ, and the n end-members in the phase form an independent set. In the asymmetric formalism, the non-ideal contributions are written
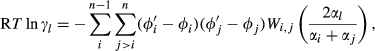 (2)
(2)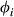 is the proportion of end-member i weighted by the van Laar parameters,
is the proportion of end-member i weighted by the van Laar parameters, 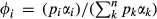 , and
, and 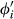 is likewise the van Laar-weighted equivalent of
is likewise the van Laar-weighted equivalent of  .
.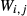 and
and 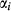 values. In addition, it is sometimes necessary to introduce an expression
values. In addition, it is sometimes necessary to introduce an expression 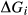 , which represents an adjustment to the Gibbs energy of end-member i relative to its function
, which represents an adjustment to the Gibbs energy of end-member i relative to its function 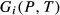 in the dataset. The
in the dataset. The 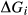 take the form a + b T + c P.
take the form a + b T + c P. 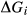 expressions were introduced into the metabasite set for a number of reasons:
expressions were introduced into the metabasite set for a number of reasons:
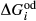 represents the
represents the 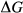 of ordering. It is applied to an end-member that represents full ordering of cations on sites, at an intermediate composition. It captures the enthalpy change of formation of the ordered intermediate end-member, when it is made by reaction of the end-members at the compositional extremes.
of ordering. It is applied to an end-member that represents full ordering of cations on sites, at an intermediate composition. It captures the enthalpy change of formation of the ordered intermediate end-member, when it is made by reaction of the end-members at the compositional extremes. . This is a modification made to the thermodynamics of a dataset end-member simply in order to improve the behaviour of the a–x relations in phase diagram calculations. A non-zero value may imply that the dataset thermodynamic data for the relevant end-member might be inappropriate, or just that the end-member is accommodating various other deficiencies in the thermodynamic models.
. This is a modification made to the thermodynamics of a dataset end-member simply in order to improve the behaviour of the a–x relations in phase diagram calculations. A non-zero value may imply that the dataset thermodynamic data for the relevant end-member might be inappropriate, or just that the end-member is accommodating various other deficiencies in the thermodynamic models.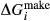 . Certain minor or ‘fictive’ end-members in the a–x models do not appear in the dataset. To approximate their
. Certain minor or ‘fictive’ end-members in the a–x models do not appear in the dataset. To approximate their  functions, a linear combination of dataset end-members is chosen that produces the right composition. The G(P,T) functions of these end-members are combined likewise, and a
functions, a linear combination of dataset end-members is chosen that produces the right composition. The G(P,T) functions of these end-members are combined likewise, and a 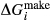 expression is added that can be calibrated to represent the
expression is added that can be calibrated to represent the 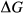 between the combination of dataset end-members and the fictive end-member.
between the combination of dataset end-members and the fictive end-member.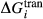 . This is a special case of
. This is a special case of 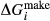 , in which a first order phase transition separates end-member i from dataset end-member j of the same composition but different symmetry. Then
, in which a first order phase transition separates end-member i from dataset end-member j of the same composition but different symmetry. Then 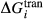 represents ΔG of the i–j transition.
represents ΔG of the i–j transition.
Examples of all of these appear in the a–x relations in the Appendix.
This paper adopts the following notational conventions: (i) as 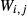 ≡
≡ 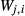 , either notation may be used for a given pair of end-members; (ii) the interaction energies between an end-member i and multiple, specified end-members j,k,… in the same phase are represented as
, either notation may be used for a given pair of end-members; (ii) the interaction energies between an end-member i and multiple, specified end-members j,k,… in the same phase are represented as 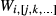 ; (iii) the expression
; (iii) the expression 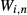 , or
, or 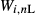 for the liquid model, represents the set of
for the liquid model, represents the set of  parameters between end-member i and all of the other end-members in the same a–x model.
parameters between end-member i and all of the other end-members in the same a–x model.
Calibration strategy
The root of the calibration approach was the fitting of key parameters in small, well-constrained chemical subsystems. Thus, each of the new a–x models has a core in a major subsystem that was developed independently of the other new models. The models were then completed sequentially. First the augite model was developed entirely in amphibole-free and melt-free assemblages. Then the clinoamphibole model was completed based on calculations in which the augite model was treated as fixed. Finally, both the augite and clinoamphibole a–x relations were treated as fixed, while the melt model was completed based on observations from a selection of experimental studies on TTG-generation. The choice of TTG-generation studies was limited to those with multiple hydrate-breakdown melting runs at ≤13 kbar, placing constraints on significant phase-in/phase-out boundaries, with bulk compositions that could reasonably be modelled in NCKFMASHTO (e.g. they should be nominally carbon-free).
In general (for variance >2), the calculations performed during the calibration process mimicked those performed when the finished models are used; they were forward calculations that gave the compositions and modal proportions of phases at equilibrium, subject to the constraint of the experimental bulk composition. In some cases, the calculations took place at the P–T conditions of an experiment, for direct comparison with the experimental run products. However, the highest priority for the calibration was to make good predictions of the major features of phase relations across P–T space, rather than to make accurate predictions of phase compositions. Consequently, the interpolated positions of key phase field boundaries (e.g. orthopyroxene-in, hornblende-out) were used directly in calibration. The final step in calibration was to calculate full P–T pseudosections for key experimental bulk compositions, ensuring that the assemblages specified during the calibration were the most stable that could be modelled.
Calibrations that are new in this work were carried out either by manual trial and error or by using a Monte Carlo method, mctc, within the thermocalc software. When mctc is invoked, thermocalc calculates a set of phase equilibria repeatedly, using a–x models with parameters drawn randomly from within specified distributions. ‘Successful’ sets of model parameters are identified by comparing the resulting calculated phase equilibria with the observations, and the distribution of successful model parameters is reviewed, leading to refinement of the initial distribution. Over the course of many mctc runs, the user will first widen the initial distributions of model parameters until, for each parameter, a peak is visible in the distribution of successful values. Then, certain model parameters may be given fixed values, especially those that are weakly constrained (their ‘successful’ distributions are wide), or strongly correlated with other parameters. The distributions of all parameters are narrowed over time, with the aim of deriving quasi-optimized values.
The mctc approach is thus a hybrid between manual trial and error and a formal, automated technique. It robustly handles two problems: the very high and multi-dimensional correlations among successful distributions of model parameters, and the presence of parameters that are essentially unconstrained by the data. A fitting method that does not take these phenomena into account is at risk of generating physically implausible parameter values, leading to a–x relations that do not extrapolate well in P–T–X space.
In order to use phase equilibrium experiments as constraints, it is necessary to infer bulk compositions that represent the experimental run products at equilibrium. Two components of bulk composition in particular are hard to estimate: those of fluid content, assumed to be all water (‘molar bulk H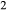 O’,
O’, 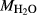 ), and of oxygen (‘molar bulk O’,
), and of oxygen (‘molar bulk O’, 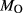 ). Experimental studies routinely provide estimates of H
). Experimental studies routinely provide estimates of H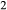 O content in the starting material, although these are uncertain, and unlikely to include H
O content in the starting material, although these are uncertain, and unlikely to include H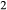 O gained by adsorption during the pulverization of the sample, which may be retained even during storage under desiccation (London et al., 2012).
O gained by adsorption during the pulverization of the sample, which may be retained even during storage under desiccation (London et al., 2012). 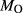 may be equated directly to molar bulk Fe
may be equated directly to molar bulk Fe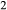 O
O , via the reaction Fe
, via the reaction Fe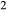 O
O = 2 FeO + O, if iron is the only element considered to have variable oxidation state. The fraction of iron present as Fe
= 2 FeO + O, if iron is the only element considered to have variable oxidation state. The fraction of iron present as Fe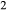 O
O in the starting material is rarely estimated. During experimental runs, values of
in the starting material is rarely estimated. During experimental runs, values of 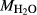 and
and 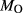 in the capsule are subject to interdependent changes. The experiments considered in this work were not formally buffered to specified
in the capsule are subject to interdependent changes. The experiments considered in this work were not formally buffered to specified 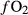 , but even in such cases, the experimental apparatus has an ‘intrinsic
, but even in such cases, the experimental apparatus has an ‘intrinsic 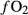 ’ that influences the oxidation state of the starting material during the run; hence
’ that influences the oxidation state of the starting material during the run; hence 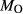 is not conserved. The process of oxidation or reduction of starting materials primarily involves diffusion of H
is not conserved. The process of oxidation or reduction of starting materials primarily involves diffusion of H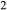 , to which experimental capsules are effectively open. If the apparatus provides an environment that is reducing with respect to the oxidation state of the starting materials, H
, to which experimental capsules are effectively open. If the apparatus provides an environment that is reducing with respect to the oxidation state of the starting materials, H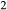 will enter the capsule and may form H
will enter the capsule and may form H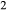 O by reduction of iron oxides, constituting an increase in
O by reduction of iron oxides, constituting an increase in 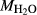 and decrease in
and decrease in 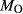 (carbon, derived from graphite furnaces, may play a under-acknowledged role in this process; see Brooker et al., 1998; Jakobsson, 2012; Matjuschkin et al., 2015). Finally, apparent loss or gain of both H
(carbon, derived from graphite furnaces, may play a under-acknowledged role in this process; see Brooker et al., 1998; Jakobsson, 2012; Matjuschkin et al., 2015). Finally, apparent loss or gain of both H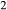 and O
and O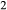 , or possibly molecular H
, or possibly molecular H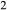 O, has been reported in several piston cylinder studies (e.g. Patiño Douce & Beard, 1994, 1995; Truckenbrodt & Johannes, 1999; Pichavant et al., 2002; Jakobsson, 2012), especially during longer and higher temperature experiments.
O, has been reported in several piston cylinder studies (e.g. Patiño Douce & Beard, 1994, 1995; Truckenbrodt & Johannes, 1999; Pichavant et al., 2002; Jakobsson, 2012), especially during longer and higher temperature experiments.
There is therefore no satisfactory way to convert the information reported in an experimental study into values of 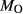 and
and 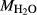 suitable for a representative pseudosection. A crucial part of the model calibration, then, is to analyse the sensitivity of calculations to the assumed values of
suitable for a representative pseudosection. A crucial part of the model calibration, then, is to analyse the sensitivity of calculations to the assumed values of 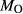 and
and 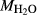 . This is done most informatively by calculating T–X or P–X pseudosections, in which X is
. This is done most informatively by calculating T–X or P–X pseudosections, in which X is 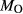 or
or 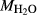 .
.
Clinopyroxene A–X Relations
Omphacite model
The ‘omphacite model’ of Green et al. (2007), modified by Diener & Powell (2012), was developed with the aim of modelling coexisting jadeite–omphacite and omphacite–diopside pairs. Previously calibrated with ds55, it was upgraded in this work for use with version 6 of the Holland & Powell dataset. It remains the only appropriate choice of a–x relations wherever diopsidic and sodic clinopyroxenes may stably coexist, since the new augitic clinopyroxene model is intended for use at temperatures higher than the closure of the jadeite–omphacite and omphacite–diopside miscibility gaps, and has no capacity to represent the ordered omphacite structure.
The omphacite model allows for cation mixing as [Mg, Fe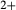 , Al, Fe
, Al, Fe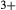 ]
]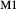 and [Ca, Na]
and [Ca, Na]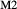 , but in order to represent ordered intermediate end-members such as omphacite (Ca
, but in order to represent ordered intermediate end-members such as omphacite (Ca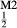 Na
Na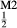 Mg
Mg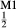 Al
Al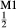 Si
Si O
O ), it treats the M1 and M2 sites as ‘split’. That is, Mg, Fe
), it treats the M1 and M2 sites as ‘split’. That is, Mg, Fe , Al and Fe
, Al and Fe mix on a M1m and a M1a site, with cations preferentially partitioned onto the M1m site in the order Fe
mix on a M1m and a M1a site, with cations preferentially partitioned onto the M1m site in the order Fe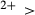 Mg > Al > Fe
Mg > Al > Fe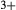 , while Ca and Na mix on a M2c and a M2n site, with Ca preferentially partitioned onto M2c (Green et al., 2007). The tetrahedral sites contain Si only.
, while Ca and Na mix on a M2c and a M2n site, with Ca preferentially partitioned onto M2c (Green et al., 2007). The tetrahedral sites contain Si only.
Slight modifications were needed in order to compensate for the change from version 5.5 to version 6 of the dataset. Following Diener & Powell (2012), modifications were made simultaneously for both the omphacite model, and the NCFMASHO core of the ds55 clinoamphibole model of Diener et al. (2007) refined by Diener & Powell (2012). For the omphacite model, the modification amounted to a change in 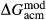 on the acmite end-member, from −4 to −7 kJ. The change was determined by manually adjusting the
on the acmite end-member, from −4 to −7 kJ. The change was determined by manually adjusting the 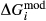 values of end-members in both models, until satisfactory calculations were obtained for equilibria in a MORB-like composition (composition Mcal, Table 1, H
values of end-members in both models, until satisfactory calculations were obtained for equilibria in a MORB-like composition (composition Mcal, Table 1, H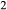 O in excess).
O in excess).
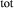 is total iron expressed as FeO. O, oxygen, combines only with FeO, via the equation 2 FeO + O = Fe
is total iron expressed as FeO. O, oxygen, combines only with FeO, via the equation 2 FeO + O = Fe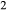 O
O ; hence
; hence 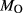 is identically equal to molar bulk Fe
is identically equal to molar bulk Fe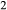 O
O ,
, 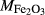 , with
, with 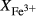 given by 2
given by 2 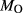 /
/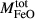 . Where no value is cited in the
. Where no value is cited in the 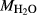 column, H
column, H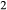 O is assumed to be in excess
O is assumed to be in excess
|
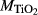
|
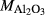
|
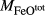
|
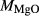
|
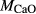
|
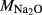
|
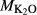
|
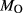
|
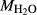
|
|
| Mcal | 55.21 | 1.01 | 8.75 | 7.84 | 12.22 | 11.75 | 2.51 | 0.22 | 0.47 | |
| SM89 | 52.47 | 1.05 | 9.10 | 8.15 | 12.71 | 12.21 | 2.61 | 0.23 | 1.47 | |
| IZ100 | 52.05 | 1.29 | 13.24 | 10.18 | 7.70 | 12.14 | 2.89 | 0.51 | ||
| dP0669 | 58.29 | 0.99 | 11.55 | 6.45 | 7.18 | 8.97 | 4.59 | 1.14 | 0.84 | |
| DR9734 | 47.05 | 0.18 | 8.77 | 5.43 | 19.02 | 17.52 | 1.39 | 0.04 | 0.60 | |
| SKA101 | 58.26 | 1.42 | 9.15 | 11.98 | 8.80 | 8.61 | 0.49 | 0.70 | 0.60 | |
| SKB116 | 53.72 | 1.75 | 9.10 | 12.40 | 7.43 | 10.85 | 2.95 | 0.42 | 1.38 | |
| PM13013 | 52.95 | 1.70 | 8.42 | 11.61 | 9.86 | 11.22 | 2.72 | 0.62 | 0.89 | |
| PM13083 | 53.24 | 0.83 | 8.62 | 9.71 | 11.32 | 12.48 | 2.41 | 0.19 | 1.19 | |
| PM13161 | 53.13 | 1.08 | 8.01 | 9.05 | 11.71 | 12.31 | 3.14 | 0.43 | 1.15 | |
| AG9 | 51.08 | 1.37 | 9.68 | 11.66 | 11.21 | 13.26 | 0.79 | 0.16 | 0.80 | |
| SQA (high-P) | 60.05 | 1.27 | 6.62 | 6.57 | 9.93 | 8.31 | 1.83 | 0.44 | 0.33 | 4.64 |
| SQA (low-P) | 59.76 | 1.26 | 6.59 | 6.54 | 9.88 | 8.27 | 1.82 | 0.44 | 0.81 | 4.62 |
| BL478 | 53.96 | 1.35 | 9.26 | 10.14 | 8.11 | 10.15 | 2.54 | 0.11 | 0.98 | 3.42 |
| WW94 | 50.09 | 0.31 | 8.91 | 7.27 | 16.50 | 15.86 | 1.00 | 0.07 | 0.35–0.86 | 3.50–5.00 |
| AGS11.1 | 58.31 | 0.75 | 8.62 | 10.90 | 8.44 | 11.44 | 1.14 | 0.41 | 0.52–1.30 | 3.50–6.50 |
| IAT | 55.99 | 0.81 | 10.41 | 6.90 | 12.12 | 10.33 | 3.24 | 0.18 | 0.33–0.82 | 3.50–6.50 |
| BL571 | 56.03 | 1.28 | 10.17 | 11.15 | 7.18 | 10.46 | 3.49 | 0.26 | 1.20–1.30 | 3.50–6.50 |
-
Mcal: MORB-like composition used in calibration. SM89: oxidized average MORB composition of Sun & McDonough (1989) (the analysed composition has
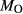 = 0.5 mol.%). IZ100: natural metabasite sample of Kunz et al. (2014),
= 0.5 mol.%). IZ100: natural metabasite sample of Kunz et al. (2014), 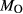 estimate from pseudosection modelling. dP0669: Breaksea Orthogneiss sample 0669 (dioritic gneiss), De Paoli (2011),
estimate from pseudosection modelling. dP0669: Breaksea Orthogneiss sample 0669 (dioritic gneiss), De Paoli (2011), 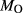 from wet chemistry. DR9734: microprobe analysis of experimental glass, ground from a garnet pyroxenite xenolith, by Adam et al. (1992);
from wet chemistry. DR9734: microprobe analysis of experimental glass, ground from a garnet pyroxenite xenolith, by Adam et al. (1992); 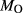 was assumed for the current study. SKA101, SKB116, PM13013, PM13083, PM13161, AG9: Natural amphibolites and low-temperature granulites (unpublished),
was assumed for the current study. SKA101, SKB116, PM13013, PM13083, PM13161, AG9: Natural amphibolites and low-temperature granulites (unpublished), 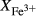 estimated at 0.10–0.25 from previous pseudosection modelling. SQA: Synthetic amphibolite composition of Patiño Douce & Beard (1995) (glass analysis). The compositions at high- and low-P are the same except for different assumed
estimated at 0.10–0.25 from previous pseudosection modelling. SQA: Synthetic amphibolite composition of Patiño Douce & Beard (1995) (glass analysis). The compositions at high- and low-P are the same except for different assumed 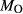 values at high-P (piston cylinder apparatus) and low-P (internally heated pressure vessel); see text.
values at high-P (piston cylinder apparatus) and low-P (internally heated pressure vessel); see text. 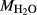 from analysis of starting material. In Fig. 5, 0.33
from analysis of starting material. In Fig. 5, 0.33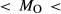 0.82, 3.50
0.82, 3.50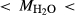 6.50. BL478: Sample 478 of Beard & Lofgren (1991). See text for
6.50. BL478: Sample 478 of Beard & Lofgren (1991). See text for 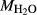 ,
, 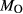 estimates. In Fig. 5, 0.52
estimates. In Fig. 5, 0.52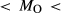 1.30, 3.50
1.30, 3.50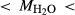 6.50. WW94: natural amphibolite composition of Wolf & Wyllie (1994). AGS11.1: natural amphibolite composition of Skjerlie & Patiño Douce (1995). IAT: meta island arc tholeiite of Rushmer (1991). BL571: Sample 571 of Beard & Lofgren (1991).
6.50. WW94: natural amphibolite composition of Wolf & Wyllie (1994). AGS11.1: natural amphibolite composition of Skjerlie & Patiño Douce (1995). IAT: meta island arc tholeiite of Rushmer (1991). BL571: Sample 571 of Beard & Lofgren (1991).
The 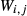 parameters were left unchanged from the previous version of the omphacite model, since these were relatively well constrained by the observed geometry of the solvi between the diopsidic, omphacitic and jadeitic portions of the solid solution. Conversely, since the solvi depend solely on the mixing properties of the models, rather than the end-member thermodynamics, solvus calculations will be unchanged from the previous model.
parameters were left unchanged from the previous version of the omphacite model, since these were relatively well constrained by the observed geometry of the solvi between the diopsidic, omphacitic and jadeitic portions of the solid solution. Conversely, since the solvi depend solely on the mixing properties of the models, rather than the end-member thermodynamics, solvus calculations will be unchanged from the previous model.
Augite model
Prompted by the compositions of clinopyroxene in TTG-genesis experiments (e.g. Patiño Douce & Beard, 1995; Rapp & Watson, 1995; Skjerlie & Patiño Douce, 2002), a new ‘augite model’ was developed for calcic clinopyroxene at high temperature, with mixing on sites as [Mg, Fe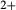 , Al, Fe3+]M1 [Ca, Na, Mg, Fe2+]M2 [Si, Al]
, Al, Fe3+]M1 [Ca, Na, Mg, Fe2+]M2 [Si, Al]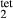 . This model is not consistent with the omphacite model, although the models overlap in composition space, and the two should not be used in the same calculation. In particular, the simple M1 and M2 sites of the augite model do not allow order–disorder to take place on either of these sites individually, unlike the split M1 and M2 sites of the omphacite model. In partial compensation for this, different values of
. This model is not consistent with the omphacite model, although the models overlap in composition space, and the two should not be used in the same calculation. In particular, the simple M1 and M2 sites of the augite model do not allow order–disorder to take place on either of these sites individually, unlike the split M1 and M2 sites of the omphacite model. In partial compensation for this, different values of 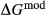 are used for some end-members that are common to both models.
are used for some end-members that are common to both models.
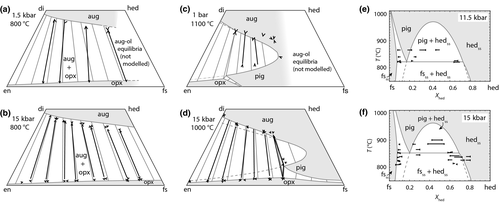
The heart of the augite model is the pyroxene quadrilateral CaMgSi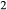 O
O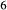 –Mg
–Mg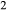 Si
Si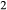 O
O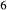 –Fe
–Fe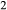 Si
Si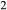 O
O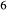 –CaFeSi
–CaFeSi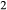 O
O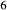 . Figure 1 shows the modelled fit to the experimental work of Lindsley (1981, 1983) and Turnock & Lindsley (1981) on clinopyroxene–orthopyroxene equilibria in this system, including the binary subsystem CaFeSi
. Figure 1 shows the modelled fit to the experimental work of Lindsley (1981, 1983) and Turnock & Lindsley (1981) on clinopyroxene–orthopyroxene equilibria in this system, including the binary subsystem CaFeSi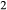 O
O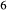 –Fe
–Fe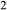 Si
Si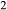 O
O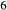 . The clinopyroxene a–x relations cover the whole of the quadrilateral composition space, with the compositional end-members in appropriate C2/c symmetry being diopside (di), clinoenstatite (cenh), clinoferrosilite (cfs) and hedenbergite (hed). The clinoenstatite and clinoferrosilite end-members are polymorphs that exist at low-pressure, high-temperature in the unary systems, and their stability fields and properties are little known. They are generated via
. The clinopyroxene a–x relations cover the whole of the quadrilateral composition space, with the compositional end-members in appropriate C2/c symmetry being diopside (di), clinoenstatite (cenh), clinoferrosilite (cfs) and hedenbergite (hed). The clinoenstatite and clinoferrosilite end-members are polymorphs that exist at low-pressure, high-temperature in the unary systems, and their stability fields and properties are little known. They are generated via 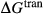 expressions from the Pbca end-members en (enstatite) and fs (ferrosilite) in the Holland & Powell dataset. An ordered intermediate end-member, fmc (Mg
expressions from the Pbca end-members en (enstatite) and fs (ferrosilite) in the Holland & Powell dataset. An ordered intermediate end-member, fmc (Mg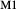 Fe
Fe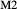 Si
Si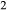 O
O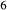 ), allows non-equal partitioning of [Mg, Fe
), allows non-equal partitioning of [Mg, Fe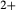 ] over the M1 and M2 sites (Holland & Powell, 2006). Since a reaction di +
] over the M1 and M2 sites (Holland & Powell, 2006). Since a reaction di + 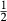 cfs = hed +
cfs = hed + 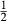 cenh can be written among the compositional end-members, the thermodynamic properties of one must be treated as dependent, and hedenbergite was chosen for this purpose. Values for model parameters on the CaMgSi
cenh can be written among the compositional end-members, the thermodynamic properties of one must be treated as dependent, and hedenbergite was chosen for this purpose. Values for model parameters on the CaMgSi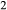 O
O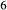 –Mg
–Mg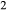 Si
Si O
O join, including
join, including 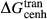 , were taken from the CMAS clinopyroxene model of Green et al. (2012a), where they were calibrated against the experimental work of Mori & Green (1975), Lindsley & Dixon (1976), Perkins & Newton (1980), Schweitzer (1982), Brey & Huth (1984), Nickel & Brey (1984) and Carlson & Lindsley (1988).
, were taken from the CMAS clinopyroxene model of Green et al. (2012a), where they were calibrated against the experimental work of Mori & Green (1975), Lindsley & Dixon (1976), Perkins & Newton (1980), Schweitzer (1982), Brey & Huth (1984), Nickel & Brey (1984) and Carlson & Lindsley (1988).
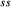 and hed
and hed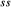 are solid solutions rich in the fs and hed end-members respectively.
are solid solutions rich in the fs and hed end-members respectively.The mctc function in thermocalc was used to fit the additional CFMS parameters 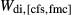 ,
, 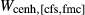 ,
,  ,
, 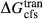 and
and 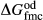 . The pressure dependence of the inherited CMAS parameter
. The pressure dependence of the inherited CMAS parameter 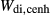 was applied to
was applied to 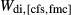 .
. 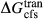 was assumed to have the same temperature dependence as
was assumed to have the same temperature dependence as 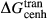 , and was required to give a fs = cfs transition curve consistent with the estimation of Lindsley (1981).
, and was required to give a fs = cfs transition curve consistent with the estimation of Lindsley (1981). 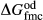 took the mean pressure and temperature dependencies of
took the mean pressure and temperature dependencies of 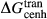 and
and 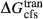 , with the constant term fitted such that the ordered end-member fmc was more stable than its fully disordered equivalent, Mg
, with the constant term fitted such that the ordered end-member fmc was more stable than its fully disordered equivalent, Mg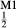 Fe
Fe Mg
Mg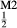 Fe
Fe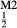 Si
Si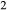 O
O , for which G is given by
, for which G is given by 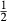 (
(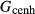 +
+ 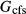 ). At 900
). At 900 C and 8 kbar, the dependent value of
C and 8 kbar, the dependent value of 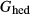 was constrained to be within 2 kJ mol
was constrained to be within 2 kJ mol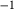 of the ds62 dataset value, with a further constraint of
of the ds62 dataset value, with a further constraint of  .
. 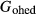 is the G function for the Pbca-symmetry orthohedenbergite end-member, derived from the quadrilateral a–x relations for orthopyroxene in the same way as
is the G function for the Pbca-symmetry orthohedenbergite end-member, derived from the quadrilateral a–x relations for orthopyroxene in the same way as 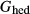 is derived for the hedenbergite end-member in clinopyroxene; thus, the latter condition specified that the monoclinic polymorph was the more stable of the two.
is derived for the hedenbergite end-member in clinopyroxene; thus, the latter condition specified that the monoclinic polymorph was the more stable of the two.
The resulting fit successfully reproduces augite–orthopyroxene tielines in the quadrilateral, and is notably successful at matching the very sensitive divariant augite–pigeonite–orthopyroxene equilibrium at 15 kbar, 1000 C (Fig. 1). It somewhat overestimates the width of the augite–pigeonite solvus towards higher FeO/(FeO+MgO) values.
C (Fig. 1). It somewhat overestimates the width of the augite–pigeonite solvus towards higher FeO/(FeO+MgO) values.
The quadrilateral model was then combined with the CMAS clinopyroxene model of Green et al. (2012a), introducing the end-member Ca-tschermak's pyroxene (cats; CaAl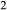 SiO
SiO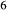 ) and associated parameters, which allowed for the substitution of Al onto the M1 and tetrahedral sites simultaneously. The cats end-member exhibits internal order–disorder of Si-Al on the tetrahedral site, with the energy and entropy of disordering reduced by a factor of four (Holland & Powell, 2011). Finally, the end-members jadeite (jd) and acmite (acm) were added to the model to accommodate Na, Fe
) and associated parameters, which allowed for the substitution of Al onto the M1 and tetrahedral sites simultaneously. The cats end-member exhibits internal order–disorder of Si-Al on the tetrahedral site, with the energy and entropy of disordering reduced by a factor of four (Holland & Powell, 2011). Finally, the end-members jadeite (jd) and acmite (acm) were added to the model to accommodate Na, Fe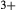 , and an excess of Al on the M1 site relative to the tetrahedral site. Values for
, and an excess of Al on the M1 site relative to the tetrahedral site. Values for 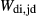 ,
, 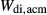 and
and 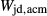 were adopted from the omphacite model. However, the jd and acm end-members serve a different role in the augite model from in the omphacite model. In the augite model, they are simply required to admit minor components, whereas in the omphacite model, they may be present in substantial proportions, with order–disorder between sodic and calcic end-members contributing heavily to the thermodynamics of mixing. Consequently it is not very significant that the values of the dependent
were adopted from the omphacite model. However, the jd and acm end-members serve a different role in the augite model from in the omphacite model. In the augite model, they are simply required to admit minor components, whereas in the omphacite model, they may be present in substantial proportions, with order–disorder between sodic and calcic end-members contributing heavily to the thermodynamics of mixing. Consequently it is not very significant that the values of the dependent 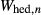 parameters in the augite model differ from their independently calibrated equivalents in the omphacite model (values are compared in the Appendix). With the same justification, a
parameters in the augite model differ from their independently calibrated equivalents in the omphacite model (values are compared in the Appendix). With the same justification, a 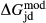 term was added to the augite jd end-member, and different
term was added to the augite jd end-member, and different 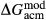 terms were used in the augite and omphacite models.
terms were used in the augite and omphacite models.
In addition to 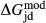 and
and 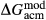 , the free parameters in this second stage of augite model calibration were
, the free parameters in this second stage of augite model calibration were 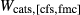 ,
, 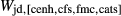 and
and 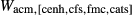 . These interaction energies were not expected to be influential compared with the
. These interaction energies were not expected to be influential compared with the 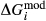 terms, so a small number of observed equilibria were carefully chosen to be fitted, primarily with the purpose of finding values for
terms, so a small number of observed equilibria were carefully chosen to be fitted, primarily with the purpose of finding values for 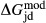 and
and 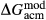 . The chosen equilibria comprised two natural rock samples, with estimated P–T values, and one experiment; Table 2 shows the equilibria and results. The process of fitting with mctc revealed very strong multicomponent correlations among the interaction energies. It was not clear a priori that these correlations would be relevant for model calculations in general, but in fact, in later calculations on melting equilibria, it was found that violating the correlations for apparently trivial parameters such as
. The chosen equilibria comprised two natural rock samples, with estimated P–T values, and one experiment; Table 2 shows the equilibria and results. The process of fitting with mctc revealed very strong multicomponent correlations among the interaction energies. It was not clear a priori that these correlations would be relevant for model calculations in general, but in fact, in later calculations on melting equilibria, it was found that violating the correlations for apparently trivial parameters such as 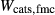 did indeed have a large and detrimental effect on the calculated compositions of all phases, particularly the anorthite content
did indeed have a large and detrimental effect on the calculated compositions of all phases, particularly the anorthite content 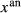 in plagioclase.
in plagioclase.
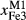 ) obtained using the rule of Droop (1987)
) obtained using the rule of Droop (1987)| Assemblage | P (kbar) | T ( C) C) |
x(aug) | y(aug) | f(aug) | z(aug) | j(aug) |
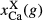
|
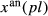
|
|
|---|---|---|---|---|---|---|---|---|---|---|
| IZ100a | cpx opx g pl ilm | 9 | 900 | 0.26 | 0.08 | 0.06 | 0.89 | 0.04 | 0.19 | 0.53 |
| 0.34 | 0.06 | 0.07 | 0.81 | 0.05 | 0.20 | 0.56 | ||||
| dP0669b | cpx opx g pl bi ilm q H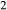 O O |
11 | 880 | 0.25 | 0.10 | 0.05 | 0.80 | 0.05 | 0.20 | 0.50 |
| 0.25 | 0.01 | 0.11 | 0.73 | 0.15 | 0.20 | 0.31 | ||||
| 1303/DR9734c | cpx g pl sp | 10 | 1000 | 0.17 | 0.19 | 0.03 | 0.77 | 0.07 | 0.21 | 0.64 |
| 0.14 | 0.09 | 0.06 | 0.81 | 0.06 | 0.18 | 0.57 |
- a Natural sample (Kunz et al., 2014). P–T estimate from pseudosection forward modelling of intercalated metapelitic rocks using the ds55 models.
- b Natural sample from De Paoli (2011). P–T estimate from the author's pseudosection forward modelling using the ds55 models. Representative values of compositional variables given to nearest 0.05.
- c Experimental run 1303 of Adam et al. (1992), with starting material DR9734.
Calculations with the augite v. omphacite models
Figure 2 shows pseudosections calculated for an oxidized MORB composition, based on that of Sun & McDonough 1989; SM89, Table 1), in the range 450–700 C and 4–20 kbar. The figure is contoured for
C and 4–20 kbar. The figure is contoured for 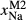 in clinopyroxene. Calculations were carried out with first the augite model (Fig. 2a,b) and then the omphacite model (Fig. 2c,d), in order to compare the two. The comparison demonstrates, firstly, that the omphacite model is the appropriate choice for the relatively low temperatures shown. When modelling is done correctly using the omphacite model (Fig. 2c,d),
in clinopyroxene. Calculations were carried out with first the augite model (Fig. 2a,b) and then the omphacite model (Fig. 2c,d), in order to compare the two. The comparison demonstrates, firstly, that the omphacite model is the appropriate choice for the relatively low temperatures shown. When modelling is done correctly using the omphacite model (Fig. 2c,d), 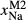 in clinopyroxene rises to >0.4 towards higher pressures, and the diopside–omphacite solvus is visible at several pressures with closure at ∼600
in clinopyroxene rises to >0.4 towards higher pressures, and the diopside–omphacite solvus is visible at several pressures with closure at ∼600 C. Meanwhile the augite model has no capacity to model omphacite-like Na contents or coexistence between omphacitic and diopsidic compositions, so no solvus appears in Fig. 2a,b. Secondly, it can be seen that the two models give substantially consistent results for < 13 kbar and > 600
C. Meanwhile the augite model has no capacity to model omphacite-like Na contents or coexistence between omphacitic and diopsidic compositions, so no solvus appears in Fig. 2a,b. Secondly, it can be seen that the two models give substantially consistent results for < 13 kbar and > 600 C, where the omphacite model takes on an augitic composition. Phase field boundaries in this region in Fig. 2a,c show agreement within 20
C, where the omphacite model takes on an augitic composition. Phase field boundaries in this region in Fig. 2a,c show agreement within 20 C, while the augite model gives values of
C, while the augite model gives values of 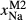 that are consistently lower than the omphacite model by ∼0.05, within the likely uncertainty in the modelling.
that are consistently lower than the omphacite model by ∼0.05, within the likely uncertainty in the modelling.
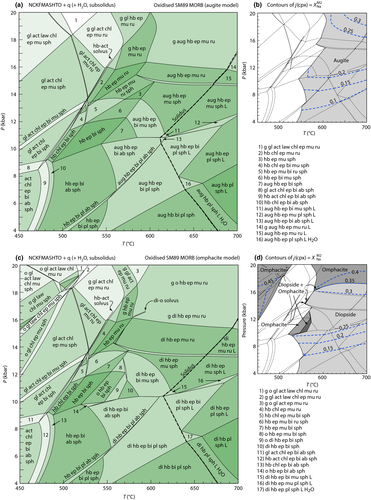
 , giving
, giving 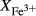 = 0.36 (SM89, Table 1). (a, b) Calculations using the augite model for clinopyroxene. (c, d) Correctly modelled using the omphacite model for clinopyroxene. Where clinopyroxene is truly augitic in composition, the two models are substantially consistent, but the augite model is unable to represent moderate to high Na contents or the coexisting clinopyroxene phases highlighted in (b) and (d). H
= 0.36 (SM89, Table 1). (a, b) Calculations using the augite model for clinopyroxene. (c, d) Correctly modelled using the omphacite model for clinopyroxene. Where clinopyroxene is truly augitic in composition, the two models are substantially consistent, but the augite model is unable to represent moderate to high Na contents or the coexisting clinopyroxene phases highlighted in (b) and (d). H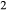 O was taken to be in excess below the solidus; above the solidus values of 5.8 mol.% were used for (a), (b) and 5.6 mol.% for (c), (d), such that assemblages are just H
O was taken to be in excess below the solidus; above the solidus values of 5.8 mol.% were used for (a), (b) and 5.6 mol.% for (c), (d), such that assemblages are just H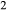 O-saturated at the solidus. Removal of K
O-saturated at the solidus. Removal of K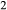 O, TiO
O, TiO from the amphibole model has negligible effect on phase boundaries. The bulk composition is the same as in Diener & Powell (2012), fig. 1c, which was calculated with the previous generation of models.
from the amphibole model has negligible effect on phase boundaries. The bulk composition is the same as in Diener & Powell (2012), fig. 1c, which was calculated with the previous generation of models.The nature of phase relations in Fig. 2c are discussed in a later section. Subsequent figures will demonstrate the behaviour of the augite model in the < 13 kbar, > 600 C regime for which it was calibrated.
C regime for which it was calibrated.
Clinoamphibole A–X Relations
The clinoamphibole model of Diener et al. (2007) and Diener & Powell (2012), in NCFMASHO, is suitable for calculations on metabasic rocks under subsolidus conditions, using version 5.5 of the dataset (Holland & Powell, 1998). As described above, it was updated for use with version 6.2 in conjunction with the omphacite model, by adjustments to the end-member thermodynamics. The resulting modifications affected the following end-members: pargasite (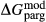 changed from 15 kJ to −10 kJ), glaucophane (
changed from 15 kJ to −10 kJ), glaucophane (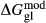 changed from 3 kJ to −3 kJ), cummingtonite (
changed from 3 kJ to −3 kJ), cummingtonite (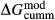 changed from −6.4 kJ to 0 kJ), grunerite (
changed from −6.4 kJ to 0 kJ), grunerite (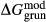 changed from −5 kJ to −3 kJ) and magnesioriebekite (
changed from −5 kJ to −3 kJ) and magnesioriebekite (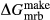 changed from 8 kJ to 0 kJ). These were pleasing in that generally the absolute values of the
changed from 8 kJ to 0 kJ). These were pleasing in that generally the absolute values of the 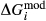 terms decreased, making the end-member
terms decreased, making the end-member 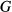 curves more similar to the dataset functions.
curves more similar to the dataset functions.
By granulite facies temperatures, the components K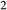 O and TiO
O and TiO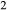 are significant in hornblende (e.g. Robinson et al., 1982). The core model was therefore expanded to include the components K
are significant in hornblende (e.g. Robinson et al., 1982). The core model was therefore expanded to include the components K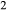 O and TiO
O and TiO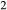 , with the intention that the full model in NCKFMASHTO would be applicable both above and below the solidus. K
, with the intention that the full model in NCKFMASHTO would be applicable both above and below the solidus. K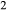 O was introduced via a potassium-pargasite end-member (kprg, KCa
O was introduced via a potassium-pargasite end-member (kprg, KCa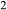 Mg
Mg Al
Al Si
Si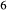 O
O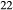 (OH)
(OH)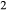 ), such that K
), such that K mixes with Na
mixes with Na on the partially filled model A site. A deprotonation-style substitution was adopted to introduce TiO
on the partially filled model A site. A deprotonation-style substitution was adopted to introduce TiO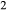 via an end-member Ti-tschermakite (tts, Ca
via an end-member Ti-tschermakite (tts, Ca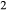 Mg
Mg Ti
Ti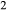 Al
Al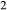 Si
Si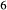 O
O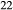 ), allowing hornblende to persist to higher temperatures in equilibrium with melt by lowering its water activity
), allowing hornblende to persist to higher temperatures in equilibrium with melt by lowering its water activity 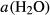 , although in reality, the substitution whereby TiO
, although in reality, the substitution whereby TiO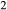 enters metamorphic hornblende is more likely to be a tschermakite-like and/or glaucophane-like substitution (Schumacher, 2007). The new end-members tts and kprg are not present in the Holland & Powell dataset, but are made via the reactions kprg = mu − pa + parg +
enters metamorphic hornblende is more likely to be a tschermakite-like and/or glaucophane-like substitution (Schumacher, 2007). The new end-members tts and kprg are not present in the Holland & Powell dataset, but are made via the reactions kprg = mu − pa + parg + 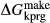 and tts = dsp − 2 ru + ts +
and tts = dsp − 2 ru + ts + 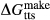 (mu: muscovite; pa: paragonite; ru: rutile; dsp: diaspore).
(mu: muscovite; pa: paragonite; ru: rutile; dsp: diaspore).
A key equilibrium is the first introduction of hornblende and glaucophane to the assemblage act + chl + ep + ab + sph + q + H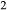 O ± bi, that is, the junction of the greenschist, blueschist and amphibolite facies. This occurs at around 8–10 kbar and 450–500
O ± bi, that is, the junction of the greenschist, blueschist and amphibolite facies. This occurs at around 8–10 kbar and 450–500 C on most metamorphic facies diagrams. The presence of three coexisting amphiboles in this equilibrium make the calculated values of P, T and compositional variables extremely sensitive to the parameterization of the amphibole a–x relations. It was required that minimal amounts of K
C on most metamorphic facies diagrams. The presence of three coexisting amphiboles in this equilibrium make the calculated values of P, T and compositional variables extremely sensitive to the parameterization of the amphibole a–x relations. It was required that minimal amounts of K O and TiO
O and TiO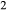 should be taken into the amphiboles at this temperature, but the prejudice was nevertheless imposed that the amphibole phases would incorporate K
should be taken into the amphiboles at this temperature, but the prejudice was nevertheless imposed that the amphibole phases would incorporate K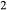 O in the order hb >gl ≈ act, and TiO
O in the order hb >gl ≈ act, and TiO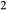 in the order hb ≈ gl > act. The full list of P–T and compositional constraints placed on this equilibrium during fitting, and the results obtained, are given in Table 3. The table also compares calculations and observations for several upper amphibolite facies rocks, for which likely values of P–T and
in the order hb ≈ gl > act. The full list of P–T and compositional constraints placed on this equilibrium during fitting, and the results obtained, are given in Table 3. The table also compares calculations and observations for several upper amphibolite facies rocks, for which likely values of P–T and 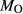 have been established by previous calculations with older versions of the models. Since some of these equilibria contain clinopyroxene, this was also an opportunity to check the behaviour of the ds6-omphacite and augite models.
have been established by previous calculations with older versions of the models. Since some of these equilibria contain clinopyroxene, this was also an opportunity to check the behaviour of the ds6-omphacite and augite models.
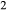 O). Observed or other target values (see footnotes) of compositional variables are shown in roman font, calculated values in italics. Compositional variables for the clinoamphibole and augite models are defined in the Appendix. Bulk compositions used in the calculations are given in Table 1. Phase→0 indicates the zero-mode isopleth (the phase-out boundary) for phase
O). Observed or other target values (see footnotes) of compositional variables are shown in roman font, calculated values in italics. Compositional variables for the clinoamphibole and augite models are defined in the Appendix. Bulk compositions used in the calculations are given in Table 1. Phase→0 indicates the zero-mode isopleth (the phase-out boundary) for phase| Assemblage | P (kbar) | T ( C) C) |
Composition variables | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y(hb) | z(hb) | a(hb) | c(hb) | f(hb) | y(gl) | z(gl) | a(gl) | c(gl) | f(gl) | ||||
| Mcala | hb gl act bi ep chl | 10±1 | 480±20 | 0.55–0.70 | 0.3–0.4 | 0.35–0.45 | 0.6–0.7 | 0.1 | 0.7–0.8 | 0.8–0.9 | 0.1 | 0.1 | 0.1 |
| ab sph; | 9.3 | 474 | 0.63 | 0.38 | 0.37 | 0.61 | 0.08 | 0.78 | 0.89 | 0.07 | 0.11 | 0.09 | |
| hb, gl→0 | |||||||||||||
| y(act) | z(act) | a(act) | c(act) | f(act) | |||||||||
| 0.15–0.25 | 0.15–0.25 | 0.1 | 0.75–0.80 | 0.05 | |||||||||
| 0.17 | 0.22 | 0.07 | 0.78 | 0.03 | |||||||||
| a(hb) | k(hb) | t(hb) | y(aug) | z(aug) | j(aug) | 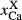 (g) (g) |
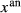 (pl) (pl) |
||||||
| SKA101b | hb g pl bi ilm sph | 10 | 770 | 0.41 | 0.31 | 0.08 | – | – | – | 0.27 | 0.86 | ||
| 0.65 | 0.34 | 0.07 | 0.28 | 0.83 | |||||||||
| SKB116b | hb cpx g pl bi sph | 11 | 770 | 0.56 | 0.38 | 0.12 | 0.03 | 0.87 | 0.02 | 0.30 | 0.47 | ||
| 0.72 | 0.16 | 0.07 | 0.09 | 0.86 | 0.11 | 0.43 | 0.26 | ||||||
| PM13013b | hb pl ilm | 4 | 700 | 0.71 | 0.31 | 0.11 | – | – | – | – | 0.36 | ||
| 0.39 | 0.35 | 0.05 | 0.38 | ||||||||||
| PM13083b | hb cpx pl sph | 4 | 700 | 0.44 | 0.11 | 0.07 | 0.07 | 0.93 | 0.04 | – | 0.51 | ||
| 0.51 | 0.14 | 0.05 | 0.06 | 0.92 | 0.04 | 0.49 | |||||||
| PM13161b, c | hb cpx pl sph | 4 | 700 | 0.65 | 0.18 | 0.07 | 0.08 | 0.52 | 0.02 | – | 0.26 | ||
| 0.49 | 0.19 | 0.04 | 0.02 | 0.89 | 0.08 | 0.29 | |||||||
| AG9d | hb g pl ilm; | 6±3 | 650 | 0.29 | 0.17 | 0.04 | – | – | – | 0.96 | |||
| g→0 | 6.3 | 0.32 | 0.19 | 0.04 | 0.47 | 0.95 | |||||||
- a
Hb, gl, act were assumed to have negligible K
 O, TiO
O, TiO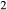 , with k(hb) > k(gl) ≈ k(act) and t(hb) ≈ t(gl) > t(act); calculated values are 0.02 < k < 0.04, t≤0.01, with appropriate differences among the three phases.
, with k(hb) > k(gl) ≈ k(act) and t(hb) ≈ t(gl) > t(act); calculated values are 0.02 < k < 0.04, t≤0.01, with appropriate differences among the three phases.
- b P–T estimated from pseudosection forward modelling with ds55 models.
- c Measured j(aug) looks suspect.
- d Garnet has 20% spessartine, unmodelled.
Fitting was carried out in mctc, to find values for 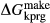 ,
, 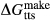 , and the new interaction energies
, and the new interaction energies 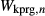 and
and 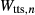 . Because the number of interaction energies to be fitted was large, and they were expected to be poorly constrained due to the small amounts of the K
. Because the number of interaction energies to be fitted was large, and they were expected to be poorly constrained due to the small amounts of the K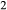 O and TiO
O and TiO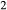 end-members present, the fitting problem was initially reduced by assuming that K
end-members present, the fitting problem was initially reduced by assuming that K and Na
and Na would mix with similar energetic consequences on the A-site, and therefore fixing values of
would mix with similar energetic consequences on the A-site, and therefore fixing values of 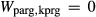 and
and 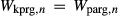 . The possibility of allowing other, less well constrained parameters to vary in order to improve the fit was also explored. Ultimately, however, better results were obtained by allowing the
. The possibility of allowing other, less well constrained parameters to vary in order to improve the fit was also explored. Ultimately, however, better results were obtained by allowing the 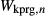 parameters to diverge from the equivalent
parameters to diverge from the equivalent 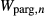 values by up to 5 kJ, while the parameters from the core NCFMASHO model could not convincingly be improved upon. The asymmetry of interactions was inherited from the Diener et al. (2007) model, with the addition of the terms
values by up to 5 kJ, while the parameters from the core NCFMASHO model could not convincingly be improved upon. The asymmetry of interactions was inherited from the Diener et al. (2007) model, with the addition of the terms  and
and  . As in the Diener et al. (2007) model and the new augite model, the entropy of Si–Al mixing on the tetrahedral sites was reduced by a factor of four.
. As in the Diener et al. (2007) model and the new augite model, the entropy of Si–Al mixing on the tetrahedral sites was reduced by a factor of four.
Calculations on Subsolidus Phase Relations
We now return to Fig. 2c, a pseudosection calculated between greenschist–blueschist facies conditions and the solidus using the metabasite set of a–x relations, with the omphacite model representing clinopyroxene. The bulk composition (SM89, Table 1) is based on the MORB composition of Sun & McDonough (1989), but considerably oxidized, with 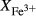 = Fe
= Fe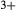 /(Fe
/(Fe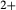 +Fe
+Fe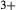 ) = 0.36. The same bulk composition was previously used by Diener & Powell (2012), fig. 1c, allowing the ds55 and ds6x generations of a–x relations to be compared.
) = 0.36. The same bulk composition was previously used by Diener & Powell (2012), fig. 1c, allowing the ds55 and ds6x generations of a–x relations to be compared.
Subsolidus phase relations in the greenschist and amphibolite facies remain similar, with hornblende replacing actinolite and chlorite at ∼480  C as in the older calculations, and diopside now joining the assemblage at ∼550
C as in the older calculations, and diopside now joining the assemblage at ∼550 C rather than 600
C rather than 600 C. Calculations at 12–20 kbar and <550
C. Calculations at 12–20 kbar and <550 C now generate gl + act + chl + ep ± law ± o assemblages that resemble natural blueschists, whereas the ds55 generation of a–x relations found omphacite stable rather than glaucophane. At 16–20 kbar, between 530 and 580
C now generate gl + act + chl + ep ± law ± o assemblages that resemble natural blueschists, whereas the ds55 generation of a–x relations found omphacite stable rather than glaucophane. At 16–20 kbar, between 530 and 580 C, the blueschist assemblages give way to higher temperature eclogite assemblages containing garnet, omphacite and hornblende.
C, the blueschist assemblages give way to higher temperature eclogite assemblages containing garnet, omphacite and hornblende.
Phase relations below 650 C are negligibly affected if the K
C are negligibly affected if the K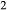 O and TiO
O and TiO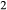 components are excluded from amphibole. The Diener & Powell (2012) figure was calculated without a melt phase, since no suitable melt a–x relations existed at that time; the new figure, using the metabasite melt model described in the next section, shows the start of H
components are excluded from amphibole. The Diener & Powell (2012) figure was calculated without a melt phase, since no suitable melt a–x relations existed at that time; the new figure, using the metabasite melt model described in the next section, shows the start of H O-saturated melting at 615–700
O-saturated melting at 615–700 C.
C.
Melt A–X Relations
Existing silicate melt a–x relations for use with the Holland & Powell dataset include the ds5 haplogranitic model of Holland & Powell (2001), its expansion into NCKFMASH for use in metapelite melting calculations (White et al., 2001 2007), the ds6 equivalent of the metapelite melt model (White et al., 2014), and the mafic melt model of Jennings & Holland (2015). These models are exceedingly simple, reproducing the macroscopic mixing properties of melt over a limited compositional range while making no attempt to capture melt speciation, or otherwise to separate the enthalpic and entropic contributions in the models in a way that resembles reality. Like the a–x relations for solid solutions, the melt is treated as a regular solution with the non-ideal enthalpy of mixing expressed using the symmetric formalism. The end-members are mineral-like compounds that mix as molecules.
The metapelite melt model has proved very successful in calculations (e.g. White et al., 2001 2007; Johnson et al., 2008; Grant, 2009; White et al., 2011). It is desirable that the new metabasite melt model and the metapelite melt model should share a core in NKASH, defined by the end-members qL–abL–kspL–h2oL (see Appendix for end-member definitions). However, with respect to the CaO, FeO and MgO components, the metabasite melt model requires a different parameterization and structure from the metapelite model, in order to allow the melt composition to become sufficiently calcic, and to become metaluminous if required.
The qL–abL–kspL subsystem of the White et al. (2014) metapelite melt model was strongly constrained by the experiments of Boyd & England (1963), Lindsley (1966), Ostrovsky (1966) and Jackson (1976), and could be retained without change to form the core of the metabasite melt model. In the qL–abL–kspL–h2oL subsystem, a number of changes are planned for a forthcoming revision of the White et al. (2014) metapelite melt model, and these have been incorporated directly into the metabasite melt model as presented in this study. The changes to the qL–abL–kspL–h2oL core, relative to the White et al. (2014) version of the metapelite melt model, are as follows. (1) The interaction energies 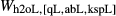 have been refined by comparison with the subsystem experiments of Kennedy et al. (1962), Stewart (1967), Goldsmith & Jenkins (1985), Goldsmith & Peterson (1990) and Behrens (1995). (2) In ds63, the constant-pressure heat capacity of the h2oL end-member has been lowered to improve the calculated H
have been refined by comparison with the subsystem experiments of Kennedy et al. (1962), Stewart (1967), Goldsmith & Jenkins (1985), Goldsmith & Peterson (1990) and Behrens (1995). (2) In ds63, the constant-pressure heat capacity of the h2oL end-member has been lowered to improve the calculated H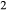 O isopleths for melts. In fig. 9 of Holland & Powell (2001), the H
O isopleths for melts. In fig. 9 of Holland & Powell (2001), the H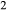 O isopleths in granitic liquid are spuriously concave downwards in pressure, as a result of too high heat capacity for h2oL; this heat capacity has now been optimized such that the isopleths become approximately straight lines, as required by the experimental data of Holtz et al. (1995). (3) The formula of the end-member silL has been changed from
O isopleths in granitic liquid are spuriously concave downwards in pressure, as a result of too high heat capacity for h2oL; this heat capacity has now been optimized such that the isopleths become approximately straight lines, as required by the experimental data of Holtz et al. (1995). (3) The formula of the end-member silL has been changed from  Al
Al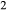 SiO
SiO to Al
to Al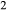 SiO
SiO .
.
In the metapelite model, the Ca-rich vertex of composition space is represented by the anorthite-liquid end-member, anL, but the metabasite model has been extended as far as a wollastonite-liquid end-member, woL, in order to encompass metaluminous compositions. However, the woL end-member is compositionally distant from the melts of metabasic rocks, and its thermodynamics are poorly constrained. To compensate for this, an anL-composition end-member was restored to the metabasite melt model in the form of an ordered intermediate, made via the reaction anL = woL + silL with a 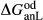 term applied. The thermodynamic properties of CaAl
term applied. The thermodynamic properties of CaAl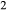 Si
Si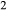 O
O -composition liquid were approximated by fitting to the anorthite melting curve. This aspect of the model structure follows, e.g. Hastie (1983), Bonnell & Hastie (1985), Hastie & Bonnell (1985), Besmann & Spear (2002) and Green et al. (2012b), in which the ordered intermediate end-members are termed ‘associate species’. The inclusion of an ordered intermediate end-member, intL, in the melt a–x relations adds flexibility in fitting the available constraints, since the
-composition liquid were approximated by fitting to the anorthite melting curve. This aspect of the model structure follows, e.g. Hastie (1983), Bonnell & Hastie (1985), Hastie & Bonnell (1985), Besmann & Spear (2002) and Green et al. (2012b), in which the ordered intermediate end-members are termed ‘associate species’. The inclusion of an ordered intermediate end-member, intL, in the melt a–x relations adds flexibility in fitting the available constraints, since the 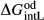 term provides a free parameter and the presence of the intL compound contributes to model entropy. However, it should be stressed that speciation is not represented in any meaningful way in the metabasite melt model, either by the choice of end-member mixing units or by the ordering taking place among them.
term provides a free parameter and the presence of the intL compound contributes to model entropy. However, it should be stressed that speciation is not represented in any meaningful way in the metabasite melt model, either by the choice of end-member mixing units or by the ordering taking place among them.
To complete the calibration of the metabasite melt model, values had to be found for 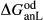 and the new interaction energies
and the new interaction energies 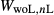 and
and 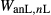 . Parameters such as
. Parameters such as 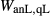 are not strictly the same as the equivalently named parameter in the metapelite melt model, because the anL end-member in the metabasite melt model is not the dataset end-member but an ‘ordered’ end-member that coexists with a 1:1 mixture of woL + silL ‘molecules’, even at the anorthite composition. Due to the significant difference in composition range between the metapelite and metabasite melt models, the non-core parameters from the metapelite melt model were considered to be potentially subject to variation in mctc, namely the interaction energies
are not strictly the same as the equivalently named parameter in the metapelite melt model, because the anL end-member in the metabasite melt model is not the dataset end-member but an ‘ordered’ end-member that coexists with a 1:1 mixture of woL + silL ‘molecules’, even at the anorthite composition. Due to the significant difference in composition range between the metapelite and metabasite melt models, the non-core parameters from the metapelite melt model were considered to be potentially subject to variation in mctc, namely the interaction energies 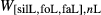 and the
and the 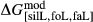 . A finite
. A finite 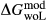 was also explored.
was also explored.
Calibration in mctc was carried out simultaneously on (i) the wet and dry melting curves of anorthite (the experiments of Stewart (1967), Yoder (1976) and Goldsmith (1980), constraining the woL–silL and woL–silL–h2oL compositional joins of the melt model), (ii) the inferred position of the hb + di + opx + an + q + L + H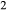 O invariant point in the CMASH system, from Ellis & Thompson (1986), (iii) two reported melt compositions at large melt fraction, from the TTG-genesis studies of Patiño Douce & Beard 1995, SQA composition) and Beard & Lofgren (1991) Sample 478), and (iv) nine estimates of phase boundary positions (H
O invariant point in the CMASH system, from Ellis & Thompson (1986), (iii) two reported melt compositions at large melt fraction, from the TTG-genesis studies of Patiño Douce & Beard 1995, SQA composition) and Beard & Lofgren (1991) Sample 478), and (iv) nine estimates of phase boundary positions (H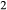 O-out, orthopyroxene-out, hornblende-out, melt-out, quartz-out, plagioclase-out) in the same two experimental bulk compositions. The studies of Patiño Douce & Beard (1995) and Beard & Lofgren (1991) were chosen because the experiments represent a comprehensive P–T grid for ≤ 12.5 kbar. The results of the calibration are shown below.
O-out, orthopyroxene-out, hornblende-out, melt-out, quartz-out, plagioclase-out) in the same two experimental bulk compositions. The studies of Patiño Douce & Beard (1995) and Beard & Lofgren (1991) were chosen because the experiments represent a comprehensive P–T grid for ≤ 12.5 kbar. The results of the calibration are shown below.
Calculations on Experimental Compositions
Figures 3 and 4 present pseudosections calculated for hydrate-breakdown melting using bulk compositions SQA (Patiño Douce & Beard, 1995) and Sample 478 (Beard & Lofgren, 1991, hereafter BL478). Bulk composition is treated as constant for experiments on one starting material in one type of apparatus.
Experiments of Patiño Douce & Beard (1995)
The experiments of Patiño Douce & Beard (1995) on SQA, a synthetic quartz amphibolite, yielded assemblages of q + pl + ilm/ru ± hb ± opx ± g ± cpx. Experiments at >6 kbar were performed in a piston cylinder and experiments at <6 kbar in an internally heated pressure vessel (IHPV). In Fig. 3a, calculations at >6 kbar used a value of 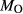 that gave
that gave 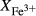 = 0.1, while calculations <6 kbar took place with
= 0.1, while calculations <6 kbar took place with 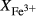 = 0.25. These values reflect the more oxidizing environment of the IHPV relative to the piston cylinder, and were chosen because they span a range of
= 0.25. These values reflect the more oxidizing environment of the IHPV relative to the piston cylinder, and were chosen because they span a range of 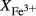 values inferred from modelling of natural amphibolites and granulites (see Table 1), although they may not correspond closely to the unknown
values inferred from modelling of natural amphibolites and granulites (see Table 1), although they may not correspond closely to the unknown 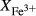 values developed in the experimental apparatus. For each of the two bulk compositions, calculated values of
values developed in the experimental apparatus. For each of the two bulk compositions, calculated values of 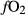 fall within the ranges estimated in the experiments, but this does not sensitively constrain appropriate values for
fall within the ranges estimated in the experiments, but this does not sensitively constrain appropriate values for 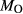 . A single estimate for
. A single estimate for 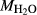 was applied to both high- and low-pressure calculations, obtained by Patiño Douce & Beard (1995) through electron probe analysis of the melted starting mixture. In reality, the starting material likely underwent substantial reduction or oxidation in each of the two assemblies, mediated by infiltration or loss of hydrogen and associated with changes in
was applied to both high- and low-pressure calculations, obtained by Patiño Douce & Beard (1995) through electron probe analysis of the melted starting mixture. In reality, the starting material likely underwent substantial reduction or oxidation in each of the two assemblies, mediated by infiltration or loss of hydrogen and associated with changes in 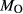 and
and 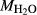 . However, we did not attempt to simulate the relationship between
. However, we did not attempt to simulate the relationship between 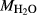 in the high-pressure, low-
in the high-pressure, low-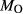 experiments v. the low-pressure, high-
experiments v. the low-pressure, high- experiments, given that the initial value of
experiments, given that the initial value of 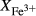 in the starting material is unknown.
in the starting material is unknown.
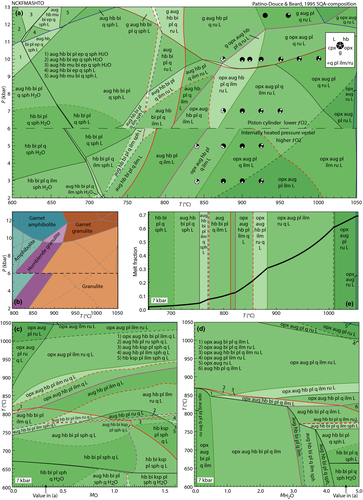
 values are used at higher and lower pressure, corresponding to different sets of experimental apparatus (see text). (b) Summary of (a) highlighting the implied facies transition. (c) T–
values are used at higher and lower pressure, corresponding to different sets of experimental apparatus (see text). (b) Summary of (a) highlighting the implied facies transition. (c) T–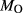 section at 7 kbar, representing values of
section at 7 kbar, representing values of 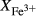 ≤0.5. (d) T–
≤0.5. (d) T– sections at 7 kbar. (e) Melt fraction as a function of temperature at 7 kbar; melt fraction is molar with phases represented on a 1-cation basis, approximating the volumetric melt fraction. Boundaries are ornamented and coloured to highlight the continuation of phase-out curves through different assemblages.
sections at 7 kbar. (e) Melt fraction as a function of temperature at 7 kbar; melt fraction is molar with phases represented on a 1-cation basis, approximating the volumetric melt fraction. Boundaries are ornamented and coloured to highlight the continuation of phase-out curves through different assemblages.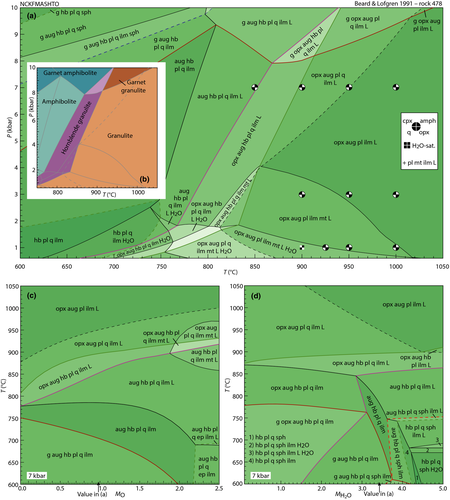
 section at 7 kbar, representing values of
section at 7 kbar, representing values of  0.5. (d) T–
0.5. (d) T–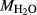 sections at 7 kbar. Boundaries are ornamented and coloured to highlight the continuation of phase-out curves through different assemblages. In calculating this figure, the clinoamphibole model was used with
sections at 7 kbar. Boundaries are ornamented and coloured to highlight the continuation of phase-out curves through different assemblages. In calculating this figure, the clinoamphibole model was used with 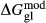 = 0 kJ, rather than the preferred value of −3 kJ; however, this affects the position of phase field boundaries by
= 0 kJ, rather than the preferred value of −3 kJ; however, this affects the position of phase field boundaries by  C.
C.The calculations successfully reproduce the major assemblage changes of the amphibolite–granulite transition as characterized by the experiments, specifically through the up-temperature appearance of orthopyroxene and exhaustion of hornblende (summarized in Fig. 3b). The hornblende-out boundary is well defined by the experiments, and the calculations match this constraint reasonably well, although they predict a shallower dP/dT slope for the boundary than the experiments suggest. For the chosen values of  and
and 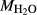 , the calculations progressively underestimate the temperature of hornblende exhaustion towards lower pressure. Garnet appears up to 0.6 kbar below the minimum pressure permitted by the experiments, and at the highest pressures the orthopyroxene-in boundary moves rapidly towards excessive temperatures. In the experiments at 840
, the calculations progressively underestimate the temperature of hornblende exhaustion towards lower pressure. Garnet appears up to 0.6 kbar below the minimum pressure permitted by the experiments, and at the highest pressures the orthopyroxene-in boundary moves rapidly towards excessive temperatures. In the experiments at 840 C and at 875
C and at 875 C, 10 kbar, the experimental assemblage is hb + pl + q + Fe-Ti oxides, while the calculations additionally contain aug + L ± opx ± g. The experimental assemblage is unchanged from that of the starting materials, so an approach to the stable equilibrium assemblage cannot be demonstrated. Despite the moderate temperatures and very long run durations of 1–2 weeks, the shortage of vapour or a detectable volume of melt may inhibit equilibration, and it is likely that stable assemblages at these conditions do indeed include clinopyroxene ± orthopyroxene ± melt.
C, 10 kbar, the experimental assemblage is hb + pl + q + Fe-Ti oxides, while the calculations additionally contain aug + L ± opx ± g. The experimental assemblage is unchanged from that of the starting materials, so an approach to the stable equilibrium assemblage cannot be demonstrated. Despite the moderate temperatures and very long run durations of 1–2 weeks, the shortage of vapour or a detectable volume of melt may inhibit equilibration, and it is likely that stable assemblages at these conditions do indeed include clinopyroxene ± orthopyroxene ± melt.
Figure 3c shows the effect of oxidation state on the calculated assemblages at 7 kbar, over a range of 0 < 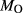 < 1.62 mol.% (0 <
< 1.62 mol.% (0 < 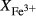 < 0.50). Under the relatively reduced conditions assumed for the piston cylinder assembly, the temperature of the hornblende-out boundary in particular is a strong function of
< 0.50). Under the relatively reduced conditions assumed for the piston cylinder assembly, the temperature of the hornblende-out boundary in particular is a strong function of  , rising from 830
, rising from 830 C to 905
C to 905 C over the range 0 <
C over the range 0 < 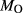 < 0.5 mol.% (0 <
< 0.5 mol.% (0 < 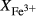 < 0.15), although further increase in
< 0.15), although further increase in  to 1.62 mol.% raises the hornblende-out temperature by only 40
to 1.62 mol.% raises the hornblende-out temperature by only 40 C. The sensitivity of the boundary under low-
C. The sensitivity of the boundary under low- conditions demonstrates the difficulties of extracting calibration information from even the best devised and most careful experimental study, and also highlights the sensitivity of future forward-modelling results to the assumed bulk O content. This sensitivity should always be quantitatively investigated via T–
conditions demonstrates the difficulties of extracting calibration information from even the best devised and most careful experimental study, and also highlights the sensitivity of future forward-modelling results to the assumed bulk O content. This sensitivity should always be quantitatively investigated via T– and P–
and P– plots (e.g. White et al., 2000; Diener & Powell, 2010; Korhonen et al., 2012).
plots (e.g. White et al., 2000; Diener & Powell, 2010; Korhonen et al., 2012).
The equivalent analysis for 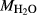 at 7 kbar is shown in Fig. 3d. At
at 7 kbar is shown in Fig. 3d. At 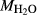 =4.6 mol.%, the value used in Fig. 3a, the calculations predict a H
=4.6 mol.%, the value used in Fig. 3a, the calculations predict a H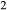 O-present solidus at 665
O-present solidus at 665 C, leading to a volumetric melt fraction of 0.33 at 900
C, leading to a volumetric melt fraction of 0.33 at 900 C (Fig. 3e). By contrast, the experiments are thought to represent hydrate-breakdown melting and produce only modest melt fractions at 900
C (Fig. 3e). By contrast, the experiments are thought to represent hydrate-breakdown melting and produce only modest melt fractions at 900 C. However, by reducing the estimate of
C. However, by reducing the estimate of 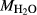 in Fig. 3a from 4.6 mol.% to 3.0 mol.%, a fluid-absent solidus could be calculated at 800
in Fig. 3a from 4.6 mol.% to 3.0 mol.%, a fluid-absent solidus could be calculated at 800 C without significantly degrading the fit to the experimental hornblende-out boundary, the latter being only a weak function of
C without significantly degrading the fit to the experimental hornblende-out boundary, the latter being only a weak function of 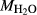 . A value of
. A value of 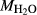 = 3.0 mol.% is in fact close to the estimate of bulk H
= 3.0 mol.% is in fact close to the estimate of bulk H O in the starting materials based on mineral modes (
O in the starting materials based on mineral modes (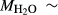 3.3 mol.%, Patiño Douce & Beard, 1995). For a boundary as sensitive to bulk H
3.3 mol.%, Patiño Douce & Beard, 1995). For a boundary as sensitive to bulk H O as the water-undersaturated solidus, it is difficult to make a meaningful comparison between calculations and observations, given that the appropriate value of bulk H
O as the water-undersaturated solidus, it is difficult to make a meaningful comparison between calculations and observations, given that the appropriate value of bulk H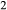 O in the experimental run products is poorly known.
O in the experimental run products is poorly known.
Experiments of Beard & Lofgren (1991)
Sample 478 from the study of Beard & Lofgren 1991; BL478) is a naturally occurring low-K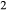 O andesite, less siliceous and less potassic than the SQA material of Patiño Douce & Beard (1995) and with higher bulk FeO/(FeO+MgO). Hydrate-breakdown melting experiments, conducted in an IHPV, produced assemblages of pl + melt + Fe-Ti oxides ± cpx ± opx ± hb ± q, as shown in Fig. 4a.
O andesite, less siliceous and less potassic than the SQA material of Patiño Douce & Beard (1995) and with higher bulk FeO/(FeO+MgO). Hydrate-breakdown melting experiments, conducted in an IHPV, produced assemblages of pl + melt + Fe-Ti oxides ± cpx ± opx ± hb ± q, as shown in Fig. 4a.
Calculations on this bulk composition again describe an amphibolite to granulite facies transition that is broadly consistent with the experiments, summarized in Fig. 4b. As for the SQA composition, the calculated prediction of clinopyroxene stability conflicts with the lowest temperature experiment at 850 C, 6.9 kbar. This experiment yielded pargasitic amphibole + q + pl + Fe-Ti oxides + 6.2 wt% L, whereas the starting assemblage was actinolitic amphibole + q + pl + Fe-Ti oxides. We tentatively suggest that the small quantity of melt present in an otherwise dry experiment may again have been insufficient to allow the stable crystalline assemblage to form. If this is the case, the experiments again primarily define an upper temperature limit on the hornblende-out boundary. The calculated quartz-out boundary lies at too high a temperature, but is shown in Fig. 4c,d to be particularly sensitive to
C, 6.9 kbar. This experiment yielded pargasitic amphibole + q + pl + Fe-Ti oxides + 6.2 wt% L, whereas the starting assemblage was actinolitic amphibole + q + pl + Fe-Ti oxides. We tentatively suggest that the small quantity of melt present in an otherwise dry experiment may again have been insufficient to allow the stable crystalline assemblage to form. If this is the case, the experiments again primarily define an upper temperature limit on the hornblende-out boundary. The calculated quartz-out boundary lies at too high a temperature, but is shown in Fig. 4c,d to be particularly sensitive to 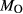 and
and 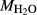 . At 900
. At 900 C and 1 kbar the calculations predict H
C and 1 kbar the calculations predict H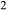 O as a free phase, so they are compared with the results of an H
O as a free phase, so they are compared with the results of an H O-saturated experiment on the same starting material, but fail to reproduce the observed amphibole + quartz assemblage. This is not a significant concern, as the focus of the model calibration was on the more geologically relevant situation of hydrate-breakdown melting (Brown & Fyfe, 1970).
O-saturated experiment on the same starting material, but fail to reproduce the observed amphibole + quartz assemblage. This is not a significant concern, as the focus of the model calibration was on the more geologically relevant situation of hydrate-breakdown melting (Brown & Fyfe, 1970).
The value of 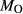 chosen for the calculations in Fig. 4a corresponds to
chosen for the calculations in Fig. 4a corresponds to 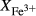 = 0.2, which was assumed to be plausible for the natural starting material, and consistent with exposure to the IHPV assembly over moderate run durations of around 90–120 h. The T–
= 0.2, which was assumed to be plausible for the natural starting material, and consistent with exposure to the IHPV assembly over moderate run durations of around 90–120 h. The T–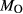 plot (Fig. 4c) shows that, for the relatively oxidized conditions imposed, the calculated 7 kbar position of the hornblende-out boundary varies only from 885
plot (Fig. 4c) shows that, for the relatively oxidized conditions imposed, the calculated 7 kbar position of the hornblende-out boundary varies only from 885 C at
C at 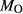 = 0.76 mol.% (
= 0.76 mol.% (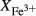 = 0.15) to 902
= 0.15) to 902 C at
C at 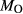 = 1.27 mol.% (
= 1.27 mol.% (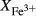 = 0.25). The hornblende-out boundary is also almost indifferent to
= 0.25). The hornblende-out boundary is also almost indifferent to 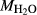 in the range 0.5–4.5 mol.% (Fig. 4d). The value of
in the range 0.5–4.5 mol.% (Fig. 4d). The value of 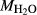 chosen for Fig. 4a is 3.42 mol.%, larger than the 1.72 mol.% estimated by loss on ignition from the starting materials by Beard & Lofgren (1991). In our modelling, this choice of
chosen for Fig. 4a is 3.42 mol.%, larger than the 1.72 mol.% estimated by loss on ignition from the starting materials by Beard & Lofgren (1991). In our modelling, this choice of 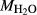 leads to the coexistence of orthopyroxene and hornblende over a narrow (∼50
leads to the coexistence of orthopyroxene and hornblende over a narrow (∼50 C) temperature range, whereas for values of
C) temperature range, whereas for values of 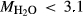 mol.%, orthopyroxene joins the assemblage at rather low temperatures and creates a wide field of hornblende-granulite.
mol.%, orthopyroxene joins the assemblage at rather low temperatures and creates a wide field of hornblende-granulite.
Hornblende-out boundaries in various experimental studies
Since only two bulk compositions from TTG-genesis experiments were used in the model calibration, Fig. 5 summarizes the results of calculations on the hornblende-out boundary in four additional bulk compositions that were not involved in the calibration process, taken from the hydrate-breakdown melting studies of Beard & Lofgren (1991), Rushmer (1991), Wolf & Wyllie (1994) and Skjerlie & Patiño Douce (1995). Comparable calculations for SQA and BL478, the compositions used in calibration, are also shown. In each case, the true temperature of the hornblende-out boundary could be inferred with some confidence from an isobaric sequence of experiments, in which the final hornblende coexisted with a moderate melt fraction and had an apparently equilibrated composition. The calculations, shown as blue bars, locate the hornblende-out boundary for each experimental phase assemblage. Where possible, calculations were performed over generous ranges of 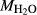 (3.5–6.5 mol.%, equivalent to ∼1–2 wt%) and
(3.5–6.5 mol.%, equivalent to ∼1–2 wt%) and 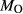 (such that 0.1
(such that 0.1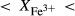 0.25), varied simultaneously, which we expect to encompass the true experimental values in most cases. For bulk compositions WW94 and BL571, the experimental assemblage could only be calculated over a reduced range of
0.25), varied simultaneously, which we expect to encompass the true experimental values in most cases. For bulk compositions WW94 and BL571, the experimental assemblage could only be calculated over a reduced range of 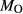 or
or 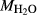 ; see Fig. 5 and Table 1.
; see Fig. 5 and Table 1.
 and
and 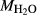 values (blue bars). Except in the case of compositions labelled
values (blue bars). Except in the case of compositions labelled  , calculations were performed for a range of
, calculations were performed for a range of 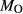 such that 0.1
such that 0.1 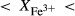 0.25, and for 3.5
0.25, and for 3.5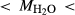 6.5 mol.% (∼1–2 wt% H
6.5 mol.% (∼1–2 wt% H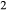 O), varied simultaneously. For compositions
O), varied simultaneously. For compositions  , the blue bars represent calculations for the restricted range of
, the blue bars represent calculations for the restricted range of  or
or 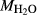 over which positive modes of phases were predicted (Table 1). For composition WW94, TiO
over which positive modes of phases were predicted (Table 1). For composition WW94, TiO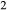 was omitted as hornblende is the only Ti-bearing model involved. In compositions
was omitted as hornblende is the only Ti-bearing model involved. In compositions 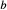 , only trace hornblende was detected at the lower-T end of the experimental bracket. Calculations were made on each experimental assemblage without checking that it was the most stable assemblage that the models could generate, except for compositions
, only trace hornblende was detected at the lower-T end of the experimental bracket. Calculations were made on each experimental assemblage without checking that it was the most stable assemblage that the models could generate, except for compositions  , which were used in calibration. For BL478, the experimental assemblage is ambiguous, while in the calculations, stable assemblages ± quartz are needed to cover the full range of
, which were used in calibration. For BL478, the experimental assemblage is ambiguous, while in the calculations, stable assemblages ± quartz are needed to cover the full range of 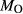 and
and 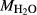 .
.The calculations generally reproduce the experimental hornblende-out temperatures well, although they considerably overestimate the temperature for the IAT (island arc tholeiite) composition of Rushmer (1991). Temperatures are probably underestimated for the natural amphibolite composition AGS11.1 of Skjerlie & Patiño Douce (1995), and the calibration composition SQA. Over- or under-estimation of hornblende-out temperature may be correlated with molar bulk values of Al O
O /(CaO + Na
/(CaO + Na O + K
O + K O), of which IAT has the highest value and AGS11.1 and SQA relatively low values.
O), of which IAT has the highest value and AGS11.1 and SQA relatively low values.
To a considerable extent, the variation of modelled boundaries with bulk composition is a function of the well established Holland & Powell (2011) dataset calibration, combined with the superimposed 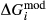 and
and 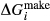 terms. Therefore, it is perhaps unsurprising that the results of these calculations are reasonable, although only two of the TTG-genesis studies were incorporated into the fitting.
terms. Therefore, it is perhaps unsurprising that the results of these calculations are reasonable, although only two of the TTG-genesis studies were incorporated into the fitting.
Discussion
The newly calibrated a–x relations extend the scope of phase-equilibrium forward-modelling methods to include metabasic rocks at high temperature. A pseudosection approach to thermobarometry is now feasible for such rocks, and other questions that incorporate a bulk composition constraint, such as limits on melt loss, may now be addressed. Methods of this kind have previously brought insight into metamorphic processes in metapelites (e.g. Kelsey et al., White et al., 2003; 2003; Johnson & Brown, 2004; Halpin et al., 2007; Streule et al., 2010; Korhonen et al., 2010; Palin et al., 2012). Strictly the calibration of the a–x relations described in this paper was limited to ≤13 kbar, owing to the lack of a thermodynamic model for aqueous fluid containing dissolved silicate material. However, it is reasonable to use the metabasite models with caution whenever the results can be compared with observations to demonstrate that appropriate stable assemblages are calculated. In the companion paper, Palin et al. (2016b), we examine calculations with the metabasite models on a variety of natural compositions, comparing the calculated assemblages and melt compositions with expectations drawn from observation and experiment.
Through the above comparison of phase diagram calculations with experiments, it is possible to comment on the uncertainties and limitations of the models. The models can probably be expected to give a correct sequence of up-temperature assemblages, with respect to major phases. Within the calibration range of the a–x relations, phase-in/phase-out boundaries are likely to be constrained to within 50–100 C, or 1–2 kbar for a strongly pressure-dependent boundary, allowing for the difficulty of assessing
C, or 1–2 kbar for a strongly pressure-dependent boundary, allowing for the difficulty of assessing  and
and  during model calibration. Comparable magnitudes of uncertainty are associated with estimating a representative bulk composition for an equilibrium assemblage in a natural rock sample (Palin et al., 2016a). As in all forward modelling of phase equilibria, careful consideration of the sensitivity of results to
during model calibration. Comparable magnitudes of uncertainty are associated with estimating a representative bulk composition for an equilibrium assemblage in a natural rock sample (Palin et al., 2016a). As in all forward modelling of phase equilibria, careful consideration of the sensitivity of results to 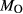 and
and 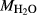 will be essential for meaningful interpretation.
will be essential for meaningful interpretation.
As metabasic rocks typically contain fewer phases than metapelites, fields on P–T pseudosections tend to be larger, providing a less useful constraint on the pressure and temperature of mineral preservation. It may therefore be desirable to estimate P–T more precisely by comparing the observed and calculated compositions of phases. An appropriate way to do this, that correctly takes account of the uncertainties in the thermodynamic modelling, is the ‘average P–T’ method of Powell & Holland (1988) and Powell & Holland (1994). This can be carried out in thermocalc, using the standard input files for the Holland & Powell (2011) dataset and metabasite set of a–x relations, just as for pseudosection calculations (Powell & Holland, 2008). The average P–T method finds the least-squares best estimate of P-at-T or T-at-P using the thermobarometric information contained in multiple independent reactions among model end-members. Starting from the activities calculated for the model end-members at the analytical phase compositions, it makes minimal uncertainty-weighted adjustments to the activities and enthalpies of the end-members, until the constraint is satisfied that all end-member reactions must meet at an equilibrium P or T (both P and T can be constrained using the uncertainty output). When good statistical diagnostics are obtained from the procedure, they suggest both that the analysed phases are well equilibrated, and that the thermodynamic models are sufficiently well calibrated to reflect this.
The a–x relations presented in this paper should be considered only as a starting point for the modelling of high-temperature metabasic assemblages. Future a–x development is expected to include a single model for clinopyroxene, replacing the current omphacite and augite models, and a single model for tonalitic–trondjhemitic to granitic melt, replacing the current metabasite and metapelite melt models. The set of metabasite a–x models will be refined over time, as was the metapelite set of models before it, to correct systematic problems that emerge in calculated phase equilibria. We welcome feedback from users on the performance of the models.
Acknowledgements
We are grateful to S. Fischer for his efforts in compiling an experimental database, and to L. Ziberna for illuminating discussions about experimental methods. We thank K. Evans, D. M. Jenkins and G. Stevens for their insightful and constructive reviews, and M. Brown for his editorial handling. This work was supported by DFG grant WH 110/4-1 awarded to R. W. White.
Appendix
The thermodynamic models discussed in this paper may be conveniently used with the software thermocalc (Powell & Holland, 1988). The thermocalc software may be downloaded from the University of Mainz thermocalc website at http://www.metamorph.geo.uni-mainz.de/thermocalc/, along with input files containing the a–x relations, versions of the Holland & Powell (2011) dataset, and explanatory notes. thermocalc versions tc340 and above should be used. Versions ds62 and ds63 of the Holland & Powell (2011) dataset have not been formally published, so anyone wishing to use them independently of thermocalc must extract parameters from the thermocalc input files. To assist in doing so, thermocalc may be run in mode 0 with the appropriate dataset and a–x relations, generating tables of G values as functions of pressure and temperature for each end-member, including those that do not appear explicitly in the dataset. The G values include any 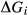 expressions applied to the end-members (identified in a–x input files by the script ‘DQF’).
expressions applied to the end-members (identified in a–x input files by the script ‘DQF’).
Full thermodynamic descriptions of the new a–x relations for clinopyroxene (augite model), clinoamphibole and metabasite melt are given below. 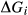 terms are specified relative to end-members that appear in the Holland & Powell (2011) dataset. Interaction energies
terms are specified relative to end-members that appear in the Holland & Powell (2011) dataset. Interaction energies 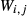 and
and 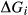 parameters are specified as functions of pressure P in kilobar and T in kelvin:
parameters are specified as functions of pressure P in kilobar and T in kelvin: 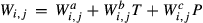 and
and 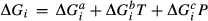 .
.
Clinopyroxene models
In the augite model, the following independent set of end-members is used, with the cations shown on their mixing sites, and the tetrahedral site split into T1 and T2 in order to describe Si–Al ordering in the cats end-member (the latter is an intrinsic property of the cats end-member of the Holland & Powell (2011) dataset, written out explicitly in the a–x model):
| M1 | M2 | T1 | T2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mg | Fe | Al | Fe3 | Mg | Fe | Ca | Na | Si | Al | Si | Al | |
| di | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| cenh | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| cfs | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| jd | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| acm | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| ocats | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| dcats | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
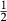
|
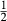
|
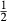
|
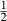
|
| fmc | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
Cenh and cfs are the C2/c polymorphs of the dataset Pbca end-members en and fs, and are derived from them via 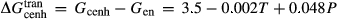 kJ and
kJ and 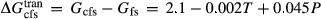 kJ. Fmc is the ordered end-member for which
kJ. Fmc is the ordered end-member for which 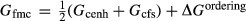 . Because
. Because 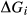 terms are described relative to dataset end-members,
terms are described relative to dataset end-members, 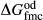 incorporates
incorporates 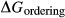 ,
, 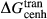 and
and 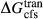 :
: 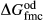 =
= 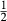 (
(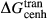 +
+ 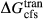 ) +
) + 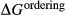 = −1.6−0.002T+0.0465P kJ. Ocats and dcats are the fully ordered and fully disordered forms respectively of the dataset cats end-member. Together they reproduce the thermodynamics of the cats end-member via prescribed values for
= −1.6−0.002T+0.0465P kJ. Ocats and dcats are the fully ordered and fully disordered forms respectively of the dataset cats end-member. Together they reproduce the thermodynamics of the cats end-member via prescribed values for 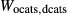 and the term
and the term 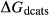 =3.8−0.0028816T+0.01P kJ.
=3.8−0.0028816T+0.01P kJ. 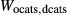 ,
, 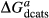 and
and 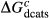 can be found in Holland & Powell (2011), table 2c, while
can be found in Holland & Powell (2011), table 2c, while 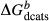 represents the configurational entropy involved in disordering. Jd and acm are subject to
represents the configurational entropy involved in disordering. Jd and acm are subject to 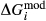 terms of 2 kJ and −5 kJ respectively.
terms of 2 kJ and −5 kJ respectively.
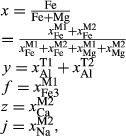
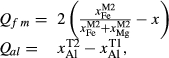
 (cenh + cfs) and dcats = ocats. The site fractions are
(cenh + cfs) and dcats = ocats. The site fractions are
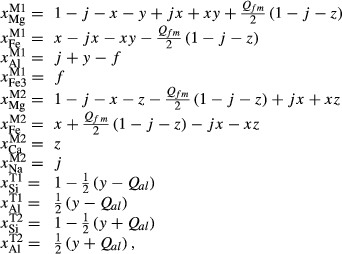
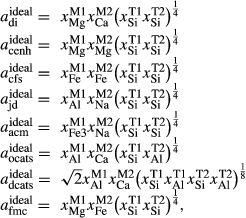
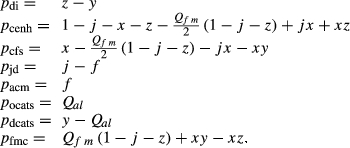
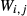 (kJ) (kJ) |
cenh | cfs | jd | acm | ocats | dcats | fmc |
|---|---|---|---|---|---|---|---|
| di | 29.8−0.03P | 25.8−0.03P | 26 | 21 | 12.3−0.01P | 12.3−0.01P | 20.6−0.03P |
| cenh | 2.3 | 50 | 62 | 45.7−0.29P | 45.7−0.29P | 4 | |
| cfs | 60 | 58 | 48 | 48 | 3.5 | ||
| jd | 5 | 40 | 40 | 40 | |||
| acm | 35 | 35 | 60 | ||||
| ocats | 3.8+0.01P | 50 | |||||
| dcats | 50 |
with asymmetry introduced by the van Laar parameters 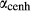 =
= 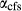 =
= 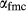 = 1,
= 1, 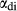 =
= 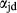 =
= 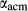 = 1.2, and
= 1.2, and 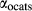 =
=  = 1.9.
= 1.9.
We reiterate that the augite model does not have a structure suitable for calculations where coexisting clinopyroxenes may be expected. To calculate two-clinopyroxene equilibria, the ‘omphacite’ model should be used for both phases, using appropriate starting guesses for the compositional parameters in each. The omphacite model is described in Green et al. (2007), with new 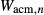 values given Diener & Powell (2012) and a new value for
values given Diener & Powell (2012) and a new value for 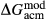 , of −7 kJ, given in this paper. The change to
, of −7 kJ, given in this paper. The change to 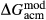 entails a corresponding change to the parameter
entails a corresponding change to the parameter 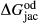 . The jac end-member is the ordered intermediate Na
. The jac end-member is the ordered intermediate Na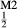 Na
Na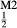 Fe
Fe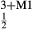 Al
Al Si
Si O
O , and is formed through the reaction jac =
, and is formed through the reaction jac = 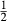 (jd + acm) +
(jd + acm) + 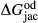 , such that
, such that 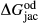 =
= 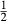 (
(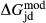 +
+ 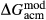 ) − 1 kJ. With
) − 1 kJ. With 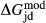 = 0, the change to
= 0, the change to 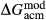 leads to
leads to 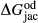 = −4.5 kJ, rather than the previous value of −5 kJ.
= −4.5 kJ, rather than the previous value of −5 kJ.
For comparison between the omphacite and augite models, the dependent parameters associated with the hed end-member, CaFeSi O
O , in the augite model are compared here with their equivalents in the omphacite model.
, in the augite model are compared here with their equivalents in the omphacite model.
| parameter (kJ) | augite model | omphacite model |
|---|---|---|
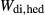
|
2.9 | 4 |
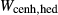
|
26.6−0.03P | – |
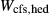
|
20.9−0.03P | – |
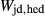
|
42.4 | 24 |
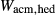
|
17.4 | 20.8 |
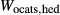 , , 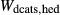
|
8.7−0.01P | – |
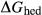 at 8 kbar, 900 at 8 kbar, 900 C C |
1.5 | 0 |
There is, however, no discordance of symmetry between the two models, as they both feature 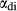 =
= 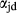 =
= 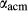 =
= 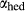 . For the method of determining the dependency relationships, see Powell & Holland (1999).
. For the method of determining the dependency relationships, see Powell & Holland (1999).
Clinoamphibole model
The following independent set of end-members is used, based on an amphibole formula calculated for 23 oxygen atoms, with the mixing sites only shown (v = vacancy):
| A | M13 | M2 | M4 | T1 | V | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| v | Na | K | Mg | Fe | Mg | Fe | Al | Fe3 | Ti | Ca | Mg | Fe | Na | Si | Al | OH | O | |
| tr | 1 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 0 | 2 | 0 |
| ts | 1 | 0 | 0 | 3 | 0 | 0 | 0 | 2 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | 0 |
| parg | 0 | 1 | 0 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | 0 |
| gl | 1 | 0 | 0 | 3 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 4 | 0 | 2 | 0 |
| cumm | 1 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 4 | 0 | 2 | 0 |
| grun | 1 | 0 | 0 | 0 | 3 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 4 | 0 | 2 | 0 |
| a | 1 | 0 | 0 | 3 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 4 | 0 | 2 | 0 |
| b | 1 | 0 | 0 | 0 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 4 | 0 | 2 | 0 |
| mrb | 1 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 2 | 4 | 0 | 2 | 0 |
| kprg | 0 | 0 | 1 | 3 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 2 | 2 | 0 |
| tts | 1 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | 2 | 2 | 0 | 2 |
As the end-member thermodynamics are in general not well known, it is assumed that that dataset end-member tr is correct, while the other compositional end-members ts, parg, gl, cumm and grun are modified relative to this via terms 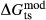 = 10 kJ,
= 10 kJ,  = −10 kJ,
= −10 kJ, 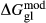 = −3 kJ,
= −3 kJ, 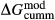 = 0 kJ,
= 0 kJ, 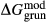 = −3 kJ. Order–disorder of Fe–Mg on the M13, M2 and M4 sites is governed by end-members a =
= −3 kJ. Order–disorder of Fe–Mg on the M13, M2 and M4 sites is governed by end-members a = 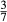 cumm +
cumm + 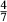 grun +
grun + 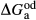 and b =
and b = 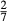 cumm +
cumm +  grun +
grun + 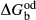 , where the
, where the 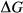 relative to the dataset values of the end-members are given by
relative to the dataset values of the end-members are given by 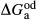 =
= 
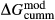 +
+ 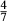
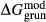 – 9.5 = −11.2 kJ and
– 9.5 = −11.2 kJ and  =
= 
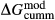 +
+ 
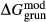 – 11.7 = −13.8 kJ. The ferric end-member mrb, and the new end-members kprg and tts, have to be ‘made’ from dataset end-members via the reactions mrb = gl − gr + andr +
– 11.7 = −13.8 kJ. The ferric end-member mrb, and the new end-members kprg and tts, have to be ‘made’ from dataset end-members via the reactions mrb = gl − gr + andr + 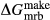 , kprg = mu − pa + parg +
, kprg = mu − pa + parg + 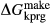 , and tts = ts + 2 ru − 2 dsp +
, and tts = ts + 2 ru − 2 dsp + 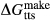 respectively, where the dG terms are
respectively, where the dG terms are 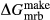 = 0 kJ,
= 0 kJ,  = −7.06+0.02T kJ and
= −7.06+0.02T kJ and 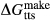 = 95 kJ (gr: grossular; andr: andradite; mu: muscovite; pa: paragonite; ru: rutile; dsp: diaspore). Diener et al. (2007) describe the structure and calibration of the core NCFMASHO model more fully.
= 95 kJ (gr: grossular; andr: andradite; mu: muscovite; pa: paragonite; ru: rutile; dsp: diaspore). Diener et al. (2007) describe the structure and calibration of the core NCFMASHO model more fully.

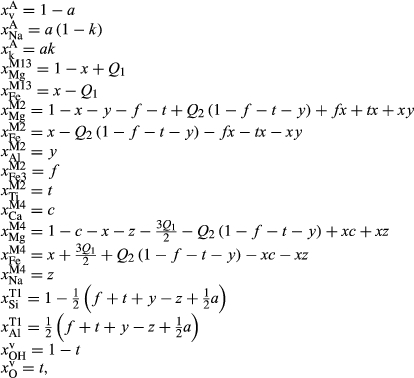
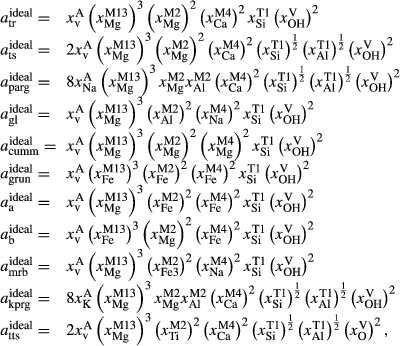
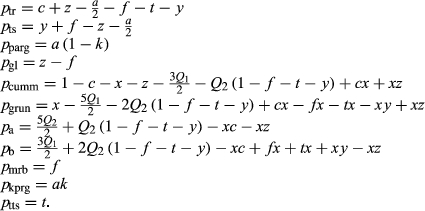
 (kJ) (kJ) |
ts | parg | gl | cumm | grun | a | b | mrb | kprg | tts |
|---|---|---|---|---|---|---|---|---|---|---|
| tr | 20 | 25 | 65 | 45 | 75 | 57 | 63 | 52 | 30 | 85 |
| ts | −40 | 25 | 70 | 80 | 70 | 72.5 | 20 | −40 | 35 | |
| parg | 50 | 90 | 106.7 | 94.8 | 94.8 | 40 | 8 | 15 | ||
| gl | 100 | 113.5 | 100 | 111.2 | 0 | 54 | 75 | |||
| cumm | 33 | 18 | 23 | 80 | 87 | 100 | ||||
| grun | 12 | 8 | 91 | 96 | 65 | |||||
| a | 20 | 80 | 94 | 95 | ||||||
| b | 90 | 94 | 95 | |||||||
| mrb | 50 | 50 | ||||||||
| kprg | 35 |
with asymmetry introduced by the van Laar parameters 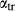 =
= 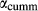 =
= 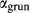 =
= 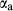 =
= 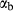 = 1,
= 1, 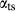 =
= 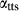 = 1.5,
= 1.5, 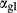 =
= 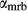 = 0.8, and
= 0.8, and 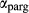 =
= 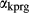 = 1.7.
= 1.7.
These a–x relations are suitable for all of the clinoamphibole solid solutions hornblende, glaucophane, actinolite and cummingtonite, when appropriate starting guesses are given for the compositional variables.
Melt model
The end-members are mixing units with mineral-like formulae:
| end-member | formula |
|---|---|
| qL | Si O O
|
| abL | NaAlSi O O
|
| kspL | KAlSi O O
|
| woL | CaSiO
|
| silL | Al SiO SiO
|
| faL | Fe Si Si O O
|
| foL | Mg Si Si O O
|
| h2oL | H O O |
| anL | CaAl Si Si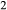 O O
|
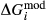 terms are imposed on some end-members:
terms are imposed on some end-members: 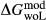 = 1.3 kJ,
= 1.3 kJ, 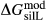 = −7.8 kJ,
= −7.8 kJ, 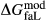 = −8.2−1.4P kJ, and
= −8.2−1.4P kJ, and 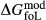 = −4. The end-member anL is made by the reaction anL = woL + silL +
= −4. The end-member anL is made by the reaction anL = woL + silL + 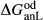 , with
, with 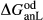 = −46.5−0.25P.
= −46.5−0.25P.
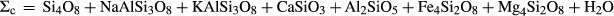 :
:
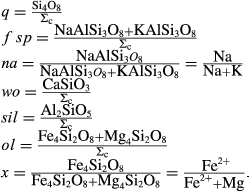
 is defined, where
is defined, where  . The full set of end-member proportions can now be written as:
. The full set of end-member proportions can now be written as:

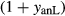 terms arise because the reaction woL + silL = anL leads to an overall change in the number of ‘molecules’ present, for a fixed number of atoms of liquid.
terms arise because the reaction woL + silL = anL leads to an overall change in the number of ‘molecules’ present, for a fixed number of atoms of liquid.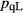 ,
, 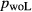 ,
, 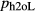 ,
,  ,
, 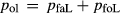 ,
, 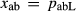 ,
,  , and additionally the expressions
, and additionally the expressions
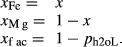
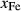 and
and 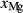 terms allowing for an extra entropic contribution from Fe-Mg mixing in addition to that of the mixing of foL and faL units, and the
terms allowing for an extra entropic contribution from Fe-Mg mixing in addition to that of the mixing of foL and faL units, and the 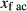 term allowing for extra entropy in the addition of H
term allowing for extra entropy in the addition of H O:
O:
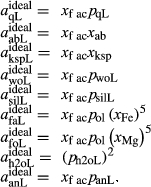
 (kJ) (kJ) |
abL | kspL | woL | silL | faL | foL | h2oL | anL |
|---|---|---|---|---|---|---|---|---|
| qL | 12−0.4P | −2−0.5P | −5 | 0 | 0 | 42+1.0P | 18.1−0.68P | −29.5−0.1P |
| abL | −6+3.0P | −12 | 10 | −30+0.8P | −47.3+0.3P | −4.4−0.17P | 8.6+0.4P | |
| kspL | −13 | 0 | −11.3 | 6.8 | 10.4−0.39P | −16−0.25P | ||
| woL | −1.6 | 6.5 | 4 | 21 | 3.5 | |||
| silL | 12 | 12 | 11−0.5P | 6.4 | ||||
| faL | 18 | 29 | −43.5−0.95P | |||||
| foL | 29−0.5P | −26−0.6P | ||||||
| h2oL | 9.75−0.5P |
In version 6.3 of the Holland & Powell (2011) dataset, the thermodynamic properties of the h2oL end-member, incorporating the new constant-pressure heat capacity, are as follows. Enthalpy of formation (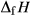 ): −281.68 ± 0.26 kJ, entropy (S): 66.60 kJ K
): −281.68 ± 0.26 kJ, entropy (S): 66.60 kJ K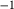 , volume (V): 1.363 J bar
, volume (V): 1.363 J bar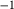 , at 1 bar, 298 K. Heat capacity (
, at 1 bar, 298 K. Heat capacity (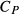 ): 0.0650 kJ K
): 0.0650 kJ K . Thermal expansivity (
. Thermal expansivity (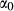 ): 57.80 K
): 57.80 K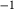 . Bulk modulus at 1 bar, 298 K, and its first and second pressure derivatives (
. Bulk modulus at 1 bar, 298 K, and its first and second pressure derivatives (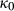 ,
, 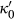 ,
,  ): 47.92 kbar, 4.00, −0.08350 kbar
): 47.92 kbar, 4.00, −0.08350 kbar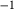 .
.
Other models
The a–x relations for biotite, garnet and orthopyroxene were first presented in White et al. (2014). As used in White et al. (2014), the a–x relations for epidote were taken from Holland & Powell (2003), those for feldspar from Holland & Powell (2011), and those for spinel–magnetite from White et al. (2002). For ilmenite, the Mg-bearing model used by White et al. (2002). has been replaced, in both the metabasite set and the metapelite set, with the older model of White et al. (2014) in the system FeO–Fe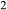 O
O –TiO
–TiO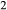 , as the more recent model appears to predict excessive values of MgO/(FeO+MgO) in the phase.
, as the more recent model appears to predict excessive values of MgO/(FeO+MgO) in the phase.



 O
O melts
melts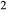 O–K
O–K O–CaO–MgO–FeO–Fe
O–CaO–MgO–FeO–Fe O
O –Al
–Al O
O –SiO
–SiO –TiO
–TiO –H
–H O–CO
O–CO
 O
O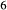 , and albite, NaAlSi
, and albite, NaAlSi O
O , in the range up to 50 kilobars
, in the range up to 50 kilobars Si
Si O
O –CaMgSi
–CaMgSi O
O
 in melt and cordierite: implications for dehydration, partial melting and graphite precipitation
in melt and cordierite: implications for dehydration, partial melting and graphite precipitation O–CaO–FeO–MgO–Al
O–CaO–FeO–MgO–Al O
O –SiO
–SiO –H
–H O–O
O–O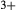 concentrations in ferromagnesian silicates and oxides from microprobe analyses, using stoichiometric criteria
concentrations in ferromagnesian silicates and oxides from microprobe analyses, using stoichiometric criteria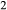 O
O + SiO
+ SiO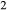 + H
+ H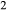 O system under water-excess and water-deficient conditions to 10 kb: some implications for the origin of peraluminous melts from mafic rocks
O system under water-excess and water-deficient conditions to 10 kb: some implications for the origin of peraluminous melts from mafic rocks O–SiO
O–SiO fluid up to 1300
fluid up to 1300 C and 20 kbar based on the chain reaction formalism
C and 20 kbar based on the chain reaction formalism O
O as microcline and sanidine
as microcline and sanidine -TiO
-TiO -Al
-Al O
O -Fe
-Fe O
O -CaO-MgO-FeO-K
-CaO-MgO-FeO-K O-Na
O-Na O-H
O-H O-CO
O-CO
 O
O –SiO
–SiO and CaO–MgO–Al
and CaO–MgO–Al O
O –SiO
–SiO to 50 kbar and 1800
to 50 kbar and 1800 C
C O
O –SiO
–SiO and CaO–MgO–Al
and CaO–MgO–Al O
O –SiO
–SiO : thermodynamic models and an experimental conflict
: thermodynamic models and an experimental conflict –H
–H O near the upper critical end point based on quartz solubility experiments at 500–1100
O near the upper critical end point based on quartz solubility experiments at 500–1100 C and 5–20 kbar
C and 5–20 kbar BeF
BeF and GeO
and GeO at elevated pressures
at elevated pressures –H
–H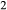 O
O O
O : effect of pressure up to 40 kb
: effect of pressure up to 40 kb to 1400
to 1400 C 5 to 35kb
C 5 to 35kb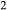 O in the lower crust and upper mantle
O in the lower crust and upper mantle O at 700
O at 700 and 10 kbar: evidence for Al–Si complexing at high pressure and temperature
and 10 kbar: evidence for Al–Si complexing at high pressure and temperature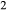 O
O –Mg
–Mg Si
Si O
O at high pressures and temperatures
at high pressures and temperatures SiO
SiO –quartz geobarometer
–quartz geobarometer –H
–H O fluid near the upper critical end point from quartz solubility measurements at 10 kbar
O fluid near the upper critical end point from quartz solubility measurements at 10 kbar to 60 kbar: a re-evaluation of the regular solution model
to 60 kbar: a re-evaluation of the regular solution model –H
–H O
O O loss from hydrous melts during uid-absent piston cylinder experiments
O loss from hydrous melts during uid-absent piston cylinder experiments O
O –SiO
–SiO at 900
at 900 –1,100
–1,100 C and high pressures
C and high pressures O content of high-MgO magmas in island arc settings: an experimental study of a primitive calc-alkaline basalt from St. Vincent Lesser Antilles arc
O content of high-MgO magmas in island arc settings: an experimental study of a primitive calc-alkaline basalt from St. Vincent Lesser Antilles arc + enstatite
+ enstatite at 15kbar
at 15kbar Si
Si O
O –SiO
–SiO –H
–H O
O C
C O–FeO–MgO–Al
O–FeO–MgO–Al O
O –SiO
–SiO –H
–H O–TiO
O–TiO –Fe
–Fe O
O
 O-CaO-K
O-CaO-K O-FeO-MgO-Al
O-FeO-MgO-Al O
O -SiO
-SiO -H
-H O (NCKFMASH)
O (NCKFMASH) and Fe
and Fe O
O on metapelitic assemblages at greenschist and amphibolite facies conditions: mineral equilibria calculations in the system K
on metapelitic assemblages at greenschist and amphibolite facies conditions: mineral equilibria calculations in the system K O–FeO–MgO–Al
O–FeO–MgO–Al O
O –SiO
–SiO –H
–H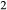 O–TiO
O–TiO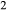 –Fe
–Fe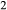 O
O
 , BeF
, BeF and GeO
and GeO at elevated pressures
at elevated pressures
