Quantitative flood hazard assessment methods: A review
Funding information: Italian Ministry of University and Research, Grant/Award Number: 2017T4JC5K
Abstract
Flood hazard assessment is a fundamental step in flood risk mapping. Quantitative assessment requires hydrodynamic modelling of the flooding process in order to calculate the spatial distribution of suitable flood hazard indicators representative of flooding intensity and frequency, hence its potential to result in harm. Flood hazard indicators are usually defined by combining relevant flooding parameters, mainly flood depth and flow velocity, but also flooding arrival time, flooding duration, sediment or contamination load, and so forth. A flood hazard classification is commonly introduced to assign a hazard level to areas potentially subject to flooding. This article presents a systematic review of quantitative methods proposed in the scientific literature or prescribed by government authorities to assess the hazard associated with natural or anthropic flooding. Flood hazard classification methods are listed and compared by specifying their underlying approach (heuristic, conceptual, empirical), the exposed element which they were designed for (people, buildings, vehicles, etc.), and their fields of application (river overflow, dam-break, levee breach, debris flow). Perspectives and future challenges in quantitative flood hazard analysis are also discussed. This review aims to help modellers and practitioners to select the most suitable flood hazard assessment method for the case study of interest.
1 INTRODUCTION
Inundations are among the most destructive disasters, with the potential to create dramatically negative impact on populations in terms of fatality, injury, displacement of people, and damage to infrastructure, cultural and environmental heritage, and economic activities (CRED-UNDRR, 2020; Doocy et al., 2013). Flooding can be induced by natural phenomena (such as river floods causing overflow or breaching of river embankments, coastal storms, tides, or intense rainfall in urban areas), or anthropic causes (such as incorrect operations of hydraulic structures, or uncontrolled release of water resulting from an accident, or the partial or total collapse of a dam). Over the last 20 years, floods have been the most recurrent type of natural disaster (accounting for 44% of all events recorded by CRED's Emergency Events Database during this period) and affected 1.65 billion people worldwide (the highest figure compared to the other disaster types), with $651 billion in economic losses (CRED-UNDRR, 2020).
Flooding creates a risk when anthropic and environmental systems can be potentially damaged. According to the EU Floods Directive (European Council, 2007), flood risk is defined as “the combination of the probability of a flood event and of the potential adverse consequences to human health, the environment and economic activity associated with a flood”. In analogy with the standard definition of risk of extreme events, flood risk is to be considered as the combination of three components (IPCC, 2012; Kron, 2002): flood hazard (i.e., flood frequency and severity); exposure (i.e., the presence of people, buildings, infrastructure, economic and social activities in floodable areas); and vulnerability (i.e., the propensity of exposed elements to be damaged by flooding). The increase in human settlements and economic assets in floodplains and coastal areas, along with the alteration in flood magnitude and frequency due to climate change, leads to a higher degree of flood risk (Hirabayashi et al., 2013), thus highlighting the need to adopt national and local risk reduction and adaptation strategies to improve the resilience of communities to the negative impacts of floods (Hammond et al., 2015; Nofal & van de Lindt, 2022).
Flood risk mapping is an effective, increasingly used tool in the risk-based approach to flood risk management (Sayers et al., 2013). Flood risk maps visualise the spatial distribution of flood risk, expressed in terms of expected damage and potential consequences for a given flooding event (Merz et al., 2007), and are essential to plan a prompt response to emergencies, prevent occurrence of new risks (by orienting land-use planning and land management), reduce existing risks (through the implementation of protection and mitigation measures), and increase public awareness of flood risk, thereby fostering the adaptation of society to changing risk factors (Martini & Loat, 2007).
On an international level, there exist many examples of flood mapping for purposes of flood risk management (de Moel et al., 2009; Klijn et al., 2008). Among these, the U.S. National Flood Insurance Program (NFIP, 2021; Luke et al., 2018); the French Flood Risk Prevention Plan (Decree 2019-715, 2019; Guillier, 2017); the Flood Risk Management Plan of the Rhine, Germany (ICPR, 2021); the Danube Flood Risk Management Plan (ICPDR, 2021); the plan PLUIES (Flood prevention and control and effects of floods on victims) in Wallonia, Belgium (PLUIES, 2003); the DREAM and UP DREAM programs in the Philippines (Santillan et al., 2016; UP DREAM, 2016); the recent update of hazard and flood risk maps for several thousand kilometres of river courses and coastal sectors in Spain (Olcina-Cantos & Díez-Herrero, 2021). The EU Floods Directive (European Council, 2007) requires member states to produce flood hazard and risk maps as a preparatory step to the development of flood risk management plans (de Moel et al., 2009).
Catalogues of interactive flood maps or databases are often made available on websites as a result of national flood mapping programs (e.g., Environment Agency, 2019; Géorisques, 2020; HORA, 2022; UmweltAtlas, 2022). Flood inundation maps for selected return periods are published in these online resources, thereby providing a flood hazard zonation based on flooding probability. Furthermore, various reports, guidelines and handbooks have been produced with the purpose of guiding flood risk assessment and management, typically targeted to a specific geographic area (e.g., CHARIM, 2021; Díez-Herrero et al., 2009; ESCAP, 1991; FEMA, 2013; FEMA, 2021; INTEGEMS, 2017; LAWA, 2006; Lumbroso et al., 2008; National Research Council, 2009; NSWG, 2005; The Mekong River Commission Secretariat, 2009), or offering an overview of the techniques used in different countries across the world (e.g., Prinos, 2008; Ranzi et al., 2011; van Alphen & Passchier, 2007). Recently, several national and international research programs have been devoted to investigating extreme flood events and promoting advances in methods, strategies, and flood simulation techniques to enhance flood risk management (e.g., FloodRISE: UCI, 2022; FLOODsite: FLOODsite, 2009 and Samuels et al., 2009; KULTURisk: KULTURisk, 2011; IMPACT: Morris & Hassan, 2005).
Flood hazard is defined as the threat represented by a flood of certain frequency and magnitude to a particular location (de Moel et al., 2015; Nofal & van de Lindt, 2022); it is a key component of flood risk and can be evaluated via qualitative, semi-quantitative, or quantitative methods (Chen et al., 2015). Qualitative methods are heuristic and solely based on expert judgement. Semi-quantitative methods are based on the concept of ranking flood hazard by weighting the contributions of different geographic and morphometric factors. Typically, they exploit the potential of GIS (e.g., Albano et al., 2014; Albano et al., 2019; Araújo et al., 2019; Bathrellos et al., 2016; Bhat et al., 2019; Chen et al., 2015; Islam & Sado, 2000; Kittipongvises et al., 2020; Kourgialas & Karatzas, 2011; Kumar, 2016; Skilodimou et al., 2021; Toosi et al., 2019), and are very efficient, especially in large-scale (regional or basin-scale) analysis, or in situations characterised by scarcity of data. Finally, quantitative methods are based on hydrological scenarios and hydraulic modelling, and imply the definition and calculation of a suitable flood hazard index to be referred to in order to draw up a hazard level classification. Flood hazard indexes are usually defined by combining relevant flow parameters; therefore, applying such methods requires setting up complex hydrodynamic models and having a large number of input data available (elevation models, land use and cover data, etc.). In addition, a great computational effort is needed, especially when a large floodable area must be covered, and high accuracy and spatial resolution must be guaranteed (Banks et al., 2014). Figure 1 illustrates the main steps of quantitative flood hazard assessment. The hydrodynamic inundation model, usually based on the two-dimensional shallow water equations (FEMA, 2020; Mudashiru et al., 2021; Néelz & Pender, 2009; Teng et al., 2017), provides a physically based description of the flooding process for selected scenarios and allows predicting the relevant hydraulic parameters needed to characterise flooding intensity. The flooding parameters mostly used to quantify flood hazard are flood depth (FEMA, 2013; Martini & Loat, 2007; Merz et al., 2007; National Research Council, 2009) and flow velocity (Kreibich et al., 2009), taken separately or in combination to define a suitable flood hazard indicator (often, the product of flood depth and flow velocity; e.g., AIDR, 2017; Merz et al., 2007). In particular, flood depth is the most used intensity parameter in flood damage functions (Hammond et al., 2015; Merz et al., 2010; Nofal & van de Lindt, 2022). Other parameters relevant to flooding hazard assessment are flood arrival time, flood duration, flood depth rise rate (Ahmadisharaf et al., 2015; de Bruijn et al., 2015; FEMA, 2013; Merz et al., 2007; Muñoz et al., 2020; Naeem et al., 2021; Santillan et al., 2016; Vu & Ranzi, 2017), as well as standing water depth following the flood, erosive potential of the flooding (Luke et al., 2018), and debris or contaminant load.
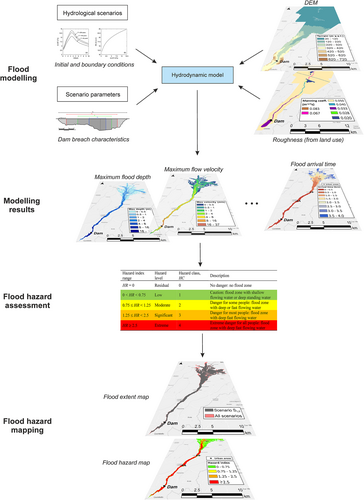
Typical outcomes of quantitative flood hazard assessment are inundation and flood hazard maps (Figure 1), which depict the extent of the areas potentially subject to flooding and the spatial distribution of the flood hazard, respectively, for a selected hydrological scenario (Carrasco et al., 2012; de Moel et al., 2009; Merz et al., 2007; van Alphen & Passchier, 2007). However, lack of standardisation can be observed in flood hazard mapping (de Moel et al., 2009; van Alphen et al., 2009; van Alphen & Passchier, 2007). Probabilistic approaches have recently been proposed, which, unlike deterministic ones, provide information about the uncertainty associated with flood hazard predictions (e.g., Beven et al., 2015; Di Baldassarre et al., 2010; D'Oria et al., 2019; Vorogushyn et al., 2010).
This article systematically reviews existing quantitative flood hazard assessment methods either prescribed by national government authorities or developed by academic institutions during research programs, with a special focus on the criteria proposed for flood hazard level classification. Despite recent valuable efforts to provide critical reviews on various aspects of flood risk modelling (e.g., Cea & Costabile, 2022; Moreira et al., 2021), a comprehensive review on quantitative flood hazard assessment methods is still missing in the literature. Stability conditions for people and vehicles are not considered here since they identify two possible states only (i.e., safe/unsafe) without introducing an actual classification in different flooding hazard levels. Besides, extensive reviews of these stability conditions are already available, for both people (Jonkman & Penning-Rowsell, 2008; Xia et al., 2014) and vehicles (Bocanegra et al., 2020; Martínez-Gomariz et al., 2018; Shah et al., 2021), often with particular reference to urban flooding (Mignot & Dewals, 2022).
The methods reviewed here are categorised in terms of basic approach (heuristic, conceptual, empirical); exposed element (people, buildings, vehicles); and field of application (riverine or coastal flooding, dam-break, levee breach, debris flow, etc.). For each method, the indicator used to express flood hazard is specified along with the parameters involved.
- offer an overview of the state of art in quantitative flood hazard assessment by presenting an updated list of quantitative methods currently used for flood hazard ranking and mapping based on hydrodynamic modelling;
- describe the main characteristics of these methods in terms of basic approach, jeopardised elements, and application fields;
- help practitioners and modellers to identify the most suitable flood hazard ranking method for the application of interest by providing essential information to compare the different classification methods and evaluate their potential and limitations;
- provide relevant references in which the flood hazard ranking methods are proposed, analysed, or applied;
- discuss present issues and future challenges in quantitative flood hazard assessment;
- serve as an essential basis for the development of new and improved flood hazard assessment methods.
2 STATE OF THE ART ON QUANTITATIVE FLOOD HAZARD ASSESSMENT METHODS
The quantitative flood hazard methods retrieved during the literature review are divided into two main categories and listed in two distinct tables. Table 1 shows the methods based on flood intensity only, which do not explicitly include information on frequency of flooding in the flood hazard classification. The resulting hazard maps represent the spatial distribution of the hazard index for a specific flood event (historical or synthetic). Table 2 includes the methods that take into account probabilistic information (i.e., the return period of the flood event or the probability of the flooding scenario), as well as the intensity of flooding. In this case, the flooding hazard maps represent the spatial distribution of flood hazard assessed on the basis of intensity-probability matrices. The methods usually adopted for the identification of river hazard zones also belong to this category. In both tables, the methods are listed in chronological order.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
|---|---|---|---|---|---|---|---|---|
| No. | Institution/country | References | Approach | Variables involved | Flood hazard indicators | Flood hazard classification | Exposed elements | Applications |
| 1 | ACER, USA | ACER (1988) | Empirical | Flood depth h, flow velocity v | h, v (graphical depth-velocity relationships) | Graphical partition (depending on the jeopardised element): Low danger zone Judgement zone High danger zone |
People, houses on foundation, mobile homes, passenger, vehicles | Flooding (Di Baldassarre et al., 2009; Musolino et al., 2020); levee breach (Mazzoleni et al., 2014); dam-break (Ahmadisharaf et al., 2013) |
| 2 | N/A | Abt et al. (1989) | Empirical | Flood depth h, flow velocity v, mass of a person mp, height of a person hp |
vh | Manoeuvrability and stability condition: vh < f(mp, hp) vh < 0.0929[exp(0.01927mphp + 1.088)]2 (vh in m2/s, mp in kg, and hp in m) |
People (adults) | Flooding |
| 3 | Ministry of Environment, Spain | Ministerio de Medio Ambiente (1996) | Heuristic | Flood depth h, flow velocity v |
h, v (graphical depth-velocity relationships) |
Graphical partition of the h-v plane (different for urban and rural areas): Low danger zone Judgement zone High danger zone |
N/A | Dam-break (Musolino et al., 2020) |
| 4 | France | MATE-METL (1999) | Heuristic | Flood depth h |
h | Low or Medium: h < 1 m High: h ≥ 1 m |
N/A | Flooding |
| 5 | France | MATE-METL (1999) | Heuristic | Flood depth h, flow velocity v |
h, v | Hazard matrix in which four hazard levels are defined (very high, high, medium, low) as a combination of: Three flood depth classes: h < 0.5 m 0.5 m ≤ h < 1 m h ≥ 1 m Three flow velocity classes: Low: v < 0.2 m/s Medium: 0.2 m/s ≤ v < 0.5 m/s High: v ≥ 0.5 m/s |
N/A | Flooding (flash flood) |
| 6 | RESCDAM Project (Development of rescue actions based on dam-break flood analysis) | Karvonen et al. (2000) | Empirical | Flood depth h, flow velocity v, mass of a person mp, height of a person hp |
vh | Manoeuvrability and stability condition: vh < f(mp, hp) (being f a function of flow and environmental conditions: good, normal, poor; vh in m2/s, mp in kg, and hp in m) Good environmental conditions: vh < 0.006 mphp + 0.3 Normal environmental conditions: vh < 0.004 mphp + 0.2 Poor environmental conditions: vh < 0.002 mphp + 0.1 |
People (adults) | Flooding (in urban areas; Xia et al., 2011); dam-break (Xia et al., 2011) |
| 7 | Finland; ISPRA, Italy |
Maijala (2001), Clausen and Clark (1990), ISPRA (2012) | Empirical | Flood depth h, flow velocity v |
vh, v | Damage classification based on the building type: - Not anchored wooden buildings Partial damage: vh ≥ 2 m2/s Total damage: vh ≥ 3 m2/s - Anchored wooden buildings Partial damage: vh ≥ 3 m2/s Total damage: vh ≥ 7 m2/s - Concrete and masonry buildings Inundation damage: v < 2 m/s and vh < 3 m2/s (Clausen & Clark, 1990) Partial damage: v ≥ 2 m/s and vh ≥ 3 m2/s Total damage: v ≥ 2 m/s and vh ≥ 7 m2/s |
Buildings | Flooding; dam-break (Clausen & Clark, 1990) |
| 8 | N/A | Aleotti et al. (2004) | Heuristic | Flood depth h, flow velocity v |
h, v | Very low: h < 0.25 m and v < 0.25 m/s Low: (0.25 m ≤ h < 0.5 m and v < 0.5 m/s) or (h ≤ 0.25 m and 0.25 m/s ≤ v < 0.5 m/s) Medium: (0.5 m ≤ h < 1 m and v < 1 m/s) or (h ≤ 0.5 m and 0.5 m/s ≤ v < 1 m/s) High: h ≥ 1 m or v ≥ 1 m/s |
Buildings | Flooding (in alluvial fans; Aleotti et al., 2004) |
| 9 | N/A | Penning-Rowsell et al. (2005), DEFRA Environment Agency (2006a) | Heuristic | Flood depth h, flow velocity v, debris flow parameter DF |
HR = h(v + 1.5) + DF DF = 0, 1, 2 (depending on the probability that debris will lead to a significant greater hazard: 0 — unlikely; 1 — possible; 2 — likely) |
Very high: HR ≥ 10 High: 7 < HR < 10 Medium/Low: HR < 7 |
People | Flooding (Penning-Rowsell et al., 2005) |
| 10 | N/A | Tingsanchali and Karim (2005) | Empirical | Flood depth h, flooding duration d |
h, d | Based on flood intensity: Low: h < 0.6 m (0.8 m) Medium: 0.6 (0.8) m < h < 1 m High: 1 m < h < 3.5 m Very high: h > 3.5 m Based also (qualitatively) on flood duration: Low: Short duration Medium: Medium duration High: Long duration Very high: Very long duration |
N/A | Flooding (Shrestha & Lohpaisankrit, 2017; Tansar et al., 2020; Tingsanchali & Karim, 2010) |
| 11 | DEFRA, UK | Wade et al. (2005), DEFRA Environment Agency (2006a), DEFRA Environment Agency (2006b) | Empirical | Flood depth h, flow velocity v, debris flow parameter DF |
HR = h(v + 0.5) + DF DF = 0, 0.5, 1 (depending on the probability that debris will lead to a significant greater hazard) |
Low: HR < 0.75 Moderate: 0.75 ≤ HR < 1.25 Significant: 1.25 ≤ HR < 2.5 Extreme: HR ≥ 2.5 |
People | Flooding (Kvočka et al., 2016; Kvočka et al., 2018; Musolino et al., 2020); |
| 12 | N/A | van Alphen and Passchier (2007), Luke et al. (2018) | Heuristic | Flood depth h | h | Classification based on flood depth in relation to a human body scale (van Alphen & Passchier, 2007): Dark blue: ankle-deep Light blue: knee-deep Light rose: hip-deep Orange: head-deep Red: submerged Human body scale classification used by Luke et al. (2018): 1 cm — ankle (0.01 m < h < 0.11 m) Ankle — knee (0.11 m < h < 0.45 m) Knee — waist (0.45 m < h < 1 m) Waist — head (1 m < h < 1.7 m) Above head (h > 1.7 m) |
People | Flooding (Luke et al., 2018; Sanders et al., 2020; van Alphen & Passchier, 2007); levee breach (Mazzoleni et al., 2014) |
| 13 | N/A | Aureli et al. (2008) |
Heuristic | Flood depth h, Froude number Fr |
Total depth D = h(1 + 2Fr2)1/2 |
Low: D < 0.5 Medium: 0.5 ≤ D < 1 High: 1 ≤ D < 1.5 Very high: D ≥ 1.5 |
N/A | Flooding; levee breach (Ferrari et al., 2019; Ferrari et al., 2020); dam-break (Aureli et al., 2008) |
| 14 | N/A | Cançado et al. (2008) | Heuristic | Flood depth h, flow velocity v |
h, v | Low: 0.1 m < h < 0.5 m and 0.1 m/s < v < 0.5 m/s Medium: 0.5 m < h < 1.5 m or 0.5 m/s < v < 1.5 m/s High: h > 1.5 m or v > 1.5 m/s |
N/A | Flooding (in urban areas; Cançado et al., 2008; Hurtado-Pidal et al., 2020) |
| 15 | Environmental Assessment Agency, Netherlands | Pieterse et al. (2009) | Heuristic | Flood depth h, arrival time ta |
h, ta |
Hazard matrix in which nine hazard levels are defined as a combination of three water depth classes (shallow, intermediate, deep) and three flood arrival time classes (slow, intermediate, rapid) | N/A | Flooding; levee breach (de Bruijn et al., 2015) |
| 16 | Australian Government | Cox et al. (2010) | Empirical | Flood depth h, flow velocity v |
h, v, vh | Different classifications (in four hazard classes) depending on the type of person (infants, children, adults). For example, for adults: for h < 1.2 m and v < 3 m/s, Low: vh < 0.4 m2/s Moderate: 0.6 < vh < 0.8 m2/s Significant: 0.8 < vh < 1.2 m2/s Extreme: vh > 1.2 m2/s; otherwise: Extreme |
People (infants, children, and adults) |
Flooding (Musolino et al., 2020; Smith et al., 2014) |
| 17 | Australian Government | Shand et al. (2011), Smith et al. (2014) | Empirical | Flood depth h, flow velocity v |
h, v, vh | Different stability conditions depending on the vehicle type (small or large or 4WD) | Vehicles | Flooding |
| 18 | N/A | Xia et al. (2011) | Conceptual/empirical | Flow velocity U, critical velocity Uc |
Degree of hazard HD = min(1; U/Uc) |
HD → 0: element safe HD → 1: element in danger |
People, vehicles | Flooding (in urban areas; Xia et al., 2011); dam-break (Xia et al., 2011) |
| 19 | N/A | Masood and Takeuchi (2012) | Heuristic | Flood depth h | Hazard index H (ranging from 0 to 5) | H = 0: h = 0 m H = 1: 0 m < h < 1 m H = 2: 1 m ≤ h < 2 m H = 3: 2 m ≤ h < 3 m H = 4: 3 m ≤ h < 4 m H = 5: h ≥ 4 m |
N/A | Flooding (Masood & Takeuchi, 2012) |
| 20 | National Disaster Management Authority, Pakistan; National Weather Service, USA |
ERG (2013), NDMA (2016) | Heuristic | Flood depth h | h | Hazard zone 1 (Low): h < 3 ft (≈1 m) Hazard zone 2 (Medium/Moderate): 3 ft (≈1 m) < h < 6 ft (≈2 m) Hazard zone 3 (High): 6 ft (≈2 m) < h < 9 ft (≈3 m) Hazard zone 4 (Very high/Extreme): h > 9 ft (≈3 m) (in NDMA, 2016, calculated for T = 10, 25, 50, and 100 years) |
N/A | Flooding (Farooq et al., 2019 [with a reclassification of the hazard zones]; Longenecker et al., 2020) |
| 21 | N/A | Russo et al. (2013) | Empirical | Flood depth h, flow velocity v |
h, v | For 0.09 m < h < 0.16 m: High: v ≥ 1.88 m/s Moderate: 1.5 m/s ≤ v < 1.88 m/s Low: v < 1.5 m/s |
Pedestrians (in flooded streets) |
Flooding (Garrote et al., 2021) |
| 22 | N/A | Mani et al. (2014) | Empirical | Flood depth h, flow velocity v, flooding duration d |
h, vh, d |
Very low: h < 0.2 m and vh < 0.3 m2/s and d < 50 h Low: 0 < h < 0.2 m and 0 < vh < 0.3 m2/s and d > 50 h Low: 0.2 m < h < 0.6 m or 0.3 m2/s < vh < 0.7 m2/s and 0 < d < 25 h Medium: 0.2 m < h < 0.6 m or 0.3 m2/s < vh < 0.7 m2/s and d > 25 h Medium: 0.6 m < h < 1.5 m or 0.7 m2/s < vh < 1.2 m2/s and 0 < d < 25 h High: 0.6 m < h < 1.5 m or 0.7 m2/s < vh < 1.2 m2/s and d > 25 h High: 1.5 m < h < 3.5 m or 1.2 m2/s < vh < 1.6 m2/s and 0 < d < 25 h Very high: 1.5 m < h < 3.5 m or 1.2 m2/s < vh < 1.6 m2/s and d > 25 h Very high: h > 3.5 m or vh > 1.2 m2/s and d > 0 |
N/A | Flooding (Mani et al., 2014) |
| 23 | N/A | Mani et al. (2014) | Empirical | Flood depth h, flow velocity v, flooding duration d |
h, vh, d | Flood hazard classification based on flood variables considered individually: h Very low: h < 0.2 m Low: 0.2 m < h < 0.6 m Medium: 0.6 m < h < 1.5 m High: 1.5 m < h < 3.5 m Very high: h > 3.5 m vh Very low: vh < 0.3 m2/s Low: 0.3 m2/s < vh < 0.7 m2/s Medium: 0.7 m2/s < vh < 1.2 m2/s High: 1.2 m2/s < vh < 1.6 m2/s Very high: vh > 1.6 m2/s d Very low: d < 25 h Low: 25 h < d < 50 h Medium: 50 h < d < 100 h High: 100 h < d < 175 h Very high: d > 175 h |
N/A | Flooding |
| 24 | Australian Government | Smith et al. (2014) |
Empirical | Flood depth h, flow velocity v |
h, v, vh | H1: vh ≤ 0.3 m2/s and h < 0.3 m and v < 2 m/s H2: (vh ≤ 0.6 m2/s and h < 0.5 m and v < 2 m/s) \ H1 H3: (vh ≤ 0.6 m2/s and h < 1.2 m and v < 2 m/s) \ H2 H4: (vh ≤ 1 m2/s and h < 2 m and v < 2 m/s) \ H3 H5: (vh ≤ 4 m2/s and h < 4 m and v < 4 m/s) \ H4 H6: vh > 4 m2/s or h > 4 m or v > 4 m/s |
People, vehicles, buildings | Flooding (AIDR, 2017; Costabile et al., 2020; Costabile et al., 2021); dam-break (Abdulrahman et al., 2022; CDSO, 2020) |
| 25 | Australian Government | Smith et al. (2014) | Empirical | Flood depth h, flow velocity v |
h, v, vh | Different stability conditions depending on the building type | Buildings | Flooding |
| 26 | Ministry of Land, Infrastructure and Transport, Japan; Korea |
MLIT (2015), Lee et al. (2019), Udmale et al. (2019) | Heuristic | Flood depth h | h | Very low: h < 0.5 m Low: 0.5 m < h < 1 m Medium: 1 m < h < 2 m High: 2 m < h < 5 m Extreme: h > 5 m In Japan and Korea, flood maps are produced by the central and local governments, and the hazard classification may vary |
People (evacuation) |
Flooding (Mihu-Pintilie et al., 2019; Ongdas et al., 2020; Quiroga et al., 2016); levee breach (Kim et al., 2019) |
| 27 | N/A | Milanesi et al. (2015) | Conceptual | Admissible flood depth h (function of flow velocity v), sliding depth hs, toppling depth ht, drowning depth hd |
h = min(hs(v), ht(v), hd) |
Flood hazard classification into three classes (low, medium, high) based on two different stability thresholds for children and adults | People (children and adults) | Flooding (in flat and mountain areas and in the presence of debris) |
| 28 | N/A | Arrighi et al. (2016) | Empirical | Froude number Fr, height of the vehicle HV, height of the planform hc, car width l, car length L, water density ρ, car density ρc, flow orientation β |
Mobility parameter θVcr/θV θV = f(HV, hc, l, L, ρ, ρc, β) θVcr = f(Fr2) |
The (colour) scale of the parameter goes from 0.25 (very low hazard) up to 1.5 (very high hazard). Areas where θVcr/θV = 1 are those likely to be prone to incipient motion of vehicles (high hazard) |
Vehicles | Flooding (Arrighi et al., 2016) |
| 29 | N/A | Kramer et al. (2016) | Empirical | Flood depth h, flow velocity v |
Total head Ht = h + v2/(2g) |
For passenger cars: Low: Ht ≤ 0.3 m Transition: 0.3 m < Ht < 0.4 m High: Ht ≥ 0.4 m For emergency vehicles: Low: Ht ≤ 0.6 m Transition: 0.6 m < Ht < 0.7 m High: Ht ≥ 0.7 m |
Vehicles | Flooding (in urban areas) |
| 30 | N/A | Kvočka et al. (2016) | Conceptual | Flow velocity v, toppling incipient velocity vt, sliding incipient velocity vs |
HR = min[1, v/min(vt, vs)] | Low: HR < 0.3 Moderate: 0.3 ≤ HR < 0.6 Significant: 0.6 ≤ HR < 1 Extreme: HR = 1 |
People | Flooding (Kvočka et al., 2018) |
| 31 | N/A | Silvestro et al. (2016) | Empirical/heuristic | Flood depth h, flow velocity v |
h, v, vh | Low: (h < 0.2 m and vh < 1.35 m2/s) or (0.2 m < h ≤ 0.5 m and v < 1 m/s) Moderate: (h < 0.2 m and vh > 1.35 m2/s) or (0.2 m < h ≤ 0.5 m and v > 1 m/s and vh < 1.35 m2/s) or (h > 0.5 m and vh < 1.35 m2/s) High: h ≥ 0.2 m and vh > 1.35 m2/s Very high: vh ≥ 5 m2/s and v ≥ 2 m/s |
People | Flooding (Silvestro et al., 2016) |
| 32 | Philippines | UP DREAM (2016) | Heuristic | Flood depth h | h | Low: h ≤ 0.5 m Medium: 0.5 m < h ≤ 1.5 m High: h > 1.5 m |
N/A | Flooding (Santillan et al., 2016) |
| 33 | N/A | Vojtek and Vojteková (2016) | Empirical | Flood depth h, flow velocity v |
FI = 0 if h = 0 m FI = h if h > 0 m and v ≤ 1 m/s FI = vh if v > 1 m/s |
Low: FI ≤ 0.3 Medium: 0.3 < FI ≤ 1 High: FI > 1 |
People, buildings | Flooding (Vojtek & Vojteková, 2016) |
| 34 | N/A | Álvarez et al. (2017) | Heuristic | Flood depth h, flow velocity v |
h, v, vh | Low: h < 0.5 m or v < 0.5 m/s or vh < 0.25 m2/s Medium: 0.5 m ≤ h ≤ 1 m or 0.5 m/s ≤ v ≤ 1 m/s or 0.25 m2/s ≤ vh ≤ 0.5 m2/s High: h > 1 m or v > 1 m/s or vh > 0.5 m2/s |
N/A | Dam-break (Álvarez et al., 2017) |
| 35 | N/A | Farid et al. (2017) | Heuristic | Flood depth h | h | Low: h < 0.8 m Moderate: 0.8 m < h < 1.2 m High: h > 1.2 m |
N/A | Flooding (in urban areas; Farid et al., 2017) |
| 36 | Germany | Krieger et al. (2017) | Heuristic | Flood depth h | h | Low: h < 0.1 m Moderate: 0.1 m < h < 0.3 m High: 0.3 m < h < 0.5 m Very high: h > 0.5 m |
Buildings | Flooding (in urban areas; Bhola et al., 2020) |
| 37 | Federal Ministry for Agriculture, Forestry, Environment and Water Management, Austria | Neuhold et al. (2018), van Alphen and Passchier (2007) | Heuristic | Flood depth h, flow velocity v |
h, v |
High hazard (red zone): h > 1.5−0.5v [m/s] or v > 2 m/s Medium hazard (yellow zone): h < 1.5−0.5v [m/s] and v < 2 m/s (calculated for the return period T = 100 years) |
N/A | Flooding (van Alphen & Passchier, 2007) |
| 38 | Malaysia | Ghazali and Osman (2019) | Heuristic | Flood depth h | h | Low: h < 0.5 m Moderate: 0.5 m ≤ h ≤ 1.2 m High: 1.2 m < h ≤ 2.5 m Very high: h > 2.5 m (calculated for T = 5, 10, 20, 50, and 100 years) |
People | Flooding (Ghazali & Osman, 2019) |
| 39 | N/A | Khaing et al. (2019) | Heuristic | Flood depth h | h | Very low: h ≤ 0.2 m Low: 0.2 m < h ≤ 0.5 m Medium: 0.5 m < h ≤ 1 m High: 1 m < h ≤ 2 m Very high: 2 m < h ≤ 3 m Extremely high: h > 3 m |
N/A | Flooding (Khaing et al., 2019) |
| 40 | N/A | Patra et al. (2019) | Heuristic | Flood depth h, flow velocity v, time to peak tp |
h, v, tp | Low: h < 0.25 m or v < 0.2 m/s or tp > 12 h Medium: 0.25 m ≤ h < 1 m or 0.2 m/s ≤ v < 0.8 m/s or 6 h < tp ≤ 12 h High: 1 m ≤ h < 2 m or 0.8 m/s ≤ v < 1.2 m/s or 3 h < tp ≤ 6 h Very high: 2 m ≤ h < 5 m or 1.2 m/s ≤ v < 2 m/s or 1 h < tp ≤ 3 h Extreme: h > 5 m or v > 2 m/s or tp ≤ 1 h |
N/A | Dam-break (Patra et al., 2019) |
| 41 | N/A | Al Baky et al. (2020) | Heuristic | Flood depth h | h | Low: h ≤ 2 m Medium: 2 m < h ≤ 4 m High: h > 4 m (calculated for different return periods T = 2.33, 10, 20, 50, and 100 years) |
N/A | Flooding (Al Baky et al., 2020) |
| 42 | N/A | Evans et al. (2020) | Heuristic | Flood depth h | h | Low: h ≤ 0.1 m Medium: 0.1 m ≤ h < 0.3 m High: h ≥ 0.3 m |
Vehicles, traffic flows | Flooding in urban areas (Evans et al., 2020; Padulano et al., 2021) |
| 43 | Kazakhstan | Ongdas et al. (2020) | Heuristic | Flood depth h, flow velocity v, flooding duration d |
h, v, d | Low: h < 1 m, v < 0.01 m/s, d < 5 h Medium: 1 m < h < 3 m, 0.01 m/s < v < 0.05 m/s, 5 h < d < 24 h High: 3 m < h < 5 m, 0.05 m/s < v < 0.1 m/s, 24 h < d < 72 h Crisis: 5 m < h < 7 m, 0.1 m/s < v < 1 m/s, 72 h < d < 120 h Catastrophic: h > 7 m, v > 1 m/s, d > 120 h |
N/A | Flooding (Ongdas et al., 2020) |
| 44 | N/A | Liu et al. (2021) | Empirical | Flood depth h | h | Extremely low: h ≤ 0.3 m Low: 0.3 m < h ≤ 0.5 m Medium: 0.5 m < h ≤ 1 m High: 1 m < h ≤ 3 m Extremely high: h > 3 m |
People | Flooding (in urban areas; Liu et al., 2021) |
| 45 | N/A | Phakonkham et al. (2021) | Heuristic | Flood depth h | Hazard index H (ranging from 0 to 1 according to a h-H relationship) | Small (H ≤ 0.25): h ≤ 0.3 m Medium (0.25 < H ≤ 0.5): 0.3 m < h ≤ 0.6 m High (0.5 < H ≤ 0.75): 0.6 m < h ≤ 2 m Very high (H > 0.75): h > 2 m |
N/A | Flooding (Phakonkham et al., 2021) |
| 46 | N/A | Psomiadis et al. (2021) | Heuristic | Flood depth h, flow velocity v |
vh | Low/Medium: vh < 2.1 m2/s High: 2.1 m2/s ≤ vh ≤ 3 m2/s Very high: vh > 3 m2/s |
N/A | Dam-break (Psomiadis et al., 2021) |
| 47 | N/A | Lazzarin et al. (2022) | Heuristic | Flood depth h, Froude number Fr |
Impact parameter W = (h/hW)α× (1 + βFr2) where hW: reference water depth; α and β: calibration factors Special cases (Kreibich et al., 2009): α = 1 and β = 0: W expresses flow depth; α = 1 and β = 1/2: W expresses energy head; α = 2 and β = 2: W expresses flow force |
N/A | People, vehicles, buildings | Flooding (Lazzarin et al., 2022) |
| 48 | N/A | Tingsanchali and Promping (2022) | Heuristic | Flood depth h, flow velocity v, flooding duration d |
Flood hazard index, FHI = α FHId + β FHIh + μ FHIv where FHId = 1 for d ≤ 60 h FHId = 2 for 60 h < d ≤ 100 h FHId = 3 for 100 h < d ≤ 120 h FHId = 4 for 120 h < d ≤ 140 h FHId = 5 for d > 140 h FHIh = 1 for h ≤ 0.6 m FHIh = 2 for 0.6 m < h ≤ 2 m FHIh = 3 for 2 m < h ≤ 2.25 m FHIh = 4 for 2.25 m < h ≤ 2.5 m FHIh = 5 for h > 2.5 m FHIv = 1 for v ≤ 0.1 m/s FHIv = 2 for 0.1 m/s < v ≤ 0.5 m/s FHIv = 3 for 0.5 m/s < v ≤ 0.6 m/s FHIv = 4 for 0.6 m/s < v ≤ 0.7 m/s FHIv = 5 for v > 0.7 m/s α, β, μ: weighting factors (summing to 1) |
Very low: FHI ≤ 1 Low: 1 < FHI ≤ 2 Medium: 2 < FHI ≤ 3 High: 3 < FHI ≤ 4 Very high: 4 < FHI ≤ 5 |
N/A | Flooding (in urban areas; Tingsanchali & Promping, 2022) |
| 49 | N/A | García-Martínez and López (2005) | Heuristic | Flood depth h, flow velocity v |
h, vh | For flooding: Low: 0.1 m < h < 0.5 m and vh < 0.5 m2/s Medium: 0.5 m < h < 1.5 m or 0.5 m2/s < vh < 1.5 m2/s High: h > 1.5 m or vh > 1.5 m2/s For mud or debris flows: Low: 0.2 m < h < 1 m and vh < 0.2 m2/s Medium: 0.2 m < h < 1 m and 0.2 m2/s < vh < 1 m2/s High: h > 1 m or vh > 1 m2/s |
N/A | Mud or debris flow; flooding (Erena et al., 2018) |
| 50 | Icelandic Meteorological Office | Pagneux and Roberts (2015) | Heuristic | Flood depth h, flow velocity v, debris and sediment load index l (= 0 or 1), water temperature index t (= 0 or 1) |
h, vh, l, t | Extreme: vh ≥ 7 m2/s (or, when flow velocities are not known, h > 6 m) High: vh > 1.3 m2/s (or h > 1 m) or l = 1 or t = 1 Moderate: 0.25 m2/s ≤ vh ≤ 1.3 m2/s (or 0.5 m ≤ h ≤ 1 m) and l = 0 and t = 0 Low: vh < 0.25 m2/s (or h < 0.5 m) |
N/A | Jökulhlaups (volcanogenic floods; Pagneux & Roberts, 2015) |
- Note: N/A = not applicable; not available.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) |
|---|---|---|---|---|---|---|---|---|
| No. | Institution/country | References | Approach | Variables involved | Flood hazard indicators | Flood hazard classification | Exposed elements | Applications |
| 1 | USACE, USA | USACE (1995) | Heuristic | Flood depth h, return period T |
h, T | Primary flood hazard area: h > 0 for T = 100 years Secondary flood hazard area: outside |
N/A | Riverine flooding |
| 2 | Po River Basin Authority, Italy | Po River Basin Authority (1999) | Heuristic | Flood depth h, flow velocity v, flow discharge Q, return period T |
h, v, Q, T | Zone A: h > 0 for T = 200 years and Q = 0.8QT = 200, v > 0.4 m/s Zone B: (h > 0 for T = 200 years) \ Zone A Zone C: (h > 0 for T = 500 years) \ (Zone A ∪ Zone B) |
N/A | Riverine flooding |
| 3 | Czech Republic | Beffa (2000), Dráb and Říha (2010) | Heuristic | Flood depth h, flow velocity v, return period T |
R = (0.3 + 1.35IP)p with IP = 0 if h = 0, IP = h if h > 0 and v ≤ 1 m/s, IP = vh if h > 0 and v > 1 m/s; p = 1 – e−1/T |
Four flood hazard categories calculated for different return periods T (5, 20, 100, 500 years): High: R ≥ 0.1 or IP ≥ 2 Medium: 0.01 ≤ R < 0.1 Low: R < 0.01 Residual: p < 0.0033 |
N/A | Flooding (Klemešová, 2016) |
| 4 | South Africa (Vaal River) | Stephenson (2002) | Heuristic | Flood depth h, flow velocity v, return period T |
HRI = HI × RI with HI (Hazard Index, ranging from 1 to 3) being a function of h, v and vh, and RI (Risk Index, ranging from 0 to 2) being a function of T | Matrix method, which defines six hazard classes ranging from 0 to 6 (excluding 5) | Buildings vehicles, people |
Flooding |
| 5 | Government of Wallonia, Belgium | PLUIES (2003) | Heuristic | Flood depth h, return period T (flow velocity v, flood duration d) |
h, T (v, d) |
Hazard matrix in which three hazard levels are defined (high, medium, low) as a combination of: Three submersion classes: Low: h < 0.3 m Medium: 0.3 m ≤ h < 1.3 m High: h ≥ 1.3 m Three flood recurrence classes: Frequent: T = 25 years Occasional: T = 50 years Rare: T = 100 years Corrective factors are applied to intensity if v > 1 m/s or d > 3 days and to recurrence if flood defences are present |
N/A | Flooding (Beckers et al., 2013; van Alphen & Passchier, 2007) |
| 6 | Sicilian District Basin Authority, Italy | Sicilian Region (2004) |
Heuristic | Flood depth h, return period T |
h, T | Hazard matrix in which four hazard levels are defined (P1, P2, P3, and P4, for increasing hazard levels) Four flood magnitudes: Very high: h > 2 m High: 1 m < h < 2 m Average: 0.3 m < h < 1 m Low: h < 0.3 m Three flood frequencies: Frequent: T = 50 years Average: T = 100 years Rare: T = 300 years |
N/A | Flooding |
| 7 | Adige River Basin Authority, Italy | Adige River Basin Authority (2005) | Heuristic | Flood depth h, flow velocity v, return period T |
h, v, T | Four different classes (low, moderate, high, very high) according to the values attained by h and v calculated for different return periods T (30, 100, and 200 years) | N/A | Flooding; levee breach (Maranzoni et al., 2022) |
| 8 | Germany | LAWA (2006) | Heuristic | Flood depth h, flow velocity v, return period T |
h, v, T | Hazard matrix in which four hazard levels are defined (extreme, moderate, low, residual) as a combination of: Three flood magnitudes: - In flat areas: High: h > 2 m Medium: 0.5 m < h < 2 m Low: h < 0.5 m - In steep areas: High: v > 2 m/s Medium: 0.5 m/s < v < 2 m/s Low: v < 0.5 m/s Four flood probabilities: High: T = 20 years Medium: 20 < T < 100 years Low: T = 100 years Residual: T = 200 years |
N/A | Flooding |
| 9 | Netherlands | van Alphen and Passchier (2007) | Heuristic | Flood depth h, return period T |
HR | HR = 0 if h < 1 m HR = 1 if h > 1 m for T = 4000 years |
N/A | Flooding (van Alphen & Passchier, 2007) |
| 10 | Mosel Basin, Rheinland-Pfalz, Germany | van Alphen and Passchier (2007) | Heuristic | Flood depth h, flow velocity v, return period T |
Flood intensity I(h, v), T | Hazard matrix in which four hazard levels are defined (high, moderate, low, residual) as a combination of: Three flood magnitudes: High, average, low Four flood frequencies: Frequent: T = 50 years Average: T = 100 years Rare: T = 200 years Residual: T > 200 years (extreme) |
People, animals, property |
Flooding (van Alphen & Passchier, 2007) |
| 11 | Switzerland | Loat and Petrascheck (2008), Loat (2010) | Empirical | Flood depth h, flow velocity v, return period T |
h, vh, T | Hazard matrix in which four hazard levels are defined (high, moderate, low, residual) as a combination of: Three flood magnitudes: High: h > 2 m or vh > 2 m2/s Average: 0.5 m < h < 2 m or 0.5 m2/s < vh < 2 m2/s Low: h < 0.5 m or vh < 0.5 m2/s Four flood frequencies: Frequent: T < 30 years Average: 30 < T < 100 years Rare: 100 < T < 300 years Residual: T > 300 years |
People, animals |
Flooding (Ţîncu et al., 2018; van Alphen & Passchier, 2007; Werren et al., 2016) |
| 12 | Spanish Geological Survey | Díez-Herrero et al. (2009) | Heuristic | Flood depth h, flow velocity v, return period T |
h, v, vh, T | High hazard zone: h ≥ 1 m or v ≥ 1 m/s or vh ≥ 0.5 m2/s (T = 100 years) Medium hazard zone: h < 1 m and v < 1 m/s and vh < 0.5 m2/s (T = 100 years) Low hazard zones: h ≈ 0 and v ≈ 0 (T = 500 years) |
People | Flooding |
| 13 | N/A | Aronica, Candela, et al. (2012) |
Empirical | Flood depth h, flow velocity v, return period T |
h, vh, T | Different hazard classes (H1, H2, H3, H4, from low to high) depending on T (50, 100, and 300 years). Graphical partition based on: h < 0.3 m, vh < 0.7 m2/s, vh > 0.7 m2/s, h > 1.5 m | N/A | Flooding (Aronica, Franza, et al., 2012; Garrote et al., 2021) |
| 14 | Netherlands | de Bruijn et al. (2015) | Conceptual/heuristic | Flood depth h, flow velocity v, water level rise rate dh (over the first 1.5 m), flood scenario probability Pi, evacuation fraction fevacuation, flee fraction ffleeing |
FFH (flood fatality hazard) | FFH = FD = 1 for vh ≥ 7 m2/s and v > 2 m/s FD = ΦN[(ln(h) – 7.60)/2.75] for h < 2.1 m or dh < 0.5 m/h FD = ΦN[(ln(h) – 1.46)/0.28] for h > 2.1 m and dh < 4.0 m/h where ΦN is the cumulative standard normal distribution function |
People | Flooding; levee breach (de Bruijn et al., 2015) |
| 15 | Netherlands | de Bruijn et al. (2015) | Conceptual/heuristic | Flood depth h, flood scenario probability Pi |
FDH (flood damage hazard) | FDH = VD is a (graphic) damage function of h depending on the type of building |
Buildings, infrastructure | Flooding; levee breach (de Bruijn et al., 2015) |
| 16 | Castile and León Region, Spain | Garrote et al. (2020) | Heuristic | Flood depth h, return period T |
h, T | Hazard matrix in which six hazard levels are defined (extreme, high, medium-high, medium, medium-low, low) as a combination of: Flood type (flash/normal flood) and basin area (small/large basin) Four flood depth classes: h < 0.9 m 0.9 m ≤ h < 1.8 m 1.8 m ≤ h ≤ 3.6 m h > 3.6 m Three flood recurrence classes: Frequent: T = 10 years Average: T = 100 years Rare: T = 500 years |
Cultural heritage sites | Flooding (Garrote et al., 2020) |
| 17 | FEMA, USA | FEMA (2021) | Heuristic | Flood depth h, return period T |
h, T | Zone A (areas of special flood hazards) h > 0 for T = 100 years in floodplains [Zones AO and AH: 0.3 m < h < 0.9 m for T = 100 years, for areas of ponding or sloping terrain, respectively] Zone B or X-shaded (areas of moderate flood hazards): (h > 0 for T = 500 years) \ Zone A Zone C or X-unshaded (areas of minimal flood hazards): outside Zones A and B Note: Zone A is named Zone V along coasts |
N/A | Flooding |
| 18 | N/A | Efstratiadis et al. (2022) | Heuristic | Flood depth h, probability P, return period T |
P, probability that at least one hydrologic event (in a selected design time) causes h > 0.1 m (under a fixed confidence limit) or P, probability of h > 0.1 m for a hydrologic event of given T |
N/A | N/A | Flooding (Efstratiadis et al., 2022) |
| 19 | Switzerland | Lateltin (1997), Raetzo et al. (2002), Loat and Petrascheck (2008) | Empirical | Depth of debris deposition h, debris flow velocity v, return period T |
h, v, T | Hazard matrix in which four hazard levels are defined (high, moderate, low, residual) as a combination of: Three debris flow magnitudes: High: h > 1 m and v > 1 m/s Average: h < 1 m or v < 1 m/s Low: h = 0 Four debris flow frequencies: Frequent: T < 30 years Average: 30 < T < 100 years Rare: 100 < T < 300 years Residual: T > 300 years |
People, animals |
Debris flow (van Alphen & Passchier, 2007) |
| 20 | N/A | Rickenmann (2005) | Empirical | Depth of debris deposition h, debris flow velocity v, return period T |
h, v, T | Hazard matrix in which four hazard levels are defined (high, moderate, low, very low) as a combination of: Four debris flow magnitudes: High: h > 1 m or v > 1.5 m/s Medium: h < 1 m and 0.4 m/s < v < 1 m/s Low: h < 0.4 m and v < 0.4 m/s Non affected areas: h = 0 Three probability of occurrence: High, medium, low |
N/A | Debris flow (Hürlimann et al., 2008) |
| 21 | Andorra | Hürlimann et al. (2006) | Empirical | Depth of debris deposition h, debris flow velocity v, return period T |
h, v, T | Hazard matrix in which four hazard levels are defined (high, moderate, low, very low) as a combination of: Four debris flow magnitudes: High: h > 1 m and v > 1 m/s (direct impact) Medium: h < 1 m or v < 1 m/s (direct impact) Low: indirect impact (after flow) Non affected areas: h = 0 Three probability of occurrence: High: T < 40 years Medium: 40 < T < 500 years Low: T > 500 years |
N/A | Debris flow (Hürlimann et al., 2006) |
| 22 | N/A | Aronica, Biondi, et al. (2012) | Heuristic | Flood depth h, flow velocity v, return period T |
h, impact pressure ∑, T | Hazard matrix in which four hazard levels are defined (H1: low; H2: medium; H3: high; H4: very high) as a combination of: Four event intensities: h < 0.1 m ∑ < 20 kPa 20 kPa < ∑ < 35 kPa ∑ > 35 kPa (∑ = ρmv2 + 1/2 ρmgh, where ρm is the density of the solid–liquid mixture) Three probabilities: T = 50 years T = 100 years T = 300 years |
N/A | Debris flow (Aronica, Biondi, et al., 2012) |
- Note: N/A = not applicable; not available.
The tables consist of nine columns.
Column 1 reports a progressive number for the reader's convenience.
Column 2 indicates which government authority or national guidelines prescribe or suggest the method; state-of-the-art methods proposed in academic research projects are labelled as “N/A”.
Column 3 provides the fundamental references of each method, especially those where they were first proposed (if available).
In Column 4, the methods are classified according to the basic approach: (a) “heuristic”, if the flood hazard classification is defined on the basis of the author's expertise, well-established local uses, or choices made in previous studies, without providing specific supporting reasons; (b) “conceptual”, if the flood hazard classification is defined on the basis of theoretical stability models specifically designed for the exposed element considered; and (c) “empirical”, if the flood hazard classification is defined on the basis of experimental data.
Column 5 lists the hydraulic parameters and flooding variables involved in the definition of the flood hazard indicator for each method considered.
The flood hazard index used to provide a quantitative measure of flood hazard is specified in Column 6, while the related flood hazard classification is detailed in Column 7. The complexity of the classification is mainly related to the number of flooding parameters involved and the inclusion of information on flood frequency.
The exposed elements considered with each method are specified in Column 8 (people, buildings, vehicles, etc.).
Finally, Column 9 reports the fields of application of the methods, along with some references in which the methods are applied to real cases. In this column, “flooding” indicates the application to generic inundation events having various causes (severe rainfall, river overflow, coastal storm); labels “levee breach” and “dam-break” indicate the application of the method to flooding caused by levee system- and dam-failure, respectively; “debris flow” indicates the application to debris flow events. Hazard assessment methods specifically proposed for debris flows are listed at the bottom of Tables 1 and 2.
3 DISCUSSION
The present review shows that a large number of quantitative flood hazard assessment methods have been proposed in the past decades and are currently in use. These methods differ in many respects, including the basic approach (heuristic, conceptual, or empirical), the indicator used to assess flood hazard, and details on flood hazard ranking. Table 3 reports some statistics regarding the entire set of methods listed in Tables 1 and 2.
| (1) | (2) | (3) | (4) |
|---|---|---|---|
| Data type | Item | Sample sizea | Appearance rate (%) |
| Category | Intensity (Table 1) | 50 | 69.4 |
| Intensity and probability (Table 2) | 22 | 30.6 | |
| Flooding variables involvedb | Water depthc | 70 | 97.2 |
| Flow velocityc | 49 | 68.1 | |
| Return period/scenario probability | 22 | 30.6 | |
| Flooding duration | 6 | 8.3 | |
| Flooding arrival time | 1 | 1.4 | |
| Debris parameter | 3 | 4.2 | |
| Others | 8 | 11.1 | |
| Exposed elementd | Not specified | 38 | 52.8 |
| People (adults or children)e | 24 | 33.3 | |
| Animals | 3 | 4.2 | |
| Vehicles | 9 | 12.5 | |
| Buildings | 10 | 13.9 | |
| Others | 4 | 5.6 | |
| Applicationf | Flooding (general)/river overflow | 62 | 86.1 |
| Levee breach | 9 | 12.5 | |
| Dam-break | 10 | 13.9 | |
| Debris/mud flow | 5 | 6.9 | |
| Others | 1 | 1.4 | |
| Approach | Heuristic | 42 | 61.1 |
| Conceptual | 2 | 2.8 | |
| Empirical | 22 | 30.6 | |
| Mixed | 4 | 5.5 |
- a The methods analysed are N = 72.
- b Some methods use several flow variables.
- c The product of water depth and flow velocity is used in 29.2% of cases; flood depth only is used as representative of flood hazard in 18.1% of cases.
- d Some methods are applied to different exposed elements.
- e The methods designed specifically for people are 20.8% of the sample considered.
- f Some methods are used in different applications.
Most of these methods (i.e., the 50 listed in Table 1 out of 72 total, approximately 7 out of 10) are based on estimating the hazard through flooding intensity only, generally referring to a specific (extreme or historical) flood scenario or fixed hydrological events with selected return periods. Accordingly, the same flooding hazard indicator and classification are used regardless of the exceedance probability of the potentially hazardous flood event. Fewer methods (i.e., the 22 listed in Table 2 out of 72 total, approximately 3 out of 10) combine flooding intensity and flood exceedance probability. For example, Aronica, Candela, et al. (2012) used distinct hazard level classifications for hydrologic events of different return periods so that, for a given flooding magnitude, the hazard level is higher for more frequent flood events. Therefore, including flooding probability in hazard assessment enables different consideration of a potentially damaging situation (i.e., more tolerable or less tolerable) depending on its probability of occurrence. Methods that use intensity-probability matrices are based on a similar concept and are very popular (e.g., LAWA, 2006; PLUIES, 2003; Stephenson, 2002) due to the simplicity of visualisation and application. An alternative effective method of combining inundation intensity and probability is based on defining the hazard classes through conditions set on flooding hazard indexes calculated for flood scenarios of different return periods (Adige River Basin Authority, 2005). Accordingly, a univocal hazard level can be attributed to a fixed location while starting from flood events of different return periods.
Tables 1 and 2 show that various flooding hazard indicators are currently used in the literature and in practical applications by scientists and practitioners. The most used is flood depth, followed by flow velocity, because these parameters reasonably have the greatest influence on flooding consequences (e.g., Merz et al., 2007). Indeed, flood depth is involved in defining flood hazard in almost all cases in Tables 1 and 2 (except items 18 and 30 in Table 1), either alone as representative itself of flood hazard (in approximately 18% of cases), or in combination with flow velocity or other relevant flooding parameters. Meaningful indexes representative of inundation intensity are obtained by combining flood depth and flow velocity. Among these, the most used is the product of flood depth and flow velocity, which is involved in almost 30% of the flood hazard assessment methods considered. Other basic hydraulic quantities are sometimes used as flood hazard indicators, namely energy head (e.g., Kramer et al., 2016) and total flow momentum, expressed as hydrostatically equivalent total depth (Aureli et al., 2008). Besides flood depth and flow velocity, other flooding quantities are rarely considered in flooding hazard assessment, despite their potential impact on the safety of people and the resilience of buildings and infrastructure. These quantities are mainly flooding arrival time (Pieterse et al., 2009), flooding duration (e.g., Mani et al., 2014; Ongdas et al., 2020; Tingsanchali & Promping, 2022), and other factors, such as turbidity (e.g., DEFRA Environment Agency, 2006b). The possible transport of floating objects (e.g., large wood debris) or pollutants is normally disregarded. National authorities in charge of soil defence from flooding and water resource management often identify distinct riverine hazard zones on the basis of the areas that are prone to flooding as a result of flood events of selected return periods (e.g., FEMA, 2021; Po River Basin Authority, 1999). According to this approach, flooding hazard is expressed by means of selected classes of inundation probability or, equivalently, through the probability of exceedance of a selected threshold flood depth (Efstratiadis et al., 2022).
Quantitative flood hazard classifications are commonly tailored to specific elements at risk, such as people (e.g., DEFRA Environment Agency, 2006b; Liu et al., 2021; Xia et al., 2011), vehicles (e.g., Shand et al., 2011; Xia et al., 2011), or buildings (e.g., de Bruijn et al., 2015; Krieger et al., 2017; Maijala, 2001), sometimes accompanied by a qualitative description of the hazardous implications expected (e.g., García-Martínez & López, 2005; Priest et al., 2009; Wade et al., 2005) and by recommendations on planning limitations and protection measures (e.g., Beffa, 2000). Garrote et al. (2020) even proposed a specific hazard ranking for cultural heritage sites. The graphical hazard classification by ACER (1988) changes depending on the jeopardised element (people, houses, vehicles, etc.). The hazard classification for people by Cox et al. (2010) is differentiated according to age (infants, children, adults), while the hazard categories defined by Kramer et al. (2016) for vehicles differ for passenger cars and emergency vehicles. It is indeed reasonable that the hazard level, which provides a concise interpretation of the flooding information in terms of potential hazard, is tailored to the exposed element. For instance, a given flooding intensity (expressed, e.g., in terms of water depth) can be very hazardous for a person and much less damaging for a building. On the other hand, other methods provide a general evaluation of the flooding hazard in an anthropised area (e.g., an urban area, as in Cançado et al., 2008 and in Tingsanchali & Promping, 2022), with no reference to specific elements at risk (e.g., Smith et al., 2014). Most of the methods considered in this review (about 1 out of 2) belong to this category. Hazard classes can be defined either mathematically (e.g., DEFRA Environment Agency, 2006b; Khaing et al., 2019; Mani et al., 2014; Patra et al., 2019) or graphically (e.g., ACER, 1988; Aronica, Candela, et al., 2012; Ministerio de Medio Ambiente, 1996) through conditions set on relevant flooding variables.
Most of the hazard assessment methods reviewed (approximately 86% of the total) are applied indifferently to flooding phenomena, regardless of their causes, and hence their use can be found in multiple contexts in the literature. For example, the flood hazard classification methods by ACER (1988) and DEFRA Environment Agency (2006b) have been applied to riverine and coastal flooding, as well as to levee breach flooding; the method by Loat (2010) has been applied to both flooding and landslides. On the other hand, some methods have been specifically proposed for a certain flood disaster, such as dam-break (e.g., Ministerio de Medio Ambiente, 1996; Patra et al., 2019) or debris flow (e.g., Loat & Petrascheck, 2008; Rickenmann, 2005). In this case, specific flood intensity parameters and hazard categorizations suitable for the particular hazardous process are used (e.g., Aronica, Biondi, et al., 2012).
Finally, Table 3 shows that the approach used to derive most of the quantitative methods considered (about 61%) is heuristic — that is, the selection of the hazard indicator and the classification adopted are not soundly motivated theoretically or empirically; rather they are based on the expert judgement of the practitioner/modeller or, more simply, on previous studies (Rufat et al., 2015). The remaining methods derive from the analysis of experimental data (in approximately 31% of cases), conceptual models (in approximately 3% of cases), or mixed approaches (in approximately 5% of cases; see items 18 and 31 in Table 1, or items 14 and 15 in Table 2).
- The definition of a hazard indicator and the associated hazard ranking, as well as the definition of a flood hazard matrix in matrix-based methods, is often tailored to a specific case study and based on expert (subjective) judgement. In addition, different flooding hazard classifications are adopted by government authorities, even in the same country. This lack of standardisation on an international (but also national) scale appears obvious when considering the various geographical, environmental, and socio-economic contexts in which flooding can occur, the variety of assets potentially threatened by floods, and the different aims of flood hazard assessments. However, having unified and standardised hazard assessment methods would favour their transferability to different contexts, and allow for a consistent quantitative comparison of flooding hazard assessments performed in different regions of the world. It is worth considering the convenience to directing efforts towards standardisation of flooding hazard assessment. In this regard, the simplest methods, based on an intuitive and physically based hazard index, appear more suitable for wide and shared use, despite the trade-off with the requirement (discussed in the following point) that the hazard index is sufficiently representative. In addition, a standard format of flood hazard maps (including graphical elements, symbols, colours, etc.) is desirable (e.g., see the recommendations by FEMA, 2013).
- The flooding hazard indicator and the associated hazard classification ought to be suitably chosen according to the ultimate aim of the flood hazard assessment: spatial planning, emergency management and people evacuation, structural safety of constructions or infrastructures, protection of threatened assets, and so forth (de Bruijn et al., 2015). The methods currently in use mainly consider flood depth as the primary flood hazard indicator regardless of the aim of the hazard assessment, yet additional flooding parameters might be relevant in specific application contexts. For example, in emergency management, flooding arrival and duration times also play a crucial role since they provide information about the time available for people evacuation and the time that evacuated people need to stay away from home. Moreover, flooding duration time is perhaps the main parameter for estimating potential damages to flooded agricultural and production areas (Förster et al., 2008). Water temperature instead is a relevant factor in volcanogenic floods (Pagneux & Roberts, 2015). A current challenge is to improve flood hazard assessment by introducing new empirical or physically based representative flood hazard indicators that take into account all relevant flooding parameters for the application of interest (Lazzarin et al., 2022; Tingsanchali & Promping, 2022).
- Flood hazard can be highly variable during the stages of a flooding event due to its unsteady character (Xia et al., 2011). The usual choice of considering the local maximum value attained by the hazard indicator (e.g., Santillan et al., 2016) allows a conservative hazard estimation, especially suitable for very rapid flood events. However, for long flooding events, the temporal aspect becomes relevant in flood hazard assessment, as for social vulnerability (Rufat et al., 2015). For this reason, the choice of flood hazard indicator could change depending on the temporal phases of the flooding. For example, in the pre-flood phase (preparedness), flooding arrival time and flood frequency can be assumed as the most significant flood hazard parameters; in the during-flood phase (response), flood intensity (e.g., flood depth) is the key flooding quantity, along with flood rise ratio; finally, the post-flood phase (recovery) is mainly characterised by flooding duration time and long-term flood depth. However, including unsteadiness in flood hazard assessments would require providing hazard maps for the different stages of the flood event, thereby making the communication of flood hazard to public, practitioners, and stakeholders more complex and likely less effective.
- Flood hazard must be considered a dynamic variable due to the non-stationarity of inundation events (Tsakiris, 2014). Indeed, climate change (Shrestha & Lohpaisankrit, 2017; Toosi et al., 2020) and the reduction in natural water retention due to modified land use are increasing the recurrence, magnitude, and spatial extent of flood events (IPCC, 2012; Kundzewicz et al., 2018), and consequently the likelihood of adverse impacts (Blöschl et al., 2019). Accordingly, possible future climate scenarios and changes in hydrological regimes and land cover and use are being increasingly accommodated in risk management studies (e.g., Phakonkham et al., 2021) in order to estimate future changes in flood hazard and prioritise areas where protection and risk reduction measures are required. This is particularly challenging in urban areas, where growing wealth and the increasing presence of strategic assets can exacerbate the impact of floods (Padulano et al., 2021; Skougaard Kaspersen et al., 2017). Caution must be exerted in these projections due to the complex impact of climate change on flood hazard and the considerable uncertainty associated, especially on the regional or local scale (Kundzewicz et al., 2018).
- Flooding hazard is commonly categorised into classes and identified using qualitative attributes, such as “very high”, “high”, “moderate”, “low” and “very low”, or similar (also depending on the number of hazard classes considered). Such classifications are typically heuristic since they are based on the proposer's judgement and experience. An exhaustive explanation of the meaning and implications of the different flood hazard classes is unfortunately rarely provided (e.g., Beffa, 2000; Priest et al., 2009; Wade et al., 2005). A detailed description of the practical implications of an event of a given hazard level for the elements at risk ought to be added, especially for those heuristic methods that are not oriented to specific exposed elements. A more objective hazard assessment is ensured by physically based (conceptual or experimental) approaches. In this regard, data obtained from laboratory experiments or collected after real-field events are important to understand the potentially damaging effects of flooding events of a given magnitude on exposed elements.
- The literature review has revealed a general lack of validation of the flood hazard methods against real case studies. It would be desirable to assess and compare the predictive capabilities of different hazard classifications against benchmarks, mainly to verify if hazard (and risk) assessments are accurate enough to allow practitioners and decision-makers to reach a confident decision. To enable this, rich, high-quality databases on observed distributed hazard parameters and flooding consequences of well-documented real events ought to be made available and easily accessible. Unfortunately, few flood hazard data are actually available because flood parameters are difficult to measure and collect during or after an actual flooding event (Molinari et al., 2019). New recent opportunities to collect data that can support validation and calibration of flood hazard models are provided by satellite or airborne remote sensing, crowd sourcing, and footage from security cameras (Bates, 2004; Molinari et al., 2019; Rosser et al., 2017).
- Flood hazard assessment is affected by uncertainties, both aleatory and epistemic, from many different sources (Beven et al., 2015; de Moel et al., 2015; Merwade et al., 2008), and information on these uncertainties would be desirable. Probabilistic hazard maps are very useful to this end, and to address the problem of lack of flood hazard model validation (Aronica, Franza, et al., 2012; Efstratiadis et al., 2022; Garrote et al., 2021; Maranzoni et al., 2022) since they are based on a multiplicity of flooding scenarios with different likelihood, unlike deterministic maps, which are based on a single (worst) scenario. In particular, probabilistic flood hazard maps illustrate the spatial distribution of the probability of the hazard levels considered (D'Oria et al., 2019), thereby providing information about the uncertainty associated with the occurrence of a given flood hazard level. Probabilistic maps can hence ensure a sufficiently concise and clear representation of flood hazard along with the associated uncertainty, the knowledge of which can support more informed decision-making strategies (Efstratiadis et al., 2022). However, validating probabilistic models is still a challenging task (Environment Agency, 2021; Molinari et al., 2019).
- When considering homogeneous methods (i.e., based on the same approach or referring to the same jeopardised element), a priori none seems better than another, especially among the heuristic ones. Indeed, the lack of flood hazard model validation does not grant full awareness of the limitations of the models. Different methods could therefore be used in the same study to estimate the sensitivity of the predicted flood hazard level with respect to the classification method adopted. It is, however, worth noting that some of the methods listed in Table 1 are very similar, differing in minor details only, such as the thresholds used to separate the hazard classes (e.g., compare items 9 and 11, or items 26 and 44 in Table 1).
- Effective communication of flooding hazard contributes to raising public awareness and forming a correct perception of flood hazard in floodable areas (Correia et al., 1998), thereby reducing social vulnerability, and consequently positively modifying the resilience and adaptive capacity of communities (IPCC, 2012). Indeed, communicating flood hazard promotes the preparedness of individuals and communities to cope with flooding, and enhance their capability to respond adequately, also in relation to the local attitude to deal with floods. Therefore, it is crucial to produce compelling, clear, understandable, and actionable flood hazard maps, which can satisfy the specific expectations and needs of different stakeholders and end-users and can be correctly interpreted by non-experts too (Feldman et al., 2016; Hagemeier-Klose & Wagner, 2009; Henstra et al., 2019). To this end, 3D flood hazard mapping (e.g., FEMA, 2013; Macchione et al., 2019) may be a powerful and effective tool to improve flood hazard perception. Finally, it is advisable that flood hazard maps be freely available through public web portals and GIS applications (Environment Agency, 2019; Géorisques, 2022), together with practical advice to reduce the impact of flooding (OPW, 2022).
4 CONCLUSIONS
Flood hazard assessment is a key step in flood risk analysis, which in turn translates into emergency planning, flood risk management strategies, and mitigation and protection measures to improve the resilience of communities living in flood-prone areas. This justifies the great attention paid to this topic in the past decades.
A comprehensive literature review of the quantitative methods currently used by scientists and practitioners for flood hazard assessment is presented in this article. Such methods are typically based on the quantitative categorisation of a suitable flood hazard index, defined as a combination of relevant flooding parameters. Hydrodynamic numerical modelling of the flooding process is required to calculate the flood hazard index and determine the flood hazard level (based on the associated classification). Basic details on quantitative methods proposed in scientific studies or adopted by government agencies were reported in summary tables, indicating the mode of expression for flood hazard (flood intensity only, or flood intensity in combination with flood probability), the methodological approach (conceptual, empirical, or heuristic), the exposed elements considered (people, vehicles, buildings, etc.), and the contexts of application (riverine flooding, dam-break or levee breach flooding, flooding in coastal or urban areas, debris flow, etc.).
This review aims to help modellers and practitioners select the most appropriate flood hazard assessment method for the specific needs and the application of interest, as well as identify references where relevant application examples and case studies can be found. A flood hazard analysis based on thorough knowledge of the features of existing flood hazard methods can support more informed assessments, consequently more effective decision-making.
Aspects that are worth improving and represent future challenges in flood hazard assessment analysis were discussed in detail. These range from the representativeness of the flood hazard indicator depending on the flooding cause and the stage of the flood event, to the standardisation and validation of the flood hazard classification methods, as well as the mapping of flood hazard uncertainty. The effective communication of the outcomes of a flood hazard analysis increases public awareness of the potential harm of flooding, thereby reducing its negative impact in terms of loss of life, economic and social damage, and loss of cultural and environmental heritage.
The comprehensive analysis of the current quantitative flood hazard assessment methods might encourage new contributions for improved hazard evaluation in flood risk mapping.
ACKNOWLEDGEMENT
This work was supported by the Italian Ministry of University and Research through the PRIN 2017 Project RELAID (REnaissance of LArge Italian Dams), project number 2017T4JC5K.
Open Research
DATA AVAILABILITY STATEMENT
Data availability statement is not applicable for this article.




