Species richness responds to buffer effectiveness and competitive priorities in simulations of alpine microrefugia
Abstract
Aim
Microrefugia on alpine slopes may allow species to persist in a warming climate. How plant species richness could respond to of the effectiveness of climatic buffering, defined as the difference in climate change in a microrefugium in comparison to that of an open alpine slope as mediated by competitive priority effects, is explored.
Location
Alpine habitat anywhere.
Taxon
Vascular plants.
Methods
A simple spatially explicit model of plant species with adaptations across a climatic gradient simulates reproduction, dispersal, and mortality through climatic change. The effectiveness of microrefugia in buffering climate change and levels of competitive priority effects are included as factors that alter demographic rates in an experimental framework. Spatial patterns of microrefugia and differences in dispersal are also simulated. Differences in mean species richness were analysed.
Results
The number of species conserved, relative to an instantaneous equilibrium calculation with the same climatic change, decreases with inclusion of a period of change (transient vs. instantaneous, equilibrium change) and further with competitive priority effects. In these simulations, the number of species conserved does not simply increase with buffer effectiveness, as hypothesized, but instead is bimodal.
Main Conclusions
The dip in number of species conserved in the middle range of buffer effectiveness occurs because barriers develop. These are temporal ecological traps, wherein species adapted to the middle of a climatic gradient become extinct, because their colonization of microrefugia is blocked by an extinction debt of resident species. The inertia that allows these demographic consequences is increased by competitive priorities. The highest levels of buffering and resulting inertia will not be ubiquitous but the bimodal pattern indicates that assessments of the role of microrefugia need to recognize the temporal species-environment and species-species interactions that will change the number of species conserved versus extinctions.
1 INTRODUCTION
Mountains are warming faster than the planetary average and the isolation of mountaintops makes it difficult for species to migrate latitudinally, yet topographic heterogeneity among and within elevational zones creates microclimatic heterogeneity that can support a diversity of plant species and communities. Most of the literature on alpine microrefugia focuses on the habitat diversity created by topographic variation at multiple scales in mountainous environments. Mesoscale differences in slope and aspect in relation to solar radiation, prevailing winds, and synoptic variation in precipitation create a context within which the microclimates experienced by plants will reflect regional climate change (e.g. Graham et al., 2012; Malanson et al., 2022). Furthermore, other research has asserted that sensitivity is a critical component; heath and grassland species in local refugia (down to 100 m cells) would persist in the future because species have broader tolerances than expected (Maclean & Early, 2023). On single slopes, the simultaneously observed range of temperatures can exceed the increase in average global projected over the next century (Scherrer & Körner, 2010, 2011). Here we consider this within-slope scale, with microtopography and microclimates being the variation at extents of 1–10 m. The cooler of these areas have been identified as potential microrefugia in a warming climate that might reduce the loss of cold-adapted species (Scherrer & Körner, 2010), but how their microclimates change is poorly known. As a conceptual contribution to widening discussion, we evaluate two characteristics of microrefugia, buffer effectiveness and inertia, which could affect species conservation especially if a ‘barrier’ develops, that is, if inertia, the conditions created by time-lags between the outcomes of demographic processes and the inputs that drive them (i.e. climate) (e.g. Cole, 1985; Malanson, 1993; Scherrer et al., 2020; Theurillat & Guisan, 2001) constrains or retards colonization of microrefugia. We focus on plants because they would seem to be more limited relative to climate velocity, but the spatial tracking of the climate to which most organisms are adapted is a central issue of their response to climate change (e.g. Chan et al. 2024).
1.1 Buffering
The concept of buffering in microrefugia is not always clear. In many cases, areas currently with a below-average range of temperatures are cited as buffering climate change or buffering its impact on species or systems (Dobrowski, 2011; García et al., 2020; Gentili et al., 2015; Pastore et al., 2022; Shi et al., 2014; Suggitt et al., 2018). In partial contrast, research has reported that larger potential refugia (at >20 m extent) more effectively modify climate (Chytrý et al., 2023). In a stricter sense, buffering means that some change, or the impact of that change, is less pronounced than it would be without the buffer. More mechanistically for microrefugia, we would have a formula for change in temperature or moisture as a function of their change on the surrounding open slope (e.g. 0*T and 1*T for 100% and 0% effectiveness, with T the surrounding change). 100% effectiveness would be rare, but could include the coldest sites (e.g. Wipf et al., 2013) or wet sites where the thermal properties absorb energy (e.g. Björk and Molau, 2007; Isaak et al., 2015). Most microrefugia would respond between the extremes and with other variations, for example, by buffering change outside the summer season (Aalto et al., 2018), Buffering effectiveness can be thought of as the degree of partial decoupling of the micro- and meso-scale climates that can lower the correlations between them, while the energy fluxes of mechanistic coupling never equal zero.
1.2 Competitive priority effects
Competitive priority effects (CPE) include both resource and scramble competition or facilitation (Michalet et al. 2006), with the former as a gradient of the effect of competition on demographic processes and the latter as limited space favouring early arrivals (e.g. Ezard & Purvis, 2016) (we add facilitation only in supporting analyses). Also described but moderately quantified is how inertia affects resulting patterns. Inertia can limit species losses by extending the time for effective tracking but also alter new establishment because competition and facilitation can affect different vital rates in response to different environmental drivers in the same situation (Collins et al., 2022; Dullinger & Hülber, 2011; Liang et al., 2018; Scherrer et al., 2020). Together these processes of inertia create time lags in extinctions and colonization that have been identified as extinction debts (Lewis, 2006; Malanson, 2008) and colonization credits (Rumpf et al., 2019). Inertia may be common for alpine species, for example, those with exceptional longevity including persistence through clonal regeneration (Jiménez-Alfaro et al., 2016), and because many species of alpine habitats have ranges that extend into the subalpine (e.g. Jiménez-Alfaro et al., 2021; Rundel, 2011). However, thermophilisation, the increase in species adapted to warmer mean temperatures (at least in the growing season) now occurs widely (Steinbauer et al., 2018) while exceptionally cold sites can resist it (Lamprecht et al., 2018).
1.3 Approach and hypotheses
Given habitat heterogeneity on alpine slopes, here we focus on a single, heterogeneous slope. Using a spatially explicit simulation model as a virtual microcosm (Winsberg, 2003), we evaluate buffer effectiveness from no effect (0%, microrefugia climates change in parallel with those of the rest of the slope) to full effect (100% effective, microrefugia climates hold constant while the rest of the slope changes). We include transient dynamics, that is, the demographic process during the period of climate change, which include time lags, Transient dynamics cause differences in simulated outcomes from equilibrium calculations for a given climate change. These dynamics interact with buffer effectiveness in their effect on tracking success, for example, by creating temporal barriers (discussed below). We additionally include CPE, We compare simulation outcomes that include or exclude CPE, and we vary the spatial pattern to compute differences in the losses of virtual species while maintaining a similar distribution of climate gradient values among runs.
- Increased inertia, seen in the simulations with transient climate change versus the equilibrium calculation for an instantaneous climate change and in simulations with CPE versus those without it, will reduce the number of virtual species conserved Buffer effectiveness will increase the number of virtual species conserved.
- Buffer effectiveness will increase the number of virtual species conserved.
We compare the outcomes of simulation experiments (sensu Peck, 2004) in terms of number of virtual species conserved. Although the model has many simplifying assumptions, for example, regarding habitat heterogeneity and the period of climate change, it is a sensible representation of the system, and an unexpected outcome illustrates the complex interactions of a subset of the processes involved in responses to climate change. Key assumptions are that 100 species are represented by Gaussian or normal curves on a single gradient, 0–1, that represents climate.
We focus on plants that, while sessile, disperse offspring to other sites every generation and model iteration. The inclusion of animals, especially those that move with volition or intent relative to the environment, would alter the outcomes and interpretation significantly. Animals can be expected to find microrefugia and to move to others as conditions change. Behaviours, such as territoriality, would be important even if they do not change, and competitive priority effects would be more complicated.
2 MATERIALS AND METHODS
2.1 Simulation model
Our simulations create a virtual microcosm of a slope in a spatially-explicit agent-based model developed in Netlogo (Wilensky, 1999, cf. Malanson et al., 2023). The details of the following summary of model design are presented in a modified OOD Protocol format, as recommended by (Grimm et al., 2020), in Supporting Information, Appendix S1. Simulation experiments include manipulation of buffering and CPE.
2.1.1 Initial patterns and virtual species
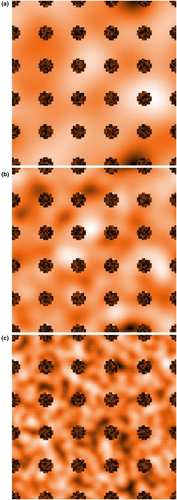
Scherrer and Körner (2010, 2011) reported that a wide range of temperatures could be observed on a single slope and that their distribution was shaped so that the extremes were relatively small (i.e. with the warmest and coldest 30% of the gradient occupying 15% or less of the slope) (e.g. Scherrer & Körner's, 2010, Figure 1 and 2011, Figure 6). We created patterns on a 100 × 100 cell grid that have a similarly shaped one-dimensional distribution of values, which represents a cool to warm climatic gradient (this could also represent a wet to dry or combined temperature and moisture gradient). We use a topography subroutine in Netlogo to create patterns of pseudo-elevation that we rescaled to 0.3–1 as a climate gradient and superimposed microrefugia scaled 0.0–0.3 on this gradient. Three levels of pattern complexity were generated, but the individual patterns vary with random initial conditions (Figure 1). In preliminary analyses, reported in Supporting Information Appendix S2, Table A2.1, Figure A2.1, we compared cases with single/few large versus several smaller refugia (1, 25, 64, 400, 1500) holding total refugia area constant. Size/numbers of refugia did not affect the number of virtual species conserved in these simulations. Thereafter, we used only one of these variations (25 refugia patches) in further analyses.
We created 100 virtual species in the simulation. Each species has a Gaussian response function over the environmental gradient (illustrated in Supporting Information, Appendix S1, Figure A1.2; the modes are evenly spaced at 0.01 intervals on the 0–1 environmental gradient, and the standard deviation is 0.005, which produce breadths of 0.08 at R ix of 0.5) The response of species i can be calculated for any position x on the gradient as R ix. The initial distribution of species to cells applied a Monte Carlo test of the R ix of each species and cell to a random number, 0–1; at the end of this procedure individuals were randomly removed from cells until 10 remained.
2.1.2 Processes of establishment and mortality
We simulated establishment and mortality on these patterns using the Monte Carlo method to represent stochastic demographic processes. Processes and parameter values for establishment and mortality are reported in Supporting Information, Appendix S1. In a heuristic simulation the outcomes are artefacts of the parameter values, even if they are derived from observations, and we evaluated alternatives with results in Supporting Information, Appendix S3, Figure A3.1. The qualitative pattern of species conserved relative to buffer effectiveness does not change.
To introduce CPE, Rix was reduced as the number of individuals on a cell increased, which created more and less stringent competition. We used different levels of reduction, JRix and KRix, which we applied to the mortality of seedlings (0–2 years) and established plants (>2 years), respectively.
The species were further divided into two groups with different dispersal abilities. Every other species along the gradient had either ubiquitous dispersal, with seed rain on every cell in every iteration from anywhere on the grid, or dispersal limited to seed rain to a cell only if present in a radius of ca. three cells (see Supporting Information, Appendix S1 for justification).
Seed rain of the ubiquitous dispersers added an individual to each cell in every year. The dispersal-limited species did so if the distance criterion was met. This seed rain would be extraordinarily high if it resulted in establishment. However, the mortality subroutine for new individuals is used immediately and the individual is eliminated if its priority-reduced JRix is less than a random number; ubiquitous dispersers have a higher mortality rate than the dispersal limited species, as expected from a tradeoff on an r-K continuum (Bonte et al., 2012), and cells with lower densities because of climate have greater opportunity for seedling establishment (see Meineri et al., 2020).
The mortality rates for seedlings in alpine tundra are high, and we follow Dullinger et al. (2012) for the limited dispersal species. For the ubiquitous dispersing species, in preliminary analyses we incrementally increased mortality to the point where it affected whether all 100 virtual species were maintained in the pre-climate change period; that is, we used as high rate as possible that still maintained all 100 virtual species on the grid prior to climate change to balance the high seed rain. Defining two types of dispersal covers a full range of potential tracking while maintaining model simplicity.
Additional seed rain is contributed to the grid by the ubiquitous dispersers, independent of whether they are still represented in the landscape or not, at the rate of one individual placed randomly on the grid in each year. This procedure is meant to account for rare long-distance dispersal, for which there is evidence of new species appearing (e.g. Lamprecht et al., 2018). We interpret this seed rain as a potential rescue effect for local extinctions.
Mortality is then imposed on all older individuals using the less severe competitive reduction of fitness, KRix. We ran additional simulations with less and greater difference between the dispersal types to assess sensitivity (Supporting Information, Appendix S2, Figure A2.3).
2.2 Simulation experiments
2.2.1 Climate change and buffering
We changed the climate by adding to the climate gradient value of each cell over a 100-year period, and the response functions of the virtual species per cell are recalculated at every iteration. We assumed climate change to shift by a 50% of the currently realized gradient and added 0.005 each year to the non-refugia cells (those initially in the range 0.3–1.0). While Scherrer and Körner (2011) illustrated a much smaller change along the gradient for 2°C of warming, 50% change approximates the effect of a 5° change. The climate values of the refugia cells (those initially in the range of 0.0–0.3) were increased by differing amounts to represent buffer effectiveness as a treatment in simulation experiments. Buffer effectiveness is the degree to which the climates of the refugia cells remain constant (100% effective) versus increasing at the same rate as the rest of the landscape (i.e. zero buffering). We ran simulations with levels of effectiveness from 0% to 100% in 10% increments, We ran these 11 levels for each of the three levels of initial pattern complexity. We repeated these simulation runs without the competitive priority multipliers to assess the interaction of inertia and buffer effectiveness. We repeated these runs 3 times; these 198 runs constitute the focal simulation experiment.
To these simulation experiments we added two special cases. We ran simulations with each of the 25 refugia having a unique amount of buffering during the period of climate change. We divided annual change of the climate, 0–0.005 into 25 increments of 0.0002 and added each of these to one of the 25 microrefugia, in a randomly selected order, during the 100-year transient period. We repeated the set of three initial patterns three times. Last, we compared an equilibrium response to climate change with the simulated transient response. The equilibrium response takes the climate at the end of the 100 years and initializes the distribution of species with no further population dynamics.
2.2.2 Competitive priority effects
Competition and facilitation are included by adding a simple linear multiplier to reduce the establishment of new seedlings based on the number of seedlings and older plants already on each plot, and we calculated two multipliers to differentiate the effects of extant competitors on seedlings and older plants. The term is negative for CPE and positive for the additional cases of facilitation. See Supporting Information, Appendix S1 for details.
2.2.3 Additional cases
To the simulation experiments above we added two special cases. We ran simulations with each of the 25 refugia on slope having a unique amount of buffering so that the microrefugia were as heterogeneous as possible. We added 25 increments of 0.0002 of increase in the climate value to the 25 microrefugia, in a randomly selected order, during the 100-year transient period. We repeated the set of three initial patterns three times. Last but importantly, we calculated an equilibrium response to climate change for the 11 levels of buffer effectiveness. The equilibrium calculation takes the final climate and initializes the distribution of species with no further population dynamics.
2.3 Analyses
We compared the number of virtual species (#VS) conserved on the grid in the various simulation runs. In such a simplified simulation, the values are not meaningful in terms of actual species distributions, and we are looking for statistically significant differences between simulation experimental treatments. To this end we have limited the number of simulations to what might be achieved with physical microcosm experiments to avoid driving p-values lower by inflating N, and thus we circumvent the problem as presented by White et al. (2014).
We visually compared the mean number of species and its 95% confidence interval for the 11 levels of buffer effectiveness, with and without CPE, and the equilibrium calculation that does not include any iterations of the demographic processes. This comparison reveals the direct effects of (a) eliminating one-half of the climate gradient on which species have their optimum fitness, (b) the spatial tracking of changing climates on the grid cells, and (c) species interactions in the focal simulations. For these, we examined the population sizes for the 100 species at the 11 levels of buffer effectiveness to uncover how it conserves some species and eliminates others.
We defined pattern complexity as an ordinal variable because no true zero provides a scale basis. The patterns differ in mean climate and its standard deviation, and we calculated an index of connectivity across the grid by counting the number of potential steppingstones for cooler adapted species, defined as those with an initial climate gradient value 0.0–0.4 within a 6-cell radius and taking its average; these are continuous scale variables.
Given the variable levels, we computed a mixed effects model (Minitab v.20) for the focal simulations with CPE with #VS as the dependent variable, pattern as a random factor, and buffer effectiveness as a fixed factor, and climate mean, climate standard deviation, and steppingstones as covariates.
3 RESULTS
3.1 Buffer and competitive priority effects: Number of virtual species conserved
Of our two hypotheses, the first is supported. The number of virtual species (#VS) conserved differs markedly between the cases with and without CPE and between the equilibrium (special case) and transient simulations (Figure 2). The differences develop with moderate to high buffer effectiveness. Our second hypothesis is not supported; instead of an increase in the number of virtual species conserved, unimodal and bimodal results are seen. A unimodal response to buffer effectiveness occurs in the equilibrium result because with the highest buffer effectiveness, the microrefugia support only a few species with their modes of Rix any higher than 0.3. In contrast, incorporating climate change in 100 years of simulated establishment and mortality resulted in a bimodal pattern in the transient simulations with and without CPE, that is, microrefugia cells that become 5%–10% and 40%–45% warmer conserve more species than those with 0% and 50% change and much more than those with 25% change (Figure 2). Without CPE, results hardly differ from equilibrium simulations at low buffer effectiveness but then #VS is reduced in parallel with the high CPE (except for maximum buffer capacity). The greatest differences are seen in the middle range of buffer effectiveness where the no-CPE outcomes conserve 10% fewer species than the equilibrium result, and the high-CPE lead to an additional loss of 15% facilitation has a minor effect; Supporting Information, Appendix S3, Table A3.1; negative buffering, that is, the climate of the microrefugia worsens, for example, as with a state change in snowbeds, comparing −20 to +20% and −80% to +80% buffering, decreased the number of species conserved by 26% and 59%, respectively, to the lowest levels of all simulations (Supporting Information, Appendix S3, Table 3.2). Details of the transient dynamics show that lags in initial loss of species and a small rescue effect without CPE are evidence of inertia, but some payoff of extinction debt occurs with CPE (Supporting Information, Appendix S3, Figure A3.2). Further, the number of species conserved without CPE is similar to the equilibrium result through a buffer effect of 30, which clearly indicates that CPE affects inertia, and more demographic consequences can be developed and expressed. These might be seen in the increase in process-pattern relationships in the greater confidence limits among the mean results in Figure 2 when CPE is added to buffer effects.
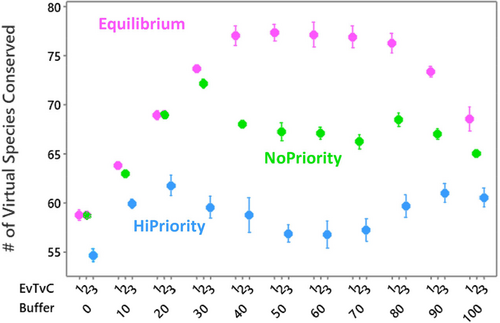
The mixed effects model provides detail on the differences in the simulations (Supporting Information, Appendix S3, Table A3.3). The random factor, pattern, is not significant but the fixed factors, buffer effectiveness, and CPE, are. Of the covariates, the steppingstone variable is significant. The overall model fit the data (<0.001) and had a R 2 of 85.88%. The levels of buffer effectiveness affect the outcomes differently. Withholding 100% to avoid complete collinearity, the buffer levels that are significant (p < 0.01) are those that decrease the #VS relative to the overall mean, that is, all except 60%, 70% and 90%.
3.2 Buffer effects: Inertia in species populations
Buffering causes inertia, or time lags within which the demographics differ in relation to climate change. With minimal buffering effectiveness, the 60% of species with their peak fitness on the climate gradient at 0.4 or higher survive in the new climate range of 0.5–1.5. The species adapted to the most extreme warmer/drier conditions can expand into the new habitat while maintaining their initial populations, but unevenness is high. The cooler-adapted species become extinct (Figure 3a).
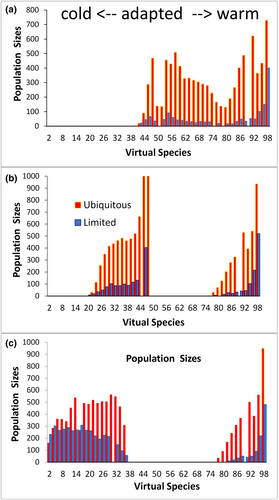
With high buffer effectiveness (Figure 3c), the 0.0–0.3 range of the climate gradient that comprises the microrefugia remains cooler, the species that are adapted to that range already occupied those cells initially, and their continued survival is not threatened. The other cells are then in the range of 0.8–1.5 on the climate gradient, and the species with their peak fitness at 0.7 and higher persist. A gap in the climates remaining on the grid, from 0.3 to 0.8, leaves no habitat for the species with their fitness in this range.
In contrast, with a middle level of buffer effectiveness (Figure 3b), both the species of the microrefugia and those adapted to the upper middle of the climatic gradient are lost. As the sites slowly become warmer and drier the species adapted only to the coolest end of the gradient can persist until a tolerance threshold is reached and they go extinct one by one. The climate range of 0.5–0.8 is temporarily absent and the species adapted to it become extinct before that climate is reached by the microrefugia cells. The species adapted to the lower middle gradient persist because the microrefugia sites reach their climate level sooner. Thus, a portion of the climatic gradient that covers part of the landscape at the end of the period of climate change is unoccupied because the species adapted to it became extinct during the change.
In the additional simulations with the full range of buffer effectiveness allocated among the 25 microrefugia, nearly all virtual species are conserved (from 9F8.44 ± 1.22, 95% ci), depending on initial pattern. No part of the climate gradient is ever absent.
4 DISCUSSION
Simulated microrefugia create a template of climatic heterogeneity that increases the probability of spatial tracking, but buffer effectiveness mediates the inertia in establishment and mortality and thus alters the balance of colonization and extinction. Competitive priority effects introduce further inertia, which allows some species to persist in their preferred microclimate longer, but it can leave others without any preferred microclimate space as the regional climate changes. A bimodal response of species conserved to buffer effectiveness develops because the rates of colonization and extinction differ. Inertia favours persistence early in the period of climate change by incurring extinction debt and colonization credit. The differences between the equilibrium and experimental simulations clearly illustrates the general importance of the dynamics of establishment and mortality that underly colonization and extinction and how these inertial effects are complementary in their consequences. In the Alps, high elevation species have been lost before the arrival of competitors, and inertia may be limited to less extreme sites (Rumpf et al., 2019, Steinbauer et al., 2020).
The conservation of alpine species in the simulation does not consistently increase with the buffer effectiveness of microrefugia. More species are conserved when buffer effectiveness is either high or low, and it reaches a low when effectiveness is near 50%. The result can be explained in part by a theorized ecological trap process (Hale & Swearer, 2016), which could be reinforced by local adaptation (Wessely et al., 2022) and in part by an adjunct to the theory involving a barrier effect by competitors; the latter complements the idea of predatory walls (Durant et al., 2023).
Microrefugia can conserve species with or without buffering the climate (i.e. buffer effectiveness >0 or = 0). They will still provide habitat for some species that could not otherwise continue to exist if the range of climate never included those microrefugia. In our simulations, with no buffering in the microrefugia, that is, starting cooler, they change temperature at the same rate as the rest of the alpine slope, and they would support the species adapted to the remaining cool climate. However, species adapted to the coolest climates are lost. With strong buffering, the species adapted to the coolest sites are conserved but species adapted to less extreme conditions will not find suitable space. On actual alpine slopes such conditions would be rare (e.g. Wipf et al., 2013). At the middle level of buffering, the microrefugia sites slowly become warmer or drier, and they no longer conserve the species adapted to the coolest end of the gradient. Meanwhile, several of the species adapted to the new range in climate were lost because they were excluded by CPE before the slowly warming microrefugia either reached climatic values suitable to them and/or persistent cold adapted species reached them.
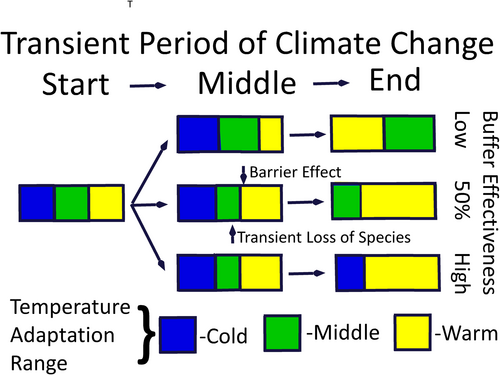
The loss of these moderately warm or dry tolerant species indicates a temporal ecological trap. Mountaintops have been associated with the concept of ecological traps (Sauer et al., 2011), which was developed to identify animal behaviours that placed them in environments where their probability of extinction increased. The concept can also apply to plant species in systems where spatial tracking is possible and creates colonization credits. If the extinction-debt persistence of their competitors on moderately buffered microrefugia precludes tracking while faster climate change of current, unbuffered habitat exceeds their tolerances, they can become extinct before the new habitat is available. The competitors, demonstrating inertia and extinction debt in their persistence, barrier the colonization-credit species into the cooler spaces. The former are eventually lost with extinction debt payoff, while the species that might have contributed to colonization credit become locally extinct while they are excluded by CPE. They are barriered in a temporal ecological trap because of the difference in timing of the local extinctions associated with extinction debt and colonization credit. At the end, the sum of extinctions exceeds the range of climatically suitable habitat that eventually is lost from the landscape. Figure 4 illustrates this conceptual addition to the discussion of alpine microrefugia.
The case for robust alpine vegetation in the face of climate change (e.g. Körner, 2023; Körner & Hiltbrunner, 2021) implies minimal loss of species. While most simulations resulted in substantial losses, the special case in which multiple types of microrefugia coexist, and thus microclimates are maintained at least in small areas of the grid, indicates that on some slopes alpine vegetation may be truly robust to climate change without buffer effectiveness. This co-occurrence implies different drivers for similar initial levels of the climatic gradient, such as cooler locations caused by cold-air pooling, persistent nearby snowbeds, seeps or springs, effective topographic shading, or coldest summits (Gentili et al., 2015; Wipf et al., 2013). Most research to date does not address multiple kinds of microrefugia on single slopes. Heterogeneity at larger scales does not seem to solve the problem although it creates the potential for conserving more species (e.g. Chytrý et al., 2023; Maclean & Early, 2023), but only if the species can track their preferred climate.
This simulation focuses on a specific aspect of microrefugia, the potential differences in positive buffer effectiveness. The potential for negative buffering, that is, such as the conditions in now cooler microrefugia worsening, the potential for facilitation mitigating the loss of species, and the distribution of buffer effectiveness need further empirical research.
Not attempted here are simulations of animals on slopes with microrefugia. Simulations with volitional animal movement, in which the landscape and its changing resources are learned, require species specific knowledge for parameterization. For example, Bennett and Tang (2006) identified needs for modelling procedures that include the varied amount of bounded knowledge of geographical space maintained by individuals, their accumulation of this knowledge through experiential learning when the environment (such as microrefugia, but in their case refugia at macroscale for elk) changes continually (e.g. seasonally). The basic information is lacking for most alpine organisms that would use microrefugia (see Shi et al., 2016). Simple assumptions, such as 100% movement to refugia, would require information on the species-area relationship but otherwise would maintain all species regardless of CPE. The extension to aquatic biogeography would complicate both the organismal and environmental aspects of any modelling attempt (e.g. Muhlfeld et al., 2011).
5 CONCLUSION
Our conceptual model for part of the microrefugia construct identifies potential weaknesses in the current interpretation of the biogeographic effects of climate change. The effectiveness of microrefugia in buffering climate change, as defined here, does not correspond linearly to effectiveness in conserving species. The significant differences in numbers of virtual species among our simulations could be the basis for larger or smaller absolute differences on many, but not all, alpine slopes. Thus, the role of microrefugia in conserving alpine species needs to be rethought with greater precision. The types of microrefugia can be differentiated in multiple dimensions based on their plant communities, and the changes in their microclimates can be better modelled with process-orientated calculations of energy and water fluxes. How these combinations respond to changes in the mesoscale climate can become a basis for assessing the degrees to which they conserve species, recognizing that not all responses are linear.
ACKNOWLEDGEMENTS
This research was supported by NSF award 1853665 to GPM, funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 883669) to SD, and from the Spanish Research Agency (PID2019-108636GA-100) to BJ-A. No permits were required for this research.
CONFLICT OF INTEREST STATEMENT
The authors declare that no conflicts of interest exist.
Open Research
DATA AVAILABILITY STATEMENT
An example of the code that generated the results is included in Supporting Information, Appendix S4. Upon publication the code will be archived in the NetLogo model library.
REFERENCES
BIOSKETCH
The research interests of the team members have been in the plant species diversity of alpine environments.
Author Contributions: GPM conceived the ideas and wrote the model based on prior ideas by SD, HP, MW, and BJ-A, modelling by SD, and field observations by HP, MW, and BJ-A. All participated in the writing.




