Comparing deregression methods for genomic prediction of test-day traits in dairy cattle
Summary
We aimed to investigate the performance of three deregression methods (VanRaden, VR; Wiggans, WG; and Garrick, GR) of cows’ and bulls’ breeding values to be used as pseudophenotypes in the genomic evaluation of test-day dairy production traits. Three scenarios were considered within each deregression method: (i) including only animals with reliability of estimated breeding value (RELEBV ) higher than the average of parent reliability (RELPA ) in the training and validation populations; (ii) including only animals with RELEBV higher than 0.50 in the training and RELEBV higher than RELPA in the validation population; and (iii) including only animals with RELEBV higher than 0.50 in both training and validation populations. Individual random regression coefficients of lactation curves were predicted using the genomic best linear unbiased prediction (GBLUP), considering either unweighted or weighted residual variances based on effective records contributions. In summary, VR and WG deregression methods seemed more appropriate for genomic prediction of test-day traits without need for weighting in the genomic analysis, unless large differences in RELEBV between training population animals exist.
1 INTRODUCTION
Pseudophenotypes are commonly used as response variables in two-step genomic prediction (Meuwissen, Hayes, & Goddard, 2001; VanRaden, 2008). In dairy cattle, when the raw phenotypic data are available, the yield deviations (YD, VanRaden & Wiggans, 1991) and the daughter yield deviations (DYD, VanRaden & Wiggans, 1991) are used to summarize the phenotypic performance for genomic analysis of cows and bulls, respectively. However, when YD and DYD are not available, estimated breeding values (EBVs) derived from genetic evaluations have been used (Calus, Vandenplas, Ten Napel, & Veerkamp, 2016).
In order to avoid double-counting of information and double shrinkage of the direct genomic values (DGVs) using EBVs as pseudophenotypes, computation of deregressed EBVs (dEBVs) has been suggested as a feasible alternative to perform genomic predictions (Garrick, Taylor, & Fernando, 2009). In general, the use of dEBV as response variable can contribute to reduce the bias and increase the reliability of DGVs in genomic prediction of breeding values when compared to the traditional EBVs (Guo, Lund, Zhang, & Su, 2010; Ostersen et al., 2011). Methods of deregression reported in the literature vary from the simplest form of deregression, just dividing each EBV by its reliability (Goddard, 1985), to more sophisticated deregression procedures. The latter involves setting up the complete mixed model equations (MME) for all animals in the pedigree (Jairath et al., 1998). Thus, to simplify and avoid to reconstruct the complete MME, different strategies have been proposed (Garrick et al., 2009; VanRaden et al., 2009). In this way, the challenge is to find the most efficient deregression method that provides the best advantages of using dEBV as pseudophenotype in the second step of genomic prediction.
In a recent study based on simulated data, Calus et al. (2016) compared the performance of different deregression methods for non-longitudinal traits. These authors did not analyse the direct impact of deregression methods on the GEBVs, but showed that the majority of the methods yielded biased dEBVs when compared to EBVs, especially for cows. As an attempt to reduce the influence of bias of cow genetic evaluations and improve their contribution for the genomic selection accuracy, an adjustment to decrease the variance and mean of cow's EBVs and dEBVs was proposed for accumulated milk traits (Wiggans, Cooper, VanRaden, & Cole, 2011).
Although some countries are still using accumulated yields for genetic selection in dairy cattle, there are several advantages of using yields recorded on test-day for genetic evaluations (Schaeffer, 2004). Some of these advantages are more precise adjustment for environmental effects, accounting for the shape of lactation curves, and the possibility to evaluate animals with incomplete lactation through random regression models (RRM). Especially regarding genomic predictions, the application of RRM in both steps of two-step genomic selection could provide suitable opportunities to select genotyped animals based on the complete pattern of the production curve, without changing the genetic evaluation systems used in several countries. However, besides all progress achieved in the field of genomics in the last decade, to our knowledge, there are no reports evaluating deregression of EBVs for genomic predictions of test-day traits, especially in breeding programs with small training populations including cows’ records. In this context, the objective of this study was to investigate the performance of the most used deregression methods for non-longitudinal traits in the deregression of cows’ and bulls’ EBVs for genomic evaluation of test-day traits in the Canadian Jersey breed.
2 MATERIALS AND METHODS
The Canadian Dairy Network (CDN; Guelph, ON, Canada) provided the pedigree, genotypes and two official genetic evaluations for milk (MY), fat (FY) and protein (PY) yield and somatic cell score (SCS) from the first lactation of Jersey cows. The two official genetic evaluations were from December 2012 to December 2016 and contained the estimates of lactation curve random regression genetic coefficients and reliabilities for 134,631 and 160,241 animals, respectively. Details about the model used by CDN are presented in Interbull (2016a,b).
To preserve the shape of the genetic lactation curves, EBVs for each day in milk (from 5 to 305 days) were derived using the genetic coefficients for each trait, and, then, three different deregression methods were contrasted: (i) VR (VanRaden et al., 2009); (ii) WG (Wiggans et al., 2011); and (iii) GR (Garrick et al., 2009). The implementation of these single-trait deregression methods is described in the next section.
2.1 Deregression methods
2.1.1 VR method
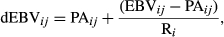 (1)
(1)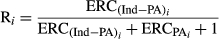 (2)
(2)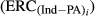 , and for the PA (
, and for the PA (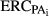 ) of the animal i were estimated based on (VanRaden & Wiggans, 1991):
) of the animal i were estimated based on (VanRaden & Wiggans, 1991):
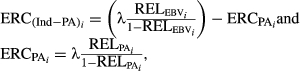 (3)
(3)in which, λ = (1 - h
2)/h
2, and 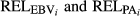 are the average of reliabilities for the EBV and PA of the animal i for each analysed trait, respectively. Heritabilities (h
2) considered in all deregression methods were 0.37, 0.29, 0.31 and 0.14 for MY, FY, PY and SCS, respectively (Interbull, 2016a,b).
are the average of reliabilities for the EBV and PA of the animal i for each analysed trait, respectively. Heritabilities (h
2) considered in all deregression methods were 0.37, 0.29, 0.31 and 0.14 for MY, FY, PY and SCS, respectively (Interbull, 2016a,b).
2.1.2 WG method
It consists in adjusting the EBVs and dEBVs of cows, estimated as in the VR method, to make them similar to those of bulls. In summary, for longitudinal traits, the following scheme was implemented:
- Estimate dEBV ij for all cows and bulls based on Equation 1 without adding the PA ij effect;
- Group the animals present in the official 2012 genetic evaluation run by similar
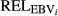 (from 0.00 to 0.20, 0.20 to 0.40, … , 0.80 to 1.00);
(from 0.00 to 0.20, 0.20 to 0.40, … , 0.80 to 1.00); - Estimate the variance adjustment (VA j ) for each group of animals in each day j as standard deviation of dEBV j of bulls divided by the standard deviation of dEBV j of cows;
- Estimate the mean adjustment (MA j ) for each group of animals in each day j as the difference between the average of dEBV j of bulls and cows after VA;
- Average VA j and MA j across groups (all genotyped cows and dams of genotyped animals will receive the same adjustment for each day j);
- Estimate the adjusted PA (PAadj) and the adjusted dEBV for all genotyped bulls (dEBVadj,bulls) and cows (dEBVadj,cows) as follow:
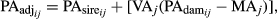 (4)where
(4)where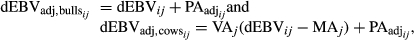
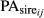 and
and 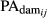 are the fraction of PA from the sire and dam of the animal i in the day j, respectively.
are the fraction of PA from the sire and dam of the animal i in the day j, respectively. - Reverse the deregression to obtain the adjusted EBV (EBVadj) for animal i in the day j as follows:
where R i was computed as described in Equation 2.
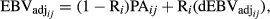 (5)
(5)
2.1.3 GR method
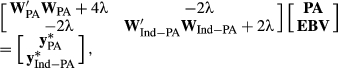 (6)
(6)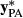 and
and 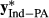 are the amount of information equivalent to the right-hand-side elements due to PA and animal effect free of PA, respectively. The
are the amount of information equivalent to the right-hand-side elements due to PA and animal effect free of PA, respectively. The  and
and 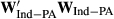 represent the unknown information content of the PA and animal effect free of PA, respectively. These terms are estimated as follows:
represent the unknown information content of the PA and animal effect free of PA, respectively. These terms are estimated as follows:
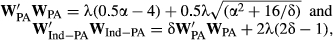 (7)
(7)where α = 1/(0.5 – REL PA ), δ =(0.5 – REL PA ) / (1–REL EBV ) and λ = (1 - h 2)/h 2 as previously defined. Programming codes in R (R Core Team, 2016), written to create the dEBVs using the different methods of deregression, are available in Table S1.
2.2 Statistical analysis
To compare the efficiency of deregression methods, we have performed genomic predictions of breeding values using pseudophenotypes calculated based on each deregression method (described below). The training population included genotyped animals from 2012 official genetic evaluation provided by CDN. Genotyped individuals born after 2011 that were not included in the training population were used as validation population. Thus, animals in the training and validation populations were born between 1960 and 2010, and between 2011 and 2014, respectively.
Three scenarios were considered for each trait: (i) including only animals with RELEBV higher than the average of RELPA for the analysed trait in the training and validation populations (SCEN1); (ii) including only animals with RELEBV higher than 0.50 in the training population and RELEBV higher than the average RELPA in the validation population (SCEN2); and (iii) including only animals with RELEBV higher than 0.50 in the training and validation populations (SCEN3). Average of RELPA was 0.35, 0.35, 0.34 and 0.31 for MY, FY, PY and SCS in the training population, respectively, and 0.34, 0.33, 0.33 and 0.27 for MY, FY, PY and SCS in the validation population, respectively. Genotyped animals that did not have own performance or progeny information 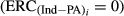 were excluded from all scenarios. This is because they would not contribute to the marker effect estimation and could cause double-counting of information. In other words, an animal without own phenotype or without phenotype of daughters would have an EBV calculated solely based on PA and, therefore, this would be duplicated information in the analysis.
were excluded from all scenarios. This is because they would not contribute to the marker effect estimation and could cause double-counting of information. In other words, an animal without own phenotype or without phenotype of daughters would have an EBV calculated solely based on PA and, therefore, this would be duplicated information in the analysis.
2.2.1 Genotype quality control
Originally, a total of 499 animals were genotyped using low-density panels (3K, 7K, 8K or 15K), 57 animals were genotyped using medium-density panels (20K or 30K), 1,046 animals were genotyped using 50K panels, and 202 animals were genotyped using high-density panels. All genotypes were imputed to 50K using FImpute software (Sargolzaei, Chesnais, & Schenkel, 2011). Details about the accuracy of imputation for Canadian dairy cattle breeds can be found in Larmer, Sargolzaei, and Schenkel (2014). After the imputation process, single nucleotide polymorphisms (SNPs) with Mendelian conflicts, call rate less than 0.95, minor allele frequency (MAF) less than 0.01 and SNPs with departure from expected heterozygosity higher than 0.15 were removed using the PreGSF90 software (Aguilar, Misztal, Tsuruta, Legarra, & Wang, 2014). After the quality control, 38,166 SNPs on the 29 bovine autosomes remained in the analysis.
2.2.2 Random regression GBLUP
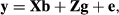 (8)
(8)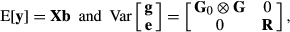 (9)
(9)where G
0 and R are the additive genetic and residual variance–covariance matrices, respectively. Residual variance was initially assumed homogenous along lactation for all traits 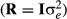 , as the official genetic evaluation carried out by CDN already accounted for heterogeneous variance (Interbull, 2016a,b). The G is the genomic relationship matrix, constructed according to VanRaden (2008). The AIREMLF90 software (Misztal et al., 2002) was used to estimate the variance components and the solutions of the MME for the regression coefficients.
, as the official genetic evaluation carried out by CDN already accounted for heterogeneous variance (Interbull, 2016a,b). The G is the genomic relationship matrix, constructed according to VanRaden (2008). The AIREMLF90 software (Misztal et al., 2002) was used to estimate the variance components and the solutions of the MME for the regression coefficients.
2.2.3 Weights
In general, there is a high variability of RELEBV between animals in dairy cattle populations, especially between bulls and cows. Thus, considering this variability may yield more reliable predictions (Vandenplas & Gengler, 2015). To verify whether the performance of the deregression methods is influenced for this variability, all analyses were carried out considering no weight (first subscenario), and considering the ERC of an animal, excluding the PA information (ERC(Ind-PA)), as weight for the inverse of residual variance matrix (second subscenario). Hereafter, the first subscenario will be referred as “UW” and the second one as “WT”, in the subscript of each scenario. For instance, the first scenario considering the second subscenario will be called SCEN1WT. Finally, a total of 18 analyses were carried out for each trait (3 deregression methods × 3 scenarios × 2 subscenarios).
2.2.4 Direct genomic values
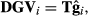 (10)
(10)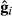 is the vector of predicted genomic random regression coefficients, and T is a matrix of orthogonal covariates associated with the fourth-order Legendre polynomials.
is the vector of predicted genomic random regression coefficients, and T is a matrix of orthogonal covariates associated with the fourth-order Legendre polynomials.2.3 Comparison of different deregression methods
The different deregression methods were compared by contrasting reliabilities and bias (slope of the linear regression of dEBV on DGV; bDGV), considering all days in milk (i.e., from 5 to 305), for each trait in the validation population. Realized reliabilities of dEBV 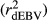 and DGV
and DGV 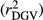 were calculated as the square of Pearson correlation between dEBV and EBV, and between DGV and dEBV, respectively. To adjust
were calculated as the square of Pearson correlation between dEBV and EBV, and between DGV and dEBV, respectively. To adjust 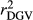 for the inaccuracy of dEBVs, adjusted realized reliabilities (
for the inaccuracy of dEBVs, adjusted realized reliabilities ( ) were calculated dividing
) were calculated dividing 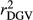 by
by 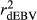 . Regression coefficients (bDGV) were used as indicator of bias of DGV, which assumes that the dEBVs were unbiased.
. Regression coefficients (bDGV) were used as indicator of bias of DGV, which assumes that the dEBVs were unbiased.
To evaluate the influence of deregression methods on cows’ and bulls’ DGV separately, they were split into two data sets after the GBLUP, and average and standard deviation of DGV and bDGV were calculated for cows (COWS), bulls (BULLS) and all animals combined (COMB).
3 RESULTS
Descriptive statistics of the training population in the COWS, BULLS and COMB data sets are shown in Table 1. Similar descriptive statistics for the validation populations are shown in Table S1.
| Scenario | Traits | N | Mean (SD) | ||||
|---|---|---|---|---|---|---|---|
| RELEBV | EBV | dEBVVR | dEBVWG | dEBVGR | |||
| COMB | |||||||
| Average RELPA | MY | 1,257 | 0.68 (0.18) | 8.23 (1.59) | 8.40 (2.06) | 7.76 (2.00) | 8.53 (2.54) |
| FY | 1,226 | 0.66 (0.19) | 0.38 (0.07) | 0.39 (0.09) | 0.35 (0.08) | 0.39 (0.12) | |
| PY | 1,249 | 0.65 (0.19) | 0.26 (0.07) | 0.27 (0.10) | 0.24 (0.09) | 0.27 (0.10) | |
| SCS | 1,199 | 0.56 (0.20) | −1.09 (0.31) | −1.09 (0.47) | −1.06 (0.48) | −1.09 (0.93) | |
| 0.50 | MY | 1,001 | 0.74 (0.15) | 8.14 (1.64) | 8.25 (1.91) | 7.60 (1.85) | 8.32 (2.14) |
| FY | 944 | 0.73 (0.15) | 0.38 (0.07) | 0.39 (0.08) | 0.34 (0.07) | 0.39 (0.09) | |
| PY | 944 | 0.73 (0.15) | 0.26 (0.07) | 0.27 (0.07) | 0.24 (0.07) | 0.27 (0.08) | |
| SCS | 544 | 0.74 (0.16) | −1.08 (0.34) | −1.08 (0.38) | −1.06 (0.38) | −1.08 (0.48) | |
| BULLS | |||||||
| Average RELPA | MY | 747 | 0.72 (0.21) | 8.21 (1.64) | 8.32 (2.05) | 7.81 (2.01) | 8.41 (2.51) |
| FY | 731 | 0.71 (0.21) | 0.37 (0.07) | 0.37 (0.08) | 0.34 (0.08) | 0.38 (0.11) | |
| PY | 741 | 0.71 (0.22) | 0.26 (0.07) | 0.26 (0.08) | 0.24 (0.08) | 0.26 (0.10) | |
| SCS | 721 | 0.63 (0.22) | −1.07 (0.33) | −1.06 (0.48) | −1.05 (0.48) | −1.05 (0.97) | |
| 0.50 | MY | 574 | 0.81 (0.15) | 8.07 (1.71) | 8.08 (1.89) | 7.58 (1.85) | 8.11 (2.06) |
| FY | 556 | 0.81 (0.15) | 0.37 (0.07) | 0.37 (0.08) | 0.34 (0.07) | 0.37 (0.08) | |
| PY | 554 | 0.81 (0.15) | 0.25 (0.07) | 0.25 (0.07) | 0.23 (0.07) | 0.25 (0.08) | |
| SCS | 450 | 0.78 (0.14) | −1.07 (0.35) | −1.07 (0.38) | −1.06 (0.38) | −1.08 (0.45) | |
| COWS | |||||||
| Average RELPA | MY | 510 | 0.61 (0.10) | 8.25 (1.52) | 8.52 (2.07) | 7.67 (1.99) | 8.71 (2.57) |
| FY | 495 | 0.58 (0.09) | 0.39 (0.06) | 0.41 (0.09) | 0.35 (0.09) | 0.42 (0.13) | |
| PY | 508 | 0.57 (0.09) | 0.27 (0.06) | 0.28 (0.12) | 0.24 (0.11) | 0.29 (0.10) | |
| SCS | 478 | 0.45 (0.06) | −1.13 (0.28) | −1.13 (0.46) | −1.09 (0.47) | −1.16 (0.86) | |
| 0.50 | MY | 427 | 0.65 (0.06) | 8.22 (1.53) | 8.47 (1.94) | 7.62 (1.86) | 8.60 (2.22) |
| FY | 388 | 0.63 (0.05) | 0.40 (0.06) | 0.41 (0.08) | 0.35 (0.07) | 0.42 (0.10) | |
| PY | 390 | 0.62 (0.05) | 0.27 (0.06) | 0.28 (0.07) | 0.24 (0.07) | 0.29 (0.08) | |
| SCS | 94 | 0.54 (0.04) | −1.12 (0.28) | −1.11 (0.39) | −1.07 (0.40) | −1.11 (0.60) | |
- Average RELPA, minimum RELEBV equal to average of reliability of parent average; N, number of animals.
- Average RELPA was estimated to be 0.35, 0.35, 0.34 and 0.31 for milk (MY), fat (FY), protein (PY) yield and somatic cell score (SCS), respectively. dEBV: deregressed EBV estimated by VanRaden (dEBVVR), Wiggans (dEBVWG) and Garrick (dEBVGR) methods.
Scenarios considering only animals with RELEBV greater than 0.50 in the training population (SCEN2 and SCEN3, displayed as scenario 0.5 in Table 1) had approximately 20%, 23%, 24% and 55% less animals compared to SCEN1 for MY, FY, PY and SCS, respectively. The proportion of cows in the training population was around 40% for almost all traits and scenarios (except for SCS in SCEN2 and SCEN3, in which the proportion of cows was around 17%). As expected, RELEBV were higher for BULLS, and the mean of EBVs from each trait varied between scenarios according to direction of selection (SCEN1 had mean of EBV increased for MY, FY and PY and decreased for SCS, when compared to SCEN2 and SCEN3). The EBVs from COWS were more favourable (higher for MY, FY and PY and lower for SCS) than EBVs from BULLS, and the differences between them were higher in SCEN1 for SCS and in SCEN2 and SCEN3 for MY, FY and PY. For all traits and scenarios, the WG allowed to reduce the difference between dEBV from COWS and BULLS when compared to VR and GR methods. Among all tested methods, GR showed consistently the highest standard deviation of dEBVs for all analysed traits and scenarios. Meanwhile, the average dEBV was similar for VR and GR methods and constantly lower for WG method across the scenarios.
Table 2 shows the 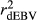 ,
, 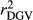 ,
, 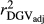 and bDGV for each deregression method, considering all scenarios in the COMB data set. According to unweighted analysis,
and bDGV for each deregression method, considering all scenarios in the COMB data set. According to unweighted analysis, 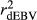 and
and 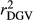 in SCEN3UW were higher than SCEN1UW and SCEN2UW. However, especially for SCEN2UW and SCEN3UW,
in SCEN3UW were higher than SCEN1UW and SCEN2UW. However, especially for SCEN2UW and SCEN3UW, 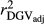 was similar for MY, FY and PY. In general,
was similar for MY, FY and PY. In general, 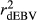 ,
, 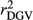 and
and 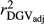 were similar for VR and WG (within each scenario), and lower reliability values were found for GR method for all traits. The DGV was overestimated for all traits and methods, as bDGV were significantly lower than 1. However, when comparing bDGV estimates, the DGVs were less biased for minimum reliability of 0.5 in the reference and the average of RELPA for validation population (SCEN2UW). Considering ERC(Ind-PA) as weight increased
were similar for VR and WG (within each scenario), and lower reliability values were found for GR method for all traits. The DGV was overestimated for all traits and methods, as bDGV were significantly lower than 1. However, when comparing bDGV estimates, the DGVs were less biased for minimum reliability of 0.5 in the reference and the average of RELPA for validation population (SCEN2UW). Considering ERC(Ind-PA) as weight increased 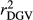 ,
, 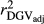 and bDGV just for PY and SCS in SCEN1WT, for VR and WG methods. For SCEN2WT, the bDGV of WG method generate undesirably decrease when compared to SCEN2UW. In addition, WG method only increased bDGV for MY and SCS in the SCEN2UW and SCEN3UW and for MY and SCS in the SCEN3WT.
and bDGV just for PY and SCS in SCEN1WT, for VR and WG methods. For SCEN2WT, the bDGV of WG method generate undesirably decrease when compared to SCEN2UW. In addition, WG method only increased bDGV for MY and SCS in the SCEN2UW and SCEN3UW and for MY and SCS in the SCEN3WT.
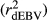 , realized and adjusted realized reliabilities of DGV
, realized and adjusted realized reliabilities of DGV 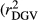 and
and 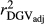 ) and regression coefficients (bDGV) for milk (MY), fat (FY), protein (PY) yields and somatic cell score (SCS) in the combined file
) and regression coefficients (bDGV) for milk (MY), fat (FY), protein (PY) yields and somatic cell score (SCS) in the combined file| Scenario | Trait | Method |
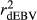
|
Without weight | ERC(Ind-PA) as weight | ||||
|---|---|---|---|---|---|---|---|---|---|
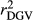
|
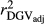
|
bDGV ± SE |
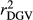
|
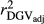
|
bDGV ± SE | ||||
| Average RELPA (SCEN1) | MY | VR | 0.71 | 0.27 | 0.38 | 0.87 ± 0.003 | 0.27 | 0.38 | 0.87 ± 0.003 |
| WG | 0.69 | 0.27 | 0.39 | 0.87 ± 0.003 | 0.27 | 0.39 | 0.87 ± 0.003 | ||
| GR | 0.55 | 0.15 | 0.27 | 0.71 ± 0.004 | 0.15 | 0.27 | 0.72 ± 0.004 | ||
| FY | VR | 0.77 | 0.22 | 0.28 | 0.72 ± 0.003 | 0.22 | 0.28 | 0.72 ± 0.003 | |
| WG | 0.73 | 0.20 | 0.27 | 0.70 ± 0.003 | 0.20 | 0.27 | 0.70 ± 0.003 | ||
| GR | 0.55 | 0.08 | 0.14 | 0.49 ± 0.004 | 0.08 | 0.14 | 0.49 ± 0.004 | ||
| PY | VR | 0.78 | 0.42 | 0.52 | 0.79 ± 0.002 | 0.46 | 0.59 | 0.88 ± 0.002 | |
| WG | 0.74 | 0.38 | 0.51 | 0.75 ± 0.002 | 0.43 | 0.58 | 0.85 ± 0.002 | ||
| GR | 0.56 | 0.24 | 0.43 | 0.72 ± 0.003 | 0.24 | 0.43 | 0.74 ± 0.003 | ||
| SCS | VR | 0.74 | 0.17 | 0.23 | 0.50 ± 0.003 | 0.18 | 0.24 | 0.54 ± 0.002 | |
| WG | 0.75 | 0.16 | 0.21 | 0.50 ± 0.003 | 0.17 | 0.23 | 0.54 ± 0.003 | ||
| GR | 0.39 | 0.02 | 0.05 | 0.17 ± 0.003 | 0.02 | 0.05 | 0.17 ± 0.003 | ||
| 0.50 for training and average RELPA for validation (SCEN2) | MY | VR | 0.71 | 0.26 | 0.37 | 0.93 ± 0.003 | 0.26 | 0.37 | 0.93 ± 0.004 |
| WG | 0.69 | 0.26 | 0.38 | 0.94 ± 0.004 | 0.26 | 0.38 | 0.90 ± 0.003 | ||
| GR | 0.55 | 0.15 | 0.27 | 0.83 ± 0.005 | 0.15 | 0.27 | 0.83 ± 0.005 | ||
| FY | VR | 0.77 | 0.24 | 0.31 | 0.86 ± 0.004 | 0.24 | 0.31 | 0.86 ± 0.004 | |
| WG | 0.73 | 0.22 | 0.30 | 0.86 ± 0.004 | 0.23 | 0.32 | 0.80 ± 0.003 | ||
| GR | 0.55 | 0.10 | 0.19 | 0.71 ± 0.005 | 0.10 | 0.19 | 0.71 ± 0.005 | ||
| PY | VR | 0.78 | 0.47 | 0.60 | 0.94 ± 0.002 | 0.47 | 0.60 | 0.94 ± 0.002 | |
| WG | 0.74 | 0.44 | 0.60 | 0.92 ± 0.002 | 0.44 | 0.60 | 0.88 ± 0.002 | ||
| GR | 0.56 | 0.25 | 0.46 | 0.86 ± 0.003 | 0.25 | 0.46 | 0.86 ± 0.003 | ||
| SCS | VR | 0.74 | 0.23 | 0.31 | 0.78 ± 0.003 | 0.23 | 0.61 | 0.78 ± 0.003 | |
| WG | 0.75 | 0.23 | 0.31 | 0.79 ± 0.003 | 0.23 | 0.31 | 0.78 ± 0.003 | ||
| GR | 0.39 | 0.03 | 0.09 | 0.53 ± 0.01 | 0.03 | 0.09 | 0.53 ± 0.01 | ||
| 0.50 (SCEN3) | MY | VR | 0.90 | 0.34 | 0.38 | 0.91 ± 0.003 | 0.34 | 0.38 | 0.91 ± 0.003 |
| WG | 0.90 | 0.35 | 0.39 | 0.92 ± 0.003 | 0.35 | 0.39 | 0.92 ± 0.003 | ||
| GR | 0.81 | 0.23 | 0.28 | 0.80 ± 0.004 | 0.23 | 0.28 | 0.80 ± 0.004 | ||
| FY | VR | 0.88 | 0.28 | 0.32 | 0.84 ± 0.003 | 0.28 | 0.32 | 0.84 ± 0.003 | |
| WG | 0.86 | 0.26 | 0.30 | 0.84 ± 0.004 | 0.26 | 0.30 | 0.84 ± 0.004 | ||
| GR | 0.72 | 0.14 | 0.19 | 0.69 ± 0.004 | 0.14 | 0.19 | 0.69 ± 0.004 | ||
| PY | VR | 0.91 | 0.56 | 0.61 | 0.93 ± 0.002 | 0.56 | 0.61 | 0.93 ± 0.002 | |
| WG | 0.89 | 0.52 | 0.58 | 0.91 ± 0.002 | 0.52 | 0.58 | 0.91 ± 0.002 | ||
| GR | 0.76 | 0.37 | 0.49 | 0.84 ± 0.003 | 0.37 | 0.49 | 0.84 ± 0.003 | ||
| SCS | VR | 0.85 | 0.32 | 0.38 | 0.80 ± 0.01 | 0.33 | 0.39 | 0.80 ± 0.01 | |
| WG | 0.85 | 0.32 | 0.38 | 0.81 ± 0.01 | 0.32 | 0.38 | 0.81 ± 0.01 | ||
| GR | 0.55 | 0.10 | 0.18 | 0.63 ± 0.01 | 0.10 | 0.18 | 0.63 ± 0.01 | ||
- SCEN, scenario.
- Average RELPA: minimum RELEBV equal to average of reliability of parent average. Average RELPA was estimated to be 0.35, 0.35, 0.34 and 0.31 for MY, FY, PY and SCS, respectively. Deregression was based on VanRaden (VR), Wiggans (WG) and Garrick (GR) methods.
Average DGV and bDGV for BULLS and COWS, for unweighted analysis, are shown in Table 3. For all traits, average DGV was more favourable (higher for MY, FY and PY and lower for SCS) in BULLS compared to COWS data set. Regarding bDGV, DGV for MY tended to be underestimated for bulls and overestimated for cows, with all different methods and scenarios. In general, values of bDGV close to 1 were observed for PY in BULLS, mainly from VR and WG methods. Similar bDGV estimates were found for FY and SCS for BULLS and COWS data sets, within each deregression method, especially in SCEN1UW and SCEN2UW.
| Scenario | Trait | Method | BULLS | COWS | ||
|---|---|---|---|---|---|---|
| DGV (SD) | bDGV ± SE | DGV (SD) | bDGV ± SE | |||
| Average RELPA (SCEN1) | MY | VR | 8.73 (1.31) | 1.13 ± 0.01 | 8.53 (1.36) | 0.86 ± 0.003 |
| WG | 8.08 (1.26) | 1.13 ± 0.01 | 7.91 (1.31) | 0.85 ± 0.003 | ||
| GR | 8.94 (1.48) | 1.02 ± 0.02 | 8.69 (1.62) | 0.70 ± 0.004 | ||
| FY | VR | 0.41 (0.07) | 0.74 ± 0.01 | 0.40 (0.06) | 0.72 ± 0.003 | |
| WG | 0.37 (0.06) | 0.70 ± 0.01 | 0.36 (0.05) | 0.69 ± 0.003 | ||
| GR | 0.42 (0.08) | 0.57 ± 0.01 | 0.41 (0.07) | 0.49 ± 0.004 | ||
| PY | VR | 0.29 (0.06) | 0.99 ± 0.01 | 0.28 (0.07) | 0.77 ± 0.002 | |
| WG | 0.26 (0.06) | 0.98 ± 0.01 | 0.25 (0.06) | 0.74 ± 0.002 | ||
| GR | 0.30 (0.07) | 0.92 ± 0.01 | 0.29 (0.07) | 0.71 ± 0.003 | ||
| SCS | VR | −1.16 (0.33) | 0.44 ± 0.01 | −1.12 (0.31) | 0.51 ± 0.003 | |
| WG | −1.13 (0.33) | 0.43 ± 0.01 | −1.09 (0.31) | 0.50 ± 0.003 | ||
| GR | −1.20 (0.63) | 0.24 ± 0.02 | −1.11 (0.55) | 0.17 ± 0.003 | ||
| 0.50 for training and average RELPA for validation (SCEN2) | MY | VR | 8.73 (1.31) | 1.13 ± 0.02 | 8.53 (1.36) | 0.93 ± 0.004 |
| WG | 8.08 (1.26) | 1.13 ± 0.02 | 7.91 (1.31) | 0.93 ± 0.004 | ||
| GR | 8.94 (1.48) | 1.04 ± 0.02 | 8.69 (1.62) | 0.82 ± 0.005 | ||
| FY | VR | 0.41 (0.07) | 0.85 ± 0.01 | 0.40 (0.06) | 0.86 ± 0.004 | |
| WG | 0.37 (0.06) | 0.80 ± 0.01 | 0.36 (0.05) | 0.86 ± 0.004 | ||
| GR | 0.42 (0.08) | 0.66 ± 0.02 | 0.41 (0.07) | 0.72 ± 0.005 | ||
| PY | VR | 0.29 (0.06) | 1.06 ± 0.01 | 0.28 (0.07) | 0.94 ± 0.002 | |
| WG | 0.26 (0.06) | 1.06 ± 0.01 | 0.25 (0.06) | 0.92 ± 0.002 | ||
| GR | 0.30 (0.07) | 0.98 ± 0.02 | 0.29 (0.07) | 0.85 ± 0.003 | ||
| SCS | VR | −1.16 (0.33) | 0.71 ± 0.02 | −1.12 (0.31) | 0.78 ± 0.003 | |
| WG | −1.13 (0.33) | 0.71 ± 0.02 | −1.09 (0.31) | 0.79 ± 0.004 | ||
| GR | −1.20 (0.63) | 0.41 ± 0.04 | −1.11 (0.55) | 0.54 ± 0.01 | ||
| 0.50 (SCEN3) | MY | VR | 8.70 (1.14) | 1.10 ± 0.01 | 8.47 (1.25) | 0.90 ± 0.003 |
| WG | 8.05 (1.10) | 1.12 ± 0.02 | 7.84 (1.19) | 0.91 ± 0.003 | ||
| GR | 8.87 (1.22) | 1.02 ± 0.02 | 8.56 (1.39) | 0.79 ± 0.004 | ||
| FY | VR | 0.42 (0.05) | 0.73 ± 0.02 | 0.40 (0.05) | 0.84 ± 0.003 | |
| WG | 0.38 (0.05) | 0.63 ± 0.02 | 0.36 (0.05) | 0.84 ± 0.004 | ||
| GR | 0.44 (0.05) | 0.53 ± 0.02 | 0.41 (0.06) | 0.69 ± 0.004 | ||
| PY | VR | 0.29 (0.06) | 0.97 ± 0.01 | 0.28 (0.06) | 0.93 ± 0.002 | |
| WG | 0.26 (0.05) | 0.96 ± 0.01 | 0.25 (0.06) | 0.90 ± 0.002 | ||
| GR | 0.30 (0.06) | 0.87 ± 0.01 | 0.28 (0.06) | 0.84 ± 0.003 | ||
| SCS | VR | −1.18 (0.22) | 0.90 ± 0.01 | −1.12 (0.24) | 0.77 ± 0.01 | |
| WG | −1.26 (0.22) | 0.90 ± 0.01 | −1.10 (0.24) | 0.78 ± 0.01 | ||
| GR | −1.21 (0.24) | 0.86 ± 0.02 | −1.13 (0.27) | 0.57 ± 0.01 | ||
- SCEN, scenario.
- Average RELPA: minimum RELEBV equal to average of reliability of parent average. Average RELPA was estimated in 0.35, 0.35, 0.34 and 0.31 for MY, FY, PY and SCS, respectively. Deregression of estimated breeding value was based on VanRaden (VR), Wiggans (WG) and Garrick (GR) methods. SE: standard error.
4 DISCUSSION
Reliable performance information and large size of the training population are crucial factors to ensure high reliability in the genomic predictions (Liu et al., 2011). Thus, to increase the size of training population in breeds with lower number of animals, females usually have been included in official genomic evaluations in several countries (Interbull, 2016c; Koivula, Strandén, Aamand, & Mäntysaari, 2016). A lower proportion of cows were observed for SCS when the minimum RELEBV was considered equal to 0.50, as most cows had RELEBV lower than this assumed threshold. In addition, average EBVs from cows were higher (in absolute values) than EBVs from bulls for all analysed traits, probably because only important cows have been genotyped in the Jersey breed. Thus, these cows might have some level of preferential treatment. Preferential treatment has been reported as one of the main causes of bias in cows evaluations (Dassonneville, Baur, Fritz, Boichard, & Ducrocq, 2012), as cows selected to be genotyped are important animals in the breed (i.e., dams or future dams of bulls with high EBV for economically important traits). Several studies have reported that preferential treatment increases linearly the bias of cow evaluations (Kuhn, Boettcher, & Freeman, 1994). However, adjustments have been developed to make these evaluations comparable with those of bulls. Besides its simple application, adjustments of WG method allowed to reduce the differences between dEBV from cows and bulls when compared to VR and GR methods (Table 1).
Efficiency of genomic predictions depends on the accuracy of estimated marker effects, which relies on the information contained in the dEBVs. In spite of the fact that dEBV is derived from EBV, they might substantially differ and the difference between them increases as the RELEBV decreases. Thus, as the deregression process is less severe for animals with high RELEBV, 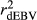 and
and 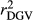 were higher in the scenario that just considered animals with RELEBV higher than 0.50 in the training and validation populations (SCEN3). However, when adjusting
were higher in the scenario that just considered animals with RELEBV higher than 0.50 in the training and validation populations (SCEN3). However, when adjusting 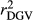 for the inaccuracy of dEBVs in the validation population
for the inaccuracy of dEBVs in the validation population 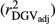 , SCEN2 and SCEN3 were similar for MY, FY and PY traits (Table 2). Especially for SCS,
, SCEN2 and SCEN3 were similar for MY, FY and PY traits (Table 2). Especially for SCS, 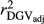 estimated in the SCEN2 were lower than those estimated in the SCEN3, probably due to the large effect of reduced number of animals in the validation population when a minimum RELEBV of 0.50 was considered (Table S1). Thus, our results suggest that the influence of RELEBV in the
estimated in the SCEN2 were lower than those estimated in the SCEN3, probably due to the large effect of reduced number of animals in the validation population when a minimum RELEBV of 0.50 was considered (Table S1). Thus, our results suggest that the influence of RELEBV in the 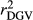 for the animals in the validation population can be easily adjusted using the
for the animals in the validation population can be easily adjusted using the 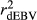 . Nowadays, several authors have opted to report reliabilities adjusted for the inaccuracy of the dEBVs in genomic selection studies (Baba et al., 2016; Koivula et al., 2016).
. Nowadays, several authors have opted to report reliabilities adjusted for the inaccuracy of the dEBVs in genomic selection studies (Baba et al., 2016; Koivula et al., 2016).
Estimated 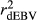 ,
, 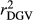 and
and 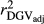 were similar for VR and WG methods, suggesting that the adjustment made by WG had small effect in the reliabilities of genomic prediction for Jersey cattle. These results corroborate with those reported by Wiggans et al. (2011) for total milk, fat and protein yield in Jersey cattle, where small difference between realized reliability estimated using adjusted and unadjusted predicted transmitting abilities were found. Contrasting all analysed methods, GR resulted in lower
were similar for VR and WG methods, suggesting that the adjustment made by WG had small effect in the reliabilities of genomic prediction for Jersey cattle. These results corroborate with those reported by Wiggans et al. (2011) for total milk, fat and protein yield in Jersey cattle, where small difference between realized reliability estimated using adjusted and unadjusted predicted transmitting abilities were found. Contrasting all analysed methods, GR resulted in lower 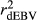 ,
, 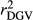 and
and 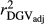 for all traits (Table 2), which is due to the strength of the deregression of EBVs in this method when compared to VR and WG. For this reason, the GR generated more variable dEBV for all traits (which is indicated by standard deviations in Table 1), suggesting that the deregression was too strong. These results corroborate with those reported by Song, Li, Zhang, Zhang, and Ding (2017), which also presented higher variance for dEBVs and lower
for all traits (Table 2), which is due to the strength of the deregression of EBVs in this method when compared to VR and WG. For this reason, the GR generated more variable dEBV for all traits (which is indicated by standard deviations in Table 1), suggesting that the deregression was too strong. These results corroborate with those reported by Song, Li, Zhang, Zhang, and Ding (2017), which also presented higher variance for dEBVs and lower 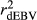 generated by the GR method. Calus et al. (2016) also concluded that the deregression by GR was too strong compared to VR method. Therefore, based on our findings, the use of the GR method is less suitable for test-day traits compared to the others methods investigated here.
generated by the GR method. Calus et al. (2016) also concluded that the deregression by GR was too strong compared to VR method. Therefore, based on our findings, the use of the GR method is less suitable for test-day traits compared to the others methods investigated here.
The ability to reduce the bias in the genomic predictions is an important factor when comparing different deregression methods. In general, a necessary (but not sufficient) condition for unbiased prediction of a model is that the slope of the linear regression of dEBV on predicted DGV should be close to one, assuming unbiased dEBVs. In this context, we found that the DGV was overestimated in all tested deregression methods. This is likely a consequence that the analysed traits are under selection pressure. When considering animals with lower RELEBV in the training population further increased the overestimation. It means that increasing the size of training population using animals with low RELEBV (in unweighted analysis) increases the bias, probably due to more heterogeneous amount of information used to generate the EBVs. The heterogeneity of information was larger for PY and SCS in SCEN1, which explains the best performance of these traits in the weighted analysis (SCEN1WT). In agreement with Guo et al. (2010), the weighted analysis in scenarios that considered minimum RELEBV of 0.50 in the training population (SCEN2WT and SCEN3WT) did not result in accuracy improvement. The WG method in the SCEN2WT (Table 2) had the bDGV significantly decreased when compared to SCEN2UW. This suggests that, for different minimum criteria for RELEBV in the training and validation populations, the weights used should consider the adjustments made in dEBVs of cows.
It is important to highlight that, in despite of the great numerical properties of GR (Garrick et al., 2009), this method showed the worst performance among all comparisons in the present study. In addition, using weighted analysis did not improve the GR method (Table 2). Thus, the stronger deregression performed by GR method (as discussed earlier) requires the use of specific weights in the inverse of residual variance matrix (R −1). Garrick et al. (2009) have deduced the optimal weights to be considered in R −1 based on heritability, RELEBV and the fraction of genetic variance not explained by markers. In this context, Song et al. (2017) tested the GR method considering the optimal weights based on different heritabilities and proportions of genetic variance not explained by markers. However, these authors found that, given a fixed heritability, increasing the proportion of genetic variance not explained by markers decreased the accuracy of genomic prediction and increased the bias. Thus, they concluded that weighting the R −1 matrix by the reliability of response variable is, generally, more stable. In our study, as the weights were just used to verify whether the performance of the methods is changed when using weighted analysis, we have opted to use the same weight for all tested methods. For this reason, we used one of the simplest weights described in the literature, that is, ERC. However, additional studies contrasting the performance of different deregression methods considering different weights are necessary.
In contrast to Table 1, breeding values in the validation population were more favourable (higher for MY, FY and PY and lower for SCS) for BULLS than COWS (Tables S1 and 3). This is probably related to the higher selection intensity for young bulls when compared to young cows, which have resulted in a small number of bulls mainly in the validation population (Table S1).
5 CONCLUSIONS
Deregressed longitudinal EBVs obtained using well-established methods of deregression for non-longitudinal traits seem a feasible alternative for genomic prediction of longitudinal traits. For all analysed test-day traits, the VR and WG deregression methods yielded to similar results, being, however, more accurate and less biased than GR independently of the minimum RELEBV considered. The scenario considering a minimum RELEBV of 0.50 in the training and minimum RELEBV equal to the average of RELPA in the validation population allowed for obtaining high reliabilities of predicted DGV and the smallest prediction biases. Weighted residual analysis only showed benefits when differences in RELEBV among animals in the training population were high.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge the financial support to this research from Agriculture and Agri-Food Canada and by additional contributions from Dairy Farmers of Canada, the Canadian Dairy Network and the Canadian Dairy Commission under the Agri-Science Clusters Initiative.




