Use of random regression model as an alternative for multibreed relationship matrix
Summary
A random regression model is presented as an approximation for multibreed variance model. The approximation is derived using the splitted multibreed model where the single breeding value is split to the breed specific and their segregation terms. The random regression model allows extending the multibreed information easily to genomic data models. We present the approach by a simple example.
Introduction
Two models of breeding value and variance component estimation for multibreed data have been presented in Lo et al. (1993), Cantet & Fernando (1995), and García-Cortés & Toro (2006). Lo et al. (1993), and Cantet & Fernando (1995) build a single covariance matrix to describe relationships between breeding values. Thus, there is one covariance matrix having breed proportion information and variance components, and one breeding value for each animal. In contrast, García-Cortés & Toro (2006) splits the single breeding value to its breed and breed segregation specific components. In this split breeding value model, each breeding value component is a random effect with a specific relationship matrix, and the breeding value components are uncorrelated in the variance structure.
The original multibreed model can be solved by standard linear mixed model equations (Henderson 1984). However, the covariance structure for the breeding values contains the variance components making its use in practice numerically expensive when variance components are estimated. When the covariance structure is built externally, the split breeding value model allows using standard variance component estimation software in analysis of multibreed data where the variance components multiply the correlation structure of breeding values. However, neither of these multibreed models can use genomic marker information. Objective of this study was to derive random regression models that are approximations to the multibreed model. The approximation allows an easy approach to use multibreed data and also allows genomic data models.
Additive multibreed linear mixed models
Multibreed models need information on observations, fixed effects, pedigree information etc. but also information on the breed composition of animals. Each animal in the pedigree must have breed proportion values that indicate proportion of genes in the animal from the different breeds in the analysis. Let  be proportion of genes in animal i from breed p. The breed proportions of animal i sum to one. For a purebred animal, only one of the breed proportion values is one, and the others are zero.
be proportion of genes in animal i from breed p. The breed proportions of animal i sum to one. For a purebred animal, only one of the breed proportion values is one, and the others are zero.
 (1)
(1)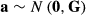 , and
, and 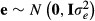 . Thus,
. Thus, 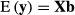 and
and  . Matrix G describes variances and covariances in a multibreed population where individual is allowed to have unique breed composition and each breed has individual genetic variance. Lo et al. (1993) describe rules for obtaining the relationship matrix G using pedigree, breed proportion and variance component information. Note that the additive covariance matrix G cannot be expressed as the numerator relationship matrix times additive genetic variance but contains the necessary variances in the matrix.
. Matrix G describes variances and covariances in a multibreed population where individual is allowed to have unique breed composition and each breed has individual genetic variance. Lo et al. (1993) describe rules for obtaining the relationship matrix G using pedigree, breed proportion and variance component information. Note that the additive covariance matrix G cannot be expressed as the numerator relationship matrix times additive genetic variance but contains the necessary variances in the matrix.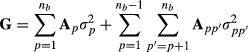 (2)
(2)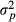 is the additive genetic variance of breed p and
is the additive genetic variance of breed p and 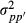 is the genetic segregation variance between breeds p and p′. The authors gave algorithms to calculate the required partial numerator relationship matrices. Splitting the covariance matrix G to its breeding value components allows using model
is the genetic segregation variance between breeds p and p′. The authors gave algorithms to calculate the required partial numerator relationship matrices. Splitting the covariance matrix G to its breeding value components allows using model
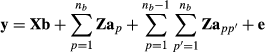 (3)
(3) and
and 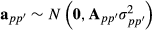 .
.The mixed model equations by model (3) is much larger than by model (1) but has the advantage of allowing separation of the variance terms from the covariance matrix as a multiplier. In practice, this allows implementation of computationally more efficient breeding value and variance component estimation approaches. Model (3) can be used in standard variance component estimation software such as ASREML (Gilmour et al. 2009) when the partial relationship matrices or their inverses are available as external covariance structures stored in files. However, special software has to be written to analyse large data sets. In addition, the model does not allow use of genomic marker information. In the following, we derive a random regression approximation to model (3) that can be easily extended to use genomic marker information.
Random regression approximation to the multibreed model
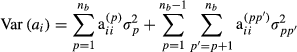
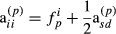
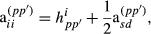
 is the proportion of genes of the animal i coming from breed p, s and d denote sire and dam of individual i, respectively, and
is the proportion of genes of the animal i coming from breed p, s and d denote sire and dam of individual i, respectively, and 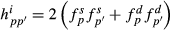 . These formulas have the same structure as diagonal of standard numerator relationship matrix A where diagonal of animal i is
. These formulas have the same structure as diagonal of standard numerator relationship matrix A where diagonal of animal i is 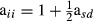 . When all animals are 100% of, say, breed one, then
. When all animals are 100% of, say, breed one, then 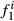 is always one,
is always one, 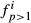 are zero and
are zero and  are zero giving A1 = A and Ap>1 = 0.
are zero giving A1 = A and Ap>1 = 0.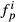 and
and  , respectively, when the partial relationship coefficients
, respectively, when the partial relationship coefficients 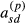 and
and  , respectively, are zero. We will assume this proportionality to hold for the terms
, respectively, are zero. We will assume this proportionality to hold for the terms 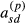 and
and 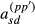 as well for all individuals. Thus, the approximation assumes that all diagonal elements have form
as well for all individuals. Thus, the approximation assumes that all diagonal elements have form 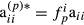 and
and  where
where 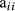 is diagonal element in A for animal i, and asterisk (*) in superscript is used to denote approximation of
is diagonal element in A for animal i, and asterisk (*) in superscript is used to denote approximation of  and
and  . In our approximate model, breeding value variance of individual i is given as follows:
. In our approximate model, breeding value variance of individual i is given as follows:
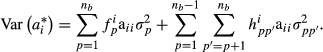
In the model (3) of García-Cortés & Toro (2006), diagonal elements of partial relationship matrices Ap and App′ are functions of relationship coefficient between parents that depend on the breed proportions of the parents. In our approximation, we assume that the diagonal elements are functions of the breed proportions of individual itself.
The formulas to calculate off-diagonal elements of the partial relationship matrices Ap and App′ are  and
and  , respectively. Corresponding formula in the standard numerator relationship matrix A has the same form
, respectively. Corresponding formula in the standard numerator relationship matrix A has the same form  . The approximation can be extended to the off-diagonal elements where we calculate
. The approximation can be extended to the off-diagonal elements where we calculate  and
and  .
.
 and
and 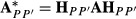 where Fp is diagonal matrix having square roots of breed proportions of individuals, and diagonal matrix Hpp′ has square roots of
where Fp is diagonal matrix having square roots of breed proportions of individuals, and diagonal matrix Hpp′ has square roots of 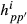 values. Note that the diagonal matrices Fp and Hpp′ contain square roots similarly as in the Cholesky decomposition of the partial relationship matrix given in García-Cortés & Toro (2006). The full approximate G matrix can be written as follows:
values. Note that the diagonal matrices Fp and Hpp′ contain square roots similarly as in the Cholesky decomposition of the partial relationship matrix given in García-Cortés & Toro (2006). The full approximate G matrix can be written as follows:

The G* matrix could be used as an approximation to G in the mixed model equations in model (1) but with the same inherent problem that the variance components are part of the covariance structure and cannot be factored as multipliers.
The split breeding value approach by García-Cortés & Toro (2006) can be used for the approximation as well. Linear mixed effects model for the approximation has the same appearance as model (3) but it is now assumed that  and
and  . Mixed model equations using these assumptions will lead to separate breeding value–specific partial covariance matrices as for model (3) where ap and app′ have been replaced by
. Mixed model equations using these assumptions will lead to separate breeding value–specific partial covariance matrices as for model (3) where ap and app′ have been replaced by  and
and  , respectively.
, respectively.
 and
and 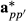 using breed proportion information Fp and Hpp′ can be relaxed by using equivalent random regression model. The matrices Fp and Hpp′ can be factored out from the covariance structure of
using breed proportion information Fp and Hpp′ can be relaxed by using equivalent random regression model. The matrices Fp and Hpp′ can be factored out from the covariance structure of  and
and 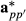 , respectively, to be part of the model equations. Then, the model is given as follows:
, respectively, to be part of the model equations. Then, the model is given as follows:
 (4)
(4)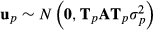 and
and  where diagonal matrices Tp and Tpp′ are incidence matrices having ones for animals with nonzero values in Fp and Hpp′, respectively. Thus, TpATp matrix has the same elements as ordinary A matrix but row and column values are zero for purebred animals of breeds other than p.
where diagonal matrices Tp and Tpp′ are incidence matrices having ones for animals with nonzero values in Fp and Hpp′, respectively. Thus, TpATp matrix has the same elements as ordinary A matrix but row and column values are zero for purebred animals of breeds other than p.Total breeding value is directly estimated in model (1). Total breeding value by the equivalent split breeding value model (3) is sum of the component breeding values:  . Similarly, total breeding value by the approximate random regression model (4) is
. Similarly, total breeding value by the approximate random regression model (4) is  .
.
Multibreed random regression model and genomic data
Genomic data models like G-BLUP have the same form as model (1), for example, VanRaden (2008). However, the G matrix given in formula (2) is replaced by genetic variance times genomic relationship matrix GM formed by using genomic SNP marker information. Often, the matrix has form GM = ZMZ′M. For example, VanRaden (2008) gave two commonly used genomic relationship matrices, which can be expressed in this form. Genomic relationship matrix GM and pedigree-based relationship matrix A describe relationships in population without trait specific variance parameter, which is included in the G matrix.
Model (4) can be applied for the genomic data model by using genomic relationship matrix GM instead of the numerator relationship matrix A. When all genotyped animals are breed crosses, that is, there are no genotyped purebred animals; matrices Tp and Tpp′ are identity matrices. Consequently, the mixed model equations simplify to using the same genomic relationship matrix for all breeding value components of the random regression model. The above-presented approximate model with genomic relationship matrix was used in Makgahlela et al. (2013) to analyse multibreed genomic data except that terms upp′ were unaccounted.
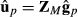 . Thus, similarly as for the random regression model, we can rewrite the multibreed G-BLUP model as a genomic marker model
. Thus, similarly as for the random regression model, we can rewrite the multibreed G-BLUP model as a genomic marker model
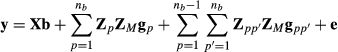
 and
and 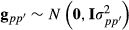 .
.Example data by García-Cortés and Toro
Pedigree data and variance components presented in García-Cortés & Toro (2006) are used to illustrate the random regression model (Table 1). A two-breed model by Cantet & Fernando (1995) is used: y = Xb + Za1 + Za2 + Za12 + e where Z is identity matrix because all animals have an observation. There are 11 animals of which animals 1, 2 and 5 are purebred animals from breed 1, and animals 3, 4 and 7 are purebred animals from breed 2. The fixed effects are herd effect and breed proportion regression effects. The animals are in two herds. Individual animal breed proportions and segregation terms were calculated using the given pedigree.
| Animal | Sire | Dam | Breedb | Herd | Record | f 1 | f 2 | h 12 |
|---|---|---|---|---|---|---|---|---|
| 1 | – | – | 1 | 2 | 11 | 1 | 0 | 0 |
| 2 | – | – | 1 | 2 | 12 | 1 | 0 | 0 |
| 3 | – | – | 2 | 2 | 13 | 0 | 1 | 0 |
| 4 | – | – | 2 | 1 | 14 | 0 | 1 | 0 |
| 5 | 1 | 2 | – | 1 | 15 | 1 | 0 | 0 |
| 6 | 3 | 2 | – | 2 | 16 | 0.5 | 0.5 | 0 |
| 7 | 3 | 4 | – | 2 | 17 | 0 | 1 | 0 |
| 8 | 5 | 6 | – | 2 | 18 | 0.75 | 0.25 | 0.5 |
| 9 | 7 | 6 | – | 1 | 19 | 0.25 | 0.75 | 0.5 |
| 10 | 9 | 8 | – | 1 | 20 | 0.5 | 0.5 | 0.75 |
| 11 | 5 | 8 | – | 1 | 21 | 0.875 | 0.125 | 0.375 |
- a García-Cortés & Toro (2006).
- b Only base animals.
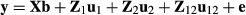
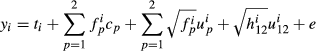
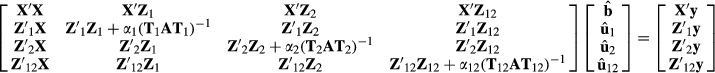
where the variance ratios are α1 = 4, α2 = 2 and α12 = 8. The fixed effects vector b has both the herd effects t and the two breed regression effects c.
Because all animals have an observation, the Z matrices are diagonal. Diagonal elements of matrices Z1, Z2 and Z12 are [1 1 0 0 1 0.707 0 0.866 0.5 0.707 0.935], [0 0 1 1 0 0.707 1 0.5 0.866 0.707 0.354] and [0 0 0 0 0 0 0 0.707 0.707 0.866 0.612], respectively.

Approximate partial relationship matrix for the random regression effect of breed one is  where diagonal matrix F1 has square roots of breed proportions f1 on the diagonal (Table 1). Thus,
where diagonal matrix F1 has square roots of breed proportions f1 on the diagonal (Table 1). Thus,  has zeros in rows and columns of the ordinary relationship matrix A for the purebred animals of breed 2, that is, animals 3, 4 and 7. Likewise, matrix
has zeros in rows and columns of the ordinary relationship matrix A for the purebred animals of breed 2, that is, animals 3, 4 and 7. Likewise, matrix  has zero rows and columns for purebred animals of breed 1, that is, 1, 2 and 5. The only nonzero elements in matrix
has zero rows and columns for purebred animals of breed 1, that is, 1, 2 and 5. The only nonzero elements in matrix  are in the lower right hand corner from animal 8 onwards. These animals have nonzero h12(Table 1). Hence, matrices
are in the lower right hand corner from animal 8 onwards. These animals have nonzero h12(Table 1). Hence, matrices  ,
,  and
and  are based on the standard numerator relationship matrix A but some columns and rows have been zeroed according to zero breed proportion or segregation value, and other elements have been weighted by breed proportion information. Mixed model equations have matrices T1AT1, T2AT2 and T12AT12 that have the same structure of zero rows and columns as the approximate partial relationship matrices. Consequently, many rows and columns of the mixed model equations will have zeros. Corresponding solutions in the mixed model equations were set to zero. In addition, herd effect one was restricted to be zero for the coefficient matrix to have full rank.
are based on the standard numerator relationship matrix A but some columns and rows have been zeroed according to zero breed proportion or segregation value, and other elements have been weighted by breed proportion information. Mixed model equations have matrices T1AT1, T2AT2 and T12AT12 that have the same structure of zero rows and columns as the approximate partial relationship matrices. Consequently, many rows and columns of the mixed model equations will have zeros. Corresponding solutions in the mixed model equations were set to zero. In addition, herd effect one was restricted to be zero for the coefficient matrix to have full rank.
 . Upper triangle of the total covariance matrix
. Upper triangle of the total covariance matrix  is given as follows:
is given as follows:

Table 2 has the diagonal elements of total genetic covariance matrix G as given in García-Cortés & Toro (2006), and the random regression model covariance matrix G*. The diagonal elements are the same for animals 1 to 7. There are small differences in the diagonal elements of animals 8 to 11. Some differences exist in the off-diagonal elements as well. Values in the G matrix by García-Cortés & Toro (2006) and our approximate G* are equal in the block of animals from one to five, and animal 7. The largest differences in the off-diagonal elements are those between animal 3 and 6, and between animal 3 and animals 8 to 11.
| Animal | CF model | APX model | ||
|---|---|---|---|---|
| diagG | EBV | diagG | EBV | |
| 1 | 1.00 | −0.29 | 1.00 | −0.33 |
| 2 | 1.00 | 0.29 | 1.00 | 0.15 |
| 3 | 2.00 | 0.69 | 2.00 | 0.30 |
| 4 | 2.00 | −0.69 | 2.00 | −0.73 |
| 5 | 1.00 | 0.24 | 1.00 | 0.10 |
| 6 | 1.50 | 1.22 | 1.50 | 1.22 |
| 7 | 2.00 | 0.67 | 2.00 | 0.43 |
| 8 | 1.62 | 1.75 | 1.69 | 1.89 |
| 9 | 2.25 | 1.26 | 2.25 | 1.29 |
| 10 | 2.15 | 1.78 | 2.23 | 1.94 |
| 11 | 1.62 | 1.46 | 1.72 | 1.60 |
- EBV, Estimated breeding values.
We illustrate reasons for differences between the G and approximate G* matrix by an example. Animal 6 is progeny of purebred animals 2 and 3 of breed 1 and 2, respectively. Thus, animal 6 has breed proportion of 0.5 for breeds one and two, and the segregation term is zero (Table 1). Covariance between animals 3 and 6 is one in G but 0.71 in G*. In matrix G, this value is due to the term  . Element (3,6) in A2 is
. Element (3,6) in A2 is  and
and  . Element (3,6) is zero in A1 and A12 because animal 3 is 100% of breed 2. Similarly, element (3,6) in G* is due to term
. Element (3,6) is zero in A1 and A12 because animal 3 is 100% of breed 2. Similarly, element (3,6) in G* is due to term  where element (3,6) in
where element (3,6) in  is
is  . The fact that animal 6 is an F1 cross between two purebred animals leads our approximation to decrease the relationship coefficient too much because this coefficient should not be influenced by breed proportion of individual but only its parents. Thus, in general, the more different are the breed proportions between parents of individual, the more different are the corresponding covariance terms of individual in G* from those in G.
. The fact that animal 6 is an F1 cross between two purebred animals leads our approximation to decrease the relationship coefficient too much because this coefficient should not be influenced by breed proportion of individual but only its parents. Thus, in general, the more different are the breed proportions between parents of individual, the more different are the corresponding covariance terms of individual in G* from those in G.
Estimated breeding values (EBV) by the methods were similar (Table 2). Largest difference was for animal 3, which had the largest differences between off-diagonal elements of G and G*. The base population had four animals numbered from 1 to 4. EBVs for the purebred animals 1 and 4 were similar by both methods because these animals had only purebred progeny. Purebred animals 2 and 3 had crossbred progeny that leads to larger differences in off-diagonal elements of G and G*, and EBVs by the two methods. Hence, the approximation is likely to work well when the population is highly admixed, that is, only a small fraction are purebred or first generation F1 crossbred animals. When the population consists of lines of purebred animals that are used to make F1 crossbred animals, the approximation is likely to work poorest. The small example (Table 1) had quite many purebred and F1 animals (63%), which should illustrate a poor case scenario for the approximation. Still, however, correlation of EBV between García-Cortés & Toro (2006) and our approximation showed a remarkably high correlation of 0.987.
Cross breeding often attempts to maximize the differences in breed composition of parent animals to attain positive heterosis. Our approximation is perhaps not well suited to such breeding structure. Our model was developed for analyses of admixed population such as the Nordic red dairy cattle (RDC). RDC population can still be roughly divided by country to subpopulations in terms of breed composition defined by breed proportions, although nowadays the population has common breeding pool of bulls. Makgahlela et al. (2013) applied subset of our approximate model in genomic model context to the RDC population. In their study, validation reliabilities by the approximate model were always at least as good as those by the model that did not account breed heterogeneity. This suggests that the approximation worked reasonably well, which can be expected because their study had only very small fraction of purebred bulls.
Conclusions
We presented a random regression model for the analysis of multibreed data. The approximate model approach presented allows a simple way to incorporate breed proportion information and different genetic variances of origin breeds into multibreed analysis and also models including genomic data.




