EXTRA-PAIR PATERNITY AND THE VARIANCE IN MALE FITNESS IN SONG SPARROWS (MELOSPIZA MELODIA)
Abstract
The variance in fitness across population members can influence major evolutionary processes. In socially monogamous but genetically polygynandrous species, extra-pair paternity (EPP) is widely hypothesized to increase the variance in male fitness compared to that arising given the socially monogamous mating system. This hypothesis has not been definitively tested because comprehensive data describing males’ apparent (social) and realized (genetic) fitness have been lacking. We used 16 years of comprehensive social and genetic paternity data for an entire free-living song sparrow (Melospiza melodia) population to quantify and compare variances in male apparent and realized fitness, and to quantify the contribution of the variances in within-pair reproductive success (WPRS) and extra-pair reproductive success (EPRS) and their covariance to the variance in realized fitness. Overall, EPP increased the variance in male fitness by only 0–27% across different fitness and variance measures. This relatively small effect reflected the presence of socially unpaired males with zero apparent and low realized fitness, small covariance between WPRS and EPRS, and large variance in WPRS that was relatively unaffected by EPP. Therefore, although EPP altered individual males’ contributions to future generations, its impact on population-level parameters such as the opportunity for selection and effective population size was limited.
The variance in fitness across individual population members has the potential to shape major evolutionary processes. Specifically, the variance in fitness determines the maximum opportunity for selection on any trait (Crow 1958; Arnold and Wade 1984), influences effective population size and hence the expected rates of inbreeding and genetic drift (Wright 1931; Nunney 1993), and shapes the distribution of relatedness within a population and hence the opportunities for subsequent inbreeding, kin selection and competition (Waples 1998; Reid and Keller 2010). Accurately quantifying the variance in fitness, and its links to mating system, is therefore central to understanding the evolutionary dynamics and potential of natural populations (Arnold and Wade 1984; Clutton-Brock 1988; Webster et al. 1995; Shuster and Wade 2003; Shuster 2009).
However, quantifying the variance in fitness across a population is challenging, requiring accurate data describing the complete life histories of all or an unbiased sample of population members (Clutton-Brock 1988; Shuster and Wade 2003; Shuster 2009). Socially monogamous birds originally proved attractive models for such studies due to the relative ease with which breeding success and survival of marked individuals can be documented (e.g., Smith 1981; Gustafsson and Sutherland 1988; Newton 1989). Subsequent genetic analyses, however, revealed frequent genetic polygynandry in socially monogamous populations (Hasselquist and Sherman 2001; Griffith et al. 2002). Due to extra-pair paternity (EPP), a substantial proportion of offspring in a substantial proportion of broods is sired by males other than the female's social mate (Hasselquist and Sherman 2001; Griffith et al. 2002). By reallocating paternity among males, EPP could substantially influence the variance in male fitness (Webster et al. 1995) and hence shape or constrain multiple evolutionary processes. Given comprehensive social (behavioral) and genetic paternity data, such populations now provide an opportunity not only to estimate the variance in male fitness, but also to explicitly quantify the consequences of monogamy versus polygynandry for that variance and consequent evolution.
Successful extra-pair sires are often postulated to be of relatively high genetic and/or phenotypic value (Jennions and Petrie 2000; Griffith et al. 2002; Akçay and Roughgarden 2007; Kempenaers 2007). EPP is consequently widely predicted to further increase the reproductive success of males whose social reproductive success is already high, thereby increasing the overall variance in male fitness beyond that resulting from the socially monogamous mating system (Møller and Birkhead 1994; Webster et al. 1995; Møller and Ninni 1998). EPP might then explain why socially monogamous species often show sexually dimorphic traits similar to those observed in socially polygynous species with obviously high variances in male mating and reproductive success (Owens and Hartley 1998; Webster et al. 2007; Albrecht et al. 2009). However, depending on the mechanisms driving and constraining EPP, extra-pair reproductive success (EPRS) could show positive, negative, or no covariance with within-pair reproductive success (WPRS) across males. Depending on the direction and magnitude of this covariance, the total variance in male fitness observed across the realized (genetic) mating system could be greater than, smaller than, or similar to that observed across the apparent (social) mating system (Webster et al. 1995; Jones et al. 2001). Key requirements are therefore to quantify and compare the variances in male apparent and realized fitness, and to rationalize the observed difference by quantifying the amount of the total variance in realized fitness attributable to the variances in WPRS and EPRS and their covariance (Webster et al. 1995; Jones et al. 2001; Freeman-Gallant et al. 2005).
Consequently, several major studies have aimed to quantify and compare apparent and realized variances in male reproductive success in socially monogamous but genetically polygynandrous populations (Table 1). Some of these studies have also decomposed the variance in realized reproductive success into components due to WPRS, EPRS, and their covariance (Table 1). However, these previous studies have limitations regarding the data that could be collected and hence the inference that can be drawn.
| Species | N years | ITa | IT | I-ratio | IW (ratio) | (ratio) | 2 × CovIW,E (ratio) | EP brood ratio | Prop. EPY assigned | Reference | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARS | Yellow Warbler (Dendroica petechia) | 2 | 0.04 | 0.53 | 13.3 | – | – | – | 0.59 | 0.35 | Yezerinac et al. 1995 | |
| Eastern Kingbird (Tyrannus tyrannus) | 3 | 0.09 | 0.85 | 9.4 | 0.35 (0.42) | 0.39 (0.46) | 0.10 (0.12) | 0.61 | Dolan et al. 2007 | |||
| North American Barn Swallow (Hirundo rustica erythrogaster) | 1 | 0.07 | 0.53 | 8.0 | 0.17 (0.33) | 0.25 (0.48) | 0.10 (0.19) | 0.50 | 1.00 | Kleven et al. 2006 1 | ||
| Mountain Bluebird (Sialia currucoides) | 2 | 0.04 | 0.27 | 7.3 | 0.16 (0.60) | 0.09 (0.34) | 0.02 (0.06) | 0.69 | 0.70 | Balenger et al. 2009 | ||
| House Martin (Delichon urbica) | 2 | 0.06 | 0.31 | 5.2 | – | – | – | 0.35 | 1.00 | Whittingham and Lifjeld 1995 | ||
| Collared Flycatcher (Ficedula albicollis) | 1 | 0.03 | 0.14 | 4.7 | 0.33 | 0.54 | Sheldon and Ellegren 1999 | |||||
| Bluethroat (Luscinia svecica svecica) | 3 | 0.08 | 0.37 | 4.5 | – | – | – | 0.54 | 1.00 | Johnsen et al. 2002 | ||
| Scarlet Rosefinch (Carpodacus erythrinus) | 7 | 0.07 | 0.23 | 3.4 | 0.32 | 0.72 | Albrecht et al. 2009 | |||||
| Scarlet Rosefinch (Carpodacus erythrinus) | 4 | 0.12 | 0.40 | 3.3 | 0.27 (0.67) | 0.09 (0.23) | 0.04 (0.10) | 0.34 | 0.73 | Albrecht et al. 2007 1 | ||
| Hooded Warbler (Wilsonia citrina) | 5 | 0.18 | 0.46 | 2.5 | 0.35 | 0.23 | Stutchbury et al. 1997 | |||||
| Black-capped Chickadee (Poecile atricapillus) | 4 | 0.04 | 0.10 | 2.5 | – | – | – | 0.29 | 0.44 | Otter et al. 1998 | ||
| Bullock's Oriole (Icterus galbula bullockii) | 2 | 0.07 | 0.17 | 2.4 | 0.46 | 0.45 | Richardson and Burke 2001 | |||||
| Song Sparrow (Melospiza melodia) | 1 | Max | 0.33 | 0.67 | 2.0 | 0.22 (0.33) | 0.30 (0.46) | 0.14 (0.14) | 0.44 | 0.99 | This study | |
| Blue Tit (Parus caeruleus) | 2 | 0.16 | 0.27 | 1.7 | 0.31 | 0.72 | Kempenaers et al. 1992 | |||||
| Common Yellowthroat (Geothlypis trichas) | 1 | 0.28 | 0.48 | 1.7 | 0.28 (0.58) | 0.10 (0.21) | 0.11 (0.22) | 0.65 | 0.83 | Whittingham and Dunn 2005 1 | ||
| Black-throated Blue Warbler (Dendroica caerulescens) | 4 | 0.48 | 0.71 | 1.5 | 0.54 (0.76) | 0.08 (0.11) | 0.08 (0.13) | 0.34 | 0.54 | Webster et al. 2001 | ||
| Dark-eyed Junco (Junco hyemalis) | 2 | 0.55 | 0.72 | 1.3 | – | – | – | 0.34 | 0.30 | Ketterson et al. 1997 | ||
| Song Sparrow (Melospiza melodia) | 16 | Overall | 1.25 | 1.37 | 1.1 | 0.79 (0.58) | 0.31 (0.23) | 0.26 (0.19) | 0.44 | 0.99 | This study | |
| Splendid Fairy-wren (Malurus splendens) | 7 | 1.47 | 1.42 | 1.0 | 0.83 (0.59) | 0.60 (0.42) | −0.01 (−0.08) | 0.55 | 0.90 | Webster et al. 2007 | ||
| Song Sparrow (Melospiza melodia) | 1 | Min | 2.07 | 1.52 | 0.7 | 1.20 (0.79) | 0.24 (0.16) | 0.08 (0.06) | 0.44 | 0.99 | This study | |
| Chestnut-sided warbler (Dendroica pennsylvanica) | 2 | – | 0.70 | – | 0.39 (0.56) | 0.31 (0.44) | 0.02 (0.03) | 0.61 | 0.87 | Byers et al. 2004 | ||
| LRS | Song Sparrow (Melospiza melodia) | 1.50 | 1.76 | 1.2 | 0.79 (0.45) | 0.31 (0.18) | 0.66 (0.37) | 0.28 | 0.99 | This study | ||
| Splendid Fairy-wren (Malurus splendens) | 1.78 | 1.98 | 1.1 | 0.84 (0.43) | 0.79 (0.38) | 0.35 (0.18) | 0.55 | 0.90 | Webster et al. 2007 | |||
| Red-winged Blackbirds (Agelaius phoeniceus)* | 0.98 | 1.36 | 1.4 | 0.26 | 0.79 | Weatherhead and Boag 1997 | ||||||
| Lance-tailed Manakin (Chiroxiphia lanceolata)* | NA | 5.5 | NA | NA | NA | NA | NA | NA | DuVal and Kempenaers 2008 |
- 1Absolute values of IW, IE, and 2 × CovIW,E were deduced from the published ratios of each variance component to IT in these studies.
First, estimating the total variance in male fitness requires fitness to be accurately measured for all or an unbiased sample of males in a population (Shuster 2009). In practice, it is often not possible to identify all males alive within a population during a breeding season, and unidentified males may be nonrandom with respect to reproductive success or fitness. Specifically, because males are often identified while defending territories or rearing dependent offspring, males that fail to obtain a territory or a social mate, or whose offspring die early, may be systematically missed (e.g., Sheldon and Ellegren 1999; Webster et al. 2001). Males with zero reproductive success may therefore be under-represented, thereby biasing the estimated mean and variance in male reproductive success (Downhower et al. 1987; Webster et al. 1995; Shuster 2009).
Second, accurate comparison between the variances in male apparent and realized fitness requires all offspring to be assigned to both their apparent (social) and true (genetic) sires. In practice, it is rarely possible to sample all offspring or assign all genetic sires with high confidence (Freeman-Gallant et al. 2005; Table 1). Such incomplete sampling and paternity assignment may affect the estimated variance in male realized reproductive success and will cause systematic underestimation of the mean (Freeman-Gallant et al. 2005). This bias is likely to cause the effect of EPP on the opportunity for selection, which is a mean-standardized variance, to be systematically overestimated (Downhower et al. 1987; Freeman-Gallant et al. 2005).
Third, studies testing whether EPP increases the variance in male fitness have measured reproductive success as the number of offspring alive a few days after hatching (when DNA samples for paternity assignment can be collected; Table 1). Measuring fitness in terms of hatched (or ideally conceived) offspring minimizes confounding between parent and offspring fitness (Wolf and Wade 2001). However, it can also be valuable to measure fitness as the number of offspring recruited to the breeding population, particularly in the contexts of estimating effective population size and “good genes” effects in sexual selection (Brommer et al. 2002). However, no studies have measured the variances in apparent or realized fitness, or the underlying variance components, in terms of recruited offspring. If offspring survival from hatching to recruitment were positively or negatively correlated with survival to hatching, or if offspring sired by within-pair versus extra-pair males were to survive at different rates (as widely hypothesized and recently observed, Jennions and Petrie 2000; Griffith et al. 2002; Akçay and Roughgarden 2007; Kempenaers 2007; Sardell et al. 2011; Reid and Sardell 2012), the effect of EPP on the variance in fitness estimated as recruited offspring may differ substantially from that estimated as hatched offspring.
Finally, almost all previous studies measured the variance in male annual reproductive success (ARS, the number of offspring produced in a single year, Table 1). However, it is the variance in total fitness, comprising an individual's total contribution to the next generation, which ultimately influences selective and evolutionary processes (Stearns 1992, pp. 72–90; Brommer et al. 2002). Depending on the magnitude and direction of covariances among ARS and survival and hence lifespan within and among individuals, the variance in ARS could be substantially larger or smaller than the variance in lifetime reproductive success (LRS, the total number of offspring produced over an individual's entire life). Only one previous study has compared and decomposed the variance in apparent and realized LRS in a socially monogamous but genetically polygynandrous species (Webster et al. 2007). However, LRS is a rate-insensitive measure of fitness. Because reproduction by offspring produced early in an individual's life may overlap with the individual's own subsequent reproductive success, estimates of the mean and variance in fitness may need to incorporate the timing of offspring production rather than solely the number of offspring produced (McGraw and Caswell 1996). No studies have quantified the effect of EPP on the variance in rate-sensitive measures of male fitness, or quantified the degree to which effects on rate-sensitive and rate-insensitive measures differ.
In summary, determining the effects of EPP on variance in male fitness and evolutionary processes requires comprehensive studies that accurately quantify and compare variances in apparent and realized male fitness in terms of ARS, rate-sensitive and rate-insensitive measures of lifetime fitness, and decompose the variances in realized reproductive success into their component parts. Such studies need to be repeated across multiple years and cohorts to determine whether effects of EPP are consistent or variable and hence evaluate their overall implications.
We used 16 years of comprehensive life-history and paternity data to quantify the variance in apparent and realized male fitness in socially monogamous but genetically polygynandrous song sparrows (Melospiza melodia) and thereby definitively test the hypothesis that EPP increases the variance in male fitness measured as ARS, LRS (a rate-insensitive measure of fitness), and λind (a rate-sensitive measure of fitness). We further decomposed the variance in male realized ARS and LRS into components due to WPRS and EPRS and their covariance and quantified the degree to which the covariance explained the ratio of realized to apparent variance in reproductive success. We quantified whether estimates or conclusions differed when fitness was measured as the number of offspring hatched, reared to independence from parental care, or recruited to the breeding population. Finally, we quantified the degree to which conclusions would have differed had we failed to sample socially unpaired males, and thereby assess the potential biases inherent in less-comprehensive field studies.
Methods
STUDY SYSTEM
A resident, socially monogamous song sparrow population on Mandarte Island, BC, Canada, has been studied intensively since 1975 (Smith et al. 2006) and averaged 30 ± 12 (SD) breeding pairs during 1993–2008. Each year during March–August, all breeding attempts are monitored and all offspring surviving to about six days posthatch (81% of all eggs laid on average) are uniquely marked with metal and colored plastic rings (Smith et al. 2006). All offspring that survived to independence from parental care (about 24 days posthatch) are identified. All immigrants are caught and ringed soon after settling (1.1 immigrant/year on average) so that all resident song sparrows are individually identifiable throughout their lives. Mandarte's small size (about 6 ha) and simple habitat structure (Smith et al. 2006) mean that the probability of observing a living individual is effectively one (Wilson and Arcese 2008). There is therefore complete knowledge of the identities of all adults (≥1-year old) alive each year (Reid et al. 2005; Smith et al. 2006; Keller et al. 2008). The high average recruitment rate of independent offspring on Mandarte (about 30%), and the rarity of marked dispersers on surrounding islands, suggests that successful dispersal from Mandarte is infrequent (Arcese 1989; Keller 1998; Wilson and Arcese 2008). Local survival to recruitment can therefore be measured unusually precisely (Keller et al. 2001; Reid et al. 2005; Keller et al. 2008).
Each year, the social parents of all offspring are identified as those incubating clutches or provisioning chicks within defended territories (Keller 1998; Sardell et al. 2010). Both sexes can breed at the age of one year and most recruited offspring survive one to three years (median 2, interquartile range 1–4). Females typically make one to three breeding attempts per year with mean clutch size 3.4 ± 0.6 (SD). Because the adult sex ratio is often male biased, a substantial proportion of males remains socially unpaired for whole breeding seasons (Hochachka et al. 1989; mean proportion of males that were unpaired during 1993–2008: 0.36 ± 0.19 [SD]). Although song sparrows show little morphological dimorphism, male song is a highly sexually dimorphic trait that functions in male–male competition and female mate choice (Arcese 1989; Reid et al. 2004).
PATERNITY ASSIGNMENT
During 1993–2008, blood samples (≤50 μl) were taken from 99.4% of all ringed offspring (2207/2221 from 811 breeding attempts), nearly all adults alive on Mandarte in 1993, and all subsequent immigrants (Sardell et al. 2010). All individuals were genotyped at 13 highly polymorphic autosomal microsatellite loci and parentage was assigned to all offspring using Bayesian full probability models that incorporated microsatellite data and the spatial location of offspring and potential sires (Sardell et al. 2010). All assigned dams had been correctly identified by social behavior. Sires were assigned to 99.2% of sampled offspring with ≥95% individual-level confidence and the estimated number of unsampled sires was approximately zero. Overall, 28% of offspring were assigned to an extra-pair male (Sardell et al. 2010), similar to the 24% estimated in a nearby mainland population (Hill et al. 2011). Because sires were assigned with high statistical confidence to nearly all offspring ringed during 1993–2008, and all independent and recruited offspring, the data provide a comprehensive record of the reproductive success of all adult males alive during 1993–2008.
ANNUAL AND LIFETIME FITNESS
For each adult male song sparrow alive on Mandarte during 1993–2008, apparent and realized ARS were estimated as the numbers of offspring reared and sired in each year. All males were classified as socially paired if they mate-guarded and/or provided paternal care, or socially unpaired if they remained unpaired for the entire season. Apparent ARS was by definition zero for socially unpaired males. ARS was calculated as the number of hatched offspring that survived to ringing (as in all previous studies, Table 1), independent offspring (surviving to independence from parental care), and recruited offspring (that survived to age one year). These measures were positively correlated across males (hatched vs. independent, rS= 0.85; independent vs. recruited, rS= 0.56; hatched vs. recruited, rS= 0.47 based on male realized ARS). Mean male ARS was lower than mean female ARS due to the male-biased adult sex ratio.
Each male's apparent and realized LRS (a rate-insensitive measure of fitness) was calculated as the total number of offspring reared and sired over its entire life. For each male, apparent and realized λind, a rate-sensitive measure of fitness that accounts for differential timing of reproduction, was calculated as the dominant eigenvalue of an individual age-structured projection matrix (McGraw and Caswell 1996). Matrices were parameterized using each individual's observed life span (with appropriate age-specific survival probabilities of 1 or 0) and age-specific reproductive success measured as hatched, independent, or recruited offspring. Because matrix fecundity elements describe the number of same-sex one-year-old offspring produced per year (McGraw and Caswell 1996; Brommer et al. 2002), elements parameterized in terms of an individual's observed number of hatched or independent offspring were multiplied by the mean population-wide proportions of hatched and independent offspring that survived to age 1 (0.187 and 0.283, respectively). All were multiplied by 0.5 because the hatching sex ratio is about 50:50 (Postma et al. 2011). λind values do not predict population growth rate due to the male-biased adult sex ratio. Estimates of LRS and λind could be biased if males that recruited on Mandarte subsequently emigrated to breed elsewhere. However, any such bias is probably very small because no such cases have been observed despite extensive study (Smith et al. 2006; Wilson and Arcese 2008).
VARIANCE IN MALE FITNESS
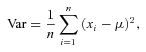
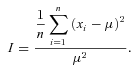
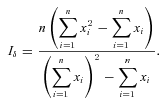
I δ measures clumping, adjusting the observed variance by the variance when reproductive success is equal across all observed individuals. It is independent of μ and equals 1 when fitness is uniformly distributed and >1 if the distribution is skewed. Morisita's index was not calculated for λind because most values of λind fell between 0 and 1, making the numerator negative.
Var, I, and Iδ were calculated for apparent and realized male fitness measured either annually (VarARS, IARS, and IδARS) or over individuals’ life spans (VarLRS, ILRS, and IδLRS). In each case, fitness was measured as hatched, independent, and recruited offspring. The relative change in variance due to EPP was then calculated as the ratios of Var, I, and Iδ calculated for realized versus apparent fitness (Var-ratio, I-ratio, and Iδ-ratio) at each offspring stage. Analyses of LRS and λind were restricted to individuals hatched during 1993–2003 because some individuals hatched during 2004–2008 were still alive in 2009. Table S1 summarizes the nomenclature and definitions of all measures of fitness and variation.
Finally, to test whether the distributions of apparent and realized ARS and LRS differed more subtly than detected by the Var-, I-, and Iδ-ratios, categorical G-tests were used to determine whether the frequencies of males that produced specific numbers of apparent and realized offspring differed significantly. Males that produced ≥10 hatched, ≥10 independent, and ≥ 5 recruited offspring were pooled to provide sufficient sample sizes in each discrete category.
DECOMPOSITION OF THE OPPORTUNITY FOR SELECTION
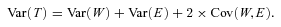
This decomposition is valid for variables of any distribution as long as the components of interest are strictly additive (Arnold and Wade 1984). For ARS and LRS, Var(W), Var(E), and 2 × Cov(W, E) were calculated from the number of within-pair and extra-pair offspring sired by each male (Webster et al. 1995) measured as hatched, independent, and recruited offspring, both across all years and cohorts combined, and within each individual year and cohort. To facilitate comparisons with other studies, Var(T) and its variance components were standardized dividing by the squared mean T; thereby decomposing the realized opportunity for selection (IT) into the opportunity for selection due to WPRS (IW), EPRS (IE), and the standardized covariance (CovIW,E). Ratios of each variance component to the total standardized variance in male reproductive success are reported. Linear regressions were used to quantify the relationship between CovIW,E and the IARS-ratios and ILRS-ratios across 16 years for ARS and 11 cohorts for LRS.
Var(W), Var(E), and Cov(W,E) could be further decomposed into subcomponents of variance (i.e., the number of mates, number of offspring per mate, and proportion of offspring sired, Webster et al. 1995). This further decomposition was not implemented because the sum of these subcomponents cannot equal Var(T), rendering their interpretation unclear (Appendix S1).
The rate-sensitive measure of male lifetime fitness (λind) is unlikely to equal the sum of λind for individual age-structured projection matrices parameterized for male WPRS and EPRS separately. This is because the dominant eigenvalues of individual projection matrices are associated with eigenvectors whose directions are likely to differ. The variance in λind could therefore not be simply decomposed as a function of the variances and covariance in WPRS and EPRS.
PAIRED VERSUS UNPAIRED MALES
To quantify the degree to which failing to identify socially unpaired males would have affected variance estimates and altered conclusions, we repeated all analyses across all males combined and across socially paired and unpaired males separately. Many unpaired males were one-year old and paired in subsequent years (Smith and Arcese 1989; Keller et al. 2008; Sardell et al. 2010). Males that were socially unpaired for their entire lifetime therefore primarily comprised males that survived only one year.
All analyses were run in R v.2.10.1 (R development Core Team 2009). All observations of ARS were retained even though many males were alive in more than one year. Any pseudo-replication does not affect the estimated variances that are our primary focus, and no individual contributed more than 1.3% of observations.
Results
VARIANCE IN ARS, ALL MALES
Apparent and realized ARS were measured for 769 male-years comprising 310 individual adult males alive during 1993–2008 (Fig. 1). Across all observations, the median, interquartile range (IQR), mean, and variance in ARS decreased as ARS was measured as hatched, independent, or recruited offspring, whereas the proportion of males with zero ARS increased (Table 2A, Fig. 1). The precise distributions of realized ARS measured at each offspring stage differed from those of apparent ARS (Fig. 1, G-tests in Table 2A). However, the median, IQR, and mean apparent ARS were identical to those of realized ARS at all offspring stages, and the proportions of males with zero ARS were very similar (Table 2A). Across all data, the variances in realized ARS were greater than in apparent ARS at all offspring stages, but only by about 2–14% (ratios in Table 2A).
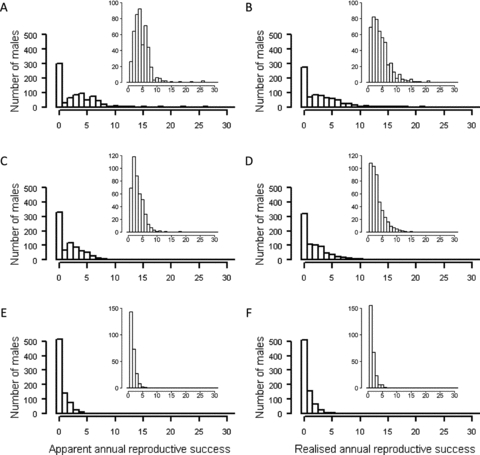
Distributions of apparent (panels A, C, E) and realized (panels B, D, F) male annual reproductive success (ARS) measured as the number of hatched (A, B), independent (C, D), and recruited (E, F) offspring produced per year. Insets show these same distributions for males with nonzero ARS for clarity.
| Apparent annual reproductive success | Realized annual reproductive success | G-test G3 (df) | Ratio | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Med | IQR | Prop. zeros | μa | VarTa(ARS) | ITa ( ARS ) 1 | I δ Ta ( ARS ) 1 | Med | IQR | Prop. zeros | μr | VarT(ARS) | IT ( ARS ) | I δ T ( ARS ) | VarARS | IARS 1 | I δ ARS 1 | |||
| (A) All males | Hatched | 2 | 0–5 | 0.39 | 2.86 | 10.16 | 1.25 | 1.89 | 2 | 0–5 | 0.36 | 2.86 | 11.14 | 1.37 | 2.01 | 957.4 (121) | 1.10 | 1.10 | 1.06 |
| Independent | 1 | 0–3 | 0.43 | 1.90 | 5.09 | 1.40 | 1.88 | 1 | 0–3 | 0.42 | 1.90 | 5.80 | 1.60 | 2.08 | 960.2 (121) | 1.14 | 1.14 | 1.10 | |
| Recruited | 0 | 0–1 | 0.67 | 0.54 | 0.87 | 2.93 | 2.09 | 0 | 0–1 | 0.66 | 0.54 | 0.89 | 3.02 | 2.18 | 645.3 (36) | 1.02 | 1.03 | 1.04 | |
| (B) Socially | Hatched | 0 | 0–0 | 1 | 0 | 0 | 0 | 0–0 | 0.84 | 0.34 | 0.83 | 7.32 | 5.39 | ||||||
| unpaired males | Independent | 0 | 0–0 | 1 | 0 | 0 | – | – | 0 | 0–0 | 0.86 | 0.23 | 0.41 | 8.10 | 4.73 | – | – | – | – |
| Recruited | 0 | 0–0 | 1 | 0 | 0 | 0 | 0–0 | 0.95 | 0.06 | 0.10 | 25.61 | 10.88 | |||||||
| (C) Socially paired | Hatched | 4 | 2–6 | 0.07 | 4.332 | 9.03 | 0.48 | 1.25 | 4 | 2–6 | 0.11 | 4.152 | 11.51 | 0.67 | 1.43 | 505.7 (121) | 1.27 | 1.38 | 1.14 |
| males | Independent | 2.5 | 1–4 | 0.13 | 2.882 | 4.90 | 0.59 | 1.24 | 2 | 1–4 | 0.19 | 2.762 | 6.38 | 0.84 | 1.47 | 587.0 (121) | 1.30 | 1.42 | 1.19 |
| Recruited | 0.5 | 0–1 | 0.50 | 0.822 | 1.08 | 1.60 | 1.38 | 0 | 0–1 | 0.52 | 0.792 | 1.12 | 1.79 | 1.53 | 475.4 (36) | 1.04 | 1.12 | 1.10 | |
- Med = median; IQR = interquartile range; Prop. Zeros = proportion of males with zero apparent or realized ARS; apparent: μa, realized: μr= mean ARS; apparent: VarTa(ARS), realized: VarT(ARS)= absolute variance in male ARS; apparent: ITa(ARS), realized: IT(ARS)= maximum opportunity for selection; apparent: IδTa(ARS), realized: IδT(ARS)= Morisita's index.
- 1 IARS, IδARS, and their ratios are undefined for apparent ARS of socially unpaired males because these individuals have zero apparent ARS by definition.
- 2The total number of offspring considered in analyses of apparent and realized ARS differs because some offspring were sired by socially unpaired males.
- 3 G-test is undefined for distributions with less than two levels such as socially unpaired males with zero ARS. All P-values < 0.00001.
However, there was substantial among-year variation in the ratio of the variances in realized versus apparent ARS (IARS-ratio) at all offspring stages (Table 3B). Specifically, IARS-ratios ranged from 0.60 to 2.00 for hatched offspring, 0.78 to 1.75 for independent offspring, and 0.58 to 1.40 for recruited offspring with considerable differences between consecutive years (Table 3B).
| Year | N | ARS hatched | ARS independent | ARS recruited | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITa (ARS) | IT (ARS) | IARS-ratio | IW | IE | 2 × CovIW,E | ITa (ARS) | IT (ARS) | IARS-ratio | IW | IE | 2 × CovIW,E | ITa (ARS) | IT (ARS) | IARS-ratio | IW | IE | 2 × CovIW,E | ||
| (A) All males | 769 | 1.251 | 1.371 | 1.101 | 0.79 (0.58) | 0.31 (0.23) | 0.26 (0.19) | 1.41 | 1.60 | 1.14 | 0.94 (0.59) | 0.35 (0.22) | 0.32 (0.20) | 2.931 | 3.021 | 1.031 | 1.93 (0.64) | 0.69 (0.23) | 0.40 (0.13) |
| (B) 1993 | 76 | 1.19 | 1.55 | 1.30 | 0.92 (0.59) | 0.44 (0.28) | 0.20 (0.13) | 1.42 | 1.90 | 1.34 | 1.28 (0.68) | 0.39 (0.21) | 0.23 (0.12) | 2.13 | 2.38 | 1.12 | 1 76 (0.74) | 0.47 (0.20) | 0.15 (0.06) |
| 1994 | 79 | 1.13 | 1.12 | 0.99 | 0.78 (0.70) | 0.24 (0.22) | 0.10 (0.09) | 1.48 | 1.41 | 0.95 | 0.93 (0.66) | 0.37 (0.26) | 0.12 (0.08) | 2.73 | 2.90 | 1.06 | 1.82 (0.63) | 0.83 (0.29) | 0.25 (0.09) |
| 1995 | 71 | 0.71 | 0.89 | 1.26 | 0.48 (0.54) | 0.29 (0.32) | 0.12 (0.14) | 0.82 | 1.00 | 1.21 | 0.56 (0.56) | 0.29 (0.29) | 0.15 (0.15) | 2.14 | 2.67 | 1.25 | 1.31 (0.49) | 0.83 (0.31) | 0.53 (0.20) |
| 1996 | 82 | 1.07 | 1.36 | 1.26 | 0.65 (0.48) | 0.36 (0.27) | 0.34 (0.25) | 1.42 | 1.72 | 1.21 | 1.16 (0.68) | 0.34 (0.20) | 0.21 (0.12) | 1.91 | 2.66 | 1.40 | 1.47 (0.55) | 0.54 (0.20) | 0.64 (0.24) |
| 1997 | 72 | 0.90 | 1.11 | 1.23 | 0.69 (0.62) | 0.23 (0.21) | 0.19 (0.17) | 1.00 | 1.18 | 1.18 | 0.71 (0.60) | 0.27 (0.23) | 0.20 (0.17) | 3.47 | 3.77 | 1.09 | 2.24 (0.59) | 1.27 (0.34) | 0.27 (0.07) |
| 1998 | 62 | 1.23 | 1.19 | 0.97 | 0.81 (0.68) | 0.30 (0.25) | 0.08 (0.07) | 1.59 | 1.67 | 1.05 | 0.96 (0.57) | 0.59 (0.35) | 0.12 (0.07) | 4.87 | 5.43 | 1.12 | 4.00 (0.74) | 0.54 (0.10) | 0.89 (0.16) |
| 1999 | 43 | 2.63 | 2.76 | 1.05 | 1.66 (0.60) | 1.26 (0.46) | −0.17 (−0.06) | 3.89 | 3.34 | 0.86 | 2.34 (0.70) | 1.26 (0.38) | −0.26 (−0.08) | 6.02 | 5.14 | 0.85 | 3.46 (0.67) | 2.11 (0.41) | −0.43 (−0.08) |
| 2000 | 40 | 2.10 | 1.82 | 0.87 | 0.77 (0.42) | 1.08 (0.59) | −0.17 (−0.09) | 2.24 | 2.95 | 1.32 | 1.42 (0.48) | 1.33 (0.45) | 0.20 (0.07) | 4.55 | 4.55 | 1.00 | 2.58 (0.57) | 2.42 (0.53) | −0.46 (−0.10) |
| 2001 | 32 | 2.07 | 1.52 | 0.73 | 1.20 (0.79) | 0.24 (0.16) | 0.08 (0.06) | 2.09 | 1.62 | 0.78 | 1.36 (0.84) | 0.16 (0.10) | 0.11 (0.07) | 2.29 | 1.84 | 0.80 | 1.68 (0.91) | 0.16 (0.08) | 0.00 (0.00) |
| 2002 | 36 | 0.70 | 0.79 | 1.12 | 0.49 (0.62) | 0.18 (0.23) | 0.12 (0.15) | 0.76 | 0.96 | 1.26 | 0.63 (0.65) | 0.14 (0.15) | 0.19 (0.20) | 2.75 | 2.25 | 0.82 | 1.93 (0.86) | 0.47 (0.21) | −0.15 (−0.07) |
| 2003 | 31 | 0.33 | 0.67 | 2.00 | 0.22 (0.33) | 0.30 (0.46) | 0.14 (0.21) | 0.39 | 0.68 | 1.75 | 0.25 (0.36) | 0.32 (0.47) | 0.11 (0.17) | 3.47 | 3.97 | 1.14 | 1.55 (0.39) | 1.18 (0.30) | 1.24 (0.31) |
| 2004 | 30 | 1.00 | 1.24 | 1.23 | 0.65 (0.53) | 0.39 (0.31) | 0.20 (0.16) | 1.07 | 1.27 | 1.18 | 0.57 (0.45) | 0.51 (0.40) | 0.19 (0.15) | 1.52 | 1.59 | 1.05 | 0.94 (0.59) | 0.59 (0.37) | 0.06 (0.03) |
| 2005 | 43 | 0.88 | 1.27 | 1.45 | 0.61 (0.48) | 0.37 (0.29) | 0.29 (0.23) | 0.92 | 1.27 | 1.39 | 0.68 (0.53) | 0.28 (0.22) | 0.31 (0.25) | 2.79 | 1.62 | 0.58 | 1.50 (0.93) | 0.45 (0.28) | −0.33 (−0.20) |
| 2006 | 28 | 0.36 | 0.46 | 1.27 | 0.20 (0.44) | 0.11 (0.23) | 0.15 (0.33) | 0.45 | 0.64 | 1.43 | 0.27 (0.43) | 0.17 (0.26) | 0.20 (0.31) | 5.31 | 6.22 | 1.17 | 3.05 (0.49) | 0.84 (0.14) | 2.33 (0.37) |
| 2007 | 13 | 0.48 | 0.29 | 0.60 | 0.30 (1.03) | 0.06 (0.22) | −0.07 (−0.25) | 0.35 | 0.31 | 0.87 | 0.27 (0.87) | 0.06 (0.18) | −0.02 (−0.06) | 0.32 | 0.34 | 1.06 | 0.28 (0.83) | 0.06 (0.16) | 0.00 (0.01) |
| 2008 | 31 | 0.55 | 0.63 | 1.14 | 0.38 (0.61) | 0.10 (0.16) | 0.15 (0.23) | 0.67 | 0.71 | 1.06 | 0.55 (0.78) | 0.09 (0.12) | 0.07 (0.10) | 2.56 | 2.56 | 1.00 | 2.51 (0.98) | 0.31 (0.12) | −0.25 (−0.10) |
| (C) Paired males | 508 | 0.48 | 0.67 | 1.38 | 0.38 (0.57) | 0.19 (0.28) | 0.09 (0.14) | 0.59 | 0.84 | 1.42 | 0.48 (0.58) | 0.21 (0.25) | 0.14 (0.17) | 1.60 | 1.79 | 1.12 | 1.18 (0.66) | 0.41 (0.23) | 0.20 (0.11) |
- N= number of males; ITa(ARS)= total variance in apparent ARS; IT(ARS)= total variance in realized ARS; IARS-ratio = the ratio between IT(ARS) and ITa(ARS); IW= variance in IT(ARS) due to within-pair reproductive success; extra-pair reproductive success (IE), and their covariance (2 × CovIW,E).
Across all males and years combined, the opportunity for selection due to male WPRS (IW) was much greater than the opportunity for selection due to EPRS (IE) whether ARS was measured as hatched, independent, or recruited offspring (Table 3A). The standardized covariance between annual WPRS and EPRS was positive but smaller than IE and substantially smaller than IW (Table 3A).
Within each year, annual IW was generally, but not always, greater than IE (Table 3B). There was substantial among-year variation in the magnitude of these standardized variances, and in the magnitude and direction of the standardized covariances (Table 3B). The IARS-ratio increased significantly with the standardized covariance between WPRS and EPRS at all three offspring stages (Fig. 2).
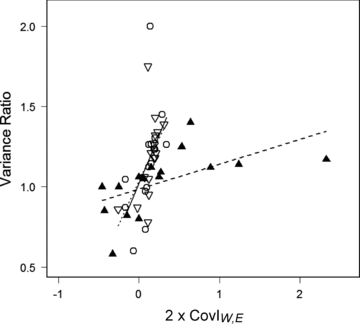
Relationship between (twice) the standardized covariance between male within- and extra-pair annual reproductive success (2 × CovIW,E) and the ratio between the variances in realized and apparent annual reproductive success (IARS-ratio). Annual reproductive success (ARS) was measured as the number of hatched (open circles), independent (open triangles pointing down) and recruited offspring produced (filled triangles pointing up). Lines show the linear models: β= 1.20 ± 0.50 (SE), t= 2.39, df = 15, P= 0.03, R2= 0.29 (ARSHatched, solid line), β= 1.07 ± 0.43 (SE), t= 2.50, df = 15, P= 0.03, R2= 0.31 (ARSIndependent, dotted line), and β= 0.15 ± 0.06 (SE), t= 2.60, df = 15, P= 0.02, R2= 0.33 (ARSRecruited, dashed line).
VARIANCE IN ARS, SOCIALLY PAIRED VERSUS UNPAIRED MALES
A total of 186 adult males alive during 1993–2008 remained socially unpaired for at least one year, totaling 261 male-years. Socially unpaired males sired up to five extra-pair offspring per year (Fig. 3). However, about 85% of these males sired zero hatched or independent offspring, and 95% sired zero recruited offspring (Table 2B). Hence, although realized IARS and IδARS for socially unpaired males were high, this primarily reflects their very low mean ARS rather than high variance (Table 2B, Fig. 3).
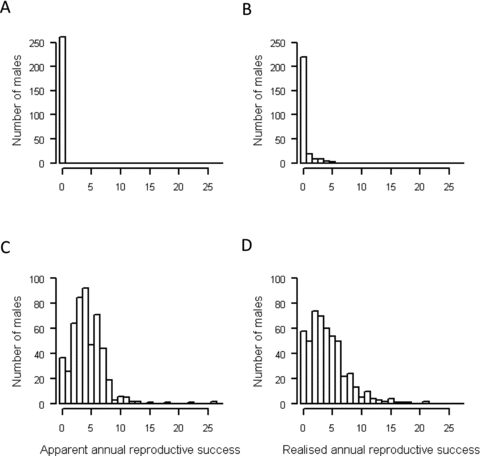
Distributions of apparent (panels A, C) and realized (panels B, D) annual reproductive success (ARS) of socially unpaired (A, B) and socially paired males (C, D) measured as hatched offspring. Scales are standardized to facilitate comparison.
A total of 219 males were socially paired for at least one breeding attempt within any single year, totaling 508 male-years. Across these males, the precise distributions of apparent and realized ARS differed to some degree (Fig. 3, G-tests in Table 2C). However, the median, proportion of zeros, IQR, and mean apparent ARS were very similar to those for realized ARS (Table 2C). Across all years and offspring stages, the variances in realized ARS exceeded those in apparent ARS by about 4–42% (ratios in Table 2C). The VarARS-, IARS-, and IδARS-ratios were consistently greater across socially paired males than across all males at analogous offspring stages (Table 2A, C).
IARS-ratios and the decomposition of realized IARS for socially paired males in each individual year are presented in Table S2. In summary, standardized variances in WPRS, EPRS, and their standardized covariance (IW, IE, and CovIW,E) were smaller across socially paired males than across all males, both across all years and in each individual year (Tables 3 and S2). However, the ratios of each variance component to the total realized IARS were similar across socially paired males to those estimated across all males both overall (Table 3A, C) and in individual years (Tables 2B and S2B).
VARIANCE IN LIFETIME FITNESS, ALL MALES
LRS was measured for 183 males hatched during 1993–2003 (Fig. 4). Across all observations, the median, IQR, mean, and variance in LRS decreased as LRS was measured as hatched, independent, and recruited offspring, whereas the proportion of males with zero LRS increased (Table 4A, Fig. 4). The distributions of realized LRS differed from those of apparent LRS (Fig. 4, G-tests in Table 4A). Across all cohorts and offspring stages, realized VarLRS, ILRS, and IδLRS were about 11–27% greater than apparent VarLRS, ILRS, and IδLRS (ratios in Table 4A). The variances in LRS were greater than the variances in ARS at analogous offspring stages, except for ILRS measured as recruited offspring (Tables 1 and 3). Furthermore, the Var-, I-, and Iδ-ratios for LRS were about 4–17% higher than those for ARS across analogous offspring stages (Tables 1 and 3).
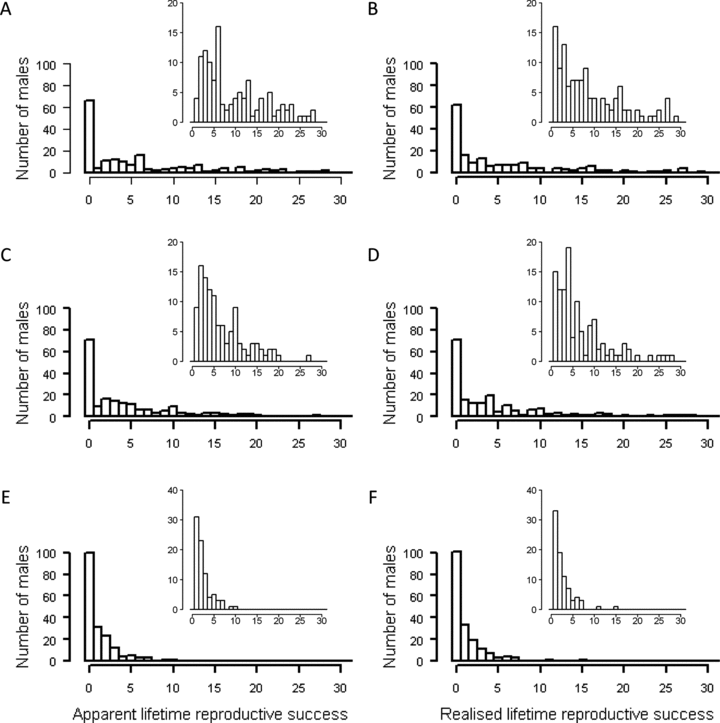
Distributions of apparent (panels A, C, E) and realized (panels B, D, F) lifetime reproductive success (LRS) measured as the total number of hatched (A, B), independent (C, D), and recruited (E, F) offspring produced over a male's lifetime. Inserts show these same distributions for males with nonzero LRS for clarity.
| Apparent lifetime fitness | Realized lifetime fitness | G-test G(df)3 | Ratio | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Med | IQR | Prop. zeros | μa1 | VarTa(LRS) and VarTa(λ) | ITa (LRS) and ITa(λ) | I δ Ta (LRS)2 | Med | IQR | Prop. zeros | μr1 | VarT(LRS) and VarT(λ) | IT (LRS) and IT(λ) | I δ T ( LRS ) 2 | VarLRS and Varλ | ILRS and Iλ | I δ LRS | |||
| (A) LRS— | Hatched | 3 | 0–10 | 0.36 | 6.19 | 57.31 | 1.50 | 2.33 | 3 | 0–9 | 0.34 | 6.27 | 68.97 | 1.76 | 2.59 | 380.9 (121) | 1.20 | 1.17 | 1.11 |
| All males | Independent | 2 | 0–6 | 0.39 | 4.10 | 27.38 | 1.63 | 2.38 | 2 | 0–6 | 0.39 | 4.18 | 34.15 | 1.96 | 2.71 | 387.3 (121) | 1.25 | 1.20 | 1.14 |
| Recruited | 0 | 0–2 | 0.55 | 1.16 | 3.35 | 2.50 | 2.64 | 0 | 0–2 | 0.55 | 1.19 | 4.24 | 2.99 | 3.15 | 249.5 (36) | 1.27 | 1.20 | 1.20 | |
| (B) λind— | Hatched | 0.53 | 0–0.98 | 0.36 | 0.52 | 0.23 | 0.87 | 0.31 | 0–0.93 | 0.34 | 0.50 | 0.24 | 0.98 | 1.04 | 1.13 | ||||
| All males | Independent | 0.53 | 0–0.94 | 0.38 | 0.51 | 0.24 | 0.91 | – | 0.38 | 0–0.94 | 0.38 | 0.50 | 0.25 | 1.00 | – | – | 1.04 | 1.10 | – |
| Recruited | 0 | 0–1.00 | 0.55 | 0.46 | 0.31 | 1.48 | 0 | 0–1.00 | 0.55 | 0.45 | 0.30 | 1.48 | 0.97 | 1.00 | |||||
| (C) LRS—Socially | Hatched | 0 | 0–0 | 1 | 0 | 0 | – | – | 0 | 0–0 | 0.86 | 0.25 | 0.50 | 8.27 | 5.42 | – | – | – | – |
| unpaired males | Independent | 0 | 0–0 | 1 | 0 | 0 | 0 | 0–0 | 0.91 | 0.12 | 0.20 | 13.43 | 6.96 | ||||||
| Recruited | 0 | 0–0 | 1 | 0 | 0 | – | – | 0 | 0–0 | 0.98 | 0.02 | 0.02 | 65 | –4 | – | – | – | – | |
| (D) LRS—Socially | Hatched | 6 | 4–13 | 0.01 | 9.60 | 56.18 | 0.61 | 1.50 | 7 | 3–14.75 | 0.05 | 9.59 | 75.77 | 0.82 | 1.71 | 222.7 (121) | 1.35 | 1.35 | 1.14 |
| paired males | Independent | 5 | 2–9.75 | 0.05 | 6.36 | 28.11 | 0.70 | 1.53 | 4 | 2–9 | 0.10 | 6.41 | 38.86 | 0.95 | 1.78 | 251.0 (121) | 1.38 | 1.36 | 1.16 |
| Recruited | 1 | 0–2 | 0.30 | 1.80 | 4.06 | 1.26 | 1.70 | 1 | 0–2.75 | 0.31 | 1.84 | 5.40 | 1.60 | 2.05 | 166.1 (36) | 1.33 | 1.27 | 1.21 | |
- Med = median; IQR = interquartile range; Prop. Zeros = proportion of males with zero apparent or realized LRS; apparent: μa, realized: μr= mean ARS; apparent: VarTa(LRS), VarTa(λ), realized: VarT(LRS), VarT(λ)= absolute variance in male LRS and λind; apparent: ITa(LRS), ITa(λ), realized: IT(LRS), IT(λ)= maximum opportunity for selection; apparent: IδTa(LRS), realized: IδT(LRS)= Morisita's index. 1Means differ because some extra-pair offspring were gained from males with incomplete LRS.2Morisita's index was not calculated for λind (see Methods). 3All P-values < 0.00001. 4Morisita's index is undefined for the number of recruited offspring of socially unpaired males because only one of these males produced one recruited offspring (making the denominator of the equation null).
However, there was substantial among-cohort variation in ILRS-ratio at all three offspring stages (Table 5B). Specifically ILRS-ratios ranged from 0.89 to 2.14 for hatched offspring, 0.85 to 2.34 for independent offspring, and 0.23 to 1.89 for recruited offspring, with considerable differences between consecutive cohorts (Table 5B).
| Year | N | LRS hatched | LRS independent | LRS recruited | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ITa (LRS) | IT (LRS) | ILRS-ratio | IW | IE | 2 × CovIW,E | ITa (LRS) | IT (LRS) | ILRS-ratio | IW | IE | 2 × CovIW,E | ITa (LRS) | IT (LRS) | ILRS-ratio | IW | IE | 2 × CovIW,E | ||
| (A) All males | 183 | 1.50 | 1.76 | 1.17 | 0.79 (0.45) | 0.31 (0.18) | 0.66 (0.37) | 1.63 | 1.96 | 1.20 | 0.91 (0.46) | 0.33 (0.17) | 0.72 (0.37) | 2.50 | 2.99 | 1.20 | 1.56 (0.52) | 0.59 (0.20) | 0.84 (0.28) |
| (B) 1993 | 27 | 2.07 | 1.95 | 0.94 | 1.07 (0.55) | 0.35 (0.18) | 0.53 (0.27) | 2.42 | 2.40 | 0.99 | 1.31 (0.55) | 0.46 (0.19) | 0.64 (0.26) | 3.25 | 3.54 | 1.09 | 1.74 (0.49) | 0.74 (0.21) | 1.06 (0.30) |
| 1994 | 23 | 1.16 | 1.43 | 1.22 | 0.67 (0.47) | 0.19 (0.13) | 0.54 (0.38) | 1.19 | 1.30 | 1.10 | 0.67 (0.51) | 0.22 (0.17) | 0.41 (0.32) | 1.57 | 1.48 | 0.94 | 0.92 (0.62) | 0.34 (0.23) | 0.22 (0.15) |
| 1995 | 31 | 2.22 | 2.51 | 1.13 | 1.21 (0.48) | 0.59 (0.24) | 0.71 (0.28) | 2.39 | 2.74 | 1.15 | 0.94 (0.34) | 0.75 (0.27) | 1.05 (0.38) | 3.47 | 4.46 | 1.29 | 1.79 (0.40) | 1.30 (0.29) | 1.38 (0.31) |
| 1996 | 30 | 1.35 | 1.63 | 1.21 | 0.81 (0.50) | 0.32 (0.19) | 0.50 (0.31) | 1.47 | 1.97 | 1.33 | 1.01 (0.51) | 0.34 (0.17) | 0.62 (0.31) | 2.23 | 4.22 | 1.89 | 1.46 (0.34) | 1.10 (0.26) | 1.67 (0.39) |
| 1997 | 21 | 3.80 | 3.78 | 0.99 | 1.49 (0.39) | 0.80 (0.21) | 1.63 (0.43) | 4.03 | 3.43 | 0.85 | 1.81 (0.53) | 0.45 (0.13) | 1.17 (0.34) | 5.48 | 6.20 | 1.13 | 3.89 (0.63) | 0.39 (0.06) | 1.92 (0.31) |
| 1998 | 11 | 1.12 | 1.59 | 1.41 | 0.50 (0.31) | 0.36 (0.22) | 0.73 (0.46) | 1.11 | 1.63 | 1.47 | 0.58 (0.36) | 0.30 (0.19) | 0.74 (0.46) | 1.29 | 2.30 | 1.79 | 1.12 (0.49) | 0.39 (0.17) | 0.80 (0.35) |
| 1999 | 6 | 1.49 | 1.37 | 0.92 | 0.73 (0.53) | 0.13 (0.09) | 0.52 (0.38) | 1.54 | 1.47 | 0.96 | 0.78 (0.53) | 0.13 (0.09) | 0.57 (0.38) | 1.57 | 1.28 | 0.81 | 1.16 (0.91) | 0.04 (0.03) | 0.08 (0.06) |
| 2000 | 5 | 0.30 | 0.26 | 0.89 | 0.10 (0.38) | 0.08 (0.30) | 0.08 (0.32) | 0.15 | 0.19 | 1.23 | 0.05 (0.25) | 0.12 (0.62) | 0.02 (0.13) | 0.51 | 0.12 | 0.23 | 0.20 (1.67) | 0.31 (2.67) | −0.39 (−3.33) |
| 2001 | 8 | 1.18 | 1.33 | 1.13 | 0.49 (0.37) | 0.24 (0.18) | 0.60 (0.45) | 1.06 | 1.12 | 1.06 | 0.43 (0.38) | 0.22 (0.20) | 0.47 (0.42) | 3.43 | 2.40 | 0.70 | 0.72 (0.30) | 0.75 (0.31) | 0.93 (0.39) |
| 2002 | 12 | 0.29 | 0.55 | 1.91 | 0.18 (0.32) | 0.15 (0.27) | 0.23 (0.41) | 0.27 | 0.64 | 2.34 | 0.23 (0.36) | 0.16 (0.25) | 0.25 (0.39) | 0.57 | 1.08 | 1.87 | 0.62 (0.58) | 0.14 (0.13) | 0.32 (0.29) |
| 2003 | 9 | 1.02 | 2.19 | 2.14 | 0.75 (0.34) | 0.51 (0.23) | 0.94 (0.43) | 1.17 | 2.26 | 1.93 | 0.74 (0.33) | 0.52 (0.23) | 1.00 (0.44) | 2.20 | 1.53 | 0.70 | 0.97 (0.63) | 0.64 (0.42) | −0.08 (−0.05) |
| (C) Paired males | 118 | 0.61 | 0.82 | 1.35 | 0.36 (0.43) | 0.17 (0.21) | 0.29 (0.36) | 0.70 | 0.95 | 1.36 | 0.43 (0.46) | 0.19 (0.20) | 0.33 (0.35) | 1.26 | 1.60 | 1.27 | 0.84 (0.52) | 0.35 (0.22) | 0.41 (0.25) |
- N= number of males; ITa(LRS)= total (mean-standardized) variance in apparent LRS; IT(LRS)= total variance in realized LRS; ILRS-ratio = the ratio between IT(LRS) and ITa(LRS); IW= variance in IT(LRS) due to within-pair reproductive success; IE= extra-pair reproductive success; 2 × CovIW,E= covariance between within- and extra-pair LRS.
Across all males and cohorts, the opportunity for selection due to lifetime WPRS (IW) was substantially greater than that due to lifetime EPRS (IE) whether LRS was measured as hatched, independent, or recruited offspring (Table 5A). The standardized covariance between lifetime WPRS and EPRS was positive (Table 5A) and substantially greater than the standardized covariance between annual WPRS and EPRS (Tables 2A and 4A).
Within each cohort, lifetime IW was generally, but not always, greater than lifetime IE (Table 5B). The standardized covariance between lifetime WPRS and EPRS was generally positive but varied substantially in magnitude and direction (Table 5B). The ILRS-ratio did not vary significantly with the standardized covariance between lifetime WPRS and EPRS at any of the three offspring stages (Fig. 5).
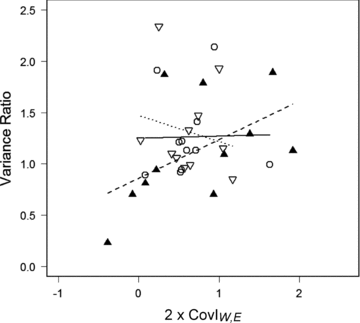
Relationship between (twice) the standardized covariance between male within- and extra-pair lifetime reproductive success (2 × CovIW,E) and the ratio between the variances in realized and apparent lifetime reproductive success (ILRS-ratio) across 11 cohorts. Lifetime reproductive success (LRS) was measured as the number of hatched (open dots), independent (open triangles pointing down), and recruited offspring produced (filled triangles pointing up). Lines show the linear models: β= 0.02 ± 0.34 (SE), t= 0.06, df = 10, P= 0.95, R2 < 0.01 (LRSHatched, solid line), β=–0.25 ± 0.43 (SE), t=–0.60, df = 10, P= 0.57, R2= 0.04 (LRSIndependent, dotted line) and β= 0.38 ± 0.20 (SE), t= 1.85, df = 10, P= 0.10, R2= 0.28 (LRSRecruited, dashed line).
Across all 183 males, the mean and variance in realized λind (the rate-insensitive measure of lifetime fitness) were similar to those for apparent λind (Table 4B). Estimates of Iλ were slightly greater for realized λind than apparent λind at all three offspring stages, but by ≤13% (ratios in Table 4B).
VARIANCE IN LIFETIME FITNESS, SOCIALLY PAIRED VERSUS UNPAIRED MALES
A total of 65 males remained socially unpaired for their entire life (median life span: 1 year, range: 1–3). These males sired up to three hatched extra-pair offspring (Fig. 6) but very few sired any recruited offspring (Table 4C). Their apparent and realized LRS therefore remained very low (Table 4C, Fig. 6).
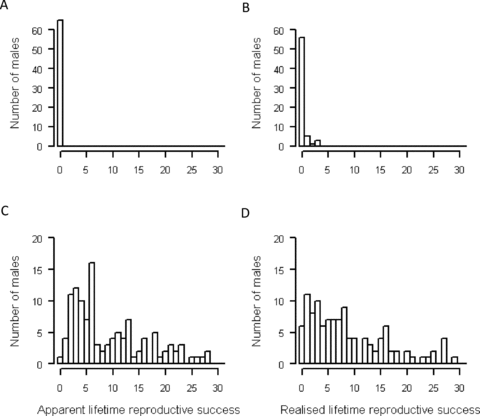
Distributions of apparent (panels A, C) and realized (panels B, D) lifetime reproductive success (LRS) of socially unpaired (A, B) and socially paired males (C, D), measured as hatched offspring. Scales are standardized to facilitate comparison.
Across 118 males that were socially paired for at least one breeding attempt during their life, the median, IQR, proportion of zeros, and mean for apparent LRS were similar to those for realized LRS (Table 4D). Across all cohorts and offspring stages, realized VarLRS, ILRS, and IδLRS were 14–38% greater than apparent VarLRS, ILRS, and IδLRS (ratios in Table 4D, Fig. 6). For the rate-sensitive measure of lifetime fitness, the variances and opportunity for selection (Varλ and Iλ) were 2% smaller to 57% greater for realized λind than for apparent λind.
Lifetime IW, IE, and CovIW,E were smaller across males that were socially paired at least once than across all males and cohorts (Tables 4C and 5A). However, the ratios of each standardized variance component (IW, IE, and CovIW,E) to the total ILRS among socially paired males were similar to those estimated across all males and cohorts (Tables 4C and 5A). ILRS-ratios and the decomposition of the realized ILRS in each individual cohort for socially paired males are presented in Table S3. In summary, standardized variances and covariances in WPRS and EPRS were consistently smaller across socially paired males than across all males, but the ratios of each variance component to the variance in male LRS across paired males were similar to those estimated across all males (Tables 4B and S3b).
Discussion
It is widely hypothesized that males with high social mating success will also be successful extra-pair sires (Jennions and Petrie 2000; Griffith et al. 2002; Akçay and Roughgarden 2007; Kempenaers 2007) and therefore that EPP will increase the population-wide variance in male fitness and influence consequent evolutionary processes (e.g., Arnold and Wade 1984; Nunney 1993; Waples 1998; Reid and Keller 2010). However, despite considerable previous effort, tests of this hypothesis are limited because apparent (social) and realized (genetic) reproductive success have not been comprehensively measured across the life spans of all males within a population. We identified all adult males alive in a free-living song sparrow population during 1993–2008 and assigned social and genetic sires to virtually all offspring with high confidence. We thereby quantified the full distributions of apparent and realized ARS and LRS, comprehensively tested the hypothesis that EPP increases the variance in male fitness, and determined the contributions of the variance and covariance in WPRS and EPRS to the realized variance in male fitness.
VARIANCE IN ARS
Across all males and years, three measures of variation in male ARS (Var, I, and Iδ) remained relatively similar whether estimated as apparent or realized ARS. This result was broadly consistent whether ARS was measured as hatched, independent, or recruited offspring (range of ratios: 2–14%). Thus, despite the relatively high EPP rate of 28%, EPP had a relatively small effect on the variance in ARS in song sparrows. There was therefore qualitative but only limited quantitative support for the hypothesis that EPP will substantially increase the variance in male fitness. These results contrast with previous (less-comprehensive) studies of socially monogamous but genetically polygynandrous bird populations, which report that EPP substantially increased male IARS. Indeed, the median ratio of realized to apparent IARS for hatched offspring across 17 published studies is 2.9, compared to 1.1 in song sparrows (Table 1).
However, there was substantial among-year variation in IARS-ratio in song sparrows, ranging from 0.57 to 2.00 across all years and offspring stages. EPP therefore approximately doubled or halved IARS in different years. Because most previous studies covered few years (Table 1), it is not yet clear whether substantial among-year variation in IARS-ratio is common, and hence whether effects estimated by short-term studies may simply reflect individual study years rather than any consistent or average effect.
VARIANCE IN LRS
Individual fitness is commonly measured as ARS (Kingsolver et al. 2001). However ARS may inaccurately predict fitness if there are cross-season trade-offs among fitness components, potentially providing misleading conclusions regarding the effect of EPP on the variance in total fitness. In song sparrows, variance in apparent LRS was substantial (see also Hochachka 2006) and consistently greater than the variance in ARS at all offspring stages. However, as with ARS, variation in realized LRS was only slightly greater than the variation in apparent LRS (11–27% measured as Var, I, or Iδ). This result is broadly consistent with the only other study that quantified variation in male apparent and realized LRS in a socially monogamous but genetically polygynandrous species; realized ILRS was 12% greater than apparent ILRS in splendid fairy wrens (Malurus splendens, Webster et al. 2007). This study and ours also report the lowest IARS-ratios published to date (Table 1), and both indicate that ILRS-ratios slightly exceed IARS-ratios. The effect of EPP on the variance in male fitness might therefore be greater when integrated over each individual's life span than over individual breeding seasons. Furthermore, the ILRS-ratio varied substantially among song sparrow cohorts, from 0.23 to 2.34 across all offspring stages. EPP therefore more than doubled ILRS or reduced it by a factor of four in different cohorts, showing that the true lifetime realized opportunity for selection may be substantially larger or smaller than the apparent opportunity in any individual cohort.
VARIANCE IN RATE-SENSITIVE LIFETIME FITNESS
A male's ability to sire within-pair and/or extra-pair offspring could vary with age, for example if young males lose paternity to older males (Richardson and Burke 1999; Schmoll et al. 2007). Rate-insensitive measures of fitness such as LRS do not incorporate any such age-specific paternity loss or gain. However, the effect of EPP on the variance in rate-sensitive measures of lifetime fitness, such as λind, has not previously been estimated.
In song sparrows, variances in λind were consistently lower than variances in LRS measured at analogous offspring stages. This may be because although variation in life span increases the variance in LRS compared to ARS, it increases the variance in λind to a lesser degree because the value of offspring produced later in a male's life is discounted (Brommer et al. 2002). Furthermore, the slight increase in the variance in male LRS due to EPP was even less evident when fitness was measured as λind. Indeed, the variance in realized λind even decreased slightly relative to the variance in apparent λind when λind was estimated as recruited offspring. Analysis of λind therefore suggests that, on average, EPP increased the variance in adult male fitness slightly or not at all in song sparrows.
MECHANISMS
The fact that EPP increased the variance in male fitness less in song sparrows than reported in other populations (Table 1) may primarily reflect the less-comprehensive paternity assignment in those studies and the consequent inflation of estimated IARS-ratios. This bias is well documented (Downhower et al. 1987; Freeman-Gallant et al. 2005). However, the distribution of EPP on Mandarte is skewed across males and repeatable within males among years (Reid et al. 2011), two conditions that underpin the potential for EPP to increase the variance in fitness (Webster et al. 1995). The observation that EPP did not substantially increase the overall variance in male fitness therefore requires further explanation.
The small overall effect of EPP on the variance in male fitness may result from the presence of socially unpaired males with zero apparent reproductive success. These socially unpaired males sired few extra-pair offspring (Sardell et al. 2010), and so also had very low realized reproductive success. The presence of socially unpaired males therefore dampens the effect of reallocation of paternity among socially paired males on the total variance in fitness. Indeed, EPP increased the variance in male ARS by 4–42% when socially unpaired males were excluded (compared to 2–14% across all males). These results support Shuster's (2009) suggestion that studies that fail to sample socially unpaired or otherwise unsuccessful males may overestimate the effect of EPP on the total variance in male fitness.
However, even after excluding socially unpaired males, the overall increase in the variance in realized versus apparent fitness was still relatively small on average. Small effects of EPP on the I-ratio might be expected if reproductive success gained through EPP is offset by reduced WPRS due to cuckoldry (Webster et al. 1995). The I-ratio is therefore expected to reflect the magnitude and direction of covariance between male WPRS and EPRS (Webster et al. 1995; Jones et al. 2001). Across all years and cohorts, the covariances between male annual and lifetime WPRS and EPRS were positive, showing that males that successfully sired within-pair offspring also sired more extra-pair offspring. However, the magnitude and direction of the covariance between annual WPRS and EPRS varied substantially among years, and explained approximately a third of the among-year variation in IARS-ratio. The covariance between lifetime WPRS and EPRS also varied substantially among cohorts, but explained only 0–28% of the among-cohort variation in the ILRS-ratio. The hypothesis that variation in I-ratio reflects the covariance between WPRS and EPRS was therefore somewhat supported with respect to ARS, but less so with respect to LRS, and substantial proportions of variation remained unexplained.
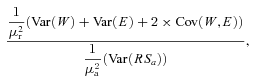
From the above expression, it is clear that the I-ratio will be close to 1 if the variance in WPRS is large relative to the variance in EPRS and is relatively unaffected by EPP. Indeed, the variance in WPRS integrates the variances in social pairing success, female fecundity, and the proportion of within-pair offspring sired (Webster et al. 1995). The occurrence of EPP is expected to influence the variance in the proportion of within-pair offspring sired, but not necessarily the variances in social pairing success or social female fecundity. How to quantify the relative contribution of these fitness components to the total variance in male realized reproductive success is unclear (Appendix S1). However, social pairing success is a major component of male fitness in Mandarte sparrows because a substantial proportion of males remains socially unpaired and have low EPRS (Sardell et al. 2010). Furthermore, there is substantial variation in female fecundity; females rear zero to four broods in a season (Smith et al. 2006, p. 34), and the number of offspring hatched per female varies substantially (median female ARS: 5, IQR: 3–6). The small difference in the variances in realized and apparent fitness in song sparrows may therefore result from the substantial variance in male WPRS that is unaffected by EPP.
Finally, the overall effect of EPP on the I-ratio across all years may be small because it combines substantial among-year variation in the variance and covariance in annual WPRS and EPRS (Table 3). This among-year variation could itself reflect among-year variation in population state such as density, breeding synchrony, operational sex ratio, or age structure (Richardson and Burke 1999; Westneat and Stewart 2003; Shuster 2009), all of which vary markedly on Mandarte (Hochachka et al. 1989; Arcese et al. 1992; Smith et al. 2006; Keller et al. 2008). The degree to which among-year and among-cohort variation in I-ratio reflects these extrinsic and intrinsic processes remains to be investigated.
IMPLICATIONS
In song sparrows, EPP increased the overall variance in male fitness by only 0–27%, but caused much larger changes in individual years and cohorts. Whether these changes are sufficient to influence evolutionary processes, however, depends on the particular process of interest.
The variance in fitness influences effective population size (Nunney and Elam 1994). However, because EPP does not affect the variance in female fitness, a small increase in the variance in male fitness due to EPP is unlikely to substantially affect effective population size or consequent rates of inbreeding and genetic drift. Indeed, previous analysis of four years of song sparrow data showed that the ratios of effective to total population size were 0.66 and 0.65 when estimated using variances in apparent and realized ARS, respectively (O’Connor et al. 2006).
However, even though EPP did not substantially increase the variance in reproductive success, it could still affect the variance in mating success. This could in turn explain the evolution of sexual dimorphism in social monogamous but genetically polygynandrous species, in terms of morphology and other traits such as song (Webster et al. 2007). Furthermore, EPP altered the distributions of male ARS and LRS in more subtle ways than detected by measures of population-wide variance. Such small changes in the distribution of fitness, if linked to heritable attributes of males that gain or lose reproductive success through EPP, could affect phenotypic variation over time (Shuster and Wade 2003). Furthermore, subtle changes in the distribution of reproductive success could also affect patterns of relatedness by changing the frequencies of full and half siblings, and hence influence inbreeding risk and kin selection and competition (Cornell and Tregenza 2007; Cornwallis et al. 2010). In summary, although EPP did not greatly alter the variance in male fitness in song sparrows, it could still influence major evolutionary processes through more subtle redistribution of paternity.
Associate Editor: M. Blows
ACKNOWLEDGMENTS
We thank the Tsawout and Tseycum First Nation bands for allowing us to work on Mandarte Island, everyone who contributed to long-term data collection and the Royal Society (JMR), the Leverhulme Trust (CL and JMR), NERC (RJS), NSERC (PA), and the Swiss National Science Foundation (LFK) for funding.




