EVIDENCE OF ADAPTATION FROM ANCESTRAL VARIATION IN YOUNG POPULATIONS OF BEACH MICE
Abstract
To understand how organisms adapt to novel habitats, which involves both demographic and selective events, we require knowledge of the evolutionary history of populations and also selected alleles. There are still few cases in which the precise mutations (and hence, defined alleles) that contribute to adaptive change have been identified in nature; one exception is the genetic basis of camouflaging pigmentation of oldfield mice (Peromyscus polionotus) that have colonized the sandy dunes of Florida's Gulf Coast. To quantify the genomic impact of colonization as well as the signature of selection, we resequenced 5000 1.5-kb noncoding loci as well as a 160-kb genomic region surrounding the melanocortin-1 receptor (Mc1r), a gene that contributes to pigmentation differences, in beach and mainland populations. Using a genome-wide phylogenetic approach, we recovered a single monophyletic group comprised of beach mice, consistent with a single colonization event of the Gulf Coast. We also found evidence of a severe founder event, estimated to have occurred less than 3000 years ago. In this demographic context, we show that all beach subspecies share a single derived light Mc1r allele, which was likely selected from standing genetic variation that originated in the mainland. Surprisingly, we were unable to identify a clear signature of selection in the Mc1r region, despite independent evidence that this locus contributes to adaptive coloration. Nonetheless, these data allow us to reconstruct and compare the evolutionary history of populations and alleles to better understand how adaptive evolution, following the colonization of a novel habitat, proceeds in nature.
Adaptation following colonization of novel habitats is influenced by the interplay of demographic and selective forces. Thus, to obtain a complete picture of the evolutionary change involved in the process of adaptation, we must reconstruct the evolutionary history of alleles under selection as well as the history of populations. Over the last years, considerable progress has been made in identifying genes that contribute to phenotypic variation in natural populations (reviewed in Stinchcombe and Hoekstra 2007; Ellegren and Sheldon 2008; Mackay et al. 2009; Stapley et al. 2010). However, the precise genetic variants that define alleles responsible for altered gene function and/or expression have yet to be identified in most cases (but see Chan et al. 2010) and/or their direct link to fitness is often missing (Barrett and Hoekstra 2011), thus limiting our ability to define and thereby study the evolution of adaptive alleles. Therefore, fundamental questions such as the primary source of beneficial mutations (i.e., pre- existing mutations segregating as standing genetic variation or de novo mutations that appear after an environmental change [but see Colosimo et al. 2005; Linnen et al. 2009]), the number of independent origins of alleles (see Feldman et al. 2009; Steiner et al. 2009; Song et al. 2011; van't Hof et al. 2011), and the timing and strength of selection acting on these alleles (see Linnen et al. 2009) remain largely unanswered.
Answering these questions also requires placing the history of fitness-related alleles in a demographic context. For example, only by comparing the evolutionary relationships of beneficial alleles with the phylogenetic relationships of populations can one infer the number of independent origins of beneficial mutations. Moreover, the ability to distinguish signatures of selection from purely demographic effects requires rigorous estimation of null demographic models (Thornton and Jensen 2007). Specifically, strong or recent demographic events, such as population bottlenecks, can reduce or even eliminate our ability to identify statistically significant departures from neutrality (i.e., selective sweeps; see review of Thornton et al. 2007). In addition to providing a framework for gaining insight into the evolution of adaptive loci, several aspects of the demographic history of colonization have intrinsic value to understand the forces involved in genetic and phenotypic divergence. Specifically, when organisms colonize new areas, they typically experience founder effects associated with reduced population size and low genetic diversity, which may limit opportunities to adapt to a new local environment (Nei et al. 1975). Moreover, ancestral and derived populations may still exchange migrants at least in the initial stages of the colonization process—because gene flow constrains genetic and phenotypic differentiation between populations, this may limit adaptive divergence (Riechert 1993; Nosil and Crespi 2004; Nosil 2009). Therefore, a complete understanding of adaptive evolution necessitates inference of the parameters of both population size change and migration.
Because patterns of genetic diversity and relationships among populations vary widely among loci, especially for recently diverged species or populations (Tajima 1983), an accurate estimation of the demographic history calls for data from multiple unlinked loci (Takahata and Nei 1985). Recent developments in high-throughput sequencing technologies and multiplex strategies now make it possible to genotype hundreds of loci distributed throughout the genome in wild populations. This, together with novel statistical and computational methods for genome-wide phylogenetic reconstruction (e.g., Guindon and Gascuel 2003; Stamatakis 2006), for demographic modeling (e.g., Thornton and Andolfatto 2006; Gutenkunst et al. 2009; Naduvilezhath et al. 2011), and for detecting targets of selection (e.g., Sabeti et al. 2002; Nielsen et al. 2005; Williamson et al. 2007; Pavlidis et al. 2010) place us in a strong position to accurately infer the history of natural populations and rigorously document the effects of selection during local adaptation.
Here, we capitalize on a system—camouflaging pigmentation in the oldfield mouse (Peromyscus polionotus)—for which alleles that contribute to phenotypic variation have been identified (Hoekstra et al. 2006; Steiner et al. 2007) and the link between phenotype and fitness is clear (Vignieri et al. 2010) to answer questions regarding the evolutionary history of fitness-related traits in a demographic context. In the dark loamy soils of the southeastern United States, these mice have dark dorsal coats, whereas conspecifics that subsequently colonized the pale sand dunes and barriers islands of Florida's Gulf Coast have pale coats with reduced pigmentation. Experimental work showed that natural selection for crypsis, via predation by visual hunters, acts on differences in pigmentation between mainland and beach forms (Vignieri et al. 2010). Along Florida's Gulf shoreline, there are five subspecies of beach mice; although all beach mice have lighter pelage than their mainland counterparts, each subspecies shows a unique color pattern (Sumner 1926; Mullen et al. 2009). A single mutation in the coding region of the melanocortin-1 receptor (Mc1r) has been identified and shown to contribute to differences between Santa Rosa Island beach mice (SRIBM) (P. p. leucocephalus), the lightest of the beach subspecies, and mainland mice (P. p. subgriseus) (Hoekstra et al. 2006). Moreover, variation in the frequency of Mc1r alleles among beach mouse subspecies is correlated with pigment differences (Mullen et al. 2009).
To gain a more complete picture of the evolution of cryptic coloration in P. polionotus following the colonization of the beach habitat, we used a targeted resequencing approach to reconstruct the demographic signature of colonization, to infer the evolutionary relationships of adaptive alleles, and to identify genomic footprints of selection. Specifically, we evaluated the competing hypotheses of single or multiple colonization events of the beach habitat. In addition, we estimated the timing of the colonization and the number of independent origins of a derived mutation in Mc1r that contributes to the reduced pigmentation in beach mice, and we evaluated our ability to detect signatures of selection in a recently colonized population while controlling for demographic effects.
Methods and Materials
MOUSE SAMPLES
We collected mice from 13 locations across the range of P. polionotus, including the five Gulf Coast beach mouse subspecies and eight mainland populations (Fig. 1A). Mice were collected using Sherman live traps, and a tissue sample (tail tip or liver) was taken and stored in 95% ethanol. We extracted genomic DNA from each tissue sample using an Autogen kit in an AutoGenPrep 965 instrument (Autogen, Holliston, MA). Mainland samples were accessioned as museum specimens in the Harvard Museum of Comparative Zoology Mammal Department.
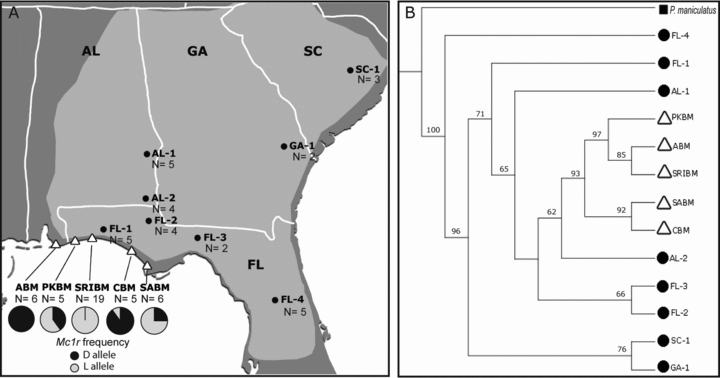
(A) Map showing the approximate distribution of Peromyscus polionotus (light gray shade) in Alabama (AL), Georgia (GA), South Carolina (SC), and Florida (FL), and sample sites of mainland populations (filled dots) and beach subspecies (open triangles) surveyed in this study. Pie charts represent the estimated frequency of Mc1r ancestral “dark” alleles (in black) and derived “light” alleles (in gray) in the beach subspecies (ABM, Alabama beach mice; PKBM, Perdido Key beach mice; SRIBM, Santa Rosa Island beach mice; CBM, Choctawhatchee beach mice; SABM, Saint Andrews beach mice). (B) Topology of P. polionotus populations generated using genomic data (211 genomic regions, totaling 161 kb). Bootstrap supports based on 100 replicates are shown on branches. Taxon labels correspond to locations shown in (A).
CAPTURE ARRAY DESIGN, TARGET ENRICHMENT, AND NEXT-GENERATION SEQUENCING
We designed a custom SureSelect capture array (Agilent Technologies, Santa Clara, CA) to enrich templates for both random “neutral” regions and for the Mc1r locus (following Gnirke et al. 2009). To obtain genome-wide data for demographic and phylogenetic analysis, we targeted 5114 regions averaging 1.5 kb in length (5.2 Mb of nonrepetitive sequence) at random locations throughout the Peromyscus genome at 3× tiling. Probes were designed from an in-house P. maniculatus bairdii∼1x draft genome assembly (3.3 million reads from Baylor College of Medicine/NCBI Trace Archive; WGS assembler [Myers et al. 2000]). To maximize recovery of unique sequence reads, we masked repetitive regions using existing data for mouse/rat (RepeatMasker open3.2.7; http://www.repeatmasker.org) and custom repeat libraries for Peromyscus constructed using Piler (Edgar and Myers 2005) and RepeatScout (Price et al. 2005). To resequence an approximately 160-kb region containing the single Mc1r exon and neighboring genes, we used sequences obtained from a Mc1r-containing BAC clone (a Sanger-sequenced 160-kb clone from P. m. rufinus BAC library at 20× coverage) to design the capture array. We tiled 120mer probes (at 5× coverage) across intervals that encompass exons and intronic regions included in the BAC.
We prepared barcoded DNA libraries for each of our samples. We used a multiplex strategy with the above-described array to enrich pools of 12 samples each. Capture probes were hybridized to target DNA in solution, and targeted regions were then selected using magnetic beads and amplified with universal primers (Gnirke et al. 2009). We then sequenced our capture libraries and generated 100-bp paired-end reads on an Illumina HiSeq 2000 (Illumina Inc., San Diego, CA). Raw sequence data are available at the Sequence Read Archive (accession number: SRA050092.2).
SHORT-READ SEQUENCE ANALYSES AND VALIDATION
We first processed raw Illumina data to generate quality-filtered files with sequences from each barcoded individual. Second, we used the Burroughs-Wheeler Alignment (BWA) tool (Li and Durbin 2009) to map reads to a composite reference sequence set consisting of P. m. bairdii genome scaffolds and P. m. rufinus BAC sequences. We performed initial mapping and alignment using default parameters values in BWA (details of final conditions are explained below). Variant discovery and diploid genotype inference were performed using the GATK software package, which simultaneously estimates individual genotypes and population allele frequencies (DePristo et al. 2011).
To assess accuracy and completeness of genotype determination, we performed a receiver-operating characteristic (ROC) analysis to compare genotypes of eight mice generated from our short-read sequence data with those obtained from a total of 690 kb of Sanger sequence for the same individuals. Regions sampled in Sanger sequencing were representative with regards to GC content and short read coverage of the Mc1r locus overall (targeted intergenic regions had equivalent GC content but lower mean coverage as expected from differential probe tilling depth). We calculated area under the curve (AUC) for threshold models of four genotype quality metrics (described in Supporting information): two individual-level metrics (mapped read depth, DP and genotype quality, GQ) and two population-level metrics (site quality, QUAL and variant quality-by-depth, QD). Comparisons of AUC showed that population-level metrics outperform individual metrics, confirming the utility of simultaneous genotype inference across multiple individuals (Fig. S1).
OPTIMIZING MAPPING AND FILTERING OUT PARALOGOUS REGIONS
Having found the best metrics to assess accuracy of genotyping, we returned to the question of optimizing mapping parameters. Because our reference assemblage consists of sequences from a different (although closely related) species, we tested performance of mapping with different parameters values (seed length, l; seed edit distance, k; and number of suboptimal alignments to sample, R) in BWA using ROC curves of population-level metrics as described above. We tested a range of parameters around BWA defaults singly and in combination (l= 35, 55, 75; k= 2, 4, 6; R= 10, 100) and concluded that the parameter set that maximized number of reads mapped and concordance of final genotypes was l= 55, k= 4, R= 10.
As the reference genome is incomplete, we expect some incidence of paralogous mapping in our aligned reads. One signature of paralogous mapping is an excess of heterozygous genotypes (which are actually divergent sites between paralogs) compared to frequencies of the two homozygous genotype classes. To filter out paralogous regions, we computed the fraction of heterozygous individuals at each variable site for the two variant calling models used to generate the final datasets (see below). In brief, we tested independently the two final models with the addition of a fixed threshold for mean fraction heterozygous genotypes ranging from 0 to 1 in steps of 0.1 (pass one), and subsequently in intervals of 0.01 (pass two), between the best pass-one models (mean heterozygous fractions of 0.5 and 0.6 in pass one, final optimum of 0.54 in pass two). We then removed regions in which the average fraction of heterozygote individuals across sites in that region exceeded 0.54.
GENERATING FINAL DATASETS
To generate final datasets, we performed mapping using the selected BWA parameters (l= 55, k= 4, R= 10) and removed paralogous regions. Based on ROC curve inflections, we selected two threshold set conditions for variant calling in GATK that produced reliable genotypes. We generated a “dataset A” using QD = 6, QUAL = 200, and GQ = 12 (99.6% concordance with Sanger data and false-positive rate of 0.0019), and “dataset B” using QD = 20 and GQ = 20 (concordance 99.8% and false-positive rate 0.0004). Although parameters in dataset A are more permissive than in dataset B, they still generate reliable genotypes and have the advantage of providing more power for analysis based on patterns of genetic variability. Finally, we imputed missing genotypes and estimated haplotype phase using a statistical model based on flexible clustering of patterns of genetic variation and linkage disequilibrium in natural populations, implemented in the software package fastPHASE (Scheet and Stephens 2006), and obtained SNP-specific linkage disequilibrium-based genotyping error rates (following Scheet and Stephens 2008).
ANALYSIS OF POPULATION GENETIC DIVERSITY AND DIFFERENTIATION
Using genome-wide SNP data, we first estimated average heterozygosity for each population as a measure of genetic diversity. To include only unlinked markers in our analysis, we used one site per genetic region recovered in dataset A, totaling 2236 SNPs. Next, we estimated Fst in the program SPAGeDi (Hardy and Vekemans 2002) to assess the extent of differentiation among beach mice and mainland populations. In addition, we estimated population structure among beach mouse subspecies using a Bayesian model based cluster method implemented in STRUCTURE version 2.3 (Pritchard et al. 2000) that assigns individuals to populations based on their genotype frequencies. We also estimated the maximum-likelihood (ML) number of subpopulations (k= 1–6) using an admixture model and assuming uncorrelated allele frequencies between clusters. First, we ran the analysis 10 times for each k using a burn-in of 100,000 Markov Chain Monte Carlo (MCMC) steps followed by 100,000 iterations. Then, we used the Greedy algorithm in CLUMPP (Jakobsson and Rosenberg 2007) to handle the results from replicate analyses. Finally, we compared posterior probabilities of each k to determine the number of subpopulations that best fit our data.
ESTIMATION OF THE P. POLIONOTUS POPULATION TREE
To reconstruct the colonization history of mice along the Florida coast, we estimated a population topology using genomic sequencing data generated with the most restrictive of our parameter sets (dataset B) to ensure that only extremely reliable genotypes were used for phylogenetic construction. We used the Maximum Pseudo-Likelihood for Estimating Species Tree (MP-EST) method (Liu et al. 2010) to estimate a “species” tree of P. polionotus under the coalescence model by maximizing a pseudolikelihood function using a set of gene trees, which accounts for gene tree heterogeneity. First, we selected sequences from regions across the genome that contained at least five polymorphic sites (211 regions, total of 161 kb) and produced 100 bootstrap replicates for each region using a nonparametric technique (Efron 1981). Second, we built gene trees for each bootstrap sample using a ML-based method with a GTRGAMMA model of nucleotide substitution implemented in the program RAxML (Stamatakis 2006). Gene trees were rooted using P. maniculatus, the sister species of P. polionotus, as an outgroup. Next, we used the rooted gene trees to construct 100 MP-EST trees. Finally, a consensus tree was built from the 100 MP-EST trees using Majority-Rule-extension (MRe) in CONSENSE from the PHYLIP package (Felsenstein 1989). The tips of the resulting tree represent the eight mainland populations and five beach subspecies used in this study.
DEMOGRAPHY OF BEACH COLONIZATION
We inferred population history of beach mice using genome-wide SNP data (dataset A) to maximize the number of variable sites and thus power. We used the mainland population from Alabama (AL-2), which was most closely related to the beach subspecies from the phylogenetic analysis described above, to represent the ancestral population. For comparison, we also repeated the analysis using a second closely related population from mainland Florida, FL-2. Demographic parameters were estimated from the joint allele frequency spectrum (AFS; the distribution of polymorphism frequencies in the populations) by applying a diffusion-based approach implemented in the program ∂a∂i (Gutenkunst et al. 2009). We polarized SNPs using P. maniculatus as an outgroup. Because the sample size needs to be the same for each SNP when constructing the AFS, we used the projection option in ∂a∂i to adjust the number of individuals included to maximize the number of segregating sites used. The final dataset consisted of: one mainland population (AL-2; N= 4), SRIBM(N= 15), Alabama beach mice (ABM; N= 5), Perdido Key Beach mice (PKBM; N= 4), Choctawhatchee beach mice (CBM; N= 4), and St. Andrews beach mice (SABM; N= 5). The number of segregating sites ranged from 163 to 495 depending on the subspecies analyzed. We estimated demographic parameters in a pairwise fashion using the mainland population with each of the beach subspecies. The AFS of the mainland population and each of the beach subspecies were fitted to an isolation-with-migration model (Fig. 2). In this model, the mainland population gives rise to a beach population, while the two populations exchange migrants. The following parameters were estimated: size of the beach populations immediately following the split (s, given as a fraction of the original population), final size of beach (nu1) and mainland (nu2) populations, time of the split (T), migration from mainland to beach (m21), and migration from beach to mainland (m12). To estimate parameter uncertainty, we used conventional bootstrapping (fitting 100 datasets resampled over loci) and to ensure that we reached convergence, we ran each dataset at least five times. We then determined the confidence interval of each parameter as the 2.5 and 97.5 percentiles of the parameter distribution in the bootstrapped data.
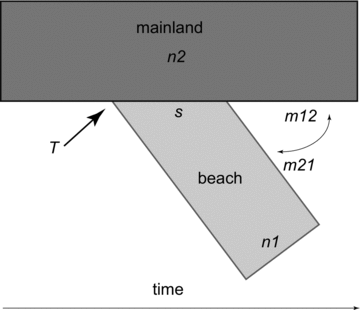
Illustration of the isolation-with-migration model used to estimate six demographic parameters. In this model, a fraction of the ancestral mainland population(s) gives rise to a derived beach population at time T in the past. Mainland and beach populations differentiate with bidirectional migration occurring between them (m21 and m12). Final beach and mainland population sizes are n1 and n2, respectively.
We next tested a less-pronounced founder event by comparing the likelihoods of the optimized model with a model of equal population size of beach and mainland populations following the population split. To explicitly test different migration scenarios, we performed likelihood ratio tests between the optimized model and the model with alternative migration rates (no migration and symmetrical migration with low and high migration rates) and determined P-values for each model comparison assuming a χ2 distribution of the test statistics.
Finally, we converted the timing of the population split (given in units of 2N generations) to years. We first obtained N from θ= 4NμLeff, where μ is the mutation rate per site per generation estimated for Mus domesticus (μ= 3.7 × 10−8, Lynch 2010), and Leff is the effective length of the genomic region used (Leff= 349,390 bp). Peromyscus polionotus achieves sexual maturity at about 30 days, and gestation lasts approximately 30 days (Clark 1938). In the wild, these mice reproduce year-round, although there is a decline in breeding activity during the summer. We estimated time in years using our estimate of N and a conservative two to three generation-per-year estimate.
PHYLOGENETIC ANALYSIS OF PIGMENTATION ALLELES
Following the approach for estimating population trees, we used the most restrictive of our parameter sets (dataset B) to generate genealogies of Mc1r alleles. We first confirmed Mc1r genotype at the Arg65Cys site for all samples using a TaqMan assay (described in Steiner et al. 2007). To determine the number of independent origins of the derived Mc1r alleles that contained the 65Cys mutation (“light allele”), we estimated a ML genealogy using a 4-kb fragment including the Mc1r exon and its neighboring sequence (comprising 35 parsimony informative sites). We used the GTRGAMMA model of nucleotide substitution and applied the rapid bootstrapping algorithm in RAxML (Stamatakis 2006). In addition, we generated MP and Bayesian phylogenies using the software Paup* version 4.0b10 (Swofford 2002) and MrBayes version 3.2 (Ronquist and Huelsenbeck 2003), respectively. Node support was evaluated with 1000 bootstrap replicates (Felsenstein 1985) in the case of ML and MP methods and posterior probabilities in the Bayesian analysis. To test if the Mc1r tree topology was statistically different from the population tree topology, we conducted an SH test (Shimodaira and Hasegawa 1999) to compare ML scores for a topology in which beach mice were forced to be monophyletic and the best ML topology for the Mc1r fragment. The SH test was performed in Paup* using the RELL approximation with 10,000 bootstrap replicates.
Because the Mc1r gene topology is expected to reflect selection, but the signature of selection should be lost as we move away from the target of selection due to recombination, we estimated genealogies using sequences at varying distances from the Mc1r gene. To first annotate the Peromyscus Mc1r BAC, we aligned Peromyscus sequences to the Rattus genome using GenomeVISTA (Bray et al. 2003; Couronne et al. 2003). Next, we chose fragments at different distances from Mc1r that contained a similar number of informative sites. All phylogenetic reconstructions were performed as described above.
DETECTING SIGNATURES OF POSITIVE SELECTION IN MC1R
Using the dataset that provides increased power for genetic diversity based analysis (dataset A), we first measured genetic diversity (e.g., number of segregating sites, average number of pairwise differences, and Waterson's θ) and characterized the skew in the frequency spectra of the 160-kb resequenced region including Mc1r, by calculating Tajima's D (Tajima 1989) and Fu and Li's D* (Fu and Li 1993) for each beach population. To test for signatures of positive selection in Mc1r, we used several approaches. First, we performed a sliding-window analysis of divergence and polymorphism using a modification of the Hudson–Kreitman–Aguade (HKA) test (Hudson et al. 1987). This analysis was conducted in the SRIBM population (which is fixed for the derived Mc1r 65Cys mutation) and the ABM population (fixed for the ancestral 65Arg state). By comparing these two beach populations, we hoped to minimize differences in genetic diversity due to effective population size (reduced following colonization) alone. To identify regions that deviate from neutral expectations, we used χ2 test statistics in which the observed numbers of polymorphic and fixed differences are contrasted with their expected numbers in 10-kb sliding windows along the 160-kb region surrounding Mc1r. Second, we focused on the SRIBM population and applied a composite likelihood method, SweepFinder, to locate regions with skewed site frequency spectrum (i.e., deviant patterns in allele frequency) in Mc1r and surrounding regions (Nielsen et al. 2005). Third, we characterized patterns of linkage disequilibrium using the ω statistics (Kim and Nielsen 2004), via a recently proposed modification of SweepFinder (Pavlidis et al. 2010)—an addition that was shown to greatly increase discriminatory power—to localize selective sweeps. Finally, we used XP-CLR (Chen et al. 2010) to compare patterns of allele frequency differentiation between SRIBM and ABM, along the 160-kb region surrounding Mc1r, that could be indicative of selective sweeps.
Results
TARGETED ENRICHMENT (SURESELECT) PERFORMANCE
A total of 601 million paired-end reads were generated in three HiSeq lanes, of which 99.6% could be confidently assigned to individual barcodes. Overall, 25–45% (mean 33%) of reads mapped to target regions. For the regions targeted at random locations throughout the Peromyscus genome, after removing putative multicopy regions, a total of 3754 and 3884 regions were retained applying the thresholds used in datasets A (QD = 6, QUAL = 200, and GQ = 12) and B (QD = 20 and GQ = 20), respectively. In dataset A, a total of 4 billion bases mapped on-target and average individual coverage of target regions ranged from 3× to 38× (average 11×), corresponding to a mean 46-fold enrichment. In dataset B, a total of 8 billion bases mapped on-target and average individual coverage of target regions ranged from 5× to 70× (average 20×), corresponding to a mean 84-fold enrichment. The difference in number of total bases mapped between dataset A and B reflects the difference in the stringency thresholds used to filter out paralogous regions. However, because the additional 4 billion bases in dataset B correspond to densely covered regions, they correspond to only 4% of the total variant sites in the dataset.
A total of 189 million bases were recovered in the targeted 160-kb region including Mc1r and surrounding sequences. Average individual coverage of target regions ranged from 5× to 49× (average 17×), corresponding to a mean 72-fold enrichment. Genotype call accuracy is shown in Table S1. SNP-specific linkage disequilibrium-based genotyping error rates associated with phasing genotypes ranged from 0 to 0.1823 (median = 0.0001).
POPULATION GENETIC DIVERSITY AND DIFFERENTIATION
We first characterized patterns of genetic diversity and differentiation among populations. Not unexpectedly, beach mice show lower levels of genetic diversity (average heterozygosity, H = 0.14– 0.19) than mainland populations (H = 0.22–0.32). We confirmed with genomic data that beach mice on the Gulf Coast are well differentiated into five subspecies. Fst values ranged between 0.38 and 0.58, and the STRUCTURE analysis supported five distinct genetic clusters, corresponding to the recognized subspecies. All individuals were correctly assigned to the cluster with their subspecies designation (Fig. S2). Fst values were also high among mainland populations (0.09–0.31), suggesting that mainland populations are also genetically differentiated.
To reconstruct the evolutionary history of beach mice, we estimated a population topology of P. polionotus using a genome-wide phylogenetic approach, which accounts for gene tree heterogeneity (Fig. 1B). Beach mice form a well-supported monophyletic group, with the closest related population from southern Alabama. These data suggest a single colonization event of the coast from northern mainland populations, followed by differentiation among the five beach mouse subspecies.
DEMOGRAPHY OF BEACH COLONIZATION
We estimated demographic parameters for the five beach mouse subspecies. Parameter estimates are similar across each of the beach subspecies (Table 1). In all cases, we obtained a recent split between beach and mainland populations (1800–3300 years; 95% confidence interval: 1600–8500 years). Moreover, estimates of the effective population size of beach populations immediately after the split are extremely small in all cases, ranging from 0.01% to 9% of the ancestral population. Four of five beach subspecies rejected the null hypothesis of equal size beach and mainland populations immediately following the split (Table 2). The one exception is SABM, the subspecies with the largest estimate of s (i.e., estimated fraction of the ancestral population that gave rise to the beach population), which showed a very small difference in –ln L between the ML model and the model with larger s, limiting our power to reject the “equal size” model. Overall, these results support a strong founder event associated with the colonization of the beach habitat.
| ABM | PKBM | SRIBM | CBM | SABM | |
|---|---|---|---|---|---|
| s | 0.020 | 0.005 | 0.001 | 0.016 | 0.090 |
| (0.000–0.213) | (0.000–0.238) | (0.001–0.225) | (0.000–0.423) | (0.000–0.249) | |
| n1 | 1.877 | 1.455 | 0.413 | 41.487 | 0.185 |
| (0.400–6.848) | (0.307–198.878) | (0.130–0.509) | (1.526–275.570) | (0.185–2.912) | |
| n2 | 117.170 | 61.320 | 222.080 | 64.274 | 698.040 |
| (46.787–996.389) | (23.636–997.544) | (57.580–960.281) | (21.946–987.185) | (36.078–996.447) | |
| T | 1.399 | 1.428 | 1.225 | 1.733 | 2.537 |
| (1.121–4.292) | (1.085–3.080) | (0.883–1.769) | (1.034–2.832) | (1.392–3.617) | |
| T (years) | 2787 | 3287 | 3040 | 2771 | 3,177 |
| (2233–8548) | (2499–7090) | (2191–4391) | (1654–4530) | (1,744–4,528) | |
| m21 | 0.072 | 0.124 | 0.203 | 0.148 | 0.236 |
| (0.021–0.122) | (0.075–0.289) | (0.121–0.495) | (0.001–0.356) | (0.015–0.236) | |
| m12 | 0.017 | 0.027 | 0.018 | 0.000 | 0.016 |
| (0.000–0.034) | (0.000–0.078) | (0.000–0.029) | (0.000–0.025) | (0.000–0.023) | |
| 102.983 | 119.043 | 128.322 | 82.708 | 64.762 | |
| lnL | –86.591 | –85.107 | –128.170 | –77.808 | −92.860 |
- s, fraction of the ancestral population that gave rise to the beach population; n1, final size of the beach population relative to the ancestral population (reference); n2, final size of the mainland population relative to the ancestral population; T, time in the past of split, in units of 2Nref generations and in years; m12, effective migration rate from beach to mainland, in units of 2Nref per generation; m21, effective migration rate from mainland to beach, in units of 2Nref per generation; θ, 4Neμ (Ne, effective population size; μ, mutation rate); lnL, logarithm of the model Likelihood.
| ABM | PKBM | SRIBM | CBM | SABM | |
|---|---|---|---|---|---|
| Large founder population size (s=0.5) | 83.5* | 72.5* | 92.1* | 60.9* | −1.78 |
| No migration (m=0) | 163.7* | 116.1* | 204.8* | 215.8* | 47.3* |
| Symmetrical migration (m21=m12; higher estimate) | 8.8* | 12.1* | 27.9* | 24.7* | 65.3* |
| Symmetrical migration (m21=m12; lower estimate) | 7.2* | 16.0* | 60.6* | 196.5* | 19.3* |
- All but one comparison is significant (*P-values < 0.001).
We detected evidence of asymmetrical migration between mainland and beach populations following colonization. Migration from the mainland into the beach populations is higher than in the opposite direction for all five cases. The models with no migration or with symmetrical migration rates were rejected by likelihood ratio tests (Table 2).
Finally, demographic results obtained using a second mainland population, FL-2, were largely consistent with estimates obtained with the first mainland population, AL-2 (Table S2). Any differences in migration rate can be attributed to differentiation of the mainland populations following colonization.
EVOLUTIONARY HISTORY OF PIGMENTATION ALLELES
To reconstruct the evolutionary history of the light Mc1r allele (defined by the derived 65Cys mutation), we first determined its frequency among subspecies and then generated genealogies based on genomic fragments at varying distance from Mc1r. Frequencies of the 65Cys Mc1r mutation in the five beach mice subspecies were consistent with previous independent results (Mullen et al. 2009). The derived mutation was fixed in SRIBM, in high frequency in PKBM (60%) and SABM (75%), low frequency in CBM (10%), and absent in ABM (Fig. 1A).
The genealogy built using the fragment that includes Mc1r and neighboring sequences (Fig. 3, red panel) shows that the 23 Mc1r alleles that contain the 65Cys mutation form a derived monophyletic clade, indicating a common ancestry of Mc1r light alleles. This Mc1r“selected” genealogy contrasts with the population “neutral” topology (Fig. 1B), as not all alleles found in beach mice cluster together. Indeed, a topology forcing all beach mice alleles to be monophyletic is significantly worse than the Mc1r ML topology (SH test, P<0.05). The Mc1r topology is recovered in genealogies that are 2-kb, 10-kb, and 20-kb downstream and upstream of Mc1r (data not shown). However, trees 35-kb and 40-kb downstream of Mc1r (Fig. 3, blue and green panels) are similar to the population tree topology as the vast majority (more than 90%) of the alleles found in the beach populations fall in a single clade.
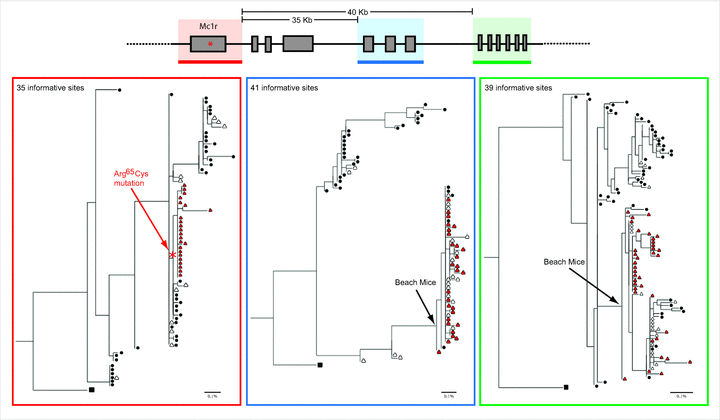
Schematic representation of a genomic region containing Mc1r and neighboring sequences and ML trees estimated from sequences along that region. Alleles found in mainland are depicted as circles; alleles found in the beach as triangles. Red panel: Mc1r genealogy of 71 alleles, estimated using a 4-kb sequence including the 954-bp Mc1r exon (note how this topology differs from population tree topology shown in Fig. 1B). Light alleles, defined by the derived 65Cys mutation (red triangles), form a monophyletic clade, indicating their common origin. Blue and green panels: Genealogies estimated from regions approximately 35- and 40-kb downstream of Mc1r, showing topologies similar to the population tree, in which alleles found in beach populations (regardless of their genotype at Mc1r position 65) fall in the same clade.
DETECTING SIGNATURES OF POSITIVE SELECTION IN MC1R
By comparing patterns of nucleotide variation between the SRIBM, in which Mc1r light alleles are fixed, and ABM, in which ancestral dark alleles are fixed, we could test for patterns consistent with selection acting on Mc1r. Overall, the complete 160-kb Mc1r sequences in beach mice showed low levels of polymorphism and negative values for Tajima's D and Fu's and Li's D* due to an excess of rare polymorphisms (Table 3). Comparison of patterns of genetic variation among the five beach subspecies reveals that SRIBM shows the most skewed frequency spectra, whereas ABM best fits the neutral equilibrium expectation. This pattern is also evident when comparing haplotypes (Fig. 4), as most polymorphisms among light Mc1r alleles are singletons, whereas variants among ancestral alleles are segregating at higher frequency. The plot of nucleotide polymorphism and divergence along the 160-kb region shows higher polymorphism than divergence in the Mc1r region in SRIBM, whereas the opposite is true for ABM (Fig. 4). Although this pattern is consistent with positive selection, the increased divergence at the Mc1r gene is not particularly striking when compared with the entire region, as several regions show biased polymorphism-to-fixed differences ratios, likely due to demographic effects. In addition, methods based on skews in AFS (SweepFinder), patterns of linkage disequilibrium (ω statistics) or allele frequency differentiation did not show a clear signature of selection in Mc1r. Thus, we identified patterns of variation consistent with positive selection acting on the light Mc1r alleles, although none were statistically significant.
| ABM | PKBM | SRIBM | CBM | SABM | |
|---|---|---|---|---|---|
| No. of segregating sites | 806 | 940 | 876 | 981 | 481 |
| Average pairwise differences | 279.293 | 318.039 | 79.901 | 338.168 | 113.349 |
| Watterson's θ | 284.909 | 332.277 | 208.493 | 346.770 | 170.027 |
| Tajima's D | -0.099 | -0.215 | -2.332 | -0.124 | -1.670 |
| Fu and Li's D* | -0.331 | -0.682 | -4.082 | -0.723 | -2.087 |
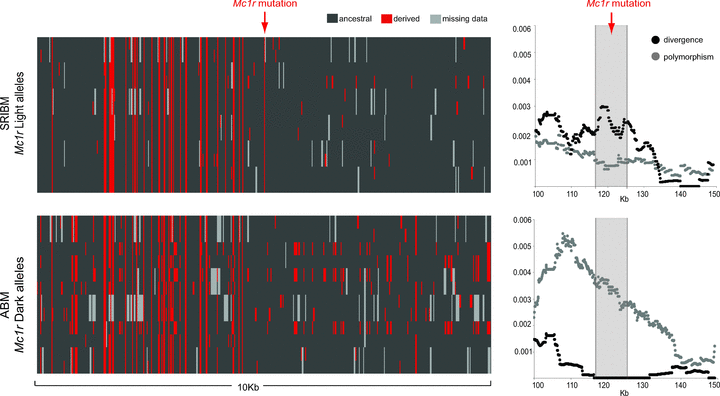
Genetic variation in Mc1r and flanking regions for SRIBM (derived mutation in Mc1r is fixed, n= 12 alleles) and ABM (derived mutation in Mc1r is absent, n= 12 alleles). On the left, haplotypes for a 10-kb region surrounding Mc1r (gray-shaded region in the graphs to the right). Rows are observed haplotypes; columns are variable nucleotide sites (black indicates ancestral, red indicates derived state, gray indicates unknown genotype). Nucleotide states were polarized using the mainland population AL-2. Graphs on the right are plots of polymorphism and divergence across a 50-kb region including Mc1r.
Discussion
Using high-throughput sequencing of targeted regions, we take a comprehensive approach to gain novel insight into the evolution of camouflaging coloration of beach mice, a well-known case of adaptation in the wild. We recreated the history of beach mouse populations in parallel with the evolutionary history of Mc1r alleles, a pigment gene that contributes to cryptic coloration in these mice. We first show that mice likely colonized the novel beach habitat less than 3000 years ago in a single founder event. In this demographic context, we demonstrate a single origin of a derived Mc1r mutation that contributes to light pigmentation in several subspecies of beach mice, and that the derived allele is old, likely first arising in the mainland populations. Further, although we show patterns of genetic variation in the region surrounding Mc1r consistent with recent positive selection, we did not detect a statistically significant signature of selection, likely due to the demographic history of these populations. Together these results retrace the evolutionary history of a beneficial allele in a demographic context, contributing to our understanding of the adaptive process in the wild.
POPULATION HISTORY
With genome-wide polymorphism data, we confirmed previous findings (Mullen et al. 2009) that the five beach mouse subspecies are highly differentiated and show no evidence of current gene flow. Given this result, the colonization of the Florida coast is consistent with two hypotheses: (1) mainland mice colonized the coast in a single event, followed by subsequent population differentiation; or (2) beach mouse subspecies resulted from independent invasions, possibly from multiple mainland source populations. To test these alternative hypotheses, we inferred the phylogenetic relationships of 13 P. polionotus populations using 211 genomic regions (161 kb) resequenced in a total of 71 individuals. Because gene trees can show discordant topologies due to variation in coalescence, especially in diverging populations or in cases of recent speciation (Tajima 1983), we used a coalescence model to account for gene tree heterogeneity (Liu et al. 2010). This method allowed us to confidently determine if beach mice form a monophyletic group, or instead, fall into distinct clades. Our genome-wide population topology clearly shows a strongly supported monophyletic clade of beach mice (Fig. 1B). Based on these results, the most likely scenario is that mainland mice colonized the sandy beaches of Florida's Gulf Coast once and that this founding population subsequently differentiated to yield the five contemporary subspecies.
DEMOGRAPHY OF BEACH COLONIZATION
Using polymorphisms obtained from targeted resequencing of approximately 5000 genomic regions and a powerful method based on the multipopulation allele frequency spectrum (AFS), we were able to estimate several demographic parameters associated with the colonization of the beach habitat. First, we estimated the time of the colonization event (i.e., time of the population split) to be between 1800 and 3300 years ago, suggesting the recent colonization of the coast. This is after the formation of the barrier islands, estimated to be approximately 6000 years old based on geological data (McNeil 1950). However, this finding strongly contradicts a previous age estimate based on mtDNA, suggesting that beach mice diverged more than 200,000 years ago from mainland mice (Van Zant and Wooten 2007). This previous anomalous result is likely due to the low-resolution phylogenetic reconstruction based on a single mtDNA marker, and specifically from estimating a divergence time for a “beach clade” that included mainland mice, leading to a large overestimate of divergence time. Our recent splitting time estimate suggests that differences in coloration between mainland and beach mice might have evolved quite rapidly. Thus, the evolution of camouflaging pigmentation in beach mice adds to the growing evidence of natural selection and adaptive divergence occurring on ecological time scales in different taxa such as in fish (Bell et al. 2004; Elmer et al. 2010), lizards (Losos et al. 2004; Herrel et al. 2008), and birds (Hendry et al. 2006). Second, we inferred a strong founder event associated with beach colonization. According to our model, only 0.1–9.0% of the genetic variation present in the mainland population was captured in the beach population at the time of divergence. Such an extreme reduction in diversity is consistent with multilocus estimates of bottlenecks associated with colonization of novel areas in a variety of other species (e.g., Rosenblum et al. 2007; Peters et al. 2008; Elmer et al. 2010), suggesting that in nature new populations often are established and adapt to novel environments from a small number of founders. Finally, we found that the split between mainland and beach mice occurred in the presence of gene flow, with most migration occurring from the mainland into the beach populations. The influx of mainland alleles to the newly established beach population might have contributed some genetic diversity to the otherwise depauperate beach gene pool, but at the same time, may have initially impeded divergence and local adaptation. As time progressed, gene flow between beach and mainland mice decreased, likely due to a combination of genetic drift, habitat preference, and/or selection against maladapted phenotypes (Garcia-Ramos and Kirkpatrick 1997; Crespi 2000; Bolnick and Nosil 2007; Nosil et al. 2008; Bolnick et al. 2009).
EVOLUTIONARY HISTORY OF A BENEFICIAL ALLELE
Our ability to precisely define beneficial alleles allowed us to reconstruct the evolutionary history of these alleles in a demographic context. Previous work demonstrated that a single mutation in the Mc1r coding region (Arg65Cys) reduces receptor activity (agonist binding and receptor signaling), consistent with the production of less pigment (Hoekstra et al. 2006). Given that this mutation is present at different frequencies in beach mouse subspecies, this raises an important question: how many times did the beneficial mutation arise, once before the ancestral beach mice population differentiated into the five subspecies or multiple times independently in more than one population? To answer this question, we conducted a phylogenetic analysis of Mc1r alleles. Given the small size of Mc1r (it is a 954-bp-long single exon) and the reduced genetic diversity observed in beach mice, we used an extended region of 4 kb including Mc1r and surrounding sequence to ensure that we had enough phylogenetic signal. A genealogy of Mc1r alleles revealed that all light Mc1r alleles (defined by the derived 65Cys mutation) cluster into a monophyletic group regardless of their population of origin. Moreover, the Mc1r genealogy does not recapitulate the population topology—unlike the population tree, the Mc1r genealogy does not show a monophyletic clade of beach mice. Instead, only light Mc1r alleles are monophyletic and ancestral dark Mc1r alleles segregating in beach mice are interspersed with the ancestral alleles found in mainland mice. Although reduced sequence variation precluded significant node support, and therefore the Mc1r topology should be interpreted with caution, we were able to reject a topology that recapitulated the population tree.
Comparison of the Mc1r allele tree with the population topology suggests a single origin of the beneficial Mc1r mutation. Thus, different frequencies of the derived alleles in the distinct beach mice subspecies could be a result of drift or, more likely, parallel selection of a single-origin mutation in similar environments (Mullen et al. 2009). In contrast, comparison of a mtDNA phylogeny of garter snakes with a genealogy of Nav1.4, a gene that confers resistance to tetrodotoxin of their newt prey, suggests that resistance to toxicity evolved independently in three species (Feldman et al. 2009). A second phylogenetic study shows that mutations in the vkorc1 locus contributing to anticoagulant rodent poison resistance, although originally thought to have originated independently in Mus musculus domesticus (Pelz et al. 2005), were in fact introduced by hybridization with M. spretus (Song et al. 2011). Together these studies illustrate how comparing beneficial alleles from different populations or species in a phylogenetic context can provide novel insight into the molecular basis and evolutionary history of adaptive traits.
In addition to determining the number of origins of the derived Mc1r light allele, we can also test hypotheses about the source of the selected mutation. The light Mc1r allele might have arisen before the mice colonized the novel beach habitat, being selected from standing genetic variation. Alternatively, it may have originated following colonization as a de novo mutation. Some have suggested that in cases of recent adaptation, mutations are likely to be derived from standing genetic variation as there is little time for new mutations to arise (Hermisson and Pennings 2005; Barrett and Schluter 2008); other studies have shown that in large populations, new mutations can contribute to rapid adaptation (e.g., Feldman et al. 2009; Linnen et al. 2009). If the derived 65Cys Mc1r mutation was of recent origin and had fixed quickly, we expect the ancestral variation surrounding the selected mutation to be low and the presence of high- frequency derived mutations in strong linkage disequilibrium (Kaplan et al. 1989). However, in SRIBM, which is fixed for the derived mutation in Mc1r, most variants are also found in the ancestral mainland populations and present at low frequency (Fig. S3). This pattern suggests that the 65Cys mutation is not of recent origin, which is surprising given the young age of beach mice populations. We therefore conclude that the mutation must have arisen in the mainland prior to population differentiation. Gene flow between mainland and beach populations would allow for recombination between light and dark alleles for extended periods of time. This scenario accounts for the lack of linkage disequilibrium around the 65Cys mutation as well as the presence of shared variants close to the selected site (Innan and Kim 2004; Hermisson and Pennings 2005; Przeworski et al. 2005). The presence of the light Mc1r allele in the ancestral mainland population would provide additional evidence to support this scenario, however, we did not find the derived Mc1r mutation in more than 500 mice caught in several locations across P. polionotus range. It is possible that the mutation is segregating at very low frequency, is restricted to specific geographic region we failed to sample, or has since gone extinct in mainland populations.
SIGNATURES OF SELECTION
Several patterns of genetic variation in the 160-kb region containing Mc1r show patterns consistent with recent positive selection. First, genealogies built with sequences at varying distances from Mc1r (along the 160-kb region) suggest a footprint of selection extending to around 20 kb on either side of Mc1r. Specifically, regions near Mc1r show a different topology compared to those that are further away—nearby genealogies show a monophyletic clustering of Mc1r light alleles, whereas those further away reflect the population topology. Second, a comparison of genetic variability between Mc1r light and ancestral alleles shows reduced variation in light alleles, consistent with recent selection. Finally, the Mc1r region shows high levels of divergence relative to polymorphism among light alleles, but the opposite pattern among ancestral alleles. Although all of these patterns are consistent with recent selection acting on Mc1r, none are statistically significant.
Perhaps one striking outcome of our study is our inability to obtain a statistically significant signature of selection in Mc1r using common population-genetics approaches that have high power to detect selective sweeps. For example, methods based on the skew in the site frequency spectrum and patterns of linkage disequilibrium (e.g., Kim and Nielsen 2004; Nielsen et al. 2005; Pavlidis et al. 2010) or those that identify regions with unusual levels of population differentiation (e.g., Chen et al. 2010), all failed to provide statistical evidence of positive selection acting on Mc1r, even when controlling for demography in our analysis. This result is puzzling given the independent evidence that selection acting on pigmentation is strong (s= 0.5; Vignieri et al. 2010) and that Mc1r is a major contributor to pigment differences (Hoekstra et al. 2006). It is important to recognize that selection from ancestral variation can be more challenging to identify than selection from new mutations. In addition, the power to detect selection may be improved by increasing sample sizes. However, this outcome likely results from the limited power of our statistical analysis due to the demographic history of these populations, for example, resulting in few variable sites in beach mouse populations. Our results illustrate how, even in a system for which there is evidence for the action of natural selection and for which the precise molecular target of selection is known, distinguishing the effects of natural selection from those of demographic events can be an elusive goal (Thornton et al. 2007). Severe population bottlenecks associated with colonization events will likely make difficult, or even prevent, the identification of genomic patterns that unambiguously implicate positive selection. This has important implications for the growing enthusiasm of using genomic scans to identify targets of natural selection in recently established populations, especially those that experienced strong demographic effects associated with colonizing novel habitat. Therefore, we suggest that careful simulations are needed to predict the power to detect signatures of selection under different demographic scenarios relevant to colonization, particularly with varying intensities of selection and population size reduction—both considering test statistics based upon standard population genetics models (i.e., the ω—statistic) as well as upon empirical distributions from the background site frequency spectrum (i.e., Sweepfinder).
Conclusion
As alleles contributing to phenotypes continue to be uncovered, we are in a strong position to reconstruct their evolutionary history and thereby gain new insights into the adaptive process, including the demographic and selective forces driving phenotypic evolution. Our integrated approach, which combines an analysis of the genomic footprint of colonization with reconstruction of the evolutionary history of specific alleles, allowed us to further understand a classic example of adaptation, the pale coloration of beach mice. Our study illustrates how targeted next-generation sequencing can be used to obtain multipopulation genomic data to accurately reconstruct the evolutionary history of both populations and beneficial alleles in nonmodel organisms. Together our results show that a phenotypic trait can evolve quite rapidly from a preexisting mutation that undergoes parallel selection in multiple closely related populations in similar habitats.
Associate Editor: J. Hermisson
ACKNOWLEDGMENTS
We thank D. Brimmer, A. Chiu, E. Kay, K. Lin, and J. Weber for assistance in the field, G. Gonçalves for help in the lab, and R. Barrett for comments on the manuscript. Sampling permits were provided by the Florida Fish and Wildlife Conservation Commission, Alabama Department of Conservation and Natural Resources, South Carolina Department of Natural Resources, Eglin AFB Natural Resources Branch, Eufala National Wildlife Refuge, Apalachee Wild Management Area, Ocala National Forest, and Tall Timbers Research Station. V. Domingues was supported by a postdoctoral fellowship from the Portuguese Foundation for Science & Technology, B. Peterson from the Jane Coffins Child Memorial Fund, Y. Poh by a National Science Foundation grant (DEB-1002785) to J. Jensen, and P. Pennings by a long-term postdoctoral fellowship from the Human Frontier Science Program. Research funding was provided by a Putnam Expedition Grant from the Harvard University Museum of Comparative Zoology and a National Science Foundation grant (DEB-0919190) to H. Hoekstra.




