THE GENETICS OF ADAPTIVE SHAPE SHIFT IN STICKLEBACK: PLEIOTROPY AND EFFECT SIZE
Abstract
The distribution of effect sizes of genes underlying adaptation is unknown (Orr 2005). Are suites of traits that diverged under natural selection controlled by a few pleiotropic genes of large effect (major genes model), by many independently acting genes of small effect (infinitesimal model), or by a combination, with frequency inversely related to effect size (geometric model)? To address this we carried out a quantitative trait loci (QTL) study of a suite of 54 position traits describing body shapes of two threespine stickleback species: an ancestral Pacific marine form and a highly derived benthic species inhabiting a geologically young lake. About half of the 26 detected QTL affected just one coordinate and had small net effects, but several genomic regions affected multiple aspects of shape and had large net effects. The distribution of effect sizes followed the gamma distribution, as predicted by the geometric model of adaptation when detection limits are taken into account. The sex-determining chromosome region had the largest effect of any QTL. Ancestral sexual dimorphism was similar to the direction of divergence, and was largely eliminated during freshwater adaptation, suggesting that sex differences may provide variation upon which selection can act. Several shape QTL are linked to Eda, a major gene responsible for reduction of lateral body armor in freshwater. Our results are consistent with predictions of the geometric model of adaptation. Shape evolution in stickleback results from a few genes with large and possibly widespread effects and multiple genes of smaller effect.
Complex traits often evolve as a correlated suite during adaptation to new environments, yet the genetic basis of such adaptation is unknown. We are still uncertain about how many genes generally underlie variation in quantitative traits, what the distributions of the effect sizes of these genes are, and what kinds of pleiotropic effects they may have (Phillips 2005). Under the “geometric” model of adaptation, most mutations fixed by selection are assumed to have pleiotropic affects (Fisher 1930). An approximately exponential distribution of effects of genes fixed by selection is expected to result (Orr 1999; Griswold and Whitlock 2003), with some genes having large phenotypic effects, but most having small effects. Because of pleiotropy, a fraction of genes is also expected to have effects opposite in direction to that of divergence (Griswold and Whitlock 2003). Alternatives to the geometric model include the “infinitesimal” model from quantitative genetics, in which all genetic effects are small, and the opposite view that genes of major effect can predominate (Orr and Coyne 1992).
Recent research indicates that at least some quantitative differences between species are influenced by QTL of major effect (Orr 2001; Slate 2005), and pleiotropic effects are commonly detected (True et al. 1997; Jiang et al. 1999; Fishman et al. 2002; Westerbergh and Doebley 2002; Cui et al. 2004; Hall et al. 2006). However, only a few studies have looked at the full distribution of genetic effects underlying adaptive differences in a complex suite of correlated traits, such as the shape of organs (Zeng et al. 2000; Klingenberg et al. 2001; Fishman et al. 2002; Workman et al. 2002; Langlade et al. 2005; Mezey et al. 2005). The distribution of effects can be difficult to determine because traits are usually measured in different units, or are scaled by a variance that differs between traits and cross types (Lynch and Walsh 1998; Flint et al. 2005; Lexer et al. 2005). Also, the direction of adaptation is rarely known. We focused on shape changes during adaptation from marine to freshwater phenotypes in sticklebacks, using measurements for a complex suite of traits all in the same units.
Threespine stickleback (Gasterosteus aculeatus) are an excellent system for studying the genetics of complex adaptations. After the retreat of the Pleistocene glaciers, marine stickleback colonized newly available freshwater habitats and underwent rapid adaptation in these new environments (Bell and Foster 1994). Freshwater stickleback diverged from their marine ancestors in many traits, including bony armor, trophic morphology (Bell and Foster 1994), and body shape (Walker 1997; Walker and Bell 2000). Recent attention has focused on the genetic basis of changes in single traits (Peichel et al. 2001; Aguirre et al. 2004; Colosimo et al. 2004, 2005; Cresko et al. 2004; Shapiro et al. 2004; Kimmel et al. 2005), but studies of complex traits in stickleback are lacking.
Shape changes in threespine stickleback involve shifts in the positions of multiple skeletal elements that have repeatedly been modified together in lake populations descended from the same ancestral marine species (Walker and Bell 2000). Reductions in defensive armor have occurred simultaneously with changes in shape. These changes have occurred repeatedly and independently in different lakes (Walker and Bell 2000; Schluter et al. 2004), implying adaptation in response to novel lake environments. Indirect methods have not detected genes of large effect on stickleback shape, suggesting that body shape might have a polygenic basis (Schluter et al. 2004).
Here we report the results of an investigation into the genetic basis of shape differences between a marine species and the freshwater benthic species from Paxton Lake in British Columbia (Fig. 1A). These populations represent the extremes of shape variation within the threespine stickleback complex. We mapped changes in the x and y positions of 27 morphological landmarks, 54 traits in total, to answer the following questions: (1) How many quantitative trait loci (QTL) underlie divergence in shape between marine and benthic sticklebacks? (2) Do QTL affect components of shape together, or are separate coordinates under independent genetic control? (3) What is the distribution of effect sizes of these QTL? (4) Do the same QTL affect shape that has been shown to affect bony armor?

Fish species and landmark positions used. Fish have been stained with alizarin red to highlight bony tissue. (A) Examples of the ancestral marine form (above) and the Paxton benthic (below). (B) The locations of the 27 landmarks used to describe shape. The landmarks are described more fully in Table 1.
Methods
SHAPE ANALYSIS
We crossed a female Pacific marine stickleback from Japan to a male benthic stickleback from Paxton Lake, Texada Island, British Columbia (details in Colosimo et al. 2004). The Japanese marines have a body shape that is almost identical to marines from British Columbia (Schluter et al. 2004) giving us a good estimate of genetic differences involved in shape evolution while providing more genetic differentiation at neutral markers used for mapping. F1 siblings of this cross were mated to produce multiple F2 families. In this report we measured the shape of 372 individuals from a single F2 family. The x and y coordinates for 27 shape landmarks were obtained by taking digital photographs of the right side of the body, and then placing 27 landmarks (Fig. 1B, Table 1) on each digital photo using tpsDig (Rohlf 2001a). The 27 landmarks (Fig. 1B) were chosen to highlight important changes in shape associated with adaptation to freshwater, including fin insertion points, pelvic girdle features, and the relative locations of jaw bones (Walker 1997). These landmarks are similar to those used in previous studies of stickleback shape (Walker 1997; Schluter 2003; Schluter et al. 2004). The x and y coordinates of all 27 landmarks were aligned and then corrected for geometric size using tpsRelw (Rohlf 2001b).
| Landmark number | Landmark positions |
|---|---|
| 1 | Posterior extent of caudal peduncle |
| 2 | Posterior insertion of anal fin |
| 3 | Anterior insertion of anal fin |
| 4 | Insertion point of pelvic spine into the pelvic girdle |
| 5 | Dorsal extent of the ascending branch of the pelvis |
| 6 | Posterior extent of ectocorocoid |
| 7 | Dorsal extent of ectocorocoid |
| 8 | Anterior extent of ectocorocoid |
| 9 | Ventral extent of operculum |
| 10 | Posteriodorsal extent of operculum |
| 11 | Anteriodorsal extent of operculum |
| 12 | Dorsal extent of preopercular |
| 13 | Posterioventral extent of preopercular |
| 14 | Anterioventral extent of preopercular |
| 15 | Posterior extent of premaxilla |
| 16 | Posterior extent of maxilla |
| 17 | Anterior extent of maxilla |
| 18 | Anterior extent of nasal |
| 19 | Lachrymal at nasal capsule |
| 20 | Anterior extent of orbit |
| 21 | Ventral extent of orbit |
| 22 | Posterior extent of orbit |
| 23 | Posterior extent of supraoccipital |
| 24 | Anterior insertion of first dorsal spine |
| 25 | Anterior insertion of second dorsal spine |
| 26 | Anterior insertion of third dorsal spine |
| 27 | Posterior insertion of dorsal fin |
A significant amount of variation in shape resulted from vertical bending of the preserved specimens. To remove this effect we used the 54 aligned x and y coordinates of the F2s as traits in a principal components analysis. The first eigenvector (principal component, PC1) explained 34.4% of the variation between the F2s, and described a U-shaped displacement upward of the most anterior and posterior landmarks and a simultaneous downward displacement of landmarks near the center of the body. When we used PC1 as a trait in QTL mapping, it failed to map to any location, suggesting that vertical bending represented mainly measurement error. To remove the influence of this variation on landmarks we back-transformed the PC scores to the original 54 x and y coordinates after deleting the first eigenvector and the corresponding eigenvalue from the set of 54. These error-corrected x and y coordinates were the traits used in all subsequent analyses.
Although the alignment of the landmarks by tpsRelw (Rohlf 2001b) corrects for isometric size, there is still the possibility of allometric size effects on the landmark positions. As a check on the possible influence of size we measured and mapped standard body length of the F2s. Only one QTL for size was detected and it mapped to a unique location, on linkage group 13 (away from another QTL for x20). This suggests that size does not explain any of the shape mapping results presented here. We also calculated the residuals of separate linear regressions of every x and y coordinate against the standard length of the fish. Using these residuals in the QTL mapping resulted in no substantial difference in the number and location of detected QTL.
To obtain the magnitude and direction of divergence from the ancestral marine to the derived benthic phenotype, we measured 25 marine and 24 benthic laboratory-raised adult fish from the parental populations. The mean difference per landmark between the marine and benthic species was 0.82 mm ± 0.12 SE (range: 0.01–2.01) for x coordinates, and 0.39 mm ± 0.04 SE (range: 0.02–0.77) for y coordinates. The total Euclidean distance between the means of the two parent species was 5.58 mm.
SEXUAL DIMORPHISM
We discovered substantial sexual dimorphism by comparing the means of males and females for each x and y coordinate position using two-sample t-tests. Forty-four of the 54 landmark positions were significantly different between the sexes (P < 0.05).
In addition to controlling for sex using Multiple QTL Mapping (MQM) (see mapping methods below), we carried out interval mapping on the sexes separately. This resulted in fewer total QTL, because the sample size for each mapping run was reduced. However, in most cases males and females had similar log of odds (LOD) score profiles, and there was very little indication that a QTL present in one sex was absent from the other. Hence we present results only from the MQM analysis that included both sexes.
QTL MAPPING
We genotyped the 372 F2 progeny at 248 microsatellite loci, and at a length polymorphism in isocitrate dehydrogenase (IDH), which was used as a proxy for sex in our analysis. IDH is within 0.6 cM of the sex-determining region in sticklebacks and in a previous study only two recombinants between sex and IDH were found out of 328 individuals (Peichel et al. 2004). The sex ratio was 51% females and 48% males in our F2 family.
We used the same settings as Peichel et al. (2001) in JoinMap 3.0 (Van Ooijen and Voorrips 2001) to construct a linkage map for the F2s, in which the average distance between markers was 5.35 ± 0.45 cM, and the total map length was 1220 cM (see online Supplementary Fig. S1). We used this linkage map and MapQTL 5.0 (Van Ooijen 2004) to determine the locations of QTL separately for all 54 x and y shape coordinates. Because sexual dimorphism accounted for a large proportion of the variation in the F2s we controlled for the effects of sex by using IDH as a cofactor in MQM. MQM mapping is a modified form of interval mapping that allows cofactors (other markers) affecting a trait to be fitted simultaneously. First, we mapped the trait using IDH as a cofactor. Then we chose all loci identified as significant QTL as cofactors in a new round of MQM mapping. This was continued until no new QTL were detected. QTL were considered significant if they exceeded a LOD score of 4.5 (Van Ooijen 1999). This is slightly more conservative than the LOD of 4.3 identified as the average threshold in genome-wide permutation tests carried out for single traits in MapQTL 5.0 (Van Ooijen 2004).
We mapped individual shape coordinates instead of their principal components (“relative warps”), unlike previous studies of shape (e.g., Zeng et al. 2000; Langlade et al. 2005; Mezey et al. 2005). The reason is that, although the principal components are orthogonal phenotypically, they did not correspond to independent dimensions of genetic variation. Sexual dimorphism provides a good illustration of the problem: although caused by a single gene, four of the first six principal components mapped to the sex-determining region. All these effects vanished once sex was added as a covariate in mapping. We ran into similar issues with other QTL. In other cases, two or more landmark coordinates that together loaded a given principal component were found to map to nonoverlapping QTL when tested separately. Therefore, rather than attempt to define a priori “independent” traits for mapping, we located QTL by mapping coordinates one at a time, and then subsequently assessed the total effect on landmarks of individual QTL detected.
We identified chromosome regions (QTL) influencing many coordinates by examining the MQM LOD profiles for all coordinates mapping to a similar region. We assigned traits to the same QTL if they had overlapping 2 LOD support intervals. This likely leads to an underestimate of the number of QTL present, while simultaneously overestimating their total and pleiotropic effects. Nevertheless, the identification of chromosome regions is a significant step toward ultimately identifying genes important for shape differences.
Because of the large potential for type I errors with so many traits, we calculated a false discovery rate for our analysis using the method of Storey and Tibshirani (2003). We used the χ2 approximation described in Van Ooijen (2004) to calculate P-values associated with LOD scores obtained at every marker position for all 54 x and y coordinates (over 13,000 tests in total). The LOD scores used were those derived in the first pass of mapping including only IDH as a cofactor. Using this distribution of P-values and the P-value corresponding to the LOD threshold of 4.5, we estimated the false discovery rate of our analysis to be 0.006, or about 6 per thousand. This suggests that our LOD cutoff of 4.5 is sufficiently conservative to ensure that virtually all of the QTL identified here are real.
QTL EFFECT SIZE
Estimated effect size of a QTL on a single coordinate was the effect on the coordinate position of replacing two marine alleles (MM) at the nearest marker with two benthic alleles (BB), as predicted by MQM analysis of the F2 cross. The effect is positive if the BB genotype is more similar to the benthic species than the MM genotype, otherwise the effect is negative. We excluded the pelvic landmarks 4 and 5 because they are absent in the Paxton benthic (Fig. 1). To convert QTL effects to millimeters all effects were multiplied by a constant, calculated as the mean standard length of all the fish divided by the mean distance between the most anterior and posterior landmark coordinates (x1 and x17). The distribution of these individual effects was then compared to exponential and gamma distributions to see which distribution fit best. We also calculated the overall (pleiotropic) effect size of each QTL as the Euclidean distance between the means of individuals having two marine alleles (MM) and individuals having two benthic alleles (BB) at the nearest marker, as predicted by the MQM model. This calculation used all x and y coordinates that were significantly affected by the QTL, which probably underestimates total QTL effects. Direction of effect was not incorporated into this measure.
BIAS
We evaluated the influence of two biases potentially affecting estimated QTL effect sizes (in addition to detection limits, which are well known to lead to an underestimate of the frequency of small effect QTL; Otto and Jones 2000). The first is the Beavis effect, the overestimation of effect sizes of detected QTL (Beavis 1994). The second is the “Noor effect,” the exaggeration of QTL effect sizes in genomic regions of low recombination caused by the cumulative effects of multiple smaller effect genes present there (Noor et al. 2001).
We used the parametric bootstrap (Efron and Tibshirani 1994) to measure the contribution of the Beavis effect to our estimated QTL effects. Details of the methods are provided in the online Supplementary Material. Briefly, each bootstrap replicate randomly drew a QTL effect size from the gamma distribution best fitting the positive effects in the data (see Results). Using simulation tools available in Rqtl 1.05–2 (Broman et al. 2003), we placed the QTL randomly on the original linkage map (see online Supplementary Fig. S1) and then generated a distribution of phenotypes by adding normal random errors to each fixed QTL effect. Finally, we carried out QTL mapping using a LOD threshold of 4.5 and “reestimated” the effect size of the QTL if detected. This procedure was repeated 500 times. In a second bootstrap we used the best-fit exponential distribution to the QTL effects instead, but the results were identical and we do not present them. If the Beavis effect is influential then the reestimated effect sizes of detected QTL should overestimate the true effects of simulated QTL placed on the map. These 500 simulations also provided us with estimates of the probability of QTL detection (see online Supplementary Fig. S2). A QTL of effect size 0.1 mm had a probability of detection of approximately 0.5, whereas an effect of 0.2 mm had a detection probability of approximately 0.9.
We could not fully evaluate the Noor effect because we lack a recombination map of the stickleback genome. Instead, we used the local density of markers on the linkage map as a surrogate for recombination rate. We assumed that locally dense concentrations of markers on the map likely reflect areas of low recombination, defined as higher numbers of kilobases per centiMorgan (see online Supplementary Fig. S1). Evidence of a Noor effect was examined in the data by regressing single-trait and total effect sizes of QTL against local marker density (number of markers within 10 cM of each QTL).
Results
Sexual dimorphism made up a significant portion of shape variation among the F2s. Thirty of 54 landmark coordinates mapped to the marker nearest the sex-determining locus (Peichel et al. 2004). The effect of sex on shape was remarkably similar to the shape differences between species, particularly in head shape and fin position (Fig. 2A, B). In addition, the amount of sexual dimorphism in shape is reduced in the freshwater benthic population (Fig. 3), suggesting that selection on sex-limited expression of genes may have contributed to shape evolution.
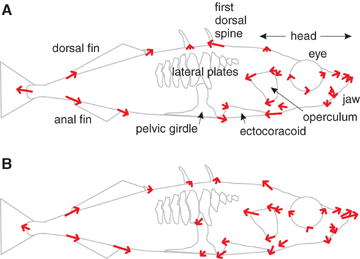
Shape differences. (A) Differences between the species in landmark positions. Arrows extend from the mean of the marine species to the mean of the benthic species. Changes involving the pelvic girdle are not indicated because the structure is missing in the benthic species. (B) Shape differences between the sexes in the F2s. Arrows multiply by five the distance from the mean position of females to the mean position of males for those landmarks mapping significantly to IDH, the closest known marker to the sex-determining locus.

Sexual dimorphism of shape in the parental species. Box plots of sexual dimorphism in shape in the Japan marines (left), and the Paxton benthics (right). Shape here is the first principal component of the variation in landmark positions between species. The asterisk (*) indicates an outlier.
In total, 47 of 54 x and y landmark coordinates mapped to 26 chromosome regions (QTL) on 17 linkage groups, including the sex-determining region (see online Supplementary Table S1). Some coordinates mapped to just one QTL, but most mapped to at least two. The x and y coordinates of individual landmarks almost always mapped to different QTL, justifying their treatment as separate traits here.
The frequency distribution of the number of coordinates affected by a QTL had a mode of one and was steeply right-skewed (Fig. 4). QTL on linkage groups 1, 4, 7, 12, and 21 affected at least seven coordinates apiece. The average number of coordinates affected by QTL was 3.5.
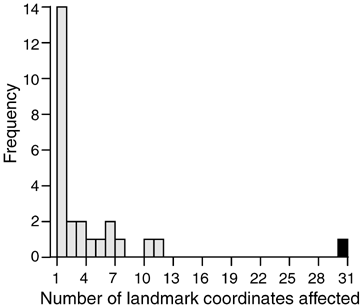
The frequency distribution of pleiotropic effects of QTL detected by MQM mapping. The horizontal axis shows the number of landmark coordinates mapping significantly to each QTL. The vertical axis gives the frequency of QTL. The black bar on far right indicates the sex-determining region.
Linkage group 4 had the highest number of QTL, four in total. One of these produced a relatively large effect, and influenced multiple landmarks in the head and pelvic regions. Figure 5 shows overall change in shape linked to a selected marker on linkage group 4. We cannot be certain that a given QTL represents one mutation, multiple mutations in the same gene, changes in multiple, tightly linked genes, or linkage to a causal gene. There were 117 individual QTL effects on traits—this exceeds the number of QTL because of pleiotropy.
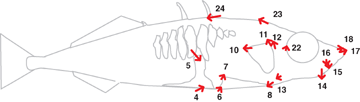
Shape changes linked to the major gene responsible for lateral plate reduction on linkage group 4 (see online Supplementary Fig. S1). Arrows multiply by five the effect of substituting two benthic alleles at the microsatellite marker Gac4174 for two marine alleles, as predicted by an MQM analysis that conditioned only upon sex. Arrows are shown for landmarks whose x or y coordinates were significantly associated with Gac4174 with a LOD of 2 or higher.
As predicted by theory, a few of the single-trait effect sizes were large—several exceeded 0.4 mm—but most were small (Fig. 6A). Also as expected, negative effects were present but positive effects surpassed them in frequency (80% vs. 20%, respectively) and in mean absolute magnitude (0.21 ± 0.011 mm vs. −0.17 ± 0.013 mm, respectively). Frequency distributions of positive and negative effects deviate from the back-to-back exponential distributions predicted by theory (Orr 1999), but this prediction does not take into account the difficulty of detecting QTL of very small effect. When detection limits are incorporated, the predicted distribution of effect sizes should be closer to a gamma distribution having a shape parameter exceeding one (Otto and Jones 2000). In support, both positive and negative effect sizes fit gamma distributions, with shape parameters 4.5 and 9.6, respectively (Fig. 6A), better than exponential distributions (Log-likelihood ratio tests, χ2= 63.68, df = 1, P= 1.4 × 10−15 and χ2= 28.42, df = 1, P= 9.8 × 10−8; these P-values are heuristic because of nonindependence of effect sizes).

Effect sizes of QTL, as estimated by MQM mapping. (A) Effects on single traits. (B) Overall effects. Overall effect size includes only landmark coordinates mapping significantly to a QTL, and so is an underestimate. The black bar indicates the effect of the sex-determining region.
The total effect sizes of QTL ranged from 0.09 to 1.23 mm (Fig. 6B). This compares with the total Euclidean distance of 5.58 mm between the parent species. The frequency distribution of effect sizes is right-skewed, with several having relatively large effects but most having small effects. Again, small effects are underrepresented compared with the predicted exponential distribution. Pleiotropy was an important component of overall effect size. Overall effect size of a QTL was predictable from the number of coordinates it affected (r= 0.91, df = 20, P= 6.4 × 10−9; excluding the QTL linked to sex: r= 0.87, df = 19, P= 3.97 × 10−7).
Shape in lake stickleback has evolved together with a reduction in bony armor. Are armor and shape genetically linked? None of the landmark coordinates, other than the four associated with the pelvic girdle, mapped to the region of Pitx1, the major gene responsible for loss of the pelvic girdle in some freshwater populations (Shapiro et al. 2004). However, QTL on linkage group 4 affected pelvic girdle landmarks as well as head shape (Fig. 5). One of these QTL mapped to the marker nearest Ectodysplasin (Eda), the major gene responsible for a reduced number of lateral armor plates in freshwater stickleback (Colosimo et al. 2005), indicating pleiotropy or tight linkage.
The latter explanation (linkage) is supported by measurements of 26 complete and 31 low-plate morphs of threespine stickleback from Friant Lake, California. This population is polymorphic at the Eda locus, and previous work has shown that only a narrow genomic region of 16 kb, which includes the Eda gene, is presently in linkage disequilibrium with lateral plate phenotype (Colosimo et al. 2005). We placed landmarks on photographs of complete and low-plated Friant fish. All fish were genotyped at IDH to confirm sex, and at Stn381, a microsatellite marker for Eda (Colosimo et al. 2005), to confirm the plate locus genotypes. Using the aligned landmarks we compared the landmark coordinates using ANOVA with sex and plate morph as factors. We found no significant head shape differences between Eda genotypes in Friant Lake, suggesting that shape QTL on linkage group 4 (Fig. 5) are not in this same interval.
EVALUATION OF BIAS
A Beavis effect, if present, should cause bootstrap estimated effect sizes to overshoot the “true” effect sizes of QTL placed on the map, on average. Our bootstrap results indicated that estimated effect sizes of the smallest QTL were indeed slightly inflated (see online Supplementary Fig. S3), but the overall impact of the bias was slight. The bootstrap estimate of variance in effect size was 99% that of the “true” detected QTL. These results are based on simulations using a gamma distribution of true effect sizes, but the results using an exponential distribution instead were almost identical. The small impact of the Beavis effect on our study likely results because our sample size and LOD threshold for significance are large, and because the distribution of true effect sizes of QTL for shape is very broad.
The effect sizes of QTL on single coordinates were unrelated to local marker density (Fig. 7A; positive effects, r= 0.05, df = 49, P= 0.75; negative effects, r= 0.14, df = 15, P= 0.60; sex-linked effects are excluded), suggesting that the “Noor effect” on single coordinates is minimal. This is to be expected when the number of QTL affecting a single trait is few and the genome is large (Noor et al. 2001). However, we observed a positive effect of local marker density on total QTL effect size in the data (Fig. 7B; r= 0.58, df = 19, P= 0.0062). The most pleiotropic QTL with the largest total effects exist in regions of relatively high marker density. The likely reason for the difference from the single-coordinate result is that here we mapped a large number of traits, which increases the chances that multiple genes will occur together in any given region of the genome. Those landing in regions of low recombination might appear as a single pleiotropic QTL when mapped. Therefore, our estimates of pleiotropy and total QTL effect size are probably overestimated to an unknown degree by this effect. It is not possible to determine the magnitude of the bias without finer scale mapping. This caveat does not apply to the sex-determining region in which single gene likely influences a large number of shape traits.

QTL effect size in relation to the local density of markers (number of markers within 10 cM). (A) Influence of marker density on the effect sizes of QTL on individual traits. The dashed line separates positive effects from negative effects. (B) Influence of marker density on overall QTL effect sizes, including all traits mapping significantly to each QTL.
Discussion
Body shape of freshwater stickleback populations that formed at the end of the last ice age represents a complex suite of traits that diverged rapidly from an ancestral marine phenotype similar to the one used in our cross (Walker and Bell 2000). Different aspects of shape have changed together repeatedly in different populations, raising the question whether shape divergence might be determined by a few genes having large and pleiotropic effects. Our results show that the distribution of effect sizes of QTL followed neither the major genes model of adaptation nor the infinitesimal model of quantitative genetics. Instead, the distribution of detected effect sizes approximately followed a gamma distribution, which is the expected distribution from the geometric model of adaptation when detection limits are present (Otto and Jones 2000). This does not mean, of course, that the geometric model is correct, but it provides a better approximation for the genetics of adaptation than its simplistic alternatives.
Under the geometric model of adaptation, the distribution of QTL effects fixed by selection in the new environment should be approximately exponential (Orr 1999). We interpret our gamma distribution of effect sizes for single traits as a consequence of detection limits, but several other processes might contribute to a shortage of QTL of very small effects. The most interesting is that gene flow between diverging populations might prevent the fixation of small effect mutations between them (Griswold 2006). Although our Paxton Lake benthic population is not sympatric with any marine population, it coexists and may hybridize with another species, the Paxton Lake limnetic (McPhail 1992), which has some morphological similarities to marine stickleback (Schluter and McPhail 1992). A second possible reason for a shortage of very small effect QTL is that they are under weak selection in the freshwater environment and few have yet spread to fixation.
Our counts of small- or moderate-effect QTL are comparable to other studies that have identified QTL for shape differences in specific structures between populations or species: 25 QTL for mouse mandible shape (Klingenberg et al. 2001), 18 QTL for mouse molar shape (Workman et al. 2002), 19 QTL for male Drosophila genital arch shape (Zeng et al. 2000), 21 QTL for Drosophila wing shape (Mezey et al. 2005), and 15 QTL for leaf size and shape differences in Antirrhinum (Langlade et al. 2005). However, we also identified several major QTL for body shape. We cannot determine whether each of them represents one gene with widespread effects or multiple genes in close linkage. Total effect size of QTL, but not effects on individual traits, increased with local density of markers, suggesting that QTL of widespread effect might represent multiple genes (Fig. 7B).
A subset of QTL effects was in the direction opposite to that of the difference between the parental species (antagonistic effects) (Fig. 6A). Antagonistic effects are a predicted outcome of adaptation when genes have pleiotropic effects, because selection on a particular trait causes the fixation of antagonistic effects as a by-product (Griswold and Whitlock 2003). A substantial number of the QTL found here had effects on multiple coordinates, suggesting that pleiotropy may indeed have influenced the directions of effects fixed during evolution. However, antagonistic effects are also expected under stabilizing selection and random genetic drift (Rieseberg et al. 2002; Griswold and Whitlock 2003). The proportion of antagonistic effects (20%) in our study was similar to that detected in other taxa (Rieseberg et al. 2002).
QTL for shape are linked to, or have pleiotropic effects on, some armor traits that have evolved together with shape in freshwater populations. A major QTL on linkage group 4 affected landmarks on the pelvic girdle as well as multiple landmark coordinates in the head region (Fig. 5). This QTL was strongly linked to Eda, the major gene responsible for reduction in the number of lateral plates. Such effects might help to explain why body shape and plate number evolve together during adaptation to freshwater. No shape traits other than landmarks on the pelvic girdle mapped to the marker nearest Pitx1 on linkage group 7, which controls pelvic girdle loss (Shapiro et al. 2004), suggesting that the effects of the Pitx1 mutation do not include changes in body shape. This is in agreement with previously detected effects of the Pitx1 mutation on Pitx1 expression, which appear specific to the pelvic region during pelvis development (Cole et al. 2003; Shapiro et al. 2004, 2006).
A surprising number of landmark coordinates mapped to the sex-determining region. This region also had the largest total effect of any other QTL, reflecting sexual dimorphism for shape in this cross (see also Kitano et al., 2007; Jones et al. 2006). Landmarks affected include those marking the position of the operculum, a trait whose shape was found also to map to the sex-determining chromosome in another QTL study of stickleback species differences (Kimmel et al. 2005). Remarkably, shape differences between the sexes in the F2s are similar (although not identical) to the shape differences between the species (Fig. 2). This suggests that in the newly formed freshwater population, becoming more male-like would have represented a significant step toward becoming more benthic-like. Perhaps this could be accomplished in a simple step such as turning off sex-limited expression of some genes, allowing for rapid adaptation in certain structures. In support of this scenario, we found that sexual dimorphism has been largely lost in the Paxton benthics in the principal component axis that describes most of the variation in shape between the two parent species (Fig. 3).
A key assumption of the geometric model of the genetics of adaptation is that mutation is the sole source of advantageous alleles during adaptation in the new environment (Orr 1999). However, we already know that a major armor trait in stickleback has evolved via standing variation rather than new mutation (Colosimo et al. 2005), and it is reasonable to suppose that the same is at least partly true for shape. This is another reminder that finding a gamma distribution of QTL effects does mean that the details of existing geometric theory are correct. The predicted distribution of effect sizes from standing genetic variation has not been modeled.
A goal of future work is to compare these findings with crosses made between the marine species and other freshwater populations, including other benthic species, to determine whether parallel changes in shape are controlled by the same genes as in the current cross. Another goal is to further disentangle the effects of pleiotropy and genetic linkage in the evolution of body shape, and to identify the actual genes underlying shape differences. Together, these findings would allow us to better understand how suites of traits can evolve in correlated and repeated ways during adaptation to new environments.
Associate Editor: M. Noor
ACKNOWLEDGMENTS
We thank S. Rogers, L. Harmon, R. Barrett, K. Marchinko, J. Weir, M. Whitlock, and the SOWD group for helpful discussions on data analysis and organization. We also thank J. Kelly, M. Noor, and an anonymous reviewer for valuable comments on the manuscript. This work was supported in part by a Center of Excellence in Genomic Science grant from the National Institutes of Health (1P50HG02568; DMK), the Natural Sciences and Engineering Research Council of Canada (NSERC) (DS), and the Canada Foundation for Innovation (DS). AA was supported by a NSERC postgraduate scholarship, TV by a Marie Curie Outgoing International Fellowship, BS by a National Science Foundation predoctoral fellowship, and CM by a Jane Coffin Childs postdoctoral fellowship. DS is a Canada Research Chair, and DMK is an Investigator of the Howard Hughes Medical Institute.




