MALE VERSUS FEMALE MATE CHOICE: SEXUAL SELECTION AND THE EVOLUTION OF SPECIES RECOGNITION VIA REINFORCEMENT
Abstract
Male mate choice, expressed through courtship preferences, sometime occurs even under the mating system of polygyny, when the operational sex ratio is skewed toward males. The conditions under which male mate choice may be expected during polygyny are not well established. Servedio and Lande (2006, Evolution 60:674–685), assuming strict polygyny where all females have equal mating success, show that when having a preference does not increase the amount of energy that a male can put into courtship, male preferences for “arbitrary” female ornaments should not be expected to evolve; direct selection acts against them because they place males that carry them into situations in which there is high competition for mates. Here I explore in detail two situations under which logic dictates that this effect may be overcome or reversed. First I determine the contributions that direct and indirect selection place on male versus female preferences for traits that increase viability, using notation that allows the exact expression of these measures of selection. I find that direct selection against male preferences still predominates in the male mate choice model, causing less evolution by male than female preferences under these conditions. Second I address whether male mate choice is likely to evolve as a mechanism of premating isolation leading to species recognition, driven by the process of reinforcement. Reinforcement is compared under male and female mate choice, using a variety of models analyzed by both analytical techniques assuming weak selection and numerical techniques under broader selective conditions. I demonstrate that although under many conditions stronger premating isolation evolves under female mate choice, reinforcement may indeed occur via male mate choice alone.
Mate choice is of great interest to evolutionary biologists both in its own right, as shown by the vast literature on sexual selection (e.g., Andersson 1994), and due to the role that it plays in other evolutionary phenomena such as speciation. During polygyny, the most common breeding system (e.g., Thornhill and Alcock 1983), mate choice is generally exercised by females and based upon male display traits, even in cases in which males provide no resources (e.g., Darwin 1871; Andersson 1994). Similarly, male mate choice during polygyny can occasionally be based upon female display traits (e.g., color, Burley and Coopersmith 1987; Hill 1993; Amundsen et al. 1997; Hunt et al. 1999; Amundsen and Forsgren 2001; see Amundsen 2000) that may or may not be correlated with any immediate benefit to the male. Far more often, however, male choice is associated with the direct benefit of mating with females that are more fecund (e.g., Olsson 1993; Verrell 1995; Monaghan et al. 1996; Jones et al. 2001; Szykman et al. 2001; Werner and Lotem 2003; Herdman et al. 2004; Saeki et al. 2005; for review see Andersson 1994, table 6a; Bonduriansky 2001). This begs the question, assuming that males are limited in their number of mates during polygyny, why is male choice only rarely based on “arbitrary” traits?
Although there is a rich theoretical literature on the conditions affecting the evolution of female preferences during polygyny (reviewed in Andersson 1994; Mead and Arnold 2004; Kokko et al. 2006), theoretical investigations of the evolution of male preferences for “arbitrary” traits during polygyny are in their infancy. These models do indicate, however, that male and female mate choice may behave very differently (e.g., Servedio and Lande 2006). When female preferences are not assumed to directly affect viability or fecundity (e.g., there is no “direct” selection on preferences), they will evolve solely due to their genetic correlation (linkage disequilibrium) with the evolving male trait (“indirect” selection, see e.g., O'Donald 1967; Lande 1981; Kirkpatrick 1982). Servedio and Lande (2006) developed a series of haploid population genetic models of male mate choice, which like these prior female choice models, assume strict polygyny, where all females have equal mating success. They demonstrated that an allele for male mate choice for an “arbitrary” female trait (not favored by selection or indicating good genes) will automatically be directly selected against, even if it is not assumed to affect viability or fecundity; the male preference allele is lost because it causes itself to be placed disproportionately in situations in which there is high competition among males for mates. The conditions for the evolution of male preferences would therefore be expected to be more restricted than those for the evolution of female preferences.
Servedio and Lande (2006) explored several cases in which the direct selection occurring against male preferences during polygyny could be reversed or overcome, leading to the evolution of male choice. Direct selection can actually favor male choice, for example, in certain cases in which having a preference leads to males putting more energy into courtship, or if females are more likely to mate if they are courted sufficiently more often. Male preferences may also evolve via direct selection if males prefer to court females that have sufficiently higher fecundity, predicting the common preferences of males for more fecund females noted above. Finally, when there are pleiotropic effects of preference or trait genes causing expression in both sexes, male preferences may evolve due to selection occurring in the female choice components of the system, although if pleiotropy is absent male and female mate choice does not affect one another during mutual mate choice (Servedio and Lande 2006).
Female preferences have been found to evolve not only due to natural and sexual selection within a single species, but also due to evolutionary forces that promote preference divergence during the development of premating reproductive isolation. Theoretical models have examined the evolution of female preferences during sympatric speciation (e.g., van Doorn et al. 1998; Higashi et al. 1999; Kondrashov and Kondrashov 1999), along a cline (e.g., Lande 1982; Day 2000), and during the process of reinforcement (defined as the evolution of premating isolation after secondary contact due to selection against hybrids or hybridization, e.g., Liou and Price 1994; Kelly and Noor 1996; Kirkpatrick and Servedio 1999; Servedio 2000). Similar preference evolution during speciation could be imagined to occur via male choice for female traits. Although this has seldom been explored theoretically (out of the context of simple assortative pairing, but see Lande et al. 2001), empirical evidence from many systems suggests that male choice may play a role in species recognition between closely related species pairs (e.g., Wiernasz 1995; Seehausen et al. 1999; Gabor and Ryan 2001; Deering and Scriber 2002; Shine et al. 2004; Albert and Schluter 2004)
The goal of the current article is to examine two conditions under which male choice may evolve during strict polygyny, using techniques that yield new insights into the selective forces operating during male mate choice. Logic dictates that it may be possible for male preferences to evolve when the preferred female trait improves female viability. Servedio and Lande (2006) find some support for this idea through numerical analysis, but do not explore it fully. In the first part of this article I use very simplified models of sexual selection to explore the evolution of male preferences for traits that improve female viability and compare this with female preferences for male traits, using a methodology that allows analytical comparisons of direct and indirect selection on preferences (Barton and Turelli 1991). This allows a much more detailed description of the differences between the male and female mate choice models than presented in Servedio and Lande (2006), and provides a clear explanation for the ultimate outcomes of the models. In the second case, I ask whether male mate choice can evolve during a scenario of reinforcement. The results provide the first theoretical demonstration of reinforcement via male courtship. I also compare reinforcement via male versus female mate choice under several types of models, using a combination of analytical and numerical techniques. I find that although reinforcement can indeed occur via male mate choice, it generally (but not always) occurs more easily via female mate choice.
Male versus Female Mate Choice for a Trait That Increases Viability
In this section, I use simplified “toy” models of sexual selection to compare male versus female mate choice for traits that increase viability. These models do not attempt to be biologically realistic, as they make several restrictive assumptions discussed below. Despite their lack of biological realism, these models are very revealing in that they clearly illustrate the differences in direct and indirect selection that act during male versus female mate choice. They, thus, illuminate general properties of male and female mate choice that can be applied, with some restrictions detailed below, to more realistic biological scenarios. The models are based on the classic sexual selection model of Kirkpatrick (1982).
ASSUMPTIONS
Both the male and female mate choice models are based on the same set of assumptions. The models are haploid. Two loci are included, one (locus T) for a display trait, and the other (locus P) for a mating preference. The display trait is assumed to be expressed only in males in the female mate choice model and only in females in the male mate choice model. The trait locus has two alleles, T1 and T2. In the sex in which it is displayed, the trait T2 is favored by viability selection. In this sex, trait T1 thus has the relative fitness 1, whereas T2 has the relative fitness 1 +st. The opposite sex, which does not express the display trait, is assumed to gain no direct benefit from the T2 allele. The models assume that variation may be present at the trait locus, despite the fact that the sole initial effect of the T2 allele is that it improves viability; the preference can thus be assumed to be introduced into the model while the trait is in the process of fixing from a low frequency of introduction. Although this is not very realistic, it serves the purpose of investigating the behavior of the toy models (and mirrors the assumptions of Kirkpatrick 1982, in which the male trait is selected against).
The preference locus P is expressed by the choosing sex, specifically by females in the female mate choice model and by males in the male mate choice model. The preference locus also contains two alleles, P1 and P2. In the female choice model, females with the P1 allele mate at random, whereas females with the P2 allele are 1 +α times as likely to mate with a T2 male than a T1 male upon encounter. The model assumes polygyny where all females have equal mating success. The assumptions for the female choice model are thus identical to those of Kirkpatrick 1982, with the exception of natural selection favoring the trait T2 in the present model, instead of acting against it (and where Kirkpatrick's a2= 1 +α). A fitness equation that includes both natural and sexual selection, derived from these assumptions, is presented in Appendix 1. This uses the notation of Barton and Turelli (1991), which will ultimately allow the extraction of specific expressions for the strength of direct and indirect selection on the preference allele P2.
In the male choice model, the preference locus determines how a male will distribute his courtship. All males, regardless of the preference allele they carry at this locus, are assumed to have the same amount of energy that they can devote to courtship (vs. foraging, protection from predators, etc.). Males that carry the P1 allele court females at random, based solely on their rate of encounter with T1 and T2 females. Males that carry the P2 allele, on the other hand, bias their courtship toward T2 females. Specifically, a male will be 1 +α times as likely to court a T2 female as a T1 female if he encounters one of each. This can also be thought of as choosy males being more likely to decide not to bother courting some females (in this case the T1 females), with the consequence that they are able to court other females (in this case the T2 females) more, given a limited amount of energy for courtship. The male choice model, like the female choice model, assumes strict polygyny. Females will chose from among the males that are courting them, where a male's apparentness to a female is directly proportional to the amount of courtship a male is directing toward that female. As in the female choice model, all females are assumed to have equal mating success. Equations derived from these assumptions are presented in Appendix 1, also using the notation of Barton and Turelli (1991). The assumptions in the male mate choice model are identical to those for male mate choice in Servedio and Lande (2006; with the exception of selection favoring, instead of acting against, the male trait T2).
The current model makes several assumptions (e.g., regarding strict polygyny, a lack of pleiotropy, no costs to preferences) that will often not be realistic in specific natural cases. The violation of these assumptions and others are reviewed in the discussion.
Note that in the absence of pleiotropy, the male mate choice model used here also describes the male mate choice portion of mutual mate choice; in the absence of pleiotropy, and with the assumptions of strict polygyny used here, the male and female mate choice portions of mutual mate choice behave independently of one another (Servedio and Lande 2006).
ANALYSIS
These toy models of male and female mate choice are analyzed in two ways below. By evaluating the dynamics of the spread or loss of the male or female preference allele over a single generation, the first type of analysis, it is possible to obtain a full understanding of the action of direct versus indirect selection on preferences in these models. The second type of analysis, an analysis of the equilibrium values that preference and trait alleles will obtain, allows the determination of whether male versus female mating preferences would ultimately be expected to be present in populations. Together these analyses provide a full picture of both the evolutionary outcome of male versus female mate choice and the selective processes that produce this outcome.
Dynamics and partitions of selection
Female and male mate choice differs significantly in the fundamental biological processes that determine whether preference alleles will increase or decrease. Adaptive allele frequency evolution in any model can be attributed to either direct selection, where changes in the allele frequency are due to the direct effects of that allele on the viability or fecundity of individuals that possess it, or indirect selection, where changes in the allele frequency are due solely to the fact that the focal allele is genetically associated with other alleles that are themselves changing in frequency. Direct and indirect selection act differently on preference alleles in male versus female mate choice models.
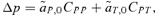 (1)
(1)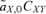 gives the amount that the frequency of an allele at locus Y changes due to (1) selection at locus X (
gives the amount that the frequency of an allele at locus Y changes due to (1) selection at locus X (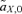 , averaged over males and females) and (2) the genetic association between locus X and locus Y (CXY). Equation (1) is general and applies to both the male choice and female choice models presented in Appendix 1.
, averaged over males and females) and (2) the genetic association between locus X and locus Y (CXY). Equation (1) is general and applies to both the male choice and female choice models presented in Appendix 1.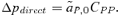 (2)
(2)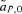 , times the genetic variance at the P locus, CPP. Likewise, indirect selection is represented by the second term in equation (1),
, times the genetic variance at the P locus, CPP. Likewise, indirect selection is represented by the second term in equation (1),
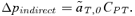 (3)
(3)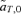 ) but changes the frequency of alleles at the P locus due to the genetic association, or linkage disequilibrium, between P and T, CPT. The
) but changes the frequency of alleles at the P locus due to the genetic association, or linkage disequilibrium, between P and T, CPT. The  s in equations (2) and (3) can be calculated for both the male and female mate choice models, using the equations and procedure described in Appendix 1. Equations (2) and (3) can then be used to compare Δpdirect and Δpindirect for male versus female mate choice, illustrating the differences between the ways that direct and indirect selection act in these two models.
s in equations (2) and (3) can be calculated for both the male and female mate choice models, using the equations and procedure described in Appendix 1. Equations (2) and (3) can then be used to compare Δpdirect and Δpindirect for male versus female mate choice, illustrating the differences between the ways that direct and indirect selection act in these two models.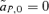 (see also Barton and Turelli 1991), yielding Δpdirect= 0. During female mate choice there is thus no direct selection on the preference allele, as expected from the results of Lande (1981) and Kirkpatrick (1982). For male mate choice, however,
(see also Barton and Turelli 1991), yielding Δpdirect= 0. During female mate choice there is thus no direct selection on the preference allele, as expected from the results of Lande (1981) and Kirkpatrick (1982). For male mate choice, however,
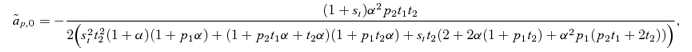 (4)
(4)where the lower case letters indicate the frequencies of the corresponding alleles (note that this expression, and the others in this section, are exact and do not assume weak selection). Δpdirect for male mate choice will be equal to expression (4) times the genetic variance at the P locus, CPP=p1p2. Expression (4) can be seen to be a complex function of the current female trait frequency t2 (which is affected by the viability of the trait st), the current frequency of the male preference allele p2, and the preference strength α. Because expression (4) is clearly negative, as, consequently, is Δpdirect for male mate choice, this analysis clearly confirms that direct selection acts against the male preference allele P2. Because much of the equilibria and stability of many female mate choice models (e.g., a line of equilibria with polymorphic preferences and traits, Lande 1981, Kirkpatrick 1982) depends critically on a lack of direct selection on the preference allele (Δpdirect= 0 for female choice), the finding that Δpdirect< 0 for male mate choice indicates that it will behave very differently from female mate choice.
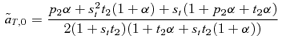 (5)
(5)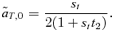 (6)
(6)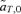 times the linkage disequilibrium in each model between the preference and trait loci, CPT, which is always positive. Both expressions (5) and (6) can be seen to be positive; indirect selection therefore favors the spread of the mating preference allele under both male and female mate choice. With male mate choice, the strength of selection on the female trait (expression 6) only shows the effect of viability selection on the T locus; a factor of 1/2 is present because the trait is only expressed in females. Selection on the female trait therefore does not depend upon the strength of the male preference, α. This illustrates that when male mate choice acts during strict polygyny, sexual selection is not actually exerted on the female trait. This is a logical consequence of the assumption that all females, despite the trait they carry, have equal mating success when polygyny is absolute. Selection on the male trait during female choice (expression 5), on the other hand, is a complex expression that includes both the selection coefficient on the trait (st) and the strength of sexual selection (α). Because I assume in this model that sexual selection always favors allele T2, selection on a male trait during female choice (expression 5, Fig. 1A), will be greater, for a given α, than selection on a female trait during male choice (expression 6, Fig. 1B).
times the linkage disequilibrium in each model between the preference and trait loci, CPT, which is always positive. Both expressions (5) and (6) can be seen to be positive; indirect selection therefore favors the spread of the mating preference allele under both male and female mate choice. With male mate choice, the strength of selection on the female trait (expression 6) only shows the effect of viability selection on the T locus; a factor of 1/2 is present because the trait is only expressed in females. Selection on the female trait therefore does not depend upon the strength of the male preference, α. This illustrates that when male mate choice acts during strict polygyny, sexual selection is not actually exerted on the female trait. This is a logical consequence of the assumption that all females, despite the trait they carry, have equal mating success when polygyny is absolute. Selection on the male trait during female choice (expression 5), on the other hand, is a complex expression that includes both the selection coefficient on the trait (st) and the strength of sexual selection (α). Because I assume in this model that sexual selection always favors allele T2, selection on a male trait during female choice (expression 5, Fig. 1A), will be greater, for a given α, than selection on a female trait during male choice (expression 6, Fig. 1B).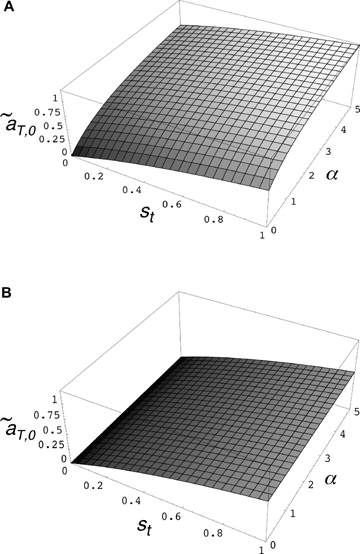
.
Value of  for p2= 0.5 and t2= 0.5. (A)
for p2= 0.5 and t2= 0.5. (A)  for female mate choice, (B)
for female mate choice, (B) 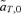 for male mate choice.
for male mate choice.
How do these differences in direct and indirect selection between the models affect the total change in the frequency of preference alleles over a generation? For female mate choice, because there is no direct selection on preferences (Δpdirect= 0), the preference changes only due to indirect selection (the total Δp=Δpindirect). Because Δpindirect > 0 with selection favoring the preferred trait (st > 0), the total change in the preference allele frequency during female mate choice will always be positive (Δp > 0). An allele for female preference will therefore always spread when selection favors the male trait, given the assumptions of the model.
For male mate choice, however, direct and indirect selection have opposing effects on the preference allele; Δpdirect < 0, whereas Δpindirect > 0. The sign of the total change in the preference allele frequency, Δp=Δpdirect+Δpindirect, is therefore determined by the relative magnitude of the effects of direct and indirect selection. I examined several cases with numerical simulations that iterated the exact recursion equations. The male preference allele was observed to increase in some cases, but for many parameter values, direct selection was seen to have a larger effect than indirect selection for male mate choice, causing the total change in preference Δp to be negative (e.g., Fig. 2, shown also for negative st). Figure 2 also demonstrates that the change in frequency of the preference allele due to indirect selection (Δpindirect) is consistently larger with female mate choice than with male mate choice; this is true because Δpindirect is affected by natural selection alone during male mate choice (expression 6), but also includes increases due to sexual selection during female mate choice (expression 5).
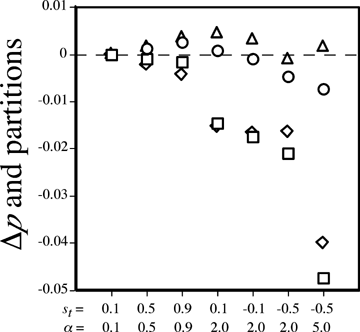
. Values of Δp and its partitions for male and female mate choice. Under male mate choice, squares represent the total Δp, diamonds representΔpdirect, and circles represent Δpindirect. Triangles represent Δpindirect (= total Δp) with female mate choice. These measures are shown for various values of st and α, as labeled on the x-axis. A dashed line is drawn at 0 on the y-axis to aid in interpretation. Values of p2, t2, CPT, and CPP were obtained from numerical simulations after one generation of evolution starting with allele frequencies p2=t2= 0.5.
Equilibrium analyses
A better sense of the ultimate outcome of the evolution of male and female preferences can be obtained by determining the equilibrium frequency of the preference and trait alleles under male and female mate choice. Again we are concerned here with the situation in which viability selection favors the preferred trait. Recursion equations for each of the models, following the exact assumptions above, were thus analyzed to determine the equilibria and their stability.
For the female mate choice model, the recursion equations can be obtained from Kirkpatrick (1982), changing the sign of selection on the male trait T2 to have it increase viability. Analysis of these equations shows that there is a line of equilibrium where the male trait is lost, and a line of equilibrium where the male trait is fixed, but, in contrast to the case in which there is selection against the male trait (Kirkpatrick 1982), there is no line of equilibrium that is polymorphic for both the preference and the trait. The line of equilibrium where the trait is lost can be shown to be unstable, whereas the line of equilibrium where the trait is fixed can be shown to be stable. This conclusion is consistent with the finding above that the net selection on the trait allele, 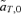 , is always positive (and that selection on the preference allele, which could technically change the frequency of the trait allele through indirect selection, is zero).
, is always positive (and that selection on the preference allele, which could technically change the frequency of the trait allele through indirect selection, is zero).
The final frequency of the preference allele in a given case will depend upon the starting frequencies of the preference and trait in this female choice model. The more quickly variation at the trait locus is lost, the sooner the preference allele will stop increasing in frequency, because the preference changes only through its association with the trait locus. The trait allele T2 will be fixed more quickly when viability selection favoring it is strong (remembering that sexual selection also uniformly favors this allele). The preference allele thus ends up increasing in frequency the most when, conversely, the viability selection (st) favoring the trait allele T2 approaches zero. Some representative increases of the frequency of the preference allele at equilibrium under female mate choice are shown in Figure 3A.
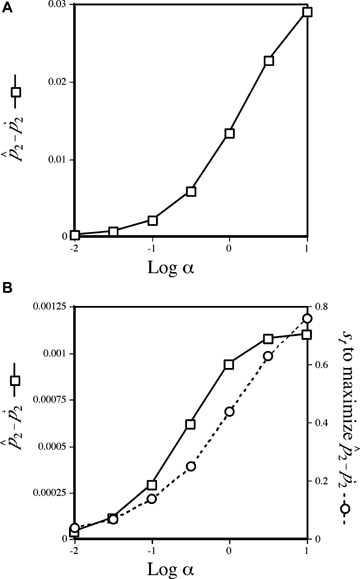
Increases in p2 during mate choice from its starting value, measured at equilibrium. Starting values for the trait allele T2 and preference allele P2 are 0.5 and 0.1, respectively. The x-axis shows the log of the preference strength parameter α. (A) Plot for female mate choice. The left-hand y-axis (squares, solid lines) displays the maximum difference seen between the equilibrium value of the preference allele p2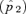 and its starting value of (p′2), given α,p′2, and the starting value for t2. The spread of the preference allele is at its maximum when st= 0 (see text), which are the conditions shown in the figure. Under these conditions preferences will not spread during male mate choice. (B) Plot for male mate choice. The left-hand axis is as in 3A. The right-hand axis (circles, dashed lines) shows the value of st that produces the maximum value of
and its starting value of (p′2), given α,p′2, and the starting value for t2. The spread of the preference allele is at its maximum when st= 0 (see text), which are the conditions shown in the figure. Under these conditions preferences will not spread during male mate choice. (B) Plot for male mate choice. The left-hand axis is as in 3A. The right-hand axis (circles, dashed lines) shows the value of st that produces the maximum value of  for each value of α. The values of
for each value of α. The values of  can be seen to be relatively low, despite the fact that they are the maximal values for each α given the starting conditions (for any st). Equilibrium values of p2 are lower for lower starting values of p2, so the values shown, for a relatively high starting value of p2 if P2 is considered to arise through a new mutation, are conservatively large.
can be seen to be relatively low, despite the fact that they are the maximal values for each α given the starting conditions (for any st). Equilibrium values of p2 are lower for lower starting values of p2, so the values shown, for a relatively high starting value of p2 if P2 is considered to arise through a new mutation, are conservatively large.
Recursion equations for the male mate choice model can be obtained from Servedio and Lande (2006), again changing selection so that it favors the trait T2, now expressed in females. Analysis of this model also shows two lines of equilibrium, one when the trait is lost and the other where the trait is fixed. As in the case with female mate choice, it can again be shown that the line of equilibrium where the trait is lost is unstable, whereas the line of equilibrium where the trait is fixed is stable. The differences between the male and female mate choice models are thus not in the stability of the lines of equilibrium, but ultimately in the position that the preference allele will reach along the line of equilibrium where the trait allele T2 is fixed.
Under male mate choice, the trait allele T2 increases due to viability selection, but it can actually be selected against by indirect selection; it is genetically associated with the preference allele P2, which is often decreasing in frequency. The preference allele will only evolve when there is variation at the male trait (note that 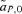 in expression (4) will equal zero if either t1 or t2 are zero). The maintenance of variation at the trait allele and the strength of indirect selection on the preference, due in part to the viability advantage of the T2 allele, combine to determine an intermediate value of st for which male preference evolution will be maximized. For a given numerical case, it is possible to find the value of st that will result in the greatest increase in P2. These values, and the subsequent equilibrium values for the preference allele P2, are shown for some examples in Figure 3B.
in expression (4) will equal zero if either t1 or t2 are zero). The maintenance of variation at the trait allele and the strength of indirect selection on the preference, due in part to the viability advantage of the T2 allele, combine to determine an intermediate value of st for which male preference evolution will be maximized. For a given numerical case, it is possible to find the value of st that will result in the greatest increase in P2. These values, and the subsequent equilibrium values for the preference allele P2, are shown for some examples in Figure 3B.
The analysis of equilibrium values of preference and trait alleles thus reveals no fundamental differences in the stability of the lines of equilibria in the female versus male mate choice models. The numerical analyses above, which present the maximum amount of evolution of preferences given a set of starting frequencies for the preference and trait (i.e., the maximum for any value of viability selection on the trait, st) indicate that female mate choice is likely to result in a substantially greater amount of preference evolution than male mate choice. The amount of evolution of male preference alleles is very minimal. Even female mate choice can be quite restricted, however, due to the loss of variation of the male trait.
Can Male Mate Choice Evolve via Reinforcement?
In the situation of reinforcement, matings between individuals from partially diverged populations result in low fitness for the mated pair, often through the low fitness of hybrid offspring. The production of offspring with low fitness has been shown in theoretical models to drive the divergent evolution of female preferences under certain conditions (e.g., Liou and Price 1994; Kelly and Noor 1996; Servedio and Kirkpatrick 1997; Kirkpatrick and Servedio 1999; Kirkpatrick 2000; Servedio 2000, 2004; Servedio and Sætre 2003). Here I examine whether selection against hybrids can drive the evolution of species-specific male courtship preferences to cause reinforcement, even when females mate indiscriminately. I compare the conditions for reinforcement through female and male choice, using both computer simulations (with two-island models) and an analytical approach assuming weak selection (with a continent-island model).
I analyze reinforcement via male and female choice using haploid, four locus models. In the “preference” models, the choice locus (locus P) codes for male or female preferences for specific traits in the opposite sex, whereas in the “assortative mating” models the choice locus codes for a preference to mate assortatively (locus B; see Servedio 2000, 2004). The preference model is a “two-allele model” sensu Felsenstein (1981), whereas the assortative mating model is a “one-allele model”; evaluating both models assures that the results are robust to this important distinction. The second locus in both models, T, codes for a trait that acts as a mating cue, here assumed to be expressed in both sexes. The final loci (the “background” loci), N and M, interact epistatically to produce low fitness in hybrids (e.g., Carvajal et al. 1996; Palopoli and Wu 1994; Noor et al. 2001; Orr and Irving 2001). Each locus has two alleles.
TWO-ISLAND MODELS—ASSUMPTIONS
I begin with a haploid two-island model that will be analyzed numerically via computer simulations. The island populations are assumed to have undergone a period of allopatry during which some amount of population divergence has taken place. I assume that the trait allele T1 is locally adapted on island 1 whereas the allele T2 is locally adapted on island 2 (these traits therefore represent mating cues that are both ecologically important and targets of sexual selection, e.g., body size). The locally adapted allele starts at a high frequency in each population. I assume that alleles at the background loci have also diverged in allopatry, so that N1M1 is initially fixed in island 1 and N2M2 is initially fixed in island 2.
The populations are assumed to come into secondary contact through the introduction of migration between them (symmetrical with rate m). Migration is the first step in the life cycle, followed by selection at the mating cue (T) and the background loci (N and M). Selection favors the locally adapted trait (T1 or T2) in each population with a strength determined by the selection coefficient st. Hybrid recombinant genotypes at the background loci, N1M2 and N2M1, are selected against with the selection coefficient sE. Sexual selection, if any, follows natural selection, followed in turn by free recombination between all loci. An initial equilibrium is reached at the trait and background loci, T, N, and M, due to a balance between selection and migration (the equilibrium is considered to have been reached when the change per generation in each genotype has dropped below 1×10−11).
After the initial equilibrium is reached, an allele causing premating isolation is introduced at the preference locus (P) or assortative mating locus (B), which up until now have been fixed for a single, ancestral allele; if this new allele spreads, then reinforcement is considered to have occurred. Preferences have the same function in the female choice and male choice reinforcement models as in the female and male choice models in the first half of this article; female preferences directly affect a female's choice whereas male preferences affect biases in courtship given to different types of females.
In the preference model, allele P1 is initially fixed in both populations under both male and female mate choice. P1 codes for a preference of strength α1 for mates with the T1 trait (P1 females, for example, are 1 +α1 times as likely to mate with T1 males during female mate choice if encounter rates are equal, whereas P1 males are 1 +α1 times as likely to court T1 females during encounter; if α1= 0 then mating or courtship is random). Allele P2, which causes a preference for the trait T2 in the opposite sex (of strength α2), is introduced at a low frequency (0.002) in both populations, keeping linkage equilibrium between the preference (P) locus and all other loci in the system. If the preference allele P2 is established it reaches a polymorphic equilibrium across the system (under both female and male mate choice), resulting in some premating isolation between P1T1 and P2T2 individuals.
In the assortative mating model both populations are initially fixed for the random mating allele B1. Nonrandom mating occurs through the introduction of the assortative mating allele B2, which causes individuals to prefer mates that share their trait at the T locus (self-referent phenotype matching, see Hauber and Sherman 2001). Assortative mating also functions via preferences that work in essentially the same way as in the female and male choice models above. With female mate choice, for example, females with the genotype B2T1 prefer males with the trait T1, whereas females with the genotype B2T2 prefer males with the trait T2. Females are 1 +α2 times as likely to mate with males that they prefer in the female choice model, whereas in the male choice model males are 1 +α2 times as likely to court females that they prefer.
As in the toy models of male and female mate choice above, males in the male choice reinforcement models are assumed to put equal energy into courtship regardless of whether they have a preference, and in both models all females are assumed to have equal mating success (there is no direct selection on female preferences). Strict polygyny is thus assumed. Specific equations expressing the frequency of each type of mated pair for female mate choice, under both the preference and assortative mating models, can be found in equation (1) of Servedio 2000, where ak=ck= 1 +αk and αk= 0 when k= 1 for the assortative mating model. For male mate choice under the preference model the equations for the frequency of mated pairs at the preference and trait loci when α1≠ 0 can be found in equations (2) through (5) in Servedio and Lande (2006), where af= 0 and for equation (2)am=α2, d= 1 if (1) i is odd and j is between 1 and 4 or between 9 and 12 inclusive or (2) i is even and j is between 5 and 8 or 13 and 16 inclusive, and d= 0 otherwise. Parallel equations can be constructed when α1 0 (not shown). For the assortative mating model with male mate choice, using these same equations from Servedio and Lande (2006), af= 0 and for equation (2)am=α2, and if j is between 5 and 8 or 13 and 16 inclusive, d= 1 if i and j are odd or if i and j are even, and d= 0 otherwise.
TWO-ISLAND MODELS—NUMERICAL ANALYSIS
Computer simulations of these models were written in C; the simulations step through the life cycle to determine changes in genotype frequencies resulting from the exact recursion equations for each model. The genotype frequencies are then translated into allele frequencies for each locus.
In general, I find that reinforcement can occur under favorable conditions via the spread of alleles for male mate choice through biased courtship. Previous work shows that with female mate choice, reinforcement is restricted (occurs under some conditions but not others) with a preference model, whereas it always occurs with an assortative mating model that includes local adaptation (Servedio 2000); this appears to be true of male choice as well. I provide more details of the dynamics of the spread of alleles causing reinforcement, as well as equilibrium results.
Dynamics
Analyses were first performed to compare the rate of spread of an allele causing reinforcement (P2 for the preference model or B2 for the assortative mating model) through female versus male mate choice. In both the preference model (Fig. 4A, when P1 individuals express no preference, i.e., the preference strength α1= 0) and the assortative mating model (Fig. 4B), the genes causing reinforcement via male choice spread at a slower rate than the genes causing reinforcement via female choice, but the differences are very slight. Figure 4B confirms that, for both male and female mate choice, although an assortative mating gene will evolve in the absence of selection against hybrids (via preferences for locally adapted trait alleles, see Kirkpatrick and Servedio 1999; Servedio 2004), selection against hybrids (sE > 0) increases its rate of spread. The dynamics of the preference model become complicated when the preference allele P1 expresses a preference for T1 males (i.e., when the preference strength α1 > 0); in this case the initial equilibrium (before the preference allele P2 is introduced) differs between the male and female mate choice models. These differences make it difficult to assess whether reinforcement occurs more easily in the male versus female mate choice model, although under some conditions reinforcement occurs more easily (requires weaker selection against hybrids) with male rather than with female mate choice (not shown).
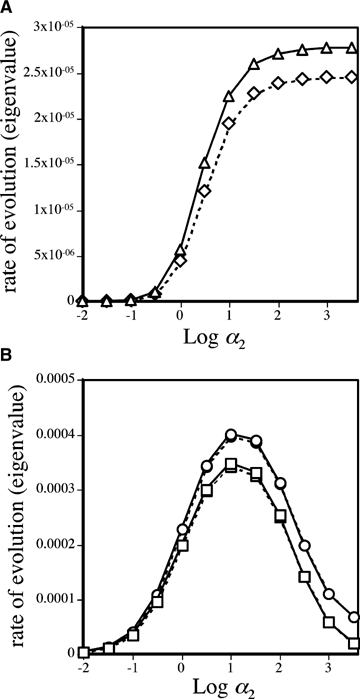
Rate of spread of the nonrandom mating allele, leading to reinforcement. The rate of spread is shown as the eigenvalue estimated (using P2 as an example) as 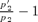 , where p2 andp′2 are the frequencies of P2 from subsequent generations close to the p2= 0 equilibrium point, taken when estimates of the eigenvalues calculated from multiple allele frequencies have stabilized (see Servedio 2000 for the exact procedure used). (A) Rate of spread of the P2 allele in the preference model. Parameter values are m= 0.001, st= 0.1, and sE= 0.4. The P1 allele causes random mating (α1= 0). Triangles (solid lines) represent reinforcement via female mate choice and diamonds (dashed lines) represent reinforcement via male mate choice. (B) Rate of spread of the B2 in the assortative mating model. Parameter values are m= 0.001 and st= 0.1. Solid lines represent reinforcement via female mate choice and dashed lines represent reinforcement via male mate choice. Squares show values when sE= 0 and circles show values when sE= 0.1.
, where p2 andp′2 are the frequencies of P2 from subsequent generations close to the p2= 0 equilibrium point, taken when estimates of the eigenvalues calculated from multiple allele frequencies have stabilized (see Servedio 2000 for the exact procedure used). (A) Rate of spread of the P2 allele in the preference model. Parameter values are m= 0.001, st= 0.1, and sE= 0.4. The P1 allele causes random mating (α1= 0). Triangles (solid lines) represent reinforcement via female mate choice and diamonds (dashed lines) represent reinforcement via male mate choice. (B) Rate of spread of the B2 in the assortative mating model. Parameter values are m= 0.001 and st= 0.1. Solid lines represent reinforcement via female mate choice and dashed lines represent reinforcement via male mate choice. Squares show values when sE= 0 and circles show values when sE= 0.1.
Equilibrium analyses and long-term dynamics
Other analyses address longer-term dynamics. In the preference model, I assess the equilibrium value of the preference allele P2 under male and female mate choice in the case in which individuals with the preference allele P1 mate at random (α1= 0; this assures that the initial equilibria under male vs. female mate choice are identical). Although the rates of evolution via male and female mate choice, measured by the eigenvalues, are similar, and although the equilibrium values under both models are small, the equilibria are substantially lower under male mate choice than under female mate choice (Fig. 5). Male mate choice therefore appears to be a significantly less-potent mechanism of reinforcement in this particular case.
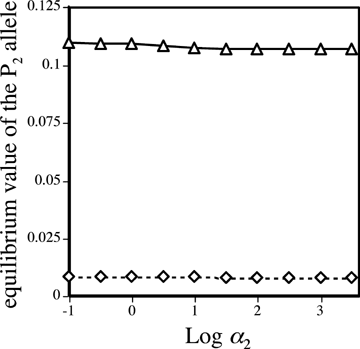
Equilibrium values of the P2 allele under male and female mate choice. Parameter values are m= 0.001, st= 0.1, sE= 0.4, and α1= 0. Triangles (solid lines) represent reinforcement via female mate choice and diamonds (dashed lines) represent reinforcement via male mate choice.
In the assortative mating model reinforcement always occurs under both male and female mate choice (the assortative mating allele B2 always spreads to fixation at equilibrium), so I examine longer-term dynamics by assessing how many generations it takes for an allele causing premating isolation to reach a value an order of magnitude above its starting frequency. I find that evolution continues to occur somewhat more rapidly under female mate choice than under male mate choice (not shown), although the differences are very small (indistinguishable on the scale of the previous figures).
CONTINENT-ISLAND MODEL—ASSUMPTIONS
I also compare reinforcement via female versus male mate choice in the context of a continent-island model that assumes weak selection. This allows a comparison of the two models using analytical means. A “preference” model, as opposed to an “assortative mating” model was used for this analysis (for comparisons of the behavior of a preference vs. and assortative mating model in a continent-island context see Servedio 2000, 2004).
The assumptions of this preference model are identical to those of the two-island preference model above, where population 1 is now a source (“continental”) population, contributing migrants unidirectionally to population 2 (now the “island” population). Specifically, as in the two-island model, I assume that the display trait is expressed in both males and females (allele T2 is favored on the island in both sexes with coefficient st). At the preference locus the ancestral allele P1 causes a preference (of strength 1 +α1) for trait T1 in the opposite sex, whereas the derived allele P2 causes a preference (of strength 1 +α2) for the trait T2. Female preferences are again involved directly in mate choice, whereas male preferences are expressed in biased courtship; strict polygyny is once more assumed. The background loci M and N interact to cause low hybrids fitness in the same manner described above for the two-island model.
The island is assumed to have diverged from the continent at the trait and background loci prior to secondary contact (the island has a high frequency of the trait allele T2 and the background alleles N2 and M2). The continent is likewise assumed to have a high frequency of the trait allele T1 and the background alleles M1 and N1. I assume that the continental population predominantly carries the preference allele P1, but also has some small frequency of the preference allele P2 (this might occur if the preference were polymorphic at equilibrium, as in the sexual selection models above, or if there were recurrent mutation at the preference locus). I ask whether the preference allele P2 will increase on the island, causing premating isolation between the continent and island populations.
Kirkpatrick and Servedio (1999) also performed an analysis of reinforcement by female preferences in a continent-island context, using the notation of Barton and Turelli (1991). They describe in full the derivation of an estimate of the difference in the frequency of a preference allele between a continent and an island population that has undergone reinforcement, using a weak selection analysis. Their analysis includes an expression of this difference in a four-locus model that is virtually identical to the female preference model used here (Kirkpatrick and Servedio 1999, eq. 30; the only difference lies in sex-limited expression of the display trait in the Kirkpatrick and Servedio model). I do not propose to redo that analysis in its entirety using male mate choice. Instead, I contrast the effects of male and female mate choice by comparing key terms that differ between the models in a weak selection approximation of the equation for the change in the frequency of a preference allele, under the conditions of quasi-linkage equilibrium (QLE). QLE conditions assume that linkage disequilibria equilibrate quickly in comparison to the rate at which allele frequencies change, as would eventually occur when selection is weak compared to recombination (e.g., Barton and Turelli 1991).
CONTINENT-ISLAND MODEL—WEAK SELECTION ANALYSIS
Dynamics and partitions of selection
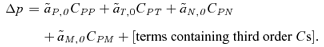 (7)
(7)The general structure of this equation, and the definitions of the  s (measures of selection) and the Cs (measures of disequilibria), are identical to those presented in equation (1). With weak selection, to obtain a first-order approximation in the selection parameters (sE, st, α1, α2), the terms containing the third-order disequilibria (the third-order Cs) will be small enough to be ignored. With weak selection and migration I find that the QLE approximations for the genetic associations (the Cs) in equation (7) are identical between the male and female mate choice models (using a first-order approximation in the migration rate and natural and sexual selection coefficients). Migration can also be shown to have identical effects on both the selection measures (the
s (measures of selection) and the Cs (measures of disequilibria), are identical to those presented in equation (1). With weak selection, to obtain a first-order approximation in the selection parameters (sE, st, α1, α2), the terms containing the third-order disequilibria (the third-order Cs) will be small enough to be ignored. With weak selection and migration I find that the QLE approximations for the genetic associations (the Cs) in equation (7) are identical between the male and female mate choice models (using a first-order approximation in the migration rate and natural and sexual selection coefficients). Migration can also be shown to have identical effects on both the selection measures (the  s) and the genetic associations (the Cs) between the models. Natural and sexual selection, on the other hand, will cause differences in the selection measures (the
s) and the genetic associations (the Cs) between the models. Natural and sexual selection, on the other hand, will cause differences in the selection measures (the  s) between the models. Because I am only interested in these differences, I can therefore compare the expressions for the
s) between the models. Because I am only interested in these differences, I can therefore compare the expressions for the  s in equation (7) by deriving them for male and female mate choice using the fitness equations in Appendix 2 (note that these fitness equations exclude the effects of migration, which will act identically in both types of reinforcement model).
s in equation (7) by deriving them for male and female mate choice using the fitness equations in Appendix 2 (note that these fitness equations exclude the effects of migration, which will act identically in both types of reinforcement model).
As described for the toy models of sexual selection above, preferences in the reinforcement model can once again evolve via two forces, direct selection, which acts on the preference locus specifically, or indirect selection, which acts on other loci in the system. As described in equations (2) and (3) above, direct selection is caused by selection on the preference locus, measured by 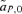 , whereas indirect selection is caused by selection at the other loci, measured in the reinforcement model by
, whereas indirect selection is caused by selection at the other loci, measured in the reinforcement model by 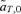 ,
, 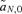 , and
, and 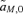 .
.
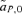 , between the female and male mate choice reinforcement models, assuming weak selection. I find that for female mate choice selection on the preference locus,
, between the female and male mate choice reinforcement models, assuming weak selection. I find that for female mate choice selection on the preference locus, 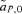 , is exactly equal to zero, whereas with male mate choice, although to first order in the natural and sexual selection coefficients
, is exactly equal to zero, whereas with male mate choice, although to first order in the natural and sexual selection coefficients 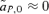 , to the second order
, to the second order
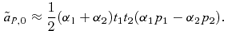 (8)
(8)In the scenario of reinforcement on an island with weak selection, if the preference allele P2 is uncommon on the continent, it is likely to be rare on the island at QLE (see, e.g., Kirkpatrick and Servedio 1999 table 1—the value on the island is only slightly different from the continental value). When the preference strength of P1 males, α1, is similar to the preference strength of P2 males, α2, expression (8) is therefore likely to be positive (because p1 will be big and p2 will be small). This will tend to make reinforcement on an island stronger with male mate choice than female mate choice.
This positive selection for male preference allele P2 contrasts with expression (4) for male mate choice in a simple polygyny scenario, for which, to the second order in the natural and sexual selection coefficients, 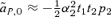 . A comparison of this approximation with expression (8) shows that they are identical in the case in which the preference strength of P1 males α1= 0; the difference in sign is solely due to the presence of a preference in P1 males. When the P1 allele represents random mating (α1= 0), term (8) will therefore tend to make reinforcement on an island weaker with male mate choice than female mate choice.
. A comparison of this approximation with expression (8) shows that they are identical in the case in which the preference strength of P1 males α1= 0; the difference in sign is solely due to the presence of a preference in P1 males. When the P1 allele represents random mating (α1= 0), term (8) will therefore tend to make reinforcement on an island weaker with male mate choice than female mate choice.
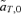 , also differ between the models of reinforcement by male and female mate choice. For female mate choice,
, also differ between the models of reinforcement by male and female mate choice. For female mate choice,
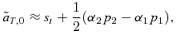 (9)
(9)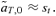 (10)
(10)For the models of female and male mate choice under polygyny described above, the first-order approximations of selection on the trait in expressions (5) and (6) are 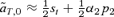 and
and 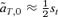 , respectively. These approximations correspond exactly to (9) and (10) when natural selection at the T locus occurs in one sex instead of two (accounting for the factors of one-half), and when there is no preference from allele P1 (α1= 0). When the preference allele P1 codes for random mating (α1= 0), the second term in (9) will be positive, tending to cause more preference divergence with female mate choice than male mate choice. In contrast, with similar preference strengths of the P1 and P2 preference alleles (similar α1 and α2, and with a low frequency of P2 on the island), the second term in (9) will tend to be negative, causing reinforcement to be a stronger effect with male mate choice than female mate choice.
, respectively. These approximations correspond exactly to (9) and (10) when natural selection at the T locus occurs in one sex instead of two (accounting for the factors of one-half), and when there is no preference from allele P1 (α1= 0). When the preference allele P1 codes for random mating (α1= 0), the second term in (9) will be positive, tending to cause more preference divergence with female mate choice than male mate choice. In contrast, with similar preference strengths of the P1 and P2 preference alleles (similar α1 and α2, and with a low frequency of P2 on the island), the second term in (9) will tend to be negative, causing reinforcement to be a stronger effect with male mate choice than female mate choice.
The first-order approximations for selection at the background loci, 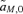 and
and 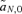 , are exactly equivalent between the male and female mate choice models. The loci causing hybrid incompatibilities are therefore not expected to affect the male and female mate choice models very differently and thus are not considered in this analysis, which is focused on assessing differences between the models.
, are exactly equivalent between the male and female mate choice models. The loci causing hybrid incompatibilities are therefore not expected to affect the male and female mate choice models very differently and thus are not considered in this analysis, which is focused on assessing differences between the models.
To the first-order approximation, the differences between the change in the preference locus in one generation at QLE in the models of reinforcement by male and female mate choice can therefore be summarized by the presence of the term  in the model of female mate choice versus the term stCPT in the model of male mate choice (from eqs. 7, 9, and 10). Both these effects and that from the second-order approximation of selection on the preference,
in the model of female mate choice versus the term stCPT in the model of male mate choice (from eqs. 7, 9, and 10). Both these effects and that from the second-order approximation of selection on the preference, 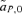 , will tend to make reinforcement a stronger effect with male mate choice than with female mate choice when P1 and P2 individuals have similar strengths of preferences (α1≈α2), due to sexual selection driven by the characteristic continental preference allele P1. When P1 individuals have no preference (α1= 0), a comparison of the reinforcement models behaves very similarly to a comparison of the sexual selection models discussed earlier in this article; under these conditions reinforcement is a stronger effect with female mate choice.
, will tend to make reinforcement a stronger effect with male mate choice than with female mate choice when P1 and P2 individuals have similar strengths of preferences (α1≈α2), due to sexual selection driven by the characteristic continental preference allele P1. When P1 individuals have no preference (α1= 0), a comparison of the reinforcement models behaves very similarly to a comparison of the sexual selection models discussed earlier in this article; under these conditions reinforcement is a stronger effect with female mate choice.
Equilibrium and strong selection—–numerical analyses
A larger effect of reinforcement under male mate choice when the continental preference allele P1 and island preference allele P2 have similar preference strengths (α1≈α2) can be confirmed under both weak and strong selection by numerical simulations of the exact recursion equations (not shown). The higher rate of preference evolution under male choice also corresponds to a higher frequency reached by a male preference allele than by a female preference allele at equilibrium (e.g., Fig. 6, circles). Reinforcement is thus stronger via male choice under these conditions in its eventual evolutionary outcome.
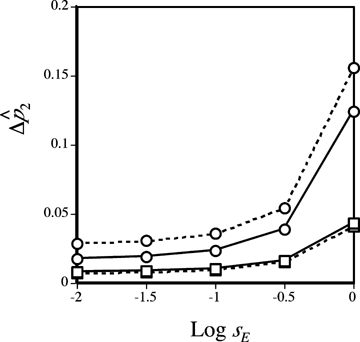
Reinforcement via male versus female mate choice on an island. Plotted points show the difference 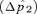 between the frequency of P2 on the island at equilibrium
between the frequency of P2 on the island at equilibrium 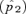 and the frequency of P2 on the continent (in this case 0.1); this provides a measure of the amount of reinforcement. The T1N1M1 genotype is assumed to be fixed on the continent. The island starts the simulation with the frequency of the genotype P1T1N1M1= 0.1 and the frequency of genotype P1T2N2M2= 0.9 (results are robust to changes in the starting frequency provided the N2M2 genotype is high on the island). See Kirkpatrick and Servedio 1999 for a full description of comparable simulations. Migration occurs at rate m= 0.001 from the continent to the island, st= 0.5 and α2= 0.2 (qualitatively similar results are found with weaker selection and preferences, e.g., st= 0.01 and α2= 0.005). Solid lines show the equilibrium frequency of the P2 allele when reinforcement occurs via female mate choice and dashed lines show the equilibrium frequency of the P2 allele when reinforcement occurs via male mate choice. Circles show the case in which α1=α2 and squares show the case in which α1= 0.
and the frequency of P2 on the continent (in this case 0.1); this provides a measure of the amount of reinforcement. The T1N1M1 genotype is assumed to be fixed on the continent. The island starts the simulation with the frequency of the genotype P1T1N1M1= 0.1 and the frequency of genotype P1T2N2M2= 0.9 (results are robust to changes in the starting frequency provided the N2M2 genotype is high on the island). See Kirkpatrick and Servedio 1999 for a full description of comparable simulations. Migration occurs at rate m= 0.001 from the continent to the island, st= 0.5 and α2= 0.2 (qualitatively similar results are found with weaker selection and preferences, e.g., st= 0.01 and α2= 0.005). Solid lines show the equilibrium frequency of the P2 allele when reinforcement occurs via female mate choice and dashed lines show the equilibrium frequency of the P2 allele when reinforcement occurs via male mate choice. Circles show the case in which α1=α2 and squares show the case in which α1= 0.
Likewise, numerical simulations confirm that when individuals with the characteristic continental allele P1 mate at random (α1= 0), reinforcement is a stronger effect with female choice than with male choice both under weak and strong selection, both in the dynamic and in the equilibrium results (the latter shown in Fig. 6, squares).
Discussion
Male and female mate choice differs sharply under the assumptions of strict polygyny. When females have equal mating success, alleles for female preferences are not under direct selection, and so evolve via indirect selection through genetic correlations with the preferred male trait (e.g., Lande 1981, Kirkpatrick 1982). Alleles for male preferences, in contrast, do undergo direct selection under the assumptions of polygyny; male preferences cause biased courtship, which places the male preference allele disproportionately in situations in which there is high competition for mates (Servedio and Lande 2006). This direct selection against male preferences could presumably be countered successfully by indirect selection favoring male preferences, allowing male mate choice to evolve. I explore two situations that could allow this male preference evolution, (1) when viability selection favors the female trait preferred by males, and (2) when male preferences are involved in species recognition and evolve through the process of reinforcement. Both of these cases are examined using both the notation of Barton and Turelli (1991), which allows unique biological insights, as well as through computer simulation. I also directly compare male mate choice to female mate choice under each set of assumptions.
DIRECT AND INDIRECT SELECTION IN MALE AND FEMALE MATE CHOICE
Several insights result from the comparison of male and female mate choice in the situation in which viability selection favors a display trait. When a trait that is preferred by the opposite sex also increases viability, the net selection placed on that trait is always positive, and the trait will always spread. A preference for such a trait is therefore always favored by indirect selection, through its genetic association with the trait; offspring of individuals with the preference tend to inherit the high fitness trait as well (e.g., Lande 1981; Kirkpatrick 1982). In the situation of female mate choice under polygyny, indirect selection is the sole determinant of the evolution of a preference allele. Female preferences for male traits that improve viability will therefore always spread (until a line of equilibrium is reached in the haploid case, Kirkpatrick 1982). Male preferences, on the other hand, undergo both direct and indirect selection when polygyny is assumed. Although indirect selection under this viability regime favors the spread of the male preference, direct selection always acts against it.
The fate of a male preference allele is therefore determined by the balance between direct selection (a negative effect) and indirect selection (a positive effect). The positive effects of indirect selection can sometimes outweigh the negative effects of direct selection, but simulations indicate that the evolutionary gains of the male preference allele in this situation are very small. Male preference evolution can therefore generally not be explained by viability selection favoring preferred female traits. This result is consistent with that of Kirkpatrick and Barton (1997), who showed, for the case of female preferences, that direct selection will generally outweigh indirect selection in magnitude. The result for traits conferring a viability advantage contrasts sharply, however, with the situation of males preferring females that have higher fertility. Servedio and Lande (2006) showed that in this case, the sign of direct selection on male preferences can itself be reversed, provided that the fertility benefit of the preferred trait is strong enough. Male preferences can thus increase by direct selection if males prefer a trait that confers high fertility on females, but can at most increase only slightly due to indirect selection (and be opposed by direct selection) if males prefer a trait that confers high female viability.
Parallel analyses of male and female mate choice also yield a comparison of the strength of indirect selection acting in each case. In the scenario of female mate choice for a male trait, selection on the trait is a combination of viability selection (assumed here to favor the preferred trait) and sexual selection. Male mate choice, however, does not place sexual selection on the female trait. Selection on the female trait arises solely from the viability selection that affects it. This is a direct consequence of the assumption of polygyny; if females control mating, and, as assumed here, have equal mating success regardless of the display traits they carry (provided that they survive until mating), sexual selection is not actually placed on those display traits. Because male traits during female choice are favored by viability and sexual selection, but female traits during male choice are only favored by viability selection, indirect selection favoring female preferences is stronger than indirect selection favoring male preferences.
BIOLOGICAL SIMPLIFICATIONS AND COMPLICATIONS
The results of these analyses depend upon a number of assumptions of the model. One of the most important of these is strict polygyny. Both the male and female mate choice models used here assume a very pure form of polygyny, where choice is ultimately by females and every female has equal mating success (see, e.g., Kirkpatrick 1982). This obviously includes many simplifying assumptions that may not be met in nature (e.g., Andersson 1994). Females, for example, are not assumed to accrue benefits simply by receiving courtship, as would be the case when males confer nuptial gifts (reviewed in Andersson 1994; Vahed 1998; but see Vahed 2007), or when it is beneficial to mate quickly (reviewed in Reynolds and Gross 1990; Wong and Candolin 2005). Likewise, females are not assumed to pay a cost of excessive courtship due to male harassment (e.g., Magurran and Seghers 1994; Watson et al. 1998; Schlupp et al. 2001; Bateman et al. 2006; reviewed in Clutton-Brock and Parker 1995; but see Head and Brooks 2006). The assumption of strict polygyny could potentially be relaxed in several different ways. It is possible, for example, that females that are courted more often are more likely to acquire a mate. This case is examined in Servedio and Lande (2006), who find a threshold advantage, over which male preference alleles will increase instead of decrease in frequency within a generation.
As discussed above, females may also differ in their fecundity; this can be a trait that males base their mate choice upon. Assuming that males prefer traits that honestly indicate higher female fecundity is mathematically identical in this simple two-locus framework to the assumption that preferred females mate more often, and thus also can cause male preferences to evolve if the fecundity advantage is over a certain threshold (Servedio and Lande, 2006). Chenoweth et al (2006) consider male choice when female quality varies, but assume that quality trades off with the strength of the signal; energy put into display can thus not be put into fecundity. They find that these assumptions can lead to the evolution of stabilizing male preferences for female display traits. Variation in female quality is also an important component of several models that predict the evolution of male choice and sex role reversal (e.g., Parker 1970; Trivers 1972; Forsberg 1987; Owens and Thompson 1994; Johnstone et al. 1996).
Several other biological simplifications are also included in the toy sexual selection models. Servedio and Lande (2006) consider the effects of a number of these on the outcome of the male mate choice model. They find, for example, that pleiotropy between male traits and female traits or male preferences and female preferences during mutual mate choice can allow the evolution of male preferences under certain circumstances. They also show the degree to which costs to preferences (e.g., Byers et al. 2005) can further depress the evolution of male preferences (see also Deustsch and Reynolds 1995; Johstone 1997). Direct selection favoring male preferences occurs in another model variant analyzed by Servedio and Lande (2006), which assumes that males with a preference can have greater overall courtship output than males that mate at random. There are, however, many different ways that direct selection can be assumed to benefit male and female preferences. In general, direct selection on mating preferences will have a stronger ultimate effect on preference evolution than indirect selection on preferences (Kirkpatrick and Barton 1997). If direct selection benefiting male preferences were layered on top of the toy model used in this article, by simply assuming a viability benefit to the male preference allele, it would tend to counter the direct selection against male preferences that results from the competitive interactions between males in the model. The net result would simply depend upon the strength of the direct selection benefit assumed.
An additional assumption of the toy models is that all males with a preference behave identically and have identical abilities. This leads to the result that all males with a preference suffer identically from the fact that they are placing themselves in a situation of high competition. More complex models, that allow the quality of males to vary, yield different results. Fawcett and Johnstone (2003) and Härdling and Kokko (2005), for example, show using game theory models that males with low-quality and low courtship ability do best courting low-quality females, for whom there is little competition among males. High-quality males, with good competitive abilities, likewise benefit by courting high-quality females. This leads to assortative mating based on quality in these models. Ihara and Aoki (1999) also allowed males to differ in quality, basing this on their amount of available resources. The polygyny version of their model, which assumed that female mating success was based partially on the resources available to their mated male, predicted that coevolution of male preferences and female traits would be restricted compared to the case of monogamy.
SPECIES RECOGNITION VIA REINFORCEMENT
In addition to the situation in which males prefer a trait that reflects female viability, male preferences may also be expected to be favored when they allow males to preferentially court members of their own species. Such preferences could potentially be recruited into species recognition through the process of reinforcement. Under reinforcement, selection against hybrids can place indirect selection upon mating preferences for conspecifics, causing premating isolation to evolve (e.g., Dobzhansky 1937). Previous work on reinforcement has concentrated on the evolution of female mating preferences (e.g., Liou and Price 1994; Kelly and Noor 1996; Servedio and Kirkpatrick 1997; Kirkpatrick and Servedio 1999; Kirkpatrick 2000; Servedio 2000, 2004; Servedio and Sætre 2003).
I address reinforcement by male mate choice using both two-island and continent-island models. The analyses in two-island models demonstrate through numerical simulations that reinforcement can occur via male mate choice; this, to my knowledge, is the first theoretical demonstration of reinforcement via male courtship alone. When the ancestral condition is random mating, reinforcement occurs via male choice slightly less rapidly than if it occurs via female mate choice. This result holds over both a two-allele “preference” model and a one-allele “assortative mating” model. In the preference model, the equilibrium value of male preferences under these conditions can be substantially lower than the corresponding equilibrium value for female preferences. When the ancestral condition is a preference for one type of trait, and reinforcement occurs by the spread of a novel preference (e.g., both α1 and α2 > 0), reinforcement may, however, occur under broader conditions with male mate choice than female mate choice. This may be unlikely, however, because it may be difficult to maintain or evolve an ancestral male preference for an “arbitrary” trait, for the reasons described in the first half of the article.
The weak selection analyses of the continent-island models of reinforcement concentrate on pinpointing differences between the male and female mate choice models, specifically those that affect the change in the frequency of a preference allele in a generation under the conditions of QLE. The selection measures 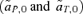 that result from these analyses show clear parallels with those from the models of male versus female mate choice in the first half of this article; the differences in the reinforcement models can be accounted for without reference to selection through the loci causing hybrid incompatibilities. In the continent-island model, reinforcement can be shown to occur more strongly through female choice than male choice when the only preference in the system is specifically for mates with the characteristic island phenotype, and prior to the evolution of this preference mating occurs at random. In this situation, as in the basic model of sexual selection presented earlier, there is direct selection against the spread of a male courtship preference. When the ancestral condition is not random mating, but a preference for mates with the trait characteristic of the continent, it can again be shown through both weak selection analyses and computer simulation that reinforcement occurs more easily through male preferences. As in the two-island model, these ancestral conditions may be unlikely for male preferences if traits are “arbitrary.” In this case, however, direct selection against the new, and rare, male preference that causes reinforcement is outweighed by direct selection against the more common, ancestral preference allele for continental males; the new allele should therefore spread, unless it, too, becomes too common.
that result from these analyses show clear parallels with those from the models of male versus female mate choice in the first half of this article; the differences in the reinforcement models can be accounted for without reference to selection through the loci causing hybrid incompatibilities. In the continent-island model, reinforcement can be shown to occur more strongly through female choice than male choice when the only preference in the system is specifically for mates with the characteristic island phenotype, and prior to the evolution of this preference mating occurs at random. In this situation, as in the basic model of sexual selection presented earlier, there is direct selection against the spread of a male courtship preference. When the ancestral condition is not random mating, but a preference for mates with the trait characteristic of the continent, it can again be shown through both weak selection analyses and computer simulation that reinforcement occurs more easily through male preferences. As in the two-island model, these ancestral conditions may be unlikely for male preferences if traits are “arbitrary.” In this case, however, direct selection against the new, and rare, male preference that causes reinforcement is outweighed by direct selection against the more common, ancestral preference allele for continental males; the new allele should therefore spread, unless it, too, becomes too common.
These models of reinforcement clearly indicate that the combination of sexual selection for locally adapted alleles (see, e.g., Kirkpatrick and Servedio 1999; Servedio 2004) and selection against hybrids during reinforcement can overcome direct selection against male preferences to drive the evolution of species-specific male courtship. Reinforcement can thus be added to the list of situations under which male mate choice can evolve. Furthermore, both female and male mating behavior can therefore diverge after secondary contact between incipient species under favorable conditions. Reinforcement may thus be expected via both of these mechanisms, although the selection for male mate choice may be expected to diminish as premating isolation via female mate choice accumulates, and vice versa.
RELATIONSHIP TO GOOD GENES MODELS
The evolution of mating preferences during reinforcement is in some ways related to good genes models of mate choice. In reinforcement models, the choosing sex ends up with the highest fitness if it avoids the production of hybrid offspring. One way to potentially produce hybrid offspring is to mate with a hybrid; because hybrids have low fitness this is similar in its effect to the outcome of mating with a poor condition mate in a good genes scenario. Reinforcement differs from good genes, however, in that another way to produce a hybrid is to simply mate with an individual from the wrong population; these individuals do not themselves have low fitness.
The toy sexual selection models of male and female mate choice from the first half of the article also relate to good genes models in that the display trait directly reflects high viability; individuals that mate with these display carriers therefore inherit the high fitness trait for their offspring. This increases the indirect selection that favors the preference in both the female and male mate choice models. Typically, however, good genes models do not assume that the trait itself also causes high viability, but assume that the trait is an indicator of high quality at other loci (e.g., Kirkpatrick 1986; Pomiankowski 1988; Tomlinson 1988; reviewed in Andersson 1994). The outcomes of these models vary based on several details, including how genes for quality may become associated with the indicator trait. The “good genes” process in all of these models ultimately depends upon indirect selection on the preference caused originally by selection favoring the high viability genes at the loci that determine quality. This indirect selection is passed through two links of genetic associations, one between the quality locus and the indicator locus and another between the indicator locus and the preference. It is very likely that under certain assumptions, a good genes process could cause increases in the evolution of male preferences under this same mechanism.
IMPLICATIONS
The empirical literature on male mate choice and courtship preferences during polygyny remains patchy (for reviews see Amundsen 2000; Bonduriansky 2001). Theoretical work in this article and in Servedio and Lande (2006) makes some clear predictions concerning under which biological scenarios male mate choice would be expected (e.g., for female traits that indicate high fertility, when increased courtship improves the chances females will mate, when preferences increase male courtship effort, in some cases when preferences act during species recognition), versus when its evolution would be minimal at best (e.g., when preferences are for “arbitrary” traits or for traits that increase female viability and when preferences are not correlated with courtship effort). Male mate choice for “arbitrary” traits may ultimately act as a potential indicator that reinforcement may have occurred; such preferences are not expected to evolve with male mate choice outside of a speciation context, whereas the presence of species-specific preferences in females is confounded by the possibility that they have evolved due to sexual selection in allopatry. More empirical data and synthetic reviews across taxa will ultimately be needed to evaluate all of these predictions.
Associate Editor: J. Wolf
ACKNOWLEDGMENTS
I would like to thank A. Chunco, S. Diamond, H. Olofsson, J. Wolf, and two anonymous reviewers for comments on the manuscript and S. Otto for the suggestion that male mate choice for arbitrary traits may provide an indicator of reinforcement. MRS was funded by the National Science Foundation Grants DEB-0234849 and DEB-0614166 and was supported in this work by the National Evolutionary Synthesis Center (NESCent), NSF #EF-0423641.
Appendices
Appendix 1.
FITNESS EQUATIONS FOR FEMALE MATE CHOICE FOR A TRAIT FAVORED BY SELECTION
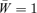 , here and for the other fitness equations below, so equation (A1) is equal to the equation for relative fitness):
, here and for the other fitness equations below, so equation (A1) is equal to the equation for relative fitness):
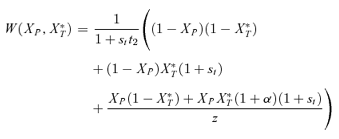 ((A1))
((A1))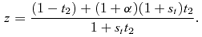
Equation (A1) is simply a slight modification of the fitness equation in Barton and Turelli (1991, table 4), which is in turn a reanalysis of the model of Kirkpatrick (1982). The notation has here been modified slightly to match the main text, and selection in equation (A1) has been changed to favor allele T2, instead of act against it.
Equation (A1), and the subsequent equations in these Appendices, can be used to calculate the  terms present in equation (1) of the main text. To calculate the
terms present in equation (1) of the main text. To calculate the  s, the specific fitness equation for a model (e.g., eq. A1) is set equal to a generic equation for fitness in terms of the
s, the specific fitness equation for a model (e.g., eq. A1) is set equal to a generic equation for fitness in terms of the  s, Cs (see eq. 1) and a function of the Xs (Barton and Turelli 1991). Terms are then matched to extract expressions for the
s, Cs (see eq. 1) and a function of the Xs (Barton and Turelli 1991). Terms are then matched to extract expressions for the  s for the particular model under consideration. The exact procedure for doing this is thoroughly described in appendix B of Kirkpatrick and Servedio (1999).
s for the particular model under consideration. The exact procedure for doing this is thoroughly described in appendix B of Kirkpatrick and Servedio (1999).
FITNESS EQUATIONS FOR MALE MATE CHOICE FOR A TRAIT FAVORED BY SELECTION
 ((A2))
((A2))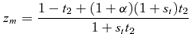
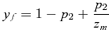
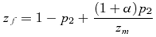
Appendix 2.
FITNESS EQUATIONS FOR REINFORCEMENT VIA MALE AND FEMALE MATE CHOICE
Fitness equations can be written for the scenario of reinforcement described in the continent-island model in the text, for both female mate choice and male mate choice. These equations exclude migration, and so describe fitness in a population due to natural selection and sexual selection alone. Migration does have a very important effect in these models (e.g., Kirkpatrick and Servedio 1999) but that effect can be shown to be identical in the male and female mate choice reinforcement models, so it does not need to be considered in this weak selection analysis, the purpose of which is only to pinpoint differences between the models of reinforcement in male versus female mate choice. The equations below, like those in Appendix 1, account for changes throughout the life cycle in allele frequencies, so the various stages of the life cycle do not need to be accounted for independently in equation (7).
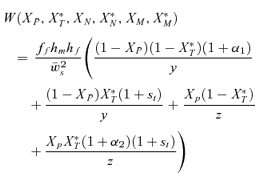
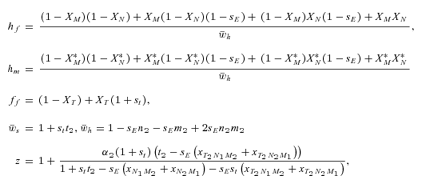
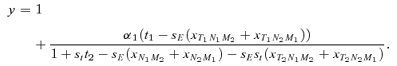
The Xs are defined as consistent with the definitions in Appendix 1, where expression in males is designated by an asterisk. The components in the numerators of the fitness equation are derived from first principles, whereas the normalizations in the denominators are derived from writing out the full recursion equations for viability selection and mating, following the assumptions described in the main text. The expressions z and y are normalizing coefficients that account for the assumption that female fitness is independent of her genotype at the preference locus. The expressions hf and hm describe fitness at the loci that cause low hybrid fitness, in females and males, respectively, whereas ff describes fitness due to viability selection at the trait locus T in females. The terms  and
and 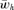 denote the mean fitness from selection favoring the trait T2 and selection against hybrids, respectively. Lower case designations of alleles represent their frequencies whereas lower case xs represent the frequencies, in zygotes, of the genotype named in the subscript.
denote the mean fitness from selection favoring the trait T2 and selection against hybrids, respectively. Lower case designations of alleles represent their frequencies whereas lower case xs represent the frequencies, in zygotes, of the genotype named in the subscript.
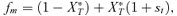
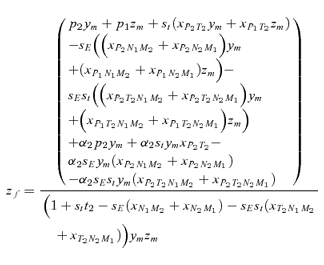
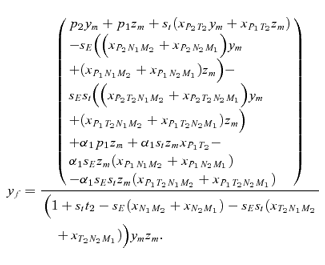
Here zm and ym are normalizing coefficients that account for the fact that males have an equal amount of energy to put into courtship, whereas zf and yf account for the fact that all female preference genotypes have equal fitness.




