Do Insurance Companies Possess an Informational Monopoly? Empirical Evidence From Auto Insurance
ABSTRACT
This article investigates the impact of policyholder tenure on contractual relationships in nonlife insurance markets. For a sample of auto insurance policies, we find that average risk decreases with policyholder tenure, but the effect is entirely due to the impact of observable information. We reject the hypothesis that the incumbent insurer is privately learning faster about quality of their policyholders. We highlight the importance of a public signal regarding policyholders' claims experiences and suggest alternative explanations for the unconditional relationships in the data.
INTRODUCTION
In the United States, approximately one-quarter of auto insurance premiums are used to pay expenses related to actuarial and underwriting activities (Insurance Information Institute, 2010), which help insurance companies set prices and manage risk. These activities help reduce natural information asymmetries between customers and the owners and managers of an insurance company. Indeed, the theoretical justification for the existence of many financial intermediaries relies on the intermediary capturing the scale economies inherent in the production of information. Throughout the course of repeated underwriting and occasional claims settlement, insurance companies produce valuable information concerning the risk profiles of their policyholders. Natural follow-on questions concern the availability and consequences of this information once it has been generated by a particular intermediary. Does this information become the proprietary property of the incumbent insurer? And could it create a subsequent information monopoly that destroys policyholder welfare?
This article addresses these questions empirically by testing two hypotheses generated from models of asymmetric learning and policyholder lock-in. These models assume repeated contractual interactions and a complete lack of commitment by both the insurer and the policyholder, as is common in most nonlife insurance markets, including auto insurance.1 First, if an insurance company gains an information advantage relative to its rivals, the incumbent insurer should strategically retain a larger fraction of lower risk policyholders, because these policyholders are unable to reveal their higher quality to outside competitors. As a result, the average risk of a group of policyholders will decrease as the policies age. Second, insurers will earn higher average profits on policyholders with longer tenure, because insurers use discounts to attract new customers and gradually increase prices as the information monopoly grows over time.
Using a large set of policy level data from a single Australian automobile insurer, the results strongly suggest that policyholder tenure is related to average risk. However, the relationship is driven by the effect of policyholder characteristics (e.g., the insured's age and claims history) that are easily observable by competing insurers, and the conditional relationship between risk and policyholder tenure is considerably weaker. We conclude that there is no evidence supporting the hypothesis that hidden (unobservable) information is a source of policyholder lock-in.
We draw this conclusion based on estimated claim risk and severity models that explicitly account for unobserved heterogeneity. By exploiting the occurrence of multiple claims for some policyholders during the sample period, we permit the risk distributions to vary at the policyholder level according to characteristics unobservable to us as econometricians and to competing insurers. We find that claim severity distributions do not have residual heterogeneity, meaning that we cannot reject the null hypothesis that all policyholders have the same mean claim severity, conditional on observable characteristics. For claim frequency distributions, we do find evidence of residual heterogeneity; we confidently reject the null of zero variance in the mixing distribution that determines the Poisson parameter that governs claim frequency. Importantly, however, we do not find any evidence that the level of heterogeneity varies with policyholder tenure, which we interpret as corroborating evidence that insurers are not strategically retaining a select group of low-risk policyholders.
We do observe a strong negative relationship between loss ratios—the ratio of claim costs to premium, a traditional measure of nonlife insurance company profitability—and policyholder tenure. However, we show that premiums charged by the insurance company do not systematically increase with policy age after conditioning on observable characteristics. Alternatively, the loss ratio pattern can be explained by the combination of a pricing policy that includes a fixed component in premiums and the decline in expected claim costs as policies age. Based on a fixed charge that is roughly one-third of the average premium, which is what we estimate in the data, we can closely match the empirical relationship between loss ratios and policy age. Because expected claim costs decrease so dramatically with policy age, the impact of a fixed charge becomes an increasingly large share of charged premiums, resulting in lower loss ratios. We are left with a puzzle, however, why observably less risky policyholders are more likely to persist with the insurer. In our data, the annual frequency of claims for the oldest policies is less than one-half that of the youngest policies, and the average severity of claims is about 60 percent that of the youngest policies.
Several theoretical papers have considered the potential threat of policyholder “lock-in” created by information monopoly power on behalf of an incumbent intermediary. In a nonlife insurance environment, Kunreuther and Pauly (1985) demonstrate that asymmetric learning can result in prices and profits that increase over time, as insurers utilize their subsequent monopoly power to increase their economic rents. Sharpe (1990) and Rajan (1992) generate a similar prediction in the market for loans, where lenders learn about the quality of their assets over time. These models rely on the assumption that intermediaries are unable to commit to contracts that stipulate the manner in which revealed information is used. In a similar model for the nonlife insurance market, Kofman and Nini (2006) highlight the important implication that the incumbent retains a higher share of privately known lower risk policyholders, as these are precisely the policyholders where the incumbent's monopoly power provides economic rents. This is the prediction that we fail to confirm empirically.
Conditioning on observable information is quite important when interpreting insurance premium and claims data. Although unconditional statistics are consistent with the hypothesis of asymmetric learning, the conditional tests remove the impact of publicly available information and suggest that the statistical and economic impact of asymmetric information is in fact quite small. Our conditional tests become a significant improvement over studies that use only aggregate data, such as D'Arcy and Doherty (1990) and Dionne and Doherty (1994). Furthermore, by observing ex post realizations of claims, we can compute accurate measures of risk and profitability. This is a significant improvement over the empirical work on relationship banking that uses only ex ante proxies for risk, such as Petersen and Rajan (1994) and Angelini, Di Salvo, and Ferri (1998).
Our analysis is most closely related to the work in Cohen (2012), who examines the temporal pattern of profitability in a panel of auto insurance customers of a single Israeli insurer. Cohen finds that the ratio of premiums to losses is larger for repeat policyholders, particularly for policyholders with better than average claim experience. This happens because premiums do not fall as quickly as claim costs for repeat customers with good claim experience, suggesting that the insurer earns excess profits on repeat customers. Because Cohen controls for a large set of observable characteristics, her results are consistent with asymmetric learning and monopoly power by the incumbent insurer.
One possibility for the different conclusion drawn from our results and Cohen (2012) is the prevalence of public information available to insurers in Australia.2 Like many insurance markets around the world, the Australian insurance market uses a bonus-malus scheme of tracking the claims history of insured drivers. All drivers receive a “no claims discount” (NCD) that adjusts over time based on the quantity, timing, and nature of claims made. This discount is publicly observable by all insurance companies and provides a useful mechanism for sharing information. However, as the NCD tracks only the occurrence of at-fault claims, incumbent insurers have access to additional information because they observe the entire history of all claims and claim amounts, which may provide additional information about policyholder risk. Nonetheless, one interpretation of our results is that the bonus-malus scheme, combined with other observable policyholder characteristics, removes any information asymmetry between competing insurers in Australia. In the absence of any information asymmetry, it would be expected that there would be no residual relationship between policyholder tenure and average claim risk or profitability.
Our work fits into the recent literature on testing for asymmetric information in insurance markets, which has found only weak evidence for information asymmetries between insurers and policyholders.3 Chiappori and Salanié (2000) highlight the importance of conditioning on observable attributes of policyholders and propose using the realized claim experience of policyholders to measure risk. Chiappori and Salanie (2000) find no evidence that French policyholders are more informed about their risk profile than their insurer. Abbring, Chiappori, and Pinquet (2003) focus on the experience rating structure for automobile insurance in France and find no evidence of asymmetric information. Dionne, Gouriéroux, and Vanasse (2001) find no evidence that Canadian insurance companies use deductibles to screen applicants who may be more informed about their risk profile than the insurer. Similarly, Saito (2006) fails to find evidence of asymmetric information in Japan, despite the fact that rate regulation suppresses certain attributes in setting premiums. Alternatively, Wang, Chung, and Tzeng (2008) do find evidence of asymmetric information based on the intertemporal (within policy year) deductible choice of policyholders in Taiwan's automobile insurance market. Kim et al. (2009) find that a decomposition of (optional) insurance coverage choice for South Korea's automobile insurance market also provides evidence supporting asymmetric information. One possibility for the mixed results is variation in the underwriting process that can help limit the information asymmetry between the insurance company and the policyholder. Experience rating, often implemented through bonus-malus schemes such as the NCD in Australia, can be an important component of underwriting. Our results suggest that underwriting information can also limit information asymmetries between competing insurance companies, particularly when the information is readily observable.
The data from our sample insurer do confirm a strong unconditional relationship between policyholder tenure and risk, as shown in D'Arcy and Doherty (1990) for a sample of U.S. insurers. Moreover, even conditional on observable characteristics, brand new policies appear to receive a small premium discount relative to their realized risk, suggesting some sort of intertemporal pricing strategy by the sample insurer. We conjecture that more traditional sources of monopoly power may be important in explaining these facts, such as consumer search costs. For example, Israel (2005) points out that insurance exhibits the properties of an experience good, meaning that consumers only learn slowly about the quality of the insurance product. Moreover, he finds that consumers of auto insurance do learn about the quality of their match with the insurer but that the learning is quite slow due to the slow arrival of claims. We conjecture that similar frictions likely have an important impact on the strategies of nonlife insurers and should be further explored both theoretically and empirically.
The remainder of the article is structured as follows. The next section positions and develops our empirical analysis by deriving two testable hypotheses that follow from models of asymmetric learning. The “Data and Summary Statistics” section describes our cross-sectional sample of comprehensive automobile insurance policies and their claim experience. We provide summary statistics on the unconditional relationship between policy age, claim experience, and loss ratios. The “Policy Age and Claim Risk” section tests the hypothesis regarding the conditional relationship between policy age and claim risk, and the “Policy Age, Premiums, and Profitability” section shows how the inclusion of a fixed component of premiums can explain the loss ratio pattern. The final section concludes.
THEORETICAL BACKGROUND AND TESTABLE PREDICTIONS
The theoretical models developed in Kunreuther and Pauly (1985) and Kofman and Nini (2006) yield positive empirical predictions concerning the makeup of a nonlife insurer's portfolio over time. In a repeated contracting situation where the incumbent insurer receives private signals concerning the policyholder's true risk type, an insurance company can use the private information as a source of pricing power. Given an optimal response by less informed competing insurers, the incumbent strategically offers prices that encourage less risky customers to remain with the incumbent although more risky customers are encouraged to switch to a competitor. The incumbent earns positive profits on average across the costumers that remain, and the size of the profits is directly related to the size of the information asymmetry.
Kofman and Nini (2006) show that there is a strong positive correlation between the occurrence of an insurance claim and the lapsation of a policy.4 This result is consistent with the model of asymmetric learning, as both claiming and lapsing can be thought of as endogenous events that are influenced by an unobservable risk type. The equilibrium prediction from the model is that high-risk drivers are more likely to lapse than are low-risk drivers, although both types lapse in equilibrium. Because high risks are also more likely than low risks to make a claim, the model predicts that lapsing and claiming are positively correlated in a cross-section of an insurer's portfolio. Of course, there are many reasons why we might observe a positive correlation between claiming and lapsing, so in this article we explore two additional predictions of the asymmetric learning model.
- H1: Conditional on publicly available information, insurance risk is negatively related to the age of the policy.
Risk can be defined in several manners, but insurance companies typically measure risk by a combination of claim frequency and claim severity. Claim frequency refers to the random variable capturing the number of claims a particular policy generates during a policy period, and claim severity refers to the random variable capturing the size of the claim conditional on occurrence. Empirically, we test the prediction by examining the correlation between the age of a policy and both claim frequency and claim severity, conditional on other observable variables likely to be correlated with claim risk.
- H2: Conditional on publicly available information, insurance profitability is positively related to the age of the policy.
This final hypothesis has been explored in previous empirical research. D'Arcy and Doherty (1990) show evidence of a positive relationship between the profitability of a cohort and the age of the cohort within a survey of U.S. automobile insurance companies. Conversely, Dionne and Doherty (1994) find evidence that profitability increases with premium growth for a sample of California automobile insurers, which is evidence that younger cohorts are more profitable than older cohorts. However, in both prior studies, the aggregate data omits explanatory variables that may be correlated with the age and profitability of a cohort. Because the model predicts a positive relationship between policy age and profitability created by private information, it is important to condition on characteristics observable to competing insurers to remove the influence of symmetric information. Our results highlight the influence of controlling for public information, because empirically there are strong correlations between policy age and observable characteristics that are also correlated with claim risk.
We measure profitability in two ways. First, we use the ratio of expected claim costs to charged premiums, a traditional measure of insurance profitability. Because this measure does not account for any costs other than claim costs, we also examine the charged premiums, conditional on observable underwriting characteristics. By conditioning on observable policyholder characteristics, we hope to account for differences in expected claims costs and any other source of pricing power. Our functional form assumption allows charged premiums to have a fixed component that does not vary with policyholder characteristics, so the insurer's pricing strategy is permitted to cover any fixed costs associated with insuring a policyholder.
We conclude this section by noting that the relevant null hypothesis is no relationship between the age of a policy and either average claim risk or average profitability. In the absence of any information monopoly power, standard theory provides no reason why policyholder tenure decisions should be related to policyholder risk, so we should not see any systematic relationship between tenure and average claim frequency or average claim severity.
DATA AND SUMMARY STATISTICS
Data
We use policy level data from a single Australian automobile insurer to test the empirical hypotheses. The data set is composed of all comprehensive automobile insurance policies that were in force as of July 1, 1996. Comprehensive insurance policies provide first-party protection for damage to the covered automobile, including at-fault accidents, nonfault accidents, theft, and various other perils. We have data on all claims related to these policies during the 1-year period from July 1, 1996 to June 30, 1997. Observations are heterogeneous with respect to their exposure to loss during the sample period, so we control for this difference in all empirical models. We have a single observation for each policy, and after limiting the sample to more homogeneous policies, we are left with a cross-section of 290,804 policies covering 134,699 years of exposure.6
For each policy observation, we have a large set of policyholder characteristics that are known to be correlated with expected claims costs, which we obtain from the insurer's administrative records. We observe all of the variables that would be readily available to a competing insurer to set premiums, including the policyholder's age, gender, residence, and the automobile's value, crash worthiness, and intended use. All of the characteristics are quite standard and universally used to price auto insurance, and they permit us to condition on information available to competing insurers at the time the contract was written.
Importantly, the data also include a measure of the policyholder's claim history, known as the NCD in the Australian market. Australian automobile insurance utilizes a bonus-malus pricing scheme, with prices being determined by a rating class and the policyholder specific NCD.7 The rating class is a function of the policyholder's characteristics, such as age, gender, residence, make and model of car, etc. The NCD rating takes one of 15 different levels and provides up to a 60 percent premium benefit for policyholders in the best class. In short, every policyholder begins as level 6 and improves by one step following a year without an at-fault claim and drops by two steps following a year with an at-fault claim. The data provide the NCD rating for the primary driver named on each policy at the time the contract was written.
We also observe all of the important contractual features of the policy. In the Australian auto insurance market, it is common for insurers to require a particular level of deductible. So although we restrict the sample to policies with a chosen $400 deductible, we have some variation in the level of the compulsory deductible. We observe the level of the premium charged to the policyholder as well as the number of claims made during the sample period along with their associated payments. We also observe the inception date of the policy, which permits us to account for differences in exposure during the sample period.
Table 1 presents a description of the variables included in the data set that we use as control variables in all of our empirical specifications. We separate the variables into four sections: policyholder characteristics, automobile characteristics, policy characteristics, and policy performance. The policyholder and automobile characteristics are specific to the primary policyholder and primary covered vehicle. All of these variables are considered exogenous and observable. Throughout the analysis, an important assumption is made regarding the availability of information contained in the data set. We assume that all information available in the data set is publicly available information and could not be a source of private information. This assumption is reasonable as competing insurance companies likely collect similar information; many of the variables are observed very cheaply, including the insured's NCD rating. Consequently, all of our econometric tests focus on the impact of policy age after controlling for other variables.
| Policyholder characteristics | |
| Insured age: | Age, in years, of the primary driver of the covered automobile. |
| Male: | Dummy variable indicating that the primary driver is a male. |
| Insured location: | Set of 12 dummy variables indicating insurer determined aggregation of postal codes. |
| No claims discount: | No claims discount of the primary policyholder, ranging from class 9 to class 1 for 6 consecutive years. We create a set of 13 dummy variables that combines the lowest 3 levels. |
| Automobile characteristics | |
| Vehicle age: | Age, in years, of the insured automobile. |
| Insured value: | Value, in A$1,000, of insured automobile in case of total loss. |
| Car make and model: | Set of 600+ dummy variables for the make and model of the insured vehicle. |
| Insurance category: | Insurance industry provided category indicating the crash worthiness of the automobile, converted to set of 12 dummy variables. |
| Is financed: | Dummy variable indicating that the insured automobile is financed, with the only alternative being a privately owned car. |
| Policy characteristics | |
| Policy age: | Age, in years, that the policy has been in-force, converted to a set of 15 dummy variables. |
| Days in-force: | Number of days the policy was in force during the accident period (July 1, 1996—through June 30, 97). Used to compute exposure. |
| Inception month: | Starting month of the current policy, converted to 12 dummy variables. |
| Full premium: | Total premium charged on the policy. |
| Has compulsory excess: | Dummy variable indicating a nonzero deductible imposed by the insurer. |
| Rating protection: | Dummy variable indicating that the insured selected rating protection, meaning that the NCD is not affected by an at-fault claim. |
| Policy performance | |
| N: | Number of claims on the policy incurred during the policy period. |
| Claims cost: | Total value, in A$, of claims made on the policy during the accident period. |
- Note: This table lists the variables available in the data set, including all of the control variables used in the regression models.
Unconditional Claim Risk and Profitability by Policy Age
Figure 1 displays sample averages for claim risk, premium, and profitability by policy age. As shown in the figure, the average total loss per policy decreases from around A$430 to less than A$125 as policies age over 18 years. This reflects a reduction in both claim frequency, which falls from over 12 percent per year to less than 5 percent per year, and a reduction in average claim severity, which falls from about A$3,500 per policy to less than A$2,000 per policy. The combination results in the oldest policies generating less than one-quarter of the total costs per policy than the youngest policies. The unconditional averages paint a striking picture: the oldest policies are considerably less risky than the youngest policies.
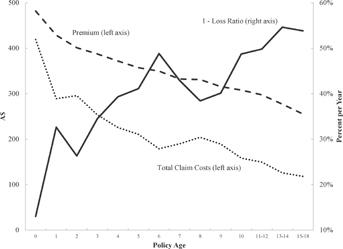
Note: This figure presents unconditional averages of total premium, total claim costs, and the loss ratio by policy age. The sample is the 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section. Premium (measured on the left axis) is the annual premium charged for a policy. Total claim costs (measured on left axis) include all payments made on all claims. The loss ratio is the ratio of total losses to total premium, and the figure plots 1–Loss Ratio (measured on the right axis), which represents the fraction of premium remaining after claim costs.
Figure 1 also shows that the average premium charged per policy also trends down with policy age, but at a slightly slower rate than claim costs, falling from just under A$500 to about A$250. As a result of the difference in slopes, the unconditional loss ratio—defined as the ratio of total claim costs to total premiums—decreases with policy age. Conversely, one minus the loss ratio, a standard measure of insurance profitability, trends up with policy age. Comparing the youngest policies with the oldest policies, the fraction of premiums remaining after claims payments increases more than fivefold, rising from just over 10 percent to more than 50 percent. These unconditional averages are consistent with the United States-based data presented in D'Arcy and Doherty (1990), who show that loss ratios decrease notably with policy age for many insurers.
The unconditional statistics are unequivocal. Expected losses decrease markedly with policy age as both the frequency of claims and the average severity of claims fall over time. Premiums also decrease over time, but at a slower rate than losses, resulting in a loss ratio that decreases with policy age. These results are consistent with a story of asymmetric learning between competing insurers: as policies age, the incumbent insurer is retaining increasingly better risk policyholders at increasingly unfair prices, with the higher risks leaving for a better premium offer at a competing insurer. However, for the story to remain attributable, even in part, to asymmetric learning, the patterns should remain after controlling for information that is publicly available to competitors. If any of the patterns can be completely explained by changes in characteristics that are observable to competitors, it cannot be private information that explains the unconditional relationships. Indeed, in the next section of the article, we show that the relationship between claim risk (both frequency and severity) and policy age can be explained by policy-level observable information, which also changes markedly with policy age.8
Summary Statistics
Panel A of Table 2 shows summary statistics for many of the control variables available in the data set, and Panel B shows how the distribution of these variables changes with policy age. As of the start of the sample, the average policyholder was about 48 years old, and slightly more than one-half of primary insured drivers were male. The average insured vehicle was roughly 10 years old and insured for up to about A$10,000. The average premium for comprehensive coverage was about A$400. Importantly, there is substantial variation in the control variables, which will be used to identify the correlations between observable characteristics and claim risk.
| Panel A: Distribution of Control Variables | |||||||
|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Minimum | 25th Percentile | Median | 75th Percentile | Maximum | |
| Insured age | 47.844 | 15.874 | 16.000 | 35.000 | 47.000 | 60.000 | 95.000 |
| Male | 0.564 | 0.496 | 0.000 | 0.000 | 1.000 | 1.000 | 1.000 |
| Vehicle age | 9.896 | 5.405 | 1.000 | 6.000 | 9.000 | 13.000 | 30.000 |
| Insured value | 10.728 | 7.793 | 1.200 | 4.500 | 9.000 | 14.500 | 45.500 |
| Has rating protection | 0.072 | 0.258 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| Is financed | 0.062 | 0.242 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| Has comp. excess | 0.021 | 0.143 | 0.000 | 0.000 | 0.000 | 0.000 | 1.000 |
| Total premium | 399.401 | 171.059 | 101.000 | 300.000 | 367.000 | 438.000 | 3,576.000 |
| Panel B: Sample Means by Policy Age | ||||||||
|---|---|---|---|---|---|---|---|---|
| Policy Age | Insured Age | Male | Vehicle Age | Insured Value | Has Rating Protection | Has Comp. Excess | Is Financed | Share With Top Rating |
| 0 | 41.938 | 0.562 | 7.376 | 14.315 | 0.094 | 0.033 | 0.137 | 0.263 |
| 1 | 44.255 | 0.563 | 8.029 | 13.223 | 0.073 | 0.016 | 0.094 | 0.340 |
| 2 | 46.151 | 0.557 | 8.992 | 11.804 | 0.084 | 0.015 | 0.063 | 0.351 |
| 3 | 47.820 | 0.555 | 9.592 | 10.782 | 0.067 | 0.016 | 0.037 | 0.380 |
| 4 | 49.598 | 0.558 | 10.283 | 9.608 | 0.064 | 0.017 | 0.019 | 0.388 |
| 5 | 50.861 | 0.562 | 10.757 | 8.561 | 0.068 | 0.018 | 0.010 | 0.400 |
| 6 | 50.984 | 0.558 | 11.670 | 7.618 | 0.075 | 0.016 | 0.009 | 0.554 |
| 7 | 52.546 | 0.575 | 12.676 | 6.647 | 0.064 | 0.016 | 0.005 | 0.581 |
| 8 | 54.460 | 0.570 | 13.088 | 5.964 | 0.041 | 0.016 | 0.004 | 0.577 |
| 9 | 56.744 | 0.578 | 13.991 | 5.058 | 0.038 | 0.017 | 0.003 | 0.614 |
| 10 | 57.590 | 0.572 | 14.369 | 4.804 | 0.032 | 0.016 | 0.001 | 0.648 |
| 11–12 | 60.090 | 0.590 | 15.802 | 4.464 | 0.025 | 0.021 | 0.001 | 0.724 |
| 13–14 | 63.051 | 0.579 | 18.091 | 3.573 | 0.017 | 0.027 | 0.001 | 0.775 |
| 15–18 | 66.034 | 0.619 | 20.021 | 3.011 | 0.015 | 0.026 | 0.001 | 0.780 |
- Note: This table presents summary statistics of policyholder characteristics and contract choice variables for the sample of 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section. Table 1 provides a description of the variables. Except for Total premium, these variables are used as control variables in subsequent models for claim frequency and claim severity.
Panel B of Table 2 shows sample means for these variables by policy age. There are major differences in observable variables between younger and older policies. The average age of policyholders and vehicles increases monotonically with policy age, and the average value of the insured automobile decreases monotonically with policy age. Older policies are more likely to be insured by males and less likely to cover cars that are financed. Finally, there is a notable improvement in the average NCD rating of policyholders with older policies; the final column shows the share of the sample with the very top NCD rating.9 Whereas only about one-quarter of new policies are for policyholders with the top rating, more than three-quarters of the oldest policies are for policyholders with the same high-quality driving history. As we will show in the next section, all of these variables are related to claim risk, and controlling for these factors dramatically reduces the independent impact of policy age.
POLICY AGE AND CLAIM RISK
Empirical Setup
Let the discrete random variable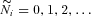 
denote the number of claims on policy i, and the random variable 
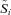denote the severity of a claim conditional on occurrence. We model N and S as independent random variables drawn from a Poisson distribution and a lognormal distribution, respectively. As in Pinquet (1997), we account for unobserved heterogeneity in both the claim risk and severity distributions. Pinquet (1997) derives the relevant statistics to test for unobserved heterogeneity and provides empirical evidence that such heterogeneity exists in French auto insurance claims. In addition to providing a sensible empirical model for claim risk, the models allow us to directly test for unobserved heterogeneity and examine its relationship with policy tenure.
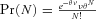, where
is the expected value of the number of claims and 
is a random variable with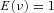 
and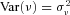 
. The random variable 
captures unobserved heterogeneity in the claim process and controls the variance of number of claims,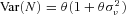 
. For partial year policies, the Poisson parameter becomes 
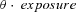, where exposure represents the fraction of the year during which the policy was in force. We permit the Poisson parameter 
to vary by observable policy characteristics by modeling it as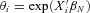 
, for a vector of coefficients 
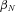and observable variables Xi. We model the random variable 
as a Gamma random variable with mean 1 and variance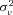 
, which leads to a negative binomial model for the number of claims:
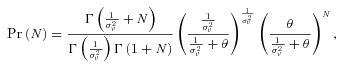
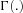denotes the gamma function. We estimate the unknown coefficients 
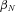and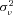 
by maximum likelihood. The estimate of 
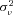provides an indication of the amount of unobserved heterogeneity in claim frequency risk. Intuitively, 
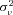is identified by the frequency of multiple claims by the same policyholder. In the special case when 
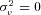, the frequency distribution reduces to a standard Poisson distribution, and the likelihood of two claims in a full year by the same policyholder is the same as the likelihood of a single claim for each of two policyholders for one-half of a year. More instances of multiple claims by the same policyholder are evidence of unobserved heterogeneity and leads to a larger estimate of 
.
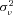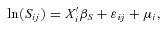
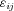is a standard regression residual assumed to be normally distributed with mean zero and variance 
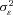. The random variable 
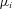is a mean zero, normally distributed random variable with variance 
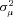that captures heterogeneity at the policyholder level; the variable varies only by i, so the random draw is constant for all claims for a given policyholder. With the normality assumptions, we can estimate the parameters 
, 
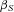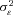, and 
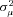by maximum likelihood. The estimate of 
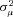provides an indication of the amount of unobserved heterogeneity in claims severity. The parameter 
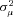is identified by the within-policyholder correlation of claim amounts, conditional on removing the effect of observable characteristics. Intuitively, if residuals from a standard regression tend to be positively correlated within the claims of a particular policyholder, there is evidence of unobserved heterogeneity that leads to a larger estimate of 
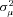.Among other observable control variables, we include various sets of dummy variables to account for the age of the policy. We use three different specifications with decreasing flexibility: (A) a complete set of unconstrained policy-age dummies, (B) a single dummy for new policies (policy age 0), and (C) no controls for policy age. We use likelihood ratio statistics to test for improvements in the fit of the model and test hypotheses about the importance of policy tenure. In each of the three specifications, we use a full set of control variables in addition to the controls for policy ages. We use dummy variables for obviously categorical variables (e.g., make and model of car), and enter continuous variables (e.g., insured age) as fourth-degree polynomials.10 In total, we run three different specifications for frequency risk and severity risk, with each specification differing only in the degree of flexibility of the policy age variables.
Claim Frequency Results
Before discussing the results of the hypothesis tests regarding policy age, we first briefly discuss the impact of the control variables on frequency risk.11 As expected, many of the variables are significantly related to the likelihood of claims. NCD ratings are significantly related to the frequency of claims, with risk falling notably for better NCD ratings. The age and gender of the insured, the age of the insured vehicle, and various policy provisions are all related to the claim risk of the policyholder. In many cases, comparing the sign of the estimated effects with the means presented in Panel B of Table 2 suggest that older policies are considerably less observably risky than younger policies.
Figure 2 confirms that observable variables can explain the large majority of the reduction in claim risk that happens over the lifetime of a policy. The figure plots average actual claim risk by policy age along with predicted claim risk based on the estimated negative binomial model. The predicted values are based on the specification that includes no controls for the age of the policy (specification (C), shown by the dashed line) and the specification that includes a dummy for brand new policies (specification (B), shown by the dotted line).12 The impact of observable variables is highlighted by comparing the fit of models with the actual frequency of claims. Much of the decline in risk that happens with policy age can be predicted based simply on variation in observable characteristics that happens coincidentally as policies age. Table 3 confirms this by providing a formal statistical test of whether accounting for the age of the policy can improve the fit of the claim frequency model.
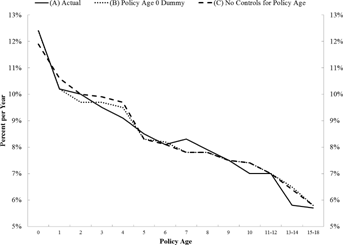
Note: This figure presents mean predicted annual claim frequencies by policy age for the models summarized in Table 3. The actual claim frequency is shown by the thin black line, which corresponds to the predicted values from model (A) that includes a full set of controls for policy age. Model (B), the dotted blue line, includes a control for only policy age 0. Model (C), the dashed red line, includes no controls for the age of the policy. The sample is the 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
| Dependent Variable: Number of Claims | |||
|---|---|---|---|
| (A) | (B) | (C) | |
| Policy age | |||
| 0 | 0.098 (0.023) | ||
| 1 | −0.100 (0.029) | ||
| 2 | −0.071 (0.031) | ||
| 3 | −0.123 (0.035) | ||
| 4 | −0.159 (0.039) | ||
| 5 | −0.210 (0.042) | ||
| 6 | −0.250 (0.046) | ||
| 7 | −0.191 (0.054) | ||
| 8 | −0.249 (0.067) | ||
| 9 | −0.261 (0.069) | ||
| 10 | −0.318 (0.076) | ||
| 11−12 | −0.283 (0.067) | ||
| 13−14 | −0.398 (0.087) | ||
| 15−18 | −0.328 (0.114) | ||
 |
0.100 (0.049) | 0.100 (0.049) | 0.101 (0.049) |
| Parameters | 135 | 123 | 122 |
| Log-likelihood | −51,501 | −51,506 | −51,515 |
| AIC | 103,273 | 103,260 | 103,275 |
| BIC | 104,701 | 104,572 | 104,577 |
- Note: This table presents coefficient estimates (and standard errors in parentheses) from three negative binomial models for the number of claims during the sample period. Specification (A) includes 13 policy age dummy variables for each of the policy age groups, specification (B) includes a single dummy for policy age 0, and specification (C) includes no controls for policy age. All models include controls for the variables listed in Table 2, with discrete variables entered as dummy variables and forth-order polynomials for continuous variables. The row labeled parameters shows the number of estimated parameters. AIC refers to the Akaike information criterion, and BIC is the Bayesian information criterion. The sample is the 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
Table 3 reports the estimated coefficients on the policy age dummy variables for each of the three models. Each specification includes a full set of control variables, which results in 122 additional parameter estimates. The table also reports the estimate of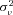 
, which captures the importance of unobserved heterogeneity in the data. In all specifications, the estimate is significantly larger than zero, suggesting that there is residual heterogeneity in the data. However, the size of the estimate is nearly unchanged by the inclusion of policy age variables, suggesting that unobserved heterogeneity does not vary with policy age, which we confirm formally below. The table also reports several measures of goodness of fit for each specification, which can be used to evaluate if adding more controls for policy age improves the fit of the model. Under the null hypothesis that all of the additional coefficients are zero, two times the difference in log-likelihood values is distributed as a chi-square random variable with degrees of freedom equal to the number of additional parameters. Comparing the full set of dummies (A) with the model with only a policy age 0 dummy (B), the likelihood ratio statistic is 9.30, which falls at the 75th percentile of the chi-square distribution with 12 degrees of freedom. A 5 percent critical value of the null distribution is 21.03, so there is no evidence to suggest that the policy age dummy variables are collectively significant beyond policy age 0. Comparing model (B) with model (C) shows that the policy age 0 dummy is statistically significant, however. The estimated coefficient is positive, and the associated t-statistic is greater than 4, suggesting strong statistical significance. Moreover, the likelihood ratio statistic is 17.42, which is statistically significant at well below the 1 percent level; the 1 percent critical value is 6.63.
We conclude from the evidence that, after controlling for a full set of control variables, there is no statistically significant monotonic relationship between claim frequency risk and policy age. Given the large sample size and the accuracy of the fit presented in Figure 2, we do not interpret this result as simply reflecting a lack of statistical power. However, there is evidence that brand new policies are significantly riskier than the remainder of the portfolio. After controlling for a wide range of observable characteristics, the policy age 0 dummy variable suggests that new policies have about 1 percent more claims per year than otherwise similar policies, which results into about 10 percent more claims.
Claim Severity
We now turn to the conditional relationship between policy age and claim severity by replicating the preceding analysis. We estimate the lognormal severity model allowing for unobserved heterogeneity on the sample of policyholders with at least one claim. The results are shown in Figure 3 and Table 4.
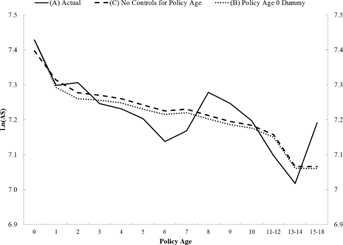
Note: This figure presents mean predicted log claim amounts by policy age for the models summarized in Table 4. The actual mean claim severity is shown by the thin black line, which corresponds to the predicted values from model (A) that includes a full set of controls for policy age. Model (B), the dotted blue line, includes a control for only policy age 0. Model (C), the dashed red line, includes no controls for the age of the policy. The sample is the 13,272 claims from 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
| Dependent Variable: Ln(Claim Severity) | |||
|---|---|---|---|
| (A) | (B) | (C) | |
| Policy age | |||
| 0 | 0.066 (0.027) | ||
| 1 | −0.062 (0.036) | ||
| 2 | −0.023 (0.038) | ||
| 3 | −0.082 (0.043) | ||
| 4 | −0.090 (0.047) | ||
| 5 | −0.101 (0.051) | ||
| 6 | −0.153 (0.057) | ||
| 7 | −0.128 (0.066) | ||
| 8 | −0.001 (0.082) | ||
| 9 | −0.016 (0.085) | ||
| 10 | −0.056 (0.094) | ||
| 11−12 | −0.129 (0.083) | ||
| 13−14 | −0.119 (0.108) | ||
| 15−18 | 0.058 (0.140) | ||
 |
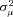0.000 (0.523) | 0.000 (0.475) | 0.000 (0.717) |
 |
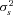1.226 (0.008) | 1.226 (0.008) | 1.226 (0.008) |
| Parameters | 116 | 103 | 102 |
| Log-likelihood | −21,532 | −21,537 | −21,540 |
| AIC | 43,296 | 43,282 | 43,286 |
| BIC | 44,165 | 44,062 | 44,058 |
- Note: This table presents coefficient estimates (and standard errors in parentheses) from three OLS models for the log of the amount of a claim. Specification (A) includes 13 policy age dummy variables for each of the policy age groups, specification (B) includes a single dummy for policy age 0, and specification (C) includes no controls for policy age. All models include controls for the variables listed in Table 2, with discrete variables entered as dummy variables and forth-order polynomials for continuous variables. The row labeled Parameters shows the number of estimated parameters. AIC refers to the Akaike information criterion, and BIC is the Bayesian information criterion. The sample is the 13,272 claims from 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
Figure 3 shows that, similar to frequency risk, observable variables can account for the large drop in average claim amounts that happens as policies age. The figure plots average actual claim severity by policy age along with predicted severity based on the estimated lognormal model. The predicted values are based on the specification that includes no controls for the age of the policy (specification (C), shown by the dashed line) and the specification that includes a dummy for brand new policies (specification (B), shown by the dotted line). Without explicitly controlling for policy age, predicted claim severity amounts fall sharply with policy age due to the impact of observable characteristics that are correlated with policy age.13 Table 4 provides the formal statistical test to show that explicitly accounting for the policy cannot significantly improve the fit of the claim severity model.
Table 4 reports the estimated coefficients on the policy age dummy variables for each of the three models. Each specification includes a full set of control variables, which results in 102 additional parameter estimates.14 The table also reports the estimates of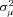 
, which capture the importance of unobserved heterogeneity in the data, and 
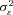, which is the unconditional variance of log-severity. Unlike with claim frequency, there is no evidence of unobserved heterogeneity, as the estimates of 
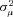are not statistically different from zero.15 In terms of goodness of fit, comparing the specification with a full set of dummies (A) with the model with only a policy age 0 dummy (B), the likelihood ratio statistic is 10.14, which can be compared to the 5 percent critical value of 21.03. There is no evidence to reject the null hypothesis that all of the additional policy age dummy variables are zero; the p-value for the likelihood ratio statistic is 0.60. In model (B), however, the dummy variable capturing policy age 0 is statistically significant. The estimated coefficient is positive, and the associated t-statistic is 2.42, suggesting fairly strong statistical significance. The likelihood ratio statistic comparing (B) and (C) is 5.90, which is larger than the 5 percent critical value of 3.84. The p-value on the likelihood ratio statistic is 0.015, again suggesting fairly strong statistical significance.
Similar to the results on frequency risk, we conclude from the evidence that, after controlling for a full set of control variables, there is no statistically significant monotonic relationship between claim severity risk and policy age. Because the claim severity model is based on a much smaller sample size of observed claims, a lack of statistical power is more relevant than with claim frequency. However, given the accuracy of the model fit presented in Figure 3, we still conclude that the fall in average claim severity as policies age is due to observable policyholder characteristics, not asymmetric information.
Unobserved Heterogeneity
As a final test of the importance of private information held by the incumbent insurer, we examine how our estimates of unobserved heterogeneity vary with the age of the policy. As shown in Table 3, we do find evidence of unobserved heterogeneity in claim frequency, suggesting that there is scope for the incumbent insurer to possess superior information. To provide a sense of the magnitude of the 0.1 estimate, recall that, conditional on 
, the number of claims is distributed as a Poisson random variable with mean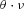 
. As a result, a one standard deviation change in 
results in a 10 percent change in the expected claim frequency. At the unconditional claim frequency of 4.5 percent per year, this translates into a roughly 0.5 percent per year increase in the number of claims.
as a function of several policy age dummy variables. Specifically, we let the variance vary with several large policy age buckets: policy age 0, policy ages 1 through 9, and policy ages 10 and above16
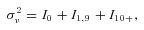
Reestimating the claim frequency model with some flexibility in the variance of the mixing distribution provides some evidence that unobserved heterogeneity increases with policy age, although the estimates are measured with considerable noise. The point estimate (standard error) of the three dummy variables is 0.001 (0.029), 0.111 (0.597), and 0.519 (0.310). There is strong evidence that there is no unobserved heterogeneity for brand new policies, and modest evidence of more heterogeneity for older policies. However, the maximized log-likelihood from this model is –51,504, which can be compared to the log-likelihood from model (B) in Table 3, –51,506. The likelihood ratio statistic is 3.62, which is distributed as a chi-square random variable with two degrees of freedom under the null that all of the dummy variables are equal. A 5 percent critical value for this distribution is 5.99, and the 3.62 value yields a p-value of 0.16. We cannot confidently reject the null hypothesis that the level of unobserved heterogeneity is constant across policy ages.
For claim severity, recall that there is no evidence that there is unobserved heterogeneity in the data. However, we reestimate the lognormal model by permitting the variance of the individual random effect,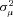 
, to vary by the same three policy age buckets. The results provide no evidence that unobserved heterogeneity varies by policy age. Indeed, the point estimate of 
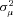is negative in all three buckets, which provides no evidence that we can reject the null of equal (and zero) unobserved heterogeneity in claim severity.
POLICY AGE, PREMIUMS, AND PROFITABILITY
The second hypothesis following from the theory of asymmetric learning is that the profitability of policies should increase with policy age. The evidence in Figure 1 is consistent with this hypothesis: the unconditional average loss ratio—the ratio of total losses to total premiums—decreases with policy age, suggesting that profit margins (1–Loss Ratio) do increase over time. However, loss ratios do not account for any costs of production besides claim costs. In this section, we show that a simple pricing strategy which includes a fixed charge plus a charge that is proportional to a policies' expected loss can account for the decreasing pattern in loss ratios. Because expected losses decrease sharply with policy age, the impact of a fixed cost on charged premiums is much bigger for older policies. Reasonable levels of a fixed cost can account for the decline in loss ratios seen in the data.
Policy Age and Charged Premiums
We explore the relationship between policy age and charged premiums in Table 5. Figure 2 shows that, unconditionally, premiums decrease with policy age at a rate slower than total claim costs, which results in a loss ratio that decreases with policy age. Table 5 shows the relationship between premiums and policy age after conditioning the set of control variables used in the claim risk regressions. We estimate ordinary least squares (OLS) regressions where the dependent variable is the log of the total premium and use specifications identical to those in Tables 3 and 4. The explanatory variables now provide a control for both the risk associated with policy age and any other factors that might affect charged prices, such as insurer market power or consumer search costs. Importantly, the policy age variables now pick up only premium changes that vary with tenure after removing the impact of expected losses and other sources monopoly power.
| Dependent Variable: Ln(Premium) | |||
|---|---|---|---|
| (A) | (B) | (C) | |
| Policy age | |||
| 0 | −0.005 (0.000) | ||
| 1 | 0.005 (0.000) | ||
| 2 | 0.005 (0.001) | ||
| 3 | 0.008 (0.001) | ||
| 4 | 0.006 (0.001) | ||
| 5 | 0.003 (0.001) | ||
| 6 | 0.003 (0.001) | ||
| 7 | 0.002 (0.001) | ||
| 8 | 0.012 (0.001) | ||
| 9 | 0.006 (0.001) | ||
| 10 | −0.006 (0.001) | ||
| 11–12 | 0.009 (0.001) | ||
| 13–14 | 0.014 (0.001) | ||
| 15–18 | −0.007 (0.001) | ||
| Parameters | 134 | 122 | 121 |
| Log-likelihood | 341,580 | 341,345 | 341,255 |
| AIC | –682,894 | –682,448 | –682,270 |
| BIC | –681,487 | –681,167 | –681,000 |
- Note: This table presents coefficient estimates (and standard errors in parentheses) from three OLS models for the log of the amount of the charged premium. Specification (A) includes 13 policy age dummy variables for each of the policy age groups, specification (B) includes a single dummy for policy age 0, and specification (C) includes no controls for policy age. All models include controls for the variables listed in Table 2, with discrete variables entered as dummy variables and forth-order polynomials for continuous variables. The row labeled Parameters shows the number of estimated parameters. AIC refers to the Akaike information criterion, and BIC is the Bayesian information criterion. The sample is the 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
The table shows that, after controlling for observable characteristics, charged premiums vary very little with policy age. Although the log-likelihood ratios (and unreported statistics) suggest that the model with a full set of dummy variables (A) provides a significantly better fit, there is no systematic pattern to the estimated coefficients. Based on specifications (A) and (B), there is some evidence that premiums are a bit lower for brand new policies, but the estimated effect is only 0.5 percent. At the mean premium of A$400, this translates into an effect of only A$2. The remaining coefficients in specification (A) are all between –0.007 and 0.014—a range of 0.021—and do not show a pattern increasing with policy age. A difference of 2.1 percent translates into a dollar effect of less than A$10 at the mean premium. There is little evidence that, after controlling for observable characteristics, the insurer is strategically varying premiums based on the age of the policy.
Policy Age and Loss Ratios
Given that charged premiums do not systematically vary with policy age, we now show that a pricing strategy that includes a fixed component can account for the dramatic decrease in loss ratios that happens with policy age.17 We do this by creating an estimated loss ratio based on generating charged premiums as a simple linear function of expected losses, which we compute using the models estimated in the “Policy Age and Claim Risk” section. We can then compute expected loss ratios as the ratio of expected losses to generated charged premiums, which we then compare with actual loss ratios.
We assume independence between claim frequency and claim severity and compute expected losses as the product of expected claim frequency and expected claim severity. Given the evidence that charged premiums do not vary systematically with policy age, we use the specifications without any controls for policy age (specification (C)). Although expected losses are computed in sample, it is important to note that they are not conditioned on policy age, so all of the variation across policy ages is driven by changes in other observable characteristics.
We generate charged premiums based on estimates of the pricing policy used by the insurance company.18 First, we regress charged premiums on our estimate of expected losses, using an errors-in-variables regression to account for the estimation error in our estimate of expected losses.19 The point estimates are A$160 for the intercept and 0.85 for the slope. We use these parameter estimates to generate our first set of charged premiums. Second, we repeat the same regression but restrict the slope coefficient to be 1.0, which prevents any cross-subsidization between policies. The estimated intercept is A$107. We use a more round number of A$110 to generate our second set of charged premiums as the expected loss plus A$110.20
Figure 4 illustrates the impact of these pricing policies on expected loss ratios. For each policy age, we compute an expected loss ratio based on our model of expected claim costs and the two pricing formulas that include a fixed charge. Because expected losses decrease so dramatically with policy age (based on the claim risk models that do not include any controls for policy age), expected loss ratios fall with policy age as the fixed component becomes a larger share of charged premiums. For the oldest policies, expected loss ratios are quite low. Based on the pricing formula that includes the larger A$160 fixed charge, the estimated loss ratio matches the actual loss ratio quite well. For the smaller A$110 fixed charge, actual loss ratios fall faster than estimated loss ratios. We conclude that the observed pattern of loss ratios that decrease with policy tenure can be explained by three features of the data. First, charged premiums contain a fixed charge, which represents a larger fraction of premiums for policies with low expected losses. Second, expected losses decrease sharply with policy tenure, which makes the fixed charge more important for older policies and results in lower loss ratios. Finally, the estimated pricing policy suggests some cross-subsidization from policyholders with low expected losses to policyholders with high expected losses, which contributes to the high loss ratios for younger policies and low loss ratios for older policies. For our specific purposes however, the temporal pattern of loss ratios can be explained entirely with the evolution of observable policyholder characteristics, which rules out asymmetric learning about claim risk as a source of monopoly power.
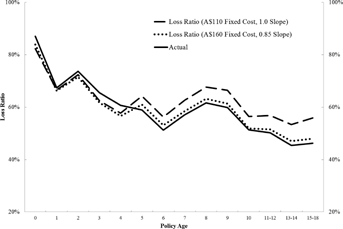
Note: This figure presents average actual loss ratios and two expected loss ratios by policy age. The two estimated loss ratios are based on a simple pricing formula that charges a premium equal to a fixed cost plus a percentage of expected losses. In one case (the dashed line), premiums are assumed to be $110 plus expected losses; in the other case (the dotted line), premiums are assumed to be $160 plus 85 percent of expected losses. Expected loss ratios are the ratio of expected claim costs to charged premiums. Expected claim costs are based on the models for claim frequency and claim severity including all control variables and no policy age dummy variables. The sample is the 290,804 policies representing 134,699 years of exposure described in the “Data and Summary Statistics” section.
CONCLUSIONS
The analysis presented in this article extends the empirical literature on the value of long-term relationships in nonlife insurance contracting. Theoretically, models conjecture that a potential downside of repeated relationships is information monopoly power and policyholder lock-in. The results from this Australian auto insurance company indicate that this particular insurance market has evolved to a stage where publicly available data capture all relevant information about policyholders, with the possible exception of brand new policies. The public nature of the NCD rating removes one potential source of asymmetric learning, namely, claims history. Due to the inexpensive nature of tracking the NCD rating, it is likely that the sharing of such information is economically sensible as it prevents subsequent monopoly power. Methodologically, the results confirm the importance of conditioning on publicly observable variables to properly identify the role of asymmetric information, and the importance of using ex post realizations to properly measure risk.
The impact of relationships on insurance contracting may very well be different in other markets, so we encourage additional testing in other environments. Personal automobile insurance is a rather straightforward line of business where underwriting has evolved to a stage where there is likely very little residual private information. Commercial lines of insurance, where insurance brokers are prevalent, may provide different results. Our results suggest that simply examining the relationship between loss ratios and policy age is not enough to confirm an information monopoly. We advocate testing whether the riskiness of policyholder declines with policy age after conditioning on observable underwriting variables.
The empirical results from this market also point to another direction for future theoretical research. The aggregate statistics indicate that observable risk decreases significantly over time, meaning that policyholder persistence is much higher for less risky consumers. Moreover, there is evidence that brand new policies are a bit riskier than expected and receive a premium discount relative to their risk. We conjecture that models of search and two-sided matching might be useful in explaining these facts. Although we do not want to downplay the importance of information in insurance markets, the evidence from this market is inconsistent with the theoretical predictions of asymmetric learning and points to alternative sources of frictions to explain the importance of relationships in insurance markets.
REFERENCES
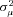is negative in all three specifications, which is feasible in the estimation routine, but provides strong evidence that there is no unobserved heterogeneity in the data.
