A Savings Plan With Targeted Contributions
ABSTRACT
We consider a simple savings problem where contributions are made to a fund and invested to meet a future liability. The conventional approach is to estimate future investment return and calculate a fixed contribution to be paid regularly by the saver. We propose a flexible plan where contributions are systematically adjusted and targeted. We show by means of stochastic simulations that this plan has a reduced risk of a shortfall and is relatively insensitive to errors in the planner's estimate of future returns. Sensitivity analyses in terms of parameter values, stochastic return models and investment horizons are also performed.
INTRODUCTION
We consider a simple savings problem where an individual puts aside funds in order to meet a certain liability at a given date in the future. The individual may contribute to a medium-term investment and savings vehicle, for example, to meet school or college fees for his children in 5 years time. Another example is where the individual wishes to purchase property. He may save for, say 5 years, and then withdraw some or all of his investment and use it as a deposit or down payment as part of a home loan. A longer-term example is a retirement or pension fund, where the individual saves out of labor income to provide a lump sum at retirement. This may then be used to buy an annuity.
In most problems of this kind, a financial planner or adviser will assist the individual to determine how much he should save and invest every month (say), depending on his household finances. Two related decisions must be made: how much the monthly contribution will be and where the savings will be invested. In this article, we do not consider the second decision, that is, asset allocation, although we discuss this briefly later. We assume instead that the individual saves in a variable-rate bank account or in a low-risk mutual fund.
A very risk-averse investor could save in a term-deposit bank account or in a zero-coupon bond, yielding a fixed interest rate. However, it could be that a medium-term fixed-income investment like this is unavailable or pays unattractive rates. A less risk-averse investor, such as a young worker aspiring to home ownership, may instead wish to invest in a stock market fund to try and achieve the largest possible future down payment as part of a home loan. If his stock market investment performs poorly after 5 years, this may mean that a smaller home loan, or a more expensive loan with a higher debt-to-equity ratio, will be available to him. On the other hand, a worker who is close to retirement age is usually advised to invest in less risky, bond-like, assets so as to secure a comfortable retirement.
In standard economic theory, this savings problem can be cast as a consumption–investment problem, with consumption (or saving) and asset allocation as decision variables, and with a utility or loss function as an objective criterion that is optimized dynamically. Even though idealized assumptions may be made, this approach can lead to decision rules that are simple to implement and that can be used to benchmark performance. In practice, however, financial planners do not employ stochastic dynamic optimization to provide retail advice to individual savers. They will suggest instead that the individual sets aside a given amount every month, or possibly a fixed percentage of income, and will also offer suggestions regarding asset allocation. Dynamic optimization is not used regularly by financial planners at a retail level because of the complications caused by real-world features such as taxes, transaction costs, and investment charges, because of imperfect knowledge about asset return distributions, and because it is difficult to capture individuals' varying financial circumstances and requirements.
One example is in the deterministic lifestyling strategies commonly employed in target-date funds and in pension planning (Shiller, 2005; Blake, Cairns, and Dowd, 2001). Advisers typically suggest a fixed monthly contribution based on a range of assumed investment rates of return (Employee Benefits Security Administration, 2006). Another example is work-related savings vehicles, such as an employer-sponsored pension plan, where a fixed proportion of salary is determined (McGill et al., 2004). The new Florida public sector pension plan described by Lachance, Mitchell, and Smetters (2003) requires that individuals save a uniform 9 percent of pay. The Actuarial Foundation and WISER (2004) suggest a rule of thumb of saving 15 percent of pay toward retirement.
Our approach in this article is to try to improve upon the conventional fixed-contribution approach. We suggest a flexible targeted-contribution savings plan that has variable contributions that depend on current and historic investment performance. We investigate whether this new plan performs robustly, in terms of meeting an investment target at a given horizon, under a wide range of investment conditions. We show, by means of simulations, that this plan is less risky than the conventional fixed-contribution plan. Our proposed savings plan is based on a method used in industrial process control (e.g., Box and Luceño, 1995). The method has also been proposed in the econophysics literature (Gandolfi, Sabatini, and Rossolini, 2007) and is applied in the pensions literature to defined benefit pension funding with deterministic economic scenarios (Owadally, 2003). The innovation in this article is to apply this method to a savings problem with a simple stochastic investment environment.
In the next section, we describe the targeted-contribution plan. We then run stochastic simulations with serially independent normally distributed log-returns to compare the performance of this plan over a 5-year saving period with a conventional plan. We measure the risk that end-of-period wealth falls short of the target liability using both the standard deviation and 95th percentile. The sensitivity of our proposed plan to the financial planner's assumptions is verified by repeating the simulations with different parameter values. We also run simulations with constraints imposed on the flexible contributions, with non-Gaussian investment returns incorporating jumps, and with serially correlated returns. Finally, we consider an application in pension funding with a long investment horizon and with a bootstrap stochastic asset model using 59 years of investment data on equities and bonds.
FIXED- AND TARGETED-CONTRIBUTION PLANS
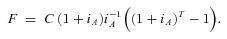 (1)
(1)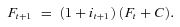 (2)
(2)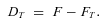 (3)
(3)The risk for the individual saver is that there is a large deficit at time T. (A surplus is just a negative deficit here.)
The second plan that we consider is a targeted-contribution plan. This is based on the pension funding method discussed by Owadally (2003) and adapted from industrial process control (Box and Luceño, 1995). Although we do not consider the asset allocation problem in this article, it is worth noting that Gandolfi, Sabatini and Rossolini (2007) propose a similar method for tactical asset allocation in an investment portfolio.
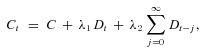 (4)
(4)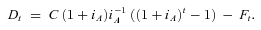 (5)
(5)Equation (4) therefore requires that, at time t, an overpayment at a rate of λ1 is made based on the notional deficit Dt. If actual returns on the fund are persistently lower than the anticipated return iA, then deficits will recur systematically. Therefore, Equation (4) also imposes a further overpayment, at a rate of λ2, based on the cumulative sum of deficits up to time t. If there is no persisting deficit, that is, positive and negative deficits cancel each other out on average, then the additional overpayment represented by the third term on the right-hand side of Equation (4) is on average zero.
We do not directly address the optimal choice of parameters λ1 and λ2 here. Instead we assume a set of practical parameter values and investigate the targeted-contribution plan under various conditions such as the presence of parameter estimation errors, persistence and jumps in investment returns, investor cash flow constraints, and long-term retirement planning objectives. Our aim is to establish robustness of the targeted-contribution approach, and we leave formal optimization to future work.
Practical values for λ1 and λ2 in Equation (4) are likely to be small because a saver may be unable or unwilling to make additional contributions, and tax advantages may also mean that he is unwilling to reduce his contributions. In the following, our base parameter values are 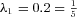 , as this represents paying a deficit over approximately 5 months (ignoring interest), and λ2 = 0.01 as a charge or tax of 1 percent per month thereafter on the deficit in any month. These parameter values are comparable to values employed by Box and Luceño (1995) and Owadally (2003) in other contexts. In a later section, we consider other values for λ1 and λ2 and we also discuss parameter choice by reference to an ARMA time series process.
, as this represents paying a deficit over approximately 5 months (ignoring interest), and λ2 = 0.01 as a charge or tax of 1 percent per month thereafter on the deficit in any month. These parameter values are comparable to values employed by Box and Luceño (1995) and Owadally (2003) in other contexts. In a later section, we consider other values for λ1 and λ2 and we also discuss parameter choice by reference to an ARMA time series process.
RESULTS OF STOCHASTIC SIMULATIONS
Stochastic simulations are performed to compare the terminal deficits under the two plans described in the preceding section. An investment horizon of T = 60 months and a target fund of F = 100 are assumed, along with values λ1 = 0.2 and λ2 = 0.01 in the targeted-contribution plan in Equation (4). A set of 10,000 simulations was carried out throughout, with frequent checks for convergence using 5,000 and 20,000 simulations, and with a fixed seed for the random number generator to minimize sampling error when comparing results.
The monthly logarithmic return δt = ln (1 + it) on the fund is simulated as an independent and identically distributed (i.i.d.) sequence of normally distributed random numbers with mean 0.3792 percent and standard deviation 2 percent. The mean arithmetic return is thus 0.4 percent per month. These are representative values for a relatively conservative investment fund.1
A financial planner has to estimate future investment return and make an assumption iA as to the return on the fund. Since he does not have perfect foresight, he may over- or underestimate future average investment return. For example, if iA = 0.7 percent, the planner overestimates the mean return by 0.3 percent per month. Henceforth, we define the estimation error as the excess of iA over the average return on the fund. When iA = 0.7 percent, the planner's estimation error is therefore 0.3 percent per month.
Histograms of Terminal Deficit
Figure 1 shows the distributions of the terminal deficit under the two plans, for iA = 0.4 percent and 0.7 percent. Since the accumulated fund has a right-skewed distribution, the distribution of the deficit is left-skewed. We make two observations.
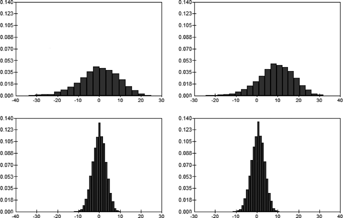
Note: F = 100, 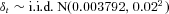 , λ1 = 0.2 and λ2 = 0.01. Statistics appear in Table 1.
, λ1 = 0.2 and λ2 = 0.01. Statistics appear in Table 1.
Observation 1
The fixed-contribution plan is riskier than the targeted-contribution plan (where we measure risk in terms of the fund falling short of the target at the end-date).
The terminal deficit is more dispersed under the fixed-contribution plan (top panels in Figure 1) than under the targeted-contribution plan (bottom panels in Figure 1). The fixed-contribution plan is riskier than the targeted-contribution plan in that end-wealth is more volatile and has a heavier-tailed distribution in the former case than in the latter case.
Observation 2
Risk in the fixed-contribution plan is sensitive to the error in the financial planner's estimate of future investment return, whereas risk in the targeted-contribution plan is relatively insensitive to this. (Again, we measure risk in terms of the shortfall or deficit from the target at the end.)
When the return assumption is 0.7 percent, rather than 0.4 percent, the adviser's return assumption overstates the mean return on the fund and we anticipate that the plans will, on average, fall short of the target. The distribution of the terminal deficit does indeed shift to the right when the return assumption changes from 0.4 percent to 0.7 percent in the fixed-contribution plan. However, it remains centered around zero in the targeted-contribution plan. If the planner's return assumption turns out to be overoptimistic, the risk of a shortfall is greater in the fixed-contribution plan than in the targeted-contribution plan.
Percentiles and Moments of Terminal Deficit
Table 1 shows how various statistics concerning the terminal deficit change as the estimation error in iA changes.
| Error in iA | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | Mean Square Deficit | ||||
|---|---|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | FC | TC | |
| −0.3% | −9.841 | −0.497 | 10.385 | 3.223 | 6.219 | 4.697 | 204.701 | 10.636 |
| −0.2% | −6.499 | −0.336 | 10.068 | 3.214 | 9.073 | 4.843 | 143.600 | 10.442 |
| −0.1% | −3.230 | −0.171 | 9.760 | 3.205 | 11.863 | 4.998 | 105.691 | 10.299 |
| 0 | −0.036 | −0.003 | 9.458 | 3.195 | 14.591 | 5.155 | 89.453 | 10.210 |
| 0.1% | 3.086 | 0.169 | 9.163 | 3.186 | 17.256 | 5.315 | 93.478 | 10.178 |
| 0.2% | 6.135 | 0.344 | 8.875 | 3.176 | 19.859 | 5.472 | 116.394 | 10.207 |
| 0.3% | 9.112 | 0.523 | 8.593 | 3.167 | 22.401 | 5.641 | 156.866 | 10.301 |
- Note: The error in iA is the excess of iA over the average return. F = 100,
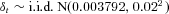 , λ1 = 0.2, and λ2 = 0.01.
, λ1 = 0.2, and λ2 = 0.01.
First, note that the 95th percentile and standard deviation of the terminal deficit are smaller in the targeted-contribution plan than in the fixed-contribution plan for all values of errors in iA in Table 1. The histograms in Figure 1 illustrate this visually for errors of 0 and 0.3 percent. This confirms Observation 1 above.
Second, note that the more iA overestimates the average return (i.e., the greater the error in iA), the greater the terminal deficit in the fixed-contribution plan: both the mean deficit and the 95th percentile of the deficit increase. The targeted-contribution plan, however, is much less sensitive to the error in iA: the mean, standard deviation, and 95th percentile of the deficit change, but not as much as in the fixed-contribution case. This confirms Observation 2 above. The mean square deficit column in Table 1 gives the second noncentral moment of the deficit around zero. We note that the mean square deficit in the targeted-contribution plan is fairly constant regardless of the size of the error.
Finally, we also computed skewness and kurtosis. The coefficients of skewness are −0.319 and −0.107 (to 3 d.p.) for the fixed-contribution and targeted-contribution plans, respectively, for all estimation errors in Table 1. The top panels in Figure 1 exhibit a more pronounced left skew than the bottom panels. The respective coefficients of kurtosis are 3.305 and 3.002 (to 3 d.p.) for all estimation errors in Table 1.
DISCUSSION OF RESULTS AND SENSITIVITY ANALYSIS
Observations 1 and 2
Observation 1, that is, the targeted-contribution plan is less risky than the fixed-contribution plan, in terms of meeting the target at the investment horizon, is not surprising. The targeted-contribution plan is flexible and contributions can be varied to make up any shortfall gradually. In other words, the flexible contributions pick up part of the investment risk, thereby reducing the risk to end-wealth.
Observation 2, that is, the targeted-contribution plan is relatively insensitive to errors in the planner's estimate of investment return, is less intuitively obvious. Whereas the first observation could arise from any plan that allows flexible contributions, the second observation requires that the contributions be flexible and be targeted systematically, so as to counter the effect of the estimation error. The third term on the right-hand side of Equation (4) ensures that any notional deficit that accumulates over time is “taxed” at a rate λ2, thereby adjusting the contribution to restore the savings plan on a path to target.
This is illustrated in Table 2 which shows the average path of the two plans over time for a return assumption of 0.7 percent. The fund builds up gradually from 0 to about 90 on average in the fixed-contribution plan, leaving an average terminal shortfall of 10. By contrast, the fund builds up to nearly 100 on average in the targeted-contribution plan, leaving almost no terminal shortfall on average. Whereas the contribution is constant under the fixed-contribution plan, the mean contribution in the targeted-contribution plan gradually increases so that the plan is on average on target after 60 months.
| Time (Months) | Mean Fund | Mean Contribution | ||
|---|---|---|---|---|
| FC | TC | FC | TC | |
| 0 | 0.0000 | 0.0000 | 1.3375 | 1.3375 |
| 10 | 13.6729 | 13.7782 | 1.3375 | 1.3677 |
| 20 | 27.9042 | 28.5406 | 1.3375 | 1.4166 |
| 30 | 42.7163 | 44.4238 | 1.3375 | 1.4685 |
| 40 | 58.1330 | 61.4937 | 1.3375 | 1.5220 |
| 50 | 74.1847 | 79.8185 | 1.3375 | 1.5778 |
| 60 | 90.8881 | 99.4771 | 1.3375 | 1.6369 |
- Note: F = 100,
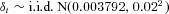 , iA = 0.7%, λ1 = 0.2, and λ2 = 0.01.
, iA = 0.7%, λ1 = 0.2, and λ2 = 0.01.
An estimation error in the financial planner's investment return assumption can arise in several ways. The planner's model of asset returns may be wrongly calibrated because of insufficient or inaccurate data (parameter risk). The model itself may be misspecified (model risk). For example, the planner may fit a normal distribution to asset returns that, in fact, have a heavy-tailed distribution, thereby discounting the effect of market corrections and underestimating tail risk. An estimation error may also occur because of a large unexpected shift in the economic environment (such as after a market crash or following a revision in monetary policy targets by the central bank). Finally, and more subtly, the financial planner may exhibit behavioral biases, leading to overconfidence in an economic boom (Akerlof and Shiller, 2009; Kahneman and Riepe, 1998) and decisions influenced by framing and mental accounting issues (Thaler, 1999). Observation 2 therefore suggests that the targeted-contribution plan performs fairly robustly regardless of all these sources of estimation errors in the future investment return.
Terminal Wealth and Interim Consumption
The targeted-contribution savings plan shifts uncertainty from terminal wealth to intermediate contributions. For a short-term savings plan, or one where contribution is a small proportion of income, the variability in contributions may have a negligible impact on the saver and on the saver's consumption during the saving period. On the other hand, for a long-term savings plan, or one where the contribution is a large proportion of income, large contribution requirements over a long period could be unaffordable.
To investigate this, we repeat the simulations of the earlier section with an unbiased estimate iA = 0.4 percent. First, we calculate the variance of the fund and contribution at intermediate time steps.2 The results are displayed in Table 3. The contribution variance over time in the fourth column is significantly smaller than the variance in terminal wealth (at time t = 60) for either the fixed-contribution plan (88.363) or the targeted-contribution plan (10.095). Much more of the “total variance” is allocated to end-wealth than to interim contributions.
| Time (Months) | Var Fund | Var Contribution TC | |
|---|---|---|---|
| FC | TC | ||
| 0 | 0 | 0 | 0 |
| 10 | 0.3581 | 0.1764 | 0.0089 |
| 20 | 2.7890 | 0.8225 | 0.0443 |
| 30 | 9.7172 | 2.0260 | 0.1102 |
| 40 | 23.9019 | 3.8799 | 0.2104 |
| 50 | 48.9548 | 6.5508 | 0.3520 |
| 60 | 88.3625 | 10.0954 | 0.5393 |
- Note: Contribution under FC has zero variance. F = 100,
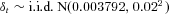 , iA = 0.4%, λ1 = 0.2, and λ2 = 0.01.
, iA = 0.4%, λ1 = 0.2, and λ2 = 0.01.
 in the targeted-contribution plan
in the targeted-contribution plan
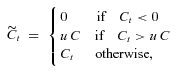 (6)
(6)We anticipate that, the more budget constrained the saver is, the more increases in contribution will be limited, and the less effective the targeted-contribution plan will be in compensating for lower than anticipated investment returns. Table 4 does indeed show that the lower u is, the more end-wealth risk increases in the targeted-contribution plan: the volatility and 95th percentile of terminal deficits in the targeted-contribution plan increase with decreasing u.
| Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | ||||
|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | |
| No constraint | −0.036 | −0.003 | 9.458 | 3.195 | 14.591 | 5.155 |
| u= 2 | −0.036 | −0.015 | 9.458 | 3.249 | 14.591 | 5.185 |
| u= 1.75 | −0.036 | 0.044 | 9.458 | 3.310 | 14.591 | 5.465 |
| u= 1.5 | −0.036 | 0.270 | 9.458 | 3.530 | 14.591 | 6.189 |
| u= 1.25 | −0.036 | 1.072 | 9.458 | 4.215 | 14.591 | 8.560 |
| u= 1.1 | −0.036 | 2.451 | 9.458 | 5.153 | 14.591 | 11.806 |
| u= 1.05 | −0.036 | 3.313 | 9.458 | 5.631 | 14.591 | 13.397 |
- Note: FC is independent of u but statistics are shown for comparison. F = 100,
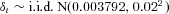 , iA = 0.4%, λ1 = 0.2, and λ2 = 0.01.
, iA = 0.4%, λ1 = 0.2, and λ2 = 0.01.
The upper constraint u does not affect the fixed-contribution plan, of course, but statistics are shown in Table 4 for the sake of comparison. We observe from Table 4 that the targeted-contribution plan, even when constrained, performs better than the fixed-contribution plan in terms of achieving a lower end-wealth risk. It is also of practical interest to note that, even if contributions in the targeted-contribution plan are constrained to be no more than 110 percent of the planned contribution under the conventional fixed-contribution plan (and no less than zero), the standard deviation of the terminal deficit is reduced by almost half.
Constraining contributions as in Equation (6) may be realistic to the extent that individuals are able to budget and form a view of an upper limit as to how much they can save every month. Nevertheless, the analysis in this article is limited in that risk is measured in terms of terminal wealth only. We note, as a direction for future research, that one could consider utility over both end-wealth and the interim consumption stream. Labor income risk then becomes relevant (Campbell and Viceira, 2002). If labor income is inversely correlated with investment return, a hedging effect is induced that may reduce combined risk in terms of both consumption and end-wealth.
The intermediate consumption pattern also matters in conventional fixed-contribution plans, in fact. A prudent financial adviser will underestimate future investment return (i.e., he will end up with negative values of the estimation error in Table 1) so as to minimize the 95th percentile of deficits. However, this can also result in large surpluses, in the individual making larger contribution payments than he can afford, and in a consequent loss in utility of consumption during the saving period. Again, we note this here as an item for further research.
Variables λ1 and λ2
Simulations for a wider range of values of λ1 and λ2 are described in the Appendix. Our main conclusion is that the targeted-contribution plan is less risky than the fixed-contribution plan, in terms of volatility and 95th percentile of the deficit, for all but impractically large values of λ1 and λ2. For example, the targeted-contribution plan is less risky than the fixed-contribution plan for λ1 ≤ 2 when λ2 = 0.01 (Table A3 in the Appendix) or λ2 ≤ 3 when λ1 = 0.2 (Table A4 in the Appendix). We also find that the volatility of contributions increases as λ1 and λ2 increase. This is to be anticipated since, the larger λ1 and λ2 are in Equation (4), the more variable contributions will be as random deficits arise from random investment returns. A time-series analysis shows that for very large values of λ1 and λ2, the deficit in the targeted-contribution plan becomes nonstationary. A practical conclusion for financial planners is that large values of λ1 and λ2 should be avoided as they can lead to very volatile contributions and to loss of utility of consumption for the individual saver.
Asset Return Model and Asset Allocation
In the earlier sections, we assumed that asset returns were normally distributed and serially independent. We investigate the relative performance of the fixed and targeted-contribution plans under two alternative investment return models here.
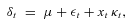 (7)
(7)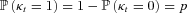 . Here p is small and is the probability of a “rare event,” such as a market correction, in a given month. Finally, {xt} is an i.i.d. sequence of Gaussian random variables with mean μx and standard deviation σx. Given that a market correction occurs in month (t − 1, t), the size of the market correction is represented by xt.
. Here p is small and is the probability of a “rare event,” such as a market correction, in a given month. Finally, {xt} is an i.i.d. sequence of Gaussian random variables with mean μx and standard deviation σx. Given that a market correction occurs in month (t − 1, t), the size of the market correction is represented by xt.We repeat the work of the earlier section, with unconstrained contributions and with λ1 = 0.2, λ2 = 0.01 and iA = 0.4 percent. Table 5 shows that the volatility and 95th percentile of terminal deficits are lower in the targeted-contribution plan than in the fixed-contribution plan, for various values of p, μx, and σx. The targeted-contribution plan is effective at reducing end-wealth risk compared to the fixed-contribution plan, even when asset returns have fat-tailed nonnormal distributions.
| p | μx | σx | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | |||
|---|---|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | |||
| No jump | −0.036 | −0.003 | 9.458 | 3.195 | 14.591 | 5.155 | ||
| 1/60 | −7% | 0.1 | 3.234 | 0.203 | 11.210 | 3.838 | 21.414 | 6.052 |
| 2/60 | −7% | 0.1 | 6.381 | 0.342 | 12.450 | 4.407 | 26.322 | 7.323 |
| 3/60 | −7% | 0.1 | 9.273 | 0.502 | 13.394 | 4.870 | 31.183 | 8.990 |
| 1/60 | −7% | 0.1 | 3.234 | 0.203 | 11.210 | 3.838 | 21.414 | 6.052 |
| 1/60 | −10% | 0.1 | 4.629 | 0.282 | 11.509 | 4.039 | 23.750 | 6.437 |
| 1/60 | −13% | 0.1 | 5.958 | 0.358 | 11.963 | 4.296 | 25.889 | 6.916 |
| 1/60 | −7% | 0.1 | 3.234 | 0.203 | 11.210 | 3.838 | 21.414 | 6.052 |
| 1/60 | −7% | 0.2 | 2.489 | 0.188 | 15.102 | 4.990 | 26.140 | 6.547 |
| 1/60 | −7% | 0.3 | 1.206 | 0.148 | 20.914 | 6.659 | 31.584 | 7.473 |
In Table 5, p = 1/60 means that on average one jump occurs in a 5-year period. As p increases, market corrections become more frequent. As μx becomes more negative, the severity of downward market corrections increases. As σx increases, the volatility of market corrections increases.3 Table 5 shows that if a financial planner does not allow for jumps in asset returns, both the fixed and targeted contribution plans will experience greater end-wealth risk as either the frequency or severity or volatility of market corrections increases. However, end-wealth risk remains lower in the targeted-contribution plan compared to the fixed-contribution plan.
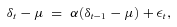 (8)
(8)Table 6 shows that the volatility and 95th percentile of terminal deficits are smaller in the targeted-contribution plan than in the fixed-contribution plan, for various values of parameter α. The lag 1 autocorrelation in {δt} increases as the autoregressive parameter α increases. (The variance of {δt} also varies with α.)
| α | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | |||
|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | |
| −0.6 | 0.341 | 0.014 | 6.000 | 2.385 | 9.795 | 3.875 |
| −0.4 | 0.270 | 0.011 | 6.795 | 2.516 | 10.998 | 4.070 |
| −0.2 | 0.155 | 0.060 | 7.894 | 2.784 | 12.436 | 4.503 |
| 0 | −0.036 | −0.003 | 9.458 | 3.195 | 14.591 | 5.155 |
| 0.2 | −0.386 | −0.018 | 11.836 | 3.814 | 17.663 | 6.074 |
| 0.4 | −1.135 | −0.049 | 15.882 | 4.797 | 22.338 | 7.539 |
| 0.6 | −3.246 | −0.120 | 25.425 | 6.555 | 30.232 | 10.039 |
The targeted-contribution plan therefore appears to be less risky than the fixed-contribution plan, even with investment returns that exhibit nonnormality and serial correlation.
It is also worth highlighting that the asset allocation decision has been ignored in this article, for simplicity. As set out in the introduction, we assume that the individual is saving for a medium term of 5 years in a vehicle such as a variable-rate savings bank account or in a low-risk mutual fund. Asset allocation becomes more important with longer-term savings, and this is explored in detail by Campbell and Viceira (2002) among others. Asset allocation depends on the individual's coefficient of risk aversion and elasticity of intertemporal substitution of consumption, as well as on his labor income risk and investment horizon, and on issues such as taxation and transaction costs, etc. In the insurance and actuarial literature, asset allocation is discussed by Vigna and Haberman (2001), Taylor (2002), Owadally and Haberman (2004), Battocchio and Menoncin (2004), Cairns, Blake, and Dowd (2006), Emms and Haberman (2008), among others.
The asset allocation decision can be incorporated in future research. It is possible to model lifestyling portfolios, such as life-cycle or target-date funds (Shiller, 2005; Blake, Cairns, and Dowd, 2001). The method employed to adjust contributions can also be used to adjust asset allocation, as in Gandolfi, Sabatini, and Rossolini (2007).
Implementation Issues
There are several practical investment considerations that are worth highlighting here. First, market frictions such as taxes and transaction costs are ignored in the above, but can be included in future simulations. Our purpose here is to model tax-free accounts such as the TFSA (Tax-Free Savings Account) in Canada or the ISA (Individual Savings Account) in the United Kingdom. The performance of the targeted-contribution savings plan under the traditional and Roth IRAs (Individual Retirement Accounts) in the United States, along the lines of Adelman and Cross (2010), would be illuminating. Various related issues must be considered in this context, namely, investor behavior during the accumulation and payout phases, reinvestment scenarios, tax rates before and after retirement, and social security.
Second, we have not explored the riskiness of the targeted-contribution plan as the maturity T of the plan varies. Starting such a plan at different points of the economic cycle (e.g., during the 1990s and 2000s) and over different horizons may produce very different results.
Third, the targeted-contribution plan can be said to follow a contrarian investment style in that a greater (smaller) contribution is required if the fund performs poorly (well). This can be contrasted with the momentum style of investing. For example, if a fixed number of units of an open-end mutual fund are bought regularly, the dollar contribution increases as the net asset value increases. The contrarian style of the targeted-contribution plan means that it can take advantage of investor overreaction and market reversal effects, specially over the long term (DeBondt and Thaler, 1985; Chopra, Lakonishok, and Ritter, 1992). This is something worth investigating in future work using historical data.
Finally, we investigated above whether the targeted-contribution plan performs robustly under a range of conditions but did not consider the optimal choice of the λ1 and λ2 parameters for a practical implementation of the targeted-contribution plan. A suitable utility function may be optimized for this purpose, in order to minimize end-wealth risk as well as risk to intermediate consumption. Historical data (e.g., with the bootstrap model of the last section) and a genetic algorithm could also be used so as to minimize the 95th percentile wrt λ1 and λ2. We mention these here as items for future research.
AN APPLICATION TO PENSION FUNDING
In this section, we consider a long investment horizon and we use a bootstrap stochastic asset model resampled over 59 years of equity and bond return data. We implement the targeted-contribution method in the funding of a defined-benefit pension plan and investigate whether it leads to a better long-term funding position compared to a typical actuarial funding method. It is assumed that an employer sponsors the pension plan and pays contributions into a pension fund to provide retirement benefits to its employees.
We use the model pension plan described by Owadally (2003), except that he uses deterministic economic scenarios whereas we use a stochastic asset model. A key assumption is that employees' salaries, and also their pensions in retirement, grow in line with price inflation. All the monetary quantities that appear below are therefore be expressed in real terms, that is, net of price inflation.
Pension liabilities have a simplified structure. Employees join at the age of 20. The age profile of the pension plan membership is constant, as is the number of new entrants to the plan every year. A pension, indexed with price inflation, is paid when employees retire at the age of 65. Mortality follows a standard actuarial life table (English Life Table No. 12 for males). Payroll is constant in real terms and the real yearly benefit outgo is normalized to 1. The actuarial liability is calculated at 16.94 (in real terms) using the projected unit credit method and a real annual discount rate of 4 percent (McGill et al., 2004, p. 665).
On the asset side, the pension fund is assumed to be invested in UK equities and long-term Treasury bonds (gilts) only. We use the bootstrap method to simulate real returns on these assets (Efron and Tibshirani, 1993). We resample real annual returns from the equity and gilt indices calculated by Barclays Capital (2009) from 1950 to 2008, with income reinvested. The returns are net of price inflation, as given by the cost of living index also calculated by Barclays Capital (2009). The pension fund portfolio is rebalanced every year and a 60:40 equity:gilt ratio is maintained.
Annual actuarial valuations take place and the sponsor's contributions are varied to make up any deficit in the plan. The deficit, also known as an unfunded liability, is the excess of the actuarial liability over assets, and a surplus is just a negative deficit. We assume that there is no deficit initially, for example, from setting up the plan or from recent improvements to employee benefits. That is, the initial unfunded liability is zero. Alternatively, any initial unfunded liability could be amortized by means of a separate schedule of payments from the plan sponsor. (see, e.g., McGill et al., 2004, p. 620).
The pension plan actuary calculates actuarial gains and losses at yearly valuations of the pension plan. A gain (loss) occurs if experience is more (less) favorable than was assumed at the previous valuation (McGill et al., 2004, p. 621). We assume here that the only source of gains and losses is the investment performance of the pension fund. That is, all other economic and demographic factors turn out to be as assumed.
The typical actuarial practice is to amortize investment gains or losses over 5 years (McGill et al., 2004, p. 686), which is also assumed here. If investment returns are consistently lower than the investment return assumption iA made by the actuary at each actuarial valuation, then investment losses will occur and will build up into a deficit. Higher employer contributions are then required as these losses are amortized. Our aim is to compare the amortization method with the targeted-contribution method given by Equation (4) (with a time unit of 1 year as opposed to 1 month).
Figure 2 shows the distribution of deficits after 40 years when the investment return assumption iA overstates the long-term average real return on the fund by 3 percent per annum. (Using the data from Barclays Capital, (2009, the pension fund makes an average annual real return of 6.15 percent, so iA = 9.15 percent here. Parameters λ1 and λ2 in Equation (4) are equal to 0.5 and 0.03, respectively. A 40-year horizon is appropriate because employees typically have a 40- to 50-year working lifetime.) The spread of deficits, and the probability of large deficits, appear to be smaller when the targeted-contribution method is used than when amortization is used.
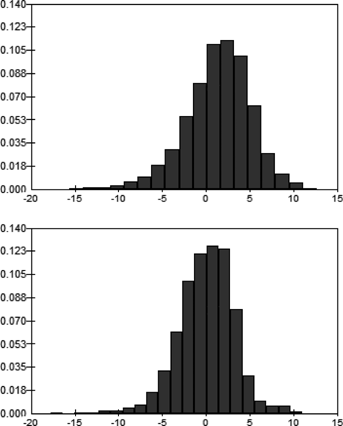
Table 7 displays various statistics for the deficits under both the amortization and the targeted-contribution method, for different errors in the investment return assumption iA. The standard deviation and 95th percentile of the deficit show that the targeted-contribution method is less risky than the amortization method in the sense that large deficits are less likely under the former. The targeted-contribution method is also less sensitive to errors in the investment return assumption, as the 95th percentile and standard deviation do not change considerably for different investment return assumptions. This mirrors earlier results.
| Error in iA | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | Mean Square Deficit | ||||
|---|---|---|---|---|---|---|---|---|
| A | TC | A | TC | A | TC | A | TC | |
| −3% | −1.607 | −0.069 | 4.673 | 3.257 | 5.186 | 4.537 | 24.414 | 10.613 |
| −2% | −1.046 | −0.048 | 4.503 | 3.252 | 5.515 | 4.551 | 21.370 | 10.579 |
| −1% | −0.512 | −0.027 | 4.342 | 3.248 | 5.826 | 4.565 | 19.118 | 10.547 |
| 0 | −0.003 | −0.007 | 4.190 | 3.243 | 6.115 | 4.579 | 17.559 | 10.516 |
| 1% | 0.483 | 0.014 | 4.046 | 3.238 | 6.420 | 4.593 | 16.605 | 10.487 |
| 2% | 0.948 | 0.033 | 3.910 | 3.234 | 6.671 | 4.606 | 16.182 | 10.459 |
| 3% | 1.391 | 0.053 | 3.780 | 3.229 | 6.937 | 4.619 | 16.222 | 10.432 |
Various commentators (e.g., Watson Wyatt Worldwide, 2009) have noted a shift from equities to bonds in pension fund asset allocation over the past few years. We repeated the simulations above for equity:gilt allocations of 50:50 and 40:60. The conclusions are essentially unchanged; that is, the targeted-contribution method results in smaller deficits and is less sensitive to the return assumption.
The average values of the pension fund assets and contribution over 40 years are shown in Table 8 for a 40:60 equity:gilt portfolio, which has a long-term average real return of 4.82 percent, and a real return assumption iA of 5.82 percent (so that the error in iA is 1 percent). Because the investment return assumption iA is too optimistic, both the amortization and targeted-contribution methods start off with a low contribution from the employer initially. As deficits mount in the pension fund, the targeted-contribution method demands larger contributions more quickly than the amortization method. After 40 years, the fund levels off at an average value of 16.92 in the targeted-contribution case and 16.45 in the amortization case, compared to the actuarial liability value of 16.94. The average deficit is therefore almost zero with the targeted-contribution method, whereas it is never completely removed under amortization and a higher contribution is permanently required on average.
| Time (Years) | Mean Fund | Mean Contribution | ||
|---|---|---|---|---|
| A | TC | A | TC | |
| 0 | 16.9364 | 16.9364 | 0.0680 | 0.0680 |
| 1 | 16.7734 | 16.7734 | 0.1044 | 0.1544 |
| 2 | 16.6463 | 16.6964 | 0.1393 | 0.2001 |
| 3 | 16.5433 | 16.6597 | 0.1753 | 0.2268 |
| 4 | 16.4751 | 16.6521 | 0.2108 | 0.2391 |
| 5 | 16.4374 | 16.6539 | 0.2469 | 0.2467 |
| 6 | 16.4485 | 16.6731 | 0.2438 | 0.2450 |
| 7 | 16.4478 | 16.6844 | 0.2443 | 0.2469 |
| 8 | 16.4393 | 16.6924 | 0.2455 | 0.2502 |
| 9 | 16.4497 | 16.7183 | 0.2432 | 0.2438 |
| 10 | 16.4503 | 16.7320 | 0.2419 | 0.2431 |
| 15 | 16.4348 | 16.7877 | 0.2471 | 0.2407 |
| 20 | 16.4433 | 16.8390 | 0.2456 | 0.2328 |
| 25 | 16.4576 | 16.8750 | 0.2405 | 0.2261 |
| 30 | 16.4588 | 16.8939 | 0.2378 | 0.2240 |
| 35 | 16.4454 | 16.9007 | 0.2420 | 0.2262 |
| 40 | 16.4541 | 16.9194 | 0.2423 | 0.2209 |
Note that under both methods, the pension fund is in balance after 40 years. In the amortization case, a fund of 16.45, with contribution income of 0.24 and benefit outgo of 1, accumulates at an investment return of 4.82 percent to 16.45 again after a year. In the targeted-contribution case, a fund of 16.91, with contribution income of 0.22 and benefit outgo of 1, accumulates at an investment return of 4.82 percent to 16.91 again after a year. However, the pension fund is in balance with a nearly zero average deficit in the latter case.
On the Barclays Capital (2009) data, autocorrelations on real equity returns up to a lag of 10 years were not significant at 5 percent. Autocorrelations on real gilt returns up to lag 10 were not significant at 5 percent, except at lag 5. This appears to have little physical meaning. Nevertheless, we also incorporated serial correlation in the simulations by resampling using blocks of 3 years and 5 years (Efron and Tibshirani, 1993). Again, the qualitative conclusions above are unchanged. (The detailed results are not included here to save space and are available from the authors.)
CONCLUSION
We considered a savings plan where contributions are received and invested for the purpose of meeting a given liability in the future. An example could be an investment and savings vehicle being used to meet school or college fees in 5 years time. In practice, financial advisers recommend a fixed and level regular contribution, based on an assumed investment return on the fund. Since investment returns are random and will be different from the assumed investment return, the fund usually undershoots or overshoots the target fund objective, leading to a deficit or surplus, respectively.
We investigated an alternative savings plan, based on a method borrowed from industrial process control and econophysics. Under this method, contributions are flexible and are adjusted and targeted systematically so that the fund objective is met. We used stochastic simulations to measure the risk that a terminal deficit occurs, that is, that end-of-period wealth falls short of the target fund. The targeted-contribution method appears to be less risky than the fixed-contribution method, in the sense that the volatility and 95th percentile of the deficit are smaller in the former case. In particular, the size of deficits in the targeted-contribution plan is less sensitive to errors in the financial planner's estimate of future investment return than in the fixed-contribution plan. These results appear to be robust under a wide range of parameter values, with and without constraints on contributions, with asset returns that are serially correlated, and with returns that incorporate large but rare market corrections and exhibit nonnormality. Finally, we applied the targeted-contribution method to a defined-benefit pension plan, with a long investment horizon and using bootstrap resampling from actual equity and bond market data. The standard deviation, mean square and 95th percentile of the deficit in the pension fund were again lower with the targeted-contribution funding method than with a conventional pension funding method.
A practical implication of this research for financial planners is that savings plans can be designed that are more flexible for individuals. A suitable design, such as the one described in this article, should be not only flexible but also targeted in a systematic way to achieve robust outcomes for individual investors.
This research can be extended in several directions, as discussed in the article. First, the asset allocation decision should be explored. Lifestyling portfolios can be readily included (Shiller, 2005). The method employed to adjust contributions can also be used to adjust asset allocation, as in Gandolfi, Sabatini, and Rossolini (2007). Second, the investment objective considered in this article was simple and related to the end-of-period wealth only. If the targeted-contribution plan is used for longer-term savings, such as retirement plans, then the utility of both wealth at retirement and consumption during the accumulation phase must be considered. Third, the choice of parameters for the targeted-contribution plan was discussed but further work, to optimize these parameters and with back-testing on historical data, is required. Fourth, practical considerations such as taxes and transaction costs can be included. Finally, the distribution of the deficit and the evolution of contributions in the targeted-contribution method are also of interest.
Appendix: Variables λ1 and λ2
The effect of varying λ1 and λ2 on the targeted-contribution plan is considered here.
Effect on Interim Contributions
Tables A1 and A2 show the variance of the contributions paid at different points in time by an investor in the targeted-contribution savings plan. Variation with λ1 is displayed in Table A1 and variation with λ2 is in Table A2. Contributions become more volatile as either λ1 or λ2 increases. This is a reasonable result since higher values of λ1 and λ2 in Equation (4) will magnify the effect of random deficits {Dt}, resulting in greater variability in contribution Ct. We also illustrate this in Figure A1 which shows three sample paths for contribution in the targeted-contribution plan, for λ2=0, 0.01 and 0.3. As anticipated, there is more variability in the contributions required from the investor in the targeted-contribution plan when λ2 = 0.3 than when λ2 = 0.01. When λ2 = 0.3, contributions are briefly negative so that the investor is actually required to withdraw monies from the fund.
Note: The three sample paths correspond to the same sample path of investment returns on the fund. F = 100, 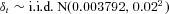 , iA = 0.7%, λ1 = 0.1.
, iA = 0.7%, λ1 = 0.1.
| Time (Months) | Values of λ1 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.25 | 0.5 | 0.75 | 1 | 1.25 | 1.5 | 1.75 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0.0004 | 0.0010 | 0.0259 | 0.0470 | 0.0784 | 0.1281 | 0.2197 | 0.4532 |
| 20 | 0.0072 | 0.0485 | 0.1127 | 0.2031 | 0.3367 | 0.5542 | 0.9709 | 2.0829 |
| 30 | 0.0354 | 0.1207 | 0.2691 | 0.4864 | 0.8149 | 1.3551 | 2.3960 | 5.2960 |
| 40 | 0.0962 | 0.2516 | 0.5456 | 0.9546 | 1.5593 | 2.5528 | 4.5084 | 10.1899 |
| 50 | 0.2051 | 0.4133 | 0.8861 | 1.5701 | 2.6174 | 4.3769 | 7.8158 | 17.5756 |
| 60 | 0.3891 | 0.6450 | 1.3724 | 2.4449 | 4.0635 | 6.7603 | 12.1910 | 28.3791 |
- Note: F = 100,
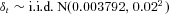 , iA = 0.7%, and λ2 = 0.01.
, iA = 0.7%, and λ2 = 0.01.
| Time (Months) | Values of λ2 | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.25 | 0.5 | 0.75 | 1 | 1.5 | 2 | 2.5 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0.0062 | 0.0428 | 0.0843 | 0.1398 | 0.1993 | 0.3568 | 0.6269 | 1.1035 |
| 20 | 0.0308 | 0.2297 | 0.4646 | 0.7296 | 1.0452 | 1.8979 | 3.3338 | 6.0679 |
| 30 | 0.0778 | 0.5920 | 1.1826 | 1.9173 | 2.8354 | 5.3257 | 8.8990 | 16.4625 |
| 40 | 0.1611 | 1.2385 | 2.4884 | 3.9304 | 5.5867 | 10.1383 | 18.2761 | 32.2095 |
| 50 | 0.2654 | 2.0423 | 4.2115 | 6.7278 | 9.6970 | 18.2082 | 30.9891 | 57.3088 |
| 60 | 0.4151 | 3.1767 | 6.7304 | 10.7284 | 15.3809 | 28.7585 | 48.4475 | 87.6670 |
- Note: F = 100,
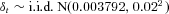 , iA = 0.7%, and λ1 = 0.2.
, iA = 0.7%, and λ1 = 0.2.
For large values of λ1 and λ2, the targeted-contribution plan appears to overcompensate for past deficits leading to large undesirable swings in contribution payments. Since investors may be unable to afford large increases in their monthly savings and contributions, large values of λ1 and λ2 should be avoided.
Effect on End-Wealth
We also investigate the effect of varying λ1 and λ2 on the risk of a terminal deficit. Tables A3 and A4 show various statistics for the deficit at time 60, for various values of λ1 and λ2, respectively. Figure A2 contains a volatility surface, that is, a plot of the standard deviation of the terminal deficit as both λ1 and λ2 vary. For very large values of λ1 and λ2 beyond those shown in Tables A3 and A4 the simulations did not converge and near-infinite standard deviations were obtained.
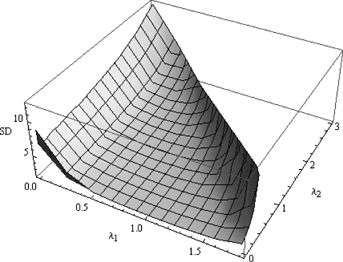
Note: F = 100, 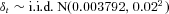 , iA = 0.7%.
, iA = 0.7%.
| λ1 | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | |||
|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | |
| 0 | 9.1119 | 0.1658 | 8.5931 | 6.5359 | 22.4008 | 10.3859 |
| 0.1 | 9.1119 | 0.5603 | 8.5931 | 4.0277 | 22.4008 | 6.9879 |
| 0.2 | 9.1119 | 0.5230 | 8.5931 | 3.1667 | 22.4008 | 5.6414 |
| 0.4 | 9.1119 | 0.4060 | 8.5931 | 2.4673 | 22.4008 | 4.3927 |
| 0.6 | 9.1119 | 0.3242 | 8.5931 | 2.1766 | 22.4008 | 3.8536 |
| 0.8 | 9.1119 | 0.2685 | 8.5931 | 2.0409 | 22.4008 | 3.5995 |
| 1 | 9.1119 | 0.2287 | 8.5931 | 1.9958 | 22.4008 | 3.4647 |
| 1.2 | 9.1119 | 0.1992 | 8.5931 | 2.0273 | 22.4008 | 3.5217 |
| 1.4 | 9.1119 | 0.1764 | 8.5931 | 2.1521 | 22.4008 | 3.7612 |
| 1.6 | 9.1119 | 0.1582 | 8.5931 | 2.4426 | 22.4008 | 4.1814 |
| 1.8 | 9.1119 | 0.1423 | 8.5931 | 3.2023 | 22.4008 | 5.3520 |
| 2 | 9.1119 | 0.1171 | 8.5931 | 9.7901 | 22.4008 | 16.1378 |
- Note: Fixed-contribution plan (FC) is independent of λ1 but statistics are shown for comparison. F = 100,
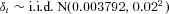 , iA = 0.7%, and λ2 = 0.01.
, iA = 0.7%, and λ2 = 0.01.
The first observation that can be made is that the point at λ1 = λ2 = 0 on Figure A2 corresponds to the fixed-contribution plan. Volatility of the deficit improves dramatically even for small values of λ1 and λ2 in the neighborhood of this point. Tables A3 and A4 bear this out: the risk of a deficit is lower under the targeted-contribution plan than under the fixed-contribution plan except for very large values of λ1 or λ2.
A second observation from Figure A2 is that the standard deviation of the deficit is globally minimized at λ1 = 1 and λ2 = 0 in the targeted-contribution plan. This is also a reasonable result since, from Equation (4), this leads to Ct = C + Dt, thus requiring the investor to make up immediately for a poor investment performance in any month by paying off the entirety of the deficit at the beginning of the next month. Since investors will typically wish to smooth their consumption and savings, this is a not a desirable parameterization for the targeted-contribution plan.
Third, we find that risk in the terminal deficit decreases and then increases as λ1 increases. There are minima in the standard deviation and 95th percentile of deficits in the targeted-contribution plan at λ1 ≈ 1 (see Table A3). This can be explained as follows. Suppose that returns were poor and there was a deficit in the previous month. When λ1 < 1 (approximately), larger values of λ1 mean that larger contributions are paid at the beginning of the current month. Deficits will therefore accumulate more slowly over successive months, and the risk of a large terminal deficit is lower for larger values of λ1. However, for very large values of λ1 (when λ1 > 1 approximately), the additional contribution required because of a deficit in the previous month is larger than the deficit itself. As the contributions are fed back into the plan, an amplification or overcompensation effect is induced and this results in larger deficits.
| λ2 | Mean Deficit | Standard Deviation of Deficit | 95th Percentile of Deficit | |||
|---|---|---|---|---|---|---|
| FC | TC | FC | TC | FC | TC | |
| 0 | 9.1119 | 1.3856 | 8.5931 | 3.2492 | 22.4008 | 6.5924 |
| 0.005 | 9.1119 | 0.8151 | 8.5931 | 3.1864 | 22.4008 | 5.9590 |
| 0.01 | 9.1119 | 0.5230 | 8.5931 | 3.1667 | 22.4008 | 5.6414 |
| 0.02 | 9.1119 | 0.2818 | 8.5931 | 3.1510 | 22.4008 | 5.3726 |
| 0.04 | 9.1119 | 0.1456 | 8.5931 | 3.1407 | 22.4008 | 5.1856 |
| 0.05 | 9.1119 | 0.1169 | 8.5931 | 3.1398 | 22.4008 | 5.1721 |
| 0.06 | 9.1119 | 0.0977 | 8.5931 | 3.1410 | 22.4008 | 5.1193 |
| 0.08 | 9.1119 | 0.0735 | 8.5931 | 3.1484 | 22.4008 | 5.1436 |
| 0.1 | 9.1119 | 0.0589 | 8.5931 | 3.1586 | 22.4008 | 5.0992 |
| 0.2 | 9.1119 | 0.0302 | 8.5931 | 3.2185 | 22.4008 | 5.1633 |
| 0.4 | 9.1119 | 0.0139 | 8.5931 | 3.3056 | 22.4008 | 5.3811 |
| 0.6 | 9.1119 | 0.0089 | 8.5931 | 3.4172 | 22.4008 | 5.5390 |
| 0.8 | 9.1119 | 0.0079 | 8.5931 | 3.5055 | 22.4008 | 5.6934 |
| 1 | 9.1119 | 0.0058 | 8.5931 | 3.6229 | 22.4008 | 5.8245 |
| 1.5 | 9.1119 | 0.0051 | 8.5931 | 4.0118 | 22.4008 | 6.5897 |
| 2 | 9.1119 | 0.0009 | 8.5931 | 4.6413 | 22.4008 | 7.4038 |
| 2.5 | 9.1119 | 0.0036 | 8.5931 | 5.6160 | 22.4008 | 9.0884 |
| 3 | 9.1119 | 0.0022 | 8.5931 | 7.5552 | 22.4008 | 12.4082 |
| 3.5 | 9.1119 | -0.0722 | 8.5931 | 19.0858 | 22.4008 | 30.9285 |
- Note: Fixed-contribution plan (FC) is independent of λ2 but statistics are shown for comparison. F = 100, δt ∼ i.i.d. N(0.003792, 0.022), iA = 0.7%, and λ1 = 0.2.
A similar effect as above occurs when λ2 increases. In Table A4, the turning points in the standard deviation and 95th percentile of deficits in the targeted-contribution plan occur at λ2 ≈ 0.055, compared to the turning point at λ1 ≈ 1. Since λ2 acts as a tax rate on the sum of all past deficits, whereas λ1 operates only on the latest deficit (see Equation (4)), λ2 has a larger effect on the dynamics of the plan compared to λ1, and the amplification effect described earlier happens more readily as λ2 increases.
We also note from Figure A2 that for large λ1, the volatility in the deficit does not decrease as λ2 increases: it is minimized when λ2 = 0. Again, this may be explained using the earlier tax analogy. When the current deficit is taxed at a large enough rate λ1, even a small tax rate λ2 on the historic sum of deficits is enough to induce overcompensation and make deficits more volatile.
Time Series Analysis
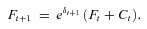 (A1)
(A1)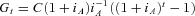 . This target therefore increases every month according to
. This target therefore increases every month according to
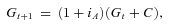 (A2)
(A2)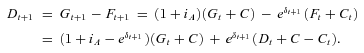 (A3)
(A3)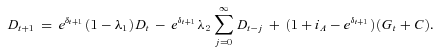 (A4)
(A4)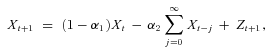 (A5)
(A5)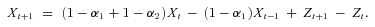 (A6)
(A6)Comparing Equations (A4) and (A5), we find that the deficit process {Dt} resembles an ARMA(2, 1) process except that: (1) {Dt} has random coefficients; (2) its innovations process, 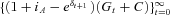 , is an independent sequence if investment returns {δt} form an independent sequence; (3) its innovations process is not identically distributed since Gt in Equation (A2) is deterministic but time varying; (4) its innovations process has a zero mean if
, is an independent sequence if investment returns {δt} form an independent sequence; (3) its innovations process is not identically distributed since Gt in Equation (A2) is deterministic but time varying; (4) its innovations process has a zero mean if 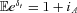 , which will only hold approximately because the planner's estimate of return iA will likely differ from the true mean, as argued earlier.
, which will only hold approximately because the planner's estimate of return iA will likely differ from the true mean, as argued earlier.
The variance of a weakly stationary process (which does not start from equilibrium) converges to a finite value as 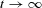 . Notwithstanding the differences between {Dt} and {Xt} mentioned earlier, the similarity that {Dt} has to an ARMA(2, 1) process may lead us to surmise that the volatility of the terminal deficit will stabilize if λ2 > 0, 2λ1 + λ2 < 4, and 0 < λ1 < 2, approximately. Our numerical simulations are indeed consistent with this. The simulations did not converge for {λ1 > 2, λ2 = 0.01} in Table A3, and for {λ2 > 3.5, λ1 = 0.2} in Table A4. The volatility surface in Figure A2 turns sharply upward roughly along the line 2λ1 + λ2 = 4.
. Notwithstanding the differences between {Dt} and {Xt} mentioned earlier, the similarity that {Dt} has to an ARMA(2, 1) process may lead us to surmise that the volatility of the terminal deficit will stabilize if λ2 > 0, 2λ1 + λ2 < 4, and 0 < λ1 < 2, approximately. Our numerical simulations are indeed consistent with this. The simulations did not converge for {λ1 > 2, λ2 = 0.01} in Table A3, and for {λ2 > 3.5, λ1 = 0.2} in Table A4. The volatility surface in Figure A2 turns sharply upward roughly along the line 2λ1 + λ2 = 4.
The simulations and time series analysis in this section have a practical implication for financial planners: λ1 and λ2 should not be large (say λ1 < 0.5 and λ2 < 0.06) since typical investors wish to smooth consumption and will find volatile and unstable contributions undesirable.
REFERENCES
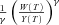 of terminal wealth W(T) relative to terminal income Y(T) at time horizon T. However, in our setting, scaling contribution and end-wealth by nonrandom labor income will simply scale Var Ct and Var Ft.
of terminal wealth W(T) relative to terminal income Y(T) at time horizon T. However, in our setting, scaling contribution and end-wealth by nonrandom labor income will simply scale Var Ct and Var Ft.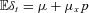 does not change as σx increases, but that the mean arithmetic return
does not change as σx increases, but that the mean arithmetic return 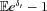 increases as σx increases, since
increases as σx increases, since 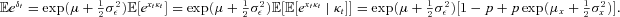 The mean deficit for both fixed and targeted-contribution plans thus decreases as σx increases in Table 5. The standard deviation and 95th percentile of deficit nevertheless increase as σx increases, highlighting the greater risk to end-wealth posed by volatile market corrections.
The mean deficit for both fixed and targeted-contribution plans thus decreases as σx increases in Table 5. The standard deviation and 95th percentile of deficit nevertheless increase as σx increases, highlighting the greater risk to end-wealth posed by volatile market corrections.



