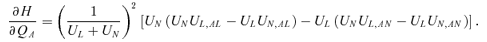Consumption Externality and Equilibrium Underinsurance
Dr. Tzeng can be contacted via e-mail: [email protected]
Abstract
Relative consumption has been found to be crucial in many areas, such as asset pricing, the design of taxation, and economic growth. This article extends this line of research to the individual's insurance decision. We first define “keeping up with the Joneses” in the purchase of insurance and find that jealousy does not necessarily give rise to “keeping up with the Joneses.” We also identify several sufficient conditions that cause the optimal coverage in the private market to be less than the social optimum (equilibrium underinsurance). Jealousy is found to be neither a sufficient nor a necessary condition for equilibrium underinsurance. We further show that a social welfare maximizing government could adopt a tax system to correct for the consumption externality and make individuals better off.
Introduction
There has been a long debate in the literature over whether the government should intervene in the individual's choice of insurance if there exists a market for private insurance. Some studies (see Kaplow, 1992a,b; Selden, 1993; Blomqvist and Johansson, 1997) have shown that the government's intervention in insurance may distort the incentive of the individual to purchase insurance in the private market and thereby reduce the social welfare, whereas certain other studies have shown that the government's intervention in the insurance market could improve social welfare by taking into consideration government efficiency (see Diamond, 1992; Mitchell, 1998; Huang and Tzeng, 2007a,b), redistribution (see Rochet, 1991; Cremer and Pestieau, 1996; Coronado, Fullerton, and Glass, 2000; Gustman and Steinmeier, 2001; Liebman, 2002; Brown, 2003), and asymmetric information in the private insurance market (see Akerlof, 1970; Eckstein, Eichenbaum, and Peled, 1985).
Although the previous literature has provided many ingenious findings, as far as we know, none of the studies has ever considered the consumption externality, which is a very important factor discovered recently in support of the view that the government's intervention might increase social welfare.1 Besides the government's intervention, relative consumption has been found to be crucial in many other areas, such as asset pricing2 and economic growth.3 This article extends this line of research to the individual's insurance decision. In this article, we intend to analyze the effect of the consumption externality on insurance and to examine whether the government could make individuals better off by intervening in the private insurance market.4
In the literature discussing the consumption externality and government intervention, Dupor and Liu (2003) have found that if the preference of the individual exhibits jealousy, then the individual will consume more than the socially optimal amount since the individual does not take the consumption externality into consideration. In this article, we intend to ask another question: if the preference of the individual exhibits jealousy, does the individual take more risks (i.e., purchase less insurance) than that supporting the social optimum? The above problem is closely related to, but not the same as, the issue in Dupor and Liu (2003) since the insurance decision could influence the individual's consumption not only in both the loss state and the no-loss state but also in the opposite direction. It is worth recognizing that by purchasing less insurance, the individual can generally save part of the insurance premium and consume more when the loss does not occur. However, if the individual purchases less insurance and the loss occurs, the net loss of the individual will increase and the individual will be forced to consume less since the risk is not well covered. By noting that the insurance decision is critical for the individual's consumption, we intend to analyze the optimal insurance choice for the individual with regard to relative consumption. Moreover, we further analyze whether the private optimum in terms of the insurance purchased is the same as the social optimum and whether or not it is necessary for the government to intervene in the private insurance market in order to correct for the consumption externality.
When examining how the consumption externality affects the individual's decision, researchers usually assume that the individual's utility is a function of his or her own consumption level and the per capita consumption level in the economy (Gali, 1994; Dupor and Liu, 2003). In other words, there is only one reference point, per capita consumption, in the setting of the previous research. However, we observe that in addition to per capita consumption, the individual's utility may also be affected by the average consumption level of some specific groups. For example, an individual may be jealous of people who do not suffer losses in their consumption. On the other hand, the individual may also show mercy toward the people who suffer losses in their consumption. This means that individuals may have multiple reference points in their utility. In order to capture this behavior, we first assume that individuals are identical and suffer a random loss following a Bernoulli distribution. Therefore, we have two different groups of individuals: one group is in the loss state and the other group is in the no-loss state. The group in the loss state will have less final wealth to consume while the group in the no-loss state will have more final wealth to consume. Second, we assume that in the representative agent's utility function, there are three reference points: the average per capita consumption, the per capita consumption of the group in the loss state, and the per capita consumption of the group in the no-loss state.
In this article, we first examine the two effects caused by relative consumption: jealousy and “keeping up with the Joneses.” We measure jealousy and admiration according to each reference point since we have three reference points rather than one reference point in our utility setting. We define the individual's preference in terms of whether his or her utility exhibits jealousy (admiration) with regard to the per capita consumption in the loss state [the per capita consumption in the no-loss state, the average per capita consumption], if the marginal utility of the per capita consumption in the loss state [the per capita consumption in the no-loss state, the average per capita consumption] is negative (positive). Note that, in the article, we allow the preference of the individual to exhibit jealousy in one state but to exhibit admiration in the other state.
As regards “keeping up with the Joneses,” our definition is similar to, but not exactly the same as, that in the literature. Researchers define “keeping up with the Joneses” as meaning that an increase in per capita consumption will increase the individual's consumption level.5 In our model, the individual's consumption level is affected by his or her insurance decision. Thus, we pay attention to whether individuals change their purchase of insurance coverage when other people increase their purchase of insurance coverage, and we redefine “keeping up with the Joneses” as referring to the case where an individual increases the amount of his or her insurance when the amount of the insurance per capita increases. We find that jealousy does not necessarily give rise to “keeping up with the Joneses.” The condition for “keeping up with the Joneses” depends on how the change in the three reference points affects the marginal rate of substitution between the individual's consumption in the loss and no-loss states.
Second, we seek to determine whether the equilibrium in the private market under a consumption externality is socially optimal. If the optimal coverage in the private market is less (greater) than the social optimum, we refer to this case as “equilibrium under- (over-) insurance.” We find that jealousy is not able to generate equilibrium underinsurance. The condition for equilibrium underinsurance depends on how the change in the three reference points affects the individual's utility. Note that we do not assume that the individual utility function is measured by expected utility or is separable as is commonly assumed in the literature. Our results hold for a large set of individual preferences.
In the case where the utility of the individual is not related to average per capita consumption, we find that the individual will be equilibrium underinsured if the marginal rate of substitution between the consumption in the loss state and the per capita consumption in the loss state is larger than that between the consumption in the no-loss state and the per capita consumption in the no-loss state. It is very important to note that equilibrium underinsurance cannot be determined by only the jealousy preference. If the preference of the individual exhibits jealousy in both the loss state and the no-loss state, then the individual may not be equilibrium underinsured. On the other hand, even if the preference of the individual exhibits admiration in the loss state or in the no-loss state, then the individual may still choose to be equilibrium underinsured. Thus, we show that jealousy is neither a sufficient nor a necessary condition for equilibrium underinsurance.
In the case where the average per capita consumption is the only source of the consumption externality, we find that the optimum in the private insurance market is also a social optimum if the insurance price is actuarially fair. Moreover, we find that if the insurance price is actuarially unfair, the individual will be equilibrium underinsured when the utility of the individual exhibits jealousy.
Finally, we demonstrate how the government corrects for the consumption externality by providing tax deductions on the individual's net losses and on the insurance premium. To analyze how a social optimum under the consumption externality can be reached, we focus on the case of equilibrium underinsurance.6 We try to find the optimal tax deduction rates for the individual's net losses and insurance premium. We find the condition for arriving at the private optimum to be the same as the social optimum. Specifically, we find that, to correct for the consumption externality, the optimal tax deduction rate on the individual's net losses should be lower than the optimal tax deduction rate on the insurance premium.
The remainder of the article proceeds as follows. The model is established in the second section. “Keeping up with the Joneses” is then defined in the third section. The condition of equilibrium underinsurance is derived in the fourth section. This is followed by a further analysis of the optimal tax deduction. The final section concludes the article.
Model Setting
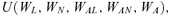 (1)
(1)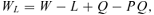 (2)
(2)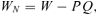 (3)
(3)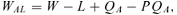 (4)
(4)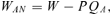 (5)
(5)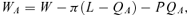 (6)
(6)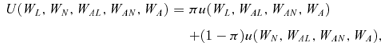 (7)
(7)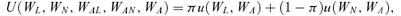 (8)
(8)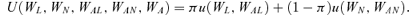 (9)
(9)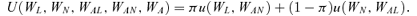 (10)
(10)Assume that U is twice differentiable. Let Ui denote the first derivative of the utility function with respect to Wi, i=L, N, AL, AN, and A. Furthermore, let Ui,j denote the derivative of Ui with respect to Wj, i, j=L, N, AL, AN, and A. Assume that UL > 0 and UN > 0, which means that an increase in the individual's own consumption will increase his or her utility.
We further characterize UAL < 0 (UAL > 0) as meaning that the preference of the individual exhibits jealousy (admiration) with regard to the per capita consumption in the loss state. In Case II above, UAL < 0 (UAL > 0) is equivalent to 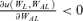 (
(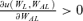 ), which means that individuals in the loss state envy (admire) an increase in the consumption of others who are also in the loss state. In Case III above, UAL < 0 (UAL > 0) is equivalent to
), which means that individuals in the loss state envy (admire) an increase in the consumption of others who are also in the loss state. In Case III above, UAL < 0 (UAL > 0) is equivalent to 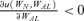 (
(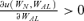 ), which means that individuals in the no-loss state will envy (admire) an increase in the consumption of those suffering a loss.
), which means that individuals in the no-loss state will envy (admire) an increase in the consumption of those suffering a loss.
Similar to the above definition, UAN < 0 (UAN > 0) denotes that the preference of the individual exhibits jealousy (admiration) with regard to the per capita consumption in the no-loss state. UA < 0 (UA > 0) denotes that the preference of the individual exhibits jealousy (admiration) with regard to the average per capita consumption.
We further assume that UL+UAL > 0 and UN+UAN > 0, which indicates that if every one at the same state increases consumption by one dollar, the individual will be happy with the increase. These two conditions confine the decision makers to a set where individuals care more about their own consumption than another's consumption although they could also be jealous.
Keeping up With the Joneses
In this section, we would like to examine the condition for “keeping up with the Joneses.” As mentioned in the Introduction, we define “keeping up with the Joneses” as 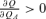 , which refers to the case where an increase in per capita insurance coverage will increase the individual's optimal choice of insurance coverage. This is not the same as the traditional concept of “keeping up with the Joneses” because an increase in Q increases the consumption of the individual in the loss state but decreases it in the no-loss state. Furthermore, an increase in QA does not necessarily result in an increase in the reference consumption levels in our setting. From Equations (4) and (5), we know that an increase in QA represents an increase in the per capita consumption in the loss state and a decrease in the per capita consumption in the no-loss state. From Equation (6), if the premium is unfair, i.e., P > π, then an increase in QA is the same as a decrease in average per capita consumption. If the premium is fair, i.e., P=π, then an increase in QA does not change the average per capita consumption. The following theorem11 provides the condition for “keeping up with the Joneses”:
, which refers to the case where an increase in per capita insurance coverage will increase the individual's optimal choice of insurance coverage. This is not the same as the traditional concept of “keeping up with the Joneses” because an increase in Q increases the consumption of the individual in the loss state but decreases it in the no-loss state. Furthermore, an increase in QA does not necessarily result in an increase in the reference consumption levels in our setting. From Equations (4) and (5), we know that an increase in QA represents an increase in the per capita consumption in the loss state and a decrease in the per capita consumption in the no-loss state. From Equation (6), if the premium is unfair, i.e., P > π, then an increase in QA is the same as a decrease in average per capita consumption. If the premium is fair, i.e., P=π, then an increase in QA does not change the average per capita consumption. The following theorem11 provides the condition for “keeping up with the Joneses”:
 if
if
 . Furthermore,
. Furthermore,
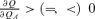 if
if
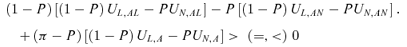
It is very important to recognize that the condition of “keeping up with the Joneses” is not the same as that of jealousy. Lemmas 1–3 further characterize “keeping up with the Joneses” as shown below:
Lemma 1: If U L,AL=UN,AL= 0 and U L,AN=UN,AN= 0, then
- (i)
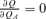 when
P=π.
when
P=π. - (ii)
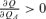 when
P > π and UNUL,A−ULUN,A < 0.
when
P > π and UNUL,A−ULUN,A < 0.
Proof: From Theorem 1, given that UL,AL=UN,AL= 0 and UL,AN=UN,AN= 0, 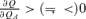 , if (π−P)[(1 −P)UL,A−PUN,A] > (=, <) 0. Thus,
, if (π−P)[(1 −P)UL,A−PUN,A] > (=, <) 0. Thus, 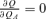 when P=π. On the other hand, when P > π,
when P=π. On the other hand, when P > π, 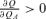 if (1 −P)UL,A−PUN,A < 0. Note that
if (1 −P)UL,A−PUN,A < 0. Note that 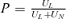 from Equation (11). Thus,
from Equation (11). Thus, 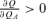 when P > π and UNUL,A−ULUN,A < 0. Q.E.D.
when P > π and UNUL,A−ULUN,A < 0. Q.E.D.
Lemma 1 discusses the case where the individual's utility function is additively separable between own consumption in both states and per capita consumption in the loss state, and between own consumption in both states and per capita consumption in the no-loss state. Case I referred to in the previous section is one of the examples where UAL=UAN= 0, implying that UL,AL=UN,AL= 0 and UL,AN=UN,AN= 0. In Case I, the average per capita consumption is the only reference consumption. Under an actuarially fair premium, an increase in per capita insurance coverage does not have any influence on the average per capita consumption. Since the only source of reference point does not change, the individual's insurance decision will remain the same. Thus, individuals will never try to “keep up with the Joneses” under an actuarially fair premium.12
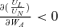 . In Case I, the above condition is equal to
. In Case I, the above condition is equal to
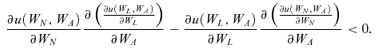 (12)
(12)Thus, even if individuals exhibit jealousy due to the increase in the average per capita consumption level,13 they may or may not increase their demand for insurance when other people increase their purchase of coverage. This is an example showing that only jealousy cannot ensure “keeping up with the Joneses.”
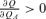 when
when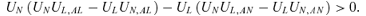
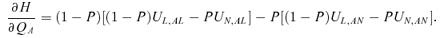
Therefore, 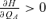 if UN(UNUL,AL−ULUN,AL) −UL(UNUL,AN−ULUN,AN) > 0.
if UN(UNUL,AL−ULUN,AL) −UL(UNUL,AN−ULUN,AN) > 0.
Q.E.D.
Lemma 2 analyzes the case where the individual's utility is additively separable between own consumption in both states and average per capita consumption. Cases II and III are two examples where UA= 0, implying that UL,A=UN,A= 0. Note that UN(UNUL,AL−ULUN,AL) −UL(UNUL,AN−ULUN,AN) > 0 can be further rewritten as 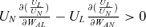 . Thus, the condition of “keeping up with the Joneses” is correlated with whether an increase in WAL and WAN increases the marginal rate of substitution between individual consumption in the loss state and in the no-loss state. For example, if
. Thus, the condition of “keeping up with the Joneses” is correlated with whether an increase in WAL and WAN increases the marginal rate of substitution between individual consumption in the loss state and in the no-loss state. For example, if 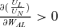 and
and 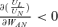 , then the condition of “keeping up with the Joneses” always holds.
, then the condition of “keeping up with the Joneses” always holds.
Lemma 3: If
U
L,A=UN,A= 0
and
U
L,AN=UN,AL= 0, then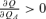 whenU
whenU UL,AL+U
UL,AL+U UN,AN > 0.
UN,AN > 0.
Proof: Lemma 3 immediately follows Lemma 2. Q.E.D.
U
L,AN=UN,AL= 0 means that the individual's utility is additively separable between the individual's own consumption in the loss state and per capita consumption in the no-loss state, as well as between the individual's own consumption in the no-loss state and the per capita consumption in the loss state. Case II is one of the examples described by Lemma 3. The condition shows that if UL,AL > 0 and UN,AN > 0 (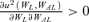 and
and 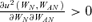 in Case II), then we could observe “keeping up with the Joneses” in this case.
in Case II), then we could observe “keeping up with the Joneses” in this case.
Equilibrium Underinsurance
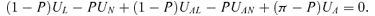 (13)
(13)Assume that the second-order condition holds to support the interior solution. By comparing Equations (11) and (13), we can find the relationship between the optimum in the private market and the social optimum as in the following theorem:
Theorem 2: The equilibrium of the private insurance market is smaller than (equal to, larger than) the social optimum if(1 −P)UAL−PUAN+ (π−P)UA > (=, <) 0.
Proof: Let Q* denote the interior solution of Equation (11) under symmetric equilibrium (QA=Q*). Define the left-hand side of Equation (13) as Γ (Q). Thus, from Equations (11) and (13), Γ (Q*) = (1 −P)UAL−PUAN+ (π−p)UA. Therefore, Γ (Q*) > (=, <) 0 if (1 −P)UAL−PUAN+ (π−P)UA > (=, <) 0. If the second-order condition holds, then Γ (Q*) > (=, <) 0 implies that the equilibrium in the private insurance market is smaller than (equal to, larger than) the social optimum. Q.E.D.
The condition in Theorem 2 is determined by the sum of the last three terms in Equation (13). That is, not only the signs of the first derivatives of the utility function with respect to the three reference points are important, but also the intensities of jealousy or admiration with respect to the three reference points are crucial to equilibrium underinsurance.14 The last three terms in Equation (13) represent the consumption externality caused by the private insurance decision. Specifically, given that 1 >P > π > 0, the first (second, third) term in the condition is positive if and only if UAL > 0 (UAN < 0 and UA < 0), respectively. If the individual purchases more insurance, then he or she consumes more when the loss occurs but consumes less when the loss does not occur. Note that UAL > 0 (UAN < 0), respectively, indicates that the preference of the individual exhibits admiration (jealousy) with regard to the consumption of other people when they suffer a loss (do not suffer a loss). Thus, if the individual purchases more insurance, the decision increases the utility of other people if UAL > 0 (UAN < 0). Furthermore, since the insurance premium is actuarially unfair, an increase in insurance decreases average per capita consumption and thus increases the other people's utility if UA < 0, indicating that the preference of the individual exhibits jealousy with regard to the average per capita consumption. To sum up, individuals care about the level of other people's consumption in the private market but fail to note that the change in their own consumption level will also affect other people's utility. For example, if UAL > 0, UAN < 0, and UA < 0, the individual fails to recognize the positive consumption externality caused by his or her insurance decision. In the following, let us use Lemmas 4, 5, and 6 to further elaborate Theorem 2.
Lemma 4: Given that UAL=UAN= 0,
- (i)
the equilibrium in the private insurance market is socially optimal if the price of the insurance is actuarially fair (P=π);
- (ii)
the equilibrium in the private insurance market is smaller than the social optimum if the price of the insurance is not actuarially fair (P > π) and UA < 0.
Proof: If P=π, then Equation (11) is identical to Equation (13) in the case where UAL=UAN= 0. Thus, the equilibrium in the private insurance market is socially optimal. On the other hand, if P > π and UA < 0, then Γ (Q*) = (π−P)UA > 0, given that UAL=UAN= 0. Q.E.D.
Lemma 4 discusses the case where individuals only take the average per capita consumption level into account while making interpersonal comparisons. Case I is one of the examples. In Lemma 4, we first show that, under the consumption externality, the equilibrium of the private insurance market is socially optimal if the price of the insurance is actuarially fair. The intuition is straightforward. If the price of the insurance is actuarially fair, the average per capita consumption is fixed. Since the decision regarding the insurance is not related to the source of the consumption externality, the actuarially fair price eliminates the consumption externality. In our model, it is not necessary for the individual to purchase full insurance when the price of the insurance is actuarially fair. Thus, the actuarially fair price makes the equilibrium in the private market socially optimal even if the optimal equilibrium in the private insurance market does not represent full insurance.
In Lemma 4, we show that, under a consumption externality, the optimal insurance quantity that a jealous individual purchases in the private market is lower than the corresponding socially optimal insurance quantity if the price of the insurance is not actuarially fair. Note that an increase in the amount of the insurance decreases the average per capita consumption when the price of the insurance is not actuarially fair. Since the individual exhibits jealousy in terms of his or her preference, an increase in the insurance amount increases the utility of the individual through the consumption externality. Thus, when the individual makes the insurance decision in the private market, the individual will underinsure the loss because he or she ignores the consumption externality.
Lemma 5: If
UA= 0, the equilibrium in the private insurance market is smaller than the social optimum if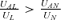 .
.
Proof: If UA= 0, Γ (Q*) = (1 −P)UAL−PUAN. Note that (1 −P)UL=PUN from Equation (11). Since UL > 0, UN > 0, by dividing the two sides of (1 −P)UAL >PUAN by (1 −P)UL and PUN, we can find that Γ (Q*) > 0 if 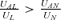 . Q.E.D.
. Q.E.D.
Lemma 5 focuses on the cases where individuals care about other people's consumption levels in the loss and no-loss states but not the average per capita consumption level while making interpersonal comparisons. Cases II and III are two examples. From Lemma 5, we find that given that UA= 0, jealousy is neither a sufficient nor a necessary condition for the individual to be underinsured. Note that 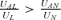 may not hold when UAL < 0 and UAN < 0.
may not hold when UAL < 0 and UAN < 0. 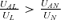 can still hold when UAL≥ 0 or UAN≥ 0. Interestingly,
can still hold when UAL≥ 0 or UAN≥ 0. Interestingly, 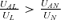 always holds if UAL > 0 and UAN < 0. In other words, if the preference of the individual exhibits admiration with regard to the per capita consumption in the loss state and jealousy in the per capita consumption in the no-loss state, then the individual always equilibrium underinsures his or her own loss.
always holds if UAL > 0 and UAN < 0. In other words, if the preference of the individual exhibits admiration with regard to the per capita consumption in the loss state and jealousy in the per capita consumption in the no-loss state, then the individual always equilibrium underinsures his or her own loss.
It is very important to recognize that in the insurance market modeled in this case, there are two sources of consumption externality, one being the loss state and the other being the no-loss state. On the other hand, in the labor-consumption market described by Dupor and Liu, there is only one source of consumption externality. Thus, Dupor and Liu only need the condition of jealousy to determine the sign of the equilibrium overconsumption, whereas we need to compare two marginal rates of substitution to determine the results of the consumption externality in the insurance market.
Lemma 6: If
P=π, the equilibrium in the private insurance market is smaller than the social optimum if(1 −P)UAL−PUAN > 0or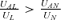 .
.
Proof: If P=π, Γ (Q*) = (1 −P)UAL−PUAN. Thus, from Lemma 5, it is obvious that the condition for equilibrium underinsurance in this case is the same as in Lemma 5. Q.E.D.
Lemma 6 provides an important result in that, under an actuarially fair premium, the social planner might think that the individuals are either under- or overinsured. Thus, a social welfare maximizing government would have an incentive to design a mechanism to “correct” the coverage level, even if the insurance price in the private market is actuarially fair.
Furthermore, we would like to show that a government might make individuals better off by forcing those individuals to deviate from full coverage when the relative consumption level could influence the individuals' utility. Assume that U(WL, WN, WAL, WAN, WA) =πu(WL, WAL, WAN, WA) + (1 −π)u(WN, WAL, WAN, WA) as in Equation (7). It is easy to show that the optimum in the private market is full insurance if the insurance price is actuarially fair (P=π). In this case, we know that the equilibrium in the private market is larger than the social optimum if (1 −π)UAL−πUAN < 0. Thus, even though the individuals purchase full coverage, the optimum in the private market is not socially optimal and the government may have an incentive to push the individual away from full coverage in order to improve social welfare.
Optimal Tax Deduction
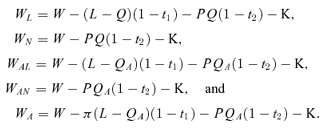
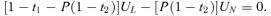 (14)
(14)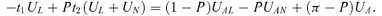 (15)
(15)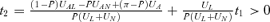 . The first term is positive under our assumption. The second term,
. The first term is positive under our assumption. The second term, 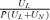 , is also positive. Since the intercept of t2 is positive and the optimal tax deduction rates will never set t1=t2, t1 is always smaller than t2, if the optimal tax deduction exists in the setting of 1 ≥t1 > 0 and 1 ≥t2 > 0.
, is also positive. Since the intercept of t2 is positive and the optimal tax deduction rates will never set t1=t2, t1 is always smaller than t2, if the optimal tax deduction exists in the setting of 1 ≥t1 > 0 and 1 ≥t2 > 0.Dupor and Liu (2003) suggested that a tax on income be employed to correct for the consumption externality caused by overconsumption. The intuition behind their suggestion is straightforward. Since the individual overconsumes, an income tax could reduce the individual's optimal consumption in the private market. In our article, we find that, to correct for the consumption externality caused by underinsurance, the government should provide a larger tax deduction with regard to the insurance premium (i.e., t2 >t1). The intuition behind our proposal is also straightforward. Since the individual underinsures, a tax deduction on the insurance premium could increase the individual's demand for insurance in the private market. Note that as shown by Kaplow (1992b), a tax deduction in relation to the individual's net losses could reduce the demand for private insurance. Since we assume that the case in this section is underinsurance, the government should try to set up a system to increase rather than decrease the demand for private insurance.
Conclusions
In this article, we analyze the relationship between the consumption externality and equilibrium underinsurance. In the case where the utility of the individual is not related to average per capita consumption, we find that the individual will be equilibrium underinsured if the marginal rate of substitution between the consumption in the loss state and the per capita consumption in the loss state is larger than that between the consumption in the no-loss state and the per capita consumption in the no-loss state. We show that jealousy is neither a sufficient nor a necessary condition for equilibrium underinsurance. In the case where the average per capita consumption is the only source of the consumption externality and the insurance is actuarially unfair, the individual will be equilibrium underinsured when the utility of the individual exhibits jealousy.
Since the consumption externality could break down the social optimum and the optimum in the private market, it provides room for the government to improve social welfare. We thus identify the conditions for an optimal tax deduction. To be specific, we show that, to correct for equilibrium underinsurance, the optimal tax deduction rate with regard to the individual's net losses should be lower than the optimal tax deduction rate related to the insurance premium.
Our article contributes to the literature by linking the consumption externality with the equilibrium underinsurance. Our results can hold for a generally large set of individual preferences. We also provide workable mechanisms and identify the conditions to enable the government to reach a social optimum. Since we do not assume asymmetric information and individual heterogeneity, including these factors in the model would be an obvious extension of our article. A dynamic model with an endogenous labor supply could also be incorporated in a future study.
Footnotes
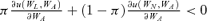 .
.




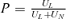 from
from