Optimal Gradual Annuitization: Quantifying the Costs of Switching to Annuities
The authors can be contacted via e-mail: [email protected],[email protected], and [email protected], respectively. This research was conducted with support from the German Research Foundation, the Fritz-Thyssen Foundation, the German Association for Insurance Research, and the German Investment and Asset Management Association. Opinions and errors are solely those of the authors and not of the institutions with whom the authors are affiliated.
Abstract
We compute the optimal dynamic annuitization and asset allocation policy for a retiree with Epstein–Zin preferences, uncertain investment horizon, potential bequest motives, and pre-existing pension income. In our setting the retiree can decide each year how much he consumes and how much he invests in stocks, bonds, and life annuities, while the prior literature mostly considered restricted so-called deterministic or stochastic switching strategies. We show that postponing the annuity purchase is no longer optimal in the gradual annuitization (GA) case since investors are able to attain the optimal mix between liquid assets (stocks and bonds) and illiquid life annuities each year. In order to assess potential utility losses, we benchmark various restricted annuitization strategies against the unrestricted GA strategy.
Introduction
In this article, we solve the optimal asset allocation problem of life annuities with fixed benefits, stocks, and bonds in the presence of pre-existing pension income for a retiree with Epstein–Zin preferences. In our setting, the retiree can decide each year how much he consumes and how much he invests in stocks, bonds, and life annuities. We refer to this unrestricted case as gradual annuitization (GA). We compare the results to restricted annuitization strategies where the retiree is only allowed to switch from a phased withdrawal plan into life annuities once (so-called switching strategies). We quantify the utility costs when the retiree is forced to follow a switching strategy for various specifications of the Epstein–Zin utility function. Using Epstein–Zin preferences, we are able to disentangle the implications of varying the relative risk aversion (RRA) and elasticity of intertemporal substitution (EIS).
Our study contributes to the literature along two essential dimensions. First, the literature has been almost entirely devoted to restricted switching strategies shifting the whole remainder of a withdrawal plan into annuities. We relax this restrictive assumption by analyzing GA and by introducing a less restrictive switching strategy that shifts an optimal wealth fraction to annuities only once (partial switching, PS).1 Second, Epstein–Zin preference, pre-existing pension income and bequest have not been analyzed in the dynamic asset allocation literature with annuities so far.
Exploring the utility impact of restricted switching restrictions can be justified from a practical viewpoint since some countries in Europe require a mandatory annuitization age for tax-induced saving plans. For instance, in the United Kingdom, accumulated assets have to be annuitized by age 75. In Germany, “Riester” plans offer a tax inducement if life-annuity payments start from age 85 on and the withdrawn amounts are either constant or increasing prior to age 85. The analysis of the optimal annuitization strategies itself is important because there is an overall increase in general awareness for longevity risk: while nations worldwide are moving from public pay-as-you-go schemes to privately funded pension systems, employers are shifting from defined benefit plans to either hybrid or defined contribution plans. The unrestricted optimal dynamic annuitization and asset allocation policy shows how longevity risk can be managed best by purchasing life annuities with constant payouts.
The constant payout or fixed benefit life annuity is a bond-based investment including longevity insurance protecting the retiree from outliving his resources (Mitchell et al., 1999).2 Not only do life annuities with fixed benefits capture the largest annuity market share, but they also play an important role in tax-induced private or corporate savings schemes. In what follows we will exclusively focus on the single premium immediate payout annuity with fixed real benefits. Such life annuities are almost identical to public pensions with respect to their payout structure. The insurer (insurance company or government) absorbs the longevity risk by pooling across a group of annuitants. There are, however, drawbacks related to life annuities. Once the individual has spent his money on the annuity premium, he loses control over the amount and surrenders his bequest potential as well as part of his financial flexibility in retirement.
We set up a discrete-time model and compute the optimal dynamic annuitization and asset allocation policy for a retiree with Epstein–Zin preferences, uncertain investment horizon, potential bequest motives, and pre-existing pension income. The irreversibility of annuity purchases and the short selling restriction require that the optimization problems are solved numerically by backward induction. Assuming Epstein–Zin utility with potential bequest motives and pre-existing pension income we are able to show for various utility specifications how switching restrictions affect the optimal annuitization and asset allocation strategy. We derive the optimal GA strategy, the optimal complete switching (CS) strategy, and the optimal PS strategy. In the GA case, the retiree can decide each year how much he consumes and how much he invests in stocks, bonds, and life annuities. The CS strategy requires the retiree to shift his entire savings into annuities at an optimal date. In the PS case, the investor can still purchase annuities only once while he is free to use any fraction of his savings.
In a final welfare analysis we evaluate utility losses by comparing certainty equivalents of following a switching strategy compared to the GA strategy. Moreover, we consider a scenario in which only stocks and bonds can be purchased (but no annuities) and one in which the retiree is forced to buy annuities only. These scenarios give insight into how high utility losses are if either the mortality credit of annuities or the equity premium of stocks is surrendered.
The remainder of this article is organized as follows. The “Prior Literature” section gives an overview of prior literature on annuities. The following section introduces the asset and annuity model and the individual's preferences, and it explains the different annuitization strategies. The next section discusses the impact of switching strategies on the asset allocation for various utility specifications. The “Welfare Analysis” section contains a robustness analysis and a comparative welfare analysis. The last section concludes.
Prior Literature
Theoretically, complete annuitization is only optimal for restrictive assumptions. Yaari (1965) finds that all assets should be annuitized by an individual with a time separable utility function—given a single riskless asset, actuarially fair annuity premiums, and no bequest motive. Davidoff, Brown, and Diamond (2005) specify weaker conditions for complete annuitization. As long as the insurance market is complete and the return on the annuity is above the reference asset, a retiree without a bequest motive completely annuitizes his entire wealth. Markets are complete if annuities pay out for one specific period and state (so-called Arrow Debreu annuities). This result does not require a time separable utility function. If the underlying assumption of complete markets is relaxed or if the individual has a bequest motive, then partial annuitization becomes optimal.
Another strand of the literature introduces incompleteness in annuity markets in respect of only life annuities being available that pay out a fixed benefit for the rest of the annuitant's lifetime. The incompleteness of the annuity market leads to the following results. The individual does not use his entire wealth to buy annuities and the purchase of annuities is delayed. Devolder and Hainout (2005) and Babbel and Merrill (2006) derive the optimal contemporaneous mix between life annuities and phased withdrawal plans at the beginning of the retirement, but they do not allow for deferring annuitization to a later age. Therefore, part of the literature searches for the optimal time to switch completely from a phased withdrawal plan into life annuities and allows for mixing withdrawal plan and life annuities inter-temporally. The recommendation is to defer annuitization until the utility gain induced by the mortality credit of annuities exceeds the opportunity costs of the forfeit equity premium and the loss of liquidity. Milevsky and Young (2002) and Kingston and Thorp (2005) argue that this real option to delay annuitization contributes to explaining the empirically low levels of annuitization (annuity puzzle). While Milevsky and Young (2002) and Kingston and Thorp (2005) derive the optimal deterministic switching time, Blake, Cairns, and Dowd (2003), Milevsky and Young (2007), Stabile (2003), and Milevsky, Moore, and Young (2006) compute the optimal stochastic CS times. Horneff et al. (2008) consider both switching tactics in a stochastic interest rate environment.
The Model
Preferences
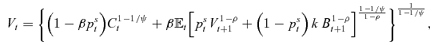 (1)
(1)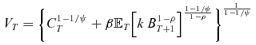 (2)
(2)GA Strategy
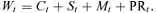 (3)
(3)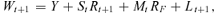 (4)
(4)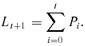 (5)
(5)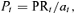 (6)
(6)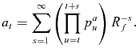 (7)
(7)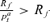 . The funds of those who die are allocated across the surviving members of a cohort. Accordingly, the lower the survival probability becomes, the higher the mortality credit is in case the retiree survives. Annuities become more attractive compared to bonds and stocks over time because the mortality credit compensates for the forfeit liquidity and equity premium of stocks. Given (6) the recursive evolution of Lt follows as
. The funds of those who die are allocated across the surviving members of a cohort. Accordingly, the lower the survival probability becomes, the higher the mortality credit is in case the retiree survives. Annuities become more attractive compared to bonds and stocks over time because the mortality credit compensates for the forfeit liquidity and equity premium of stocks. Given (6) the recursive evolution of Lt follows as
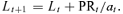 (8)
(8)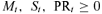 (9)
(9)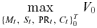 (10)
(10)PS Strategy
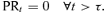 (11)
(11)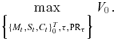 (12)
(12)CS Strategy
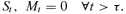 (13)
(13)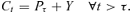 (14)
(14)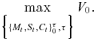 (15)
(15)Numerical Solution Method
We apply the backward optimization technique to solve the optimization problem of the optimal GA (10), PS (12), and CS strategy (15) because analytic solutions do not exist. We use the income from public pensions to normalize the state and policy variables. The normalized variables are denoted by lowercase letters.
For solving the GA and PS problem it is necessary to construct a three-dimensional state space because the optimal policy depends on three state variables: normalized cash on hand wt=Wt/Y, which represents the level of liquid financial wealth; normalized annuity payouts from previously purchased annuities lt=Lt/Y; and retirement age t. The continuous state variables cash on hand wt and annuity payouts lt have to be discretized and the only discrete state variable left is age t. Moving backward along the t dimension we calculate the optimal policy and the value of the utility function for each grid point. The expectation operator in (1) is computed by resorting to Gaussian quadrature integration and the optimization is done by numerical constrained minimization. We interpolate the policy and value functions for points that do not lie on the grid. Therefore, we compute the policy functions for GA (i= GA) and PS (i= PS) si(w, l, t), mi(w, l, t), pri(w, l, t), ci(w, l, t) and the value function vi(w, l, t) by cubic-splines interpolation. In the PS case, the policies and the value function exhibit a kink when the retiree decides to switch. In order to adjust for the kink, we use splines interpolation for the states l > 0.
When solving the CS problem, we can omit the state annuity payouts lt. Instead, we have to introduce an indicator variable I which is 1 if the optimal switching time has already been reached and 0 otherwise. For each combination of wealth and age, we compute the optimal utility for the case the retiree switches and for the case he continues to withdraw funds. Whichever policy yields a higher utility level is the one the retiree follows. After the retiree switched, utility is trivial to compute because ct, st, mt, and bt are constant from then on. Otherwise the policy functions and the value function are computed by using splines interpolation for points that do not lie on the grid. The policy functions are given by sCS(w, t, I), mCS(w, t, I), prCS(w, t, I), and cCS(w, t, I).
The Impact of Switching Restrictions on Optimal Annuitization and Asset Allocation
Base Case Results
This section presents the optimal policies for each annuitization strategy GA, PS, and CS. We choose a base case and use it as a reference point to undertake a robustness analysis regarding the parameter assumptions of the model in the section below. For the base case, we assume that the retiree is a 65-year-old woman with moderate risk aversion ρ= 5 and elasticity of inter-temporal substitution ψ= 1/5. By setting the preference parameters this way we let the Epstein–Zin utility function boil down to CRRA utility. The personal discount factor is set to β= 0.96 and the strength of the bequest motive to k= 0. The subjective belief about the mortality risk is given by the 2000 Population Basic mortality table (which we truncate to the age of 100). We set the real interest rate Rf to 2 percent, the equity premium μ−Rf to 4 percent and stock volatility σ to 18 percent. By and large, this calibration is in line with the recent life-cycle literature such as Cocco, Gomes, and Maenhout (2005). The annuity is priced fairly. The expense factor δ= 0 and the survival probabilities for pricing the annuity are also taken from the 2000 Population Basic mortality table.
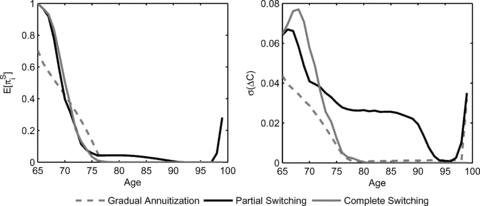
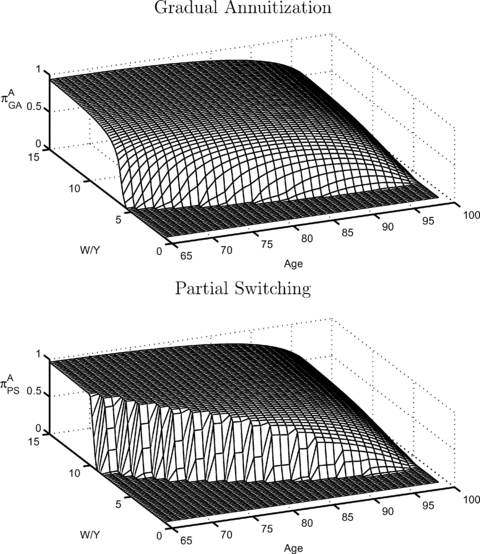
Figure 1 depicts the optimal fraction of annuity wealth πAi(w, l= 0, t), i∈{GA, PS, CS} as a function of current age t and normalized cash on hand w=W/Y. The underlying assumption is that no annuities have been purchased until t (i.e., l= 0). As a result, the figure displays the optimal first annuitization time for all ages in retirement, and the figure also illustrates to what extent the retiree annuitizes. All three policy graphs reveal two effects: the higher the level of normalized cash on hand and the older the retiree, the higher is the optimal annuity fraction. The two effects can be traced back to the relative value of pension wealth with respect to financial wealth. Pension wealth (present value of pre-existing pension income) is an implicit annuity holding. Over time the fraction between pension and financial wealth decreases. Less financial wealth (equity) is needed to maintain the optimal allocation of augmented wealth comprising pension, financial, and annuity wealth. As the mortality credit rises over time, annuities crowd out stocks completely. Comparing the GA, PS, and CS strategies, we find that it is optimal to postpone the annuity purchase into future periods for both the switching cases PS and CS. The annuitization frontier moves to the upper right corner in the wealth/age-space as compared to the GA case. Retirees have only the option to annuitize once. The exercise of the option is postponed until the ratio of pension wealth to augmented wealth is sufficiently small and the mortality credit is high enough to justify the complete or partial switch (e.g., in Milevsky and Young 2007). The left graph of Figure 2 illustrates the timing of the first annuity purchase in the wealth-age space. For instance, if w= 5, it is optimal to gradually annuitize from the age of 65 on, while in the switching cases wealth has to be more than twice as high to justify annuitization. The timing of annuitization can be deferred for up to 10 years for this level of wealth. Although the PS is less restrictive than CS, annuitization is almost as late as for the CS case. The expected level of annuity wealth E[ltat] is presented in the right graph of Figure 2. In order to calculate the expected levels of annuity wealth, we carry out Monte Carlo simulations by generating 100,000 life-cycle trajectories assuming that the investor acts according to the optimal policies. We also make the assumption that the retiree has initial savings six times as high as his pension income w0= 6. Although annuitization is postponed due to the switching restriction, the level of annuity wealth is higher than in the GA case between the ages of 70 and 75. This is the period in which switching is most likely to occur. After that period the switching restriction curtails the level of annuity wealth. A reduction of annuity wealth also implies that the level of annuity income and the level of consumption is reduced.
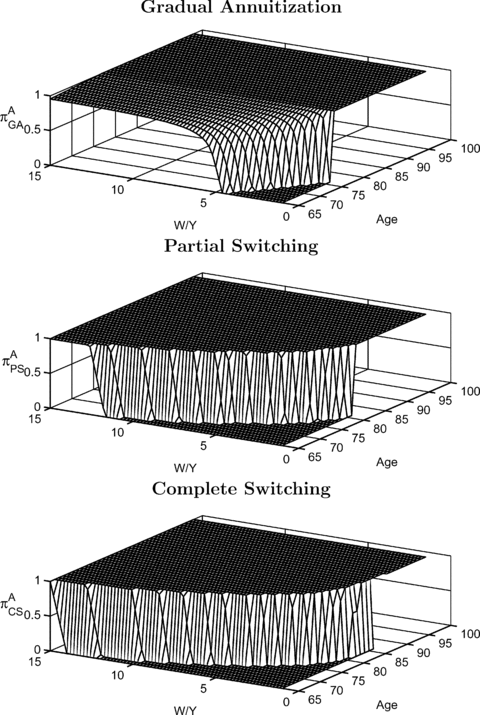
Optimal Annuity Fracton πAi(w, l= 0, t), i∈{GA,PS,CS} for Varying w and t
Note: The optimal annuity fraction is calculated according to 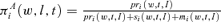 for females with RRA = 5, k= 0, and EIS = 0.2.
for females with RRA = 5, k= 0, and EIS = 0.2.
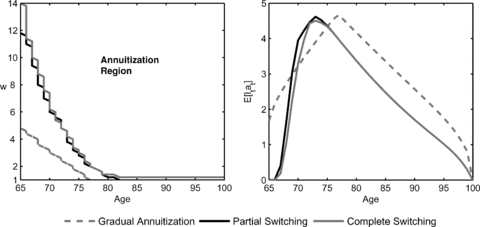
Optimal First Annuity Purchase Times and Expected Evolution of Annuity Wealth
Note: The left graph depicts which level of disposable wealth is needed to start purchasing annuities. The right graph depicts the optimal expected present value of purchased annuities E[ltat], which is computed by 100,000 Monte Carlo simulations for w0= 6.
It is also of interest to understand what effects the switching restrictions have on the composition of remaining wealth and what the impact on consumption volatility looks like. Taking into account annuity wealth, we therefore present the expected optimal stock fraction 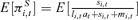 for all three annuitization strategies over time in Figure 3 (left graph). In the right graph, the volatility of the consumption change σ(ΔCt) over age is displayed. We only depict the expected stock fraction since bonds are completely crowded out by annuities due to the mortality credit. Hence, the expected annuity fraction over time is given by 1 −E[πSi,t]. To this end, we run a Monte Carlo simulation assuming that the individual has an level of initial retirement wealth that is as high as six times the annual pension income w0= 6. The simulation analysis reveals that it is optimal to start out with a stock fraction of 70 percent in the GA case. In the GA case, a gradual shift occurs from stocks to annuities until the age of 78 when wealth is completely phased into annuities. In case of CS and PS, the initial optimal stock fraction starts higher with 100 percent but drops much faster than in the GA case. The rationale is to shift equity risk into the early period of retirement because the equity markets cannot be accessed anymore after the switch to annuities. From ages 70–78, the equity exposure is below the optimal level of the GA case. However, in the PS case it is optimal to keep some stocks over the remaining retirement period. The reason is twofold. First, after the switch it is not possible to purchase additional annuities anymore. Second, bonds are not purchased as a substitute for annuities since they offer no mortality credit. The increase of the optimal equity fraction at the end of the life-cycle around age 98 is due to the decreasing value of the annuity.
for all three annuitization strategies over time in Figure 3 (left graph). In the right graph, the volatility of the consumption change σ(ΔCt) over age is displayed. We only depict the expected stock fraction since bonds are completely crowded out by annuities due to the mortality credit. Hence, the expected annuity fraction over time is given by 1 −E[πSi,t]. To this end, we run a Monte Carlo simulation assuming that the individual has an level of initial retirement wealth that is as high as six times the annual pension income w0= 6. The simulation analysis reveals that it is optimal to start out with a stock fraction of 70 percent in the GA case. In the GA case, a gradual shift occurs from stocks to annuities until the age of 78 when wealth is completely phased into annuities. In case of CS and PS, the initial optimal stock fraction starts higher with 100 percent but drops much faster than in the GA case. The rationale is to shift equity risk into the early period of retirement because the equity markets cannot be accessed anymore after the switch to annuities. From ages 70–78, the equity exposure is below the optimal level of the GA case. However, in the PS case it is optimal to keep some stocks over the remaining retirement period. The reason is twofold. First, after the switch it is not possible to purchase additional annuities anymore. Second, bonds are not purchased as a substitute for annuities since they offer no mortality credit. The increase of the optimal equity fraction at the end of the life-cycle around age 98 is due to the decreasing value of the annuity.
Expected Stock Fraction and Volatility of Consumption Changes Over Age
Note: The expected stock fraction is defined as 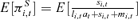 and the volatility of the consumption changes as σ(ΔCt). Both are computed by 100,000 Monte Carlo simulations in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
and the volatility of the consumption changes as σ(ΔCt). Both are computed by 100,000 Monte Carlo simulations in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
The right graph of Figure 3 reveals that switching restrictions raise the volatility of consumption changes, especially in the early stage of retirement. Obviously this is due to the higher initial equity fraction. In the later stage of the life cycle, volatility decreases to 0 in the GA and CS case since full annuitization has already occurred by then. Stock market risk does not enter into wealth development anymore. However, in the PS case the remaining stock fraction induces some volatility in consumption until the age of 90. The jump in volatility shortly before the age of 100 occurs because the optimal consumption level jumps. The sudden increase occurs because we have truncated the mortality table to 100.
Variation of Risk Aversion and EIS
In order to assess how different specifications of the preferences alter the impact of switching restrictions on optimal annuitization and asset allocation, this section varies the degree of RRA and of EIS. If we change the RRA parameter ρ, we set ψ= 1/ρ in order to maintain CRRA utility. However, we switch to Epstein–Zin utility if we vary ψ while keeping ρ= 5 constant to separate the RRA and EIS effect.
The upper panel of Figure 4 reveals that the optimal age of full annuitization is not sensitive to the level of RRA. This result suggests that the mortality credit is close to the equity premium of stocks at age 78. Before age 78 the expected annuitization rate increases with the level of RRA. In the CS case, full annuitization becomes optimal from age 78 on at the latest. In the PS case, full annuitization occurs later at age 90 since the retiree is forced to keep liquid assets instead of repurchasing annuities.
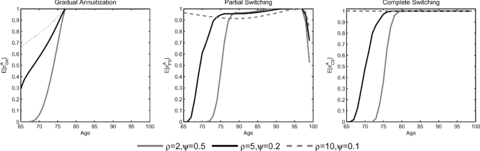
Expected Annuity Fraction Over Age for Various Levels of RRA
Note: The expected annuity fraction 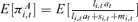 is computed by 100,000 Monte Carlo simulations, in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
is computed by 100,000 Monte Carlo simulations, in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
The effect of varying the EIS parameter ψ is depicted in Figure 5. Like Cocco, Gomes, and Maenhout (2005) as well as Gomes and Michaelides (2005), we analyze the cases ψ= 1/10, ψ= 1/5, and ψ= 1/2 and keep ρ= 5. In the case of CRRA utility the chosen degrees of EIS would correspond to ρ= 10, ρ= 5, and ρ= 2, respectively. The upper panel of Figure 5 shows that even if we vary the EIS, full annuitization is optimal at some point for most of the settings. In the PS and CS case, annuitization is postponed for higher levels of EIS. If the level of EIS is higher, the retiree accepts postpone consumption for future periods in which the mortality credit is high. While annuitization occurs much later for high EIS (ψ= 0.5) in the switching cases, the timing of annuitization remains almost unchanged for the GA strategy. The effect can be explained if the expected evolution of the sum of financial and annuity wealth is considered in the switching cases (lower panel of Figure 5). In the GA case, wealth increases further, even after full annuitization has already occurred. The reason is that substantial parts of the payouts from annuities purchased previously are used to buy new annuities offering a higher mortality credit. In turn, consumption is postponed into the late stage of retirement in order to attain the higher mortality credit. Since the continuous repurchase of annuities is not possible in the PS and CS case, it is again optimal to postpone the annuity purchase. Like in the base case, the lower panel of Figure 5 indicates that annuity wealth and annuity income are much higher in the GA case than in both switching cases.
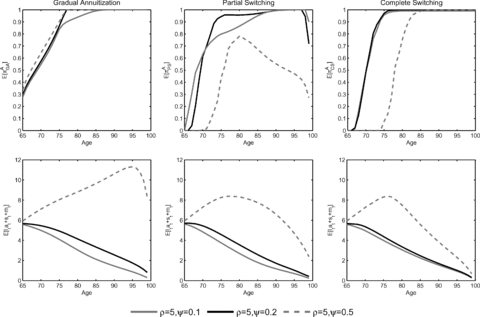
Expected Annuity Fraction and Wealth Evolution Over Age for Various Levels of EIS
Note: The expected annuity fraction 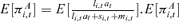 (upper panel) and expected wealth evolution E[li,tat+si,t+mi,t] (lower panel) are computed by 100,000 Monte Carlo simulations, in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
(upper panel) and expected wealth evolution E[li,tat+si,t+mi,t] (lower panel) are computed by 100,000 Monte Carlo simulations, in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
Impact of Bequest Motives
Introducing a bequest motive has substantial effects on both the retiree's asset allocation and consumption strategy. In order to ensure some estate in case the retiree dies, she has to keep some liquid wealth. In turn, full annuitization is never optimal. Marginal utility from leaving bequest becomes infinite if the estate converges to 0. Hence, the CS restriction entirely prohibits the retiree from purchasing annuities.
In order to quantify to what extent the annuity demand is reduced by a positive bequest motive (k= 2) for the GA and PS case, we present the optimal fraction of annuity wealth in Figure 6. The presence of this bequest motive results in an upward shift of the annuitization frontier. Higher levels of wealth are necessary to induce annuitization. Again the annuitization frontier of the PS case is pushed further to the upper right corner than the one of the GA case. For instance, in the PS case absolute financial wealth W has to be as high as eight times the pension income Y to make annuitization optimal at age 65. It is likely that the annuitization frontier is never reached if retirement wealth stays at low levels (i.e., if the stock market exhibits negative returns). In addition, the optimal annuitization rate decreases with age because the bequest motive becomes stronger at the end of the life cycle.
Optimal Annuity Fracton πAi(w, l= 0, t), i∈{GA,PS} With Bequest Motives k= 2 for Varying w and t
Note: The optimal annuity fraction is calculated according to 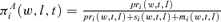 .
.
Monte Carlo simulations show that annuities are still purchased in expectation if the initial wealth is six times the pension income w0= 6 (Figure 7). Expected annuity fractions rise to 40 percent in the GA case and to 30 percent in the PS case. The optimal stock fraction shrinks with age similar to the no-bequest case due to the decrease of the human capital and the increasing mortality credit. While wealth was entirely shifted from stocks to annuities previously, the retiree prefers more liquid financial wealth that serves as estate. Thus, the desired asset allocation of total wealth is partly achieved by purchasing bonds.
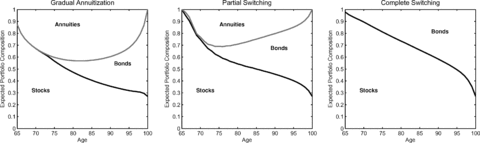
Optimal Expected Portfolio Composition With Bequest Motives
Note: The expected portfolio compositions are computed by 100,000 Monte Carlo simulations, in which we assume that the investor acts according to the optimal policies derived in the numerical optimization and has w0= 6.
Welfare Analysis
Thus far, the substantial demand for annuities suggests that considerable utility gains can be generated through the presence of annuity markets. In the preceding chapters, the annuity demand was weakened by switching regulation imposed exogenously. Annuitization was postponed or even circumvented. Exogenous restrictions cause utility losses because the mortality credit is partly foregone and the volatility of consumption is higher. In order to quantify the range of possible utility losses, we next undertake a welfare analysis based on the comparisons of certainty equivalents similar to Mitchell et al. (1999). In our analysis we increase the initial wealth of the restricted case until the level of utility is equal to the one of the GA case.
Additionally, we also introduce two new restricted strategies that are motivated by a regulatory viewpoint. Governments have an intrinsic motivation to promote longevity insurance: first, insurance products can avoid old-age poverty that might otherwise burden the social safety net; second, governments can also be interested in reducing intergenerational transfers to limit divergence in aggregate wealth distribution. Regulation of privately funded pension systems can either leave the annuitization decision entirely up to the retiree or can establish mandatory annuitization guidelines. The first idea suggests that the individual is prudent enough to decide in a responsible manner, while the second approach assumes that regulation is necessary. While in the United States annuitization is voluntary for tax sheltered retirement saving plans (401(k)), some European governments introduced tax sheltered and subsidized plans making annuitization compulsory at a certain age. For instance, in the United Kingdom, accumulated assets have to be annuitized by age 75. In Germany, “Riester” plans offer a tax inducement if life-annuity payments start from the age of 85 on and the amounts withdrawn are either constant or increasing prior to the age of 85. Both examples involve the switch from a phased withdrawal plan into annuities at a particular age. In order to assess the regulatory costs of the British and German requirements concerning annuitization, we also include a variation of the CS strategy. In the variation, the complete switch has to occur before the ages of 75 and 85, respectively.
We also assess the economic costs of not having access to annuities at all. To this end, we compute the optimal pure withdrawal plan for the case that only stock and bond markets can be accessed. This calculation offers insight into how high utility losses would be if annuity markets were ignored. Further, we quantify the utility costs for the case of complete annuitization at the beginning of the retirement period. This case isolates the effect of not having access to liquid stocks and bonds. Utility values for this strategy can be simply computed by calculating the constant consumption stream the retiree attains in exchange for his initial wealth. This stream is then plugged into the recursive utility function (1).
Table 1 displays to what extent financial wealth has to be raised in the restricted cases in order to achieve the same utility as in the unrestricted GA case. First, it becomes unequivocally clear that utility losses are the highest for the case with no annuity markets (column: no annuities). The values range between 20 to 30 percent in most cases. Only if initial wealth is sufficiently low (w0= 2) annuities are scarcely purchased in the GA case; utility losses stay at a low level. The second worst strategy is to annuitize all wealth at the start (last column: only annuities). While in the case with no annuities utility losses increase with w0, the opposite is true for the case with no liquid assets. The explanation is that the optimal annuity fraction increases with wealth w in the unrestricted GA case while the optimal stock fraction decreases with financial wealth (as shown in the previous section).
| Preferences | w 0 | Partial Switching | Complete Switching | No Annuities | Switching at Age 65 | Switching Before Age 75 | Switching Before Age 85 |
|---|---|---|---|---|---|---|---|
| (a) ρ= 2, ψ= 1/ρ, k= 0 | 2 | 4.96 | 5.89 | 19.19 | 24.74 | 7.4 | 5.89 |
| 6 | 2.83 | 3.31 | 17.76 | 14.57 | 3.54 | 3.32 | |
| 12 | 2.72 | 2.88 | 20.05 | 10.23 | 3.00 | 2.97 | |
| (b) ρ= 5, ψ= 1/ρ, k= 0 | 2 | 2.08 | 2.45 | 11.58 | 11.79 | 2.81 | 2.45 |
| 6 | 2.55 | 2.86 | 21.15 | 6.05 | 2.87 | 2.86 | |
| 12 | 3.23 | 3.73 | 32.24 | 3.89 | 3.73 | 3.73 | |
| (c) ρ= 10, ψ= 1/ρ, k= 0 | 2 | 1.35 | 1.61 | 10.48 | 6.89 | 1.69 | 1.61 |
| 6 | 2.53 | 2.98 | 31.57 | 2.97 | 2.98 | 2.98 | |
| 12 | 1.62 | 1.91 | 43.6 | 1.91 | 1.91 | 1.91 | |
| (d) ρ= 5, ψ= 1/10, k= 0 | 2 | 0.02 | 0.21 | 0.41 | 7.33 | 0.94 | 0.27 |
| 6 | 0.68 | 1.58 | 8.46 | 4.58 | 1.60 | 1.58 | |
| 12 | 0.92 | 2.82 | 20.2 | 2.95 | 2.82 | 2.82 | |
| (e) ρ= 5, ψ= 1/2, k= 0 | 2 | 77.29 | 98.64 | 189.67 | 187.28 | 119.19 | 98.84 |
| 6 | 42.29 | 53.92 | 113.77 | 77.87 | 57.26 | 53.91 | |
| 12 | 32.74 | 41.71 | 94.16 | 50.03 | 41.86 | 41.47 | |
| (f) ρ= 5, ψ= 1/ρ, k= 2 | 2 | 0.19 | 1.11 | 1.11 | n/a | n/a | n/a |
| 6 | 1.48 | 6.97 | 6.97 | n/a | n/a | n/a | |
| 12 | 2.17 | 17.32 | 17.31 | n/a | n/a | n/a | |
| (g) With annuity loads | 2 | 0.23 | 0.43 | 11.58 | 12.61 | 1.65 | 0.43 |
| ρ= 5, ψ= 1/ρ, k= 0 | 6 | 0.97 | 1.12 | 21.15 | 8.99 | 1.40 | 1.12 |
| 12 | 2.43 | 2.82 | 32.24 | 5.72 | 2.84 | 2.82 | |
| (h) With annuity loads | 2 | 42.89 | 59.61 | 189.67 | 153.80 | 86.60 | 60.10 |
| ρ= 5, ψ= 1/2, k= 0 | 6 | 24.08 | 33.06 | 113.77 | 64.52 | 40.00 | 33.12 |
| 12 | 19.32 | 26.43 | 94.16 | 40.69 | 28.18 | 26.43 |
- Note: The table depicts the additional wealth (percent) a restricted retiree requires to attain the same utility as in the gradual annuitization case.
Optimal CS and PS are less costly than the two one-and-only strategies we considered above since no asset is completely excluded. In general, utility losses vary between 2 and 6 percent. Utility costs of the CS strategy slightly increase if we add the requirement to switch completely prior to age 75 or 85. The reason is that in most settings it is optimal to switch prior to the age of 75. Higher utility costs of up to 18 percent are generated in the case with a bequest motive k= 2 (row (f)) if CS is assumed. The CS restriction completely crowds out annuity investments. Utility costs cannot be compensated if wealth has to be annuitized prior to a certain age (last three columns) since the loss would be infinite.
PS is always slightly better than CS since it contains one restriction (13) less. The highest reduction in utility costs is given in the bequest case. In the bequest case, the retiree can attain the mortality credit by purchasing annuities with a fraction of wealth and keep the remaining part of wealth invested in liquid assets to ensure bequest.
The most surprising result is given in row (e): high EIS of ψ= 1/2 and moderate RRA of ρ= 5. Although an EIS of ψ= 1/2 does not seem to be out of range—it is the EIS corresponding to ρ= 2 in a CRRA function—utility losses become huge as retirees require 30 to 100 percent more wealth in the switching cases and up to 190 percent more initial wealth in the cases with the restricted asset menu. In contrast, utility losses for low EIS ψ= 1/10 (row (d)) are smaller than in the base line case. This is also a bit surprising because one may think that the stable income of annuities is especially preferred by investors with a low EIS. The reasoning is as follows: Retirees with a high EIS of ψ= 1/2 benefit from the GA strategy. They can continuously repurchase new annuities from the income provided by annuities purchased earlier. Retirees with a low EIS prefer early consumption. In contrast, utility costs in the CRRA case with high EIS of ψ= 1/2 and low RRA of ρ= 2 are also much smaller because retirees can purchase stocks instead of annuities in order to postpone consumption.
In order to assess whether annuity loads reduce the advantage of the GA strategy we run the optimization procedure by assuming that annuities are priced according to the 1996 U.S. Annuity 2000 Aggregate Basic mortality table and that a fee of 100 basis points is deducted for each payout. Since both the asymmetric mortality beliefs and the explicit loads make annuities less attractive, utility losses are slightly reduced for the base case (row (g)). In the case with the high EIS of ψ= 1/2 (row (h)), utility losses are also reduced but still remain substantial.
Conclusion
Increasingly, workers are reaching their retirement age with a reasonable amount of wealth accumulated in a defined contribution plan or in an individual retirement account that they will be called upon to manage themselves so as not to exhaust their funds too soon. This, in turn, raises the question of how they will optimally convert their accumulated assets into a reliable stream of retirement income during their golden years. This trend becomes even more pronounced as employer-based corporate pensions are being more and more converted from defined benefit to defined contribution plans. Therefore, it is of importance to consider ways to help retirees manage different sources of risk they face during the late stage of their life cycle.
In this article, we derive the optimal dynamic asset allocation and annuitization strategies for stocks, bonds, and life annuities assuming a retiree with Epstein–Zin utility, with a potential bequest motive and pre-existing pension income. Epstein–Zin preferences allow us to disentangle both risk aversion and EIS. The prior insurance literature has so far mainly considered CS strategies, whereby the retiree is required to shift his entire savings to annuities at an optimal date. We relax this restrictive assumption by including PS and GA in our analysis. In the PS case, the investor can still purchase annuities only once while he is free to use any fraction of his savings. In the more general GA case, the retiree is allowed to purchase annuities many times and to any extent.
Taking into account a reasonable parameterization of the asset model (e.g., risk-free rate, magnitude of the equity premium, volatility of stocks, and cost structure of life annuities), our numerical assessment indicates for a moderately risk averse and endowed retiree that complete and PS restrictions cause the annuitization age to be postponed up to around 10–15 years after retirement when annuities offer a higher mortality credit, or put differently, when annuities become cheaper. Although the PS strategy is less restrictive than the CS strategy, PS occurs only slightly earlier than the CS tactic. The reason is that it is optimal to annuitize a high fraction of wealth later in life due to the increased mortality credit. Switching restrictions do not only cause annuitization to be deferred but they can also reduce annuitization. This is particularly severe in the cases with bequest: annuities are never purchased if CS restrictions are present.
In contrast to the switching cases, the retiree already starts to purchase annuities at the beginning of the retirement phase—the age of 65—if he is allowed to follow the GA strategy. In the base case, he invests 30 percent of his wealth in annuities while keeping the remainder fully invested in stocks. Doing so, the investor is able to attain both the mortality credit of annuities and the equity premium of stocks. After the age of 65, he continues to repurchase annuities until full annuitization is reached at about the age of 78. This is true for all RRA and EIS specifications considered, if no bequest motive is present. The stock fraction becomes smaller when pension wealth continuously decreases while the mortality credit increases. In turn, stocks are less attractive compared to annuities. Only in the case of a positive bequest motive does full annuitization never occur, in order to ensure estate for the heirs.
A final welfare analysis evaluates the utility costs of restricted annuitization and decumulation strategies compared to the case where GA is possible. This analysis is conducted for various degrees of RRA, EIS, bequest motives, and initial endowments. For the CRRA case, we find utility losses of up to 30 percent of financial wealth if the retiree is forced to completely annuitize his wealth at the beginning of retirement. The utility loss is of similar magnitude, if the retiree can only invest in stocks and bonds and has no access to annuities at all. Utility losses for the base case decrease to 1 to 6 percent for the optimal complete or partial switch to annuities. Even if the complete switch must occur before the age of 75 or 85, as required by the regulation of tax-induced retirement accounts in the United Kingdom and in Germany, respectively, utility costs are only slightly higher. In case the retiree has a bequest motive, utility losses increase up to 17 percent in the CS case. If PS is possible, utility costs can be reduced to 2 percent.
We also conduct the welfare analysis for Epstein–Zin preferences in order to disentangle the implications of varying the RRA and EIS. If the EIS is relatively low, utility losses are below those of the CRRA case for all restricted strategies considered. Increasing the EIS to relatively high values commonly found in the life-cycle asset allocation literature, we find utility costs of around 100 percent. The surprisingly high welfare costs can be explained by the retiree's desire to roll his annuity income over in new annuity purchases. Since the mortality credit of annuities is particularly high at the very end of the life cycle, the retiree wants to postpone consumption as long as possible.
In future work, alternative asset models exhibiting mean-reverting stock returns, interest rate risk or inflation risk, can be explored with respect to the implications for both the timing of the annuity purchase and the choice of the annuity products. The model can also be applied to alternative longevity insurance products such as deferred and equity-linked annuities in order to investigate how the timing of the annuity purchases is affected. Further, tax considerations might be important to understand the effect on the optimal annuity demand.




