Does Insurance Market Activity Promote Economic Growth? A Cross-Country Study for Industrialized and Developing Countries
The author can be contacted via e-mail: [email protected]. I am grateful for the advice and support of Rodney Lester, Senior Advisor Capital and Risk Markets Group, in preparing this article. I would also like to thank Thorsten Beck, César Calderón, Vidhi Chhaochharia, Stijn Claessens, and Kostas Tzioumis for their comments, feedback, and suggestions during its preliminary stages. The findings, interpretations, and conclusions are entirely the author's, including all errors.
Abstract
Insurance market activity may contribute to economic growth, both as financial intermediary and provider of risk transfer and indemnification, by allowing different risks to be managed more efficiently and by mobilizing domestic savings. During the last decade, there has been faster growth in insurance market activity, particularly in emerging markets, given the process of financial liberalization and integration, which raises questions about the overall impact on economic growth. This article tests whether there is a causal relationship between insurance market activity (life and nonlife insurance) and economic growth. Using the generalized method of moments (GMM) for dynamic models of panel data for 55 countries between 1976 and 2004, I find robust evidence for this relationship. Both life and nonlife insurance have a positive and significant causal effect on economic growth. For life insurance, high-income countries drive the results, and for nonlife insurance, both high-income and developing countries drive the results.
Introduction
The last two decades have seen accelerated growth in insurance markets. Total written real premiums for all countries increased by 82 percent between 1997 and 2004 (104 percent in the life insurance business and 60 percent in the nonlife insurance one), from US$1.6 trillion to US$2.9 trillion.1 Emerging markets (EMs) have recently experienced significantly faster real growth in their insurance sectors than industrialized countries have (52 percent versus 27 percent between 1997 and 2004), reflecting liberalization and financial integration after structural reforms were implemented.2
Insurance market activity, both as financial intermediary and as provider of risk transfer and indemnification, may promote economic growth by allowing different risks to be managed more efficiently. This activity would encourage the accumulation of new capital and mobilize domestic savings into productive investments. In this context, the evidence mentioned above raises questions regarding the impact that the faster growth of insurance activity would have on economic growth.
So far, most empirical work has assessed the impact of the banking sector and stock market development on economic growth (Levine, 2005). However, even though the potential contribution of insurance market activity to economic growth has been recognized, the assessment of a potential causal relationship between insurance market activity and economic growth has not been as extensively studied as that of banks and economic growth. This situation reflects both data availability and the rather arcane reputation of the insurance sector in economic circles.
In this context, the purpose of this article is to provide a systematic assessment of the causal effect of insurance market activity on economic growth, taking into account the effects that life and nonlife insurance could have because of the different benefits that they provide to households and corporations. To accomplish this task, I use measures of insurance premiums as proxies of insurance activity for a set of 55 countries between 1976 and 2004. I also use an estimation method known as the generalized method of moments (GMM) that is suited to panel data and accounts for some endogeneity in the explanatory variables. This method was developed by Arellano and Bond (1991), Arellano and Bover (1995), and Blundell and Bond (1998).
This article finds robust evidence of a causal relationship between insurance market activity and economic growth. Both life and nonlife insurance premiums have a positive and significant effect on economic growth. I also found evidence that in the case of life insurance, the impact on economic growth is driven by high-income countries only. On the other hand, in the case of nonlife insurance, the impact is driven by both high-income and developing (middle- and low-income) countries.3 Nevertheless, the results suggest that nonlife insurance has a larger effect in high-income countries than in the developing ones.
The article is organized as follows. The “Insurance Market Activity and Economic Growth” section presents a summary of the relationship between insurance market activity and economic growth. The following section provides a review of the empirical literature. The next sections describe methodology and data. The “Results” section presents and interprets the results, and the last section offers some conclusions.
Insurance Market Activity and Economic Growth
A large body of theoretical literature has emphasized how financial systems influence savings and investment decisions and hence long-run growth rates through the following functions: (1) lowering the costs of researching potential investments; (2) exerting corporate governance; (3) trading, diversifying, and managing risk; (4) mobilizing and pooling savings; (5) conducting exchanges of goods and services; and (6) mitigating the negative consequences that random shocks can have on capital investment (Levine, 2005). Financial intermediaries support development by improving these functions, i.e., ameliorating market frictions such as the costs of acquiring information, making transactions, and enforcing contracts and allowing economies to allocate resources (savings) across investments more efficiently. However, the positive effects of financial development are tailored by the macro policies, laws, regulations, financial infrastructures, and enforcement norms applied across countries and time.
Insurance activity may contribute to economic growth by improving the financial system functions, both as a provider of risk transfer and indemnification and as an institutional investor, in the following ways: (1) promoting financial stability, (2) facilitating trade and commerce (the most ancient insurance activity), (3) mobilizing domestic savings, (4) allowing different risks to be managed more efficiently by encouraging the accumulation of new capital, (5) fostering a more efficient allocation of domestic capital, and (6) helping to reduce or mitigate losses (Skipper, 1997, pp. 2–7). In addition, there are likely to be different effects on economic growth from life and nonlife insurance (property–liability) given that these two types of insurance protect households and corporations from different kinds of risks that affect economic activity in diverse ways. Moreover, life insurance companies facilitate long-term investments rather than short-term investments as is the case for nonlife insurance companies.
At the theoretical level, Greenwood and Jovanovic (1990) and Pagano (1993) have modeled the effect of financial intermediaries on economic growth. In their frameworks, financial intermediaries have an impact on growth by transforming savings into investment, i.e., funneling savings to firms by improving the allocation and productivity of capital and by altering the savings rate. With particular emphasis on insurance activity, Webb, Grace, and Skipper (2002) model the impact of financial intermediaries (banks, life, and nonlife insurers) on economic growth in the context of a neoclassical Solow-Swan model predicting that insurance and banking spur capital stock productivity, which drives the level of output and investment. Soo (1996) developed a dynamic optimization model that includes the availability of life insurance as a tax-loaded premium for individuals to maximize their lifetime utility. This analytical framework allows us both to examine life insurance effects on individual and aggregate consumption and saving rates and to evaluate whether taxing a life insurance premium would promote discouraging aggregate savings, consumption, and wealth. In this model, policies in favor of the growth of the life insurance sector increase aggregate savings and consumption and have a positive effect on economic growth.
At the empirical level, most of the extant work assesses the impact of the banking sector on economic growth, showing that developing this sector can help to explain the resulting growth (King and Levine, 1993a,b) and that there is a positive causal relationship between banking sector development and economic growth (Levine, 1998, 1999; Levine, Loayza, and Beck, 2000). Also, the impact of stock market development together with that of the banking sector on economic growth have been studied by Levine and Zervos (1998), showing that initial measures of stock market liquidity and banking sector development are both strong predictors of economic growth over the next 18 years, and by Beck and Levine (2004) who show that stock markets and banks have a positive causal relationship with economic growth.
Nonetheless, the impact of insurance market activity on economic growth has not been studied as extensively as the role of the banking sector and the stock market.4 In this context, the main task of my article is to assess whether insurance market activity has a causal effect on economic growth, distinguishing the particular effects of life and nonlife insurance activity.5 This question becomes more relevant if we take into account that many developing countries have embarked on implementing structural reforms in the last 15 years, including trade and financial liberalization. These reforms allow an increase in both the trade of financial services (e.g., insurance) and foreign direct investment in financial services (e.g., the presence of foreign insurance companies in developing countries), which may foster the role of insurance market activity in economic growth by improving the financial system functions in the economy.
Interactions Among Insurance Activity, Banks, and Stock Markets
The theoretical literature has mostly emphasized the potential complementarity or substitution effect between banks and stock markets. On the one hand, a stream of literature stresses that banks rather than stock markets play a critical role in reducing informational friction and transaction costs and in improving the allocation of resources (Boyd and Prescott, 1986; Stiglitz, 1985; Bhide, 1993). On the other hand, Allen and Gale (2000) stress the role of markets rather than banks due to the competitive nature of the markets in encouraging innovative, growth-enhancing activities. Finally, within the literature that stresses a complementarity effect, Levine (1997) points out that both banks and markets ameliorate information and transaction costs. Boyd and Smith (1998) model the increasing importance of equity markets as an economy develops, showing that equity markets complement debt markets by making debt markets operate more efficiently. Huybens and Smith (1999) present a monetary growth model where banks and secondary capital markets have a crucial allocative function in the economy, affecting long-run real performance.
Nevertheless, to my knowledge, there are no theoretical works modeling the links among banks, stock (capital) markets, and insurance activity in a unified framework. Insurance market activity may not only contribute to economic growth by itself but also through complementarities with the banking sector and the stock market. By reducing information and transaction costs, pooling risk, enhancing financial intermediation through the channeling of savings to domestic investment, and fostering a more efficient capital allocation through the gathering of substantial firm information, insurance activity may contribute to reinforcing the process of resource allocation done by banks and capital markets.
In the first case, the conjoint effect with the banking sector, insurance activity development covers banks and their customers against a range of risks, “underpinning bank lending by protecting customers against risks that might otherwise leave them unable to repay their debts” (Rule, 2001, pp. 138–139). The risk protection offered by insurance companies encourages bank borrowing by reducing companies' market cost of capital (Grace and Rebello, 1993). These results are critical because this protection could determine whether firms could develop their activities while having a direct impact on bank credit risk. In this context, for example, property insurance may facilitate bank intermediation activity by partially collateralizing credit, which would reduce a bank's credit risk exposures, promoting higher levels of lending (Zou and Adams, 2006).6 A potential negative complementarity between insurance activity, particularly life insurance, and banks may be due to the “saving substitution effect” (Haiss and Sümegi, 2006) because in the market for intermediated saving, insurance companies compete and could reduce banks' market share (Allen and Santomero, 2001). Insurers, however, may invest (part of) that savings in bank capital investments (e.g., equities) and subordinated debt, so the magnitude of the final effect has to be evaluated empirically.
At the same time, the development of the banking sector may reinforce the development of insurance activity through a much more effective payment system that allows an improved financial intermediation of services (Beck and Webb, 2003; Webb, Grace, and Skipper, 2002). In addition, the development of the banking sector provides liquidity facilities to insurance companies that enable them to pay their claims (Rule, 2001).
Finally, in the last two decades, the interdependence between banking and insurance activities has increased strongly because of risk transfer. Given that banks and insurers have mutual exposures in many areas, banks have unbundled their credit risks to insurance providers mainly through both the securitization of credit portfolios (asset-backed securities and collateralized debt obligations) and derivatives (credit default swaps). On the insurance side, insurers have transferred credit risk to banks through liquidity facilities and letters of credit (Rule, 2001).
Regarding the conjoint effect with the stock market, and capital markets in general, the development of insurance activity, particularly for life insurance companies, could promote stock and bond market development (capital markets deepening), by investing funds (savings) raised through contractual saving products in stocks and equities (Catalan, Impavido, and Musalem, 2000; Impavido, Musalem, and Tressel, 2003). Still, the channeling of savings made by insurance companies would not only develop the stock and bond markets but also foster a more efficient capital allocation because the insurance companies would gather significant information to perform their evaluation of projects and firms in order to allocate the financial capital and interest risk bearing capacity (Skipper, 1997, p. 25). In addition, it is important to mention that insurance (cat bonds) is appealing to potential investors because it is uncorrelated with other types of business activities.7
At the same time, developing the stock market may reinforce developing insurance activity because liquid capital markets help insurance companies invest their resources captured through premium payments. This is especially important for life insurance companies that want to match long-term liabilities with long-term assets (which are normally not available through banks). Finally, as is true for banks, there are also inter-linkages between insurance companies and stock markets for risk transfer reasons. According to Rule (2001), insurance companies transfer to capital markets not only market risk by hedging of embedded options in life insurance portfolios but also insurance risks related to natural catastrophes (catastrophe bonds). On the insurance side, capital markets may transfer market risk to insurance companies when the latter write options and buy bonds with embedded options (e.g., callable bonds).
In this context, the second task of my article is to assess whether the measures of insurance market activity (life and nonlife) are complementary or not to the measures of banking sector and stock market development in order to test whether banks, stock markets, and insurers complement each other.
Review of the Empirical Literature
Earlier work focuses on the relationship between insurance consumption (life and nonlife) and income level (GDP per capita) and between insurance and financial development. Beenstock, Dickinson, and Khajuria (1986) find that nonlife insurance demand is associated with GDP per capita in a sample of 12 industrialized countries between 1970 and 1981. Outreville (1990) finds that nonlife insurance demand is associated positively with GDP per capita and a measure of financial development (M2/GDP) for a sample of 55 developing counties between 1983 and 1984. However, as the author points out, a study of the causal link between insurance development and economic growth is lacking. Browne and Kim (1993) find that life insurance consumption per capita is positively associated with GDP per capita for a sample of 45 countries for the years 1980 and 1987. Outreville (1996) finds that life insurance demand is associated positively with GDP per capita but not with financial development in a sample of 48 developing countries for the year 1986. Browne, Chung, and Frees (2000) find that nonlife insurance consumption is associated positively with the income level for a sample of OECD countries over the 1986–1993 period. Beck and Webb (2003) examine the determinants of life insurance consumption for a sample of 63 countries between 1980 and 1996. The authors find that educational attainment, banking sector development, and inflation are the most robust predictors of life insurance consumption, while income is only a weak predictor. See Hussels, Ward, and Zurbruegg (2005) for a comprehensive literature review on the determinants of (life and nonlife) insurance demand.
The assessment of a potential causal relationship between insurance market activity and economic growth has not been extensively studied. The works of Ward and Zurbruegg (2000) and Webb, Grace, and Skipper (2002) are exceptions. Ward and Zurbruegg examine the potential causal relationship between economic growth and insurance market activity for nine OECD countries for the period 1961–1996, using annual real GDP as a measure of economic activity and annual real total written premiums as a measure of insurance activity.8 Long-term relationships for five countries (Australia, Canada, France, Italy, and Japan) are found using a vector autoregression error correction model on a country-by-country basis. The authors test the statistical significance of the coefficients on insurance for the long-run equation to assess causation between insurance and GDP growth for these countries.
Webb, Grace, and Skipper (2002) examine the causal relationship of banks, life, and nonlife insurance activity on economic growth in the context of a revised Solow-Swan neoclassical of economic growth model, where the authors include financial activities (bank, life, and nonlife insurance) as additional inputs in the production function, which is assumed to be a Cobb-Douglas type. The empirical specification falls in the context of the cross-country economic growth regressions literature (Barro and Sala-i-Martin, 1995), including measures of financial intermediary activity (the ratio of bank credit to GDP, the ratio of nonlife insurance premiums to GDP, and the ratio of life insurance premiums to GDP). The authors use the three-stage least squares instrumental variable approach (3SLS-IV), where the instruments used are the legal origin of the country (English, French, German, Scandinavian, or Communist) for the banking measure, a measure of corruption and quality of the bureaucracy for the nonlife insurance measure, and the religious composition of the country (fraction of the population that are Catholic, Muslim, or Protestant) for the life insurance measure.9
Among the main findings, Webb, Grace, and Skipper (2002) show that the exogenous components of the banking and life insurance measures are found to be robustly predictive of increased economic growth. These measures, however, are not significant in the presence of interaction terms between banking and life insurance, and between banking and nonlife insurance. The individual variables lose explanatory power when the interaction terms are included. The latter result would suggest the presence of complementarities among financial intermediaries.
My article, as opposed to that of Ward and Zurbruegg (2000), uses not only data on total insurance premiums but also their desegregation into life and nonlife insurance premiums in order to assess their potentially different effects on economic growth. Also, I use a broader set of countries, industrialized and developing, to evaluate whether there are similar underlying patterns among different groups of income countries. In this sense, my article is close to that of Webb, Grace, and Skipper (2002). However, I depart from those authors given that I use not only cross-country data but also time-series data to exploit the additional information provided by the over-time variation in the growth rate and its determinants, which allows for more precise estimates.
Methodology
As in Webb, Grace, and Skipper (2002), this article evaluates the effect of insurance variables on economic growth within the context of the standard growth regressions specification.
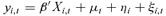 (1)
(1)I work with a pooled data set of cross-country and time-series observations (data details are given below). This article uses an estimation method that is suited to panel data, deals with static or dynamic regression specifications, controls for unobserved time- and country-specific effects, and accounts for some endogeneity in the explanatory variables. As mentioned in the introduction, this system is the GMM developed by Arellano and Bond (1991), Arellano and Bover (1995), and Blundell and Bond (1998) for dynamic models of panel data.
GMM deals with unobserved time effects through the inclusion of period-specific intercepts. Dealing with unobserved country effects is not so simple given the possibility that the model is dynamic and contains endogenous explanatory variables. Thus, unobserved country effects need to be controlled for by differencing and instrumentation. Likewise, the method relies on instrumentation to control for joint endogeneity. Specifically, it allows relaxing the assumption of strong exogeneity of the explanatory variables by allowing them to be correlated with current and previous realizations of the error term ξ.
Parameter identification is achieved by assuming that future realizations of the error term do not affect current values of the explanatory variables in that the error term ξ is serially uncorrelated and that changes in the explanatory variables are uncorrelated with the unobserved country-specific effect. As Arellano and Bond (1991), Arellano and Bover (1995), and Blundell and Bond (1998) show, this set of assumptions generates moment conditions that allow estimation of the parameters of interest. The instruments corresponding to these moment conditions are appropriately lagged values of both levels and differences of the explanatory and dependent variables (the latter if the model is dynamic). In addition, we use as instruments of banking and stock market variables the origin of the legal code (English, French, German, Communist, or Scandinavian), and measures of religious composition as instruments of insurance variables. Because the moment conditions typically overidentify the regression model, they also allow for specification testing through a Sargan-type test.
Data
I estimate economic growth regressions on a pooled (cross-country, time-series) data set consisting of 55 countries and, for each of them, at most, six nonoverlapping 5-year periods between 1976 and 2004. See Appendixes A, B, and C for a list of countries in the sample and basic descriptive statistics and correlations of the data used in the regressions.10Appendix D provides the definitions and data sources of the variables used in the article.
As it is standard in the economic growth literature, the dependent variable is the average rate of real per capita GDP growth. The regression equation is dynamic in the sense that it includes the initial level of per capita GDP as an explanatory variable. As additional control variables, the regression includes the average rate of secondary school enrollment to account for human capital investment, the average inflation rate to account for monetary discipline, the average growth of the terms of trade ratio, the average ratio of government consumption to GDP as a measure of government burden, and the ratio of the sum of exports and imports over GDP as a measure of the country's degree of openness.11 Following Beck and Levine (2004), I measure banking sector development by using the ratio of bank claims on the private sector by deposit money banks divided by GDP. This measure excludes credits by development banks and loans to the government and public enterprises. Regarding stock market development, the turnover ratio measure of market liquidity is used as a proxy. The latter equals the value of the trades of shares on domestic exchanges divided by the total value of listed shares.
The explanatory variables of interest are measures of insurance market development proxied by the ratio of life insurance premiums to GDP and the ratio of nonlife (property–liability) insurance premiums to GDP. These measures could be thought of as measures of penetration of insurance activity in the economy.12 However, the use of premiums as a proxy for insurance market activity would only capture the role of life and nonlife insurance companies as providers of risk transfer and indemnification rather than their role as institutional investors. Given data limitations, it is currently not possible to have a consistent time series of the ratio of financial investments (assets) to GDP, which would capture their role as institutional investors.13 Finally, the regression equation also allows for both unobserved time- and country-specific effects.
Results
Linear Effects of Insurance Market Activity
Table 1, columns 1 and 2, shows the linear effects of private credit and stock market turnover on economic growth. The coefficients of both variables are positive and statistically significant reflecting the proxies for banking sector and stock market development having a causal effect on economic growth, which is consistent with previous findings in the literature (Levine, 2005; Beck and Levine, 2004). Columns 3–5 show the individual and joint effect of life and nonlife premiums to GDP on economic growth. The coefficients of the insurance variables are positive and statistically significant. This result suggests that the proxies used for insurance market activity (life and nonlife premiums to GDP) have a causal effect on economic growth, both individually and jointly. The coefficient on stock market turnover is positive and statistically significant in all specifications. However, the coefficient on private credit to GDP is not significant in the specifications that include insurance variables. The latter could be explained by a significant statistical correlation between private credit to GDP and insurance variables (between 0.41 and 0.56), which would not allow the proxy of banking sector development to convey additional information.
| [1] | [2] | [3] | [4] | [5] | |
|---|---|---|---|---|---|
| Constant | 0.115*** | 0.127*** | 0.162*** | 0.151*** | 0.151*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Log. initial GDP per capita | −0.009*** | −0.012*** | −0.015*** | −0.015*** | −0.014*** |
| 0.001 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Private credit to GDP | 0.010** | 0.007** | −0.003 | −0.005 | 0.002 |
| 0.014 | 0.033 | 0.650 | 0.476 | 0.755 | |
| Stock market turnover | 0.026*** | 0.025*** | 0.026*** | 0.025*** | |
| 0.000 | 0.000 | 0.000 | 0.000 | ||
| (Life + nonlife insurance) to GDP | 0.138*** | ||||
| 0.000 | |||||
| Life premiums to GDP | 0.151** | ||||
| 0.050 | |||||
| Nonlife premiums to GDP | 0.251*** | ||||
| 0.000 | |||||
| Degree of openess | 0.399*** | 0.598*** | 0.501* | 0.564** | 0.313 |
| 0.001 | 0.004 | 0.060 | 0.019 | 0.146 | |
| Government consumption | −1.858*** | −1.679*** | −2.206*** | −1.889*** | −1.988*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.024*** | 0.046*** | 0.043*** | 0.041*** | 0.048*** |
| 0.003 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Human capital investment | 0.042*** | 0.037*** | 0.055*** | 0.054*** | 0.057*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Period shifts | |||||
| Period 1981–1985 | −0.016*** | −0.016*** | −0.015*** | −0.015*** | −0.016*** |
| Period 1986–1990 | −0.007*** | −0.011*** | −0.012*** | −0.012*** | −0.012*** |
| Period 1991–1995 | −0.017*** | −0.020*** | −0.023*** | −0.023*** | −0.024*** |
| Period 1996–2000 | −0.017*** | −0.023*** | −0.027*** | −0.027*** | −0.027*** |
| Period 2001–2004 | −0.027*** | −0.033*** | −0.040*** | −0.038*** | −0.039*** |
| Countries | 55 | 55 | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 | 263 | 263 |
| Specification tests (P-values) | |||||
| Sargan test | 0.732 | 0.766 | 0.448 | 0.447 | 0.525 |
| Second-order correlation | 0.252 | 0.586 | 0.425 | 0.429 | 0.484 |
- Note: Sample of 55 countries, 1976–2004 (5-year period observations). Dependent variable: growth in real GDP per capita. Estimation method: GMM-IV system estimator.
- P-values in italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.
Regarding the individual impact of insurance variables, an increase in one standard deviation in life insurance premiums to GDP, ceteris paribus, would imply an increase of 0.37 percent in economic growth. In the case of nonlife insurance premiums to GDP, an increase of one standard deviation would have a larger impact of 0.39 percent on economic growth. Finally, a one standard deviation increase in total insurance (life plus nonlife insurance premiums to GDP) would increase real GDP per capita growth by 0.47 percent.
With respect to the rest of the control variables, the coefficients on the degree of openness of the change in the terms of trade and the initial measures of human capital are positive and statistically significant, and the coefficients on government consumption, inflation, and initial GDP per capita are negative and significant.14 The Sargan and serial-correlation tests do not reject the null hypothesis of correct specification, lending support to our estimation results.
Moreover, Table 2 shows the coefficients of life and nonlife insurance premiums to GDP by income group.15 In the case of life insurance, only high-income countries would drive the results shown in Table 1 because the coefficient on life insurance for developing countries (low- and middle-income countries) is not significant. An increase of one standard deviation in life insurance premiums to GDP in high-income countries only, ceteris paribus, would imply an increase of 0.58 percent in economic growth in high-income countries. In the case of nonlife insurance, the results shown in Table 1 are driven not only by high-income countries but also by developing countries. However, the effect of nonlife insurance premiums to GDP is larger in high-income countries. An increase of one standard deviation in nonlife insurance premiums to GDP in high-income countries (developing countries), ceteris paribus, would imply an increase of 0.53 (0.25) percent in economic growth in high-income countries (developing countries).
| High-Income Countries | Developing Countriesa | ||||
|---|---|---|---|---|---|
| Variable | Coefficient | T-Stat | Variable | Coefficient | T-Stat |
| Life | 0.018 | 0.213 | Life | 0.249 | 2.546 |
| Life* high income dummy | 0.231 | 1.827 | Life* dev. countries dummy | −0.231 | 1.827 |
| Linear combination | 0.246 | 2.500 | Linear combination | 0.018 | 0.213 |
| Nonlife | 0.168 | 3.827 | Nonlife | 0.533 | 2.500 |
| Nonlife* high income dummy | 0.365 | 1.690 | Nonlife* dev. countries dummy | −0.265 | 1.690 |
| Linear combination | 0.533 | 2.500 | Linear combination | 0.168 | 3.827 |
- aDeveloping countries include middle- and low-income countries.
Nonlinear Effects of Insurance Market Activity
This article also evaluates the possibility that insurance variables (life and nonlife premiums to GDP) could have nonlinear effects on economic growth. Enz (2000) finds a nonlinear relationship between life and nonlife insurance penetration and GDP per capita, implying varying income elasticities. It could be the case that insurance market activity could have different effects on economic growth depending on the level of country economic development, which could be captured by the measure of the GDP per capita. In order to test this hypothesis, this article evaluates the insurance effect on economic growth for different stages of initial GDP per capita (below the 33rd percentile value of the distribution of the initial GDP per capita across our sample, between the 33rd and 66th value of the distribution, and above the 66th percentile value of the distribution).16
Table 3 presents results including interaction terms between the insurance variables and dummy variables, capturing different stages of initial GDP per capita. With respect to life insurance, the results show that the interaction term is positive and significant for the levels of GDP per capita below the 33rd percentile value of its distribution (first stage) and for the levels between the 33rd and 66th percentile value (second stage). Nonetheless, the impact on economic growth of an increase of one standard deviation in the interaction term of life insurance premiums to GDP with initial GDP per capita, first stage, is higher (0.43 percent) than the effect of the interaction term of life insurance premiums to GDP with initial GDP per capita, second stage (0.26 percent). This result would suggest that life insurance would have a bigger impact on economic growth at low and middle levels of economic development measured by GDP per capita, particularly at low levels.
| [1] Life Insurance | [2] Nonlife Insurance | [3] (Life + Nonlife) | |
|---|---|---|---|
| Constant | 0.117*** | 0.176 | 0.151*** |
| 0.000 | 0.000 | 0.000 | |
| Private credit to GDP | −0.008 | 0.004 | −0.001 |
| 0.331 | 0.504 | 0.815 | |
| Stock market turnover | 0.025*** | 0.030 | 0.023*** |
| 0.000 | 0.000 | 0.000 | |
| Insurance and interactions | |||
| Insurance* initial GDP pc (below 33rd percentile) | 1.042*** | 0.151* | 0.324*** |
| 0.000 | 0.101 | 0.006 | |
| Insurance* initial GDP pc (between the 33rd and 66th percentile) | 0.150* | 0.293*** | 0.224*** |
| 0.094 | 0.000 | 0.000 | |
| Insurance* initial GDP pc (above the 66th percentile) | 0.072 | 0.116 | 0.107* |
| 0.364 | 0.466 | 0.080 | |
| Control variables | |||
| Log. initial GDP per capita | −0.010*** | −0.019*** | −0.015*** |
| 0.003 | 0.000 | 0.000 | |
| Degree of openess | 0.626*** | 0.521** | 0.536** |
| 0.005 | 0.026 | 0.044 | |
| Government consumption | −2.163*** | −1.732*** | −2.078*** |
| 0.000 | 0.001 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.047** | 0.049*** | 0.057*** |
| 0.000 | 0.000 | 0.000 | |
| Human capital investment | 0.053*** | 0.062*** | 0.057*** |
| 0.000 | 0.000 | 0.000 | |
| Period shifts | |||
| Period 1981–1985 | −0.014*** | −0.016*** | −0.015*** |
| Period 1986–1990 | −0.011*** | −0.013*** | −0.013*** |
| Period 1991–1995 | −0.021*** | −0.024*** | −0.023*** |
| Period 1996–2000 | −0.025*** | −0.029*** | −0.028*** |
| Period 2001–2004 | −0.036*** | −0.041*** | −0.039*** |
| Countries | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 |
| Specification tests | |||
| Sargan | 0.335 | 0.309 | 0.452 |
| Autocorrelation | 0.302 | 0.501 | 0.358 |
- Note: Sample of 55 countries, 1976–2004 (5-year period observations). Dependent variable: growth in real GDP per capita. Estimation method: fixed-effects.
- P-values in italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.
Regarding nonlife insurance, the results are similar to those for life insurance. The interaction terms between the nonlife insurance premiums ratio and initial GDP per capita for the first and second stages are significant. However, the impact on economic growth of a one standard deviation increase of the interaction term for the second stage is higher (0.33 percent) than the effect of the interaction term for the first stage (0.17 percent). This result would suggest that nonlife insurance would have a bigger impact on economic growth at low and middle levels of economic development measured by GDP per capita, particularly at middle levels.
Complementarities Between Insurance and Banking and Stock Market Variables
To assess whether the measures of insurance activity (life and nonlife premiums to GDP) are complementary or not to measures of bank intermediation (private credit to GDP) and stock market (stock market turnover), an interaction term is included in the growth regressions. Insurance variables are interacted with dummy variables that capture different stages of financial and stock market development.17
Table 4 shows the results of the interaction between insurance variables and dummy variables for different stages of financial development (below the 33rd percentile value of the distribution of private credit across our sample, between the 33rd and 66th value of the distribution, and above the 66th percentile value of the distribution).
| [1] Life Insurance | [2] Nonlife Insurance | [3] (Life + Nonlife) | |
|---|---|---|---|
| Constant | 0.137*** | 0.152*** | 0.155*** |
| 0.000 | 0.000 | 0.000 | |
| Private credit to GDP | 0.007 | −0.008 | 0.000 |
| 0.253 | 0.239 | 0.947 | |
| Stock market turnover | 0.021*** | 0.028*** | 0.024*** |
| 0.000 | 0.000 | 0.000 | |
| Insurance and interactions | |||
| Insurance* private credit (below 33rd percentile) | 0.637*** | 0.229*** | 0.202*** |
| 0.002 | 0.000 | 0.000 | |
| Insurance* private credit (between the 33rd and 66th percentile) | 0.367*** | 0.085 | 0.189*** |
| 0.002 | 0.416 | 0.005 | |
| Insurance* private credit (above the 66th percentile) | −0.083 | 0.444*** | 0.111 |
| 0.277 | 0.003 | 0.123 | |
| Control variables | |||
| Log. initial GDP per capita | −0.013*** | −0.014*** | −0.014*** |
| 0.000 | 0.000 | 0.000 | |
| Degree of openess | 0.512*** | 0.359 | 0.546* |
| 0.007 | 0.179 | 0.059 | |
| Government consumption | −2.057*** | −1.918*** | −2.411*** |
| 0.000 | 0.000 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.025** | 0.057*** | 0.057*** |
| 0.033 | 0.000 | 0.001 | |
| Human capital investment | 0.055*** | 0.050*** | 0.057*** |
| 0.000 | 0.000 | 0.000 | |
| Period shifts | |||
| Period 1981–1985 | −0.015*** | −0.014*** | −0.015*** |
| Period 1986–1990 | −0.011*** | −0.010*** | −0.012*** |
| Period 1991–1995 | −0.021*** | −0.022*** | −0.024*** |
| Period 1996–2000 | −0.023*** | −0.025*** | −0.028*** |
| Period 2001–2004 | −0.033*** | −0.037*** | −0.039*** |
| Countries | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 |
| Specification tests | |||
| Sargan | 0.399 | 0.343 | 0.452 |
| Autocorrelation | 0.17 | 0.56 | 0.36 |
- Note: Sample of 55 countries, 1976–2004 (5-year period observations). Dependent variable: Growth in real GDP per capita. Estimation method: fixed-effects.
- P-values in italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.
With respect to life insurance, the results show that the interaction term is positive and significant for both the levels of private credit below the 33rd percentile value of its distribution (first stage) and the levels between the 33rd and 66th percentile value (second stage). Moreover, the impact on economic growth of a one standard deviation increase in the interaction term of life insurance premiums to GDP with private credit, second stage, is higher (0.51 percent) than the effect of the interaction term of life insurance with private credit, first stage (0.28 percent). This result would suggest that the deeper the country's financial development, the bigger the impact of life insurance on economic growth, which implies a positive complementarity between life insurance and financial development, particularly for initial and intermediate stages of financial development. For higher levels of financial development, the interaction term is negative but not significant. This could give room for further research on whether life insurance and financial development are substitutes after a particular threshold of financial deepening.
Regarding nonlife insurance, the interaction terms for different stages of financial development are positive but significant only for low and high levels of financial deepening (below the 33rd, first stage, and above the 66th, third stage, percentile value of the private credit distribution). The impact on economic growth of a one standard deviation increase in the interaction term of nonlife insurance premiums to GDP with private credit, third stage, is higher (0.69 percent) than the effect of the interaction term of life insurance with private credit, first stage (0.19 percent). These results would suggest a positive complementarity for initial and high stages of financial development. However, I do not have a particular argument, a priori, to explain why for intermediate levels of financial development there is not complementarity between nonlife insurance and financial development, even though they have a positive correlation.
Table 5 shows the results of the interaction between insurance variables and dummy variables for different stages of stock market development (below the 33rd percentile value of the distribution of stock market turnover across our sample, between the 33rd and 66th value of the distribution, and above the 66th percentile value of the distribution). With respect to life insurance, the results show that the interaction term is positive and significant for the levels of stock market turnover between the 33rd and 66th percentile value (second stage) and above the 66th percentile value for the third stage. The impact on economic growth of a one standard deviation increase in the interaction term of life insurance premiums to GDP with stock market turnover, third stage, is higher (0.43 percent) than the effect of the interaction term of life insurance with stock market turnover, second stage (0.26 percent). This result would suggest that life insurance would have a bigger impact on economic growth the deeper the country's stock market development, which implies a positive complementarity between life insurance and stock market development, particularly for intermediate and high stages of stock market development.
| [1] Life Insurance | [2] Nonlife Insurance | [3] (Life + Nonlife) | |
|---|---|---|---|
| Constant | 0.149*** | 0.147*** | 0.141*** |
| 0.000 | 0.000 | 0.000 | |
| Private credit to GDP | −0.009 | −0.007 | −0.010 |
| 0.230 | 0.239 | 0.129 | |
| Stock market turnover | 0.026*** | 0.028*** | 0.025*** |
| 0.000 | 0.000 | 0.000 | |
| Insurance and interactions | |||
| Insurance* stock market (below 33rd percentile) | 0.041 | 0.231** | 0.182*** |
| 0.603 | 0.027 | 0.005 | |
| Insurance* stock market (between the 33rd and 66th percentile) | 0.206* | 0.745*** | 0.280*** |
| 0.104 | 0.000 | 0.002 | |
| Insurance* stock market (above the 66th percentile) | 0.184** | 0.206*** | 0.144*** |
| 0.018 | 0.000 | 0.000 | |
| Control variables | |||
| Log. initial GDP per capita | −0.015*** | −0.015*** | −0.012*** |
| 0.000 | 0.000 | 0.000 | |
| Degree of openess | 0.561** | 0.592** | 0.551** |
| 0.048 | 0.017 | 0.036 | |
| Government consumption | −1.725*** | −2.167*** | −2.353*** |
| 0.000 | 0.000 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.043*** | 0.040*** | 0.055*** |
| 0.001 | 0.006 | 0.000 | |
| Human capital investment | 0.053*** | 0.061*** | 0.055*** |
| 0.000 | 0.000 | 0.000 | |
| Period shifts | |||
| Period 1981–1985 | −0.016*** | −0.015*** | −0.015*** |
| Period 1986–1990 | −0.012*** | −0.013*** | −0.011*** |
| Period 1991–1995 | −0.023*** | −0.023*** | −0.023*** |
| Period 1996–2000 | −0.027*** | −0.026*** | −0.026*** |
| Period 2001–2004 | −0.038*** | −0.037*** | −0.037*** |
| Countries | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 |
| Specification tests | |||
| Sargan | 0.343 | 0.424 | 0.425 |
| Autocorrelation | 0.42 | 0.21 | 0.24 |
- Note: Sample of 55 countries, 1976–2004 (5-year period observations). Dependent variable: growth in real GDP per capita. Estimation method: fixed-effects.
- P-values in italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.
Regarding nonlife insurance, the interaction terms for different stages of stock market development are positive and significant. The impacts on economic growth of a one standard deviation increase in the interaction term of nonlife insurance premiums to GDP with private credit for the first, second, and third stages are 0.29, 0.89, and 0.30 percent, respectively. These results suggest a complementarity for initial and intermediate stages of stock market development. For high levels of stock market development, the interaction between the variables is positive and significant but their contribution to economic growth is similar to that when initial levels of stock market development are used, implying that after a particular threshold, the combined impact of the stock market and nonlife insurance on economic growth would diminish.
Conclusions
This article finds robust evidence of a causal relationship of insurance market activity on economic growth. Both life and nonlife insurance premiums have a positive and significant effect on economic growth. In the case of life insurance, its impact on economic growth is driven by high-income countries only. On the other hand, in the case of nonlife insurance, its impact is driven by both high-income and developing (middle- and low-income) countries. However, the results suggest that nonlife insurance has a larger effect on high-income countries than in developing ones.
Regarding nonlinear effects of insurance market activity on economic growth, this article finds evidence that life and nonlife insurance have different impacts on economic growth for different levels of economic development measured by GDP per capita. Life and nonlife insurance have an impact on economic growth at the low and middle stages of economic development. However, life insurance would have a bigger impact on economic growth at low levels of economic development and nonlife insurance at middle levels.
With respect to complementarity effects between insurance and financial or stock market development, this article finds evidence of a complementarity between life insurance and financial development for initial and intermediate stages of financial development. In the case of nonlife insurance, the results suggest a complementarity for initial and high stages of financial development. Regarding the interaction with stock market development, the results suggest that life insurance would have a bigger impact on economic growth the deeper the country stock market development, particularly for intermediate and high stages of stock market development. In the case of nonlife insurance, the results suggest a complementarity effect for initial and intermediate stages of stock market development.
Footnotes
Appendices
Appendix A List of Countries
| High Income | Middle Income | Low Income |
|---|---|---|
| Australia | Argentina | Cote d'Ivore |
| Austria | Brazil | India |
| Belgium | Chile | Kenya |
| Canada | China | Nigeria |
| Denmark | Colombia | Pakistan |
| Finland | Costa Rica | Zimbabwe |
| France | Ecuador | |
| Germany | Egypt | |
| Greece | El Salvador | |
| Iceland | Indonesia | |
| Ireland | Jordan | |
| Israel | Malaysia | |
| Italy | Mexico | |
| Japan | Morocco | |
| Korea | Panama | |
| Netherlands | Paraguay | |
| New Zealand | Peru | |
| Norway | Philippines, The | |
| Portugal | South Africa | |
| Spain | Thailand | |
| Sweden | Trinidad and Tobago | |
| Switzerland | Tunisia | |
| United Kingdom | Turkey | |
| United States | Uruguay | |
| Venezuela |
- Note: Classification following the World Development Indicators, The World Bank.
Appendix B In-Sample Descriptive Statistics
| Variable | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Life | 0.021 | 0.025 | 0.000 | 0.136 |
| Nonlife | 0.022 | 0.015 | 0.003 | 0.130 |
| (Life + nonlife) | 0.042 | 0.033 | 0.005 | 0.179 |
| Private credit | 0.512 | 0.336 | 0.042 | 1.629 |
| Stock market turnover | 0.424 | 0.509 | 0.004 | 3.508 |
| GDP per capita growth | 0.019 | 0.021 | −0.065 | 0.091 |
| Openness | 0.040 | 0.005 | 0.026 | 0.054 |
| Gov. consumption | 0.027 | 0.003 | 0.014 | 0.034 |
| Inflation | 0.334 | 1.863 | −0.005 | 23.422 |
| Human capital | 0.736 | 0.304 | 0.077 | 1.607 |
| Terms of trade changes | 0.002 | 0.035 | −0.110 | 0.205 |
| Log initial GDP per capita | 9.062 | 0.957 | 6.605 | 10.439 |
Appendix C In-Sample Correlations
| Life | Nonlife | (Life + Nonlife) | Private Credit | Stock Market Turnover | GDP per Capita Growth | Openness | Gov. Consumption | Inflation | Human Capital | Terms of Trade Changes | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Life | 1 | ||||||||||
| Nonlife | 0.427 | 1 | |||||||||
| 0.000 | |||||||||||
| (Life + nonlife) | 0.935 | 0.720 | 1 | ||||||||
| 0.000 | 0.000 | ||||||||||
| Private credit | 0.520 | 0.413 | 0.562 | 1 | |||||||
| 0.000 | 0.000 | 0.000 | |||||||||
| Stock market turnover | 0.216 | 0.050 | 0.200 | 0.222 | 1 | ||||||
| 0.000 | 0.342 | 0.000 | 0.000 | ||||||||
| GDP per capita growth | 0.132 | 0.021 | 0.110 | 0.146 | 0.106 | 1 | |||||
| 0.007 | 0.677 | 0.026 | 0.000 | 0.030 | |||||||
| Openness | 0.144 | 0.121 | 0.160 | 0.220 | −0.052 | 0.145 | 1 | ||||
| 0.003 | 0.013 | 0.001 | 0.000 | 0.290 | 0.000 | ||||||
| Gov. consumption | 0.156 | 0.308 | 0.239 | 0.231 | −0.009 | −0.062 | 0.373 | 1 | |||
| 0.001 | 0.000 | 0.000 | 0.000 | 0.859 | 0.064 | 0.000 | |||||
| Inflation | −0.094 | −0.008 | −0.075 | −0.116 | −0.006 | −0.275 | −0.067 | −0.009 | 1 | ||
| 0.058 | 0.874 | −0.127 | 0.001 | 0.908 | 0.000 | 0.054 | 0.799 | ||||
| Human capital | 0.573 | 0.472 | 0.623 | 0.682 | 0.289 | 0.225 | 0.176 | 0.402 | −0.080 | 1 | |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.079 | |||
| Terms of trade changes | −0.050 | −0.030 | −0.051 | −0.044 | −0.094 | −0.024 | −0.006 | −0.059 | −0.031 | −0.080 | 1 |
| 0.339 | 0.556 | 0.329 | 0.284 | 0.065 | 0.533 | 0.883 | 0.120 | 0.437 | 0.089 |
- Note: P-values in italics.
Appendix D Definitions and Sources of Variables Used in the Regression Analysis
| Variable | Definition and Construction | Source |
|---|---|---|
| GDP per capita | Ratio of total GDP to total population. GDP is in 1995 PPP-adjusted US$ | World Development Indicators (WDI), The World Bank |
| GDP per capita growth | Log difference or real GDP per capita | Author's calculation using WDI |
| Initial GDP per capita | Initial value of ratio of total GDP to total population. GDP is in 1995 PPP-adjusted US$ | Author's calculation using WDI |
| Trade openness | Log of ratio of exports and imports (in 1995 US$) to GDP (in 1995 US$) | WDI, The World Bank |
| Government consumption | Log of the ratio of government consumption to GDP | WDI, The World Bank |
| Inflation rate | Annual change in CPI | WDI, The World Bank |
| Changes in terms of trade | Log differences of the net barter terms of trade index (1995=100) | Author's calculation using WDI |
| Human capital investment | Ratio of the total secondary enrollment, regardless of age, to the population of the age group that officially correspond to that level of education | WDI, The World Bank |
| Stock market turnover ratio | Ratio of the value of total shares traded and average real market capitalization, the denominator is deflated using the following method: Tt/P_/{(0.5) * [M/P_e + M/P_e- t-11 where T is total value traded, M is stock market capitalization, P_e is end-of-period CPI P_a is average annual CPI | Financial Structure Database, Thorsten Beck. Standard & Poor's Emerging Market Database (and Emerging Stock Markets Factbook). Data on the deflators (line 64M..ZF or, if not available, 64Q..ZFand annual CPI (line 64..ZF)) are taken from the electronic version of the IFS |
| Life insurance penetration | Life insurance premium volume as a share of GDP | Financial Structure Database, Thorsten Beck. Premium data are taken from various issues of Sigma. Data on GDP in local currency (lines 99B..ZF or, if not available, line 99B.CZF) |
| Nonlife insurance penetration | Nonlife insurance premium volume as a share of GDP | Financial Structure Database, Thorsten Beck. Premium data are taken from various issues of Sigma. Data on GDP in local currency (lines 99B..ZF or, if not available, line 99B.CZF) |
| Private credit by deposit money banks to GDP | Private credit by deposit money banks to GDP, calculated using the following deflation method:{(0.5)*[F/P_e + F +/P_e]}/[GDP/P_a] where F is credit to the private sector, P_e is end-of-period CPI, and P_a is is average annual CPI. | Financial Structure Database, Thorsten Beck. Raw data are from the electronic version of the IMF's International Financial Statistics (IFS lines 22d). Data on GDP in local currency (lines 99B..ZF or, if not available, line 99B.CZF), end-of-period CPI (line 64M..ZF or, if not available, 64Q..ZF), and annual CPI (line 64..ZF) are from the electronic version of the IFS |
Appendix E Linear Effects of Insurance Variables on Economic Growth
| [1] | [2] | [3] | |
|---|---|---|---|
| Constant | 0.233*** | 0.216*** | 0.232*** |
| 0.000 | 0.000 | 0.000 | |
| Log. initial GDP per capita | −0.024*** | −0.022*** | −0.025*** |
| 0.000 | 0.000 | 0.000 | |
| Private credit to GDP | 0.011*** | 0.011*** | 0.021*** |
| 0.005 | 0.032 | 0.000 | |
| Stock market turnover | 0.024*** | 0.025*** | 0.027*** |
| 0.000 | 0.000 | 0.000 | |
| (Life + nonlife insurance) to GDP | 0.161*** | ||
| 0.000 | |||
| Life premiums to GDP | 0.128* | ||
| 0.078 | |||
| Nonlife premiums to GDP | 0.234*** | ||
| 0.000 | |||
| Degree of openness (de jure measure) | 0.014*** | 0.014*** | 0.012*** |
| 0.000 | 0.000 | 0.000 | |
| Government consumption | −1.880*** | −1.415*** | −1.286*** |
| 0.000 | 0.000 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.027* | 0.021*** | 0.053*** |
| 0.096 | 0.033 | 0.000 | |
| Human capital investment | 0.055*** | 0.050*** | 0.053*** |
| 0.000 | 0.000 | 0.000 | |
| Period shifts | |||
| Period 1981–1985 | −0.013*** | −0.013*** | −0.013*** |
| Period 1986–1990 | −0.011*** | −0.012*** | −0.011*** |
| Period 1991–1995 | −0.025*** | −0.024*** | −0.024*** |
| Period 1996–2000 | −0.028*** | −0.029*** | −0.029*** |
| Period 2001–2004 | −0.043*** | −0.041*** | −0.043*** |
| Countries | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 |
| Specification tests (P-values) | |||
| Sargan test | 0.259 | 0.409 | 0.454 |
| Second-order correlation | 0.588 | 0.705 | 0.605 |
- Note: Sample of 56 countries, 1976–2004 (5-year period observations). Dependent variable: growth in real GDP per capita. Estimation method: GMM-IV system.
- P-values in italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.
Appendix F Interaction of Insurance Variables with Private Credit and Stock Market Turnover
| [1] Life Insurance | [2] Nonlife Insurance | [3] (Life + Nonlife) | [4] Life Insurance | [5] Nonlife Insurance | [6] (Life + Nonlife) | |
|---|---|---|---|---|---|---|
| Constant | 0.120*** | 0.137*** | 0.145*** | 0.123*** | 0.167*** | 0.156*** |
| 0.000 | 0.000 | 0.000 | 0.011 | 0.000 | 0.000 | |
| Private credit to GDP | 0.015** | 0.021** | 0.023*** | −0.002 | 0.005 | 0.004 |
| 0.032 | 0.013 | 0.000 | 0.810 | 0.379 | 0.560 | |
| Stock market turnover | 0.018 | 0.031 | 0.023 | 0.025*** | 0.033*** | 0.026*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Insurance | 0.764*** | 0.478*** | 0.490*** | 0.232*** | 0.300*** | 0.194*** |
| 0.000 | 0.000 | 0.000 | 0.011 | 0.002 | 0.000 | |
| Insurance and interactions | ||||||
| Insurance* private credit | −0.893 | −0.812*** | −0.545*** | |||
| 0.000 | 0.002 | 0.000 | ||||
| Insurance* stock market turnover | −0.160* | −0.316* | −0.120** | |||
| 0.068 | 0.081 | 0.039 | ||||
| Control variables | ||||||
| Log. initial GDP per capita | −0.009*** | −0.014*** | −0.012*** | −0.011*** | −0.017*** | −0.014*** |
| 0.000 | 0.000 | 0.000 | 0.003 | 0.000 | 0.000 | |
| Degree of openness | 0.490*** | 0.551** | 0.517** | 0.630*** | 0.362* | 0.335 |
| 0.003 | 0.025 | 0.033 | 0.004 | 0.104 | 0.162 | |
| Government consumption | −2.494*** | −1.864*** | −2.924*** | −2.175*** | −1.797*** | −2.275*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Inflation | −0.003*** | −0.003*** | −0.003*** | −0.003*** | −0.003*** | −0.003*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Terms of trade | 0.056*** | 0.045*** | 0.047*** | 0.044*** | 0.057*** | 0.050*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Human capital investment | 0.044*** | 0.052*** | 0.052*** | 0.049*** | 0.059*** | 0.054*** |
| 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | |
| Period shifts | ||||||
| Period 1981–1985 | −0.015*** | −0.016*** | −0.014*** | −0.015*** | −0.015*** | −0.015*** |
| Period 1986–1990 | −0.009*** | −0.012*** | −0.009*** | −0.012*** | −0.012*** | −0.012*** |
| Period 1991–1995 | −0.020*** | −0.024*** | −0.022*** | −0.023*** | −0.022*** | −0.023*** |
| Period 1996–2000 | −0.021*** | −0.027*** | −0.025*** | −0.026*** | −0.027*** | −0.027*** |
| Period 2001–2004 | −0.030*** | −0.038*** | −0.035*** | −0.037*** | −0.038*** | −0.039*** |
| Countries | 55 | 55 | 55 | 55 | 55 | 55 |
| Observations | 263 | 263 | 263 | 263 | 263 | 263 |
| Specification tests (P-values) | ||||||
| Sargan test | 0.456 | 0.463 | 0.321 | 0.459 | 0.315 | 0.421 |
| Second-order correlation | 0.319 | 0.525 | 0.380 | 0.336 | 0.464 | 0.325 |
- Note: Sample of 56 countries, 1976–2004 (5-year period observations). Dependent variable: growth in real GDP per capita. Estimation method: GMM-IV system estimator.
- P-values in Italics. ***, **, * denote statistical significance at the 1%, 5%, and 10% levels.




