Effects of Corporate Diversification: Evidence From the Property–Liability Insurance Industry
The authors can be contacted via e-mail: [email protected] and [email protected]
Abstract
Using a sample of property–liability insurers over the period 1995–2004, we develop and test a model that explains performance as a function of line-of-business diversification and other correlates. Our results indicate that undiversified insurers consistently outperform diversified insurers. In terms of accounting performance, we find a diversification penalty of at least 1 percent of return on assets or 2 percent of return on equity. These findings are robust to corrections for potential endogeneity bias, alternative risk measures, alternative diversification measures, and an alternative estimation technique. Using a market-based performance measure (Tobin's Q) we find that the market applies a significant discount to diversified insurers. The existence of a diversification penalty (and diversification discount) provides strong support for the strategic focus hypothesis. We also find that insurance groups underperform unaffiliated insurers and that stock insurers outperform mutuals.
Introduction
Property–liability (P/L) insurers choose whether to focus on one line of business or to diversify across multiple lines. The performance effects of this choice are unclear. Theory suggests that diversification is associated with both costs and benefits. On the one hand, diversification may be performance enhancing due to benefits associated with scope economies, larger internal capital markets, and risk reduction. On the other hand, diversification may reduce performance if it exacerbates agency costs and leads to inefficient cross-subsidization of poorly performing businesses. Thus, the net effect of diversification on the performance of property-liability insurers is an empirical question.1
There is substantial evidence on the relative efficiency and stock performance of insurers that focus on either the life–health (L/H) or P/L industry, and insurers that diversify across both industries. However, there is little evidence on the performance effect of diversification or focus within either of these industries. Given that the vast majority of insurers operate in only one of these industries, it is valuable to investigate the intra-industry effect of insurer diversification. We test two alternative hypotheses regarding diversification's effect on P/L insurer performance. The conglomeration hypothesis emphasizes the benefits associated with diversification and predicts a positive diversification-performance (D-P) relation. By contrast, the strategic focus hypothesis emphasizes the costs of diversification (and the benefits of specialization) and predicts a negative D-P relation.
We examine these hypotheses by modeling accounting and market performance measures as a function of a binary diversification indicator and a range of other performance correlates. Our results indicate that undiversified insurers consistently outperform diversified insurers. We find that diversification is associated with a penalty of at least 1 percent of return on assets (ROA) or 2 percent of return on equity (ROE). These findings are robust to corrections for potential endogeneity bias, alternative risk measures, alternative diversification measures, and an alternative estimation technique. In addition to assessing diversification's effect on accounting performance, we also examine its effect on market value for the sub-sample of publicly traded insurers. Using Tobin's Q as a proxy for firm value, we find that the market applies a significant discount to diversified P/L insurers relative to undiversified insurers. The existence of a diversification penalty (and diversification discount) provides strong support for the strategic focus hypothesis.
Our study also contributes to the debate surrounding the relative efficiency of stock and mutual insurers. Despite substantial research on the topic, there is no consensus on whether one ownership structure outperforms the other. In every regression model we find that mutual insurers are significantly less profitable than stock insurers.
The study proceeds as follows. The “Prior Literature” section reviews prior literature on line-of-business diversification in the insurance industry. The “Hypotheses Development” section develops our hypotheses. The next section describes our sample and data. The “Regression Methodology” section presents our empirical methodology. The “Results” section discusses our results, and the last section concludes.
Prior Literature
There is a paucity of studies on the effect of corporate diversification in the insurance industry in general, and in the P/L insurance industry in particular.2 This is not surprising due to the exclusion of financial services firms in most finance studies on the topic and the focus on conglomerates in much of the diversification literature. Studies that provide evidence on the strategic focus and conglomeration hypotheses in the insurance industry include Hoyt and Trieschmann (1991), Tombs and Hoyt (1994), Meador, Ryan, and Schellhorn (2000), Berger et al. (2000), Cummins and Nini (2002), and Cummins, Weiss, and Zi (2003).3
Hoyt and Trieschmann (1991) compare risk–return relationships between publicly traded insurers that specialize in either P/L or L/H insurance and those that diversify across both major segments of the aggregate insurance industry. Using capital asset pricing modeling (CAPM) and mean-variance approaches to measure risk-adjusted returns to shareholders, they find that specialized insurers performed better over the sample period of 1973–1987. Tombs and Hoyt (1994) examine the relation between stock returns and product-line focus for a panel of 26 insurers (operating in P/L and L/H) for the period 1980–1990. They measure product-line focus in terms of a Herfindahl index of premiums written across 10 business line groups. In their regression analysis of stock returns on focus and several controls, they find that stock returns are positively related to focus. Thus, both Hoyt and Trieschmann (1991) and Tombs and Hoyt (1994) provide evidence consistent with the strategic focus hypothesis.
Berger et al. (2000) compare the relative cost, revenue, and profit efficiency of diversified and focused insurers over the period 1988–1992. Their classification of the degree of diversification is similar to Hoyt and Trieschmann (1991) in that insurers that operate in either the P/L or L/H industry are deemed to be specialists while those that are joint producers are viewed as diversified. Their results suggest that neither hypothesis dominates for all firms. The strategic focus hypothesis is more applicable to small insurers that specialize in commercial lines while the conglomeration hypothesis holds more for large personal lines insurers.
Cummins et al. (2003) extend the work of Berger et al. (2000) by using data envelopment analysis to estimate the efficiency of specialists and diversified insurers. Their definition of specialist and diversified insurers is the same as that used by Hoyt and Trieschmann (1991) and Berger et al. (2000). Using data on observed firm characteristics and estimated efficiency scores for a sample of 817 firms over the period 1993–1997, they find general support for the strategic focus hypothesis.
Meador et al. (2000) focus exclusively on the L/H insurance industry. They use efficiency analysis to examine the effects of product diversification for U.S. life insurers. They compute measures of X-efficiency that are regressed on a Herfindahl index of premiums written across the six major L/H lines. Their results suggest that diversified life insurers are more X-efficient than their more focused counterparts. They conclude that their results are “consistent with the proposition that managers of multiproduct firms are able to achieve greater cost efficiencies by sharing inputs and efficiently allocating resources across product lines in response to changing industry conditions.”
Some evidence on the relation between diversification and accounting performance for P/L insurers appears in a study on insurer capitalization by Cummins and Nini (2002). Their empirical analysis includes a regression of performance (measured by ROE) on capitalization and several controls, including line-of-business diversification. They measure line-of-business diversification using a Herfindahl index of premiums written across all lines of business. They find an inverse relation between diversification and ROE. This evidence is consistent with the strategic focus hypothesis and contrary to the conglomeration hypothesis. It also invites a more thorough analysis of the D-P relationship.
The general finance literature has devoted considerable attention to the relation between diversification and firm value. In a recent review of the literature, Martin and Sayrak (2003) describe three “rounds” of research that have provided evidence regarding diversification's impact on shareholder value. The first round of research consists of empirical evidence suggesting that corporate diversification destroys shareholder value. Studies that fall into this category have found that diversified firms have lower Tobin's Q (e.g., Lang and Stulz, 1994; Servaes, 1996); that diversified firms tend to have negative excess values, implying that they trade at considerable discounts (e.g., Berger and Ofek, 1995; Lamont and Polk, 2002); and that the stock market tends to react more favorably to increases in focus than to increases in diversification (Desai and Jain, 1999; John and Ofek, 1995). One of the most recent additions to this round of research is Laeven and Levine (2007) who find evidence of a diversification discount in the banking industry, even after controlling for potential endogeneity of the diversification decision.
The second round of empirical research presents evidence that corporate diversification does not destroy value. Graham, Lemmon, and Wolf (2002) study the market reaction to acquisition announcements and calculate the excess values for firms after the acquisition. Consistent with research in the first round they find that excess values of acquirers decline after the acquisition. However, they show that this reduction in excess value for acquiring firms is due to the fact that the targets were already discounted. They argue that a firm's excess value can decline after an acquisition if it acquires a business that is already trading at a discount. Similarly, Villalonga (2004b) and Campa and Kedia (2002) argue that much, if not all, of the discount observed by previous researchers may be attributed to the fact that diversified firms would be discounted irrespective of their diversification status. Hence, it is possible that much of the evidence supporting the diversification discount is due to selection bias rather than the act of diversifying.
While the first round of research finds evidence that diversification destroys value and the second explains this value loss as a function of self-selection or endogeneity, the third round argues that diversification actually creates shareholder wealth. Round 3 of the empirical research finds evidence that diversified firms trade at a significant premium and that the discount observed in previous research is likely due to measurement error. Villalonga (2004a) investigates whether the diversification discount is simply an “artifact of segment data” and reports a diversification premium when using establishment-level census data but a diversification discount when using Compustat segment data for the same sample. Several researchers have noted concerns regarding Compustat segment data, including: (1) that the level of disaggregation (diversification) shown in segment financial reporting is much lower than the true extent of industrial diversification (Lichtenberg, 1991); (2) that the Financial Accounting Standards Board definition of “segment” allows for aggregation of multiple activities into one reported “segment” and that these segments are self-reported—thus, segments may not be comparable across firms (Davis and Duhaime, 1992); and (3) that changes in segments reported for any given firm are often not associated with any real change in operations across different activities (Denis, Denis, and Sarin, 1997).
Our study contributes to the broader diversification discount literature by examining the performance effects of corporate diversification in a setting that eliminates measurement error and managerial discretion in segment reporting. By focusing on the U.S. P/L insurance industry we are able to benefit from the richness of insurance statutory data. All licensed P/L insurers are required to file detailed annual financial statements that include highly disaggregated premium data across more than 20 distinct business lines. By contrast, firms in unregulated industries are generally not required to report revenue data on such a detailed level. Additionally, unlike managers of unregulated firms that are typically included in diversification studies, insurance managers have no discretion in deciding whether to allocate premiums to a particular line of business. The distinction between different lines of business is sufficiently clear that it is unlikely that revenues will be misallocated.
Hypotheses Development
Benefits to corporate diversification that suggest a positive D-P relation include scope economies, larger internal capital markets, and risk reduction. Diversification provides firms with the opportunity to benefit from cost and revenue scope economies. Cost scope economies arise from the sharing of fixed production costs across several businesses within the firm (Teece, 1980). Revenue scope economies may be realized due to the transfer of firm-specific intangible assets such as brand reputation and customer loyalty (Markides, 1992). Diversification also generates larger internal capital and labor markets. These internal markets may be more efficient than external capital and labor markets due to information asymmetry between the firm and the external markets (Myers and Majluf, 1984). Finally, diversification reduces income volatility by combining revenue streams that are imperfectly correlated (Lewellen, 1971). Given risk-sensitive customers, this risk reduction should increase prices that customers are willing to pay (Herring and Santomero, 1990; Sommer, 1996; Cummins and Danzon, 1997).
Among the potential costs associated with diversification are exacerbated agency costs and internal capital market inefficiencies. Agency costs are likely positively related to diversification because managerial monitoring and bonding becomes more difficult as firms become more complex. Furthermore, by creating larger internal capital markets, diversification enables managers to avoid the market discipline that comes with external financing (Easterbrook, 1984). Absent capital market discipline, managers are more inclined to engage in activities that maximize their private benefits (e.g., increased perquisite consumption) and to subsidize failing business segments (Berger and Ofek, 1995). Moreover, it is more difficult to align managerial interests with those of owners in diversified firms because divisional performance may not be observable.
The net effect of diversification is a function of firms' ability to maximize the benefits while minimizing the costs of such diversification. In terms of the conglomeration hypothesis, we should expect a positive relation between diversification and performance because diversification's benefits exceed its costs. By contrast, the strategic focus hypothesis predicts that a negative relation should exist because the costs of diversification outweigh the benefits.
The relationship between diversification and performance may be described as follows:
Performance =f (diversification | firm and industry characteristics)
The previous discussion then leads to two competing hypotheses to be tested:
-
Hypothesis 1 (Conglomeration): Diversification is positively related to performance.
-
Hypothesis 2 (Strategic Focus): Diversification is negatively related to performance.
Performance Measure Selection
Several measures of accounting performance have been used in the insurance literature. The two most commonly used measures in the literature are ROA and return on equity ROE.4 These accounting performance measures are also widely used in the D-P literature (e.g., Hill, Hitt, and Hoskisson, 1992; Hamilton and Shergill, 1993; Mayer and Whittington, 2003). Consistent with Browne et al. (2001) and Greene and Segal (2004), we perform our empirical analysis on both performance measures.
Because higher performance may simply be the result of higher risk, it is important to consider the effect of diversification on risk-adjusted performance. While the majority of prior D-P studies do not adjust for risk (Datta et al., 1991), there are two major approaches that may be followed. The first approach is to divide the relevant performance measure by its variability over a given time period. For annual data, the time period used is typically 5 years (Bettis and Hall, 1982; Johnson and Thomas, 1987) or 10 years (Browne et al., 2001). The second approach is to include a risk measure as a control variable in a linear regression model where performance is the dependent variable. This approach has been followed by Hamilton and Shergill (1993) and Lai and Limpaphayom (2003).5 The primary advantage of the latter approach is that it allows for direct interpretation of the magnitude of the effect of diversification on the dependent variable. Because our key results are unaffected by our risk-adjustment method, we focus primarily on results of regression specifications using risk as a control variable.
Diversification Measure Selection
D-P researchers use diversification measures that are either discrete or continuous. Discrete measures are designed to reflect the number of distinct business activities of the firm. Examples of discrete measures used in the literature are the number of 2-, 3-, or 4-digit Standard Industrial Classification (SIC) codes in which a firm has positive sales/assets. The richness of our data enables us to identify the specific insurance lines in which a firm operates.6 We follow the approach taken by diversification discount researchers (e.g., Lang and Stulz, 1994; Berger and Ofek, 1995; Comment and Jarrell, 1995; Servaes, 1996; Denis, Denis, and Sarin, 1997), in using a discrete measure to distinguish between undiversified firms operating in only one business line, and diversified firms that operate in multiple business lines (MULTLINE). Variable definitions and descriptive statistics are presented in Table 1.7
| Variable | Definition | Mean | Median | Standard Deviation |
|---|---|---|---|---|
| ROA | Net income/total admitted assets | 0.02 | 0.03 | 0.05 |
| ROE | Net income/policyholder surplus | 0.05 | 0.06 | 0.14 |
| SDROA5 | Standard deviation of ROA over past 5 years | 0.03 | 0.02 | 0.03 |
| SDROE5 | Standard deviation of ROE over past 5 years | 0.08 | 0.05 | 0.12 |
| LINES | Number of lines in which firm has positive direct premiums written (DPW) | 5.91 | 5.00 | 4.63 |
| MULTLINE | = 1 if LINES > 1, 0 otherwise | 0.79 | 1.00 | 0.41 |
| SIZE | Natural logarithm of total admitted assets | 17.64 | 17.47 | 2.19 |
| CAPASSET | Policyholder surplus/total admitted assets | 0.49 | 0.44 | 0.21 |
| GEODIV | 1-Herfindahl index of DPW across 57 geographic areas | 0.33 | 0.11 | 0.37 |
| WCONC | Weighted sum of market share per line multiplied by line specific Herfindahl | 0.05 | 0.05 | 0.02 |
| PCTLH | Percentage of premiums from life–health insurance | 0.44 | 0.00 | 2.16 |
| MUTUAL | = 1 if firm is a mutual, 0 otherwise | 0.48 | 0.00 | 0.50 |
| GROUP | = 1 if firm is a group, 0 otherwise | 0.34 | 0.00 | 0.47 |
| PUBLIC | = 1 if firm is publicly traded, 0 otherwise | 0.08 | 0.00 | 0.28 |
Table 2 compares medians and means of performance and risk measures between insurers that operate exclusively in one line of business (undiversified) and those that operate in multiple lines (diversified). Notably, single-line insurers earn higher ROA and ROE than multi-line insurers, but their performance volatility (SDROA5 and SDROE5) is also higher than it is for diversified insurers. Looking at risk-adjusted performance (RAROA and RAROE), single-line insurers still outperform multi-line insurers. Thus, our univariate results provide evidence consistent with the strategic focus hypothesis. Figure 1 complements our descriptive statistics with the distribution of insurers and ROA by number of lines written.8
| Variable | Single-Line Insurers (1,339 Firm-Years) | Diversified Insurers (4,951 Firm-Years) | Single-Line Minus Diversified | |||
|---|---|---|---|---|---|---|
| Mean | Median | Mean | Median | Mean | Median | |
| ROA | 0.038 | 0.036 | 0.021 | 0.025 | 0.016*** | 0.011*** |
| ROE | 0.063 | 0.063 | 0.042 | 0.056 | 0.022*** | 0.007*** |
| SDROA5 | 0.039 | 0.026 | 0.031 | 0.024 | 0.008*** | 0.003*** |
| SDROE5 | 0.102 | 0.057 | 0.080 | 0.054 | 0.022*** | 0.003 |
| RAROA | 1.850 | 1.306 | 1.478 | 1.046 | 0.372*** | 0.260*** |
| RAROE | 1.638 | 1.219 | 1.305 | 1.002 | 0.333*** | 0.218*** |
- Note: Single-line insurers are those firms where MULTLINE = 0. Diversified insurers are those where MULTLINE = 1. ROA (return on assets) is net income/total admitted assets. ROE (return on equity) is calculated as net income/policyholder surplus. SDROA5 (SDROE5) is the standard deviation of ROA (ROE) over past 5 years. RAROA (RAROE) is calculated as ROA/SDROA5 (ROE/SDROE5) and reflects risk-adjusted return of assets (equity). A t-test is used for difference of means, and a Wilcoxon rank sum test is used for difference of medians. Statistical significance at the 1%, 5%, and 10% levels is denoted by ***, **, and *, respectively.
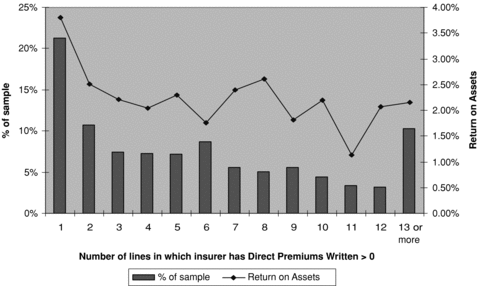
Distribution and Performance of Sample Insurers by Number of Lines
Control Variables
Datta et al. (1991) emphasize the importance, in the analysis of the D-P relationship, of controlling for the effect of both firm-specific and market factors that may explain performance variation across firms. The following firm-specific control variables are used: size, capitalization, ownership structure, geographic diversification, group status, publicly traded, and the percent of premiums attributable to L/H insurance policies.
Firm Size If larger firms have lower insolvency risk then they should be able to charge higher prices than smaller insurers (Sommer, 1996), all else equal. Additionally, to the extent that size conveys market power, we would expect larger firms to enjoy greater revenue efficiencies than their smaller counterparts (Cummins and Nini, 2002). Cummins and Nini (2002) find a positive relation between size and performance in the P/L industry. Browne, Carson, and Hoyt (1999) find that the positive size–performance relationship holds in the L/H industry as well. We therefore expect size to be positively related to performance. Size is measured as the natural logarithm of total assets.
Capitalization Sommer (1996) finds that safer insurers are able to command higher prices. Thus, we expect a positive relation between insurer capitalization and performance. We measure capitalization as the ratio of policyholder surplus to total assets.
Ownership Structure The two forms of ownership structure included in our sample (stocks and mutuals) have different inherent costs and benefits. It follows that the relation between ownership structure and performance should reflect whether, on average, the costs of each ownership structure are offset by the benefits. The advantages and disadvantages associated with each ownership structure stem from each structure's success in controlling incentive conflicts. The two primary sets of incentives conflicts in insurance are owner–policyholder conflicts and owner–manager conflicts (Mayers and Smith, 1981). Owner–policyholder conflicts are more severe, and therefore imply greater costs, for stock companies than for mutuals. The mutual form reduces the costs associated with divergent owner and policyholder interests (e.g., risk shifting) by merging the role of owner and customer. However, this reduction in owner–customer agency costs may be offset by greater owner–manager agency costs that arise out of a less effective market for corporate control.
Empirical evidence regarding the relative efficiency of stock and mutual insurers is mixed. Cummins, Weiss, and Zi (1999) examine the cost efficiency of stocks and mutuals in the P/L industry and find support for the expense preference hypothesis, which predicts that mutuals will have higher costs than stocks because control of managerial perquisite consumption is more difficult in the mutual ownership form. By contrast, Greene and Segal (2004) find no significant difference in cost efficiency, or accounting profitability, between mutual and stock life insurers. These divergent empirical results suggest that the relation between ownership structure and performance is ambiguous. We use a dummy variable (MUTUAL) to distinguish between mutuals and stocks.
Geographic Diversification Pro-conglomeration arguments suggest that geographically diversified firms are likely to have less volatile profits due to coinsurance effects. As a result of their lower risk, geographically diversified insurers should be able to charge higher prices than geographically focused insurers, all else equal. These arguments suggest a positive relation between the degree of geographic diversification and risk-adjusted performance. By contrast, pro-focus arguments suggest that geographically focused insurers are able to avoid costly monitoring that is required when operating across different states (Winton, 1999) and achieve efficiencies arising out of market specialization. Geographic diversification is measured as the complement of the Herfindahl index of premiums written across all U.S. states and protectorates (GEODIV).
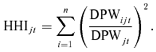
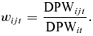
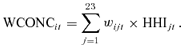
Group Status Our sample includes single-unaffiliated insurers as well as consolidated insurance groups. Cummins and Sommer (1996) and Sommer (1996) suggest that customers should be willing to pay more for insurance from unaffiliated insurers than those belonging to insurance groups because groups have the option to let one of their members fail and policyholders have difficulty in “piercing the corporate veil.” Thus, policyholders might view consolidated groups as being more risky than identical single unaffiliated insurers. Group status is measured in terms of a dummy variable (GROUP) equal to one if the unit of observation is a group. We expect a negative relation between group status and performance.
Publicly Traded Monitoring and scrutiny by shareholders and analysts implies a more effective market for corporate control for publicly traded insurers than is present for private insurers. Hence, we expect that publicly traded insurers should, on average, outperform privately held insurers. We use a dummy variable, PUBLIC, to indicate whether an insurer is publicly traded.
L/H Although our sample firms all write primarily P/L insurance, several firms in the sample also write L/H business. We control for an insurer's participation in both industries by including a variable equal to the percentage of total premiums (P/L plus L/H) attributable to operations in the L/H industry (PCTLH). To the extent that this variable indicates greater diversification, we expect it to have the same relationship with performance as our intra-industry diversification measure.
In addition to the above firm-specific controls, we include controls for time-induced variation in performance (year dummies). We also control for performance variation that is induced by companies operating in different states that have different regulatory stringency and demographics by including dummy variables indicating an insurer's participation in any given state or protectorate. Finally, to control for line-of-business effects, we include dummy variables indicating an insurer's participation in different lines.9
Sample and Data
Our initial sample includes all firms in the National Association of Insurance Commissioners (NAIC) database for the years 1995–2004. This period is chosen for two reasons. First, it is sufficiently long to include both positive and negative market conditions. For the majority of the 1990s and latter part of the 1980s, the P/L market was characterized by “soft” market conditions where prices were low and supply was abundant. After 1999, the market began to harden as prices increased and availability decreased (Ceniceros and Hofmann, 1999; Ruquet, 2000; Goch, 2001). Second, our empirical analysis includes historical risk measures that require up to 10 years of prior data, and 1985 is the first year for which we are able to obtain insurer data from the NAIC.
Our first screen is to exclude firms that are under regulatory scrutiny. Next, we exclude firms that report negative direct premiums written or total admitted assets. We then aggregate affiliated insurers, controlling for potential double counting of intra-group shareholding. This aggregation is appropriate as diversification decisions are likely made at the group level (Berger et al., 2000). Groups are assigned an organizational structure based on data collected from Best's Insurance Reports. Next, we exclude groups with substantial premium income (at least 25 percent of total premiums) from L/H insurance since our focus is on P/L insurers. Because we use historical risk measures requiring between 5 and 10 years of data, we exclude firms with less than 5 years of historical data. Finally, we exclude firms with organizational structures other than stock or mutual.
Regression Methodology
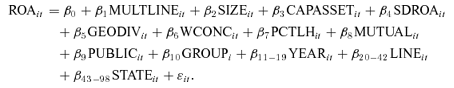 (1)
(1)Diversification discount researchers (e.g., Campa and Kedia, 2002; Villalonga, 2004b; Laeven and Levine, 2007) have used three different techniques to control for endogeneity bias. One approach used by these researchers is the fixed-effects regression estimation. The advantage of this approach is that it enables the researcher to control for unobservable (or omitted) firm-specific effects which may be correlated with other regressors in the model. A disadvantage of the fixed-effects method is that its applicability is limited to settings where key explanatory variables exhibit sufficient within-firm variation. If independent variables do not vary over time, they are “swept away” in the time-demeaning process that eliminates the time-invariant unobserved effects. For independent variables that do not vary much over time, the fixed-effects estimation technique can lead to imprecise estimates (Wooldridge, 2002). Because our key explanatory variable (MULTLINE) is almost entirely time invariant we do not apply the fixed-effects approach.11 In our sample we have a total of 914 firms (6290 firm-year observations). Of these 914 firms, 248 firms (1339 firm-year observations) operate in one line only, in at least one year. Of these 248 firms, 169 are single-line for the entire sample period. Thus, variation in MULTLINE occurs in only 79 firms, or 8.6 percent of all firms.12
Other approaches that have been used to deal with the potential endogeneity bias include estimation of Equation (1) using a two-stage least squares (2SLS) approach and a Heckman (treatment effects) approach (Campa and Kedia, 2002; Villalonga, 2004b; Laeven and Levine, 2007).13 The first stage of the 2SLS approach entails regressing MULTLINE on the other independent variables in Equation (1) and a set of instruments that do not appear in Equation (1). In the second stage, Equation (1) is estimated using the predicted values for MULTLINE obtained in the first-stage regression. The Heckman approach follows the same procedure as the 2SLS approach but also includes a self-selection parameter in the second stage that is calculated using information obtained in the first-stage regression.
Both techniques require the selection of instruments for MULTLINE. Campa and Kedia (2002) suggest an instrument set composed of current, lagged, and historically averaged measures of firm characteristics, industry growth, and general economic growth. Our initial set of instrumental variable candidates consists of lagged values of firm characteristics included in Equation (1), 5-year historical averages of firm characteristics included in Equation (1), 1-year growth in direct premiums written for the P/L industry, 1-year growth in U.S. gross domestic product, firm age, firm reinsurance use, and an index14 that captures the attractiveness of a firm's markets to single-line insurers.
Successful instrumental variable candidates must satisfy two conditions.15 The first condition, instrument relevance, requires that the instruments have a high partial correlation with MULTLINE. The second condition, instrument validity, requires that the instruments are uncorrelated with the error term in Equation (1). Instrument relevance is tested using a Wald test for the joint significance of the excluded instruments. The null hypothesis under the Wald test is that the instruments are jointly insignificant. Because multiple candidates pass the instrument relevance test we are able to test for instrument validity using Hansen's J-test of overidentifying restrictions. The null hypothesis under Hansen's J-test is that the instruments are uncorrelated with the error term (i.e., exogenous). Three candidates (age, reinsurance use, and the index reflecting the attractiveness of the insurer's markets to single-line insurers) meet both the relevance and validity conditions.
Results
Results for the effect of diversification status on ROA using each of the estimation techniques appear in Table 3.16 The coefficient estimates on MULTLINE are negative and significant in all estimations, showing that ROA for diversified firms is between 1.1 and 6.1 percent lower than for single-line firms. This negative relation between diversification and performance supports the strategic focus hypothesis.
| Model | OLS1 | OLS2 | 2SLS | HECKMAN |
|---|---|---|---|---|
| Constant | −0.122*** | −0.114*** | −0.099*** | −0.069*** |
| (0.024) | (0.024) | (0.026) | (0.012) | |
| MULTLINE | −0.011*** | −0.011*** | −0.060*** | −0.061*** |
| (0.003) | (0.004) | (0.011) | (0.008) | |
| SIZE | 0.007*** | 0.007*** | 0.008*** | 0.006*** |
| (0.001) | (0.001) | (0.001) | (0.001) | |
| CAPASSET | 0.085*** | 0.087*** | 0.073*** | 0.085*** |
| (0.009) | (0.010) | (0.010) | (0.004) | |
| GEODIV | −0.007* | −0.004 | −0.003 | −0.006*** |
| (0.004) | (0.006) | (0.005) | (0.002) | |
| WCONC | 0.119** | 0.101** | 0.019 | 0.082** |
| (0.051) | (0.051) | (0.066) | (0.032) | |
| PCTLH | −0.001* | −0.001 | −0.001 | −0.001** |
| (0.000) | (0.000) | (0.000) | (0.000) | |
| MUTUAL | −0.013*** | −0.012*** | −0.007** | −0.010*** |
| (0.002) | (0.003) | (0.003) | (0.002) | |
| PUBLIC | 0.000 | 0.004 | 0.001 | 0.001 |
| (0.003) | (0.003) | (0.004) | (0.003) | |
| GROUP | −0.013*** | −0.013*** | −0.009** | −0.012*** |
| (0.003) | (0.003) | (0.004) | (0.002) | |
| SDROA5 | 0.053 | 0.052 | 0.036 | 0.053** |
| (0.086) | (0.080) | (0.082) | (0.022) | |
| Wald test statistic | 446.870*** | |||
| Hansen J-statistic | 1.399 | |||
| Self-selection parameter | 0.030*** | |||
| (0.004) | ||||
| Number of observations | 6,290 | 6,290 | 6,290 | 6,290 |
| Adjusted/Pseudo R2 | 0.14 | 0.15 | 0.17 | 0.16 |
- Note: The dependent variable is ROA. OLS1 is an ordinary least squares regression model with year dummies. OLS2 adds state and line dummies. 2SLS is a two-stage least squares regression. The first-stage regression is a logistic regression of MULTLINE on a set of excluded instruments (age, reinsurance use, and an index capturing the attractiveness of a firm's markets to single-line insurers) and all other explanatory variables from Equation (1). Instrument relevance is tested via a Wald test of their joint significance in the first-stage regression. Instrument validity is tested in the second-stage regression using Hansen's J-test for overidentifying restrictions where the null hypothesis is that instruments are uncorrelated with the error term. HECKMAN is a two-step treatment effects regression that includes a parameter that controls for selectivity bias. The same instruments are used in HECKMAN as in 2SLS. MULTLINE is equal to one for diversified insurers, and zero otherwise. SIZE is equal to the natural logarithm of total admitted assets. CAPASSET is the ratio of policyholder surplus to total admitted assets. GEODIV is equal to one minus the Herfindahl index of premiums across 57 geographic areas. WCONC is the weighted sum of firm market share per line multiplied by each line's Herfindahl index. PCTLH is the percentage of premiums attributable to life–health insurance. MUTUAL is equal to one if the ultimate ownership form is mutual, zero otherwise. GROUP is equal to one for aggregated groups, zero otherwise. PUBLIC is equal to one if the insurer is publicly traded, zero otherwise. SDROA5 is the standard deviation of ROA over the past 5 years. Standard errors (in parentheses) in models OLS1, OLS2, and 2SLS are corrected for clustering at the insurer level. Statistical significance at the 1%, 5%, and 10% levels is denoted by ***, **, and *, respectively.
Berger and Ofek (1995) present some evidence on the size of the “diversification penalty” using accounting data for a large cross-section of nonfinancial firms for the period 1986–1991. They compare industry-adjusted ROA between single-segment firms and diversified firms and report a mean penalty of 1.5 percent. Thus, our estimates of the diversification penalty, for a subsample of financial firms, are similar to their estimates based on a broad cross-section of nonfinancial firms.17 It is important to note that the Berger and Ofek (1995) definition of single-segment firms is far broader than ours. They define single segment firms as those operating in one 4-digit SIC code. Thus, almost all of the firms in our sample (with the exception of insurer groups that participate in the L/H insurance industry and insurers that are owned by diversified conglomerates) would be classified as single-segment firms by Berger and Ofek and by other diversification discount researchers (e.g., Lang and Stulz, 1994; Servaes, 1996). This implies that diversification discount studies that compare the performance of multi-segment firms to broadly defined single segment firms are actually underestimating the size of the diversification discount.
The pattern of our results on MULTLINE across the various models differs from what has been found by Campa and Kedia (2002) and Villalonga (2004b) in their studies of the diversification discount. They find that the discount is reduced when accounting for self-selection bias. Hence, their findings are consistent with the hypothesis that firms that choose to diversify would trade at a discount irrespective of their diversification status. However, our results are consistent with those of Laeven and Levine (2007) in their study of the diversification discount in the banking industry. Similar to our findings, they show that the discount persists after controlling for potential endogeneity of the diversification decision. In several of their instrumental variables and treatment effects regressions they report larger discounts than they find using OLS, as do we.18
SIZE is positively and significantly related to performance across all models, consistent with larger firms having economies of scale and lower insolvency risk. The coefficient on CAPASSET is positive and significant, consistent with the hypothesis that higher prices paid by risk-averse policyholders to safer insurers will translate into higher risk-adjusted performance. The negative sign on GEODIV, and its significance in two of the three regressions, implies that potential benefits from risk reduction are offset by the costs associated with greater managerial discretion. The coefficients on WCONC are positive and significant in three of the models. We therefore find some support for the hypothesis that firms operating in more concentrated business lines are able to charge higher prices and earn higher profits than firms in less concentrated lines. Our control for the percentage of premiums from L/H insurance (PCTLH) is significant in the OLS regressions but not significant in the instrumental variables and treatment effects regressions.
MUTUAL is significantly negatively related to performance across all models. Thus, it appears that higher owner–manager agency costs outweigh any benefits associated with the reduction in owner–customer agency costs. Our finding is consistent with Cummins et al. (1999). The coefficient on PUBLIC is never significant. GROUP enters as negative and significant in all models. This negative relation may be due to lower prices induced by the option to let a member fail, costs of managerial discretion, or other costs associated with conglomeration. Surprisingly, our risk measure (SDROA5) is significant in only one of the four models.19
Robustness of Diversification Status Results
Alternative Performance Measure To investigate whether our results are robust to a different performance measure, we repeat our regression analysis using ROE as the dependent variable. Consistent with our ROA results, the coefficient on MULTLINE is negative and significant across all model specifications. The size of the penalty is roughly double that observed for ROA. This difference is not surprising given that the univariate size of the performance difference between single-line and multi-line insurers is almost two times larger when measuring performance in terms of ROE than when performance is measured by ROA.20 The results for our other regressors generally follow those reported in Table 3.
Alternative Risk Measures We investigate the robustness of our results to alternative risk measures by replacing SDROA5 with three alternative risk measures. First, we extend the time period over which we calculate the standard deviation of ROA, from 5 to 10 years (SDROA10). Second, we follow Klein, Phillips, and Shiu (2002) and use the standard deviation of the residual from a regression of ROA for the past 10 years on a linear time trend (KLEIN10). We also compute this measure over a 5-year period (KLEIN5). Third, we use a measure of total firm risk (FIRMRISK), based on the option pricing model of the insurance firm, introduced by Cummins and Sommer (1996).21 Results, whether based on OLS, 2SLS, or the Heckman approach indicate that the coefficient for MULTLINE using any of these alternative risk measures is very similar to that obtained using SDROA5 as a risk measure.22
Alternative Estimation Method A common method of measuring the diversification discount is the “chop-shop” (or excess value) approach applied by Lang and Stulz (1994) and others. In terms of this approach, conglomerates are broken down into businesses segments and the observed value of the conglomerate is compared to an estimate of what it would be if the conglomerate was a portfolio of specialist, or “pure-play,” firms. The “excess value” is the difference between the actual value of the conglomerate and an imputed value of the sum of its parts. A diversification discount is implied by negative excess values.
Laeven and Levine (2007) apply the chop-shop approach to the banking industry. They distinguish between two distinct activities—lending and nonlending services—and compare the Tobin's Q of banks that perform both activities with what it would be if the multi-activity bank were broken down into two specialist banks that specialize in each of the activities. They also extend the excess value methodology to a comparison of operating performance (return on assets) between multi-activity and specialist banks.
To test the robustness of our results to an alternative discount/penalty estimation technique, we apply the Laeven and Levine (2007) approach to our sample of insurance companies. A key part of the excess-value methodology is the identification of a reasonable number (usually five or more) of specialist insurers that operate in only one line of business. Unfortunately, specialist insurers do not exist for several lines of business. In order to have a sufficient number of specialist firms we broaden our definition of a specialist/undiversified insurer from one that operates in only one line to one that operates in only one group of similar insurance lines.23 Thus, the first step in applying the chop-shop approach is to aggregate the 23 lines of business into homogeneous groups.24 There are at least two approaches that can be followed. One approach is for the researcher to determine groups based on what appears most sensible (e.g., McCullough and Hoyt, 2005; Tombs and Hoyt, 1994). An alternative approach is to “allow the data to speak” and use a mathematical aggregation method that does not require prior restrictions on either the composition or structure of the aggregated groups. We follow both approaches but concentrate our discussion on the latter approach.
Following Mayers and Smith (1988), we use a variant of principal components analysis to define the groups, or bundles, of similar business lines. Specifically, we use cluster analysis to aggregate the 23 distinct lines of business into a number of clusters using the VARCLUS procedure in SAS. We apply the VARCLUS procedure to the matrix of DPW per line for all firms in our sample to identify groups of business lines that tend to be written together and are therefore assumed to be relatively homogeneous. VARCLUS initially assigns all lines to one cluster and then iteratively splits the cluster(s) until the intra-cluster correlation for all cluster members cannot be improved by further splitting the remaining clusters. The final number of clusters and membership of each cluster is determined by an algorithm that maximizes the sum across clusters of the variation accounted for by the cluster components.25 Cluster analysis of the full data set yields five clusters of insurance lines.26 We aggregate premiums for each insurer into these five clusters and treat each cluster as a separate activity.27 Specialist insurers are defined as those insurers writing premiums in only one cluster.
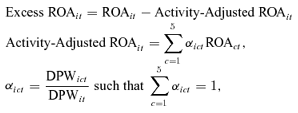
DPWit is the total direct premium written by insurer i in year t,
DPWict is the total direct premium written by insurer i in cluster c in year t,
ROAct is the average ROA for all single-cluster firms that operate in cluster c in year t.
We apply this technique to our sample of insurers to obtain excess ROA values for all firms, for each sample year. The mean Excess ROA for multi-cluster firms is –0.011 and is statistically significant at the 1 percent level. To control for other factors that affect Excess ROA we regress it on a dummy variable that indicates firm participation in either one, or several clusters (MULTCLUS), and other control variables from Equation (1). Our multivariate results, reported in Table 4, provide further support for the strategic focus hypothesis and demonstrate that our earlier results are robust to an alternative estimation technique.
| Model | OLS | 2SLS |
|---|---|---|
| Constant | −0.159*** | −0.155*** |
| (0.022) | (0.010) | |
| MULTCLUS | −0.005* | −0.012** |
| (0.003) | (0.005) | |
| SIZE | 0.007*** | 0.007*** |
| (0.001) | (0.001) | |
| CAPASSET | 0.081*** | 0.079*** |
| (0.009) | (0.004) | |
| GEODIV | −0.012*** | −0.011*** |
| (0.004) | (0.002) | |
| WCONC | 0.071 | 0.068** |
| (0.056) | (0.030) | |
| PCTLH | 0.000 | 0.000 |
| (0.000) | (0.000) | |
| MUTUAL | −0.009*** | −0.008*** |
| (0.002) | (0.002) | |
| PUBLIC | −0.001 | 0.000 |
| (0.003) | (0.003) | |
| GROUP | −0.010*** | −0.009*** |
| (0.003) | (0.002) | |
| SDROA5 | 0.042 | 0.040* |
| (0.077) | (0.022) | |
| Wald statistic | 350.120*** | |
| Hansen J-statistic | 1.539 | |
| Number of observations | 6,290 | 6,290 |
| Adjusted R2 | 0.11 | 0.12 |
-
Note: The dependent variable is Excess ROA, which is calculated as Actual ROA minus Activity-Adjusted ROA, where
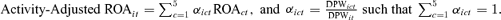 DPWit is the total direct premium written by insurer i in year t, DPWict is the total direct premium written by insurer i in cluster c in year t, and ROAct is the average ROA for all single-cluster firms that operate in cluster c in year t. OLS is an ordinary least squares regression model with year dummies. 2SLS is a two-stage least squares regression. The first-stage regression is a logistic regression of MULTCLUS on a set of excluded instruments (age, reinsurance use, and an index capturing the attractiveness of a firm's markets to single-line insurers) and all other explanatory variables from Equation (1). Instrument relevance is tested via a Wald test of their joint significance in the first-stage regression. Instrument validity is tested in the second-stage regression using Hansen's J-test for overidentifying restrictions where the null hypothesis is that instruments are uncorrelated with the error term. MULTCLUS is a binary variable equal to one if the insurer operates in more than one business line cluster, zero otherwise. SIZE is equal to the natural logarithm of total admitted assets. CAPASSET is the ratio of policyholder surplus to total admitted assets. GEODIV is equal to one minus the Herfindahl index of premiums across 57 geographic areas. WCONC is the weighted sum of firm market share per line multiplied by each line's Herfindahl index. PCTLH is the percentage of premiums attributable to life–health insurance. MUTUAL is equal to one if the ultimate ownership form is mutual, zero otherwise. GROUP is equal to one for aggregated groups, zero otherwise. PUBLIC is equal to one if the insurer is publicly traded, zero otherwise. SDROA5 is the standard deviation of ROA over the past 5 years. Standard errors (in parentheses) are corrected for clustering at the insurer level. Statistical significance at the 1%, 5%, and 10% levels is denoted by ***, **, and * respectively.
DPWit is the total direct premium written by insurer i in year t, DPWict is the total direct premium written by insurer i in cluster c in year t, and ROAct is the average ROA for all single-cluster firms that operate in cluster c in year t. OLS is an ordinary least squares regression model with year dummies. 2SLS is a two-stage least squares regression. The first-stage regression is a logistic regression of MULTCLUS on a set of excluded instruments (age, reinsurance use, and an index capturing the attractiveness of a firm's markets to single-line insurers) and all other explanatory variables from Equation (1). Instrument relevance is tested via a Wald test of their joint significance in the first-stage regression. Instrument validity is tested in the second-stage regression using Hansen's J-test for overidentifying restrictions where the null hypothesis is that instruments are uncorrelated with the error term. MULTCLUS is a binary variable equal to one if the insurer operates in more than one business line cluster, zero otherwise. SIZE is equal to the natural logarithm of total admitted assets. CAPASSET is the ratio of policyholder surplus to total admitted assets. GEODIV is equal to one minus the Herfindahl index of premiums across 57 geographic areas. WCONC is the weighted sum of firm market share per line multiplied by each line's Herfindahl index. PCTLH is the percentage of premiums attributable to life–health insurance. MUTUAL is equal to one if the ultimate ownership form is mutual, zero otherwise. GROUP is equal to one for aggregated groups, zero otherwise. PUBLIC is equal to one if the insurer is publicly traded, zero otherwise. SDROA5 is the standard deviation of ROA over the past 5 years. Standard errors (in parentheses) are corrected for clustering at the insurer level. Statistical significance at the 1%, 5%, and 10% levels is denoted by ***, **, and * respectively.
Market-Based Performance Measure The vast majority of D-P studies examine the relation between diversification and market-based performance measures. To test whether the negative relation between diversification and accounting performance extends to a market-based performance measure, we estimate diversification's effect on Tobin's Q (a standard proxy for firm value) for the subsample of publicly traded P/L insurers.28 Following Chung and Pruitt (1994), we calculate Tobin's Q as the market value of equity plus the book value of liabilities divided by the book value of assets. Market data are obtained from Compustat.
Univariate statistics for Tobin's Q across diversified and single-line insurers appear in Panel A of Table 5. Our analysis is performed for three subsamples that are defined by the percentage of sales attributable to P/L insurance (PCTPL). PCTPL is calculated using Compustat Segment data. Univariate and multivariate results are presented for “pure” publicly traded P/L insurers, where PCTPL = 100, as well as two less restrictive subsamples (PCTPL ≥ 90 and PCTPL ≥ 80). The univariate results across all three subsamples indicate that the mean and median Tobin's Q for undiversified insurers exceeds that of diversified insurers. Multivariate results are reported in Panel B of Table 5. Consistent with the univariate results, we find that multi-line insurers are discounted by the market. The magnitude of the discount is within the range reported by Lang and Stulz (1994) and Servaes (1996). These results suggest that the diversification penalty is robust to a market-based performance measure.
| Panel A: Differences in Tobin's Q Between Single-Line and Diversified Publicly Traded Insurers | ||||||||
|---|---|---|---|---|---|---|---|---|
| Subsample | (1) Single-Line Insurers | (2) Diversified Insurers | (1)–(2) | |||||
| N | Mean Tobin's Q | Median Tobin's Q | N | Mean Tobin's Q | Median Tobin's Q | Mean | Median | |
| PCTPL ≥ 80 | 41 | 1.399 | 1.196 | 375 | 1.103 | 1.048 | 0.295*** | 0.093*** |
| PCTPL ≥ 90 | 36 | 1.428 | 1.210 | 340 | 1.108 | 1.049 | 0.321*** | 0.102*** |
| PCTPL = 100 | 34 | 1.444 | 1.247 | 262 | 1.120 | 1.049 | 0.324*** | 0.127*** |
| Panel B: Multivariate Estimates of the Diversification Discount for Publicly Traded Insurers | |||
|---|---|---|---|
| Model | PCTPL ≥ 80 | PCTPL ≥ 90 | PCTPL = 100 |
| Constant | −0.682** | −0.766* | −1.080** |
| (0.320) | (0.392) | (0.488) | |
| MULTLINE | −0.178* | −0.183* | −0.214** |
| (0.101) | (0.099) | (0.108) | |
| SIZE | 0.045** | 0.049** | 0.069** |
| (0.018) | (0.022) | (0.029) | |
| CAPASSET | 0.222* | 0.216 | 0.198 |
| (0.121) | (0.141) | (0.156) | |
| GEODIV | −0.059 | −0.045 | −0.070 |
| (0.070) | (0.084) | (0.093) | |
| WCONC | 0.159 | 0.326 | −0.096 |
| (0.530) | (0.615) | (0.704) | |
| PCTLH | −0.007** | −0.010** | |
| (0.003) | (0.005) | ||
| GROUP | 0.023 | 0.021 | 0.035 |
| (0.060) | (0.066) | (0.086) | |
| Number of observations | 416 | 376 | 296 |
| Adjusted R2 | 0.25 | 0.26 | 0.29 |
- Note: The dependent variable is ln(Tobin's Q) where Tobin's Q is equal to (Market Value of Equity + Book Value of Liabilities)/Book Value of Assets. Columns 2, 3, and 4 report results of OLS regressions with year dummies for the subsample of publicly traded insurers where the percentage of sales attributable to property–liability insurance (PCTPL) is equal to at least 80%, at least 90%, and 100%, respectively. MULTLINE is equal to one for diversified insurers, and zero otherwise. SIZE is equal to the natural logarithm of total admitted assets. CAPASSET is the ratio of policyholder surplus to total admitted assets. GEODIV is equal to one minus the Herfindahl index of premiums across 57 geographic areas. WCONC is the weighted sum of firm market share per line multiplied by each line's Herfindahl index. PCTLH is the percentage of premiums attributable to life–health insurance. GROUP is equal to one for aggregated groups, zero otherwise. Standard errors (in parentheses) are corrected for clustering at the insurer level. A t-test is used for difference of means, and a Wilcoxon rank sum test is used for difference of medians. Statistical significance at the 1%, 5%, and 10% levels is denoted by***, **, and * respectively.
Persistence of the Diversification Penalty
Having established that single-line insurers outperform multi-line insurers, on average, we examine whether the negative D-P relation persists across different levels of diversification. Following Lang and Stulz (1994) and Servaes (1996), we replace MULTLINE in Equation (1) with a series of dummy variables to capture the effect on performance of operating in n or more business lines, where n goes from 2 to 10.29
The coefficient on the first dummy variable, “operates in 2 or more business lines,” is interpreted as the difference between the ROA of firms that write two lines of business and the ROA of single-line insurers. The sum of the coefficients on the first and second dummy variables is the difference between the ROA of firms that write three lines and single-line insurers. Thus, the coefficient on each dummy variable represents the marginal contribution to ROA of the nth line.
Regression results, not reported here, indicate that the first dummy variable, “operates in 2 or more business lines,” is negative and significant, while none of the other dummy variables enter as significant. Coefficient estimates on the other explanatory variables are similar to those reported for our regressions of performance on MULTLINE. Consistent with studies on inter-industry diversification (e.g., Lang and Stulz, 1994; Servaes, 1996) we find no evidence of persistence in the diversification-performance relation at the intra-industry level.30 Thus, the key distinction seems to be whether a firm is diversified or not, while the level of diversification appears to be unimportant.
Conclusion
Our study provides some of the first evidence on the relation between line-of-business diversification and performance for P/L insurers. We investigate two aspects of the D-P relationship. First, we consider the relation between diversification status and performance. We model accounting and market performance as a function of a binary diversification indicator and a range of other performance correlates. We consistently find that undiversified insurers outperform diversified insurers. Our results for accounting performance measures indicate that diversification is associated with a penalty of at least 1 percent of ROA or 2 percent of ROE. These findings are robust to corrections for potential endogeneity bias, alternative risk measures, and an alternative estimation technique. Using a market-based performance measure (Tobin's Q), we find that the market applies a significant discount to diversified P/L insurers. The existence of a diversification penalty (and diversification discount) provides strong support for the strategic focus hypothesis. Second, we explore the possibility that the diversification penalty persists. We model performance as a function of a series of dummy variables that capture the marginal contribution to performance of each additional line of business. Consistent with studies on nonfinancial conglomerates we find no evidence supporting persistence of the diversification penalty.
We also find some interesting results with respect to several of our control variables. In every regression specification we find that both size and capitalization are positively related to accounting performance. These results support the hypothesis that customers are willing to pay more for insurance from insurers that have lower insolvency risk. The relation between size and performance may also be explained in terms of scale economies. We present new evidence on the relative profitability of mutual and stock insurers. In every model we find that mutual insurers are significantly less profitable than stock insurers. We also find some support for the hypothesis that firms operating in more concentrated business lines are able to charge higher prices and earn higher profits than firms in less concentrated lines. Finally, we find that unaffiliated insurers consistently outperform aggregated insurer groups. This negative relation between insurer groups and profitability may be due to lower prices induced by the option to let a member fail, costs of managerial discretion, or other costs associated with conglomeration.
Footnotes