Adverse Selection With Frequency and Severity Risk: Alternative Risk-Sharing Provisions
He can be contacted via e-mail: [email protected]. Dr. Ligon wishes to thank the Department of Economics, Finance, and Legal Studies and the College of Commerce and Business Administration of the University of Alabama for their financial support. Dr. Thistle wishes to thank the Nevada Insurance Education Foundation for their support. An earlier version of this paper was presented at the American Risk and Insurance Association. The authors thank Christian Gollier, Harris Schlesinger, and two anonymous referees for helpful comments on a prior version.
Abstract
The analysis considers an insurance market with adverse selection where individuals' loss distributions may differ with respect to both the frequency and severity of loss. We show that the combination of deductibles and coinsurance can be used to sort rationed policyholders. Because of their screening properties, coinsurance and deductibles may both be equilibrium forms of risk sharing for a particular insurer facing asymmetric information, with different rationed consumers choosing different risk-sharing provisions.
Introduction
In practice, a single insurer will frequently offer some policies with deductibles, other policies with coinsurance (i.e., proportional coverage), and still others with a combination of these provisions. For example, these types of risk-sharing provisions are common in health insurance policies. Many HMO policies require a copayment, which operates like a per visit deductible, whereas non-HMO group and individual health insurance polices frequently include both an annual deductible and proportional coinsurance for amounts above the deductible. Deductibles (or HMO copayments) and coinsurance rates are typically higher for some kinds of treatment (e.g., dental care, mental health treatments). However, the economic rationale for the particular form of these risk-sharing provisions is not clear. In the absence of information asymmetries, full coverage is optimal for risk-averse consumers if insurance is available at an actuarially fair price. With a positive insurance cost, less than full insurance is optimal. Raviv's (1979) work suggests that with a risk-neutral insurer and costs that are linear in the payoff to the policyholder, full coverage above a deductible is the optimal form of risk sharing.1 Insurer risk aversion or convexity of insurer costs is necessary for coinsurance to be an optimal risk-sharing form. These results suggest that all contracts written by a particular insurer should feature the same form of risk sharing.
The purpose of this study is to determine whether deductibles and coinsurance can be used to solve problems of adverse selection when there is more than one rationed risk type. Our purpose is not to determine the optimal risk-sharing arrangements in a multiple-risk-type adverse selection environment but rather to determine whether the simultaneous use of deductibles and coinsurance represents an improvement over environments where only one of these forms of cost sharing is available. In general, equilibrium risk sharing might involve some combination of deductibles, coinsurance, and upper limits and could involve ex post conditioning of benefit payments. However, before one can address the multitude of possible equilibrium configurations arising from various policy form combinations or ex post adjustments to benefits, one needs to fully understand the interactions between consumer risk characteristics and basic policy forms. Accordingly, in order to focus the analysis, attention is restricted to the choice between policies with different combinations of coinsurance and deductibles.
In insurance markets with adverse selection, risk sharing has been suggested as a screening device to solve the adverse selection problem (Rothschild and Stiglitz, 1976; Wilson, 1977; Miyazaki, 1977; Spence, 1978). Most insurance models of adverse selection specify a two-point loss distribution. A loss of some fixed amount either occurs or does not occur, and high- and low-risk individuals simply differ with regard to the probability that a loss will occur. These models have proven to be quite useful for showing that self-selection methods can provide a solution to the adverse selection problem and, indeed, have been extended to provide insight into issues like insurer organizational form (Smith and Stutzer, 1990; Ligon and Thistle, 2005). Individuals with high frequency risk choose contracts with relatively higher levels of coverage (full coverage, if the price is actuarially fair) or, more generally, less risk sharing. Individuals with low frequency risk choose insurance contracts with lower prices and lower levels of coverage or, more generally, more risk sharing. An important motivation for the current research is that, with a single loss severity, the characterization of a partial coverage contract as involving a deductible or coinsurance is without content. Whether one specifies the partial coverage as a deductible or coinsurance, the analytical impact is the same.
We are not the first to analyze insurance markets under adverse selection with random loss severity, although the focus of the existing literature is different. Doherty and Jung (1993) and Landsberger and Meilijson (1996) analyze models in which there are two risk classes with different loss distributions and ask whether the first best can be achieved by, respectively, competitive and monopoly insurance markets. Both studies show that first best allocations can be equilibrium outcomes if the supports of the loss distributions are nonoverlapping. That is, there must be some values of the loss severity that can only occur if the policyholder is high risk. Then both high and low risks are offered full insurance. The low-risk policy also includes a penalty if the amount of the loss is such that it can only occur if the policyholder is high risk; the penalty deters the high risks from buying the less expensive low risk policy. In the model we analyze, the severity distributions have a common support.
Fluet and Pannequin (1995) and Young and Browne (1997) both examine the case where loss severity is random and there are two risk classes with different expected losses. In their models, differences in expected losses can arise from differences in loss frequency, loss severity, or both. This main issue in both studies is the structure of second best insurance policies. The high risks receive full insurance, and the low risks receive partial coverage. The structure of the low-risk partial coverage policy depends critically on the likelihood ratio, that is, the ratio of the high-risk to low-risk density function of losses. If the likelihood ratio is constant, then the second best low-risk policy has full coverage above a deductible, whereas if the likelihood ratio is increasing, the second best policy has coinsurance above some amount (possibly zero). However, if the likelihood ratio is nonmonotonic, then the indemnity provided by the second best policy is also nonmonotonic.2Landsberger and Meilijson (1999) allow types to have different degrees of risk aversion as well as different loss distributions. They also analyze second best insurance policies.3 They show that certainty equivalents (CEs) provide a one-dimensional characterization of types and that the second best insurance policies preserve the order of CEs. The low CE type receives full coverage, and the high CE type receives partial coverage. The high CE partial coverage policy provides an indemnity that is antithetical to (essentially, perfectly negatively correlated with) the likelihood ratio. In the model we analyze, severity distributions differ by a mean preserving spread. This implies that the likelihood ratio, and therefore the second best insurance policy, is nonmonotonic; in particular, the indemnity must be decreasing over some range. This type of policy is not common in practice.
Doherty and Schlesinger (1995) examine the effect of introducing random loss severity on insurance market equilibria, analyzing several equilibrium concepts. They assume that individuals have different frequency risks but the same severity risk, and they restrict their analysis to pure coinsurance policies. All of this literature suggests that generalizations of standard adverse selection models may provide a better understanding of empirically observed market characteristics.
The current research differs in important ways. We are interested in the use of the risk-sharing provision of the policy as an ex ante screening mechanism; consequently, in contrast to Doherty and Jung (1993) and Landsberger and Meilijon (1996), we assume that loss severity cannot be used ex post to fully distinguish types. We also wish to focus on whether the common cost-sharing forms are equilibrium mechanisms for sorting rationed insurance consumers. Accordingly, we consider an environment with four distinct types differing on both the frequency and severity distributions. Further, we assume that the severity distributions differ by a mean preserving spread. One consequence of this is that the likelihood ratio approach of Lansberger and Meilijson (1999), Fluet and Pannequin (1995), and Young and Browne (1997) becomes unproductive. The differences in our severity distributions do not obey the monotone likelihood ratio property, and we must evaluate equilibrium configurations that separate more than two types. In contrast to Doherty and Schlesinger (1995), we consider changes in severity risk rather than simply the addition of severity risk and analyze deductibles as well as coinsurance.
We begin by analyzing equilibria when policies are restricted to pure coinsurance or pure deductible policies. We show that there is no pooling of consumers with different frequency risks. In the case of pure coinsurance, consumers with different severity risks are pooled. Since it does not affect the insurer's expected profit, the insurer has no incentive to try to separate consumers by severity risk. If prices are actuarially fair, high frequency risk consumers obtain full coverage and low frequency risk consumers obtain partial coverage. In the case of pure deductible insurance, high frequency risk consumers again obtain full coverage. Low frequency risk consumers, irrespective of their severity risk, buy partial coverage policies with the same deductible. This implies that consumers with low frequency risk and low severity risk pay a premium that is higher than their expected indemnity.
We then examine the general case where consumers can choose policies with different combinations of deductibles and coinsurance. We show that if prices are actuarially fair, then high frequency risk consumers obtain full coverage. But in the general case, it is difficult to obtain any other general analytical results, so we carry out a numerical analysis. Low frequency risk consumers buy partial coverage policies. We find that consumers with low frequency risk and high severity risk choose pure deductible policies. Consumers with low frequency risk and low severity risk choose a combination of coinsurance and deductibles. Essentially, the ability to use a mixture of cost-sharing forms provides the low frequency–low severity risk type of consumer some relief from the, what is for them, overpriced deductible policy chosen by the low frequency–high severity risk types. These results lead us to conclude that the different risk-sharing provisions of the policy can be used as a screening mechanism to separate rationed consumers by the degree of severity risk.
This study is organized as follows. The next section describes the economic environment. We then analyze the cases of pure coinsurance and pure deductible insurance followed by an analysis of the general case of combinations of coinsurance and deductibles. The final section summarizes and concludes the study.
The Economic Environment
Individuals are expected utility maximizers with a standard von Neumann–Morgenstern utility function, u(·), over final wealth. Individuals have fixed initial wealth w. Individuals' preferences are assumed to satisfy standard risk aversion (Kimball, 1993). That is, preferences are nonsatiated and risk averse and exhibit decreasing absolute risk aversion and decreasing prudence. Individuals differ with respect to both the frequency and severity of losses. As in standard adverse selection models, frequency risk can be high (pH) or low (pL), where 0 < pL < pH < 1. Given that a loss occurs, the severity of the loss, x, is a random draw from one of two distributions.4 The expected severity, μ, is the same for all individuals. Loss severity is then either xF=μ+ɛF or xG=μ+ɛG, where the distribution of the random variable xF is F, and the distribution of the random variable xG is G. Both F and G are absolutely continuous, with densities f and g, respectively. Assume that E(ɛF) =E(ɛG) = 0, so that E(xF) = E(xG) =μ, and that ɛF and ɛG are independent. Also assume that F and G have the common support [a, b] with a > 0, and b < w; that is, loss severity is strictly positive but not so large as to cause bankruptcy. The assumption that F and G have a common support implies that severity cannot fully reveal risk type ex post. The occurrence and amount of any loss is assumed to be public information. Finally, G is assumed to be a Rothschild and Stiglitz (1970) increase in risk compared to F (see also Machina and Pratt, 1997).
An individual's risk type consists of both a frequency risk and a severity distribution. A type ij individual is a person with probability of loss pi who faces severity distribution j. Let Nij be the number of individuals of a type in the population and nij be the proportion of each type in the population (i.e., nij=Nij/N, where N=∑i∑j Nij). The frequency risk and severity risk of an individual is known only to that individual, but the parameters of the frequency and severity distributions and the number of all types are common knowledge. Consumers can affect neither their probability nor severity of loss, so there is no moral hazard.
 (1)
(1) (2)
(2) (3)
(3) .5
.5The uniqueness of equilibrium depends critically on whether the single crossing property holds. The conditions under which the single crossing property holds are not central to the analysis here, and we simply assume that the single crossing property holds. This assumption imposes restrictions on preferences, on the loss distributions, or both (see Gollier, 2001, pp. 99–107, for a discussion). In particular, for individuals of high frequency and low severity risk compared to individuals of low frequency and high severity risk, it requires that the frequency risk be sufficiently different to overcome the effect of the differing severity risk for single crossing to hold. In an appendix available from the authors, we show that for individuals with identical frequency but differing severity risks, single crossing holds for pure coinsurance policies, and increasing severity risk makes the indifference curves in premium-indemnity space more concave (i.e., steeper). We also show that for deductible policies (whether pure or combined with coinsurance) the single crossing property need not hold, but an increase in severity risk makes the indifference curves less flatter (i.e., less concave or more convex) in premium-indemnity space if single crossing does in fact hold.6 We simply assume that single crossing holds in all environments we consider.
Finally, for individuals the insurer regards as being in different risk classes, the Rothschild–Stiglitz condition for separation is assumed to hold.7 In the case of actuarially fair insurance, the insurer does not always regard individuals as being in different risk classes if they differ only with respect to severity risk. The focus of the article is on the use of contract form to separate types; hence, equilibria where individuals with different frequency risks are pooled, like those in Wilson (1977), are not considered. Nonetheless, and in contrast to the usual case with frequency risk only, equilibria arise where individuals with identical frequency risk but different severity risk may be pooled.
Pure Coinsurance and Deductible Policies
In this section we analyze market equilibria when insurance policies are restricted to be either pure coinsurance or pure deductible policies. We assume that actuarially fair insurance is available in a competitive market.8 In order to establish the nature of equilibrium, we first prove a result on the fair pricing of combined coinsurance–deductible insurance contracts.
Proposition 1: Let C = (π, α, δ) be an insurance policy. For the same frequency risk, an increase in severity risk does not increase the insurer's expected profit.
 (4)
(4)The intuition of Proposition 1 is simply that an increase in risk makes the probability of losses in the tails of the distribution relatively greater. For losses in the upper tail, type Gs are getting a larger indemnity. For losses in the lower tail, below the deductible, type Gs are not getting a lower indemnity. Hence, the expected indemnity under a given policy with a deductible is higher with a greater severity. At full coverage (α= 0, δ= 0), we have qF=qG=μ. This implies that if individuals differ only with respect to severity risk and premiums are actuarially fair, then both high and low severity risk types obtain full coverage.9
The corollary deals with the special case of pure coinsurance contracts.
Corollary: Let C = (π, α, 0) be a pure coinsurance contract. For the same frequency risk, an increase in severity risk does not change the insurer's expected profit.
The corollary follows directly from the fact that when the indemnity schedule is linear in loss severity, an increase in severity risk does not affect the expected indemnity and, hence, does not affect insurer expected profits. The insurer shares in both the higher and lower losses under the expected severity.
Now consider the choices of a consumer with the probability of loss pH. When actuarially fair insurance is available, individuals with the loss probability pH facing either severity risk will purchase full coverage. Since they purchase full coverage, the form of the policy is immaterial. However, the decisions of the low frequency risk consumers depend on the type of policy that is available.
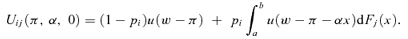 (5)
(5) (6)
(6)The resulting equilibrium is pictured in Figure 1, which is drawn so that the coverage increases (the coinsurance rate decreases) from left to right. The fair price line for the high frequency risk types, HG and HF, is the line from the origin to pHμ. Both the HG and HF types buy the full coverage policy H*. The way in which differing severity risk affects the coinsurance policies offered to low risk types can be easily seen in Figure 1. The curves UHF and UHG represent the indifference curves of the types HFs and HGs, respectively. The fair price line for the low frequency risk individuals, types LF and LG, is from the origin to pLμ. The indifference curve for the type HGs intersects this fair odds line at L, and the indifference curve for the type HFs intersect it at L*. Since the type HF's indifference curve is less steep, L* has a lower coverage level than L. The type HG's indifference curve cannot be used to define the low-risk coinsurance contract. The HF types would prefer the coinsurance policy at L to H*, causing the policy at L to lose money. Accordingly, the low-risk coinsurance policy must be defined by the intersection of the indifference curve of the HF types and the fair odds line for the low frequency risks, that is, at L*.10

Adverse Selection Equilibrium With Coinsurance Policies
This analysis leads to the following conclusion:
Proposition 2: Suppose that only pure coinsurance policies are available. Then all high frequency risk consumers obtain full coverage and all low frequency risk consumers obtain the same partial coverage policy.
The conclusion is a consequence of the corollary to Proposition 1. Since the severity risk does not affect the insurer's expected indemnity with partial coverage, the insurer has no incentive to screen policyholders by severity risk.
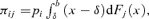 so the actuarially fair premium is decreasing and convex in δ. Proposition 1 implies that, given pi, the fair price curve for severity risk G does not lie below the fair price curve for severity risk F; at full coverage (δ= 0) the slope of the fair price line is –pi. With a pure deductible policy, expected utility is
so the actuarially fair premium is decreasing and convex in δ. Proposition 1 implies that, given pi, the fair price curve for severity risk G does not lie below the fair price curve for severity risk F; at full coverage (δ= 0) the slope of the fair price line is –pi. With a pure deductible policy, expected utility is
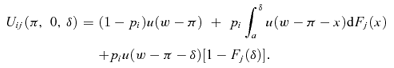 (7)
(7) (8)
(8)The resulting equilibrium is analyzed in Figure 2. The figure is drawn so that coverage increases (the deductible decreases) from left to right. Both type HG and HF individuals will purchase full coverage at a fair price; this is shown as H* in Figure 2. The type HG indifference curves are flatter than the type HF indifference curves, so the type HG indifference curves determine the self-selection constraint for the high frequency risk individuals. The fair price lines for the low frequency risk individuals, types LF and LG, are from the origin to pLμ with the type LG fair price line lying above the type LF fair price line. The indifference curve for the type HGs intersects the fair price line for the LGs at L*. Accordingly, the low-risk policy must be defined by the intersection of the indifference curve of the HGs and the fair odds line for the LGs, at L*. The type LG individuals purchase the policy at L*, with premium πL and deductible δL.

Adverse Selection Equilibrium With Deductible Policies
The type LF individuals also purchase the policy at L*. This is a consequence of the fact that the indifference curve through L* for the type LF consumers is steeper than the indifference curve for the type LG consumers. Any policy that offers a higher deductible and lower premium than L* and satisfies the self-selection constraint for the LGs (southwest of L* along ULG) is less attractive to the type LF consumers than L*. Other policies that attract type LF individuals without attracting the type LG individuals (northeast of L*) also attract type HG high frequency risk individuals and would lose money. This implies that insurers earn an expected profit of pL(qG(δL) –qF(δL)) on policies sold to individuals with low frequency and low severity risk.
This leads to the following conclusion:
Proposition 3: Suppose that only pure deductible policies are available. Then all high frequency risk consumers obtain full coverage and all low frequency risk consumers obtain partial coverage policies with the same deductible. Insurers earn positive expected profit on policies sold to individuals with low frequency and low severity risk.
The conclusion is a consequence of the effect of severity risk on consumers' preferences over policy terms, specifically, that the increase in severity risk makes the indifference curves flatter.
The positive profits implied by Proposition 3 suggest the possibility that a combination of cost-sharing forms would represent an improvement for insurance consumers. That is, a policy containing deductibles and coinsurance might allow low frequency–low severity risk consumers a lower cost signal without attracting other types. We now consider this possibility.
Combined Coinsurance and Deductible Policies
The general conclusion that emerges from the analysis so far is that when only pure coinsurance or pure deductible policies are available, then consumers are separated by frequency risk but are pooled by severity risk. This suggests that in order to separate individuals by both frequency and severity risk, it must be possible to offer policies with both coinsurance and deductible forms of risk sharing. Efforts to address this issue theoretically proved unfruitful, and thus, we carry out a numerical analysis of the types of policies bought in equilibrium.
 (9)
(9)The actuarially fair premium is linear in the coinsurance rate and decreasing and convex in the deductible. At full coverage, the slope of the premium–deductible isoprofit curve is –pi. As a result of Proposition 1, for a given level of profit, the isoprofit contour for the severity distribution F does not lie above the isoprofit contour for the severity distribution G. An increase in the coinsurance rate shifts the premium–deductible isoprofit curve downward.
 (10)
(10) . Given the coinsurance rate, the individual is willing to trade off the premium and the deductible. The premium–deductible indifference curve has slope:
. Given the coinsurance rate, the individual is willing to trade off the premium and the deductible. The premium–deductible indifference curve has slope:
 (11)
(11)This reduces to Expression (8) in the case of pure deductible policies. The indifference curve is downward sloping. The slope is equal to –pi at full coverage, which is equal to the slope of the isoprofit curve at full coverage. An increase in the coinsurance rate shifts the indifference curve downward. As with pure coinsurance and pure deductible policies, high frequency risk individuals will obtain full coverage.
The expression for the slope of the indifference curve is analytically intractable; it cannot be determined whether the indifference curve is concave or convex. Numerically, we find that the indifference curves are concave for all of the parameter values we examined. Similarly, the coinsurance–deductible indifference curve and premium–coinsurance indifference curves are downward sloping, but it cannot be determined analytically whether they are concave or convex. We can show that the increase in severity risk from F to G makes the premium–deductible indifference curves flatter.
To characterize the equilibrium insurance policies, we carry out a numerical analysis. This requires that we choose specific functional forms for the utility function and severity distribution. We employ the constant absolute risk aversion (CARA) utility function, u(w) = (–1/A)exp(–Aw), where A > 0 is the absolute risk aversion parameter. We carry out the calculations using values of A from 1/2 to 2. For absolute risk aversion levels of 3 and higher, the self-selection mechanism begins to break down. Note that for high levels of risk aversion, separating equilibria become less likely. We thus observe evidence consistent with this in our simulations. An advantage of the CARA utility function is that many commonly used utility functions are convex combinations of CARA utility functions (Brockett and Golden, 1987; Thistle, 1993). This suggests that results that hold for the CARA utility function may hold for a broader class of preferences. Nonetheless, to check that our results do not depend on the specific functional form, we also use the constant relative risk aversion (CRRA) utility function, u(w) = (–1/R)w−R, where R > –1 is the relative risk aversion parameter, as an alternative representation of preferences. We use values of R from 1/2 to 4. We set initial wealth w= 10 for computational reasons.
 (12)
(12) (13)
(13)We let the low frequency risk, pL, range from 2.5 percent to 20 percent and set the high frequency risk at pH= 2pL. For the low severity risk Weibull distributions we choose τF= 2.5 and cF= 1.384, 1.628, and 2.015; these yield expected severities of 2, 3, and 5, respectively.12 For the high severity risk Weibull distribution we choose τG= 1.25 and cG= 1.128, 2.230, and 8.177; the values of cG are chosen to equate expected severities. For the low severity risk gamma distributions we choose the shape parameter τF= 1.75 and scale parameter cF= 1.148, 1.804, and 4.861; these also yield expected severities of 2, 3, and 5, respectively. For the high severity risk gamma distribution we choose τG= 1.25 and cG= 1.163, 2.725, and 13.828; the values of cG are again chosen to equate expected severities.13
The results of the numerical analysis are reported in Tables 1 through 4.14 Each table describes the insurance policies, reporting the proportion of the loss above the deductible paid by the insurer, (1 –α), the deductible and the premium for the policy for both type LG and LF individuals. Each table also reports the proportion of losses below the deductible, F(δ), and the coverage ratio, defined as the ratio of the expected indemnity to the expected loss, CR =E{i(x, α, δ)}/μ.
| pL | High Severity Risk | Low Severity Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| Panel A: Expected Severity = 2, ARA = 1 | ||||||||||
| 2.5% | 1 | 0.916 | 0.030 | 0.291 | 0.605 | 0.832 | 0.695 | 0.027 | 0.051 | 0.547 |
| 5% | 1 | 0.944 | 0.059 | 0.300 | 0.595 | 0.827 | 0.723 | 0.053 | 0.057 | 0.533 |
| 10% | 1 | 1.005 | 0.115 | 0.320 | 0.574 | 0.818 | 0.785 | 0.101 | 0.069 | 0.504 |
| 20% | 1 | 1.147 | 0.211 | 0.365 | 0.527 | 0.798 | 0.942 | 0.174 | 0.107 | 0.434 |
| Panel B: Expected Severity = 3, ARA = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 1.156 | 0.049 | 0.231 | 0.656 | 0.874 | 0.881 | 0.046 | 0.034 | 0.620 |
| 5% | 1 | 1.20 | 0.097 | 0.241 | 0.645 | 0.870 | 0.922 | 0.091 | 0.038 | 0.605 |
| 10% | 1 | 1.296 | 0.186 | 0.262 | 0.621 | 0.861 | 1.016 | 0.172 | 0.048 | 0.574 |
| 20% | 1 | 1.527 | 0.340 | 0.311 | 0.566 | 0.842 | 1.256 | 0.299 | 0.081 | 0.498 |
| Panel C: Expected Severity = 5, ARA = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 1.512 | 0.089 | 0.127 | 0.715 | 0.902 | 1.111 | 0.088 | 0.017 | 0.703 |
| 5% | 1 | 1.589 | 0.175 | 0.135 | 0.701 | 0.898 | 1.178 | 0.172 | 0.019 | 0.688 |
| 10% | 1 | 1.761 | 0.336 | 0.153 | 0.672 | 0.890 | 1.331 | 0.327 | 0.026 | 0.655 |
| 20% | 1 | 2.192 | 0.601 | 0.198 | 0.601 | 0.870 | 1.739 | 0.572 | 0.050 | 0.572 |
| Panel D: Expected Severity = 3, ARA = 0.05 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ARA | High Severity Risk | Low Severity Risk | ||||||||
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| 0.5 | 1 | 1.582 | 0.083 | 0.323 | 0.553 | 0.769 | 1.141 | 0.072 | 0.064 | 0.482 |
| 1 | 1 | 1.20 | 0.097 | 0.241 | 0.645 | 0.870 | 0.922 | 0.091 | 0.038 | 0.605 |
| 2 | 1 | 0.870 | 0.110 | 0.168 | 0.732 | 0.894 | 0.598 | 0.108 | 0.013 | 0.717 |
- Notes: ARA is the risk aversion coefficent, α is the coinsurance rate, δ is the deductible, π is the premium, F(δ) is the percentage of loss occurrences below the deductible, CR is the coverage ratio, defined as the ratio of expected indemnity to expected loss. The analysis assumes wealth = 10, pH= 2pL, and Weibull severity distributions. The Weibull distributions have shape parameters τF= 2.5, τG= 1.25 and scale parameters cF= 1.384, 1.628, 2.015 and cG= 1.128, 2.230, 8.177. The distributions are truncated so that losses do not exceed wealth. The scale parameters cG are chosen so the expected severities are equal.
| pL | High Severity Risk | Low Severity Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| Panel A: Expected Severity = 2, ARA = 1 | ||||||||||
| 2.5% | 1 | 0.999 | 0.029 | 0.347 | 0.586 | 0.828 | 0.664 | 0.029 | 0.167 | 0.571 |
| 5% | 1 | 1.033 | 0.057 | 0.358 | 0.575 | 0.824 | 0.693 | 0.056 | 0.177 | 0.559 |
| 10% | 1 | 1.107 | 0.110 | 0.381 | 0.551 | 0.818 | 0.756 | 0.107 | 0.200 | 0.533 |
| 20% | 1 | 1.284 | 0.200 | 0.435 | 0.499 | 0.804 | 0.917 | 0.190 | 0.258 | 0.475 |
| Panel B: Expected Severity = 3, ARA = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 1.225 | 0.048 | 0.266 | 0.644 | 0.875 | 0.801 | 0.048 | 0.116 | 0.638 |
| 5% | 1 | 1.275 | 0.095 | 0.277 | 0.632 | 0.853 | 0.842 | 0.094 | 0.125 | 0.626 |
| 10% | 1 | 1.385 | 0.182 | 0.301 | 0.605 | 0.846 | 0.935 | 0.179 | 0.145 | 0.598 |
| 20% | 1 | 1.655 | 0.327 | 0.357 | 0.545 | 0.832 | 1.174 | 0.320 | 0.200 | 0.533 |
| Panel C: Expected Severity = 5, ARA = 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 1.546 | 0.089 | 0.134 | 0.709 | 0.883 | 0.996 | 0.089 | 0.050 | 0.710 |
| 5% | 1 | 1.627 | 0.174 | 0.142 | 0.695 | 0.879 | 1.062 | 0.174 | 0.055 | 0.696 |
| 10% | 1 | 1.809 | 0.3332 | 0.161 | 0.665 | 0.870 | 1.213 | 0.332 | 0.69 | 0.665 |
| 20% | 1 | 2.266 | 0.590 | 0.209 | 0.590 | 0.854 | 1.624 | 0.588 | 0.109 | 0.588 |
| Panel D: Expected Severity = 3, ARA = 5% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ARA | High Severity Risk | Low Severity Risk | ||||||||
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| .5 | 1 | 1.760 | 0.078 | 0.378 | 0.523 | 0.750 | 1.027 | 0.077 | 0.166 | 0.510 |
| 1 | 1 | 1.275 | 0.095 | 0.277 | 0.632 | 0.853 | 0.842 | 0.094 | 0.125 | 0.626 |
| 2 | 1 | 0.898 | 0.109 | 0.192 | 0.728 | 0.915 | 0.637 | 0.109 | 0.082 | 0.726 |
- Notes: ARA is the risk aversion coefficent, α is the coinsurance rate, δ is the deductible, π is the premium, F(δ) is the percentage of loss occurrences below the deductible, and CR is the coverage ratio, defined as the ratio of expected indemnity to expected loss. The analysis assumes wealth = 10, pH= 2pL, and gamma severity distributions. The gamma distributions have shape parameters τF= 1.75, τG= 1.25 and scale parameters cF= 1.148, 1.804, 4.861 and cG= 1.163, 2.725, 13.828. The distributions are truncated so that losses do not exceed wealth. The scale parameters cG are chosen so the expected severities are equal.
| pL | High Severity Risk | Low Severity Risk | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| Panel A: Expected Severity = 2, RRA = 2 | ||||||||||
| 2.5% | 1 | 1.358 | 0.023 | 0.429 | 0.464 | 0.757 | 1.192 | 0.017 | 0.184 | 0.330 |
| 5% | 1 | 1.378 | 0.046 | 0.423 | 0.458 | 0.752 | 1.217 | 0.032 | 0.193 | 0.321 |
| 10% | 1 | 1.421 | 0.089 | 0.448 | 0.446 | 0.743 | 1.273 | 0.060 | 0.213 | 0.301 |
| 20% | 1 | 1.520 | 0.168 | 0.476 | 0.419 | 0.724 | 1.409 | 0.102 | 0.266 | 0.255 |
| Panel B: Expected Severity = 3, RRA = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 1.799 | 0.038 | 0.367 | 0.506 | 0.833 | 1.599 | 0.031 | 0.143 | 0.408 |
| 5% | 1 | 1.831 | 0.075 | 0.374 | 0.499 | 0.830 | 1.637 | 0.060 | 0.150 | 0.397 |
| 10% | 1 | 1.901 | 0.145 | 0.388 | 0.485 | 0.824 | 1.720 | 0.113 | 0.169 | 0.375 |
| 20% | 1 | 2.066 | 0.271 | 0.420 | 0.452 | 0.810 | 1.928 | 0.194 | 0.218 | 0.324 |
| Panel C: Expected Severity = 5, RRA = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 2.492 | 0.069 | 0.231 | 0.554 | 0.905 | 2.240 | 0.064 | 0.092 | 0.510 |
| 5% | 1 | 2.548 | 0.136 | 0.237 | 0.545 | 0.903 | 2.300 | 0.125 | 0.098 | 0.500 |
| 10% | 1 | 2.671 | 0.263 | 0.250 | 0.527 | 0.901 | 2.435 | 0.238 | 0.112 | 0.476 |
| 20% | 1 | 2.977 | 0.482 | 0.284 | 0.482 | 0.896 | 2.783 | 0.420 | 0.153 | 0.420 |
| Panel D: Expected Severity = 3, ARA = 0.05 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ARA | High Severity Risk | Low Severity Risk | ||||||||
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| 0.5 | 1 | 2.217 | 0.064 | 0.449 | 0.424 | 0.695 | 1.917 | 0.042 | 0.215 | 0.280 |
| 1 | 1 | 2.06 | 0.068 | 0.419 | 0.453 | 0.756 | 1.806 | 0.049 | 0.188 | 0.327 |
| 2 | 1 | 1.831 | 0.075 | 0.374 | 0.499 | 0.830 | 1.637 | 0.060 | 0.150 | 0.397 |
| 4 | 1 | 1.541 | 0.084 | 0.314 | 0.563 | 0.900 | 1.411 | 0.073 | 0.106 | 0.490 |
- Notes: RRA is the relative risk aversion coefficent, α is the coinsurance rate, δ is the deductible, π is the premium, F(δ) is the percentage of loss occurrences below the deductible, CR is the coverage ratio, defined as the ratio of expected indemnity to expected loss. The analysis assumes wealth = 10, pH= 2pL, and Weibull severity distributions. The Weibull distributions have shape parameters τF= 2.5, τG= 1.25 and scale parameters cF= 1.384, 1.628, 2.015 and cG= 1.128, 2.230, 8.177. The distributions are truncated so that losses do not exceed wealth. The scale parameters cG are chosen so the expected severities are equal.
| Panel A: Expected Severity = 2, RRA = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| pL | High Severity Risk | Low Severity Risk | ||||||||
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| 2.5% | 1 | 1.643 | 0.020 | 0.531 | 0.406 | 0.791 | 1.338 | 0.018 | 0.405 | 0.406 |
| 5% | 1 | 1.674 | 0.040 | 0.539 | 0.399 | 0.789 | 1.368 | 0.035 | 0.415 | 0.348 |
| 10% | 1 | 1.741 | 0.077 | 0.555 | 0.384 | 0.784 | 1.434 | 0.066 | 0.436 | 0.331 |
| 20% | 1 | 1.897 | 0.140 | 0.591 | 0.351 | 0.776 | 1.595 | 0.118 | 0.347 | 0.295 |
| Panel B: Expected Severity = 3, RRA = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 2.061 | 0.035 | 0.436 | 0.464 | 0.848 | 1.726 | 0.032 | 0.328 | 0.428 |
| 5% | 1 | 2.104 | 0.068 | 0.444 | 0.456 | 0.846 | 1.768 | 0.063 | 0.338 | 0.419 |
| 10% | 1 | 2.199 | 0.131 | 0.461 | 0.438 | 0.843 | 1.863 | 0.120 | 0.359 | 0.400 |
| 20% | 1 | 2.425 | 0.239 | 0.500 | 0.399 | 0.836 | 2.093 | 0.215 | 0.410 | 0.358 |
| Panel C: Expected Severity = 5, RRA = 2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2.5% | 1 | 2.629 | 0.067 | 0.248 | 0.534 | 0.904 | 2.293 | 0.065 | 0.183 | 0.519 |
| 5% | 1 | 2.691 | 0.131 | 0.255 | 0.525 | 0.903 | 2.357 | 0.127 | 0.190 | 0.509 |
| 10% | 1 | 2.829 | 0.252 | 0.270 | 0.505 | 0.901 | 2.497 | 0.244 | 0.207 | 0.488 |
| 20% | 1 | 3.171 | 0.456 | 0.307 | 0.456 | 0.897 | 2.854 | 0.436 | 0.250 | 0.436 |
| Panel D: Expected Severity = 3, ARA = 5% | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ARA | High Severity Risk | Low Severity Risk | ||||||||
| 1−α | δ | π | F(δ) | CR | 1−α | δ | π | F(δ) | CR | |
| 0.5 | 1 | 2.732 | 0.053 | 0.550 | 0.351 | 0.727 | 2.125 | 0.046 | 0.416 | 0.306 |
| 1 | 1 | 2.462 | 0.059 | 0.506 | 0.393 | 0.781 | 1.981 | 0.053 | 0.385 | 0.352 |
| 2 | 1 | 2.104 | 0.068 | 0.444 | 0.456 | 0.846 | 1.768 | 0.063 | 0.338 | 0.419 |
| 4 | 1 | 1.699 | 0.080 | 0.366 | 0.536 | 0.908 | 1.496 | 0.076 | 0.275 | 0.507 |
- Notes: RRA is the relative risk aversion coefficient, α is the coinsurance rate, δ is the deductible, π is the premium, F(δ) is the percentage of loss occurrences below the deductible, and CR is the coverage ratio, defined as the ratio of expected indemnity to expected loss. The analysis assumes wealth = 10, pH= 2pL, and gamma severity distributions. The gamma distributions have shape parameters τF= 1.75, τG= 1.25 and scale parameters cF= 1.148, 1.804, 4.861 and cG= 1.163, 2.725, 13.828. The distributions are truncated so that losses do not exceed wealth. The scale parameters cG are chosen so the expected severities are equal.
Table 1 reports the results for the case of CARA utility and the Weibull severity distribution. In Panel A it is assumed that the absolute risk aversion coefficient equals 1, the expected severity equals 2, and loss frequencies pL range from 2.5 percent to 20 percent. At all frequencies, high severity risk individuals (type LGs) buy pure deductible policies. This is consistent with the result that the deductible is the optimal form of risk sharing (Raviv, 1979). The level of the deductible increases with the loss frequency. This implies that the premium rises less than proportionally to the loss frequency. As a result of the higher deductible, the proportion of uninsured losses (below the deductible) rises and the coverage ratio falls as the loss frequency increases.
The low severity risk individuals (type LFs) buy combined coinsurance–deductible policies with partial coverage above the deductible. The deductible levels for the type LF individuals are lower than those for the type LG individuals, resulting in a substantially smaller proportion of losses below the deductible. For the type LFs, the deductible increases and the proportion of covered losses above the deductible fall as loss frequency increases. Again, this implies that the premium rises more slowly than the loss frequency. The coverage ratio for the type LFs is below the coverage ratio for the type LGs and falls as the loss frequency increases.
Panels B and C report the results for expected severities of 3 and 5. The results are similar to those in Panel A. Again, the type LG individuals buy pure deductible policies and the type LF individuals buy combined coinsurance–deductible policies with lower coverage ratios. Comparing the results for the same loss frequency, the deductible for the type LGs increases with the expected severity. For the type LFs, the deductible also increases with the expected severity while the proportion covered above the deductible increases with expected severity. For both types, the coverage ratio increases with the expected severity. Panel D examines the effect of risk aversion on the policies bought, assuming that the expected severity is 3 and the loss frequency is pL= 0.05. For both type LG and LF individuals, the coverage ratio increases with the degree of risk aversion.
Table 2 reports the results for the case of CARA utility with the gamma severity distribution. The results are very similar to the results in Table 1. The high severity risk individuals buy pure deductible policies, and the low severity risk individuals buy combination coinsurance–deductible policies. The coverage ratios decrease with the frequency risk and increase with the expected severity. For both types, coverage increases with the degree of absolute risk aversion.
Tables 3 and 4 report the results for the cases of CRRA utility with the Weibull and gamma severity distributions, respectively. The results in both tables are similar to each other and to the results for the CARA utility function. The high severity risk individuals buy pure deductible policies and the low severity risk individuals buy combination coinsurance–deductible policies. Type LF individuals have lower coverage ratios for all parameter values. The coverage ratios decrease with frequency risk and increase with severity risk. For both types, coverage increases with the degree of absolute risk aversion.
The qualitative nature of the equilibrium is described in Figure 3. The figure is drawn so that the deductible decreases (coverage increases) from left to right. High frequency risk individuals obtain full coverage; this is shown as H* in the figure. Since it is flatter, the indifference curve UHG is the binding self-selection constraint for the high frequency risk individuals; this is similar to the pure deductible case.15 This indifference curve intersects the zero-coinsurance fair price curve for the type LG individuals at G*. Thus, the equilibrium policy for the type LG individuals is the pure deductible policy G*= (πG, 0, δG). The indifference curves ULG and U'LG both represent the level of expected utility that the type LGs receive from the policy G*. The curve ULG assumes a pure deductible policy, whereas U'LG assumes partial coverage above the deductible and, hence, lies below ULG. Partial coverage above the deductible also shifts the fair price curve downward. The indifference curve U'LG for the type LG individuals intersects the type LF fair price curve from the origin to pL(1 –αF)μ at the point F*. Thus, the equilibrium policy for the type LF consumers is the combined coinsurance–deductible policy at F*.

Adverse Selection Equilibrium With Coinsurance–Deductible Policies
 (14)
(14)Figure 4 illustrates the equilibrium in coinsurance–deductible space. The figure is drawn so that full coverage (α= 0, δ= 0) is at the origin, and coverage decreases as one moves away from the origin. High frequency risk individuals obtain full coverage. This is shown as H* in Figure 4 and corresponds to H* in Figure 3. The lines π–πF and π–πG in Figure 4 are fair price curves for types F and G, respectively. Since they represent the same premium, the curves are equal at pure coinsurance, otherwise π–πF lies below π–πG, reflecting the greater severity risk of the type Gs. The particular price lines drawn are the ones such that high frequency–high severity risk types just prefer H* to the pure deductible policy along the type G price line. Our numerical results show that type LG consumers choose the pure deductible policy. This is shown as G* in Figure 4, and again, this corresponds to G* in Figure 3. The fact that the type LGs choose a corner solution implies that the indifference curve, labeled UG in the diagram, is flatter than the fair price line π–πG at G*.

Adverse Selection Equilibrium With Coinsurance–Deductible Policies
Insurers cannot offer a fairly priced pure deductible policy to the type LFs. Such a policy would either attract the type G individuals and lose money or, if it satisfies the self-selection constraints, would fail to attract the type LFs. Thus, if insurers are restricted to pure deductible policies, they will offer G*, which is unfairly priced to the type LFs (recall Proposition 3). It follows that insurers' ability to offer combined coinsurance–deductible contracts makes the type LFs better off. The fact that the type F's indifference curves are steeper than the type G's indifference curves implies that, even if they were constrained to pay the same premium as G* (along π–πG), the type LFs would likely prefer a combination of coinsurance and deductible. The type LFs are willing to accept the higher coinsurance rate and overall lower coverage levels in order to obtain coverage that is both less costly than G* and fairly priced. The type G indifference curve (the self-selection constraint) intersects the type F fair price line π*F–π*F at F*. The policy F* in Figure 4 corresponds to the policy F* in Figure 3, and the fair premium curve π*F–π*F in Figure 4 corresponds to the premium π*F in Figure 3.
Summary and Conclusion
In this article, severity risk is introduced into the standard adverse selection economy. As in the standard adverse selection model, individuals may have either a high probability of loss or a low probability of loss. In addition, individuals may have a more or less risky distribution of loss severity, so that there is adverse selection with respect to both loss frequency and loss severity. The question considered is whether the form of the insurance contract (coinsurance, deductible or some combination) can be used as an adverse selection signal to separate rationed consumers.
We analyze the equilibria when policies are restricted to be pure coinsurance or pure deductible policies. In both cases, there is no pooling of individuals with different frequency risk, but there is pooling of individuals with different severity risk. If prices are actuarially fair, then all high frequency risk individuals obtain full coverage and all low frequency risk individuals obtain partial coverage. The general conclusion is that when only pure coinsurance or pure deductible policies are available, then consumers are separated by frequency risk but are pooled by severity risk. When the policy form is restricted, it cannot serve as a signal. When contract form does not serve as a signal, it is possible to pool individuals with the same frequency risk and different severity risk and such pools constitute Nash equilibria.
We examine the general case in which individuals can choose policies with different combinations of coinsurance and deductibles. We show that if prices are actuarially fair, then high frequency risk individuals obtain full coverage. In the general case, it is difficult to obtain analytical results, so we carry out a numerical analysis. We assume that preferences are described by either CARA or CRRA utility functions and that loss severity is described by either a Weibull or gamma distribution. Numerically, we find that individuals with low frequency risk and high severity risk obtain partial coverage and choose pure deductible policies. Individuals with low frequency risk and low severity risk also obtain partial coverage and choose policies that combine coinsurance and deductibles. The results are consistent across a wide range of the parameter values that we examined. The analysis leads us to conclude that the form of the policy can be used to solve the adverse selection problem and in particular that coinsurance can prove useful in separating rationed insurance customers who differ in severity risk. The level of coverage separates individuals by frequency risk and the specific risk-sharing provisions of the policy separate individuals by severity risk.




