A Two-Factor Model for Stochastic Mortality with Parameter Uncertainty: Theory and Calibration
The authors would like to thank two anonymous referees for their very helpful observations and comments. AC wishes to thank the Isaac Newton Institute in Cambridge, where he was a visitor during the preparation of this paper. This research was conducted under research grants RES-000-27-0014 and RES-000-23-1036 from the UK Economic and Social Research Council.
Abstract
In this article, we consider the evolution of the post-age-60 mortality curve in the United Kingdom and its impact on the pricing of the risk associated with aggregate mortality improvements over time: so-called longevity risk. We introduce a two-factor stochastic model for the development of this curve through time. The first factor affects mortality-rate dynamics at all ages in the same way, whereas the second factor affects mortality-rate dynamics at higher ages much more than at lower ages. The article then examines the pricing of longevity bonds with different terms to maturity referenced to different cohorts. We find that longevity risk over relatively short time horizons is very low, but at horizons in excess of ten years it begins to pick up very rapidly.
A key component of the article is the proposal and development of a method for calculating the market risk-adjusted price of a longevity bond. The proposed adjustment includes not just an allowance for the underlying stochastic mortality, but also makes an allowance for parameter risk. We utilize the pricing information contained in the November 2004 European Investment Bank longevity bond to make inferences about the likely market prices of the risks in the model. Based on these, we investigate how future issues might be priced to ensure an absence of arbitrage between bonds with different characteristics.
Introduction
Recently, it has become clear that mortality is a stochastic process: longevity has not only been improving, but it has been improving, to some extent, in an unpredictable way. These unanticipated improvements have proved to be of greatest significance at higher ages, and have caused life offices (and pension plan sponsors in the case where the plan provides the pension) to incur losses on their life annuity business. The problem is that pensioners are living much longer than was anticipated, say, twenty years ago. As a result, life offices are paying out for much longer than was anticipated, and their profit margins are being eroded in the process. The insurance industry is therefore bearing the costs of unexpectedly greater longevity. Looking forward, possible changes in lifestyle, medical advances, and new discoveries in genetics are likely to make future improvements to life expectancy highly unpredictable as well. This, in turn, will lead to smaller books of life annuity business, smaller profit margins, or both.
There are a number of possible types of systematic, mortality-related risks that annuity providers and life insurers are exposed to. For the sake of clarity, in this article we will use the following conventions.
- •
The term mortality risk should be taken to encompass all forms of uncertainty in future mortality rates, including increases and decreases in mortality rates.
- •
Longevity risk should be interpreted as uncertainty in the long-term trend in mortality rates and its impact on the long-term probability of survival of an individual. Longevity risk is normally taken to mean the risk that survival rates are higher than anticipated, although we strictly take it to mean uncertainty in either direction.
- •
Short-term, catastrophic mortality risk should be interpreted as the risk that, over short periods of time, mortality rates are much higher (or lower) than would normally be experienced. Examples of such “catastrophes” include the influenza pandemic in 1918 and the tsunami in December 2004. Once the catastrophe has past, we expect mortality rates to revert to their previous levels and to continue along previous trends.1
The idea of using the capital markets to securitize and trade specific insurance risks is relatively new, and picked up momentum in the 1990s with a number of securitizations of non-life insurance risks (see, for example, Lane, 2000). December 2003 saw the issue by Swiss Re of the first bond to link payments to mortality risk: specifically short-term, catastrophic mortality risk. A related capital market innovation, the longevity bond, provides life offices and pension plans with an instrument to hedge the much-longer-term longevity risks that they face. The idea for longevity bonds was first published in the Journal of Risk and Insurance in 2001.2 Longevity bonds are annuity bonds whose coupons are not fixed over time, but fall in line with a given survivor index.3 For example, the survivor index might be based on the population of 65-year olds alive on the issue date of the bond. Each year the coupon payments received by the life office or pension plan decrease by the percentage of the population who have died that year. If, after the first year, 1.5% of the population of what are now 66-year olds have died, then the coupon payable at the end of that first year will fall to 98.5% of the nominal coupon rate. But this is exactly what the life office or pension plan wants, since only 98.5% of their own 66-year-old annuitants (assuming these are representative of reference population) will be alive after one year, so they do not have to pay out so much.
In November 2004, BNP Paribas (in its role as structurer and manager) announced that the European Investment Bank (EIB) would issue a longevity bond. The bond had an initial market value of about £540m and a maturity of twenty-five years. Its coupon payments were to be linked to a survivor index based on the realized mortality experience of a cohort of males from England & Wales aged 65 in 2003 as published by the UK Office for National Statistics (ONS). The intended main investors were UK pension funds and life offices.4 Although this issue was ultimately unsuccessful, there are important issues to be learned about how to price such contracts (an issue which we discuss at length in this article) and about design issues (which are discussed elsewhere: see, for example, Blake, Cairns, and Dowd, 2006).
The basic cashflows under the EIB/BNP longevity bond, ignoring credit risk, are described in Appendix A. Our article focuses on the mathematical modelling that underpins the pricing of mortality-linked securities. For a full discussion of the EIB/BNP bond as well as other types of mortality-linked security, the reader is referred to Cowley and Cummins (2005), Cairns, et. al. (2005), and Blake, Cairns, and Dowd (2006).
A variety of approaches have been proposed for modelling the randomness in aggregate mortality rates over time. A key earlier work is that of Lee and Carter (1992). Their work focuses on the practical application of stochastic mortality and its statistical analysis. Aggregate mortality rates are, at best, measured annually and for this reason Lee and Carter (1992) and later authors who adopted a similar approach (see, for example, Brouhns, Denuit, and Vermunt, 2002; Renshaw and Haberman, 2003; Currie, Durban, and Eilers, 2004) worked in discrete time. Models following the approach of Lee and Carter typically adapt discrete-time time series models to capture the random element in the stochastic development of mortality rates. Other authors have developed models in a continuous-time framework (see, for example, Milevsky and Promislow, 2001; Dahl, 2004; Dahl and Møller, 2005; Miltersen and Persson, 2005; Biffis, 2005; Schrager, 2006). For further discussion and a review of previous work, the reader is referred to Cairns, Blake, and Dowd (2006).
Continuous-time models have an important role to play in our understanding of how prices of mortality-linked securities will develop over time. However, the relative intractability at the present time of such models is hindering their practical implementation. In this article, practical implementation of a model and statistical analysis are very much at the forefront of what we wish to achieve. Consequently, we choose to develop a model in discrete time and adopt an approach that is similar in vein to that of Lee and Carter (1992).
We propose a stochastic mortality model that we fit to UK mortality data and show how the calibrated model can be used to price mortality-linked financial instruments such as the EIB/BNP longevity bond. The model involves two stochastic factors. The first affects mortality at all ages in an equal manner, whereas the second has an effect on mortality that is proportional to age. We present empirical evidence that indicates that both these factors are needed to achieve a satisfactory empirical fit over the mortality term structure (that is, to model adequately historical mortality trends at different ages). The resulting model dynamics allow us to simulate cohort survival rates, thereby enabling us to model longevity risk, and to model other indices underlying alternative mortality-linked securities.
To price a mortality-linked security we adopt the risk-adjusted (or “risk-neutral”) approach to pricing adopted by, for example, Milevsky and Promislow (2001) and Dahl (2004). Given the current dearth of market data, we propose a simple method for making the adjustment between real and risk-adjusted probabilities, which involves a constant market price for both longevity and parameter risk. The magnitude of this adjustment is established by estimating the market prices of these two risks implied by the proposed issue price of the EIB/BNP longevity bond.
Once a deep, liquid market in mortality-linked securities develops, however, we will be able to determine more reliable estimates of these market prices of risk and, indeed, to test that the hypothesis are constant.
The layout of this article is as follows. The “Model Specification” section outlines the model. The “Stochastic Mortality” section fits the model to English and Welsh mortality data, and discusses the plausibility of the fit. The next section presents some simulation results for the survivor index based on the calibrated model. Two alternative sets of simulation results are presented: first, results that do not take account of parameter uncertainty, and, second, results that do take account of such uncertainty. “The Price of Longevity Risk” discusses the premium that a life office or pension plan might be prepared to pay to lay off such risk—and uses this to show how the EIB/BNP bond might be priced in a risk-adjusted framework. Specifically, we focus on the market price of risk. It also presents some illustrative pricing results. “The Risk Premium on New Issues” shows how the earlier results might be used to price new longevity bonds with different terms to maturity and following different cohorts. “Sensitivity to the EIB Interest Rate” comments briefly on sensitivity of the results to changes in interest rates. In the following section, we discuss whether the market price of risk should be positive or negative, bearing in mind the requirements of different hedgers using different types on mortality-linked contract. In the “Alternative Models” section, we give a brief discussion of alternative models including some comments on the cohort effect. The final section concludes.
Model Specification
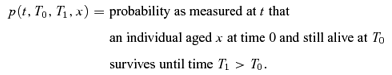
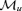 be the filtration generated by the development of the mortality curve up to time u.5 Then
be the filtration generated by the development of the mortality curve up to time u.5 Then
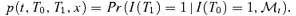
For simplicity in this exposition, we will define 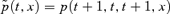 to be the realized survival probability for the cohort aged x at time 0. Additionally, define the realized mortality rate
to be the realized survival probability for the cohort aged x at time 0. Additionally, define the realized mortality rate 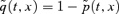 .
.
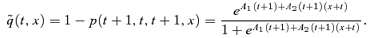 (1)
(1) ) but the chosen curve gives a significantly better fit, especially for higher ages.
) but the chosen curve gives a significantly better fit, especially for higher ages.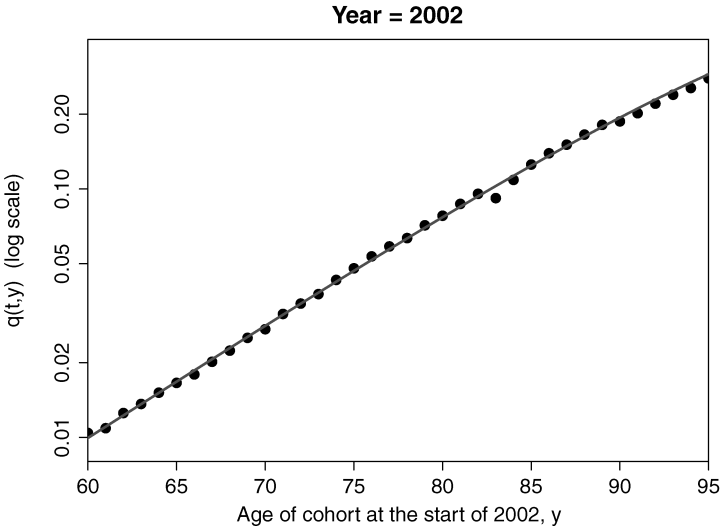
Ungraduated Mortality Rates Above the Age of 60 for England and Wales Males for the Year 2002 (dots) and Fitted Curve 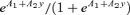 for A1=−10.95 and A2= 0.1058
for A1=−10.95 and A2= 0.1058
Stochastic Mortality
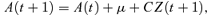 (2)
(2)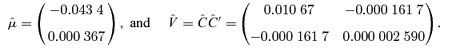 (3)
(3)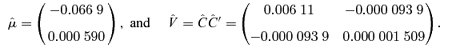 (4)
(4)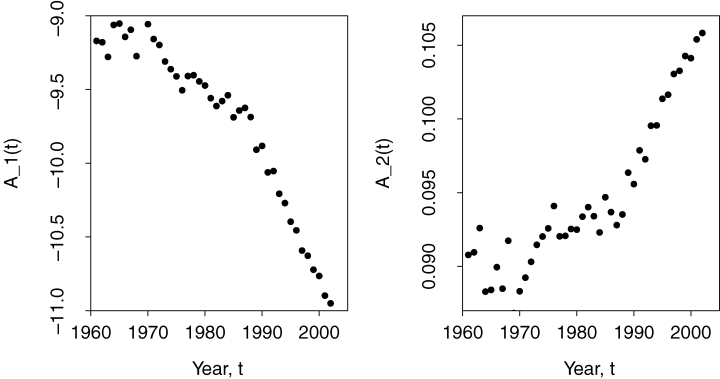
Estimated Values of A1(t) (Left-Hand Panel) and A2(t) (Right-Hand Panel) in Equation (1) from 1961 to 2002 for England and Wales Males
An important criterion for a good mortality model (see Cairns, Blake, and Dowd, 2006, for a discussion) requires the model and its parameter values to be biologically reasonable.10 The negative value for μ1 indicates generally improving mortality, with this improvement strengthening after 1982. The positive value for μ2 means that mortality rates at higher ages are improving at a slower rate. Indeed, above the very high age of 113, the model predicts deteriorating mortality.11 This might be perceived to be an undesirable feature of our model, but because this crossover point is at such a high age it is not felt to be a serious problem here as the number of lives involved is very low.
An additional criterion for biological reasonableness is that, in any given year in the future, we should normally see mortality rates for older cohorts that are higher than those for younger cohorts (that is, for fixed 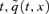 should be an increasing function of x). This criterion requires A2(t) to remain positive. In our model A2(t) could, theoretically, become negative, but the positive value for μ2 and the initial value for A2 in 2002 of 0.1058 means that A2(t) is very unlikely to do so. So the possibility of a negative A2(t) is of little significance and for all practical purposes our model be regarded as satisfying this second criterion of biological reasonableness as well.
should be an increasing function of x). This criterion requires A2(t) to remain positive. In our model A2(t) could, theoretically, become negative, but the positive value for μ2 and the initial value for A2 in 2002 of 0.1058 means that A2(t) is very unlikely to do so. So the possibility of a negative A2(t) is of little significance and for all practical purposes our model be regarded as satisfying this second criterion of biological reasonableness as well.
Cohort Dynamics
In subsequent sections we will focus on the dynamics of a survivor index, S(t). This is built up with reference to the mortality rates over time of one specific cohort, and it makes sense, therefore, to look at cohort dynamics within the context of our two-factor model. Investigating cohort dynamics also gives us the opportunity to make a further check on biological reasonableness.
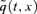 for a cohort aged x at time 0. It simplifies matters if we consider
for a cohort aged x at time 0. It simplifies matters if we consider
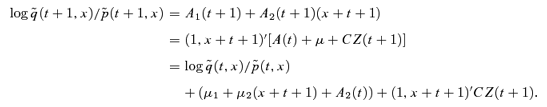
Simulation Results for The Survivor IndexS(t)
A longevity bond of the type proposed by the EIB/BNP indexes coupon payments in line with a survivor index S(t) for a specified cohort of individuals.12
We now wish to determine the distribution for S(t) for the times t= 1, 2, … , 25 that are relevant for the EIB/BNP bond. Even though the functional form for 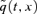 is relatively simple, its distribution for t > 2 is not analytically tractable, so we resort to Monte Carlo simulation and obtain the simulated
is relatively simple, its distribution for t > 2 is not analytically tractable, so we resort to Monte Carlo simulation and obtain the simulated 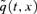 and S(t) from simulations of the underlying process A(t).
and S(t) from simulations of the underlying process A(t).
Results with No Allowance for Parameter Uncertainty
In our first experiment, we simulated the A(t) according to Equation (2) using estimates for μ and V based on data from 1961–2002 to 1982–2002. These parameter estimates were treated as if they were the true parameter values, implying that, to begin with, we ignore parameter uncertainty. The results are plotted in Figure 3. We can make the following observations:
Mean and Confidence Intervals for Projected Survival Probabilities Based on Data from 1961–2002 (Top Panel) or 1982–2002 (Bottom Panel). Each Plot Shows the Mean (Solid Curve) and the 5th and 95th Percentiles (Dashed Curves) of the Simulated Distribution of the Reference Index, S(t), with No Allowance for Parameter Uncertainty.
- •
The solid curves plot the expected values of S(t). Measured at time 0, these represent the ex ante probabilities of survival from time 0 to time t, p(0, 0, t, 65) (which we refer to as spot survival probabilities). The mean trajectory based on data from 1982 to 2002 (bottom plot) is slightly higher than that in the upper plot (based on 1961–2002 data). This is because steepening trends in A1(t) and A2(t) in the 1982–2002 data (Figure 2) signal greater improvements in the future.
- •
The dashed curves in each plot show the 5th and the 95th percentiles of the distribution of S(t). We can observe that the resulting 90% confidence interval is initially quite narrow but becomes quite wide by the 25-year time horizon (which is the maturity of the EIB/BNP longevity bond). We can also see that the confidence interval based on 1982–2002 data is a little narrower, reflecting the smaller values on the diagonal of V.
- •
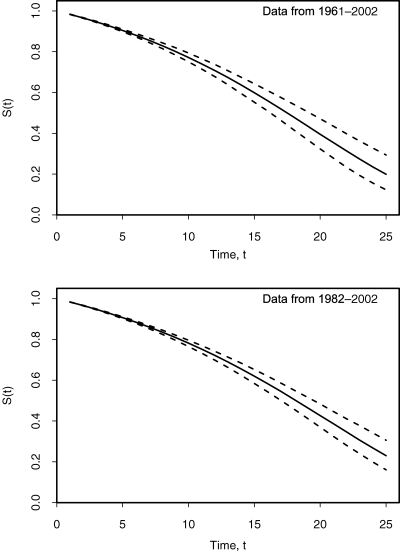
The confidence interval for S(t) grows in quite a different way from, say, that associated with an investment in equities. This point is best illustrated by looking at the variance of the logarithm of S(t), as illustrated in Figure 4. We can see that this is very low in the early years indicating that we can predict with reasonable certainty what mortality rates will be over the near future. However, after time 10 the variance starts to grow very rapidly (almost “exponentially”). This contrasts with equities where we would expect to see linear, rather than “exponential,” growth in the variance if the price process follows geometric Brownian motion.
The explanation for this variance growth is that the longer-term survival probabilities incorporate the compounding of year-by-year mortality shocks: the survival probability for year t depends on shocks applied to mortality rates in each of the years 1 to t, and each individual shock affects survival probabilities in all subsequent years.13
Plot of the Variance of log S(t) Using Data From 1961–2002 (Solid Curve) and from 1982–2002 (Dashed Curve), with No Allowance for Parameter Uncertainty
Results with Parameter Uncertainty
We consider next the impact of parameter uncertainty. It is clear that we have a limited amount of data and so the parameter estimates above must inevitably be subject to some degree of uncertainty. We will analyze this using standard Bayesian methods.14
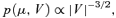
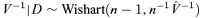 (5)
(5)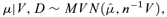 (6)
(6)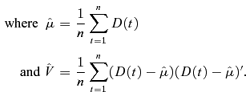
In what follows, we will restrict ourselves to an analysis based on data from 1982 to 2002.
For each simulated sample path of A(t), we simulate first μ and V from the Normal-Inverse-Wishart distribution and use these values for the whole of that sample path. The results of these simulations can be seen in Figures 5 and 6. In Figure 5, we can see the impact of parameter uncertainty on the confidence interval: specifically that parameter uncertainty becomes much more significant as a source of uncertainty in S(t) as t increases. We can see that 25 years ahead parameter uncertainty accounts for about half of the uncertainty in S(t).17 In Figure 6, we plot the variance of log S(t), and the use here of a log scale allows us to see clearly that for smaller values of t parameter uncertainty is much less important (that is, the difference between the two curves is quite small).
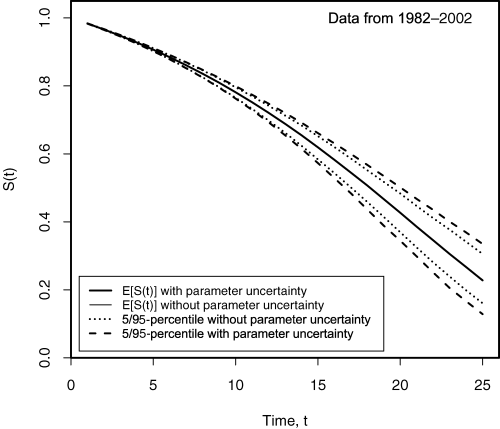
Confidence Intervals for Projected Survival Probabilities Based on Data from 1982 to 2002. Confidence Intervals Are Shown Excluding Parameter Uncertainty (Thin Dotted Curves) and Including Parameter Uncertainty (Thick Dashed Curves). The Mean Trajectories (Thin and Thick Solid Curves) for the Two Cases Are Overlapping.
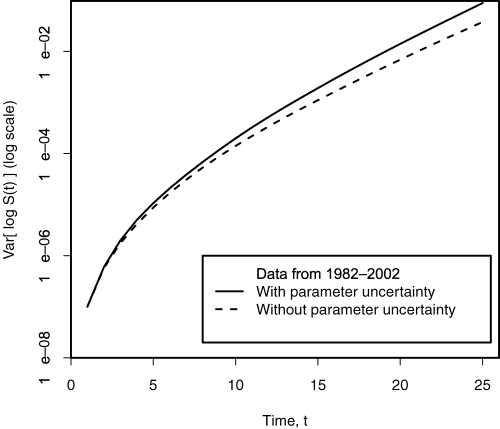
Plot of the Variance (on a Log Scale) of log S(t) Using Data from 1982 to 2002. The Variance has been Calculated Excluding Parameter Uncertainty (Dashed Curves) and Including Parameter Uncertainty (Solid Curves).
The Price of Longevity Risk
Now consider the price that a life office or pension fund might be prepared to pay to lay off its exposure to longevity risk. From 3-6 we can infer that if premiums are to be paid in respect of each future year, the premium will be much larger for the 25-year payment than, say, the 10-year payment. Furthermore, a reasonable proportion of this premium might be in respect of the desire to eliminate exposure to parameter uncertainty.
Pricing Using Risk-Adjusted Probability Measures
We propose to specify the dynamics under a risk-adjusted pricing measureQ that is equivalent to, in the probabilistic sense, the current real-world measure (which we shall refer to as P).18 The measure Q is also commonly referred to as the risk-neutral measure19 or as an equivalent-martingale measure.
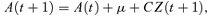
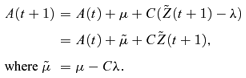
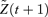 is a standard two-dimensional normal random variable21 under Q. The vector λ= (λ1, λ2) represents the market prices of longevity risk associated with the processes Z1(t) and Z2(t), respectively. Under the chosen decomposition for the matrix C (upper triangular), λ1 is associated with level shifts in mortality (specifically log q/p), while λ2 is associated with a tilt in log q/p. We assume (as part of our model) that λ is constant rather than time dependent: indeed it is difficult to propose anything more sophisticated for λ in the absence of any market price data.
is a standard two-dimensional normal random variable21 under Q. The vector λ= (λ1, λ2) represents the market prices of longevity risk associated with the processes Z1(t) and Z2(t), respectively. Under the chosen decomposition for the matrix C (upper triangular), λ1 is associated with level shifts in mortality (specifically log q/p), while λ2 is associated with a tilt in log q/p. We assume (as part of our model) that λ is constant rather than time dependent: indeed it is difficult to propose anything more sophisticated for λ in the absence of any market price data.We can make the following points about Q(λ):
- •
Complete market models such as the Black–Scholes option-pricing model force upon us a unique choice of measure Q. In contrast, here we have an incomplete market, and a range of possibilities for Q(λ).
- •
If there exists some form of market in mortality-linked securities then the choice of Q(λ) needs to be consistent with this (limited) market information (so that theoretical prices under Q(λ) match observed market prices).
- •
Beyond these restrictions, the choice of Q(λ) becomes a modelling assumption. Thus, here we have postulated that the market price of risk, λ, might be constant over time (in the same way that the market price of risk is normally assumed to be constant in the Black–Scholes model).22
- •
The assumptions embedded in Q(λ) form a testable hypothesis. However, the assumptions can only be tested once a market develops in a range of mortality-linked securities and with sufficient liquidity over time that historical price data can be used to test if the assumption that the market price of risk is constant or time varying.
Example: The EIB/BNP Longevity Bond
As an example, consider the 25-year EIB/BNP longevity bond announced in November 2004, with an issue price based on a yield of 35 basis points below LIBOR. The appropriate starting point is the EIB curve for conventional fixed-interest bonds issued typically at 15 basis points below LIBOR. This means that the new longevity bond was priced at 20 basis points below standard EIB rates. This spread below standard EIB rates will be denoted by δ in the equations that follow. We will now make the following assumptions:
- •
The projected survival rates used in the pricing of the bond (in the case of the EIB/BNP bond, this is the projection made by the UK Government Actuary's Department) are unbiased estimates at time 0 under the real-world measure P of the survival rates.
- •
The spread of 20 basis points below the standard EIB curve is accounted for entirely by the market price of longevity risk.
- •
The development of mortality rates over time is independent of the dynamics of the interest-rate term structure over time.23
We will refer to 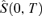 as the survivor index based upon the latest GAD projections available at time 0.24 Assumption 1 implies that
as the survivor index based upon the latest GAD projections available at time 0.24 Assumption 1 implies that 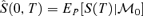 .
.
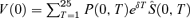 , where δ is the spread (expressed as a continuously compounding rate) below the EIB curve used in pricing the bond.25 Given assumption 1 this is equivalent to26
, where δ is the spread (expressed as a continuously compounding rate) below the EIB curve used in pricing the bond.25 Given assumption 1 this is equivalent to26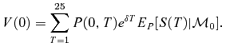 (7)
(7)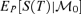 based upon parameters in (4) and without parameter uncertainty are given in Table 1, column 1. For example, if we assume that implied EIB zero-coupon prices are given by P(0, T) = 1.04−T and if we set δ= 0.0020 and λ= (0, 0)′ then we find that the price at issue of the bond on this contractual basis (Equation 7) is V(0) = 11.442.
based upon parameters in (4) and without parameter uncertainty are given in Table 1, column 1. For example, if we assume that implied EIB zero-coupon prices are given by P(0, T) = 1.04−T and if we set δ= 0.0020 and λ= (0, 0)′ then we find that the price at issue of the bond on this contractual basis (Equation 7) is V(0) = 11.442. and Market Prices Under Various Assumptions for the Market Prices of Longevity and Parameter Risk
and Market Prices Under Various Assumptions for the Market Prices of Longevity and Parameter Risk| Column Reference | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Parameter uncertainty: | N | Y | N | N | N | Y | Y |
| λ1 | 0 | 0 | 0.375 | 0 | 0.175 | 0 | 0 |
| λ2 | 0 | 0 | 0 | 0.316 | 0.175 | 0 | 0 |
| λ3 | – | 0 | – | – | – | 1.684 | 0 |
| λ4 | – | 0 | – | – | – | 0 | 1.419 |
| t | 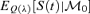 |
||||||
| 1 | 0.9836 | 0.9836 | 0.9837 | 0.9836 | 0.9836 | 0.9837 | 0.9836 |
| 2 | 0.9661 | 0.9661 | 0.9664 | 0.9662 | 0.9663 | 0.9664 | 0.9662 |
| 3 | 0.9475 | 0.9475 | 0.9482 | 0.9477 | 0.9479 | 0.9482 | 0.9477 |
| 4 | 0.9278 | 0.9278 | 0.9289 | 0.9281 | 0.9285 | 0.9289 | 0.9281 |
| 5 | 0.9068 | 0.9068 | 0.9086 | 0.9074 | 0.908 | 0.9086 | 0.9074 |
| 6 | 0.8845 | 0.8845 | 0.8872 | 0.8856 | 0.8863 | 0.8872 | 0.8856 |
| 7 | 0.861 | 0.8609 | 0.8646 | 0.8626 | 0.8635 | 0.8646 | 0.8626 |
| 8 | 0.836 | 0.8359 | 0.8408 | 0.8384 | 0.8395 | 0.8407 | 0.8383 |
| 9 | 0.8095 | 0.8095 | 0.8157 | 0.8129 | 0.8142 | 0.8156 | 0.8129 |
| 10 | 0.7816 | 0.7815 | 0.7893 | 0.7862 | 0.7877 | 0.7892 | 0.7861 |
| 11 | 0.7522 | 0.752 | 0.7616 | 0.7583 | 0.7599 | 0.7615 | 0.7582 |
| 12 | 0.7213 | 0.721 | 0.7326 | 0.7292 | 0.7308 | 0.7325 | 0.729 |
| 13 | 0.6888 | 0.6885 | 0.7023 | 0.6989 | 0.7004 | 0.7021 | 0.6987 |
| 14 | 0.6548 | 0.6545 | 0.6707 | 0.6675 | 0.6689 | 0.6704 | 0.6672 |
| 15 | 0.6195 | 0.6191 | 0.6378 | 0.635 | 0.6362 | 0.6374 | 0.6346 |
| 16 | 0.5828 | 0.5823 | 0.6036 | 0.6015 | 0.6024 | 0.6032 | 0.6011 |
| 17 | 0.5448 | 0.5443 | 0.5684 | 0.5672 | 0.5676 | 0.5679 | 0.5667 |
| 18 | 0.5059 | 0.5052 | 0.5321 | 0.5321 | 0.532 | 0.5315 | 0.5316 |
| 19 | 0.4661 | 0.4654 | 0.495 | 0.4965 | 0.4957 | 0.4944 | 0.4959 |
| 20 | 0.4258 | 0.4251 | 0.4573 | 0.4606 | 0.459 | 0.4566 | 0.4599 |
| 21 | 0.3853 | 0.3847 | 0.4191 | 0.4245 | 0.422 | 0.4185 | 0.4238 |
| 22 | 0.345 | 0.3445 | 0.3809 | 0.3885 | 0.3851 | 0.3803 | 0.3879 |
| 23 | 0.3054 | 0.305 | 0.3428 | 0.353 | 0.3486 | 0.3424 | 0.3524 |
| 24 | 0.2667 | 0.2668 | 0.3054 | 0.318 | 0.3128 | 0.3052 | 0.3177 |
| 25 | 0.2297 | 0.2302 | 0.2689 | 0.2841 | 0.278 | 0.269 | 0.284 |
| Price | |||||||
| δ= 0 | 11.240 | 11.237 | 11.442 | 11.442 | 11.442 | 11.439 | 11.439 |
| δ= 0.0020 | 11.442 | 11.439 | – | – | – | – | |
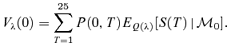 (8)
(8)We can now ask the question: What values for the market prices of risk λ1 and λ2 satisfy Vλ(0) =V(0)? Put another way, under what circumstances does the risk-adjusted price (Equation 8) match the issue price quoted in the contract (Equation 7)?
With no parameter uncertainty, and δ= 0 we found that we could obtain Vλ(0) = 11.442 with (λ1, λ2) = (0.375, 0) and (0, 0.316). For these two values for λ the values for 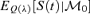 are given in Table 1 columns 3 and 4. In column 5, we have also given an intermediate value for λ between these two extremes.27 Here we can achieve Vλ(0) =V(0) with λ1=λ2= 0.175.28,29
are given in Table 1 columns 3 and 4. In column 5, we have also given an intermediate value for λ between these two extremes.27 Here we can achieve Vλ(0) =V(0) with λ1=λ2= 0.175.28,29
We next introduce parameter uncertainty into the analysis. We first simulate under P with full parameter uncertainty and the values for 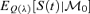 are given in Table 1, in column 2 with λ= (0, 0, 0, 0)′. We have seen in Figure 6 that parameter uncertainty presents a significant risk to annuity providers. It follows that they will be prepared to pay a premium to reduce this risk in the same way that they are prepared to pay to reduce the impact of longevity risk.
are given in Table 1, in column 2 with λ= (0, 0, 0, 0)′. We have seen in Figure 6 that parameter uncertainty presents a significant risk to annuity providers. It follows that they will be prepared to pay a premium to reduce this risk in the same way that they are prepared to pay to reduce the impact of longevity risk.
 . With parameter uncertainty, the basic model (see Appendix B) simulates first V, then calculates the upper-triangular matrix C that satisfies V=CC′, and then simulates
. With parameter uncertainty, the basic model (see Appendix B) simulates first V, then calculates the upper-triangular matrix C that satisfies V=CC′, and then simulates
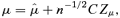
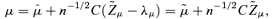
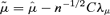 .
.We now have four market prices of risk to play with to match the single price derived by discounting expected cashflows under P at EIB minus 20 basis points. With parameter uncertainty included, the expected cashflows under P change very slightly (see Table 1, column 2), as does the price of V(0) = 11.439. The values for λ1 and λ2 required to match this price are essentially unchanged from the values that were determined before (Table 1, columns 3 and 4) and are consequently not repeated in the table. The required values for λ3 and λ4 were, respectively, 1.684 and 1.419, with the corresponding values for  quoted in Table 1, columns 6 and 7.
quoted in Table 1, columns 6 and 7.
For the various cases presented in Table 1 we have plotted in Figure 7 the expected value under P or Q(λ) of S(t) for t= 1, … , 25. This plot helps us to analyze the impact of using the different measures and, in particular, to see where most of the additional value in the longevity bond resides. The expected values in the upper plot show us two things. First, the inclusion of parameter uncertainty has almost no effect on the expected values under P. Second, the expected values under the different Q(λ) measures look similar, and all show up the largest differences compared with the P measure near t= 25.
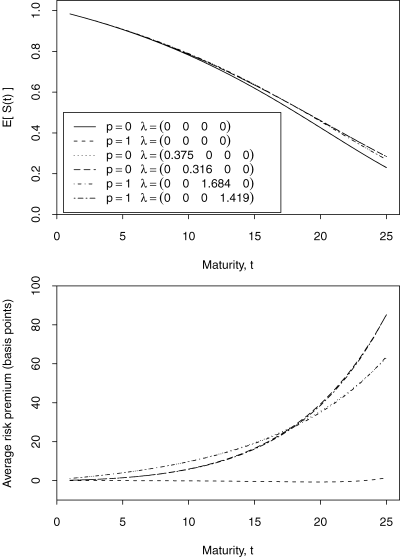
Top Panel: Expected Value of S(t) Under Different Probability Measures. Values for the Market Prices of Risk in the Six Cases Considered Are Given in the Legend; p= 0 Means without Parameter Uncertainty and p= 1 Means with Parameter Uncertainty in Both μ and V. Bottom Panel: Average Risk Premium Per Annum Is Defined as log {EQ(λ)[S(t)]/EP[S(t)]}/t on a Zero-Coupon Longevity Bond Over the Full Term to Maturity. Different Line Types Are Defined in the Top Plot.
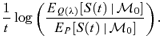
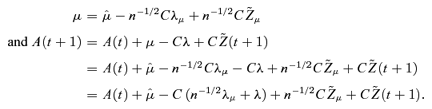
Now return to the results presented in Table 1. Why are the required values of λ1 to λ4 positive? And why does the average risk premium per annum plotted in Figure 7 differ in the way that it does for λ1 and λ2 (curves A and B)?
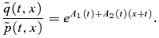
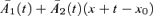 where
where 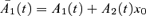 and
and 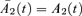 , then for a suitable choice of x0 (specifically,
, then for a suitable choice of x0 (specifically, 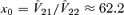 ) the processes
) the processes 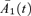 and
and 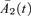 become independent random walks with drift.
become independent random walks with drift. 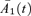 has Z1(t) as its driver with market price of risk λ1 and
has Z1(t) as its driver with market price of risk λ1 and 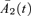 has Z2(t) as its driver with market price of risk λ2. Under this transformation we have
has Z2(t) as its driver with market price of risk λ2. Under this transformation we have
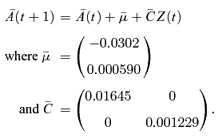
We can now see that, since both diagonal elements of  are positive, a positive shock Z1(t) will produce a level shift in
are positive, a positive shock Z1(t) will produce a level shift in 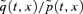 over all ages x: that is, an unanticipated deterioration in longevity. A positive value of λ1, in contrast, causes
over all ages x: that is, an unanticipated deterioration in longevity. A positive value of λ1, in contrast, causes 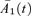 to be pushed downwards over time thereby enhancing improvements in longevity. So λ1 > 0 is required to produce a positive risk premium (that is, higher expected values of S(t) under Q(λ)).
to be pushed downwards over time thereby enhancing improvements in longevity. So λ1 > 0 is required to produce a positive risk premium (that is, higher expected values of S(t) under Q(λ)).
We have to be slightly more careful when we analyze the impact of positive shocks Z2(t). Specifically, for x+t above age x0= 62.2, a positive value for Z2(t) will increase 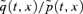 (particularly so at high ages). However, the same positive value for Z2(t) will cause
(particularly so at high ages). However, the same positive value for Z2(t) will cause 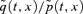 to fall for values of x+t less than 62.2. Now in our analysis we are considering a cohort who are all aged 65 at time 0, so that S(T) is constructed from the experienced mortality rates
to fall for values of x+t less than 62.2. Now in our analysis we are considering a cohort who are all aged 65 at time 0, so that S(T) is constructed from the experienced mortality rates 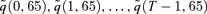 . Since the minimum age is 65, a positive shock in Z2(t) will cause an increase in each of
. Since the minimum age is 65, a positive shock in Z2(t) will cause an increase in each of 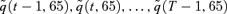 , everything else being equal. Thus, we infer that λ2 must also be positive to produce a positive risk premium.
, everything else being equal. Thus, we infer that λ2 must also be positive to produce a positive risk premium.
This discussion also helps us to explain the difference between the curves corresponding to (λ1, λ2) = (0.375, 0) and (λ1, λ2) = (0, 0.316) in the lower half of Figure 7. Specifically risk adjustments to the dynamics of A2(t) through the use of λ2 have proportionately a much greater effect on higher-age mortality than adjustments to A1(t) through λ1. This means that the probability of survival to higher ages is much more sensitive to λ2 than to λ1. Thus we see that curve A in Figure 7 corresponding to λ2 is flatter than curve B initially but then picks up at a much faster rate, ending up at a higher level.
The Risk Premium on New Issues
The announcement in 2004 of the 25-year EIB longevity bond will, we hope, be followed by other issues with different maturity dates and which will follow different cohorts.
Recall that the 25-year bond following the age-65 cohort (we will refer to this as the (T= 25, x= 65) bond), had a 20 basis-point risk premium per annum. The question now is: What risk premiums are appropriate for bonds with different terms to maturity or that follow older or younger cohorts? It is important to address this question to ensure that possible future bonds are priced in a consistent fashion.
This question can be answered relatively easily. The key is that the market prices of risk λ1 and λ2 used in pricing the (T, x) bond must be the same as those used in pricing the (25, 65) bond. Thus for each (T, x) we calculate the price of the bond by determining expectations under Q(λ) and then discounting at EIB rates as before. We then calculate the price of the bond using expectations under P, but then discounting at EIB rates minus the risk premium δ as in Equation (7). We then need to find the value of δ that equates the two prices under P and Q(λ).31
Recall that the only longevity bond so far proposed does not allow us to determine λ uniquely. Instead, for any other proposed bond (T, x), the risk premium δ(T, x, λ) will depend on λ.
Risk premia on (T, x) bonds are given in Tables 2, 3, and 4.32 We can make the following observations:
| Bond Maturity T | Initial Age of Cohort, x | ||
|---|---|---|---|
| 60 | 65 | 70 | |
| 20 | 8.9 | 14.7 | 23.1 |
| 25 | 12.7 | 20.0 | 28.7 |
| 30 | 16.9 | 24.3 | 31.5 |
| ∞ | 22.9 | 27.2 | 32.2 |
| Bond Maturity T | Initial Age of Cohort, x | ||
|---|---|---|---|
| 60 | 65 | 70 | |
| 20 | 4.8 | 12.4 | 26.1 |
| 25 | 9.2 | 20.0 | 36.1 |
| 30 | 15.0 | 27.6 | 42.3 |
| ∞ | 27.1 | 34.8 | 44.7 |
| Bond Maturity T | Initial Age of Cohort, x | ||
|---|---|---|---|
| 60 | 65 | 70 | |
| 20 | 6.8 | 13.4 | 25.1 |
| 25 | 11.0 | 20.0 | 33.3 |
| 30 | 16.2 | 26.6 | 37.9 |
| ∞ | 25.5 | 33.7 | 39.6 |
- •
In each table we see that older cohorts attract a higher risk premium. As we take younger and younger cohorts, the mortality rates get closer to zero, so even if we introduce a market price of risk, the probability of survival will still be close to 1. In contrast, at higher ages the market price of longevity risk will have a proportionally greater impact on the survival probability. These differences between ages 60, 65, and 70 are illustrated by the Var[log S(t)] plot in Figure 8. We can see that the longevity risk for the age-60 cohort is much lower than the age-65 and age-70 cohorts. Consequently, a lower risk premium is appropriate.
- •
In each table, we see that the longer the maturity of the bond, the greater the risk premium. This reflects our earlier observations (for example, Figure 7, bottom) that longer-dated cashflows have a higher risk premium per annum.
- •
In each table, consider the diagonal running from cohort 60, term 30 up to cohort 70, term 20. In each case the terminal age is 90. As we move up the diagonal, there are two conflicting trends influencing the risk premium. The shortening maturity serves to push the risk premium down,33 while the increasing initial age serves to push the risk premium up. However, we can see from the table that the latter trend dominates and the risk premium increases as we move up the diagonal.
Compare, for example, one cohort currently aged 60 with another currently aged 70 and consider the contracted cashflow at age 90. This cashflow is clearly subject to greater uncertainty for the age-60 cohort. However, the observation above indicates that the overall impact of this greater uncertainty on the 30-year longevity bond is much reduced by the effect of discounting.
- •
The risk premium δ(T, x, λ) varies most with (T, x) when λ= (0, 0.315) (Table 3). The greater variation with T reflects the development of the risk premium illustrated in Figure 7, bottom. The greater variation with x reflects the fact that Z2(t) affects mortality rates in different ways at different ages. The market price of risk λ2 has a positive effect on mortality at higher ages and a negative effect at lower ages.
- •
From Table 4 with the intermediate λ= (0.175, 0.175) we see that the risk premia lie between those given in Tables 2 and 3.
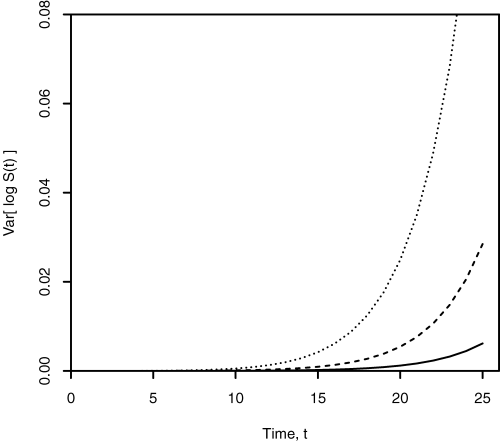
Plot of the Variances of log S(t) for the Age 60 (Solid Line), 65 (Dashed Line), and 70 (Dotted Line) Cohorts, Based on Data from 1982 to 2002, with No Allowance for Parameter Uncertainty
Table 5 shows the impact in the truncated expected future lifetime e(x, T) when we move from the real-world measure, P, to the risk-neutral measure Q(λ) when λ= (0.175, 0.175).34 The trends in this table match those in Table 4 with the exception of the trend along the diagonal from (x, T) = (60, 30) to (70, 20) where the trend is reversed. As we move upwards along the diagonal we have the same two factors working in opposite directions as before: decreasing term and increasing age. In Tables 2–4, the impact of discounting was sufficient to allow the increasing-age effect to dominate. In Table 5 the absence of discounting means that the decreasing-term effect is dominant.
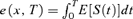 . Upper Part of Table Shows e(x, T) Under the Real-World Measure P and the Lower Part of the Table Shows the Increase in e(x, T) When We Change to the Risk-Neutral Measure Q(λ).
. Upper Part of Table Shows e(x, T) Under the Real-World Measure P and the Lower Part of the Table Shows the Increase in e(x, T) When We Change to the Risk-Neutral Measure Q(λ).| Initial Age of Cohort, x | ||||
|---|---|---|---|---|
| 60 | 65 | 70 | ||
| eP(x, T) | ||||
| Maximum | 20 | 16.95 | 15.15 | 12.74 |
| Years | 25 | 19.59 | 16.78 | 13.45 |
| T | 30 | 21.30 | 17.53 | 13.64 |
| ∞ | 22.43 | 17.79 | 13.66 | |
| e Q(λ)(x, T) −eP(x, T) | ||||
| Maximum | 20 | 0.12 | 0.20 | 0.28 |
| Years | 25 | 0.28 | 0.40 | 0.47 |
| T | 30 | 0.54 | 0.65 | 0.60 |
| ∞ | 1.22 | 1.02 | 0.66 | |
Sensitivity to the EIB Interest Rate
We can also investigate the impact of a change in interest rates. Specifically, let us take λ as given but change the EIB interest rate from 4% to 5% per annum. In this case we find that the impact on the risk premium is relatively small. Specifically, if λ= (0.375, 0) then δ(25, 65) = 19.1 basis points and if λ= (0, 0.315) then δ(25, 65) = 18.9 basis points. This reduction in the risk premium reflects the relative lowering, in present-value terms, of the later, more-uncertain cashflows under the bond.
The Sign of the Market Price of Risk
In previous sections, we focused on the EIB/BNP longevity bond and used the information contained in the offer price to make inferences about the market price of risk. We concluded that this particular bond had a negative risk premium: that is, holders of the bond were being asked to pay a premium in order to reduce their exposure to longevity risk.35
Now consider a bond that allows life insurers to hedge their exposure to short-term catastrophic mortality risk in their term-insurance portfolios (for example, the Swiss Re mortality bond issued in 200336). One might argue that life insurers will be prepared to pay a premium to reduce their exposure to the risk of high mortality rates. Indeed this is the case with the Swiss Re mortality bond (see, for example, Beelders and Colarossi, 2004). The problem is that this suggests that the market prices of risk in our model should take the opposite sign to those estimated in the section titled “Example: the EIB/BNP Longevity Bond.”
We can offer some partial answers to this apparent paradox.
- •
The apparent differences between implied market prices of risk would suggest the existence of arbitrage opportunities. However, market frictions limit the ability of annuity providers and life insurers to take advantage of these opportunities. These firms can arbitrage away some differences between the different market prices of risk, for example, by exploiting natural hedging. However, there are limits to how much arbitrage they can realistically carry out because the dynamic strategies involved are not costless to implement. There might also be regulatory constraints that prevent annuity providers and life insurers from taking advantage of apparent arbitrage opportunities. Thus, as in any other “imperfect” market, a certain amount of price differentiation will remain, and we cannot rule out the possibility that the different market prices of risk might have different signs.
- •
The individual lives associated with annuity and term-assurance portfolios are not subject to exactly the same rates of mortality. The age distributions of the two populations and the average terms of the policies are quite different, and it is evident from historical data that mortality improvements at different ages are not perfectly correlated. The two groups are subject to quite different levels of underwriting. It is also likely that their social backgrounds and family status are different. All of these differences will have an impact on their mortality prospects. To some degree, therefore, it might be possible to apply different market prices of risk to the different policy groups and over different age ranges.
- •
Annuity providers seem to be focused on the risk associated with the long-term trend in mortality (in our case, driven by a two-dimensional Brownian motion, Z(t)). In contrast, life insurers and reinsurers seem to be more focused on short-term catastrophic mortality risk (as is the case in the Swiss Re bond): it is this risk factor, much more than longevity, that is the critical determinant of a life insurer's profit or loss. In order to model this type of risk, it would be appropriate to add to our model an additional source of risk that captures more reasonably these extreme mortality risks (see, for example, Beelders and Colarossi, 2004). This additional risk will have its own market price of risk.
If we combine life insurers and annuity providers, it seems quite plausible that there is, in aggregate, a significant, positive net exposure to both short-term catastrophic mortality risk and longevity risk. However, natural hedging (Cox and Lin, 2004) can only succeed at the global level (encompassing life insurers and annuity providers) if this aggregate exposure is close to zero. If these net exposures are, in reality, positive, there remains an opportunity for the financial markets to charge both life insurers and annuity providers a premium to hedge their risks.
Alternative Models
General Models
We have deliberately chosen to use a simple (linear) parametric form for 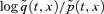 . In part this is because the data seem to justify this assumption over the 60–90 age range (see, for example, Figure 1). In addition, the simple model allows us to focus attention on the key issues in this article: highlighting the risk associated with future mortality-linked cashflows; and the calculation of the risk-adjusted price of these cashflows.
. In part this is because the data seem to justify this assumption over the 60–90 age range (see, for example, Figure 1). In addition, the simple model allows us to focus attention on the key issues in this article: highlighting the risk associated with future mortality-linked cashflows; and the calculation of the risk-adjusted price of these cashflows.
A variety of alternative stochastic models have, of course, been proposed (see, for example, Cairns, Blake, and Dowd, 2006, and references therein). However, rigorous statistical analysis has, in the main, been limited to the the approach proposed by Lee and Carter (1992) and their successors (see, for example, Brouhns, Denuit, and Vermunt, 2002; and Renshaw and Haberman, 2003). The model analyzed in this article might be considered as a special case of a two-factor Lee and Carter model (Renshaw and Haberman, 2003)37.
Despite the relative simplicity of our model we have chosen to use two stochastic factors rather than one. We did so partly because our earlier analysis suggests that we need two factors to get the best fit. However, we also did so because our later analysis highlights the importance of the longer-term longevity risks (that is, the risks associated with survivorship to very old ages), and we need the second mortality factor to model these particular risks adequately. Finally, we wish to consider a range of bonds with different maturity dates and following different cohorts, and this merits an additional factor if the historical data supports it.
Modelling the Cohort Effect
A number of authors have recently focused attention on what has become known as the cohort effect. These analyses (see, for example, Willets, 1999, 2004; Richards, Kirkby, and Currie, 2005; and MacMinn et al., 2005) have demonstrated that, for a fixed age x, the improvement in mortality from one calendar year to the next is critically dependent on the year of birth (that is t−x). Richards, Kirkby, and Currie found, for example, that the largest improvements in mortality rates in England and Wales have been consistently experienced by individuals born around 1930. We have not attempted to capture this effect in the current article. A recent paper by Renshaw and Haberman (2006) has adapted the Lee and Carter approach to incorporate a cohort effect and we anticipate more work along these lines in the coming years.
We can note that the change in pattern in A1(t) and A2(t) around 1985, observable in Figure 2, is also consistent with the cohort effect.38 For example, suppose the slope parameter, A2(t), would naturally be constant in the absence of a cohort effect. If we then introduce a cohort effect, we would find that as the “golden” cohort moves through the 60–90 age range, we would initially see the fitted curve steepen for 15 years and then fall back to its original slope over the next 15 years (that is, A2(t) would rise from its normal stable level and then fall back). In Figure 2, we can see that A2(t) was reasonably level, before starting to climb after 1985. If the cohort effect persists then we might anticipate that A2(t) will start falling around the time when the 1930 cohort passes age 75 (the mid-point of our age 60–90 data sets). Thus, we might expect to see A2(t) start to fall back again over the next few years, instead of continuing to rise.
Conclusions
In this article, we have used a simple two-factor model for the development of the mortality curve over time that seems, nevertheless, to fit the data well. The model allows us to simulate the distribution of a survivor index over various time horizons under both the real-world probability measure and under a variety of possible risk-adjusted measures. By taking expectations under the latter measure, this model enables us to price the longevity risk inherent in longevity bonds, given the known longevity risk premium (of 20 basis points) contained in the world's first longevity bond, namely the November 2004 EIB 25-year bond designed by BNP Paribas with a reference cohort of 65-year-old English and Welsh males. The chosen model is well suited to pricing longevity bonds. For other types of contracts, that involve, for example, derivative characteristics on future mortality rates (such as guaranteed annuity options) models formulated within the forward-mortality model (such as the Olivier–Smith model described in Olivier and Jeffrey, 2004) or the mortality-market model (Cairns, Blake, and Dowd, 2006) frameworks are likely to prove more efficient to implement.
We find that the premium increases with both term and the initial age of the reference cohort. In the latter case, this is caused by the greater volatility that is associated with the higher mortality rates of older people compared with younger people. For example, in the worst-case scenario considered (where the entire longevity risk premium is associated with the second (i.e., volatility) factor), the premium for a 30-year bond with a reference cohort aged 70 is 42.3 basis points.
Another key finding of the article is that the reference cohort's initial age is more important for determining the premium than the bond's maturity. To illustrate, again in the context of the worst-case scenario, the premium for a 20-year bond with a reference cohort aged 70 is 26.1 basis points, whereas the premium for a 30-year bond with a reference cohort aged 60 is 15.0 basis points. This shows that the greater uncertainty in death rates at higher ages dominates the greater discounting of the more distant cash flows of longer maturing bonds.
These findings suggest that open-ended survivor bonds that continue to pay out as long as members of the reference cohort are still alive would not have an excessively high longevity risk premium. However, they might be unattractive in other respects, such as the administrative inconvenience associated with paying very small coupons fifty years or so after the bond was issued. So fixed-term longevity bonds might well dominate for practical considerations. Our results also suggest that fixed-term longevity bonds might also be favored by investors wishing to avoid ultra-long longevity risk being dominated by parameter risk.
We propose in future research to investigate alternatives to the random walk model with drift used here. Possibilities include models drawn from the ARIMA class of time series models.39 By taking this approach, we will be investigating the important issue of model risk in addition to the parameter risk considered in this article.
In this article, we have assumed that the fitted values of A(t) are known with certainty. A further line of research is to relax this assumption and to use instead filtering approaches or Markov Chain Monte Carlo (MCMC) methods to estimate jointly the posterior distribution of the parameters and of the current values of A(t).
Footnotes
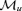 represents the history of the mortality curve up to time u.
represents the history of the mortality curve up to time u.
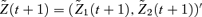 where
where 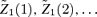 and
and 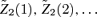 are independent sequences of i.i.d. N(0, 1) random variables under Q(λ).
are independent sequences of i.i.d. N(0, 1) random variables under Q(λ).
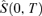 are specified in the offer document issued by BNP Paribas.
are specified in the offer document issued by BNP Paribas.
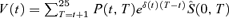 : that is, still with reference to the initial estimate
: that is, still with reference to the initial estimate 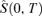 , and with reference to an easily-observable zero-coupon curve at time t.
, and with reference to an easily-observable zero-coupon curve at time t.
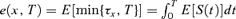 .
.
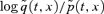 in place of the usual
in place of the usual 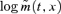 where
where 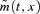 is the central death rate.
is the central death rate.
Appendices
Appendix A The EIB/BNP Longevity Bond
The EIB/BNP Paribas longevity bond makes reference to a cohort (aged x at time 0) index that is calculated along the following lines. We start, for convenience, by letting t= 0 correspond to the beginning of 2003 and set the reference index S(0) = 1. Changes in the reference index, S(t), from one year to the next are determined by reference to national mortality rates which are made publicly available. Thus, for 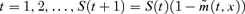 , where
, where 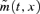 is the central death rate for individuals aged x+t in year t (that is, age 65 in 2003, age 66 in 2004, and so on) published by the UK Office for National Statistics (ONS).
is the central death rate for individuals aged x+t in year t (that is, age 65 in 2003, age 66 in 2004, and so on) published by the UK Office for National Statistics (ONS).
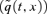 published, for example, by the UK Government Actuary's Department (GAD) (for example, as with those for 2002 plotted in Figure 1). For a full discussion of the differences between
published, for example, by the UK Government Actuary's Department (GAD) (for example, as with those for 2002 plotted in Figure 1). For a full discussion of the differences between 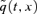 and
and 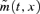 the reader is referred to standard texts such as Benjamin and Pollard (1993) or Bowers et al. (1986). A key approximation connecting the two is given by
the reader is referred to standard texts such as Benjamin and Pollard (1993) or Bowers et al. (1986). A key approximation connecting the two is given by
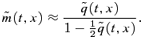
Appendix B Simulation of the Normal-Inverse-Wishart Distribution
Equation (5) requires simulation of V|D using its posterior distribution, the Wishart  distribution. It is more instructive to show how to simulate from the Wishart distribution than it is to write down its density function. Thus:
distribution. It is more instructive to show how to simulate from the Wishart distribution than it is to write down its density function. Thus:
- •
Let S be the upper triangular matrix that satisfies
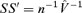 .
. - •
Now simulate n− 1 i.i.d. vectors α1, … , αn−1∼MVN(0, SS′): that is, let αi=SZi, where Zi is a standard n-dimensional normal random variable (that is, the individual elements of each Zi are independent normal random variables with mean 0 and variance 1).
- •
Let
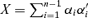 .
. - •
Then X has a Wishart
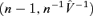 distribution.
distribution. - •
Our final step is to invert X to get our simulated covariance matrix: that is, V=X−1.
Note that 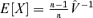 . Thus the distribution of the simulated matrices V=X−1 will be centered close to
. Thus the distribution of the simulated matrices V=X−1 will be centered close to 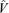 itself.
itself.
The second step of simulating from the Normal-Inverse-Wishart posterior distribution is to take the simulated V from the steps above and then sample μ from a multivariate normal distribution with mean 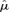 and covariance matrix n−1V. This can be simulated in the usual way.
and covariance matrix n−1V. This can be simulated in the usual way.
Appendix C Illustration of Accumulated Variance
Conside a random walk in which W(0) = 0 and, for each t, W(t+ 1) =W(t) +Z(t+ 1), where Z(1), Z(2), … is a sequence of i.i.d. standard normal random variables.
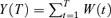 . Since W(t) =Z(1) +…+Z(t) we have
. Since W(t) =Z(1) +…+Z(t) we have
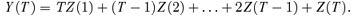
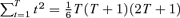 . In contrast Var W(T) =T.
. In contrast Var W(T) =T.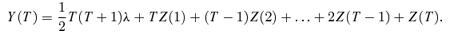
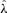 and variance σ2, then
and variance σ2, then
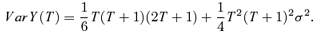
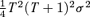 term dominates as T gets larger).
term dominates as T gets larger).



