Uncertainty Evaluation of Human Risk Analysis (HRA) of Chemicals by Multiple Exposure Routes
Abstract
The application of an ISO standard procedure (Guide to the Expression of Uncertainty in Measurement (GUM)) is here discussed to quantify uncertainty in human risk estimation under chronic exposure to hazardous chemical compounds. The procedure was previously applied to a simple model; in this article a much more complex model is used, i.e., multiple compound and multiple exposure pathways. Risk was evaluated using the usual methodologies: the deterministic reasonable maximum exposure (RME) and the statistical Monte Carlo method. In both cases, the procedures to evaluate uncertainty on risk values are detailed. Uncertainties were evaluated by different methodologies to account for the peculiarity of information about the single variable. The GUM procedure enables the ranking of variables by their contribution to uncertainty; it provides a criterion for choosing variables for deeper analysis. The obtained results show that the application of GUM procedure is easy and straightforward to quantify uncertainty and variability of risk estimation. Health risk estimation is based on literature data on a water table contaminated by three volatile organic compounds. Daily intake was considered by either ingestion of water or inhalation during showering. The results indicate one of the substances as the main contaminant, and give a criterion to identify the key component on which the treatment selection may be performed and the treatment process may be designed in order to reduce risk.
1. INTRODUCTION
In recent years, evaluation of human health risk and ecological risk has received great attention by regulation agencies, the scientific community, and workers associations. Usually, an acceptable threshold value of risk is stated by agencies. The distribution of possible risk values, i.e., the uncertainty of risk, must be considered to evaluate how much the value of risk evaluated by a human health and ecological risk assessment is under the threshold. Many U.S. EPA documents and activities(1) and the most used guide for risk analysis for contaminated sites(2,3) underline the importance of adequately characterizing uncertainty in human health and ecological risk assessment. Notwithstanding the recommendation, a standard procedure to quantify uncertainty is not yet accepted. Nevertheless, several procedures were proposed,(4–11) and the problem of uncertainty evaluation of human and ecological risk assessment is still an open question.(12)
In a site remediation approach, the numerical results of risk estimation are affected by large uncertainties, at least an order of magnitude or greater, and it is more important to identify the key site-related variables and assumptions that contribute most to the uncertainty than a precise evaluation of uncertainty.(13)
In this article, uncertainty of health risk and the contribution of each variable to uncertainty are evaluated following, where it is possible, the procedures reported in the Guide to the Expression of Uncertainty in Measurement (GUM),(14) a standard guide that establishes general rules for evaluating and expressing uncertainty. GUM is supported by seven international organizations (BIPM, IEC, IFCC, ISO, IUPAC, IUPAP, OIML) and it is published in their name; GUM is intended to be applicable to a broad spectrum of measurements in different fields.
The procedures were previously(5) tested on a single exposure route for a single substance in human risk evaluation. In the present article, GUM procedures are tested on a much more complex situation, i.e., three substances by two exposure routes.
Some terms, commonly used to indicate several components of uncertainty, might generate confusion; thus a definition of uncertainty helps in understanding the approach.
Uncertainty is a parameter associated with the results of a measurement, e.g., a risk estimation, that characterizes the dispersion of the values that could reasonably be attributed to the measurand,(14,15) i.e., to the risk. In other words, uncertainty reflects the lack of exact knowledge about the value of the risk.(14) GUM(14) lists in Clause 3.3.2 a wide range of possible sources of uncertainty and points out that some of these may be interdependent.
EPA(16) has advised risk and exposure assessors to distinguish between variability and uncertainty; otherwise GUM allows to consider variability as a component/source of uncertainty, GUM procedures may be used either on the whole uncertainty or on a single component of the uncertainty, e.g., the variability.
In the risk evaluation context, the following sources of uncertainty have particular importance: incomplete definition of risk (i.e., definition of receptors, routes, diseases, etc.), imperfect modeling of the definition (i.e., models used to calculate risk), sampling and analysis of chemical concerns, the choice of a representative target of receptors (adults, children, country, residents, etc.), and the variation in repeated observations (i.e. variability). In this article, the term uncertainty includes variability as a component.
The evaluation of uncertainty in risk assessment deals with the estimation of the level of confidence that risk is under a threshold of acceptability.
Thus in risk assessment, one needs not only to evaluate uncertainty but also to provide a coverage interval. The aimed at coverage probability and the threshold values are still in debate; in any case 95% and 10−6 and 10−4 are at the moment the main terms of reference in the world. The choice of the appropriate values for the coverage probability and threshold is a political decision and not the task of risk evaluators.
This article aims at the estimation of the risk to contract cancer as a consequence of daily consumption of water and inhalation during showering, termed R0 and Ri, respectively. An RME (reasonable maximum exposure) deterministic approach and a Monte Carlo stochastic approach were used for risk estimation; the evaluation of uncertainty was performed in both cases. This article is aimed to show and discuss GUM procedures applied to the same model and the same data (Superfund site in northeastern United States.) used by Smith(17) that is considered as the main reference for the use of Monte Carlo method in risk estimation.
2. METHODS
2.1. Substances
The description of the industrial site and data is reported in the literature.(17) The three contaminant substances with carcinogenic potency were considered, i.e., 1,1 dichloroethene, tetrachloroethene, and trichloroethene; they are indexed in the following by i= A, B, or C, respectively. Slope factor and parameters of statistical distribution of concentration values for each substance are reported in Table I.
| Substance | Oral Slope Factor kg day/mg | Inhaled Slope Factor kg day/mg | Distribution | Mean mg/L | Standard Deviation mg/L | Reference | |
|---|---|---|---|---|---|---|---|
| 1,1 Dichloroethene | A | 0.600 | 0.175 | LogNormal | 0.0690 | 0.00426 | [17] |
| Trichloroethene | B | 0.0110 | 0.00600 | LogNormal | 0.00491 | 0.00237 | [17] |
| Tetrachloroethene | C | 0.0520 | 0.00203 | LogNormal | 0.00267 | 0.00133 | [17] |
2.2. Cancer Risk Estimation
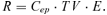 (1)
(1)The risk evaluation in this article considers the direct ingestion of contaminated water without any other attenuation factor and the inhalation of vapors of the contaminant substances during a shower.
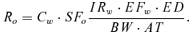 (2)
(2)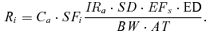 (3)
(3)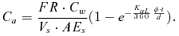 (4)
(4)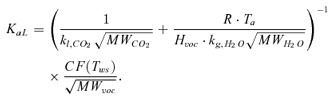 (5)
(5)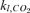 and kg,H2O are the mass transfer coefficient of CO2 in water and H2O in air at 20°C (cm/h); MW are the molecular weight (g/mol); CF is the temperature correction that depends on Tws, given in K, as it follows:
and kg,H2O are the mass transfer coefficient of CO2 in water and H2O in air at 20°C (cm/h); MW are the molecular weight (g/mol); CF is the temperature correction that depends on Tws, given in K, as it follows:
 (6)
(6)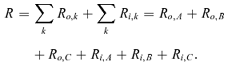 (7)
(7) (8)
(8)The model reported in Equation (8) is strongly nonlinear; moreover, temperature affects the most variables that are thus correlated.
2.3. GUM Procedure for Evaluating Uncertainty
The uncertainty characterizing the value of risk is evaluated by applying the procedure proposed by GUM(14) for combined standard uncertainty for the discussed input quantities. Their correlation is at first neglected and the procedure for uncorrelated was thus applied. More specifically, “r” is the best estimate of the value of total risk R calculated by Equation (8) and u(r), the standard uncertainty associated with “r,” is a combination of the standard uncertainties of the input quantities.
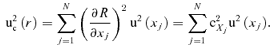 (9)
(9)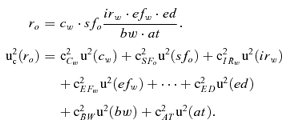 (10)
(10)Equation (9) is used to evaluate the combined uncertainty of risk uc(ro). Sensitivity coefficients are limited to first-order Taylor series when nonlinearity of risk expression is considered negligible, i.e., sensitivity coefficients are the partial derivatives of Equation (2) calculated at the point at which risk is evaluated.
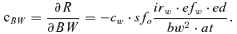 (11)
(11)When health and safety of humans are involved, GUM(14) prescribes to state not the uncertainty associated with the value of the measurand, but the so-called expanded uncertainty (U), which provides the boundaries of a coverage interval that is expected to encompass the value with a stated probability.
Extensive experience with and full knowledge of the uses to which an estimation result will be used can facilitate the selection of the proper value of the coverage factor. The coverage probability is, as mentioned above, subject to political decisions. However, the GUM and many regulations require a coverage probability of 0.95. This implies for a Gaussian that the so-called coverage factor, i.e., the ratio between U and u(y), has the value 1.96 or, rounded, 2. If the probability density function (PDF) is not symmetric (see GUM(14) G 5.3), one can introduce U− and U+ or simply state the boundaries of the shortest coverage interval. U− and U+ may be calculated as the difference between 95th percentiles of distribution and (best) estimate of the value. In the standard framework of GUM, one has reason to assume—except for certain cases—that the PDF for the measurand is a Gaussian. In this case, the coverage interval is symmetric about the expectation that is taken as (best) estimate of the value, and the expanded uncertainty is the half width of that coverage interval.
The GUM procedure permits to create a “budget of uncertainty” that underlines the sources of uncertainty for the risk and ranks the sources based on their sensitivity coefficients. The budget is a very useful tool to point out how to reduce uncertainty, how to determinate the boundary conditions for the reduction, and which are the relevant variables that affect uncertainty.
The budget of uncertainty is a table that summarizes in each row the parameters of a variable (refer to Tables IV–VI). Parameters are: acronym (X), units ([X]), value (x), uncertainty at value x (u (x)), relative uncertainty at value x (u (x)/x), sensitivity coefficient calculated at values x (c (x)), quadratic term (u2 (x) c2 (x)), criticism. The last row shows the parameters of the combined quantity, i.e., risk (R). X and u(x) (excluded last row) are the independent values; all the other values in the table are calculated from them.
| X | [X] | x | u(x) | u(x)/x | c(x) | [cu]2 | Criticism |
|---|---|---|---|---|---|---|---|
| ED | yr | 12.63 | 7.29 | 57.7% | 7.20E–06 | 2.76E–9 | 100% |
| BW | kg | 70 | 27 | 17.4% | 1.30E–06 | 1.23E–9 | 45% |
| AT | d | 13447 | 7764 | 57.7% | 6.77E–09 | 2.76E–9 | 100% |
| IRw | L/d | 1.053 | 0.608 | 57.7% | 4.16E–05 | 6.41E–10 | 23% |
| EFw | d/yr | 184 | 106 | 57.6% | 2.38E–07 | 6.38E–10 | 23% |
| IRa | m3/min | 0.00732 | 0.00422 | 57.7% | 6.44E–03 | 7.39E–10 | 27% |
| SDs | min/d | 12 | 4 | 33.3% | 3.93E–06 | 2.47E–10 | 9% |
| EFs | d/yr | 184 | 106 | 57.6% | 2.56E–07 | 7.38E–10 | 27% |
| FRws | L/min | 20 | 6 | 30.0% | 2.36E–06 | 2.00E–10 | 7% |
| Vs | m3 | 3 | 1.2 | 40.0% | 1.57E–05 | 3.56E–10 | 13% |
| AEs | m3/m3min | 0.0167 | 0.0058 | 34.7% | 2.82E–03 | 2.68E–10 | 10% |
| t | s | 10 | 1.2 | 12.0% | 4.44E–06 | 2.84E–11 | 1% |
| φ | - | 6 | 0.6 | 10.0% | 7.40E–06 | 1.97E–11 | 1% |
| d | mm | 1 | 0.29 | 29.0% | 4.44E–05 | 1.66E–10 | 6% |
| Tws | K | 318 | 4 | 1.3% | 3.47E–07 | 1.93E–12 | 0% |
| Ta | K | 293 | 3 | 1.0% | 7.71E–10 | 5.35E–18 | 0% |
| Cw,A | mg/L | 0.0532 | 0.0307 | 57.7% | 1.71E–03 | 2.74E–09 | 99% |
| Cw,B | mg/L | 0.00149 | 0.00086 | 57.7% | 7.92E–05 | 4.64E–15 | 0% |
| Cw,B | mg/L | 0.00287 | 0.00166 | 57.8% | 4.12E–05 | 4.68E–15 | 0% |
| SFo,A | kg d/mg | 0.316 | 0.182 | 57.6% | 1.38E–04 | 6.34E–10 | 23% |
| SFo,B | kg d/mg | 0.0274 | 0.0158 | 57.7% | 3.87E–06 | 3.75E–15 | 0% |
| SFo,C | kg d/mg | 0.00579 | 0.00334 | 57.7% | 7.46E–06 | 6.21E–16 | 0% |
| SFi,A | kg d/mg | 0.0921 | 0.0532 | 57.8% | 5.11E–04 | 7.39E–10 | 27% |
| SFi,B | kg d/mg | 0.00107 | 0.00062 | 57.9% | 1.11E–05 | 4.72E–17 | 0% |
| SFi,C | kg d/mg | 0.00316 | 0.00182 | 57.6% | 2.38E–05 | 1.87E–15 | 0% |
| HA | atm m3/mol | 0.0491 | 0.0057 | 11.6% | 4.58E–06 | 6.82E–16 | 0% |
| HB | atm m3/mol | 0.0427 | 0.0089 | 20.8% | 1.55E–09 | 1.90E–22 | 0% |
| HC | atm m3/mol | 0.0245 | 0.005 | 20.4% | 2.95E–08 | 2.17E–20 | 0% |
| klCO2 | cm/h | 20 | 2.89 | 14.5% | 2.21E–06 | 4.08E–11 | 1% |
| kgH2O | cm/h | 3000 | 289 | 9.6% | 7.53E–11 | 4.73E–16 | 0% |
| MWA | g/mol | 96.94 | 0 | 0.0% | 2.29E–07 | 0 | 0% |
| MWB | g/mol | 165.82 | 0 | 0.0% | 3.42E–11 | 0 | 0% |
| MWC | g/mol | 131.38 | 0 | 0.0% | 2.72E–10 | 0 | 0% |
| MWCO2 | g/mol | 44 | 0 | 0.0% | 5.02E–07 | 0 | 0% |
| MWH2O | g/mol | 18 | 0 | 0.0% | 6.27E–09 | 0 | 0% |
| R | atm m3/mol | 0.000082 | 0 | 0.0% | 2.75E–03 | 0 | 0% |
| R | - | 0.910E–04 | 1.22E–04 | 134.4% | 1.49E–08 |
| X | [X] | x | u(x) | u(x)/x | c(x) | [cu]2 | Criticism |
|---|---|---|---|---|---|---|---|
| ED | yr | 7.24 | 6.87 | 94.8% | 6.8E–05 | 2.2E–07 | 100% |
| BW | kg | 76.7 | 13.3 | 17.4% | 6.4E–06 | 7.3E–09 | 3% |
| AT | d | 25550 | 0.00 | 0.0% | 1.9E–08 | 0 | 0% |
| IRw | l/d | 1.12 | 0.547 | 48.9% | 3.6E–05 | 3.8E–10 | 0% |
| EFw | d/yr | 297 | 37.8 | 12.7% | 1.3E–07 | 2.6E–11 | 0% |
| IRa | m3/min | 0.00988 | 0.00384 | 38.8% | 4.6E–02 | 3.1E–08 | 14% |
| SDs | min/d | 13.3 | 2.45 | 18.4% | 3.4E–05 | 6.8E–09 | 3% |
| EFs | d/yr | 297 | 37.8 | 12.7% | 1.5E–06 | 3.3E–09 | 2% |
| FRws | l/min | 20 | 4.08 | 20.4% | 2.3E–05 | 8.5E–09 | 4% |
| Vs | m3 | 3.63 | 0.816 | 22.5% | 1.2E–04 | 1.0E–08 | 5% |
| AEs | m3/m3min | 0.0167 | 0.00340 | 20.4% | 2.7E–02 | 8.4E–09 | 4% |
| t | s | 10 | 0 | 0.0% | 4.8E–09 | 0 | 0% |
| f | - | 6 | 0 | 0.0% | 8.1E–09 | 0 | 0% |
| d | mm | 1 | 0.204 | 20.4% | 4.8E–08 | 9.8E–17 | 0% |
| Tws | K | 316 | 3.06 | 1.0% | 3.8E–10 | 1.4E–18 | 0% |
| Ta | K | 293 | 0 | 0.0% | 8.5E–13 | 0 | 0% |
| Cw,A | mg/L | 0.0538 | 0.0380 | 70.5% | 9.1E–03 | 1.2E–07 | 55% |
| Cw,B | mg/L | 0.00239 | 0.00113 | 47.1% | 1.6E–04 | 3.3E–14 | 0% |
| Cw,B | mg/L | 0.00442 | 0.00202 | 45.8% | 3.0E–04 | 3.7E–13 | 0% |
| SFo,A | kg d/mg | 0.6 | 0 | 0.0% | 6.6E–05 | 0 | 0% |
| SFo,B | kg d/mg | 0.052 | 0 | 0.0% | 2.9E–06 | 0 | 0% |
| SFo,C | kg d/mg | 0.011 | 0 | 0.0% | 5.4E–06 | 0 | 0% |
| SFi,A | kg d/mg | 0.175 | 0 | 0.0% | 2.6E–03 | 0 | 0% |
| SFi,B | kg d/mg | 0.00203 | 0 | 0.0% | 1.1E–04 | 0 | 0% |
| SFi,C | kg d/mg | 0.006 | 0 | 0.0% | 2.1E–04 | 0 | 0% |
| HA | atm m3/mol | 0.0491 | 0.00403 | 8.2% | 4.9E–09 | 3.9E–22 | 0% |
| HB | atm m3/mol | 0.0427 | 0.00630 | 14.7% | 3.9E–11 | 6.2E–26 | 0% |
| HC | atm m3/mol | 0.0245 | 0.00350 | 14.3% | 2.6E–10 | 8.1E–25 | 0% |
| klCO2 | cm/h | 20 | 0 | 0.0% | 2.4E–09 | 0 | 0% |
| kgH2O | cm/h | 3000 | 0 | 0.0% | 8.3E–14 | 0 | 0% |
| MWA | g/mol | 96.9 | 0 | 0.0% | 2.5E–10 | 0 | 0% |
| MWB | g/mol | 166 | 0 | 0.0% | 8.7E–13 | 0 | 0% |
| MWC | g/mol | 131 | 0 | 0.0% | 2.4E–12 | 0 | 0% |
| MWCO2 | g/mol | 44 | 0 | 0.0% | 5.4E–10 | 0 | 0% |
| MWH2O | g/mol | 18 | 0 | 0.0% | 6.9E–12 | 0 | 0% |
| R | atm m3/mol | 0.0000820 | 0 | 0.0% | 3.0E–06 | 0 | 0% |
| R | - | 0.000490 | 6.40E–04 | 130.7% | 4.1E–07 |
| X | [X] | x | u(x) | u(x)/x | c(x) | [cu]2 | Criticism |
|---|---|---|---|---|---|---|---|
| ED | yr | 7.24 | 6.87 | 94.8% | 6.8E–05 | 2.2E–07 | 100% |
| BW | kg | 76.7 | 23.0 | 30.0% | 6.4E–06 | 2.2E–08 | 10% |
| AT | d | 25550 | 0.00 | 0% | 1.9E–08 | 0 | 0% |
| IRw | L/d | 1.12 | 0.547 | 48.9% | 3.6E–05 | 3.8E–10 | 0% |
| EFw | d/yr | 297 | 37.8 | 12.7% | 1.3E–07 | 2.6E–11 | 0% |
| IRa | m3/min | 0.00988 | 0.00384 | 38.8% | 4.6E–02 | 3.1E–08 | 14% |
| SDs | min/d | 13.3 | 2.45 | 18.4% | 3.4E–05 | 6.8E–09 | 3% |
| EFs | d/yr | 297 | 37.8 | 12.7% | 1.5E–06 | 3.3E–09 | 2% |
| FRws | L/min | 20 | 4.08 | 20.4% | 2.3E–05 | 8.5E–09 | 4% |
| Vs | m3 | 3.63 | 0.816 | 22.5% | 1.2E–04 | 1.0E–08 | 5% |
| AEs | m3/m3min | 0.0167 | 0.00340 | 20.4% | 2.7E–02 | 8.4E–09 | 4% |
| t | s | 10 | 2.0 | 20.0% | 4.8E–09 | 9.38E–17 | 0% |
| f | - | 6 | 1.2 | 20.0% | 8.1E–09 | 9.38E–17 | 0% |
| d | mm | 1 | 0.204 | 20.4% | 4.8E–08 | 9.8E–17 | 0% |
| Tws | K | 316 | 3.06 | 1.0% | 3.8E–10 | 1.4E–18 | 0% |
| Ta | K | 293 | 58.6 | 20.0% | 8.5E–13 | 2.48E–21 | 0% |
| Cw,A | mg/L | 0.0538 | 0.0380 | 70.5% | 9.1E–03 | 1.2E–07 | 55% |
| Cw,B | mg/L | 0.0024 | 0.0011 | 47.1% | 1.6E–04 | 3.3E–14 | 0% |
| Cw,B | mg/L | 0.0044 | 0.0020 | 45.8% | 3.0E–04 | 3.7E–13 | 0% |
| SFo,A | kg d/mg | 0.6 | 0 | 0% | 6.6E–05 | 0 | 0% |
| SFo,B | kg d/mg | 0.052 | 0 | 0% | 2.9E–06 | 0 | 0% |
| SFo,C | kg d/mg | 0.011 | 0 | 0% | 5.4E–06 | 0 | 0% |
| SFi,A | kg d/mg | 0.175 | 0 | 0% | 2.6E–03 | 0 | 0% |
| SFi,B | kg d/mg | 0.00203 | 0 | 0% | 1.1E–04 | 0 | 0% |
| SFi,C | kg d/mg | 0.006 | 0 | 0% | 2.1E–04 | 0 | 0% |
| HA | atm m3/mol | 0.0491 | 0.0491 | 100.0% | 4.9E–09 | 5.8E–20 | 0% |
| HB | atm m3/mol | 0.0427 | 0.0427 | 100.0% | 3.9E–11 | 2.8E–24 | 0% |
| HC | atm m3/mol | 0.0245 | 0.0245 | 100.0% | 2.6E–10 | 3.9E–23 | 0% |
| klCO2 | cm/h | 20 | 10 | 50.0% | 2.4E–09 | 5.80E–16 | 0% |
| kgH2O | cm/h | 3000 | 1500 | 50.0% | 8.3E–14 | 1.55E–20 | 0% |
| MWA | g/mol | 96.9 | 0 | 0% | 2.5E–10 | 0 | 0% |
| MWB | g/mol | 166 | 0 | 0% | 8.7E–13 | 0 | 0% |
| MWC | g/mol | 131 | 0 | 0% | 2.4E–12 | 0 | 0% |
| MWCO2 | g/mol | 44 | 0 | 0% | 5.4E–10 | 0 | 0% |
| MWH2O | g/mol | 18 | 0 | 0% | 6.9E–12 | 0 | 0% |
| R | atm m3/mol | 0.0000820 | 0 | 0% | 3.0E–06 | 0 | 0% |
| R | - | 0.000490 | 6.5E–04 | 133.0% | 4.3E–07 |
Relative uncertainty is calculated as the ratio between standard uncertainty u(x) and the value x for each variable; sensitivity coefficients may be determined by analytical or numerical sensitivity analysis and they are calculated at the values x; quadratic terms are calculated from sensitivity coefficient c(x) and standard uncertainty u(x).
Risk value r is calculated from values x by Equation (1). The quadratic term of risk is calculated as the sum of quadratic terms u2(x)c2(x), i.e., by Equation (9). Uncertainty of risk is calculated as the square root of the quadratic term of risk.
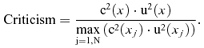 (12)
(12)Criticism mirrors and visualizes the relative impact of the variables in order to rank the contribution of the variables to the uncertainty. It is possible to state a threshold value for criticism under which variables have a negligible contribution to uncertainty, e.g., 0.1 can be considered as the threshold value.
The budget of uncertainty includes and explicates all the calculations used. A single sheet of Excell® was the only thing need to perform calculations.
2.4. Information About Independent Variables
In order to calculate risk and its uncertainty for each independent variable it is necessary to recover information. Table II lists the 37 independent variables that result from the system of Equation (8).
| Variable | Units | Variability Distribution | Reference | RME | |
|---|---|---|---|---|---|
| ED | yr | LN(11.36;13.72) | [20] | 24 | Safeguard |
| BW | kg | LN(76.11;13.2) | [21] | 70 | Mean |
| AT | d | C(25550) | [17] | 25550 | Safeguard |
| IRw | L/d | LN(1.12;1.63) | [12] | 2 | Safeguard |
| EFw | d/yr | TR(180;345;365) | [17] | 350 | Safeguard |
| IRa | m3/min | TR(0.00160;,00764;0.0204) | [22] | 0.0139 | Safeguard |
| SDs | min/d | TR(8;12;20) | [17] | 12 | Mean |
| EFs | d/yr | TR(180;345;365) | [17] | 350 | Safeguard |
| FRws | L/min | TR(10;20;30) | [17] | 20 | Mean |
| Vs | m3 | TR(2;2.9;6) | [17] | 3 | Mean |
| AEs | m3/m3min | TR(0.00833;0.0167;0.0250) | [17] | 0.0167 | Mean |
| t | s | C(10) | [23] | 10 | Mean |
| φ | - | C(6) | [18] | 6 | Mean |
| d | mm | TR(,5;1;1.5) | [18] | 1 | Mean |
| Tws | K | TR(308;318;323) | [17] | 318 | Mean |
| Ta | K | C(293) | [17] | 293 | Mean |
| Cw,A | mg/L | LN(0.00829;0.00426) | [17] | 0.101 | Safeguard |
| Cw,B | mg/L | LN(0.00267;0.00133) | [17] | 0.00284 | Safeguard |
| Cw,B | mg/L | LN(0.00491;0.00237) | [17] | 0.00545 | Safeguard |
| SFo,A | kg d/mg | C(0.6) | [24], [16] | 0.6 | Safeguard |
| SFo,B | kg d/mg | C(0.052) | [24], [16] | 0.052 | Safeguard |
| SFo,C | kg d/mg | C(0.011) | [24], [16] | 0.011 | Safeguard |
| SFi,A | kg d/mg | C(0.175) | [24], [16] | 0.175 | Safeguard |
| SFi,B | kg d/mg | C(0.00203) | [24], [16] | 0.00203 | Safeguard |
| SFi,C | kg d/mg | C(0.006) | [24], [16] | 0.006 | Safeguard |
| HA | atm m3/mol | TR(0.0359;0.0491;0.0556) | [25] | 0.04913 | Mean |
| HB | atm m3/mol | TR(0.0280; 0.0427;0.0589) | [25] | 0.04271 | Mean |
| HC | atm m3/mol | TR(0.0163; 0.0245; 0.0334) | [25] | 0.02446 | Mean |
| klCO2 | cm/h | C(20) | [18] | 20 | Mean |
| kgH2O | cm/h | C(3000) | [18] | 3000 | Mean |
| MWA | kg/kmol | C(96.94) | 96.94 | Mean | |
| MWB | kg/kmol | C(165.82) | 165.82 | Mean | |
| MWC | kg/kmol | C(131.38) | 131.38 | Mean | |
| MWCO2 | kg/kmol | C(44) | 44 | Mean | |
| MWH2O | kg/kmol | C(18) | 18 | Mean | |
| R | atm m3/mol K | C(0.0000821) | 0.0000821 | Mean | |
To implement RME risk evaluation a reasonable value must be stated for each independent variable on the basis of an approximate reasoning about the role of the variable. The more the model is complex, the less it is possible to arrange a believable reasoning about all the variables. Generally, the 95th percentile, the mode, the median, or the mean are considered as reasonable values.(19)
EPA(19) suggests values for BW, ED, EFw, AT, SFo, and SFi for RME. The RME value for contaminants concentration may be stated at the 95th percentile of the statistical distribution.(19) Smith suggested, without any explicit justification, RME values lower than the 95th percentile and greater than the mean for IRw, IRa, Cw, and RME values and equal to the mean for AEs, SD, Vs, EFs, d, FRws, and Tws. No suggestions are available for the other variables, mean values were stated as RME values according to the approach reported by Smith.(17) Nevertheless, caution would suggest a safeguard value greater than the mean for FRws and Tws. RME values and type are reported in Table II.
To implement Monte Carlo risk evaluation, a statistical distribution must be stated for each independent variable. Distribution may account for the sole variability (as it was considered by Smith(17)) or to the total uncertainty about the true value of the variable. This article deals mainly with variability because of a lack of information on the other sources of uncertainty. The statistical distributions used in this article to account for variability are the same as those used by Smith(17) and they are listed in Table II.
To implement GUM procedure a representative value and an uncertainty must be stated for each independent variable. The uncertainty u(x) of each variable must be evaluated from all the information available on the estimation of their values x using Type A or Type B evaluation of standard uncertainty.(14) All kinds of information may be used to implement a Type B evaluation of uncertainty. At least an expert evaluation about the way by which the representative value is calculated, estimated, or measured, and an expert evaluation about the possible variability of the representative value should be expressed.
Table III reports the equations used to calculate the representative value and the uncertainty from statistical distribution parameters. GUM(26) and the new development in metrology(31) do not give any indication to treat lognormal distribution. Because of the properties of the asymmetric distributions, the median was chosen as a representative value of lognormal distribution(27) and σL of lognormal distribution was chosen as relative uncertainty.
| Distribution | Constant | Uniform | Triangular | Normal | Lognormal* |
|---|---|---|---|---|---|
| Acronym | C(K) | U(h; L) | TR(h; mo; L) | N(M, SD) | LN(M;SD) |
| Value x | x = m = K | x = M = m = (h+l)/2 | 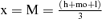 |
x = M = m =μN | 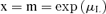 |
| Uncertainty u(x) | u = 0 | 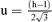 |
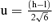 |
u =σN | 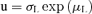 |
| X95 | K | 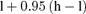 |
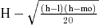 |
M + z95SD | 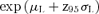 |
| Confidence of a threshold XT | 0 for XT<K | 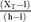 |
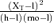 |
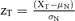 |
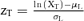 |
| 1 for XT>K | 0 for XT<l | 0 for XT<l | |||
| 1 for XT>h | 1 for XT>h | ||||
| Special properties | 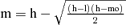 |
μN= M | 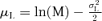 |
||
| σN= SD | 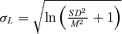 |
||||
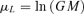 |
|||||
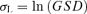 |
- Parameters of distribution: z95= 1.645; M = mean; m = median; SD = standard deviation; GM = geometric mean; GSD = geometric standard deviation; h = highest value; l = lowest value; mo = mode = highest frequency value.
- *Not treated by GUM.
Tables IV, V, and VI list the representative values and the standard uncertainty for all the independent variables for RME, variability, and total uncertainty, respectively.
3. RESULTS
GUM(14) procedures can consider more than one term of Taylor's series to account for high nonlinearity. For correlated variables the GUM(14) introduces the correlation coefficients that account for correlations.
Moreover, in the standard framework of GUM(14) one has reason to assume that the PDF for the measurand is a Gaussian; this is based on a central limit theorem and valid for models with many independent input quantities and under some assumptions for the uncertainties associated with those input quantities. GUM procedures are well tested for symmetric distributions of variables; the central limit theorem helps when few asymmetric distributions are considered.(14)
The present model of risk (Equation (8)) is surely nonlinear, many variables are correlated at least for dependence upon temperature, and most of the variables have highly asymmetric distributions (Table II).
As a first approximation, nonlinearity and correlations are neglected, yet GUM gives the instruments to overcome these approximations if the results will show that they cannot be performed. Gaussian distribution cannot be considered for risk because the asymmetry of distribution of most of the variables, i.e., the central limit theorem, cannot help in this case. Moreover, Monte Carlo simulations show clearly that the distribution is asymmetric;(17) hence, the lognormal distribution was chosen for risk as the simplest asymmetric distribution. The choices about uncertainty evaluation must be checked, keeping in mind that the uncertainty coming from the imperfect modeling of the definition of risk is not considered here, and thus it is not important to have highly accurate results.
3.1. Uncertainty of Deterministic Estimation
RME of SFo, SFi, EFw, EFs, and ED are safeguard values; they are affected by uncertainty due to caution. RME is a mean value for the other variables. Deeper information about the estimation of RME values is not available; thus some assumption must be stated in order to evaluate uncertainty.
RME safeguard values may be considered the 95th percentile of probability distribution of the variable considered.(17) Moreover, a PDF has to be assumed; the uniform distribution is the simplest one. Similar reasoning may apply to Cw and AT.
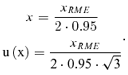 (13)
(13)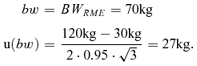 (14)
(14)If different information is available about RME values estimation, a different set of values may be calculated, but a negligible difference is expected. Similar reasoning applies to all the variables. Table IV shows the results of uncertainty estimation for RME.
By means of the equations in Table III, mean and standard deviation can be calculated from the value and the uncertainty; a lognormal distribution LN(1.53 10−3; 4.78 10−3) describes the distribution of risk. Risk results are lower than RME at 95% confidence, greater than 10−6 at 99.992% confidence, and lower than 10−4 at 16% confidence.
For the symmetric distributions mode, median and mean have the same value, but for the asymmetric distributions (as lognormal) mode, median, and mean have different values and each of them may be considered representative of the value of the risk; mean was chosen to report the results as the most representative value in the contest of risk analysis.
In the GUM procedure, one expects usually that the PDF for the output quantity tends to be a Gaussian; in this case, the coverage factor can be read off tables, and is 1.96 for a coverage probability of 0.95; this is rounded to 2.0. Nevertheless, GUM suggests to choose other values for specific applications (as for strong asymmetric distributions). In the present case, in order to reach the 95% confidence, the cover factor k was stated at 6.0. Risk estimation result may be reported(14) as r= 1.5 10−3+ 4.4 10−3. Criticism is higher than 10% for 12 variables (reported in bold in Table IV); these variables have importance in determining uncertainty. It is important to underline that only substance A (1,1 dichloroethene) has a role in determining uncertainty.
3.2. Uncertainty of Statistical Estimation
3.2.1. Variability
To evaluate variability of risk, representative value and standard uncertainty were calculated for each variable by the equations reported in Table III; the budget of variability is reported in Table V. The sole information about variability was used, so only the variability of risk is analyzed.
Henry's law constant depends on water temperature; the variability due to temperature variability was considered.
No information is considered about the way by which distributions were determined; this source of uncertainty was thus neglected.
A deeper analysis should be addressed to those variables that criticism is greater than 10% because their variability affects variability of risk. No further information is necessary for the other variables. The three variables with criticism greater than 10% (ED, IRa, CwA) are reported in bold in Table V.
A lognormal distribution was stated for risk. Mean and standard deviation can be calculated from the value r and the uncertainty u(r), the lognormal distribution LN(1.15 10−3; 2.45 10−3) results for risk. Risk is lower than RME at 97% confidence, greater than 10−6 at 99.992% confidence, and lower than 10−4 at almost 11% confidence. The 95th percentile is R95= 5.90 10−3.
Following the same procedure described in the previous section for RME, cover factor k was stated at 4.77 to reach 95% confidence and the risk estimation result may be reported(14) as r= 1.2 10−3+ 3.1 10−3.
3.2.2. Total Uncertainty
To evaluate total uncertainty of risk, information about the various sources of uncertainty is introduced.
Many statistical distributions are available for body weight;(1,17,21,28–30) median and 95th percentile value of distributions show a spread of about 10% while variability ranges from 14–25%. Thus, if no specific data about a target are available, 10% could be added to variability in order to consider uncertainty coming from the lack of knowledge about the body weight of the target.
The mass transfer coefficient in gas (kg) and liquid (kl) phases depends on fluid dynamics and its measurement is difficult and imprecise; a standard relative uncertainty of 50% was introduced. Similar reasoning is introduced for the shape factor of drop (φ) and falling time of drops (t); 20% uncertainty was introduced for φ and t.
Henry's law constant depends on temperature by a two parameter exponential relationship. Several pairs of parameters are available from the literature(25,31) for each substance. As a result, a 100% relative standard uncertainty was introduced for Henry's law constant.
It is difficult to evaluate air water temperature in a shower because it depends on water temperature and on the point of measurement; 20% of uncertainty is introduced to consider this lack of knowledge. The budget of uncertainty is reported in Table VI.
The information introduced to account for total uncertainty increases uncertainty by about 4% with respect to variability.
ED, BW, IRa, and CwA are the sole variables with a criticism greater than 10%; their uncertainty mainly affects uncertainty of risk. Henry's law constants do not contribute to uncertainty due to their 100% relative uncertainty. The nine variables with criticism greater than 1% are reported in bold in Table VI.
Mean and standard deviation of the stated lognormal distribution can be calculated from the value r and the uncertainty u(r); a lognormal distribution LN(1.19 10−3; 2.62 10−3) results for risk. As it is reported in Table VII, risk is lower than RME at 97% confidence, greater than 10−6 at 99.992% confidence, and lower than 10−4 at almost 12% confidence. The 95th percentile is R95= 4.37 10−3.
| Substance | A + B + C | A | B | C |
|---|---|---|---|---|
| Mean | 1.19E–3 | 1.18E–3 | 7.60E–7 | 2.81E–6 |
| SD | 2.62E–3 | 2.62E–3 | 1.31E–6 | 5.26E–6 |
| Median | 4.90E–04 | 4.89E–04 | 3.84E–07 | 1.32E–06 |
| Standard uncertainty (u) | 6.52E–04 | 6.50E–04 | 4.50E–07 | 1.63E–06 |
| Relative standard uncertainty | 133% | 133% | 117% | 123% |
| R95 | 4.37E–03 | 4.36E–03 | 2.64E–06 | 9.97E–06 |
| RME | 6.11E–03 | 6.10E–03 | 3.19E–06 | 1.08E–05 |
| Confidence R<10−6 | 0.0076% | 0.0076% | 79.3% | 40.9% |
| Confidence R<10−4 | 11.6% | 11.7% | 99.992% | 99.98% |
| Confidence R<RME | 97.1% | 97.1% | 99.992% | 99.992% |
| k | 4.88 | 4.9 | 4.18 | 4.4 |
| Expanded uncertainty (U) | 3.18E–3 | 3.19E–3 | 2.00E–6 | 7.00E–6 |
- A = 1,1 dichloroethene; B = trichloroethene; C = tetrachloroethene.
Following the same procedure described in the previous section for RME, cover factor k was stated at 4.9 to reach 95% confidence and the risk estimation result may be reported(14) as r= 1.2 10−3+ 3.2 10−3.
Risk evaluation for each substance is reported in Table VII. 1,1 Dichloroethene is the main substance responsible for risk. Thrichloroethene and tetrachloroethene represent a risk lower than 10−6 at 40–80% of confidence and lower than 10−4 at 99.992% of confidence. Risk is equally split between ingestion and inhalation. A water treatment before water use was considered for the reduction of risk;(17) the result of risk and uncertainty analysis indicates that water treatment must be designed for 1,1 dichloroethene as a key component. The target of water treatment should be to reduce the level of confidence of the 10−6 threshold under 95%.
3.3. Comparison: GUM vs. Monte Carlo
Figs. 1 and 2 show cumulative distribution function and probability density function, respectively, calculated by both the GUM procedure and Monte Carlo simulation.
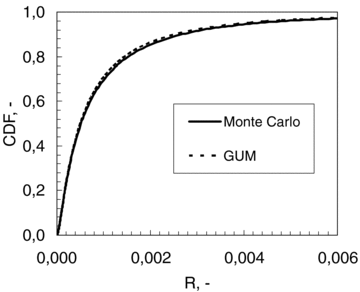
Monte Carlo and GUM cumulative density functions comparison.
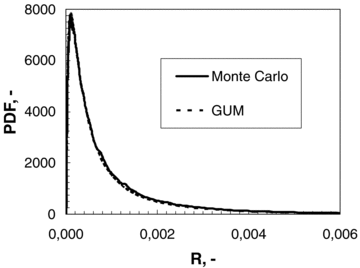
Monte Carlo and GUM probability density functions comparison.
The GUM procedure results, stating a lognormal distribution for risk, show a good fitting of Monte Carlo simulation results. The difference between 95th percentiles of risk is lower than 10%, while the difference between medians is lower than 2%. GUM gives the lowest values, but owing the large uncertainty the values of Monte Carlo and GUM may be considered the same value.
The nonlinearity of the risk model does not invalidate the applicability of a first-order Taylor series approximation. Nevertheless, if fitting is not good for strong nonlinearity in the model, the second-order Taylor series approximation may be used for approximation. Also, the approximation of neglecting correlation between variables does not affect results. Nevertheless, GUM suggests the way to overcome this kind of trouble.
This comparison confirms the validity of the choice of lognormal distribution for risk.
4. CONCLUSIONS
GUM procedure was applied to risk evaluation that considers three contaminants occurring by two exposure routes. Uncertainty of risk evaluation was quantified and the contribution of variables to uncertainty was ranked. Deterministic, statistic, and heuristic approaches to uncertainty assessment were evaluated and discussed. The model has 37 independent variables and embeds exponential functions; it considers three substances and two exposure routes. Model and data were retrieved from the paper that is widely considered as the main reference for Monte Carlo simulation.(17)
The contribution of variability to total uncertainty was considered as advised by EPA.(16)
GUM procedure can manage different kinds of information in order to have a quantitative evaluation of risk and its uncertainty. GUM procedures can couple deterministic, statistical, and heuristic approaches in order to obtain a total uncertainty value, which accounts for the main sources of uncertainty and variability. Moreover, when the distribution of a variable is not known it is possible to use all the available information to calculate the best estimate and uncertainty, avoiding further assumptions that have no meaning.
The result of the application of GUM procedures is the distribution of risk in an analytical form. It is then possible to easily and analytically calculate the level of confidence of all thresholds that are interesting for risk analysis.
The proposed procedure is easy and straightforward and the use of a simple spreadsheet program is enough to implement the algorithm; a little experience with spreadsheet programs is enough to implement the procedure. A simple table is sufficient to implement the complete procedure calculations, i.e., the budget of uncertainty, where all calculations are expressed.
GUM procedure does not have any adjusting parameter such as number of iterations, sampling technique, number, and width of intervals.
GUM procedures are widely used and accepted by different scientific and technical communities in order to evaluate uncertainty.
The calculation provided by an analytical system of algebraic equations is straightforward. Reverse calculations are simple due to the analytical form of applied equations; it enables, in principle, inverse calculations of a threshold of concentration of a carcinogen from a threshold of risk, e.g., 10−6, and a level of confidence of the threshold, e.g., 95%.
The budget of uncertainty helps in understanding which variable contributes most to the uncertainty, as requested by EPA.(12) Criticism gives a tool to judge the direct information managing the possibility of neglecting deeper insight about a variable; it helps in addressing uncertainty evaluation and reduction.
In this article, the comparison of GUM procedure and Monte Carlo approach sustains the applicability of the first-order Taylor's series approximation to the tested model of risk, albeit the model is much more complex than the simple model previously tested.(5) A balanced effect of approximations may be the cause of the result. Nevertheless, the simplicity of GUM procedures, the great information coming from the budget of uncertainty, and the possibility of reverse calculation of uncertainty suggest to apply GUM when the results are comparable with the Monte Carlo simulation.
RME value was confirmed to be over the 95th percentile of statistical distribution of risk for each substance (see Table VII).
Concerning the case study considered in this article, i.e., the risk to develop a cancer as a consequence of daily ingestion of 1,1 dichloroethene, trichloroethene, and tetrachloroethene contained in water, the result is that the presence of contaminants is a hazard and water must be treated before it is used. The main contaminant of concern is 1,1 dichloroethene, for which variation of concentration is more affecting risk variation.
The comparison of risk analysis with quantification of uncertainty (Table VII) indicates 1,1 dichloroethene as the key component on which remediation of water plan or water treatment before use must be designed.
The above consideration puts in evidence the strong role of uncertainty analysis in risk dominion as technology driver to select the more appropriate process and to design remediation process and plant. Target concentration of 1,1 dichloroethene for water treatment should be chosen in order to reduce the level of confidence of the 10−6 threshold under 95%.
5. SYMBOLS
- AEs
Air exchange rate in shower
- AT
Averaging time
- BW
Adult male body weight
- C(K)
Constant distribution
- c(x)
Sensitivity coefficienti of variable X calculated at x
- c2(x)u2(x)
Quadratic term of variable X calculated at x
- Ca
Concentration of contaminant in air
- CDF
Cumulative density function
- CF(Tws)
Correction factor for water viscosity
- C
w
Concentration of contaminant in water
- d
Diameter of drops
- ED
Adult exposure duration
- EFs
Exposure frequency for showering
- EF
w
Exposure frequency for drinking water
- FR
ws
Water flow rate
- GM
Geometric mean
- GSD
Geometric standard deviation
- h
Highest value
- H
Henry's law constant
- IRa
Adult air inhalation rate
- IR
w
Adult water ingestion rate
- KaL
Overall mass transfer coefficient
- kg
Gas phase mass transfer coefficient
- kl
Liquid phase mass transfer coefficient
- l
Lowest value
- LN(M;SD)
Lognormal distribution
- M
Mean
- m
Median
- mo
Mode, i.e., highest frequency value
- MW
Molecular weight
- N(M, SD)
Normal distribution
- PDF
Probability density function
- R
Risk
- R
Ideal gas constant
- RME
Reasonable maximum exposure
- SD
Standard deviation
- SDs
Shower duration
- SFi
Inhalation slope factor
- SFo
Oral slope factor
- t
Falling time of drops
- Ta
Air temperature
- TR(h; mo; l)
Triangular distribution
- TVo
Oral toxicity value (SF for carcinogenic)
- T
ws
Water temperature in shower
- U(h; l)
Uniform distribution
- u(x)
Standard uncertainty of variable X calculated at x
- u(x)/x
Relative standard uncertainty of variable X calculated at x
- Vs
Shower volume
- X
Variable
- [X]
Units of variable X
- x
Value of variable X
- XT
Threshold value
- z95
z score of normal distribution for 95 percentile = 1.645
- zT
z score of threshold value (values of z score and CDF for normal distribution are tabled)
- φ
Sphericity of drops
- μL
Scale parameter of lognormal distribution
- μN
Scale parameter of normal distribution
- σL
Shape parameter of lognormal distribution
- σN
Shape parameter of normal distribution.




