A Simulation Study of Quantitative Risk Assessment for Bivariate Continuous Outcomes
Department of Biostatistics, Harvard School of Public Health, Boston, MA, USA.
Department of Biostatistics and Computational Biology, Dana-Farber Cancer Institute, Boston, MA, USA.
Abstract
The neurotoxic effects of chemical agents are often investigated in controlled studies on rodents, with binary and continuous multiple endpoints routinely collected. One goal is to conduct quantitative risk assessment to determine safe dose levels. Yu and Catalano (2005) describe a method for quantitative risk assessment for bivariate continuous outcomes by extending a univariate method of percentile regression. The model is likelihood based and allows for separate dose-response models for each outcome while accounting for the bivariate correlation. The approach to benchmark dose (BMD) estimation is analogous to that for quantal data without having to specify arbitrary cutoff values. In this article, we evaluate the behavior of the BMD relative to background rates, sample size, level of bivariate correlation, dose-response trend, and distributional assumptions. Using simulations, we explore the effects of these factors on the resulting BMD and BMDL distributions. In addition, we illustrate our method with data from a neurotoxicity study of parathion exposure in rats.
1. INTRODUCTION
In toxicology studies, both binary and continuous endpoints are routinely collected. Analyzing such endpoints is an important part of risk assessment in order to find a safe dose level of exposure. Because exposures tend to affect multiple outcomes simultaneously, risk assessment procedures should account for all of the adverse events at once. While methods for quantitative risk assessment of multiple binary and even mixed outcomes have been explored, those for multiple continuous outcomes are not as widely developed.
Yu and Catalano (2005) propose a method for modeling and quantitative risk assessment via benchmark dose (BMD) estimation for bivariate continuous outcomes in dose-response studies. The purpose here is to study the properties of that approach via simulations. Motivation stems from neurotoxicology studies that assess the effects of a chemical agent on the structure and function of the nervous system. In addition, topical literature advocates risk assessment for joint as well as individual outcomes, as there may be greater overall sensitivity or ability to detect generalized effects by looking at more than one outcome (Ryan, 1992). Such studies routinely collect multiple endpoints, and risk assessment for the correlated continuous endpoints is of interest.
To estimate dose-response parameters and bivariate correlation, assume the responses (or transformations of them) are distributed bivariate normal and use likelihood-based methods for estimation. Quantitative risk assessment is accomplished by choosing two cutoffs, one for each outcome, such that the area as defined by the cutoffs defines the area of adversity. This area of adversity equals a prespecified background rate. Because the cutoffs are functions of parameters from the dose-response model, they are treated as variable rather than fixed, as in previous methods for risk assessment methods for a single continuous outcome. This background percentage then determines a BMD. One may find a lower bound on the BMD (BMDL) using a variety of methods.
In formulating this method, the authors identified several issues deserving further attention. These issues are the basis for the simulations in this article. Analogous to the issues of cutoffs to use for defining adversity are the related issues of appropriate background percentiles for risk assessment and effects of varying background rates on resulting BMD distributions. We also sought to examine the following effects on the resulting BMD distributions: sample size, level of bivariate correlation, misspecification of dose-response trend (i.e., linear versus quadratic trend), and misspecification of distribution in the parametric normal model.
Another area of interest is the method of BMDL calculation. Several advantages to the BMDL based on a likelihood-ratio method may exist over a BMDL based on the delta method (Chen & Kodell, 1989). Delta-method confidence limits may produce negative values (Crump & Howe, 1985), while the likelihood-ratio method tends to maintain better coverage and restricts the lower bound within the range of doses. For each simulation scenario, we calculated both types of BMDLs to evaluate their behaviors.
Our data come from an evaluation of the effects of parathion in rats from a study sponsored by the World Health Organization and the International Programme on Chemical Safety (Moser, 1997). One type of study in laboratory animals is the Functional Observable Battery (FOB), a series of tests where roughly 30 measures of sensory, motor, and autonomic function are collected on each animal. Each test may be grouped into a domain of neurological function (autonomic, convulsive, neuromuscular, sensorimotor, central nervous system (CNS) excitability, and CNS activity domains) (Moser, 1997). Dosing may be acute or chronic, with 8–10 rats per dose group and five dose groups. Two continuous responses of particular interest in the neuromuscular domain are the forelimb and hindlimb grip strengths. We use these outcomes in our example.
Section 2 reviews the method for modeling and risk assessment for two continuous bivariate outcomes. Section 3 provides a data example of the method for both the bivariate and the univariate settings on a neurotoxicity study of parathion in rats. Section 4 describes the procedures and parameters selected for the simulation study, with results reported in Section 5. A discussion follows in Section 6.
2. METHODOLOGY FOR CONTINUOUS BIVARIATE OUTCOMES
For N independent individuals, let F and H denote continuous forelimb grip strength and hindlimb grip strength, respectively, of the bivariate response.
2.1. Dose-Response Modeling
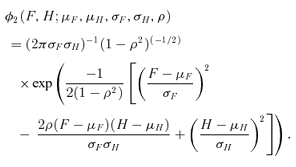
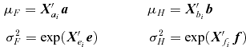
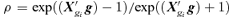
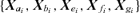 are all N×pa, N×pb, N×pe, N×pf, N×pg matrices of covariates corresponding to parameter vectors {a, b, e, f, g}, respectively. In controlled dose-response studies,
are all N×pa, N×pb, N×pe, N×pf, N×pg matrices of covariates corresponding to parameter vectors {a, b, e, f, g}, respectively. In controlled dose-response studies,  often will be simply {[1 d], …, [1 d]}, where d is the N× 1 vector of doses or some transformation of the dose metric.
often will be simply {[1 d], …, [1 d]}, where d is the N× 1 vector of doses or some transformation of the dose metric.The method of maximum likelihood allows straightforward estimation of parameters. The score equations are obtained by taking the derivatives of the log likelihood of the above bivariate distribution. The final regression parameter estimates are easily obtained using a quasi-Newton algorithm. We used the nlminb function in Splus for this purpose.
2.2. BMD Calculations
While quantitative risk assessment for bivariate data could proceed by finding BMDs for each univariate outcome separately using the above model, a joint BMD may be preferred. Topical literature has emphasized the importance of considering multiple outcomes when assessing risk (Ryan, 1992). A BMD calculated from joint risk may encompass greater overall sensitivity than computing BMDs from each individual outcome alone. One method of joint risk assessment for two outcomes, as described in Regan and Catalano (1999a, 1999b), is to consider separate fixed cutpoints for adversity for each of the two responses, and to define the probability of an adverse outcome using those cutpoints according to the methods just described.
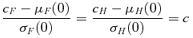
An illustration of bivariate dose response and risk assessment. Shaded areas indicate the area of adversity for each dose as defined by the cutoffs cF and cH, where P(F < cF or H < cH) equals a prespecified background rate, u.
The determination of c was best kept as a direct analogy to the univariate case. In general, the probability of the union of two events is greater than that of each marginal event; the corresponding adjustments to the cutoffs to adjust the overall probability of adversity result in the definition of c. The notion of a percentile in a bivariate distribution usually refers to contours, which contain a certain percentage of the probability under the bivariate normal surface. However, the lower probabilities defined as such are not consistent with the definitions of adversity in the univariate setting; adverse forelimb strength and adverse hindlimb strength in our example (for example “low” forelimb strength and “low” hindlimb strength) are lower tail values in the respective univariate distributions. For a bivariate distribution, the same or similar values are located on the extreme right and bottom sides of the distribution, as indicated by the shaded regions in Fig. 1.
 (1)
(1)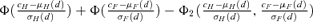 . For the control group at d= 0, the probability of an adverse outcome reduces to 2Φ(c) −Φ2(c). Note that c is dependent only upon ρ(0), the correlation in unexposed subjects, and the selected value of u. In our example, P(d) is the probability of either low forelimb strength or low hindlimb strength at dose d.
. For the control group at d= 0, the probability of an adverse outcome reduces to 2Φ(c) −Φ2(c). Note that c is dependent only upon ρ(0), the correlation in unexposed subjects, and the selected value of u. In our example, P(d) is the probability of either low forelimb strength or low hindlimb strength at dose d.The risk function, r(d), may be written as r(d) =P(d) −P(0) for additional risk, or 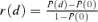 for extra risk. The
for extra risk. The 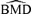 is the dose satisfying
is the dose satisfying 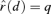 , where P(0) =u.
, where P(0) =u.
Fig. 1 illustrates a bivariate dose response. Each oval represents a contour of a three-dimensional bivariate normal surface at the respective mean response and correlation ρ. The mean responses decrease with dose while the correlation increases with dose, as shown by the “narrowing” of each contour with increasing dose. Shaded areas generally represent the region of adversity defined by the cutoffs cF and cH; note that the region of adversity includes points beyond the contour's boundary, as adversity is defined by the cutoff values (dotted lines). For a 5% background risk and a 5% additional risk, for example, the BMD is the dose where this area of adversity equals 0.10.
We present the case for two positively correlated outcomes where adversity is defined by decreasing values. When adversity is defined by increasing levels—for example, lead levels in blood—the region(s) of adversity and calculation(s) for risk would differ accordingly.
2.3. Lower Limit Calculations
A 95% lower bound on the BMD based on asymptotic normality using the delta method is 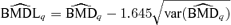 , where
, where 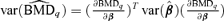 and β={a, b, e, f, g} is the vector of dose-response parameters. Because the BMDq is obtained numerically,
and β={a, b, e, f, g} is the vector of dose-response parameters. Because the BMDq is obtained numerically, 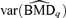 may be more conveniently obtained as
may be more conveniently obtained as 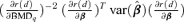 . Since
. Since 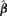 contains the estimated parameters used to calculate the cutoffs cF and cH, the BMDL calculation accounts for the variability of the background percentage. This feature is an advantage over the alternative of using a fixed cutoff or estimating the cutpoint but not taking the estimate into account in the BMDL, as in previous methods.
contains the estimated parameters used to calculate the cutoffs cF and cH, the BMDL calculation accounts for the variability of the background percentage. This feature is an advantage over the alternative of using a fixed cutoff or estimating the cutpoint but not taking the estimate into account in the BMDL, as in previous methods.
Crump and Howe (1985) point out that confidence limits based on the delta method may possess certain drawbacks such as negative values or failure to maintain nominal coverage. An alternative, more attractive approach is to construct a confidence interval based on the asymptotic distribution of the likelihood-ratio statistic (Chen & Kodell, 1989). Using this method, a BMDL is determined by finding alternative estimates of the parameters 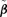 that satisfy r(d) =q, minimizing the BMD, and are subject to the constraint of
that satisfy r(d) =q, minimizing the BMD, and are subject to the constraint of 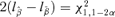 . The method is implemented by modifying a Nelder-Mead simplex algorithm to incorporate the constraint. Although more computationally intensive, the advantages of the likelihood-ratio method make its use preferable to the delta method. The confidence limits are invariant under parameter transformations and maintain better nominal coverage. Its limitation is that it requires a likelihood. While one could use GEE methods, for example, for estimation if a likelihood were not present or did not have justification, calculations for a corresponding, non-delta method BMDL are not straightforward.
. The method is implemented by modifying a Nelder-Mead simplex algorithm to incorporate the constraint. Although more computationally intensive, the advantages of the likelihood-ratio method make its use preferable to the delta method. The confidence limits are invariant under parameter transformations and maintain better nominal coverage. Its limitation is that it requires a likelihood. While one could use GEE methods, for example, for estimation if a likelihood were not present or did not have justification, calculations for a corresponding, non-delta method BMDL are not straightforward.
3. EXAMPLE
3.1. Parathion Data
Our example comes from a study evaluating the effects of parathion in rats sponsored by the World Health Organization and the International Programme on Chemical Safety (Moser, Tilson, & MacPhail, 1997). Parathion, a neurotoxic agent used as an insecticide, inhibits cholinesterase, an enzyme that is necessary for proper functioning of the nervous system in humans. For this example, we focus on the neuromuscular outcomes of forelimb and hindlimb grip strength.
As for typical neurotoxicity studies examining acute effects, the measurements for this study were taken at baseline, time of expected peak effect, one day, and one week. We are interested primarily in the responses at the time of peak effect. The data are pooled from seven different labs conducting the same experimental protocol. All laboratories had a single control group and four dosed groups, where each lab separately determined the maximum tolerated dose (MTD) from which it chose the three other lower doses. Thus, the dosed groups differed between labs. To control for intraanimal and interlab variability, we consider percent change in grip strength from baseline by subtracting the response at baseline from the response at time of peak effect, dividing by the baseline measurement, and multiplying by 100. Table I displays a summary of grip strength changes from baseline by dose group.
| Dose (mg/kg) | Mice (N) | Forelimb | Hindlimb | ||
|---|---|---|---|---|---|
| Mean | SD | Mean | SD | ||
| 0 | 74 | 11.7 | 22.8 | 1.0 | 21.3 |
| 0.38 | 8 | 12.3 | 19.5 | 24.0 | 19.2 |
| 0.56 | 17 | 4.2 | 22.8 | −4.8 | 14.3 |
| 0.60 | 10 | 1.8 | 5.6 | −0.7 | 4.7 |
| 0.75 | 8 | 11.3 | 24.8 | −7.3 | 18.2 |
| 0.84 | 18 | 9.2 | 33.0 | 0.1 | 27.5 |
| 0.85 | 10 | 9.0 | 15.8 | 0.1 | 25.1 |
| 1.10 | 18 | 1.9 | 6.1 | −0.3 | 5.7 |
| 1.13 | 10 | 5.4 | 11.6 | 2.9 | 16.3 |
| 1.27 | 10 | 19.5 | 19.5 | 1.3 | 15.7 |
| 1.50 | 8 | 14.0 | 28.0 | 4.0 | 16.4 |
| 1.69 | 28 | 9.0 | 27.6 | −0.1 | 24.2 |
| 2.25 | 9 | 4.4 | 9.4 | −7.0 | 10.8 |
| 2.30 | 18 | 2.1 | 4.6 | 1.6 | 9.3 |
| 2.53 | 10 | 4.4 | 16.3 | −1.3 | 13.5 |
| 3.00 | 8 | −2.3 | 16.0 | −26.5 | 18.8 |
| 3.38 | 28 | 2.9 | 22.6 | −3.9 | 22.3 |
| 4.50 | 26 | −6.4 | 26.3 | −15.3 | 18.0 |
| 5.07 | 10 | 0.9 | 17.8 | 7.7 | 22.2 |
| 6.75 | 22 | −27.1 | 34.4 | −15.8 | 23.0 |
| 10.13 | 6 | −25.6 | 41.6 | −33.5 | 14.2 |
- Units for grip strengths are in kilograms-to-release (percent changes from baseline).
3.2. Dose-Response Modeling
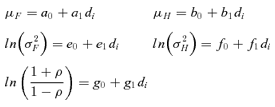
| Model Parameter | Estimate | Standard Error | Z |
|---|---|---|---|
| Forelimb grip strength mean (μF) | |||
| Intercept | 12.3 | 1.59 | 7.7 |
| Dose | −0.041 | 0.64 | −6.4 |
| Hindlimb grip strength mean (μH) | |||
| Intercept | 2.73 | 1.46 | 1.9 |
| Dose | −2.75 | 0.50 | −5.5 |
| Forelimb grip strength SD (ln (σF)) | |||
| Intercept | 6.02 | 0.099 | 60.9 |
| Dose | 0.101 | 0.031 | 3.2 |
| Hindlimb grip strength SD (ln (σH)) | |||
| Intercept | 5.96 | 0.104 | 57.6 |
| Dose | 0.014 | 0.035 | 0.4 |
Bivariate correlation 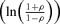 |
|||
| Intercept | 0.194 | 0.140 | 1.4 |
| Dose | 0.021 | 0.045 | 0.5 |
3.3. Quantitative Risk Assessment
We used our methods to compute bivariate BMDs for 5% and 10% additional risks at different background rates of 1%, 5%, and 10%. BMDLs were computed using the delta method and the likelihood-ratio approach (Table III).
| Background Rate | Univariate Forelimb | Univariate Hindlimb | Bivariate | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BMD | BMDL (dm) | BMDL (lr) | BMD | BMDL (dm) | BMDL (lr) | BMD | BMDL (dm) | BMDL (lr) | ||
| 5% | 1% | 2.68 | 2.10 | 2.12 | 5.04 | 3.11 | 3.46 | 2.94 | 2.38 | 2.37 |
| additional | 5% | 1.34 | 1.05 | 1.06 | 2.41 | 1.56 | 1.70 | 1.46 | 1.18 | 1.18 |
| risk | 10% | 0.95 | 0.75 | 0.76 | 1.65 | 1.11 | 1.19 | 1.01 | 0.82 | 0.82 |
| 10% | 1% | 4.04 | 3.17 | 3.20 | 7.30 | 4.75 | 5.14 | 4.31 | 3.50 | 3.49 |
| additional | 5% | 2.35 | 1.84 | 1.87 | 4.09 | 2.74 | 2.93 | 2.48 | 2.02 | 2.02 |
| risk | 10% | 1.77 | 1.39 | 1.41 | 2.99 | 2.05 | 2.18 | 1.84 | 1.49 | 1.50 |
- lr = likelihood ratio method.
- Units are in mg/kg.
- BMDLs are 95% lower bounds.
To define the joint probability of an adverse effect (large negative change in forelimb or hindlimb grip strength), we specify a background rate from which to derive cutoffs. For example, an overall background rate of 5% defines the cutoffs for percent changes in forelimb and hindlimb grip strength as −27 and −36, respectively, where the area below these cutoffs in the bivariate distribution equals 5%. Those values in the area defined by percent changes in forelimb grip strength that are less than −27 or percent changes in hindlimb grip strength less than −36 are adverse. The corresponding value of  is −1.95, with a marginal probability of 0.026 for each outcome; the estimated correlation in controls is approximately 0.1. The cutoffs for each outcome vary if we choose different background rates. For example, at 1%, the cutoffs are (−40, −48) with
is −1.95, with a marginal probability of 0.026 for each outcome; the estimated correlation in controls is approximately 0.1. The cutoffs for each outcome vary if we choose different background rates. For example, at 1%, the cutoffs are (−40, −48) with 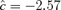 and marginal probabilities of 0.0051; at 10%, the cutoffs are (−21, −29) with
and marginal probabilities of 0.0051; at 10%, the cutoffs are (−21, −29) with 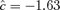 and marginal probabilities of 0.052.
and marginal probabilities of 0.052.
While the region of adversity is 100u% of the modeled bivariate surface, the actual percentage of points in the area of adversity is dependent on the fit of the model. A rough goodness-of-fit test may be implemented by finding the percentage of points lying in the modeled region of adversity. For our example, using a nominal 5% background rate, 6.8% of the actual points lie in the area of adversity as defined by our model. For a 10% background rate, 12.2% of the points lie in the adverse area; for a 1% background rate, none of the points lie in the adverse area. The simulations and discussion further address issues of appropriate background rates.
Continuing with our illustration using a 5% additional risk (r(d) = 0.05), we may estimate a BMD05. We specified the risk of an adverse effect in the control group to be 5%, which we denote as Pu(0) = 0.05. The dose satisfying the equation r(d) =Pv(d) −Pu(0) is Pv(d) = 0.10. As reported in Column 9 of Table III, this dose is the 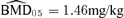 . The corresponding BMDL 05 values based on the delta method (dm) and likelihood-ratio (lr) methods are equal, 1.18 mg/kg.
. The corresponding BMDL 05 values based on the delta method (dm) and likelihood-ratio (lr) methods are equal, 1.18 mg/kg.
We wish to compare the bivariate results to the univariate cases by computing separate BMDs and 95% BMDLs for changes in forelimb and hindlimb strengths. To do so, we fit linear mean percentile regression dose-response models for both outcomes, allowing the variances for each outcome to vary linearly by dose to account for possible heterogeneity.
As for the bivariate case, we computed univariate BMDs for 5% and 10% additional risks, at background rates of 1%, 5%, and 10% for both outcomes. Fig. 2 depicts an additional risk BMD05 with background percentile of 5%. For changes in forelimb grip strength, the 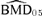 is 1.34 mg/kg with BMDL 05(dm) = 1.05 mg/kg and BMDL 05(lr) = 1.06. The results for changes in hindlimb grip strength are
is 1.34 mg/kg with BMDL 05(dm) = 1.05 mg/kg and BMDL 05(lr) = 1.06. The results for changes in hindlimb grip strength are 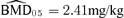 with BMDL 05(dm) = 1.56 mg/kg and BMDL 05(lr) = 1.70 mg/kg (Table III).
with BMDL 05(dm) = 1.56 mg/kg and BMDL 05(lr) = 1.70 mg/kg (Table III).
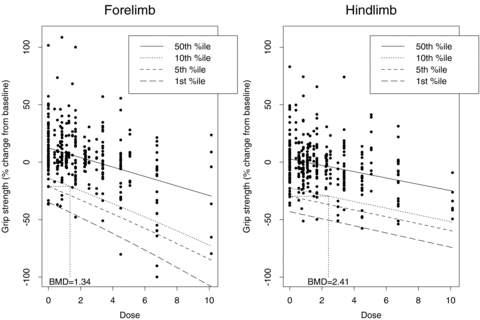
Percentile regression curves for 1%, 5%, 10%, and 50% for percent change from baseline for forelimb grip strength and hindlimb grip strength. Each plot indicates an additional BMD0.05 using a 5% background rate for each outcome.
The bivariate  fall between the two univariate
fall between the two univariate  but are closest to the more conservative univariate
but are closest to the more conservative univariate  (in this case, the forelimb grip strength change
(in this case, the forelimb grip strength change  ). This result is consistent with the explanation in Yu and Catalano (2005) for a bivariate BMD calculated with a jointly defined background rate as described.
). This result is consistent with the explanation in Yu and Catalano (2005) for a bivariate BMD calculated with a jointly defined background rate as described.
4. SIMULATION STUDY PROCEDURES
Our simulation focuses on the properties of the bivariate method. Each simulation scenario uses 1,000 BMDs and corresponding BMDLs computed from ni= 10, 20, or 50 bivariate samples at each dose group (total N= 40, 80, or 200), with a single control group and three dosed groups set arbitrarily at d= 10, 20, 30. At each dose, we generated ni bivariate normal observations about means corresponding to a dose-response model with specified intercept, slope, and variances. We modeled the bivariate correlation ρ as constant at values of ρ= 0 or ρ= 0.35 and as varying by dose at equally spaced values from 0.2 to 0.65. The background percent also varied; we used 1%, 5%, and 10% to reflect background rates typically used in bioassays where BMDs are of interest to compute. True BMDs were calculated under all possible simulation scenarios. For a linear assumption, we used a dose-response model with intercept (2, 2), slope (−0.05, −0.05), and constant variance (1, 1).
To examine the same properties for a quadratic trend, we generated bivariate normal observations as described above about means corresponding to a quadratic dose-response model with intercept (2, 2), dose coefficients (−0.078, −0.078), and quadratic coefficients (0.0013, 0.0013). To examine model misspecification, we modeled the quadratic data under (1) a linear assumption with the original four groups and (2) using only the first three dose groups to see how the curvature affects the BMD. Because of our choice of sampling distributions for both linear and quadratic trends (Fig. 3), the first three groups of the quadratic trend have means that are similar to the linear trend. The last dose group is considerably different and thus defines the curvature of quadratic dose-response trend. By eliminating the last dose group and fitting a linear trend to the remaining three groups (a common practice among dose-response modelers when the highest dose appears different from the rest of the study), we may examine the degree to which the curvature affects the BMD.
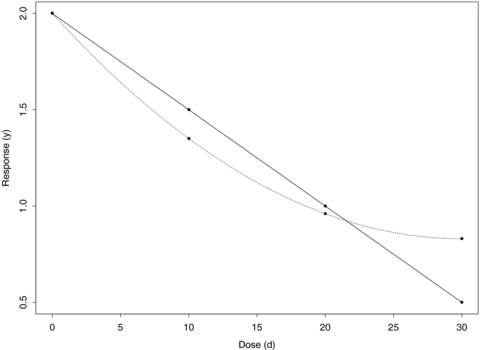
An illustration of the dose-response trends used in the simulations. For the linear trend, y= 2 − 0.05d; for the quadratic trend, y= 2 − 0.078d+ 0.0013d2. The main difference is in the last dose group, which provides the curvature in the quadratic trend.
To examine misspecification of the underlying distribution, we generated data from a bivariate lognormal distribution and analyzed them under the normality assumption. The purpose was to keep similar distributions and bivariate correlations at each dose but generate a skewed rather than a symmetric distribution about each mean. We chose this distribution because dose-response data often appear lognormal.
We used ni= 10 and 20 per dose group to reflect the sample sizes occurring in typical noncancer animal studies and used ni= 50 to examine properties resulting from a larger sample size. The choice of dose-response parameters for both linear and quadratic trends reflect good study design where the true BMD lies near the first dose. For decreasing dose-response trends, the BMD is smaller with increasing background rates; therefore, we designed the simulation study such that the BMD lies near the first dose at the 1% background rate. The quadratic trend chosen is similar to the linear trend; the main difference is the response in the last dose group, which provides the curvature in the quadratic trend (Fig. 3).
We calculate two types of 95% lower confidence bounds on the BMD: one is based on the delta method, denoted BMDL(dm); the other, on the likelihood-ratio statistic, denoted BMDL(lr). We evaluate the behavior of the BMDLs for each scenario by comparing them to the empirical 5% of the 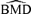 distribution and by computing coverage probabilities. We define the coverage probability as the proportion of BMDLs lying at or below the true BMD, which is calculated from the true underlying parameters used for sampling.
distribution and by computing coverage probabilities. We define the coverage probability as the proportion of BMDLs lying at or below the true BMD, which is calculated from the true underlying parameters used for sampling.
5. SIMULATION RESULTS
5.1. Linear Normal Results
Table IV presents summary statistics for estimated BMD and BMDL distributions of generated normal linear data and linear fit for true ρ= 0. Corresponding results for ρ= 0.35 and dose-varying ρ appear in Tables V and VI, respectively.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 14.02 | 13.74 | 13.15 | 3.28 | 9.5 | 7.91 | 7.92 | 1.00 | 1 | 10.05 | 9.76 | 1.83 | 0.972 |
| 20 | 13.79 | 13.57 | 2.18 | 10.76 | 9.75 | 9.68 | 1.09 | 1 | 11.00 | 10.85 | 1.42 | 0.968 | ||
| 50 | 13.93 | 13.79 | 1.42 | 11.89 | 11.37 | 11.28 | 0.98 | 0.958 | 12.02 | 11.93 | 1.07 | 0.958 | ||
| 5% | 10 | 6.45 | 6.44 | 6.13 | 1.60 | 4.44 | 3.81 | 3.81 | 0.47 | 1 | 4.71 | 4.56 | 0.86 | 0.967 |
| 20 | 6.40 | 6.28 | 1.02 | 4.97 | 4.61 | 4.58 | 0.51 | 1 | 5.11 | 5.05 | 0.66 | 0.962 | ||
| 50 | 6.67 | 6.48 | 0.66 | 5.48 | 5.30 | 5.26 | 0.45 | 0.984 | 5.55 | 5.51 | 0.50 | 0.953 | ||
| 10% | 10 | 4.28 | 4.30 | 4.09 | 1.08 | 2.95 | 2.66 | 2.66 | 0.33 | 1 | 3.14 | 3.05 | 0.57 | 0.964 |
| 20 | 4.26 | 4.18 | 0.68 | 3.30 | 3.15 | 3.14 | 0.34 | 0.998 | 3.40 | 3.36 | 0.44 | 0.961 | ||
| 50 | 4.27 | 4.22 | 0.44 | 3.64 | 3.58 | 3.55 | 0.30 | 0.979 | 3.69 | 3.65 | 0.33 | 0.951 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 14.32 | 14.35 | 13.52 | 4.02 | 9.37 | 7.47 | 7.64 | 1.41 | 1 | 10.08 | 9.77 | 2.11 | 0.969 |
| 20‡ | 14.23 | 13.84 | 2.67 | 10.67 | 9.62 | 9.58 | 1.08 | 1 | 11.01 | 10.83 | 1.60 | 0.965 | ||
| 50 | 14.29 | 14.08 | 1.70 | 11.96 | 11.40 | 11.29 | 1.08 | 0.984 | 12.08 | 11.95 | 1.22 | 0.951 | ||
| 5% | 10‡ | 6.67 | 6.81 | 6.36 | 0.66 | 4.38 | 3.62 | 3.73 | 1.01 | 1 | 4.74 | 4.59 | 0.98 | 0.963 |
| 20 | 6.67 | 6.48 | 1.27 | 4.97 | 4.60 | 4.58 | 0.51 | 1 | 5.16 | 5.07 | 0.76 | 0.961 | ||
| 50 | 6.67 | 6.58 | 0.80 | 5.58 | 5.39 | 5.34 | 0.51 | 0.983 | 5.64 | 5.57 | 0.57 | 0.951 | ||
| 10% | 10 | 4.47 | 4.58 | 4.27 | 1.46 | 2.95 | 2.51 | 2.59 | 0.72 | 1 | 3.18 | 3.07 | 0.66 | 0.962 |
| 20 | 4.48 | 4.35 | 0.85 | 3.33 | 3.15 | 3.14 | 0.35 | 1 | 3.46 | 3.40 | 0.51 | 0.961 | ||
| 50 | 4.47 | 4.41 | 0.54 | 3.74 | 3.65 | 3.62 | 0.34 | 0.98 | 3.78 | 3.74 | 0.39 | 0.951 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 14.58 | 14.84 | 13.83 | 4.45 | 9.37 | 7.15 | 7.43 | 1.69 | 1 | 10.23 | 9.78 | 2.37 | 0.960 |
| 20‡ | 14.61 | 14.13 | 2.95 | 10.71 | 9.55 | 9.53 | 1.07 | 1 | 11.13 | 10.93 | 1.71 | 0.966 | ||
| 50 | 14.62 | 14.34 | 1.88 | 12.08 | 11.48 | 11.37 | 1.15 | 0.985 | 12.24 | 12.08 | 1.32 | 0.949 | ||
| 5% | 10 | 6.78 | 7.04 | 6.47 | 2.48 | 4.37 | 3.39 | 3.56 | 1.22 | 1 | 4.78 | 4.58 | 1.05 | 0.958 |
| 20 | 6.83 | 6.59 | 1.41 | 5.00 | 4.54 | 4.52 | 0.51 | 1 | 5.19 | 5.09 | 0.81 | 0.961 | ||
| 50 | 6.82 | 6.69 | 0.89 | 5.63 | 5.40 | 5.34 | 0.54 | 0.982 | 5.70 | 5.62 | 0.62 | 0.947 | ||
| 10% | 10 | 4.56 | 4.76 | 4.37 | 1.72 | 2.91 | 2.32 | 4.54 | 0.99 | 1 | 3.21 | 3.07 | 0.72 | 0.955 |
| 20 | 4.61 | 4.44 | 0.97 | 3.37 | 3.10 | 3.10 | 0.35 | 1 | 3.49 | 3.41 | 0.55 | 0.956 | ||
| 50 | 4.59 | 4.51 | 0.61 | 3.79 | 3.67 | 3.63 | 0.37 | 0.979 | 3.83 | 3.78 | 0.42 | 0.946 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
In general, the 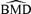 distributions are affected in similar ways by increasing sample size and background rate: they become tighter over all independent and correlated simulation scenarios, the mean and median of the
distributions are affected in similar ways by increasing sample size and background rate: they become tighter over all independent and correlated simulation scenarios, the mean and median of the 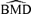 distributions grow closer to the true BMD, and the true BMD itself becomes smaller and closer to zero. For example, at ρ= 0.35, at background rates of 1%, 5%, and 10%, the true BMDs are 14.32, 6.67, and 4.47, respectively.
distributions grow closer to the true BMD, and the true BMD itself becomes smaller and closer to zero. For example, at ρ= 0.35, at background rates of 1%, 5%, and 10%, the true BMDs are 14.32, 6.67, and 4.47, respectively.
These general trends are similar for ρ= 0 and for dose-varying ρ. In particular, 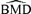 distributions at the 1% background rate tend to be wider than those at the 5% and 10% background rates. The high variability is apparent when viewing density plots of the
distributions at the 1% background rate tend to be wider than those at the 5% and 10% background rates. The high variability is apparent when viewing density plots of the  distributions (Fig. 4), where a vertical line indicates the true BMD for a specific scenario. An interesting feature on plots 4d and 4g, where the background rate is 1% and ni= 10, is a small “spike” at the maximum dose of 30. The reason for the spike, which indicates greater spread, is that our algorithm for computing the BMD limits the
distributions (Fig. 4), where a vertical line indicates the true BMD for a specific scenario. An interesting feature on plots 4d and 4g, where the background rate is 1% and ni= 10, is a small “spike” at the maximum dose of 30. The reason for the spike, which indicates greater spread, is that our algorithm for computing the BMD limits the  to the given range of doses in the study. If the estimated BMD numerically exceeds the last dose, the algorithm sets it equal to the maximum dose; a consequence is that the means of the simulated distributions are less meaningful. This “bumping up” against the maximum dose disappears with increasing sample size and background percentile because both factors decrease the variability of the distribution.
to the given range of doses in the study. If the estimated BMD numerically exceeds the last dose, the algorithm sets it equal to the maximum dose; a consequence is that the means of the simulated distributions are less meaningful. This “bumping up” against the maximum dose disappears with increasing sample size and background percentile because both factors decrease the variability of the distribution.
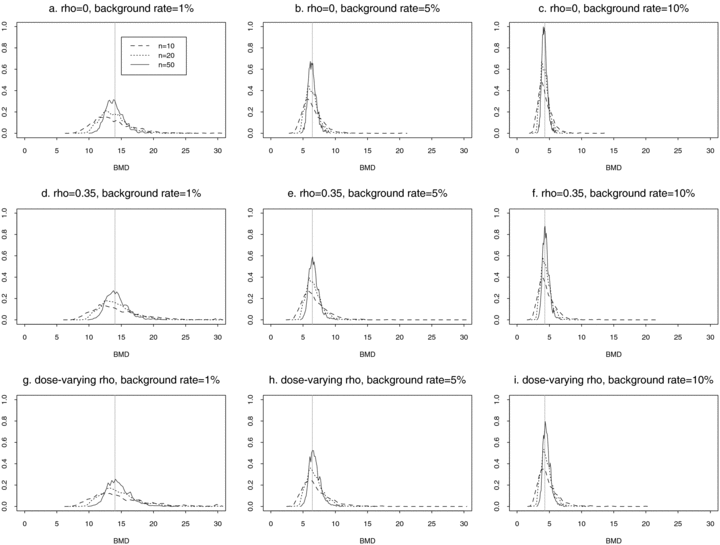
 distributions for data generated from normal distributions with linear dose-response trends and fit with a linear dose response. Vertical lines represent the true BMD.
distributions for data generated from normal distributions with linear dose-response trends and fit with a linear dose response. Vertical lines represent the true BMD.
As expected, increasing the bivariate correlation results in slightly larger BMDs. A heuristic argument is that less correlated outcomes are “more independent” and result in lower, more conservative BMDs to protect against both outcomes.
Fig. 5 displays boxplots of the estimated BMD, BMDL(dm), and BMDL(lr) distributions for two scenarios. A horizontal line represents the value of the true BMD. Both graphs are for dose-varying ρ and 10% background rate, but the sample sizes per group differ. The results are typical for the different scenarios in the simulation. The BMDL(dm) boxplot for ni= 10 in Fig. 5a displays the known tendency of BMDLs computed using the delta method to produce negative values, while the BMDL(lr) distribution remains within the range of doses. As expected, the problem is less severe as the sample size increases above 10 animals per dose (Fig. 5b). However, it indicates that in general the delta method may not be as reliable as the likelihood-based method for finding a BMDL. In general, BMDLs based on the delta method are more variable and also have poor coverage.
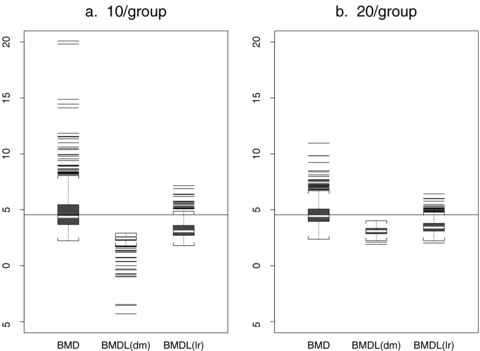
Estimated  , BMDL(dm), and BMDL(lr) distributions for dose-varying ρ and 10% background rate. The data are generated from normal distributions with linear dose-response trends and fit with a linear dose response. A horizontal line represents the true BMD.
, BMDL(dm), and BMDL(lr) distributions for dose-varying ρ and 10% background rate. The data are generated from normal distributions with linear dose-response trends and fit with a linear dose response. A horizontal line represents the true BMD.
Coverage probabilities indicate that the BMDL(dm) is extremely conservative, especially at the smaller background rates of 1% and 5%. Across all scenarios, the coverage probabilities for BMDL(dm) are wider than those for BMDL(lr). With increasing sample size, the BMDL(dm) grows closer to a 95% coverage probability, but the BMDL(lr) universally has coverage closer to the nominal 95%. In addition, the empirical 5% of the  distribution is closer to the median of the BMDL distribution with increasing sample size and background rate (Tables IV–VI). The differences for BMDL(dm) are generally higher while corresponding differences of BMDL(lr) are fairly consistent.
distribution is closer to the median of the BMDL distribution with increasing sample size and background rate (Tables IV–VI). The differences for BMDL(dm) are generally higher while corresponding differences of BMDL(lr) are fairly consistent.
The differences, especially over the three background rates, further suggest that the delta method is less adequate than the likelihood-based method for calculating the BMDL. The information also indicates that both higher sample sizes and background rates greater than 1% are more reliable for calculating the BMDL and that the BMDL(lr) is preferable over the BMDL(dm). Such results are especially interesting given that the data follow a normal distribution.
5.2. Quadratic Normal Results
Since dose-response trends often possess some degree of curvature, we examine the properties of the BMD for a quadratic dose-response trend. We generated quadratic data and looked at two main cases: one in which the model fit is quadratic and the other in which the model fit is misspecified as linear.
To examine the properties of the BMD for a true quadratic trend and quadratic fit, we generated bivariate normal observations about means corresponding to a quadratic dose-response model with intercept (2, 2), dose coefficients (−0.078, −0.078), and quadratic coefficients (0.0013, 0.0013). As stated above, this quadratic trend was chosen to be similar to the linear trend. The exception is in the last dose group, where the response chosen provides an obvious departure from linearity (Fig. 3). Tables VII–IX summarize statistics for estimated BMD and BMDL distributions of generated normal quadratic data and quadratic fit.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 11 | 10.98 | 9.33 | 5.55 | 5.12 | 1.23 | 2.48 | 14.25 | 0.977 | 6.04 | 5.49 | 2.59 | 0.966 |
| 20‡ | 10.93 | 9.93 | 3.92 | 6.32 | 4.31 | 4.20 | 5.70 | 0.983 | 6.94 | 6.51 | 1.90 | 0.966 | ||
| 50 | 10.97 | 10.67 | 2.47 | 7.65 | 6.82 | 6.65 | 1.15 | 0.993 | 8.10 | 7.96 | 1.48 | 0.956 | ||
| 5% | 10‡ | 4.46 | 4.94 | 4.00 | 3.08 | 2.26 | 0.47 | 1.17 | 4.88 | 0.997 | 2.64 | 2.41 | 0.92 | 0.952 |
| 20 | 4.66 | 4.17 | 1.81 | 2.74 | 1.89 | 1.91 | 0.35 | 0.999 | 2.98 | 2.80 | 0.77 | 0.951 | ||
| 50 | 4.53 | 4.37 | 1.00 | 3.24 | 2.89 | 2.88 | 0.35 | 0.999 | 3.39 | 3.32 | 0.58 | 0.945 | ||
| 10% | 10‡ | 2.88 | 3.34 | 2.62 | 2.25 | 1.49 | 0.19 | 0.80 | 1.88 | 1 | 1.73 | 1.57 | 0.61 | 0.945 |
| 20 | 3.07 | 2.72 | 1.26 | 1.79 | 1.20 | 1.28 | 0.34 | 1 | 1.94 | 1.82 | 0.50 | 0.947 | ||
| 50 | 2.94 | 2.83 | 0.66 | 2.11 | 1.89 | 1.89 | 0.21 | 1 | 2.19 | 2.14 | 0.37 | 0.944 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 11.31 | 11.91 | 9.73 | 6.51 | 4.99 | −0.40 | 2.10 | 24.11 | 0.961 | 6.43 | 5.59 | 3.57 | 0.947 |
| 20‡ | 11.66 | 10.37 | 4.83 | 6.19 | 3.64 | 3.74 | 9.06 | 0.971 | 7.17 | 6.58 | 2.50 | 0.944 | ||
| 50‡ | 11.49 | 11.01 | 3.12 | 7.59 | 6.39 | 6.26 | 4.27 | 0.989 | 8.25 | 7.98 | 1.76 | 0.934 | ||
| 5% | 10‡ | 4.63 | 5.55 | 4.20 | 4.07 | 2.20 | −0.04 | 0.89 | 5.90 | 0.986 | 2.77 | 2.41 | 1.47 | 0.933 |
| 20‡ | 5.04 | 4.36 | 2.38 | 2.68 | 1.54 | 1.70 | 0.87 | 0.997 | 3.06 | 2.84 | 0.95 | 0.940 | ||
| 50 | 4.77 | 4.54 | 1.26 | 3.22 | 2.76 | 2.76 | 0.31 | 0.999 | 3.45 | 3.36 | 0.70 | 0.940 | ||
| 10% | 10‡ | 3.01 | 3.89 | 2.77 | 3.47 | 1.45 | −0.54 | 0.58 | 7.88 | 0.995 | 1.81 | 1.57 | 0.83 | 0.926 |
| 20 | 3.36 | 2.86 | 1.74 | 1.76 | 0.90 | 1.14 | 0.69 | 0.999 | 2.00 | 1.84 | 0.62 | 0.938 | ||
| 50 | 3.12 | 2.97 | 0.84 | 2.1 | 1.81 | 1.83 | 0.17 | 1 | 2.25 | 2.19 | 0.44 | 0.933 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
| Background Rate | N per Dose | BMD | Empirical 5% | BMDL(dm) | BMDL(lr) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True | Mean | Median | SD | Mean | Median | SD | C.P.† | Mean | Median | SD | C.P.† | |||
| 1% | 10‡ | 11.47 | 11.63 | 9.46 | 6.69 | 4.86 | −4.88 | 1.45 | 57.08 | 0.980 | 6.57 | 5.54 | 3.99 | 0.941 |
| 20‡ | 11.97 | 10.06 | 5.88 | 6.11 | −2.05 | 3.00 | 66.93 | 0.982 | 7.47 | 6.59 | 3.55 | 0.925 | ||
| 50‡ | 11.73 | 10.87 | 3.78 | 7.49 | 4.47 | 5.14 | 6.40 | 0.997 | 8.40 | 7.99 | 2.17 | 0.929 | ||
| 5% | 10‡ | 4.66 | 5.53 | 4.17 | 4.17 | 2.2 | −0.85 | 0.64 | 8.28 | 0.993 | 2.90 | 2.46 | 1.91 | 0.919 |
| 20‡ | 5.13 | 4.37 | 2.70 | 2.68 | 0.93 | 1.51 | 2.55 | 1 | 3.14 | 2.87 | 1.09 | 0.918 | ||
| 50 | 4.81 | 4.54 | 1.31 | 3.2 | 2.52 | 2.54 | 0.26 | 1 | 3.51 | 3.39 | 0.73 | 0.933 | ||
| 10% | 10‡ | 3.04 | 3.95 | 2.77 | 3.70 | 1.45 | −1.03 | 0.42 | 8.31 | 0.995 | 1.95 | 1.63 | 1.40 | 0.912 |
| 20‡ | 3.46 | 2.89 | 2.11 | 1.79 | 0.57 | 1.03 | 1.29 | 1 | 2.07 | 1.91 | 0.69 | 0.919 | ||
| 50 | 3.16 | 2.98 | 0.88 | 2.1 | 1.69 | 1.71 | 0.15 | 1 | 2.30 | 2.22 | 0.47 | 0.927 | ||
- †Coverage probability, defined as the proportion of BMDLs lying at or below the true BMD.
- ‡Scenario where simulated BMDs exceeding the maximum dose of 30 were set as equal to the maximum dose.
The general trends for the effects of sample size and background rate on the BMD are similar to those from the normal linear results. The  distributions are more variable at lower sample sizes and background rates and become tighter as both of these factors increase. Generally, the variability is higher for each scenario than for the corresponding linear trend scenario. The results are likely due to the sampling and estimation variability from the addition of a quadratic term. Similar to the linear trend results, the 1% background rate is inadequate for BMD estimation. The BMDs at the 1% background rate are highly variable for all specified values of ρ, with noticeable spikes at the maximum dose of 30, even for ni = 50.
distributions are more variable at lower sample sizes and background rates and become tighter as both of these factors increase. Generally, the variability is higher for each scenario than for the corresponding linear trend scenario. The results are likely due to the sampling and estimation variability from the addition of a quadratic term. Similar to the linear trend results, the 1% background rate is inadequate for BMD estimation. The BMDs at the 1% background rate are highly variable for all specified values of ρ, with noticeable spikes at the maximum dose of 30, even for ni = 50.
The quadratic simulation results suggest that the delta method is inadequate for calculating the BMDL, based on the large percentage of negative values for the BMDL(dm) for all sample sizes at the 1% background rate and for ni= 10 and ni= 20 at the 5% and 10% background rates. Some of the means and medians for the BMDL(dm) distributions in Tables VII–IX are negative. As a result, the differences between the empirical 5% of the  distribution and the median of the BMDL(dm) distribution are much larger than those for the linear results. Coverage probabilities are close to 1 and do not grow closer to 95% with increasing sample size. As for the linear case, coverage probabilities are extremely wide for the BMDL(dm), whereas those for BMDL(lr) are much more consistent and closer to 95%; the BMDL(lr) is the preferable choice for a lower bound on the
distribution and the median of the BMDL(dm) distribution are much larger than those for the linear results. Coverage probabilities are close to 1 and do not grow closer to 95% with increasing sample size. As for the linear case, coverage probabilities are extremely wide for the BMDL(dm), whereas those for BMDL(lr) are much more consistent and closer to 95%; the BMDL(lr) is the preferable choice for a lower bound on the  .
.
Because most dose-response trends tend to have some curvature, it is valuable to examine how assumed quadratic data behave under different models. To assess possible model misspecification, we first modeled the quadratic data under a linear assumption. Fig. 6 displays distributions at true ρ= 0.35, with a horizontal line at the true BMD. The results suggest that fitting a linear trend to the generated quadratic data is not recommended because the resulting  are clearly biased away from the true BMD. The mean and median
are clearly biased away from the true BMD. The mean and median  tend to be higher than the true BMD.
tend to be higher than the true BMD.
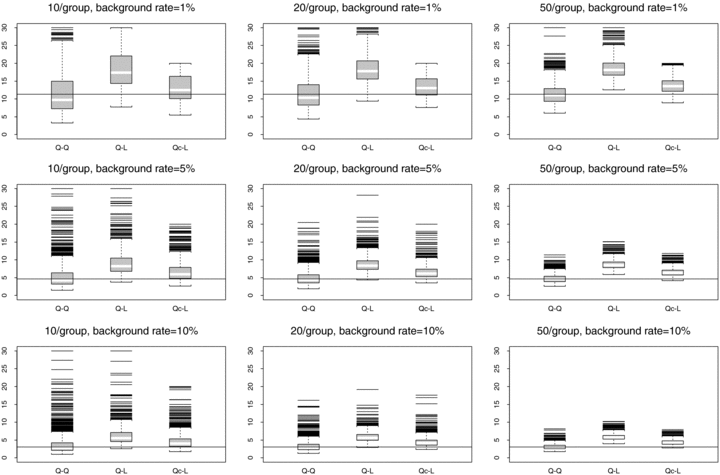
 distributions for misspecified models and true ρ= 0.35. The data are generated from normal distributions with quadratic dose-response trends. Left boxplot is fit with a quadratic trend (Q–Q), middle boxplot is fit with a linear trend (Q–L), and right boxplot is fit with a linear trend after omitting the observations from the last dose group (Qc–L). Horizontal lines represent the true BMDs.
distributions for misspecified models and true ρ= 0.35. The data are generated from normal distributions with quadratic dose-response trends. Left boxplot is fit with a quadratic trend (Q–Q), middle boxplot is fit with a linear trend (Q–L), and right boxplot is fit with a linear trend after omitting the observations from the last dose group (Qc–L). Horizontal lines represent the true BMDs.
We also examined how the curvature in the quadratic trend affects the BMD by carefully choosing sampling distributions for the linear and quadratic dose-response trends. For the quadratic trend, the choice of means for the first three doses were similar to those for the linear trend. The main difference is the last dose, where the mean response clearly defines the curvature of the quadratic dose-response trend. To see how the curvature affects the BMD, we removed the last dose of the quadratic trend and sampled only from means of the first three dose groups defined for the quadratic trend. These data are then fit with an assumed linear trend. These distributions, also shown in Fig. 6, show that there is a gain in reducing bias; the BMD estimates are considerably closer to the true BMD from generated quadratic data and quadratic fit than the mean or median 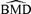 resulting from fitting a linear trend to generated quadratic data. These results show that the curvature of a nonlinear trend may greatly affect the BMD calculation and should be incorporated if possible. Fortunately, such trends are easily incorporated into dose-response models.
resulting from fitting a linear trend to generated quadratic data. These results show that the curvature of a nonlinear trend may greatly affect the BMD calculation and should be incorporated if possible. Fortunately, such trends are easily incorporated into dose-response models.
5.3. Sensitivity to Distributional Shape
The small samples typical of dose-response data may result in skewed, rather than symmetric, distributions of responses within a dose group. A way to examine the behavior of skewed distributions is to generate data from a bivariate lognormal distribution and analyze them under a normal distribution assumption.
To evaluate the sensitivity of our method to changes in distributional shape, we kept the same dose-response trends and bivariate correlations but generated a lognormal distribution about each mean. We chose means at (5, 5) to avoid distributions whose observations were primarily distributed along the x and y axes and variance parameters (2, 2) to provide a clear skewness to the distribution. The lognormal data were treated as normal for modeling and subsequent BMD calculation. Fig. 7 displays some of the simulation results for ρ= 0.35.
 distributions for misspecified distributions and true ρ= 0.35. The data are generated from lognormal distributions with linear dose-response trends and fit with a linear dose response. The assumption of normality is used to compute the
distributions for misspecified distributions and true ρ= 0.35. The data are generated from lognormal distributions with linear dose-response trends and fit with a linear dose response. The assumption of normality is used to compute the  . Thin solid vertical lines represent the true BMDs under a lognormal assumption. Dashed vertical lines represent true BMDs under a normal assumption.
. Thin solid vertical lines represent the true BMDs under a lognormal assumption. Dashed vertical lines represent true BMDs under a normal assumption.
The true BMD in this case is one for lognormally generated data calculated using a lognormal assumption. The simulations show that the resulting  , calculated under a normal assumption, are clearly biased away from the true BMD. A few of the
, calculated under a normal assumption, are clearly biased away from the true BMD. A few of the 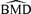 distributions at the 5% and 10% background rates do not even cover the true BMD for those scenarios.
distributions at the 5% and 10% background rates do not even cover the true BMD for those scenarios.
Misspecifying a distribution should be avoided if possible. Nonetheless, under true lognormality, a simple fix is available. Skewed data are common in bioassays, and researchers often will use a transformation of the data to make them conform to a normal distribution. In our case, taking the log of the observations corrects the problem, as seen in Fig. 8.
 distributions for log transformations of misspecified distributions and true ρ= 0.35. The data are generated from the log of the data used to create Fig. 7 and fit with linear dose-response trends. The assumption of normality is used to compute the BMD. Thin solid vertical lines represent true BMDs under a normal assumption.
distributions for log transformations of misspecified distributions and true ρ= 0.35. The data are generated from the log of the data used to create Fig. 7 and fit with linear dose-response trends. The assumption of normality is used to compute the BMD. Thin solid vertical lines represent true BMDs under a normal assumption.
6. DISCUSSION
We present a method that models two continuous bivariate outcomes and subsequently finds a BMD, where the BMD is a 100q% increase over a background rate. Calculations for lower bounds on the BMD (BMDLs) are possible through either the delta method or a likelihood-based model. Modeling the bivariate outcomes takes the bivariate correlation into account. The method is flexible as it allows variances and correlations to vary with dose. An advantage is that the definition of adversity and characterization of risk are not based on fixed and possibly arbitrary cutoffs, and the BMDL accounts for the variability of the estimated cutoff. The bivariate method presented is analogous to a univariate method using percentile regression for dose-response estimation (Yu, 2002).
One of the natural questions arising with the method is: What background rate is appropriate? From the simulations, it is clear that the 1% background rate is not precise for BMD estimation or BMDL(dm) estimation unless the sample size is quite large. The variability is large for this background rate and often results in BMDL(dm)s that are negative. The bias is also quite large when comparing the mean of the  distribution to the true BMD for any scenario with a background rate of 1%. Larger sample sizes reduced overall variability; however, even at ni= 50, the 1% background rate is not recommended.
distribution to the true BMD for any scenario with a background rate of 1%. Larger sample sizes reduced overall variability; however, even at ni= 50, the 1% background rate is not recommended.
One of the features of the combined laboratory data for our example is that each laboratory had a control group. Thus there were a substantial number of responses for defining adversity. For smaller data sets or sample sizes, fewer responses are present in the control from which to find the region of adversity. Typical neurotoxicity animal studies contain 8–10 rats per dose group and five dose groups. Unless the same experiment is conducted in different labs and the data are pooled (as for our example), one cannot realistically guarantee a larger sample size of 20 or 50 animals per group. Given the variability of the 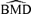 distributions at a background rate of 1%, a background rate of 5% to 10% is recommended for practical use. We note that higher background rates give slightly more conservative estimates of the BMD, a phenomenon consistent with findings from Budtz-Jørgensen, Keiding, and Grandjean (2001) for the univariate case.
distributions at a background rate of 1%, a background rate of 5% to 10% is recommended for practical use. We note that higher background rates give slightly more conservative estimates of the BMD, a phenomenon consistent with findings from Budtz-Jørgensen, Keiding, and Grandjean (2001) for the univariate case.
The simulations also confirmed another property known in the corresponding univariate procedure: that the likelihood-ratio-based BMDL is superior over the delta method BMDL for lower bound estimation. It remains within the range of doses, is based on the likelihood that is the method used for parameter estimation, maintains better coverage probability, and is less variable across all sample sizes, bivariate correlations, and background rates that were used in the simulations.
The method is not robust to model misspecification; fitting a truly quadratic trend using a linear dose response results in biased BMDs that may be nonconservative. In addition, we explored the sensitivity of our method to changes in distributional shape. To reflect bioassay data, we generated skewed rather than symmetric distributions about each mean while keeping similar bivariate correlations. We based our study on a lognormal distribution, which the method could accommodate by using a log transformation of the data. An area of future work is to explore the effects of other distributional assumptions on the method in more detail.
ACKNOWLEDGMENTS
This work was supported by Grants ES06900 and T32 ES07142-18 from the National Institute of Environmental Health Sciences and Grant CA48061 from the National Cancer Institute. The authors thank Drs. Lorenz Rhomberg, Louise Ryan, and Meredith Regan for helpful comments, and Dr. Virginia Moser at the U.S. EPA for the use of the example data.




