Phylogenetic, functional, and structural components of variation in bone growth rate of amniotes
Abstract
SUMMARY The biological features observed in every living organism are the outcome of three sets of factors: historical (inherited by homology), functional (biological adaptation), and structural (properties inherent to the materials with which organs are constructed, and the morphogenetic rules by which they grow). Integrating them should bring satisfactory causal explanations of empirical data. However, little progress has been accomplished in practice toward this goal, because a methodologically efficient tool was lacking. Here we use a new statistical method of variation partitioning to analyze bone growth in amniotes. (1) Historical component. The variation of bone growth rates contains a significant phylogenetic signal, suggesting that the observed patterns are partly the outcome of shared ancestry. (2) Functional causation. High growth rates, although energy costly, may be adaptive (i.e., they may increase survival rates) in taxa showing short growth periods (e.g., birds). In ectothermic amniotes, low resting metabolic rates may limit the maximum possible growth rates. (3) Structural constraint. Whereas soft tissues grow through a multiplicative process, growth of mineralized tissues is accretionary (additive, i.e., mineralization fronts occur only at free surfaces). Bone growth of many amniotes partially circumvents this constraint: it is achieved not only at the external surface of the bone shaft, but also within cavities included in the bone cortex as it grows centrifugally. Our approach contributes to the unification of historicism, functionalism, and structuralism toward a more integrated evolutionary biology.
INTRODUCTION
Seilacher (1970) put forward a conceptual framework (constructional morphology) to perform integrative analyses by considering that the character states observed in a given organism are the outcome of three general sets of factors: phylogenetic, adaptational, and architectural (properties inherent to the materials with which organs are constructed, and the morphogenetic rules by which they grow), which were renamed as historical, functional, and structural by Gould (2002). These sets of factors (the so-called “Seilacher's triangle”) would work together in each and every actual situation and only the integration of their influences could bring a satisfactory causal explanation of empirical data.
Nevertheless, since then, the analysis of variation of morphological characters, and the interpretation of their significance, has traditionally remained within historicism, functionalism, or structuralism (Gould 2002; Cubo 2004), taken separately, depending on each worker's emphasis and intellectual tradition (McGhee 1999). For “pure historicists” interested in the reconstruction of phylogenetic patterns, the functional adaptation to current conditions (autapomorphies) may mask a pure phylogenetic signal. For “pure functionalists,” phylogenetic patterns are constraints that may prevent organisms from reaching optimal adaptation to current conditions. Finally, “structuralists” put the accent on the self-organizing morphogenetic properties of development (Goodwin and Trainor 1980; Seilacher 1991; Kauffman 1993; Hickman 2004). These three intellectual frameworks, although useful to answer some questions, are “reality bites” which are far from a desirable integrative (holistic) approach.
Bone as a tissue has, for a long time, been an exemple of the problems raised by the exclusive use of separate sets of “explanations” (phylogenetic, functional, or structural) proposed to account for its variability. Each set has built an enormous amount of literature of its own, most often in complete separation from the other ones. This situation has been analyzed in comparative studies on bone histology (Horner et al. 2001; Padian et al. 2001; Ricqlès et al. 2001), which stressed the need for explanations in terms of a complex, multifactorial causality, in which all causal factors would be integrated. However, beyond acknowledging the complex causality of bone histodiversity, it has proved so far impossible to “sort out” the relative “weight” of the various causal factors deemed simultaneously responsible for the patterns observed.
We can wonder why Seilacher's integrative model, although intellectually satisfactory, has remained marginal in recent biological research. The answer might be that it did not provide the analytical tools necessary to perform such integrative analyses. The consequence of this is that Seilacher's framework is viewed by many “as more a heuristic concept, a working hypothesis, than a specific analytic methodology” (McGhee 1999). Here we use a new method of variation partitioning among three factors for this purpose, where the variation of bone growth rates of amniotes was partitioned among historical, functional, and structural components. This method will greatly increase the explanatory power of Seilacher's model, because it involves the extension from the qualitative analysis of the phenotypes of given organisms, to the quantitative analysis of character variation within clades.
MATERIAL AND METHODS
Biological material
This comparative study is based on 32 growing individuals belonging to 13 species of amniotes (Fig. 1). During the experiments, these specimens were maintained in controlled conditions appropriate to each species. All the procedures were carried out in accordance with the European Communities Council Directive (86/609/EEC).
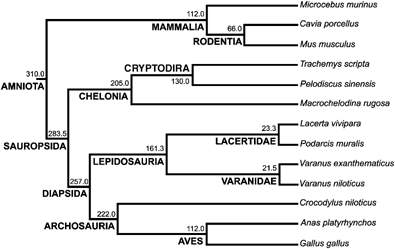
Phylogenetic relationships among the species analyzed in this study. Divergence times in millions of years and the names of the clades are given for each node. See text for the sources of the topology and divergence times.
Bone growth rate
Periosteal bone growth rate (expressed as the rate of expansion of long bone shafts during growth) was quantified using in vivo fluorescent labeling (e.g., Margerie et al. 2004) during the phase of rapid growth. Solutions corresponding to 80 mg/kg of animal fresh weight for xylenol-orange, and 40 mg/kg for fluoresceine were injected intraperitoneally to the animals at different ages. These fluorescent dyes specifically color the mineralizing zone of growing bone tissue, in deep orange for xylenol-orange, and in green for fluoresceine (Fig. 2). Animals were euthanized after a given time interval, and the left tibia was removed from each individual. It should be noted that birds have two particularities. First, tibia is fused to some tarsal elements, forming tibiotarsus. Second, some bones show pneumatization (Cubo and Casinos 2000). However, tibiae of the species used in our sample (Anas plathyrhynchos and Gallus gallus) do not show pneumatization (Margerie et al. 2005; personal observation) and are comparable to bones of the rest of species of the sample. These bones were dehydrated in graded ethanol and defatted in acetone and trichloroethylene before being embedded in a polyester resin (Matrajt et al. 1967). Transverse sections 100 ± 10 μm thick were made at the diaphyseal level using a diamond-tipped circular saw. Each thin section was ground and polished before being mounted on a slide. They were observed under fluorescent light (Zeiss Axiovert 35; Jena, Germany), and digitalized through a camera (Olympus, Japan). Bone growth rates (μm2/day) were calculated through pictorial analysis (Photoshop 7.0 on Mac OS X), using the surface either between two consecutive circular fluorescent labels or between the last label and the bone periphery, divided by the time elapsed (Fig. 2). Although we labeled animals several times, when possible we considered only the periods that corresponded to those during which the resting metabolic rates (RMRs) were measured.
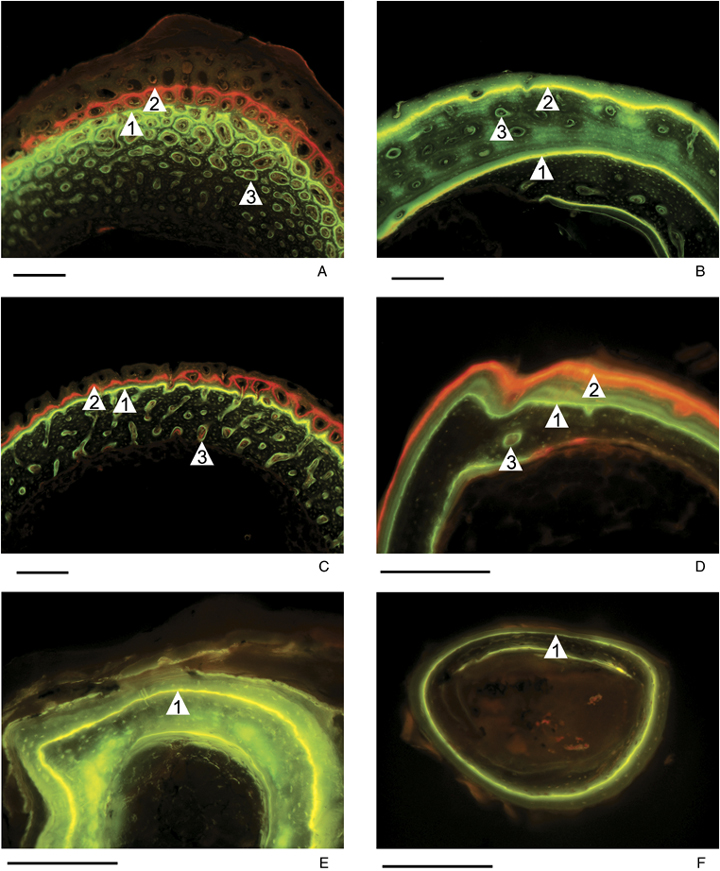
Portions of mid-shaft cross sections of the tibiae of different animals from our sample, on which fluorescent labels show the mineralizing zone of growing bone tissue at the moment of the injection. A: Anas platyrhynchos: (1) fluoresceine injection 9 days after hatching, (2) xylenol-orange injection 14 days after hatching, (3) primary osteon; B: Crocodylus niloticus: (1) fluoresceine injection 2 weeks after hatching, (2) fluoresceine injection 12 weeks after hatching, (3) primary osteon; C: Cavia porcellus: (1) fluoresceine injection 4 days after hatching, (2) xylenol-orange injection 9 days after hatching, (3) primary osteon; D: Varanus niloticus: (1) fluoresceine injection, (2) xylenol-orange injection 42 days later, (3) primary osteon; E: Pelodiscus sinensis: (1) fluoresceine injection 5 weeks after hatching; and F: Podarcis muralis: (1) fluoresceine injection. Scale bar: 200 μm.
Metabolic rate
Basal metabolic rate has been defined for adult endothermic amniotes (Daan et al. 1990). The equivalent variable for adult ectothermic amniotes is the standard metabolic rate (Lewis and Gaten 1985). In this article, we deal with growing individuals of both endothermic and ectothermic amniotes, so neither basal nor standard metabolic rates could be used. Instead, we measured the resting metabolic rate RMR, which is defined as the minimum rate of energy expenditure under postabsorptive conditions during the period of normal activity of the daily cycle (Andrews and Pough 1985). RMR was quantified as the volume of dioxygen consumed per time unit (ml O2/h) and mass-specific RMR as ml O2/h g. They were measured in endothermic species (mammals and birds) under thermoneutral conditions (in which they do not expend energy in regulating their body temperature) and in ectothermic ones (chelonians, lizards, and crocodiles) at a given typical temperature within their range of activity. The respiratory chamber was held at a controlled ambient temperature of 25 ± 0.1°C for all ectothermic species and precocial endothermic ones (birds and Cavia porcellus). For altricial endothermic species (Mus musculus and Microcebus murinus), the ambient temperature was maintained at 35 ± 0.1°C to simulate the temperature of the nest. After 30 min of acclimation under constant air flow, the chamber was closed for a duration that depended on the species. The volume of O2 consumed by each animal was calculated from initial and final concentrations of O2 in the chamber. Measurements were made using a paramagnetic gas analyzer (Analyzer 570A, Servomex Ltd., Crowborough, UK) routinely calibrated with N2 and atmospheric air assuming 21.00% O2. All individuals were deprived of food for several hours before the measurements, except young mammals that cannot be separated for a long time from their mothers. We assumed, then, that the measured RMR does not include the cost of either thermoregulation or activity (locomotion or digestion). For each species, measurements were repeated over 4 days at the same time in their daily cycle (during daytime). The values used in the comparative study are, for each species, an average of the minimal RMR measured for each individual. In order to allow comparisons among species, RMR was systematically recorded during the phase of rapid growth (see the body mass ranges in Table 1).
| Structural factorRelative perimeterof growth | Functional factorResting metabolicrate (ml/hg0.67) | Dependent variableBone growthrate (μm2/day) | Body massrange (g) | n | |
|---|---|---|---|---|---|
| Microcebus murinus | 1.687 ± 0.239 | 1.526 | 0.011472 ± 0.000344 | 7.5–24.3 | 4 |
| Cavia porcellus | 2.778 ± 0.140 | 3.477 ± 0.091 | 0.070467 ± 0.003164 | 94.0–108.0 | 3 |
| Mus musculus | 1.330 ± 0.280 | 1.696 ± 0.081 | 0.007067 ± 0.003055 | 3.9–8.2 | 3 |
| Trachemys scripta | 1.006 ± 0.011 | 0.117 ± 0.011 | 0.001316 ± 0.000121 | 13.2–18.2 | 3 |
| Pelodiscus sinensis | 1.008 ± 0.013 | 0.083 ± 0.020 | 0.001030 ± 0.000740 | 5.0–7.1 | 3 |
| Macrochelodina rugosa | 1.000 | 0.085 | 0.000131 | 27.7–30.0 | 1 |
| Lacerta vivipara | 1.000 ± 0.000 | 0.124 ± 0.061 | 0.000074 | 0.5–0.6 | 2 |
| Podarcis muralis | 1.000 ± 0.000 | 0.084 ± 0.032 | 0.000108 ± 0.000075 | 1.1–1.2 | 3 |
| Varanus exanthematicus | 1.112 | 0.173 | 0.003000 | 29.0–51.1 | 1 |
| Varanus niloticus | 1.056 | 0.157 | 0.003262 | 18.8–36.0 | 1 |
| Crocodylus niloticus | 1.853 ± 0.466 | 0.336 ± 0.250 | 0.016115 ± 0.006641 | 192.0–240.0 | 2 |
| Anas platyrhynchos | 4.962 ± 0.834 | 10.865 ± 3.668 | 0.129167 ± 0.027854 | 103.0–118.0 | 3 |
| Gallus gallus | 5.501 ± 0.925 | 8.289 ± 1.206 | 0.449150 ± 0.131542 | 80.0–94.0 | 3 |
- See “Material and Methods” for a description of these variables.
Two expressions have been proposed to correct data for the effect of body mass on the mass-specific RMR (ml O2/h g): first, the mass-independent RMR (ml O2/h gb, where “b” is the allometric exponent of raw RMR versus body mass; Withers 1992); and second, the geometry-corrected RMR (ml O2/h g0.67, where “0.67” is the allometric exponent of the ratio surface to volume versus body mass for geometrically similar organisms; Montes et al. 2007). This last correction assumes that the effect of body mass on metabolic rate is mediated by the fact that both the surface to volume ratio and the caloric loss per mass unit decrease as body mass increases (Withers 1992; White and Seymour 2005). The allometric exponent “b” of the expression corresponding to mass-independent RMR (ml O2/h gb) could not be used here because the body mass effect in our sample of growing specimens is a mixture of ontogenetic allometry and interspecific allometry. Therefore, we used the geometry-corrected RMR (ml O2/h g0.67) as an indicator of size-independent energetic expenditures by mass unit.
Surface of apposition of new bone tissue
In Lacertidae and most Chelonia of our sample, this surface corresponds to the periosteum (2, 3). In Mammalia, Varanidae, and Archosauria (crocodiles and birds), this surface corresponds to the periosteum plus the internal surface of primary osteons (2, 3). They were measured as the ratio “osteonal+peripheral_accretional_surface/peripheral_accretional_surface” to avoid a correlation between the structural factor and the dependent variable (bone growth rate) due to a size effect. These surfaces are lines (perimeters) in two-dimensional bone slides, and were quantified by using Image J (a computer program inspired by NIH Image for the Macintosh, available at http://rsb.info.nih.gov/ij/ by W. Rasband).
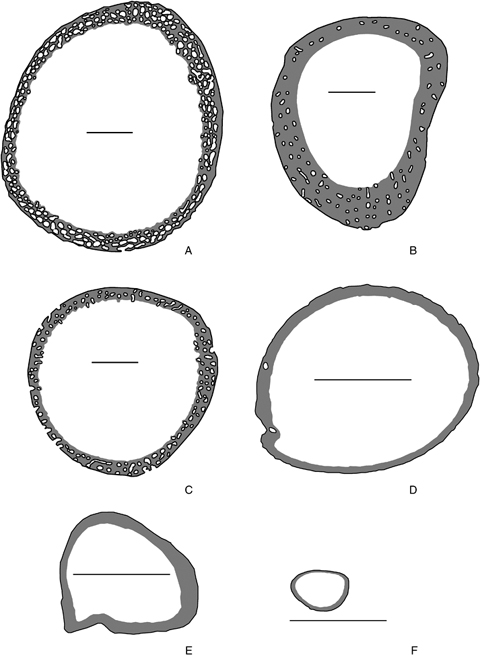
Mid-shaft cross sections of the tibiae of the same individuals as in Fig. 2 showing the bone tissue (gray) formed during the analyzed period and the surface of apposition of new bone tissue (black). These surfaces are lines in two-dimensional bone slides, and correspond to the peripheral growth only (E, F) or to the peripheral+osteonal growth (A, B, C, D). Scale bar: 500 μm.
The reference phylogeny
The phylogeny (topology and divergence times) of the 13 species of amniotes used in this study was compiled from the literature (Fig. 1). The topology for Chelonia was compiled from Gaffney and Meylan (1988). In our sample, Trachemys (Emydidae) and Pelodiscus (Trionychoidea) are sister groups, and this clade is the sister group of Macrochelodina (Pleurodira). For the squamates, the topology was compiled from Estes (1982), Estes et al. (1988), Rieppel (1988), and Caldwell (1999). Although the placement of chelonians is still controversial (Rieppel 1999; Rieppel and Reisz 1999; Zardoya and Meyer 2001), we considered them a sister-group of Diapsida, as numerous paleontological studies have argued (Laurin and Reisz 1995; Lee 2001).
The divergence time between mammals and sauropsids (310 Myr) was taken from Hedges et al. (1996) and Kumar and Hedges (1998); see Graur and Martin (2004) and Hedges and Kumar (2004) for a debate on this time estimate. Divergence time between lepidosaurs and crocodilians was taken from Reisz and Müller (2004), and those for the dichotomies between crocodiles and birds, galliformes and anseriformes, rodents and primates, and basal divergences among rodents are from Kumar and Hedges (1998).
A method of variation partitioning among three sets of explanatory variables
A method to partition the total variation of a dependent variable by two sets of explanatory variables in a phylogenetic context has previously been proposed (Desdevises et al. 2003); this, in turn, was an extension of the partitioning method proposed in ecology (Borcard et al. 1992; Borcard and Legendre 1994; Legendre and Legendre 1998). Here we use an extension of this approach where the variation of bone growth rate was partitioned among phylogenetic, functional, and structural components using a three-explanatory-matrices application. Partitioning among three sets of explanatory variables has already been used in ecology (Anderson and Gribble 1998; Cushman and McGarigal 2002; Økland 2003). However, it has been shown (Ohtani 2000) that Ezekiel's (1930) adjusted R2 (R2a) is an unbiased estimator of the real contribution of a table of explanatory variables X to the explanation of a response variable y. Peres-Neto et al. (2006) have also shown that adjusted R2a coefficients should be used in variation partitioning to obtain unbiased estimates of the fractions of variation, and Ramette and Tiedje (2007) have already used this last approach. Here we use this adjusted approach with three sets of independent variables (Fig. 4).
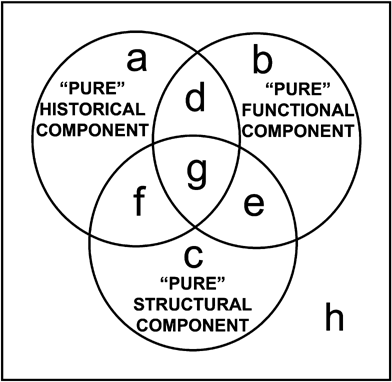
Partitioning of a dependent variable Y by three sets of independent variables (circles). The upper left circle (fraction [a+d+g+f]) is explained by phylogeny; the upper right circle (fraction [b+d+e+g]) by the functional factor; and the bottom circle (fraction [c+e+f+g]) by the structural factor. The partitioning method allows the estimation of the overlapping fractions of the variation ([d], [e], [f], [g]), as well as “pure” components ([a], [b], [c]) and the remaining unexplained variation [h].
In the present case, as described before, the three sets of variables are the phylogenetic (P), functional (F), and structural (S) components. As in Desdevises et al. (2003), variation partitioning is performed via several linear regressions followed by subtractions. Here, seven regressions are needed, where the dependent variable is sequentially regressed on P, F, S, PF (i.e., a multiple regression of the dependent variable on P and F), PS, FS, and PFS. Each of these regressions outputs a portion of the total variation of the dependent variable, via its coefficient of determination (R2). For example with P as the upper left circle (Fig. 4), R2 of the dependent variable on P is equal to [a+d+g+f]. Finally 10 subtractions are needed to quantify the fractions a–h outlined in Fig. 4, because their sum is by definition equal to 100%. The common fractions d–g cannot be tested for significance, but the others can, with the use of partial regressions. Variation partitioning and the tests of significance of the fractions were computed using the functions “varpart” and “anova.cca” from the “vegan” library (Oksanen et al. 2007) of the R statistical language (R Development Core Team 2006). All tests are performed through permutational procedures using 9999 permutations.
RESULTS
Empirical measurements of both the dependent variable (bone growth rate) and the independent variables (the explanatory factors) are shown in Table 1.
The phylogenetic (historical) component: topology and divergence times
The phylogeny of our sample of amniotes (Fig. 1) was expressed in the form of principal coordinates, the first three of which were selected by reference to a broken-stick model (Diniz-Filho et al. 1998). Variation of bone growth rate (the dependent variable) contains a significant phylogenetic signal (fraction [a+d+f+g]; P=0.0071; R2a=0.399; Table 2 and Fig. 4). However, the “pure” phylogenetic component (fraction [a]) is not significant (P=0.4511, Table 2). This means that the phylogenetic component of bone growth rate variation overlaps to a great extent (fractions [d], [f], and [g]) with the functional and structural components. In other words, most of the phylogenetic component of bone growth rate variation is linked to the two other explanatory variables, the variation of which may also have a phylogenetic structure.
| Fraction | R 2 | Adjusted Ra2 | P (9999 perm.) |
|---|---|---|---|
| [a+d+f+g] | 0.549 | 0.399 | 0.0071* |
| [b+d+e+g] | 0.569 | 0.530 | 0.0176* |
| [c+e+f+g] | 0.764 | 0.742 | 0.0001* |
| [a+b+d+e+f+g] | 0.615 | 0.422 | 0.0946 |
| [a+c+d+e+f+g] | 0.790 | 0.685 | 0.0174* |
| [b+c+d+e+f+g] | 0.869 | 0.842 | 0.0092* |
| [a+b+c+d+e+f+g] | 0.908 | 0.843 | 0.0298* |
| [a] | 0.040 | 0.0005 | 0.4511 |
| [b] | 0.118 | 0.158 | 0.0473* |
| [c] | 0.294 | 0.421 | 0.0115* |
| [d] | −0.013 | −0.057≈0 | Cannot be tested |
| [e] | −0.053 | −0.135≈0 | Cannot be tested |
| [f] | 0.006 | −0.108≈0 | Cannot be tested |
| [g] | 0.516 | 0.564 | Cannot be tested |
| [h]=resid | 0.091 | 0.157 | Cannot be tested |
- *Significant fractions.See Fig. 4 for the biological significance of each fraction.
The functional factor: RMR
Table 2 shows that this functional factor explains a significant portion of the variation of bone growth rate (fraction [b+d+e+g]; P=0.0176; R2a=0.530; Fig. 4). This relationship between the functional explanatory variable and the dependent variable is significant and positive (slope=0.027; P=0.015). This means that the higher the RMR, the greater the observed bone growth rate. This result agrees with the hypothesis according to which, considering that building new tissues at high growth rates is very energy demanding (Nagy 2000), the RMR may be a functional factor linked to bone (and overall) growth rate (Ricqlès 1978a, b). The “pure” functional component is also significant (fraction [b]; P=0.0473; R2a=0.158; Table 2 and Fig. 4).
The structural factor: relative surface of bone apposition
Bone growth is accretionary, i.e. mineralization fronts occur only at free surfaces either at the periphery of bone cortex (centrifugal growth) or at the surfaces delimitating internal cavities called osteones (centripetal growth). Thus the structural variable was defined as the ratio “osteonal+peripheral_accretional_surface”/“peripheral_accretional_surface.”Table 2 shows that this variable explains a significant portion of bone growth rate variation (fraction [c+e+f+g]; P=0.0001; R2a=0.742; Table 2 and Fig. 4). The “pure” structural component is also significant (fraction [c]; P=0.0115; R2a=0.421). The relationship between the structural explanatory variable and the dependent variable is significant and positive (slope=0.070; P<0.01). In conclusion, the greater the relative surface of apposition of new bone tissue, the higher the observed bone growth rate. These results agree with our hypothesis, according to which the accretionary mode of construction of bone tissue may be a structural factor limiting the maximum possible bone growth rate in amniotes.
DISCUSSION
As noted by Mayr (1961), biological research can be divided into two main areas that differ in method and basic concepts: whereas functional biology tries to answer “how does it work” questions and uses experimental approaches to decipher proximal causes, evolutionary biology is concerned with “how did it appear” questions, and mainly uses the comparative method to identify ultimate causes. Autumn et al. (2002) showed the advantages of combining both approaches (which they called, respectively, mechanistic, and historical biology) in the study of behavior, physiology, and development. Seilacher (1970) developed a third area (structuralism), which has its primary interest in emphasizing the properties inherent to the materials with which organs are constructed, and the morphogenetic rules by which they grow (self-organization with few genetic inputs).
Structuralist and functionalist viewpoints are rooted in pre-Darwinian times (see the excellent review by Padian 1995). Geoffroy St-Hilaire, for instance, argued in 1830 for “a pure morphology uncontaminated by functional considerations” (Hugues and Lambert 1984). Conversely, Cuvier's “conditions d'existence” clearly express the necessary adaptation of structures to functions in a given environment, but adaptation is perceived as a static “state” rather than as the outcome of a process. The advent of Darwinism introduced a historical dimension to the analysis of organic form, developed the functionalist approach, and put structuralist ways of seeing outside the mainstream of evolutionary biology. The quoted historical dimension of Darwinism concerns not only the analysis of patterns (Cuvier's concept of “type” was replaced by Darwin's concept of “last common ancestor”) but also that of process (the mechanism of natural selection involves an historical contingency component). In the last three decades, studies dealing with the analysis of the variation of morphological characters can be still classified into three traditions:
(1) Historicism: The advent of the cladistic methodology (Hennig 1966) has prompted the rise of systematics (a discipline focused on history) as one of the most active fields of morphological research. Systematists mainly use discrete characters (e.g., Mayr and Clarke 2003). We can also find historicist viewpoints in studies dealing with continuous characters. Felsenstein (1985) pointed out the statistical problems linked to the analysis of interspecific data by using standard cross-species statistical tests (as done in many allometric studies). Since then, a number of analytical methods have been devised aimed at overcoming these problems. Among all of them, independent contrasts (designed to test patterns of character covariation in a phylogenetic context) is the most popular and frequently used in comparative studies. This method can be classified in the “historicist pool” because, according to Westoby et al. (1995), it “allocates the maximum possible variation in a trait to phylogeny (i.e., fraction [a+d+f+g] in Fig. 4), considering only the residual as potentially attributable to ecology” (in our case, attributable to function: fraction [b+e] in Fig. 4). In summary, the method of independent contrasts corrects for the phylogenetic nonindependence of interspecific data values, but it cannot discriminate or quantify pure phylogenetic inertia from the part related to other factors. In contrast, the method used in this article properly quantifies all these fractions: pure functional, pure phylogenetic, and their overlap (phylogenetically structured functional variation, Cubo et al. 2005).
(2) Structuralism: Constructional morphologists follow the approach proposed by Seilacher (1970) and consider that morphological similarity is not only the outcome of shared ancestry (homology), or the outcome of similar responses to selection pressure (homoplasy), but also the outcome of shared fabricational mechanisms (Hickman 2004). They assume that intrinsic generative mechanisms may produce given phenotypes. It is often evoked that these mechanisms have, like crystal growth, the property of self-organization, and that they are under weaker biological (genetic) than direct physicochemical control. This approach has been mainly used in paleontology to analyze discrete characters (e.g., Seilacher and Hauff 2004). However, we think that an analytical quantitative, statistical approach of this view was missing. As noted above, structuralism is “more a heuristic concept than a specific analytic methodology” (McGhee 1999). Our method allows for the first time a precise (statistical) quantification of the structural component of character variation.
(3) Functionalism: Functional morphologists assume that there is a direct link between morphology and function. For them, characters are molded by natural selection to perform particular functions. Many functional morphologists have used the paradigm methodology proposed by Rudwick (1964) to find evidence for the adaptive significance of organic form. First, they postulate several functions for the structure under analysis. Afterwards, they determine the optimal mechanical design for each function (the paradigm). Finally, the paradigm design that most closely matches the original morphological structure is considered to be evidence for the actual function of this structure.
Although some functional morphologists have recognized the importance of considering history in their analyses (Lauder 1990; Biewener 2002), this approach has been criticized because it assumes a direct link between morphology and function, and considers that most traits should have a functional significance (Gould 2002). Other functional morphologists have analyzed the interspecific variation of continuous characters by using statistical methods, mainly regressions between these traits and functional or ecological variables, but without taking into account the phylogenetic relationships among species. In doing so, they assume a star phylogeny (Martins 2000), which is not realistic because of the hierarchic structure of the phylogenetic relationships among organisms. As showed by Cruz-Neto et al. (2001), this can produce quite misleading results.
An integrative approach: partitioning the variation of bone growth rate in amniotes among its phylogenetic, structural, and functional components
Our approach tries to prevent bias toward one pole or another. It is an expanded version of Seilacher's model (Fig. 5), aimed at quantifying the portion of character variation actually explained by each factor, as well as by their overlap (Fig. 4). Wake and Larson (1987) performed an integrative analysis of morphological characters in plethodontid salamanders, in which they provided evidence for the occurrence of all three factors of Seilacher's model (historical, functional, and structural). Their study dealt with discrete characters. For continuous characters, Cubo et al. (2005) quantified the phylogenetic and functional components of the variation of bone microstructural traits in sauropsids, as well as their overlap, as a first step toward more integrative analyses. The approach proposed herewith now allows the realization of holistic analyses. We were able, for the first time, to partitioning the variation of a continuous character among its historical, functional, and structural components. Bone growth rate has been selected here as the dependent variable because its variation results from a complex causality (Horner et al. 2001; Padian et al. 2001; Ricqlès et al. 2001).
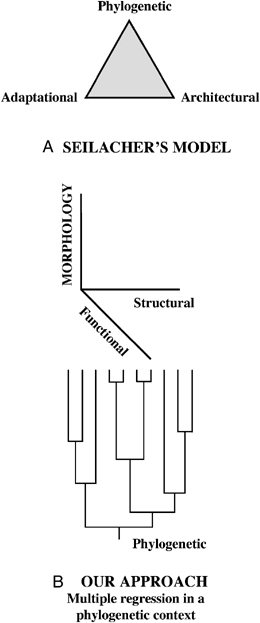
Factors explaining morphological diversity. (A) Seilacher (1970) used a ternary plotting to illustrate the basic causes of form. In his diagram, any actual feature of a given organism plots either along an edge (when it is determined only by two factors), or somewhere within the triangle (when it is determined by all three factors). This kind of triangular diagram has frequently been used by petrologists to depict the composition of actual rocks as amalgamations of three pure components. (B) Our approach greatly increases the explanatory power of Seilacher's model, because it involves the extension from the qualitative analysis of the phenotypes of given organisms, to the quantitative analysis of character variation within clades. It considers the whole space of variation of a continuous character in a clade, and quantifies the portion of variation explained by each of the three factors, as well as their overlaps (Fig. 4).
(1) Historical component of bone growth rate variation: We have found a significant global phylogenetic signal in the variation of bone growth rates, suggesting that a part of the observed patterns are the outcome of shared ancestry. This finding validates the optimizations of this variable onto an independently generated phylogenetic tree of diapsids performed by Padian et al. (2001) to estimate primitive character states.
(2) Functional component of bone growth rate variation: The analysis of the concept of function has provoked renewed interest (Gayon 2006; Bolhuis and Verhulst 2007). At least two theories of function are currently available. The “systemic concept” proposes that a function is a capacity that emerges in a system from more elementary capacities (Gayon 2006). This concept fits well with the biology of proximal (Mayr 1961) or mechanistic (Autumn et al. 2002) causes, which produce a change in an object from state 1 at time 1, to state 2 at time 2. For instance, variation in bone growth rates (our dependent variable) may be linked to variation in RMR (Ricqlès 1978a, b; Padian et al. 2001) because building new tissues at high growth rates involves high rates of protein synthesis and degradation (protein turnover) which are very energy demanding (Nagy 2000). The “etiological theory” deals with ultimate causes, and proposes that the function of a trait is the effect for which that trait was selected (Gayon 2006). Adaptations are viewed as character states exhibiting higher evolutionary fitness than other character states in the same environment (Martins 2000). In this context, the adaptive significance of observed values of bone (and overall) growth rates may be linked to the extent to which they improve survival rates. For instance, King Penguin chicks experience a first phase of rapid growth between February and early May, during which body mass increases from 0.2 to 9–12 Kg (attaining bone growth rates of up to 171 μm/day), followed by a 4.5-month period (the Austral Winter) of low feeding rate during which only those chicks that have undergone high growth rates during the first phase and have reached large size can survive (Margerie et al. 2004). Thus, high growth rates, although energy costly, may be adaptive (i.e., they may increase survival rates) in taxa showing short growth periods. High growth rates may also be adaptive in noncolonial bird species (Ixobrychus minutus), because their nestlings may undergo higher predation pressure than those of their closely related colonial breeding relatives (Bubulcus ibis, Egretta garzetta, …) (Cubo et al. 2000). Whereas this second concept of function deals with evolutionary mechanisms (survival rates, fitness), the first one analyzes evolutionary patterns. Here we performed an interspecific analysis, in which we were only concerned with emergent patterns. Thus, we hypothesized that RMR is a functional (proximal or mechanistic) factor explaining bone growth rate variation, and found empirical evidence supporting it. For instance, the low RMRs of crocodiles, lepidosaurs, and chelonia would prevent these animals from attaining high growth rates (for the body, overall, and its bones, specifically). In these three groups of organisms, adult size is attained after several cycles of slow growth, separated by periods of arrested growth. Results for mammals are ambiguous because two (of the three) studied species (M. murinus and M. musculus) are altricial and not fully endothermic at perinatal stages. These animals have lower RMRs than growing precocial mammals of similar size. The observed low RMRs may prevent these animals from attaining high growth rates, which may be the cause of the cyclical growth (periods of slow growth separated by periods of arrested growth) reported in M. murinus (Castanet et al. 2004).
Moreover, we have found that the “pure” functional component, which may correspond to autapomorphies at the level of species (immediate adaptation to current circumstances), is also significant (fraction [b]; Table 2 and Fig. 4). In fact, these autapomorphic values may have already been fixed by natural selection in species and, consequently, could also be considered to a certain extent as “historical.” However, whereas this “pure” functional component (fraction [b]) was fixed because it improves the fitness in current conditions, the functional component that overlaps with the phylogenetic component (fraction [d+g]) was selected in past conditions and was passively inherited.
(3) Structural component of bone growth rate variation: Soft tissues generally grow through a multiplicative process in which the new materials grow and produce, in turn, new material. In contrast, bone growth is accretionary (additive): new material is mineralized and cannot further contribute to growth. In other words, for a given mitotic rate and cellular activity, soft tissues may grow much faster than mineralized tissues. Accordingly, the mode of construction of bone tissue is hypothesized to be a structural (architectural) factor limiting the maximum possible bone (and overall) growth rates in amniotes. Thus, the relative surface of apposition of new bone tissue (“osteonal+peripheral_accretional_surface”/“peripheral_accretional_surface”) was considered as a structural explanatory variable. Variation of the appositional surface among species of our sample has its main origin in the fact that two variants of this accretionary mode of construction were observed (2, 3). In Lacertidae and most Chelonia in our sample, centrifugal accretional growth takes place only at the free external surface of bone, i.e., below the periosteum, a connective tissue encircling the bone shaft (2, 3). On the other hand, in Mammalia, Varanidae, and Archosauria (crocodiles and birds), accretional growth is achieved not only at the external surface of the bone shaft, but also within large cavities included in the bone cortex as it grows centrifugally (2, 3). These cavities become progressively filled by centripetal apposition of bone, forming what is called the “primary osteons.” This modified growth mode (centripetal or osteonal) allows sustained high bone growth rates (μm2/day) because it partially circumvents the topological limits imposed by the accretionary mode of construction by increasing the surface of apposition of new bone tissue for a given bone size. Hence, these two growth modes (peripheral only vs. peripheral+osteonal) represent two different levels of structural constraint on bone growth rate, which cause the variable values of our structural variable. Thus we hypothesized a positive relationship between the relative surface of apposition of new bone tissue and bone growth rate, and found empirical evidence for this hypothesis.
As shown above, we were able to successfully apply our integrative approach to the analysis of variation of bone growth rates, which was explained as a partial function of bone appositional surface and RMR in a phylogenetic context. The fact that the measured structural and functional traits are significant suggests that they are good representatives of the type. We can wonder whether results might differ if more than a single trait of each type were measured. It has recently been shown that the inclusion of other functional variables in variation partitioning analyses has the effect of decreasing the percentage of unexplained variation (Montes et al. 2007). Biomineralization mechanisms in vertebrates and in other Metazoa are particularly suitable systems to be analyzed using our approach because the functional (biological adaptation), structural (geometric and physicochemical laws), and historical (phylogenetic) components can be properly quantified. To conclude, we feel that our integrative approach contributes to the unification of historicism, functionalism, and structuralism.
Acknowledgments
This research was financed in part with funds of the UMR CNRS 7179 (Dir. M. Perret) and the IFR 101 (Dir. R. Barbault). We thank D. Wake (University of California, Berkeley) and J. Gayon (Sorbonne University, Paris) for critical readings of preliminary versions of this manuscript, and K. Padian (University of California, Berkeley) and an anonymous reviewer for their useful comments.




