Multi-trait evolution in a cave fish, Astyanax mexicanus
Abstract
SUMMARY When surface species colonize caves, a characteristic suite of traits eventually evolves over time, regardless of species. The genetic basis of the inevitable appearance of these very similar phenotypes was investigated through quantitative trait loci (QTL) mapping of 12 traits that differ significantly between the recently evolved (<1 Myr). Mexican cave tetra and its surface conspecific. The traits were a representative set, including eye size, pigment cell numbers, chemical sensitivity, body and skull morphology, standard length, and metabolism. We used both single- and multi-trait models for QTL mapping. QTL effects of these traits were significantly clustered in the genome. We mapped 13 regions in the genome with QTL effects on from three to nine traits. These clusters could be multigenic or could represent single locus with pleiotropic alleles. Given the relatively short time available to construct clusters from unlinked genes through genomic rearrangement, and the counterintuitive polarities of some of the substitution effects, we argue that at least some of the clusters must have a pleiotropic basis.
INTRODUCTION
Cave animals are ideal subjects to study multi-trait evolutionary changes (Jeffery 2001). Numerous species and populations have evolved similar suites of cave-related (troglomorphic) traits, diverging from their surface ancestors in response to the radical environmental and ecological shift to constant darkness. Most obligate cave dwellers have reduced pigmentation and nonfunctional, small eyes. To compensate for the lack of visual information, they have typically augmented chemical senses and/or mechanoreception. Metabolic and feeding efficiencies are generally enhanced as a consequence of limited food supply. We asked what features of genomic organization underlie these coordinated changes in one population of cave fish from Mexico.
The Mexican cave tetra, Astyanax mexicanus, has at least 29 separate populations, many of which have evolved independently (Mitchell et al. 1977; Dowling et al. 2002a; Strecker et al. 2003, 2004; Wilkens and Strecker 2003). All share a remarkably high degree of phenotypic similarity. Analysis of the genetic basis of troglomorphic evolution in this species is simplified because eyed surface populations are available and fully interfertile with the cave forms. To determine the changes underlying the differences between surface and cave tetras, we mapped the genome of this species (177 loci for a total 2148 cM), and used the map to find and characterize quantitative trait loci (QTL) determining typical elements of the troglomorphic suite and other changes that evolved in one specific population inhabiting Pachón cave.
In the present study, we assessed 12 traits that differ between cave adapted and surface tetras, including six that are presumably troglomorphic: these are eye size (E), melanophore numbers (M), body condition (length corrected weight; C), rate of weight loss on fast (W), number of maxillary teeth (T), and sensitivity to dissolved amino acids (A). In addition, we measured body length (L), depth of the caudal peduncle (D), the placement of the dorsal fin (P), and the size of the SO3 dermal skull bone (S); we counted numbers of anal fin rays (R) and ribs (B) (Table 1 summarizes the trait descriptions). Maximum lengths of surface fish in the laboratory exceed those of Pachón cave fish: 71 versus 68 mm for females and 67 versus 60 mm for males, respectively (unpublished). Eye sizes are smaller and pigment cell density is reduced in cave tetras in comparison with the surface tetras (Wilkens 1988). Given equal rations, cave tetras maintain better condition (length-corrected weight) than surface tetras. In the laboratory, Pachón fish weigh 11% more than surface fish, for a given length (unpublished). On limited rations, they lose weight more slowly (Huppop 1986). Cave tetras are far more sensitive to dissolved tastants and have more maxillary teeth than surface fish, traits related to food detection and feeding efficiency (Jeffery 2001). Perhaps as an adaptation to slower flow rates in cave versus surface waters, Pachón cave tetras have evolved several morphological features, including a less robust caudal peduncle, a dorsal fin set further back from the head, and fewer anal fin rays than their surface counterparts. In addition, they average fewer ribs (11 or 12 vs. 12 in surface fish) (Dowling et al. 2002b), and the SO3 dermal skull bone is smaller and fragmented in the cave versus surface forms (Yamamoto et al. 2003). Jeffery gives a thorough review of the cave-related phenotypes of this species (Jeffery 2001).
| Trait (N) | Symbol | Description and trait polarity | F2 mean, range, (N) |
|---|---|---|---|
| Eye size | E | Observed eye size divided by eye size predicted from the regression of eye size on standard length (SL). Skew corrected in MultiQTL. Cave < surface. Wilkens (1988) | 0.92, 0.39–1.76 (539) |
| Melanophore | M | Count of melanophores in an area (2.0×0.4 mm) located 3.0 mm above the left eye. See supplemental methods in Protas et al. 2007 for illustration. | 36.8, 0–80 (174) |
| Cave < surface. Wilkens (1988) | |||
| Relative condition | C | Observed weight divided by predicted weight calculated from regression of log weight on log length. Skew corrected in MultiQTL. Surface < cave | 1.01, 0.64–1.51 (534) |
| Weight loss | W | Rate of weight loss on fast expressed as percent decrease per day. Weight loss is slower in cave than in surface individuals. Huppop (1986) | −0.38, −0.92–0.05 (361) |
| Tooth count | T | The total number of maxillary teeth. | 2.59, 0–6 (227) |
| Surface < cave Yamamoto et al. (2003) | |||
| Peduncle depth | D | The minimum depth of the caudal peduncle divided by SL. The caudal peduncle is 8% deeper in surface fish compared with Pachón cave fish | 0.10, 0.06–0.13 (200) |
| Fin placement | P | The distance from the mouth to the insertion of the | 0.47, 0.42–0.51 (200) |
| dorsal fin divided by SL. The fin is set 8% posteriorly | |||
| in Pachón cave fish compared with surface fish | |||
| Anal fin rays | R | Number of branched and unbranched anal fin rays | 22, 13–26 (214) |
| Pachón cave fish average 1.8 fewer than surface fish | |||
| SO3 width | S | Width of the suborbital bone(s) SO3 divided by the distance from the preopercular canal to the orbit (structure figured in Yamamoto et al. 2003). Pachón cave < surface | 0.63, 0.44–0.78 (221) |
| Ribs | B | The number of thoracic ribs. Surface fish have 12, Pachón cave fish have 11 or 12. Dowling et al. (2002) | 12.46, 11–14 (163) |
| Length | L | Residuals of the regression of SL on age at sacrifice and dummy variables representing presence in different holding tanks. Cave < surface. | −0.03, −15.53–+16.17 (533) |
| Chemical sense | A | Threshold sensitivity to dissolved amino acids in the water assessed by searching response triggered by the addition of amino acid solution to the test aquarium. Responses were scored over the full range of concentrations and used to estimate the concentration at which response probability was 50%. This was scored as an integer (6–11) representing the concentration (10−6 to 10−11m). Pachón cave > sensitivity than surface. | 7.70, 6–11 (113) |
- QTL, quantitative trait loci; N, number of individuals phenotyped
Thus, we studied cave-evolved traits that included classic regressive (E, M) and constructive (C, W, A, and T) troglomorphies, and other traits of unknown significance (B, D, L, P, R, and S). These traits mark evolutionary alterations in diverse regions of the body brought about through a variety of developmental pathways.
It is likely that some of the traits have overlapping control. For example, rate of weight loss on fast and condition factor are surrogate measures for catabolic and anabolic metabolism, respectively, and are jointly regulated through control of circulating insulin-like growth factor activity (Peterson and Small 2004). As a second example, Jeffery has hypothesized a link between the development of eyes and feeding structures mediated by hedgehog (hh) expression; sonic hedgehog and tiggy winkle hedgehog (shh and twhh) are upregulated in Pachón cavefish embryos compared with surface embryos, leading to more robust jaw development and greater numbers of tastebuds. Hedgehog activity, however, downregulates PAX6 expression, and results in smaller eyes. If the increased sensitivity of cavefish to amino acids reflects this change in hh activity, this trait could be controlled in common with eye size (Yamamoto et al. 2004). Finally, changes in caudal peduncle depth and placement of the dorsal fin might both be influenced by the same genes affecting relative growth rates of portions of the body. It is unlikely, however, that other of the traits we studied, such as rib number and melanophore counts, are regulated in common. Nevertheless, all of these traits are united by the fact that they co-evolved in the cave environment.
MATERIALS AND METHODS
We hybridized a surface fish (Rió Valles, SLP) with a Pachón cave fish to produce an F1 and then bred two F1 individuals to produce an F2 progeny for mapping. A total of 539 F2 were used in mapping. All were full sibs. The markers used were primarily microsatellites that have been described previously (Protas et al. 2006). Markers not described previously are characterized in Supplementary materials Table S1. In addition, 12 genes were put on the map after developing primers to exploit microsatellite or single nucleotide polymorphism (SNP) variation in introns. We attempted to genotype all F2 individuals for all 177 markers, although the genotypic matrix has approximately 20% missing data.
Mapping was done with MultiPoint software (http://www.multiqtl.com), which uses an iterative algorithm to minimize the effects of chance correlations between loci (“pseudo linkages”). Loci were clustered initially under stringent conditions (threshold recombination of r <0.20), which were then relaxed in stages to aggregate initial linkage groups into larger sets. To avoid pseudo linkage, groups were combined only when linked end to end. Ordering was obtained by minimizing total map distance within each linkage group, but tested for consistency by jackknife analysis (Mester et al. 2003). Inconsistently mapping markers were excluded from further consideration. Only loci exhibiting F2 segregation within the cross could be mapped with MultiPoint. Several of the genes we mapped exhibited backcross segregation and were hand-placed on the map using recombination data from analyses with JoinMap (Van Ooijen and Voorips 2001), which can handle mixed segregation models. Hand-placed markers were not used for mapping QTL, nor did they figure in analyses based on map length.
We measured a variety of phenotypic traits in the mapping progeny (Table 1). Length and weight were measured periodically and at sacrifice. From regression analysis of log weight on log length in well-fed individuals, we calculated relative condition factor as the ratio of observed to predicted weight. Analysis of residuals was used to control for environmental variables in groups of fish that had been treated differently (e.g., variation in ages at sacrifice, broods, raising density, etc.). Other individuals were subjected to a period of fast before sacrifice, which allowed estimation of rates of weight loss under low rations. We counted anal fin rays, measured eye size, and examined each nonalbino fish for melanin pigmentation. Melanophores were counted in a defined area above the eye. Relative eye size was standardized from a regression of eye size on standard length. To phenotype osteological traits, we used alizarin red staining. In this article, we report on the number of anal fin rays, the size of the SO3 bone in the skull, and on the number of ribs.
Chemical sensitivity was assessed using an assay for a “searching” behavioral response following the addition of an equimolar mixture of four amino acids (l-alanine, l-serine, l-methionine, and l-proline) to the inflow stream of each individual's tank (2.75 l). Each tank had a bubbler to mix the water, and molarities were calculated on the basis of the assumption of complete mixture. Mixing was rapid, but local variation in concentration must have been a source of measurement noise. Additions covered the range of final concentrations from 10−6 to 10−11 molar, in 10-fold dilutions, and a pure water control. Three tests of each individual were performed for each concentration, with the orders randomized and the observer unaware of the concentrations and/or the genotypes and previous responses of the fish. The data were used to calculate threshold sensitivity for each individual and were represented for analysis as integers, representing orders of magnitude, ranging from 6 through 11. Pachón cave fish were tested in the same manner; surface fish were tested under reduced illumination. Detection of amino acid odorants is mediated by olfaction in fish (Michel 2006).
MultiQTL software (http://www.multiqtl.com) was used to search for QTL for the traits listed above. When trait distributions were significantly skewed, we used the trait transformation capabilities of MultiQTL to normalize them to the best extent possible before analyses. Generally, these transformations led to small, but significant, improvements in estimates of confidence limits and proportions of explained variance. Single-trait QTL analysis was done in two stages: in the first, we identified linkage groups with significant or suggestive trait associations (P≤0.10) using simple interval mapping (SIM) (Lander and Botstein 1989). Next, for each trait considered, all linkage groups identified in the first step were used as a starting set for multiple interval mapping (MIM) using the MIM function of MultiQTL (Korol et al. 1998). MIM assesses the significance of QTL iteratively, estimating the effects of all detected QTL on each other to minimize background variation and optimize estimation of QTL parameters (Kao et al. 1999). MIM analysis typically revealed that many of the linkage groups in the starting sets had no significant QTL, and these were eliminated from further analysis. Repeating the MIM analysis generally led to an improvement in significance and precision of the remaining QTL, although some occasionally lost significance. If so, they were eliminated and the procedure repeated until a stable set was obtained. Two final rounds of MIM analysis for each trait with parameters set at the highest stringencies confirmed that the estimates of QTL were consistent. Significances of all QTL were determined by permutation, and confidence limits on their positions were determined by bootstrap analyses. For the final program output, significance parameters were set at P=0.05 for individual QTL, with a genome-wide false detection rate of 10% (FDR=0.10). These methods detect at most one QTL per trait per linkage group.
We also used MultiQTL's capabilities to do multiple-trait QTL analysis. With this approach, the multivariate phenotype, based on three or more traits, is considered as a target and is represented in the mapping model (Jiang and Zeng 1995; Korol et al. 1995). The multi-trait algorithms implemented are based on a maximum-likelihood approach, and on transformation of the initial trait space into one of lower dimension analogous to principal component analysis (Korol et al. 1995, 1998, 2001; Ronin et al. 1998, 1999). A multi-trait QTL represents a region where one or more genetic loci control variation for some or all of the constituent traits. Multi-trait QTL analysis is better than single-trait simple interval analysis at detecting minor QTL effects because of the greater Euclidean separation of the multidimensional QTL centers and an increased heritability deriving from a greater information content as dimensionality increases (Korol et al. 2001). Not all traits could be combined into a single model because most had been measured in only subsets of animals, and some combinations with too many traits had too few individuals for analysis. We constructed six models with three or more traits. These were EMT, CRM, EMCTW, EMRDS, ADTM, and DAWM. The number of individuals included in each of the six multi-trait models are given in Supplementary materials Table S2, along with the numbers of QTL detected through analysis. As in the single-trait analyses, linkage groups with suggestive multi-trait QTL were identified at the P=0.10 level and then tested for significance using MIM. Multi QTL does not allow for the calculation of FDR for multi-trait models. All were individually significant at P≤0.0025.
This method does not guarantee that all traits in the model contribute significantly to the QTL. Therefore, we further tested the significance of the contributions of each component trait to each multi-trait QTL directly by using MultiQTL's Trait Contribution option. This tests significance by permuting values of each trait in turn against the set of other traits and marker values (Korol et al. 2001). The threshold for significance was set at P=0.05. If a multi-trait QTL lacking significant contributions from even one component trait was found, it was dropped from further analysis and the MIM procedure was repeated, sometimes eliminating more QTL. We repeated this cycle until a subset of the original candidate QTL remained that were significant by MIM and to which all traits made significant contributions.
To validate these procedures and check their false detection rates, we randomized the phenotypic values for each trait separately and repeated the analyses. With the original trait values we detected 63 single-trait QTL for the 12 traits, and with randomized data we detected six false QTL. This matches the 10% FDR we set in software. Using the iterative procedure outlined above, we detected 21 multi-trait QTL based on real data. Analysis of the permuted data produced no false QTL.
We put six genes on the map based on SNP polymorphisms: fructose-1,6-bisphosphatase 1 (FBP1), cyclin G1 (CG1), insulin (ins), insulin-like growth factor 1 (IGF1), insulin-like growth factor binding protein 5 (IGFBP5), and growth hormone (GH). RNA was extracted from liver and brain tissue of adult surface individuals (RNeasy Mini Kit, Qiagen, Valencia, CA, USA) and cDNA was synthesized (ThermoScript RT-PCR System, Invitrogen, Carlsbad, CA, USA). Portions of the genes were amplified from the cDNA using degenerate primers based on Danio, Gasterosteus, Oryzias, and/or Fugu sequences. Amplicons were sequenced (BigDye Sequencing kit, Applied Biosystems, Foster City, CA, USA) and specific primers were designed and used to find SNPs between surface and cave DNA. SNP genotyping was performed using the SNaPshot Multiplex Kit (Applied Biosystems), a primer extension analysis based protocol. SNP positions, primer sequences, polymorphisms, and Danio ENSEMBLE reference codes are given in Supplementary materials Table S3. A seventh gene, transcription factor binding to IGHM enhancer 3, Tfe3, was mapped from a size polymorphism in intron 6 revealed by sequencing a fragment amplified using degenerate primers previously used to isolate the related gene Mitf in zebrafish (Lister et al. 1999). Mapping primer sequences are given in Supplementary materials Table S3.
The linkage map and QTL were plotted using MapChart software (Voorrips 2002) and output from MultiQTL. QTL were plotted as LOD score curves and as bars indicating one LOD intervals around the maxima.
RESULTS
We calculated pair-wise phenotypic correlations among all 12 traits in the mapping F2 (Supplementary materials Table S4). Fourteen of the 78 correlations were significant at P≤0.01 level. Most of the correlations are weak, however, with an average overall R2=0.03. For the 14 significant associations, the average R2=0.09.
The map used for analysis is similar to that published earlier (Protas et al. 2007), with the addition of six new genes. Using it, we detected 63 simple QTL for 11 of these 12 traits, ranging from two QTL for anal fin ray count (R) to nine each for condition factor (C) and dorsal fin placement (P) (Table 2). On average, the QTL for a given trait account for about 50% of the total trait variance and 34% of the additive variance. Using the trait means (μ), substitution effects (d ), and heterozygote effects (h), we calculated the genotypic values of cave homozygotes (μ+d), heterozygotes (μ+h), and surface homozygotes (μ−d), for each QTL and determined the dominance status of the cave alleles. Our working criterion to determine whether the genotypic values differed significantly was nonoverlap of their standard errors. In 38 cases the cave alleles were of intermediate dominance, in eight they were dominant, in 11 recessive, and in four they appeared to be overdominant. Some of the determinations were difficult to make, but the great majority of cave alleles were semidominant. There was no significant difference among different classes of traits (sensory: A, E; metabolism/growth: C, L; meristic: R, T, B; shape/size: P, D, S) in distribution of dominance status.
| LG | Trait | LOD | P | QTL position | % V Exp. | % adV Exp. | Substitution effect | Heterozygote effect | Trait mean,range | Trait values | Dominancestatus | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cc | ce | ee | |||||||||||
| LgP1 | A | 7.3 | 0.001 | 26.8 ± 7.4 | 9.9 ± 3.1 | 4.0 ± 2.0 | −0.599 ± 0.165 | −0.519 ± 0.130 | 7.70 | 7.10 | 7.18 | 8.30 | D |
| LgP5 | 8.5 | 0.001 | 16.8 ± 4.6 | 27.1 ± 8.5 | 19.3 ± 6.5 | 1.336 ± 0.274 | −0.588 ± 0.171 | 6–11 | 9.04 | 7.11 | 6.36 | I | |
| LgP10 | 4.2 | 0.001 | 139.6 ± 28.6 | 22.1 ± 6.9 | 0.7 ± 0.9 | 0.201 ± 0.179 | 1.003 ± 0.238 | 7.90 | 8.70 | 7.50 | V | ||
| LgP20 | 10.3 | 0.001 | 7.5 ± 4.2 | 14.1 ± 2.4 | 13.8 ± 2.4 | 1.158 ± 0.117 | 0.032 ± 0.114 | 8.86 | 7.73 | 6.54 | I | ||
| LgP1 | B | 11.4 | 0.000 | 37.1 ± 3.9 | 11.7 ± 3.1 | 11.3 ± 2.9 | 0.414 ± 0.062 | 0.035 ± 0.046 | 12.5 | 12.9 | 12.5 | 12.0 | I |
| LgP5 | 8.9 | 0.001 | 90.5 ± 15.5 | 6.8 ± 1.9 | 6.3 ± 2.3 | −0.307 ± 0.066 | −0.023 ± 0.056 | 11–14 | 12.2 | 12.4 | 12.8 | I | |
| LgP9 | 4.4 | 0.001 | 44.1 ± 11.1 | 5.0 ± 2.3 | 4.5 ± 2.3 | 0.256 ± 0.072 | −0.005 ± 0.061 | 12.7 | 12.5 | 12.2 | I | ||
| LgP17 | 18.2 | 0.001 | 25.1 ± 3.1 | 32.5 ± 3.6 | 27.9 ± 3.6 | −0.624 ± 0.051 | −0.175 ± 0.042 | 11.8 | 12.3 | 13.1 | I | ||
| LgP18 | 3.6 | 0.001 | 4.1 ± 4.0 | 3.4 ± 1.4 | 0.1 ± 0.2 | 0.001 ± 0.049 | 0.155 ± 0.037 | 12.5 | 12.6 | 12.5 | V | ||
| LgP25 | 18.7 | 0.001 | 11.0 ± 3.6 | 13.1 ± 2.1 | 12.5 ± 2.3 | −0.438 ± 0.045 | −0.061 ± 0.039 | 12.0 | 12.4 | 12.9 | I | ||
| LgP4 | C | 5.5 | 0.001 | 57.3 ± 10.1 | 4.6 ± 1.7 | 4.3 ± 1.6 | −0.066 ± 0.013 | −0.004 ± 0.012 | 1.01 | 0.94 | 1.00 | 1.07 | I |
| LgP7 | 4.7 | 0.001 | 59.4 ± 23.2 | 3.7 ± 1.3 | 2.4 ± 1.3 | 0.048 ± 0.016 | −0.023 ± 0.013 | 0.64–1.51 | 1.05 | 0.98 | 0.96 | R | |
| LgP11 | 8.7 | 0.001 | 94.1 ± 11.6 | 6.1 ± 1.6 | 5.8 ± 1.7 | −0.077 ± 0.012 | 0.006 ± 0.012 | 0.93 | 1.01 | 1.08 | I | ||
| LgP14 | 7.1 | 0.001 | 81.8 ± 16.9 | 5.0 ± 1.4 | 3.8 ± 1.4 | −0.062 ± 0.012 | 0.023 ± 0.011 | 0.94 | 1.03 | 1.07 | I | ||
| LgP15 | 8.4 | 0.001 | 14.7 ± 6.3 | 5.8 ± 1.7 | 5.5 ± 1.7 | −0.075 ± 0.012 | 0.005 ± 0.009 | 0.93 | 1.01 | 1.08 | I | ||
| LgP20 | 3.4 | 0.002 | 39.6 ± 13.8 | 2.7 ± 1.1 | 2.3 ± 1.1 | 0.048 ± 0.012 | −0.006 ± 0.013 | 1.05 | 1.00 | 0.96 | I | ||
| LgP23 | 3.9 | 0.001 | 9.4 ± 9.3 | 3.1 ± 1.4 | 2.8 ± 1.4 | 0.052 ± 0.015 | −0.003 ± 0.014 | 1.06 | 1.00 | 0.95 | I | ||
| LgP25 | 9.0 | 0.001 | 19.8 ± 3.2 | 5.6 ± 1.5 | 4.6 ± 1.3 | −0.067 ± 0.010 | 0.021 ± 0.008 | 0.94 | 1.03 | 1.07 | I | ||
| LgP27 | 7.3 | 0.001 | 5.3 ± 2.5 | 4.8 ± 1.5 | 3.7 ± 1.3 | 0.061 ± 0.011 | −0.023 ± 0.009 | 1.07 | 0.98 | 0.95 | I | ||
| LgP3 | D | 3.6 | 0.001 | 15.7 ± 17.2 | 18.1 ± 10.1 | 15.4 ± 8.5 | 0.022 ± 0.010 | 0.003 ± 0.006 | 0.10 | 0.12 | 0.10 | 0.08 | I |
| LgP9 | 3.1 | 0.006 | 23.9 ± 10.6 | 7.3 ± 3.3 | 5.8 ± 3.1 | 0.013 ± 0.005 | −0.004 ± 0.003 | 0.06–0.13 | 0.11 | 0.10 | 0.09 | I | |
| LgP27 | 2.4 | 0.011 | 14.3 ± 2.6 | 5.9 ± 3.1 | 0.6 ± 0.9 | −0.002 ± 0.004 | 0.009 ± 0.003 | 0.10 | 0.11 | 0.10 | V | ||
| LgP4 | E | 4.0 | 0.000 | 43.9 ± 15.1 | 2.6 ± 1.1 | 2.4 ± 1.1 | −0.087 ± 0.022 | −0.004 ± 0.020 | 0.92 | 0.84 | 0.92 | 1.01 | I |
| LgP5 | 3.5 | 0.003 | 69.3 ± 14.7 | 2.3 ± 0.8 | 1.4 ± 0.8 | −0.065 ± 0.022 | −0.004 ± 0.038 | 0.39–1.76 | 0.86 | 0.92 | 0.99 | I | |
| LgP6 | 3.0 | 0.013 | 45.7 ± 10.9 | 1.4 ± 0.6 | 0.7 ± 0.5 | −0.045 ± 0.021 | −0.024 ± 0.024 | 0.88 | 0.90 | 0.97 | D | ||
| LgP7 | 6.8 | 0.001 | 118.1 ± 16.5 | 5.9 ± 2.0 | 3.3 ± 1.2 | −0.103 ± 0.020 | 0.061 ± 0.027 | 0.82 | 0.98 | 1.03 | I | ||
| LgP8 | 11.5 | 0.001 | 18.7 ± 17.4 | 9.0 ± 3.0 | 4.9 ± 1.6 | −0.124 ± 0.021 | 0.076 ± 0.033 | 0.80 | 1.00 | 1.05 | R | ||
| LgP13 | 3.4 | 0.002 | 20.7 ± 4.9 | 1.6 ± 0.7 | 0.1 ± 0.2 | −0.012 ± 0.018 | 0.048 ± 0.014 | 0.91 | 0.97 | 0.94 | V | ||
| LgP20 | 30.5 | 0.000 | 65.7 ± 0.1 | 17.9 ± 2.1 | 17.0 ± 2.1 | −0.238 ± 0.018 | −0.039 ± 0.013 | 0.69 | 0.88 | 1.16 | I | ||
| LgP27 | 14.6 | 0.000 | 3.0 ± 3.0 | 8.3 ± 1.7 | 7.9 ± 1.7 | −0.162 ± 0.019 | 0.020 ± 0.013 | 0.76 | 0.94 | 1.09 | I | ||
| LgP12 | L | 5.0 | 0.001 | 43.9 ± 25.0 | 6.3 ± 2.2 | 5.8 ± 2.2 | −3.30 ± 0.68 | −0.10 ± 0.70 | −0.03 | −3.33 | −0.13 | 3.27 | I |
| LgP14 | 5.1 | 0.001 | 105.1 ± 13.6 | 4.2 ± 1.6 | 3.3 ± 1.5 | −2.49 ± 0.62 | −0.79 ± 0.55 | −15.5–16.2 | −2.52 | −0.82 | 2.46 | I | |
| LgP15 | 3.7 | 0.001 | 38.4 ± 10.8 | 3.9 ± 1.7 | 1.1 ± 0.9 | −1.37 ± 0.60 | 1.63 ± 0.45 | −1.40 | 1.60 | 1.34 | R | ||
| LgP18 | 6.8 | 0.001 | 23.2 ± 5.6 | 5.4 ± 1.7 | 5.1 ± 1.7 | 3.13 ± 0.56 | −0.02 ± 0.52 | 3.10 | −0.05 | −3.16 | I | ||
| LgP26 | 5.1 | 0.001 | 45.8 ± 18.3 | 4.7 ± 1.7 | 3.2 ± 1.7 | −2.41 ± 0.68 | −0.99 ± 0.74 | −2.44 | −1.02 | 2.38 | I | ||
| LgP7 | M | 6.0 | 0.001 | 116.4 ± 21.9 | 8.5 ± 2.6 | 6.9 ± 2.8 | 13.38 ± 3.18 | −3.96 ± 2.36 | 36.8 | 50.2 | 32.9 | 23.4 | I |
| LgP9 | 16.1 | 0.001 | 31.6 ± 5.9 | 30.8 ± 3.7 | 30.4 ± 3.7 | −28.30 ± 2.47 | −1.63 ± 1.83 | 0–80 | 8.51 | 35.18 | 65.11 | I | |
| LgP14 | 4.5 | 0.001 | 137.2 ± 20.6 | 6.0 ± 2.0 | 2.3 ± 1.7 | −7.06 ± 3.49 | −6.05 ± 3.87 | 29.7 | 30.8 | 43.9 | D | ||
| LgP26 | 4.3 | 0.001 | 61.9 ± 21.1 | 14.2 ± 7.0 | 12.1 ± 7.1 | −17.19 ± 6.35 | 2.63 ± 4.64 | 19.6 | 39.4 | 54.0 | I | ||
| LgP8 | P | 6.6 | 0.001 | 78.0 ± 3.5 | 7.2 ± 2.3 | 5.7 ± 1.7 | −0.011 ± 0.002 | −0.004 ± 0.002 | 0.47 | 0.46 | 0.47 | 0.48 | I |
| LgP10 | 5.7 | 0.001 | 9.3 ± 23.3 | 6.2 ± 2.1 | 4.9 ± 2.1 | −0.010 ± 0.003 | −0.003 ± 0.002 | 0.42–0.52 | 0.46 | 0.47 | 0.48 | I | |
| LgP11 | 11.6 | 0.001 | 74.9 ± 3.3 | 12.2 ± 2.5 | 1.5 ± 1.1 | 0.005 ± 0.002 | 0.011 ± 0.002 | 0.48 | 0.48 | 0.47 | D | ||
| LgP13 | 3.7 | 0.002 | 15.2 ± 1.5 | 2.6 ± 1.1 | 0.3 ± 0.4 | −0.002 ± 0.002 | 0.005 ± 0.001 | 0.47 | 0.48 | 0.48 | R | ||
| LgP16 | 5.2 | 0.001 | 23.7 ± 5.8 | 10.9 ± 4.5 | 2.9 ± 2.3 | 0.007 ± 0.004 | 0.009 ± 0.002 | 0.48 | 0.48 | 0.47 | D | ||
| LgP24 | 6.9 | 0.001 | 66.5 ± 8.1 | 13.4 ± 3.8 | 5.1 ± 2.5 | −0.010 ± 0.003 | 0.010 ± 0.002 | 0.46 | 0.48 | 0.48 | R | ||
| LgP25 | 13.6 | 0.001 | 20.3 ± 1.6 | 10.2 ± 1.9 | 8.2 ± 1.9 | 0.014 ± 0.002 | −0.005 ± 0.001 | 0.49 | 0.47 | 0.46 | I | ||
| LgP27 | 5.9 | 0.001 | 8.8 ± 4.3 | 6.1 ± 1.8 | 2.5 ± 1.2 | −0.007 ± 0.002 | 0.006 ± 0.001 | 0.47 | 0.48 | 0.48 | R | ||
| LgP29 | 5.4 | 0.001 | 1.5 ± 3.1 | 3.8 ± 1.3 | 2.1 ± 1.0 | 0.007 ± 0.002 | −0.004 ± 0.001 | 0.48 | 0.47 | 0.47 | R | ||
| LgP3 | R | 4.8 | 0.001 | 12.5 ± 11.2 | 29.2 ± 17.3 | 15.5 ± 11.7 | 1.920 ± 1.413 | 1.312 ± 0.704 | 22.0 | 23.9 | 23.3 | 20.1 | D |
| LgP25 | 3.0 | 0.006 | 18.0 ± 7.9 | 5.3 ± 2.4 | 4.8 ± 2.4 | −1.018 ± 0.291 | 0.005 ± 0.235 | 13–26 | 21.0 | 22.0 | 23.0 | I | |
| LgP4 | S | 3.5 | 0.004 | 43.0 ± 18.2 | 8.2 ± 3.5 | 4.1 ± 2.6 | −0.031 ± 0.012 | 0.022 ± 0.008 | 0.63 | 0.60 | 0.65 | 0.66 | R |
| LgP5 | 5.5 | 0.001 | 80.0 ± 19.1 | 8.4 ± 2.9 | 4.3 ± 2.9 | −0.031 ± 0.014 | 0.018 ± 0.015 | 0.44–0.78 | 0.60 | 0.65 | 0.66 | R | |
| LgP7 | 3.9 | 0.004 | 108.3 ± 31.8 | 8.0 ± 3.0 | 6.7 ± 3.5 | 0.040 ± 0.013 | 0.002 ± 0.013 | 0.67 | 0.63 | 0.59 | I | ||
| LgP22 | 3.9 | 0.002 | 50.4 ± 8.5 | 7.6 ± 2.7 | 4.7 ± 2.4 | −0.034 ± 0.010 | −0.017 ± 0.009 | 0.60 | 0.62 | 0.67 | I | ||
| LgP25 | 3.8 | 0.001 | 17.6 ± 5.4 | 6.0 ± 2.4 | 4.4 ± 2.2 | −0.033 ± 0.009 | 0.012 ± 0.008 | 0.60 | 0.64 | 0.67 | I | ||
| LgP26 | 3.8 | 0.002 | 95.0 ± 23.3 | 13.8 ± 6.4 | 5.6 ± 3.5 | −0.037 ± 0.014 | 0.033 ± 0.010 | 0.60 | 0.67 | 0.67 | R | ||
| LgP6 | T | 5.8 | 0.001 | 21.3 ± 8.9 | 11.3 ± 3.7 | 6.3 ± 2.7 | 0.628 ± 0.155 | −0.392 ± 0.117 | 2.59 | 3.21 | 2.19 | 1.96 | R |
| LgP10 | 3.0 | 0.011 | 128.6 ± 39.1 | 9.8 ± 5.1 | 2.5 ± 2.7 | 0.276 ± 0.287 | −0.276 ± 0.404 | 0–6 | 2.86 | 2.31 | 2.31 | R | |
| LgP13 | 8.9 | 0.001 | 15.2 ± 3.9 | 11.8 ± 2.8 | 10.4 ± 3.3 | 0.821 ± 0.146 | 0.157 ± 0.145 | 3.41 | 2.74 | 1.77 | I | ||
| LgP17 | 3.4 | 0.005 | 28.0 ± 30.5 | 4.9 ± 2.0 | 3.7 ± 1.8 | 0.479 ± 0.129 | −0.147 ± 0.137 | 3.07 | 2.44 | 2.11 | I | ||
| LgP28 | 2.7 | 0.006 | 6.3 ± 10.4 | 4.5 ± 2.0 | 3.0 ± 1.8 | 0.419 ± 0.136 | 0.128 ± 0.181 | 3.01 | 2.71 | 2.17 | I | ||
- MIM, multiple interval mapping; QTL, quantitative trait loci. Trait values for cave (CC) and surface (ee) homozygotes and heterozygotes were calculated from trait means and allelic effects and used to determine dominance status of the cave allele: D, dominant; R, recessive; I, intermediate dominance; V, overdominance; % V Exp., percentage of variance explained by the QTL; % adV Exp., percentage of additive variance explained by the QTL.
The QTL appear to cluster on the map (Fig. 1), most obviously on linkage groups LgP25 (C, R, S, B, and P) and LgP27 (P, C, and E), but also on LgP5 (B, E, and S), LgP7 (E, M, and S), and LgP13 (E, T, P, and D), where, in each case, three or more QTL overlap in their one LOD score range. We tested the significance of clustering against the null hypothesis of random distribution by comparing the distribution of nearest neighbor distances based on the detected QTL versus a data set generated by placing 63 points at random on the map. For the QTL, 12 of 37 distances were below 5.0 cM, whereas for the random points, four of the 40 distances were below 5.0 cM (Fisher's exact test, P=0.0153). Thus, the neighbors among the real QTL are significantly closer than randomly placed points, suggesting that at least some of the apparent clusters are real.
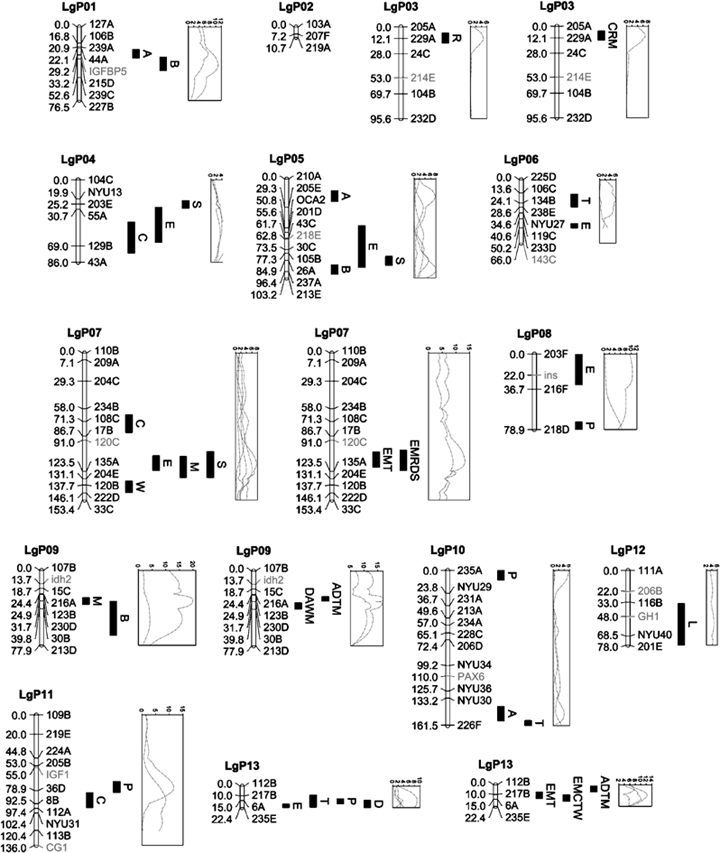
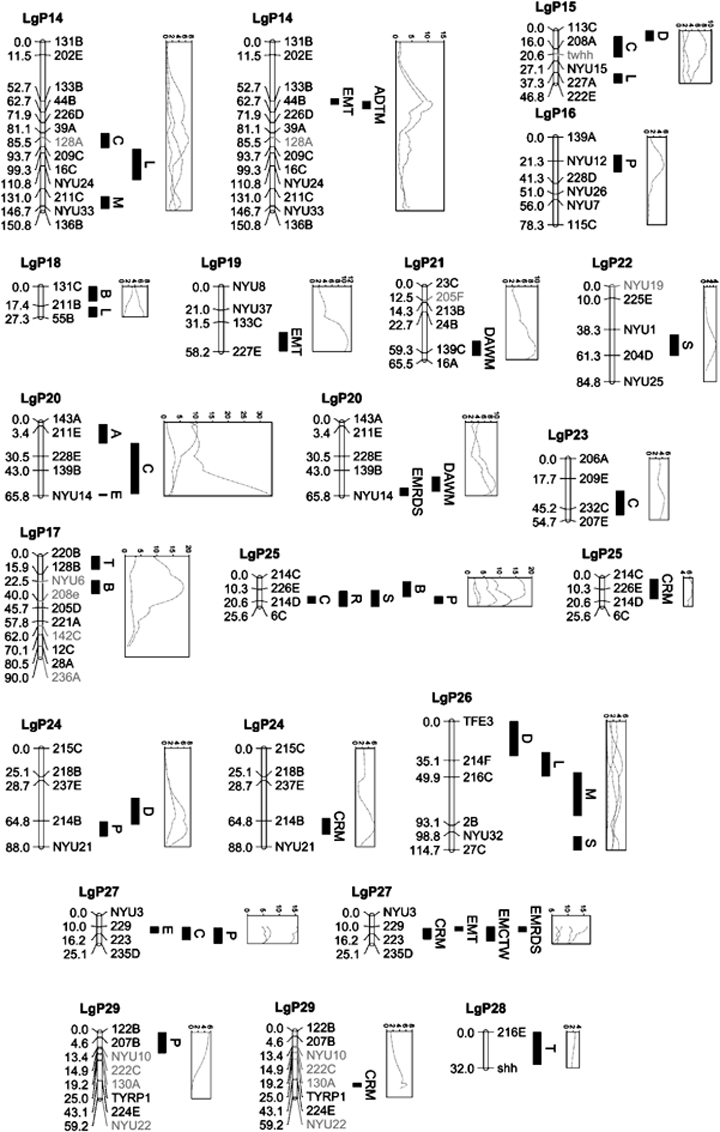
Linkage map of Astyanax mexicanus showing positions of detected QTL and their LOD score curves. Positions of markers given in cM; Bar denotes one LOD score confidence intervals. Hand-placed markers or genes are shown in gray (print version) or violet (online version). Genes newly mapped are CG1, FBP, GH, IGF1, IGFBP5, INS, and TFE3 (Table S3). Genes previously mapped are Idh2 and Oca2 (Protas et al. 2006), PAX6, shh, and twhh (Protas et al. 2007). Linkage groups with both single-trait and multi-trait QTL are shown twice to allow identification of the LOD score curves. LOD curves are unlabeled, but can be matched easily to their QTL by their positions and peak heights, or from data in Tables 2 and 3. QTL, quantitative trait loci; FBP, fructose-1,6-bisphosphatase; CG1, cyclin G1; INS, insulin; IGF1, insulin-like growth factor 1; IGFBP5, insulin-like growth factor binding protein 5.
The multi-trait QTL analysis also supports the observation that local regions harbor genetic variation influencing multiple traits. For the six models tested, we detected a total of 21 QTL (Table 3). The three-trait models detected significant QTL in five linkage groups, the four-trait models detected three, and the five trait models detect two or three.
| Chrom. | LOD | P value | Traits | Location | % V Exp | % adV Exp | Substitution effect | Heterozygote effect | |
|---|---|---|---|---|---|---|---|---|---|
| EMT | LgP7 | 12.9 | 0.0003 | E | 98.7 ± 30.8 | 14.7 ± 4.0 | 7.4 ± 3.4 | −0.173 ± 0.041 | 0.106 ± 0.064 |
| M | 12.4 ± 5.2 | 5.5 ± 3.8 | 11.599 ± 4.848 | −9.160 ± 3.968 | |||||
| T | 2.3 ± 2.2 | 1.1 ± 1.4 | −0.093 ± 0.281 | 0.012 ± 0.214 | |||||
| LgP13 | 11.7 | 0.0004 | E | 11.1 ± 2.3 | 5.7 ± 2.1 | 0.9 ± 0.8 | −0.052 ± 0.029 | −0.099 ± 0.021 | |
| M | 10.6 ± 3.7 | 9.8 ± 3.8 | −16.620 ± 3.768 | −0.681 ± 3.407 | |||||
| T | 6.8 ± 3.2 | 4.9 ± 3.2 | 0.581 ± 0.218 | 0.217 ± 0.163 | |||||
| LgP14 | 7.9 | 0.0010 | E | 56.2 ± 16.3 | 6.6 ± 1.9 | 1.7 ± 1.2 | −0.078 ± 0.032 | 0.097 ± 0.025 | |
| M | 3.5 ± 2.4 | 2.1 ± 2.0 | 6.564 ± 4.399 | 3.021 ± 3.509 | |||||
| T | 4.1 ± 3.3 | 3.4 ± 2.8 | 0.452 ± 0.243 | −0.017 ± 0.164 | |||||
| LgP19 | 10.2 | 0.0003 | E | 45.8 ± 6.7 | 16.9 ± 4.1 | 8.1 ± 3.6 | −0.176 ± 0.043 | −0.129 ± 0.033 | |
| M | 1.5 ± 1.6 | 0.8 ± 1.1 | 2.178 ± 4.195 | −0.351 ± 3.369 | |||||
| T | 2.5 ± 3.2 | 1.3 ± 1.8 | 0.167 ± 0.281 | −0.021 ± 0.220 | |||||
| LgP27 | 14.5 | 0.0002 | E | 0.8 ± 1.5 | 15.2 ± 2.8 | 12.7 ± 2.7 | −0.229 ± 0.028 | 0.069 ± 0.020 | |
| M | 2.0 ± 1.6 | 1.5 ± 1.5 | 5.356 ± 3.823 | 0.647 ± 2.619 | |||||
| T | 3.9 ± 2.5 | 2.8 ± 2.0 | 0.424 ± 0.184 | −0.165 ± 0.132 | |||||
| CRM | LgP3 | 6.3 | 0.0025 | C | 10.8 ± 9.9 | 3.5 ± 2.8 | 1.2 ± 1.6 | −0.008 ± 0.031 | 0.023 ± 0.023 |
| R | 29.7 ± 19.3 | 13.6 ± 12.4 | 1.787 ± 1.614 | 1.472 ± 0.792 | |||||
| M | 4.8 ± 5.1 | 2.8 ± 3.1 | 4.228 ± 8.361 | 0.560 ± 5.732 | |||||
| LgP24 | 6.0 | 0.0020 | C | 56.5 ± 21.6 | 8.0 ± 5.0 | 2.6 ± 2.5 | 0.035 ± 0.032 | −0.044 ± 0.023 | |
| R | 5.8 ± 3.4 | 1.2 ± 1.8 | 0.067 ± 0.530 | −0.486 ± 0.551 | |||||
| M | 4.0 ± 4.4 | 1.2 ± 1.8 | −3.333 ± 5.113 | −1.429 ± 6.313 | |||||
| LgP25 | 7.1 | 0.0005 | C | 11.6 ± 7.1 | 4.0 ± 2.1 | 2.9 ± 1.9 | −0.048 ± 0.017 | 0.015 ± 0.016 | |
| R | 6.7 ± 3.2 | 6.1 ± 3.0 | −1.164 ± 0.334 | 0.123 ± 0.238 | |||||
| M | 1.8 ± 1.8 | 0.6 ± 0.8 | 0.766 ± 4.114 | −1.460 ± 3.998 | |||||
| LgP27 | 6.2 | 0.0005 | C | 5.6 ± 2.1 | 7.8 ± 3.8 | 1.5 ± 1.6 | 0.030 ± 0.021 | −0.050 ± 0.015 | |
| R | 4.0 ± 2.4 | 2.4 ± 1.7 | 0.697 ± 0.294 | −0.383 ± 0.236 | |||||
| M | 3.2 ± 2.4 | 1.9 ± 2.2 | 5.621 ± 5.059 | 3.035 ± 3.374 | |||||
| LgP29 | 6.1 | 0.0010 | C | 45.5 ± 6.8 | 11.5 ± 4.7 | 2.7 ± 2.0 | 0.045 ± 0.020 | 0.062 ± 0.017 | |
| R | 1.4 ± 1.3 | 0.9 ± 1.1 | 0.319 ± 0.344 | −0.018 ± 0.249 | |||||
| M | 3.3 ± 2.9 | 0.7 ± 1.2 | −0.563 ± 4.653 | −4.830 ± 3.926 | |||||
| EMCTW | LgP13 | 10.2 | 0.0010 | E | 13.2 ± 3.1 | 5.5 ± 2.9 | 3.2 ± 2.2 | −0.118 ± 0.048 | −0.065 ± 0.037 |
| M | 4.2 ± 2.9 | 2.7 ± 2.4 | −7.427 ± 4.151 | −2.588 ± 3.609 | |||||
| C | 3.2 ± 2.4 | 1.1 ± 1.4 | −0.019 ± 0.025 | −0.025 ± 0.018 | |||||
| T | 10.0 ± 4.2 | 7.9 ± 4.3 | 0.746 ± 0.232 | 0.216 ± 0.184 | |||||
| W | 2.7 ± 3.0 | 1.9 ± 2.5 | −0.034 ± 0.035 | 0.002 ± 0.022 | |||||
| LgP27 | 11.4 | 0.0010 | E | 4.4 ± 3.6 | 18.9 ± 6.0 | 17.2 ± 5.3 | −0.273 ± 0.057 | 0.051 ± 0.039 | |
| M | 2.5 ± 2.8 | 1.9 ± 2.6 | 5.339 ± 4.896 | −0.731 ± 2.741 | |||||
| C | 8.3 ± 3.6 | 1.0 ± 1.4 | 0.019 ± 0.023 | −0.054 ± 0.015 | |||||
| T | 3.2 ± 2.4 | 2.1 ± 2.0 | 0.342 ± 0.206 | −0.119 ± 0.159 | |||||
| W | 1.6 ± 1.7 | 0.5 ± 0.8 | 0.008 ± 0.024 | 0.018 ± 0.018 | |||||
| EMRDS | LgP7 | 9.1 | 0.001 | E | 111.5 ± 31.8 | 3.8 ± 3.7 | 1.1 ± 1.6 | −0.191 ± 0.051 | 0.064 ± 0.051 |
| M | 13.7 ± 4.9 | 10.2 ± 4.5 | 8.150 ± 6.836 | −5.767 ± 4.652 | |||||
| R | 10.8 ± 5.4 | 8.3 ± 5.3 | 0.169 ± 0.538 | 0.238 ± 0.563 | |||||
| D | 7.6 ± 5 | 3.9 ± 4.1 | 0.002 ± 0.002 | 0.002 ± 0.002 | |||||
| S | 4.9 ± 3.9 | 2.2 ± 2.7 | 0.045 ± 0.018 | 0.007 ± 0.017 | |||||
| LgP20 | 8.3 | 0.001 | E | 49.8 ± 23.0 | 2.9 ± 3.1 | 1.1 ± 1.4 | −0.244 ± 0.068 | −0.026 ± 0.054 | |
| M | 18.8 ± 7 | 16.9 ± 7.5 | −6.335 ± 6.683 | 1.767 ± 3.779 | |||||
| R | 2.1 ± 2.2 | 1.2 ± 1.6 | −0.081 ± 0.522 | −0.263 ± 0.403 | |||||
| D | 4 ± 3.3 | 2.8 ± 3.1 | −0.001 ± 0.002 | −0.002 ± 0.002 | |||||
| S | 4.1 ± 3.3 | 1.4 ± 1.9 | 0.006 ± 0.017 | −0.004 ± 0.011 | |||||
| LgP27 | 8.1 | 0.001 | E | 4.2 ± 5.8 | 7.4 ± 3.6 | 5.4 ± 3.2 | −0.190 ± 0.040 | 0.025 ± 0.032 | |
| M | 10.8 ± 3.4 | 9.9 ± 3.7 | 4.525 ± 5.003 | 1.996 ± 3.355 | |||||
| R | 4.2 ± 2.9 | 2 ± 2.1 | 1.080 ± 0.384 | −0.405 ± 0.301 | |||||
| D | 2.6 ± 2.2 | 1.6 ± 1.9 | −0.002 ± 0.002 | 0.002 ± 0.002 | |||||
| S | 4.3 ± 3.4 | 1.8 ± 2.1 | 0.018 ± 0.014 | 0.015 ± 0.010 | |||||
| DAWM | LgP9 | 12.4 | 0.001 | D | 38.4 ± 8.4 | 11.6 ± 6.2 | 4.7 ± 4.6 | −0.003 ± 0.002 | 0.003 ± 0.002 |
| A | 6.4 ± 3.3 | 3.6 ± 2.4 | 0.634 ± 0.244 | −0.356 ± 0.242 | |||||
| W | 7.9 ± 4.7 | 3.2 ± 3 | −0.060 ± 0.044 | 0.057 ± 0.030 | |||||
| M | 38.5 ± 6.1 | 37.5 ± 6.2 | −30.127 ± 4.081 | 0.145 ± 3.482 | |||||
| LgP20 | 9.4 | 0.001 | D | 49.3 ± 9.9 | 5.8 ± 4.6 | 1.1 ± 1.8 | −0.001 ± 0.002 | −0.005 ± 0.002 | |
| A | 15.9 ± 5.3 | 4.9 ± 4.2 | 0.726 ± 0.326 | 0.783 ± 0.330 | |||||
| W | 14.9 ± 6.9 | 1.5 ± 2.3 | −0.015 ± 0.035 | −0.037 ± 0.037 | |||||
| M | 5 ± 3.4 | 3.6 ± 3.1 | −8.432 ± 4.519 | 2.064 ± 3.570 | |||||
| LgP21 | 8.0 | 0.001 | D | 19.3 ± 20.9 | 5.4 ± 5.3 | 2.4 ± 3.7 | 0.001 ± 0.003 | 0.003 ± 0.002 | |
| A | 27.7 ± 9.5 | 11.8 ± 8.7 | −0.201 ± 1.207 | −0.941 ± 0.334 | |||||
| W | 9.7 ± 6.9 | 2.2 ± 3.7 | 0.013 ± 0.053 | 0.004 ± 0.042 | |||||
| M | 6.7 ± 5.3 | 1.3 ± 2 | 2.107 ± 5.350 | −5.938 ± 5.784 | |||||
| ADTM | LgP9 | 17.1 | 0.001 | A | 30.8 ± 6.1 | 6.2 ± 4 | 4.6 ± 3.4 | 0.696 ± 0.355 | −0.030 ± 0.339 |
| D | 3.8 ± 3.3 | 2.4 ± 2.7 | −0.003 ± 0.002 | 0.000 ± 0.000 | |||||
| T | 9.9 ± 5.7 | 7.7 ± 4.9 | −0.792 ± 0.321 | 0.219 ± 0.234 | |||||
| M | 44.9 ± 4.6 | 43.5 ± 4.5 | −34.413 ± 3.092 | 3.374 ± 2.814 | |||||
| LgP13 | 7.5 | 0.001 | A | 7.4 ± 6.6 | 9.1 ± 5.7 | 5.1 ± 4.4 | 0.693 ± 0.462 | 0.196 ± 0.500 | |
| M | 0.0 | 10.1 ± 3.8 | 4.7 ± 3.4 | −10.432 ± 4.416 | −7.856 ± 3.265 | ||||
| T | 4 ± 3.5 | 2.5 ± 3.1 | 0.297 ± 0.393 | −0.055 ± 0.261 | |||||
| D | 13 ± 6.4 | 8.7 ± 5.7 | −0.006 ± 0.002 | 0.002 ± 0.002 | |||||
| LgP14 | 11.4 | 0.001 | A | 57.6 ± 13.7 | 7.5 ± 5.4 | 4.6 ± 4.6 | −0.649 ± 0.477 | 0.288 ± 0.352 | |
| D | 17.9 ± 8.5 | 14.6 ± 8.9 | 0.007 ± 0.003 | 0.002 ± 0.002 | |||||
| T | 20.7 ± 7.7 | 19 ± 7.6 | 1.293 ± 0.343 | −0.104 ± 0.265 | |||||
| M | 12.6 ± 4.4 | 7.8 ± 4.8 | 13.725 ± 5.209 | 7.073 ± 4.015 |
- MIM, multiple interval mapping; QTL, quantitative trait loci; % V Exp., percentage of variance explained by the QTL; % adV Exp., percentage of additive variance explained by the QTL.
Although MultiQTL can detect only one QTL per linkage group for any given model, analyses of multiple models allows for detection of more than one QTL region per linkage group. Based on nonoverlap of QTL ranges (+2 LOD), two QTL regions appear each to exist on LgP05, LgP08, LgP10, LgP14, LgP20, and LgP26.
Many of the single- and multi-trait QTL co-map. Limiting attention to regions where multi-trait QTL overlap with at least one single-locus QTL not included in the co-mapping multi-trait model(s), there are six linkage groups fitting the criterion: LgP9 (B and DAWM), LgP13 (P, D, and EMCTW), LgP20 (C and DAWM and EMRDS), LgP24 (P and CRM), LgP25 (S, B, P, and CRM), and LgP27 (P and EMCTW). These regions have effects on between five and nine traits (median=7.5).
We chose four traits with easily interpreted troglomorphic significance for further scrutiny, E, A, T, and M. We identified regions in which QTL with effects on at least three of the traits were found (LgP7 [E, M, and EMT], LgP9 [ADTM], LgP13 [E, T, and EMT], LgP14 [ADTM and EMT], LgP19 [EMT], LgP20 [E and DAWM], and LgP27 [EMT]), and calculated their average substitution effects within each of these regions. To characterize these regions by their substitution effects, we averaged separate estimates from single-trait (N=7 estimates) and multi-trait models (N=41 estimates), and standardized the effects for comparison among traits by dividing them by the trait range observed in the F2. The results are shown for the analysis of multi-trait models only (Fig. 2), but the results including the single-trait estimates are almost identical.

Standardized cave allele substitution effects for four traits in QTL clusters on seven linkage groups in Astyanax mexicanus. E, relative eye size; A, amino acid sensitivity; T, number of maxillary teeth; M, melanophore count. Substitution effects were standardized against the appropriate phenotypic range in the F2. Positive (negative) values denote increases (decreases) in size, sensitivity, or counts. QTL, quantitative trait loci.
Eye size effects are present in six of the seven regions and are consistently in the direction of reduction; melanophore effects are present in all seven and are variable in polarity. We observed this previously with single-trait QTL and interpreted it as evidence that eyes are selected against in the cave environment whereas melanophores decrease through random mutation and drift (Protas et al. 2007). We also expected the cave alleles to cause increased numbers of maxillary teeth and increased sensitivity to dissolved odorants (Jeffery 2001). Of the 10 effects on these two traits we detected, seven were for increases, but three were for decreases, including substantial negative effects on tooth number and amino acid sensitivity on LgP9 and LgP14, respectively.
Thus, each of these regions influences most or all of these traits with effects that are variable in magnitude and polarity. These regions also affect other traits we identified in our QTL analysis but were ignored here to simplify the analysis. Undoubtedly, other coevolved traits have escaped our attention. Thus, these clusters are both numerous and phenotypically complex.
Are these clusters simply artifacts of a clumped distribution of genes in the genome and, therefore, of trivial significance? If some areas in the Astyanax genome are gene-rich and others gene-poor, we would expect to observe clusters of cave-related or other QTL. To test whether the clumped distribution of QTL reflects variation in gene density among regions, we compared the distributions of QTL and mapped genes. We mapped 12 genes, six of which are located within the one LOD estimation intervals of single trait QTL. This exceeds the expectation of five overlaps, based on the 890 cM total coverage of these intervals, by one. The test is biased toward overlap, however, because the genes were not randomly chosen; 11 of them were mapped as candidates for cave related traits, and two of the six that overlap are candidates for the co-mapping traits. GH is a candidate for its co-mapping length QTL, and Oca2 is a candidate for its overlapping eye size QTL (with a proposed link through its effect on the composition of the retinal pigmented epithelium). Considering more general associations between genes and QTL rich linkage groups, only one gene was found in one of the nine linkage groups with both multi-trait and single-trait QTL (LgP9 and Idh2), whereas the other 11 were found in 10 of the remaining 20 linkage groups.
DISCUSSION
Trait clusters similar to those in Astyanax have been observed before (reviewed in Falconer and Mackay 1996). Genes for developmental functions in maize tend to be clustered (Khavkin and Coe 1997), as are genes for domestication traits in rice and wheat (Cai and Morishima 2002; Peng et al. 2003). In Arabidopsis thaliana, QTL for floral traits are clustered in the genome, as are QTL for vegetative (leaf) traits. There is little overlap between the two, leading to the hypothesis that the clusters represent “independent modules” largely dedicated to the development of one organ or the other (Juenger et al. 2005). Similar organ-specific modularity has been observed in Mimulus guttatus (Hall et al. 2006). One hypothesis, drawn from a review of diverse organisms, is that functionally related genes or those that are co-expressed tend to cluster in order to facilitate their coordinate expression (Hurst et al. 2004).
In some cases, the co-mapping of QTL for functionally related, although quite different, traits is striking. QTL for uptake of various mineral ions and/or survivorship co-map on three different linkage groups in wild sunflower hybrids (Helianthus spp.) raised in a salt marsh environment (Lexer et al. 2003). QTL controlling host plant-specific fecundity and host plant choice co-map in four different genomic regions of the pea aphid (Acyrthosiphon p. pisum), and at least two of the regions also correspond between different host-specialized races (Hawthorne and Via 2001). In Heliconius butterflies, a single QTL-controlling male mate preference for species specific wing color maps to the wingless locus, which is also the candidate for the forewing color switch gene (Kronforst et al. 2006). In each of these cases, the functional association of traits and the close co-mapping led to the suggestion that the basis for the clustering might be pleiotropy, although tight linkage of distinct loci could not be ruled out. In Drosophila melanogaster, a single gene, desat1, has been shown to control both the production and discrimination of sex-specific pheromones, presumably by pleiotropic effects of the single gene on different pathways (Marcillac et al. 2005).
Why are QTL for co-evolved traits clustered in the Astyanax genome? Clusters of QTL effects could result from the tight linkage of separate genes, or the pleiotropic effects of single genes. If multigenic, the sites could reflect genomic organization existing before the cave colonization, or genomic reorganization subsequent to it.
We cannot rule out any of these possibilities through QTL mapping, and some or all may play roles in the present case. Not all seem equally likely, however. Our data, although still preliminary, reveal no positive association between mapped genes and QTL, suggesting that the clustering of QTL does not reflect major genomic heterogeneity in gene density. It also seems unlikely that many of the clusters predated entry into the cave. Although some of the traits might be controlled in common, it is hard to see, for example, what unites eye size, melanophore number, condition factor, number of maxillary teeth, rate of weight loss, olfactory sensitivity, depth of the caudal peduncle, and placement of the dorsal fin—all mapping to one small region of LgP13—other than their co-evolution in a cave environment.
It also seems unlikely that there has been enough time for significant genomic rearrangement to have occurred after the fish colonized the cave. Astyanax only reached Central America from South America at the end of the Tertiary, probably not arriving in Mexico until the mid-Pleistocene (Mitchell et al. 1977). Could 1 million years (My) have been sufficient to create the observed clusters by rearrangement? In mouse and human genomes, major rearrangements (translocations and large inversions) are estimated to occur at rates on the order of 0.75 to 1.5/My (Lander et al. 2001; Pevzner and Tesler 2003; Sankoff and Mazowita 2005). Smaller inversions (300–800 bp) are more common, however, with calculations of about 8000 such events separating the two species (Kent et al. 2003; Sankoff and Mazowita 2005). The divergence of humans and mice is estimated variously at 83–96 Mya (Huchon et al. 2002; Nei and Glazko 2002), thus, the average rate of these smaller events in each line was approximately 45/My. Measurements of the nuclear DNA content of five species of Astyanax correspond to a genome size 45% that of humans (Carvalho et al. 2002). If the rate of modestly sized rearrangements, corrected for genome size, is similar in Astyanax to rates in mammals, we can estimate that about 20 such events occurred in the line leading to the cave fish after isolation from the surface. Such small numbers of modestly sized rearrangements could not account for the degree of clustering we observe. Even if the rate of genomic reorganization in Astyanax was an order of magnitude higher than in mammals the conclusion would remain the same.
Another possibility is that genomic rearrangements created these clusters much earlier in Astyanax history during previous cave-dwelling episodes. For example, in Gasterosteus aculeatus, reduction of lateral plates has proceeded in parallel in recently derived lacustrine populations due to selection for alleles at the ectodysplasin locus which exist in low frequencies in marine source populations (Colosimo et al. 2005). The widespread distribution in marine populations of an allele with no selective advantage and possible deleterious effects may reflect a history of repeated freshwater invasions by stickleback populations known to date back to the Miocene (Bell and Foster 1994). As a second example, apple-infesting populations of Rhagoletis pomonella in the Northeast United States are recently derived from stocks traditionally infesting hawthorn. The genetic changes facilitating this host switch, however, represented preadaptations evolved in allopatric Mexican populations and introduced into the Northeast by gene flow (Feder et al. 2003). If ancestral Astyanax populations have a long history of exposure to subterranean existence, genomic rearrangements might have brought genes for relevant traits into closely linked modules or supergenes, haplotypes of which were favored in evolution of the Pachón population. This seems unlikely in Astyanax, however. First, we have no evidence of such a history. Second, cave phenotypes, especially reduced eyes or pigmentation, would be quite detrimental aboveground and not likely to be carried far in fish species expanding their ranges.
Pleiotropy has often been hypothesized to drive regressive evolution in cave animals through indirect selection. Emerson (Allee et al. 1949) argued that as many traits are under the control of genes with pleiotropic effects, selection on one of these traits would produce changes in other traits, most of which would result in regression or degenerative changes, because most mutations were deleterious. In short, Emerson predicted pleiotropy as an engine of regressive evolution, a view subsequently taken as plausible or likely by others (Krekeler 1958; Barr 1968; Culver 1982; Poulson 1985; Sket 1985; Borowsky and Wilkens 2002; Yamamoto et al. 2004).
Wright argued strongly that a “practically universal pleiotropy” was key to the evolution of structural reduction and emphasized that “the momentary selective advantage of … an allele is the resultant of components, positive or negative, from effects on numerous characters. Direction of change of gene frequencies is controlled almost wholly by the more important of these components” (Wright 1964). As examples in Astyanax where regressive changes in one trait could be driven indirectly by selection for changes in another, selection for more robust jaws and more tastebuds (Yamamoto et al. 2004) or more efficient metabolism (Borowsky and Wilkens 2002) have been suggested to drive to regression of eyes or pigmentation, and at high rates not possible through random mutation and drift alone.
Although we endorse this view, we suggest that pleiotropy has a broader role in troglomorphic evolution and may be the most parsimonious explanation for the numerous QTL clusters we observe and the diversity of their component traits. Pleiotropy is more an attribute of alleles than of loci. One allele at a locus could affect one set of pathways whereas another could affect a different set. Applying Wright's insight to the present example, we hypothesize that when the fish first entered the cave environment, numerous loci were potentially capable of giving rise to QTL clusters, but only a small number eventually sustained new mutations (or had precave rare allelic variants) with relevant sets of pleiotropic effects. These alleles were fixed by selection on the consensus of their strongest positive effects, creating the modern day associations. This scenario would account for the large number of clusters we observe, their richly diverse phenotypic contents, as well as the sometimes counterintuitive polarity of substitution effects of some of their constituents. For example, if more teeth and greater sensitivity to dissolved odorants are really of advantage in the cave environment, how would we explain the relatively large negative substitution effects for these traits on LgP9 and LgP14 (Fig. 2)? The directions of these effects would be difficult to account for if every trait in a cluster was controlled by its own locus. On the other hand, if each cluster of trait effects represents a single pleiotropic allele, then the positive effects on some traits could outweigh the negative effects on others. On LgP9, for example, the increase in amino acid sensitivity might outweigh the decrease in number of teeth; on LgP14, the decrease in eye development and the increased number of teeth might outweigh the loss of amino acid sensitivity.
Thus, while not excluding the possibility that some of the QTL clusters have a multigenic basis, the data suggest that a significant portion of the complexity and diversity of the QTL clusters in Astyanax may reflect pleiotropy. This hypothesis is testable through its two predictions: the first is that independently derived cave populations of this species will prove to have comparable numbers of QTL clusters with similar constituent traits, but they will appear at different loci. The second is that when the genes underlying some of these QTL are identified and tested by transgenesis, multiple traits will be rescued or altered by wild-type alleles differing from cave alleles by single substitutions.
Acknowledgments
This study was supported by grants from the US National Science Foundation (IBN0217178; CT and RB) and US National Institutes of Health (1RO3EYE016783-01; RB). We thank A. Korol for invaluable advice on the analyses, L. Mekios for numerous contributions to the maintenance and phenotyping of the animals, B. Borowsky, for fruitful discussion and criticism, and H. Ajmera, B. Esenther, L. Nirenstein, and M. Saraghi for phenotyping.




