A Rapid-Response Economic Evaluation of the UK NHS Cancer Reform Strategy Breast Cancer Screening Program Extension via a Plausible Bounds Approach
ABSTRACT
Objectives: The 2007 National Health Service Cancer Reform Strategy includes a proposed extension of the UK breast screening program to women aged 47 to 49 years. The aim of this study is to undertake a preliminary assessment of this proposal to identify the key factors determining its cost-effectiveness and to determine whether there is sufficient uncertainty that requires more thorough analyses.
Methods: An economic model was constructed. For simplicity, the health impact of screening was estimated by calculating the lives saved through shifts in prognostic group. A “plausible bounds” approach was used to derive distributions for model parameters for probabilistic sensitivity analysis. UK data were used to populate the model.
Results: The cost-effectiveness of the extension is estimated to be £27,400 per quality-adjusted life-year (QALY) with a 29% probability of cost-effectiveness at a threshold of £20,000 per QALY. The deterministic estimate of benefit becomes negative if the anxiety due to a false-positive result is set at 0.028 QALYs. Including a small positive benefit from a negative screen has a dramatic impact on the cost-effectiveness of screening. The impact of other factors appears less marked.
Conclusions: Because the vast majority of women aged 47 to 49 years will test negative when screened for breast cancer and most of those who test positive will actually be free of the disease, the psychological impacts of screening are likely to drive cost-effectiveness for this age group. Therefore, a research priority should be to better understand and quantify these effects.
Introduction
The UK National Health Service breast cancer screening program (NHSBSP) was introduced in 1988. Initially targeted at women aged 50 to 64 years, it was extended to include women aged 65 to 70 years following the recommendations of the 2000 NHS Cancer Plan [1]. The program involves inviting women to be screened once every 3 years and has led to a reduction in UK breast cancer mortality [2]. Following the recommendations of the 2007 NHS Cancer Reform Strategy [3], further extension of the NHSBSP is planned in England, including an extra screening round targeted at women aged 47 to 49 years.
Randomized control trials have demonstrated the ability of screening by mammography to reduce breast cancer mortality [4]. Nevertheless, a significant period of time has passed since these trials were conducted. Improvements in breast cancer screening and treatment prevent the direct application of findings from these trials to policy proposals such as the Cancer Reform Strategy. Furthermore, the age of the population being screened and the proposed frequency of screening differ from trial protocols. Mathematical modeling can be used to synthesize trial results, routine data, and resource use information to evaluate the cost-effectiveness of specific screening programs [5]. The Cancer Information and Surveillance Modelling Network (CISNET) breast cancer screening project represents a state-of-the-art example of the use of modeling to evaluate the relative contribution of screening and adjuvant therapy to reducing breast cancer mortality in the United States between 1975 and 2000 [6]. The CISNET project involved a range of modeling approaches with different biologic assumptions and illustrated the challenges involved in modeling the effectiveness of breast cancer screening, and the level of research time and resources required to develop such models.
The analysis necessarily becomes even more complex if it is to address cost-effectiveness as well as efficacy. The direct costs of screening can be assessed with little difficulty. Nevertheless, by leading to detection at an earlier stage, screening will reduce the need for more aggressive treatments such as mastectomy. The resource implications of this are difficult to estimate [7]. A further complication arises in determining the scope of costs and benefits to include in the analysis. In particular, assessing the psychological impact of screening on participants is far from straightforward. If a woman is told that she has, or may have, breast cancer, it will clearly cause considerable distress in the short term, although the longer-term consequences will depend on whether or not the disease is actually present. This harm will be subjective, personal, and difficult to measure, which makes its inclusion in any quantitative evaluation of the screening program problematic. Nevertheless, the anxiety induced in the short term is likely to be marked, and any such evaluation would be strengthened greatly by including it. In younger women, breast cancer prevalence is lower, and mammography has a lower positive predictive value [8]. This will increase the impact of anxiety from false positives on the cost-effectiveness of screening for this age group.
Receiving such a false-positive diagnosis may also influence a woman's decision to attend further screening rounds, although the impact is not easy to predict. It may lead to a loss of faith in screening, and hence reduced participation; alternatively, it may lead to greater awareness of the disease and an increase in compliance. A recent systematic review of this issue found that compliance among women who had previously received a false-positive diagnosis, compared with those who had not previously been screened, was 20% lower in Canada, comparable in Europe, and 7% higher in the United States [9]. A study of women who had received false-positive results in the NHSBSP found that their compliance rate fell by 2.7% [10].
Objective
As a result of the complexities described above, an exhaustive evaluation of the proposed screening program extension would be a lengthy exercise. Policymakers may be willing to trade off a degree of precision for timeliness in a rapid-response analysis. This initial work would have two goals—to provide a timely order-of-magnitude estimate of the cost-effectiveness of the proposal and to determine which factors do and do not have a meaningful impact on the estimate, to guide the scope of any further analysis or data collection that may be considered necessary. Our objective was to perform this rapid-response evaluation for the proposed screening round aimed at women aged 47 to 49 years.
Methods
The length of time needed to carry out model-based evaluations of breast cancer screening is driven by the difficulties of developing and populating complex representations of breast cancer natural history and the impact of screen detection on prognostic factors and subsequent outcomes [11]. Our aim was to develop a model structure that reduced, where practicable, the number of parameters and biomedical assumptions required. To ensure that the model was populated in a timely fashion and that the degree of uncertainty was accurately reflected, an approach was adopted that we describe as a “plausible bounds” method. This method can be used in situations when data that directly inform a parameter value are not readily available (in this case, because data are not available specifically for the age groups at which the intervention is targeted). If data can be identified which, for well-grounded clinical reasons, give an underestimate of the parameter, this places a lower limit on the value needed. If a second data set can be identified that provides an overestimate, then an upper limit can be defined, giving a range that is highly likely to contain the true value. Plausible bounds for the screening model were represented as distributions on the parameters to inform probabilistic sensitivity analysis (PSA). Data that reflected the UK context of the decision were preferred. This led us to rely on data from the existing screening program, supplemented with data from a UK trial of screening in women aged 40 to 49 years [12], for the bulk of information used.
Model Structure
The model (Fig. 1) simulates the experience of a hypothetical cohort of 10,000 women aged 47 to 49 years attending a single breast cancer screening appointment. Initially, the number of women who are referred for further investigation is estimated. From this group, a proportion of women receive diagnoses of breast cancer. Both the initial cost of screening and the costs of further investigation to identify those with breast cancer are included in the model. For those who have breast cancer, disease severity is classified according to the Nottingham Prognostic Index (NPI) prognostic groups—ductal carcinoma in situ (DCIS), excellent, good, moderate, and poor [13]. The model estimates the proportion of screen-detected cases in each of these groups. As a comparator, it also estimates the proportions that would be observed if the screening round under evaluation had not taken place. Using data on the treatment costs and 10-year survival (a proxy for cure) for each group, the model estimates the impact of the screening program on treatment costs and mortality for the cohort. A basic model of the impact of screening on mortality is used, which assumes that all those who are saved through screen detection (i.e., the difference in mortality resulting from improved prognosis, multiplied by the size of the cohort) would otherwise have died 5 years after the date of screening.
Model structure and information requirements.
The model translates improved mortality into disease-free quality-adjusted life-years (QALYs) gained, using data on age-adjusted quality of life [14]. This allows a full cost-utility analysis to be carried out. Where appropriate, parameters used in the model are specified as stochastic variables. This allows PSA to be performed via Monte Carlo simulation, and a cost-effectiveness acceptability curve to be produced, for a reference case where the impact of screening was limited to improved survival, direct costs of screening, and changes in treatment cost. There were additional factors for which the uncertainty could not be quantified for inclusion in the PSA. These were the impact of false-positive results on short-term anxiety and on compliance with future screening rounds, the reassurance arising from a negative screen and the impact of technological improvements to mammography. Separate one-way sensitivity analyses were carried out for these factors. These analyses represented psychological impacts in QALY terms, because a common yardstick is required to combine mortality and morbidity, and the National Institute for Health and Clinical Excellence (NICE) methods guide recommends the use of the QALY for this purpose [15].
Derivation of Model Parameters
To estimate the number of cancers detected by screening, the model samples the number of positive results in the cohort and combines this with an estimate of the percentage of women testing positive that would actually have breast cancer. Data from the UK age trial and the 2006/2007 NHSBSP (Table 1) were used to construct sampling distributions for these parameters for the 40- to 49-year cohort. These data do not provide direct evidence of the required parameters for the relevant cohort, but it allows the construction of a plausible range from which to derive sampling distributions. The UK age trial provides randomized control trial (gold standard) evidence. Nevertheless the age group of interest is older than that reported in the trial and is likely to include significantly more menopausal women. Because mammography is known to have a lower positive predictive value in younger women [8], the trial results can be seen as a lower bound for the model parameters given in Table 2. Conversely, the NHSBSP provides data from an older cohort, which will therefore have a higher percentage of menopausal women than the age group of interest, thus providing an upper bound. Combining upper and lower bounds creates sampling distributions for these model parameters, if it is assumed they represent a 95% confidence interval from a normal distribution. These sampling distributions are given in Table 2.
| Source | Number screened | Referrals | Cancers detected | Referral rate | Positive predictive value |
|---|---|---|---|---|---|
| NHSBSP 2006/2007 first attendees aged 50–52 | 201,627 | 17,400 | 1,515 | 8.63% | 8.71% |
| UK age trial—first attendees aged 40–41 | 35,846 | 1,655 | 37 | 4.58% | 2.2% |
- NHSBSP, National Health Service breast cancer screening program.
| Parameter | Lower bound | Upper bound | Mean | Standard error |
|---|---|---|---|---|
| Referral rate | 4.58% | 8.63% | 6.6% | 1.0% |
| PPV | 2.20% | 8.71% | 5.5% | 1.7% |
The model assumes that all referrals will undergo either a further mammography or an ultrasound and uses the average cost of the two procedures. It also assumes, based on practice in the current screening program, that all patients who ultimately receive diagnoses of breast cancer receive a biopsy, and 2.4% of those who are referred but subsequently found to be disease-free will also undergo this procedure (in the 2006/2007 screening round, there were 69,000 false positives, of whom 1700 [31%] underwent a biopsy) [16]. The vast majority (96%) of these were core biopsies. The costs used are given in Table 3. All costs were obtained from NHS Reference Costs 2005/2006 and uplifted to 2006/2007 prices using standard indices [17].
| Activity | 2005/2006 cost (£) | 2006/2007 cost (2005/2006 + 4.6%) (£) |
|---|---|---|
| Initial two-view mammography | 40 | 42 |
| Further mammography | 67 | 70 |
| Ultrasound examination | 74 | 78 |
| Biopsy—open | 241 | 253 |
| Biopsy—core | 117 | 122 |
To predict the impact of screening on costs and outcomes, the model predicts the proportions of screen-detected cancers in each NPI group and compares this with the proportions for cancers presenting symptomatically. The source data for this are taken from the UK age trial, in combination with analysis from an economic evaluation [7] of the impact of the NHSBSP on treatment costs (Table 4). The proportion of cancers in each NPI group was used to calculate a weighted average treatment cost and survival probability for intervention and control arms of the age trial. The difference between these averages, multiplied by the number of screen-detected cancers, gives the deterministic estimate of the impact of screening the cohort on lives saved and change in treatment costs. Lives saved were translated into life-years gained using standard mortality tables [18] and converted into QALYs using established tariffs for health-related quality of life by age [14]. To avoid lead-time bias, the time of death from breast cancer was assumed to be the same irrespective of screening history, rather than calculating survival from the point of detection. All costs and benefits were discounted at 3.5%, as recommended by the UK NICE [15].
| Prognosis | 10-year survival | Treatment costs £2006/2007 [7] | UK age trial—intervention arm | UK age trial—control arm | UK NHSBSP 2006/2007 | |||
|---|---|---|---|---|---|---|---|---|
| No. | (%) | No. | (%) | No. | (%) | |||
| DCIS | 100 | 7,106 | 69 | 14.7% | 54 | 6.9% | 3185 | 21.3% |
| Excellent | 98 | 8,280 | 31 | 6.7% | 28 | 3.6% | 2628 | 17.3% |
| Good | 90 | 9,392 | 84 | 17.9% | 101 | 13.0% | 4213 | 28.3% |
| Moderate | 79 | 10,481 | 206 | 43.9% | 422 | 54.2% | 4175 | 27.6% |
| Poor | 47 | 12,441 | 79 | 16.8% | 173 | 22.2% | 778 | 5.5% |
| Weighted average: survival | 80.0% | 75.4% | 88.1% | |||||
| Weighted average: treatment cost | £9972 | £10,452 | £7917 | |||||
- NHSBSP, National Health Service breast cancer screening program; DCIS, ductal carcinoma in situ.
The intervention arm of the UK age trial will not necessarily give the correct prognostic profile of the cancers that would be detected by the proposed screening round. The population is younger on average, and the intervention arm includes interval cancers and nonattenders. These factors will lead to the stage shift from screen detection being underestimated. At the same time, using the prognostic profile of screen-detected cancers will lead to an overestimate of the benefits of screening due to length bias—the fact that less aggressive cancers will be over-represented in a screen-detected group of cancers. Furthermore, the estimate does not take into account the fact that some of the cancers detected in the proposed screen may have been picked up in the first screen of the current screening program. In a UK context of triennial screening, this omission is unlikely to be material because most cancers will have either presented within 3 years or have progressed markedly. Nevertheless, it will add to the degree of overestimation of the benefits of screening.
To represent the additional uncertainty, we again applied the plausible bounds approach. Table 4 gives the NPI profile for cancers detected in the current UK screening program and presents a calculation of the weighted average survival and treatment cost for this group. Because this represents an older population, who will have proportionately fewer aggressive tumors, this group will have a more favorable prognostic profile than the cancers detected in the 47- to 49-year age group. It was therefore used to set the upper bound for the improvement in survival and treatment costs saved due to screen detection. Zero is a natural lower bound for the survival impact and treatment cost savings due to screen detection. Therefore, a log-normal distribution was used to represent the uncertainty around these parameters in the PSA, with a mean given by the difference in the arms of the UK age trial (4.6%, £480) and a 97.5 percentile given by the difference between the age trial control arm and the UK NHSBSP (12.7%, £2535). Because both survival and treatment cost depend on stage shift, the two distributions were assumed to be perfectly correlated.
Results
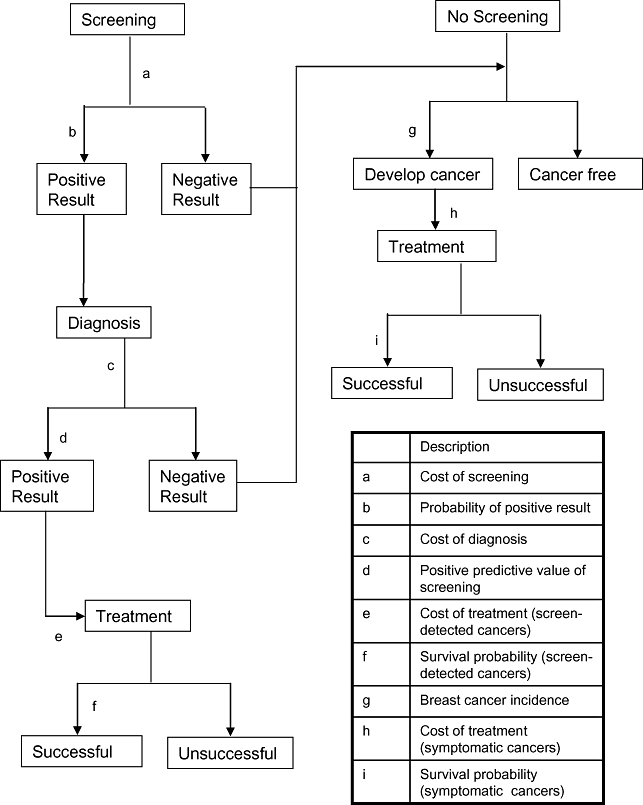
Using point estimates for all parameters, it was estimated for the base-case that 36 cancers would be detected per 10,000 women screened. Table 4 suggests that the point estimate for the absolute improvement in survival from screen detection is 4.6% (80.0% minus 75.6%), giving a total of 1.66 (36 × 4.6%) lives saved per 10,000 women screened. Using UK all-cause mortality data and age-adjusted QALY tariffs, as described above, this translated into a gain of 17.5 QALYs. Screening costs for the cohort were £420,000. The cost of diagnosis for positive results would be £70,000, and screening would lead to a saving in treatment costs of £17,000 (£480 per screen-detected cancer, calculated from the difference in treatment costs for the trial control and intervention arms in Table 4), giving a net cost of screening of £473,000 per 10,000 screened and an incremental cost-effectiveness ratio (ICER) of £27,400. Figure 2 presents the results of the PSA. The base-case PSA suggests that there is a moderate possibility that the intervention is cost-effective for the 47- to 49-year cohort. At a willingness-to-pay threshold of £20,000 per QALY, there is an estimated 29% probability that the additional screening round is cost-effective, rising to 52% if the threshold is set to £30,000 per QALY gained. The probabilistic mean was £23,700 per QALY gained.
Cost-effectiveness acceptability curve.
Several one-way sensitivity analyses were undertaken on parameters where plausible bounds could not be established. First, the model assumes that survival from screen detection for cancers that would prove fatal if not screen-detected is 5 years. Extending this by 2 years increases the ICER to £30,100 per QALY gained. This suggests that varying the estimated mean survival time for a fatal cancer does not have a dramatic impact on the cost-effectiveness of screening this cohort.
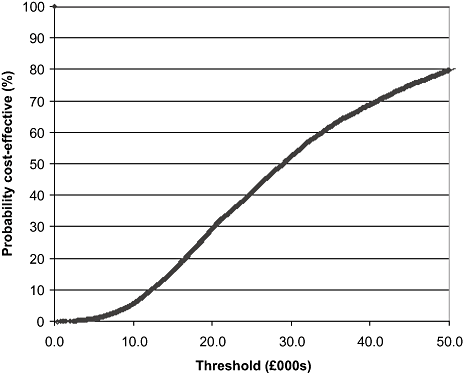
The deterministic base-case was then repeated adding a disutility, in terms of a QALY loss, reflecting the short-term anxiety of a false-positive screen. Table 5 shows the impact on cost-effectiveness of assigning a range of values to this disutility. Even if the anxiety caused by the false-positive result is assumed to be low, the impact is marked. At 0.002 QALYs per false-positive result, the deterministic estimate of cost-effective rises to £30,000 per QALY. Beyond 0.028 QALYs per false-positive result, the expected impact of screening on the health of the cohort is negative and the intervention is not cost-effective at any threshold. A similar sensitivity analysis within the probabilistic model was performed. Figure 3 shows the impact of increasing values for short-term anxiety on the probability that the intervention is cost-effective at the thresholds commonly used by NICE in the UK. Even if quite low values are used, this parameter once more has a noticeable impact on the strength of the model's conclusions. At 0.03 QALYs per person, the probability that the intervention is cost-effective falls to 2% at a threshold of £20,000 per QALY, and 3% at a threshold of £30,000 per QALY.
| Anxiety due to false-positive result (QALYs) | 0 | 0.01 | 0.02 | 0.03 |
| Incremental cost-effectiveness ratio (£) | 27,000 | 43,000 | 96,000 | Dominated |
- QALY, quality-adjusted life-year.
Impact on probability of cost-effectiveness of including false-positive anxiety. QALY, quality-adjusted life-year.
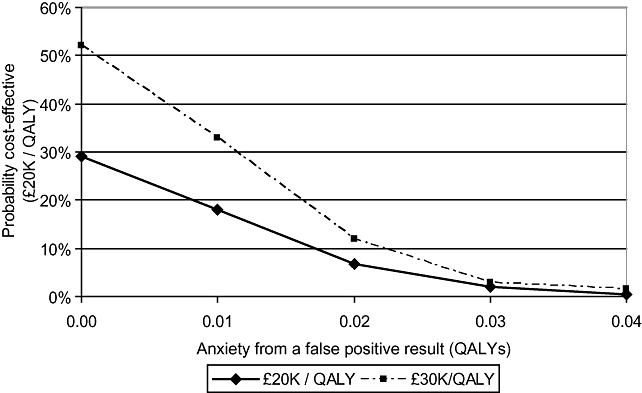
There may be positive, as well as negative, psychological consequences from being screened. A recent study of attitudes to mammography in women aged more than 70 years found that some valued the reassurance that a negative result gave them [19], and there is no reason to suppose this would be different for other age groups. Figure 4 illustrates the degree to which reassurance can offset the anxiety from false-positive diagnoses, by illustrating the combined values at which the deterministic estimate of incremental cost-effectiveness is £30,000 per QALY gained. It suggests that even if the individual benefit (in QALY terms) of this reassurance is low, the cumulative impact on cost-effectiveness is dramatic.
Combinations of false-positive anxiety and reassurance giving a cost-effectiveness ratio of £30,000 per QALY. ICER, incremental cost-effectiveness ratio; QALY, quality-adjusted life-year.
False-positive results may also have an impact on participation in subsequent screening rounds. The influence of this factor on the overall incremental cost-effectiveness of the additional screening round will depend on the direction and degree of the change in compliance, and the cost-effectiveness of the screens missed. Therefore, substantial data collection and analysis is required to quantify this influence. To assess whether such an effect is justified, a simple estimate of its size was determined. It was assumed that the total costs per attendee of each screening round are likely to be similar to those in the proposed intervention, which the model suggests are approximately £45. If the existing program is assumed to be moderately cost-effective at around £15,000 per QALY gained, this would imply a benefit of 0.003 QALYs per participant. It was assumed that compliance would either be complete or nil, so that all those who comply with the main program attend seven screening rounds. Discounting at 3.5%, this gave net present costs and benefits of attending the NHSBSP of £208 and 0.014 QALYs. These were assumed to be the costs and benefits lost per person choosing not to attend the existing program. Applying this approximation to a one-way sensitivity analysis of our base-case, it was found that a 40% reduction in participation was required in the false-positive group to raise the ICER to £30,000 per QALY gained, and that an increase of a similar magnitude would reduce the ICER to £25,000 per QALY gained. Therefore, even substantial changes in participation have a modest impact on cost-effectiveness.
Technological change can affect the performance, and therefore the cost-effectiveness, of a screening test. It has been demonstrated that digital mammography has significantly greater sensitivity (up to 40% relative improvement) than film-based mammography in the less than 50s [20]. The model can be used to explore the likely implications of improved technology on the cost-effectiveness of the proposed intervention using threshold analysis. Assuming an ability to detect 40% more cases of breast cancer in the model cohort (50 rather than 36 cases per 10,000 screened) improves the QALYs gained through screening from 17.5 to 24.2 per 10,000 screened. Offsetting this gain will be an increase in the costs of the test itself. This has been assumed to be £42 for the standard test. To restore the cost-effectiveness ratio found in the base-case, the cost of digital mammography would need to be at most 45% higher (£61). Beyond £69, the overall cost-effectiveness of the extra screening round exceeds £30,000 per QALY gained, the upper range of commonly quoted willingness-to-pay thresholds. This is only an exploratory analysis, but it does suggest that even a substantial improvement in test performance would be outweighed by fairly modest increases in cost.
Discussion
Our aim in this preappraisal was to assist decision-makers in two ways. First, we aimed to assess the need for a detailed analysis of the extension to the UK breast screening program proposed by the Cancer Reform Strategy by exploring how likely it was that it would be cost-effective compared with the status quo. Second, and perhaps more importantly, it was our aim to investigate the importance of factors that are cumbersome to evaluate and include in the decision analysis, to determine whether their impact on the conclusions made such an effort worthwhile. We acknowledge that our analysis has involved considerable simplification and approximation. Nevertheless, based on our use of the plausible bounds approach and data that are both recent and directly relevant to the decision being evaluated, we believe that our results are of the correct order of magnitude. Our estimate is not markedly different to results from assessments of the cost-effectiveness of screening programs targeting the 40- to 49-year age group [21–23].
Our aims, described above, drove our approach to representing uncertainty in the analysis. The “plausible bounds” approach we have adopted was in response to the gap between the information given by the available data and the information needed to populate the model. This is similar to the issue of “external validity” encountered in attempting to base clinical and policy decisions on trials whose circumstances differ from the decision context. If this additional source of uncertainty is ignored, this will lead to PSA that underestimates the true degree of uncertainty facing the decision-maker.
Our approach to this issue was to identify data that gave biased estimates in a direction that could be determined a priori, based on established clinical knowledge. For example, it is known that both the incidence of breast cancer and the sensitivity of mammography are higher in postmenopausal women [8]. It follows that the cancer detection rate in the current screening program will be higher than that in a screened cohort of women aged 47 to 49 years. This process allowed us to include the uncertainty implied by the gap between the available data and the parameters in the models and to represent a priori knowledge quantitatively to avoid overstating the uncertainty in the available evidence base. If every effort is made to confirm with decision-makers and clinical experts that appropriate data have been selected to define the bounds, this process is an efficient way to capture uncertainty in a “rapid response” analysis of the type we have performed.
We have used the plausible bounds approach to capture uncertainty around model parameters wherever possible. The key exception was the QALY impact of the psychological consequences of the screening round. Although there is considerable literature on the potential psychological harm of false-positive mammographies, we are not aware of any attempts to quantify the impact of such harm for inclusion in analysis of the cost-effectiveness. We are also unaware of any quantitative analysis in the literature of a possible psychological benefit to those who receive a true negative diagnosis, despite reassurance being mentioned as an important benefit of screening by some women [19]. Therefore, we undertook one-way sensitivity analyses to identify thresholds at which these effects had a marked impact. This analysis suggests that even at modest levels, psychological effects may drive estimates of the cost-effectiveness of screening. For false-positive anxiety, a value of 0.01 QALYs would reduce the probability that the extension is cost-effective to 25%. If the false positive only leads to distress until the correct result is provided, then this implies the distress is equivalent to a reduction from full health of 0.1 QALYs (assuming a delay of around 5 weeks). If, however, a false-positive result has long-term consequences for mental well-being in a significant proportion of cases, then the short-term impact need not be as severe. A priority for further research should be the quantification of these effects to support decision-making, assessing their magnitude and duration.
The psychological consequences described above have not explicitly been included in decisions to implement the existing screening program. It might therefore be argued that it would be inconsistent to consider these effects in the younger population alone. We would argue that anxiety from false positives will be a significantly less important issue in the current screening program, particularly in later rounds. This is because mammography is more definitive in postmenopausal women [24]. The age of menopause is approximately normally distributed, with mean 51 years and ranging from 40 to 58 years [25]. The cohort benefiting from the proposed extension will therefore have a higher percentage of premenopausal women. This will lead to a higher false-positive rate, which is supported by the data—the false-positive rate was 97.8% in the UK age trial (see Table 1), but only 84% for the current screening program [16]. Even if the psychological impact of screening in the current screening program was thought to be comparable with the proposed extension, we would still argue that it would be inappropriate to ignore such a significant consequence of the policy solely because previous decisions did not explicitly take it into account. If short-term anxiety is found to have a key impact on the cost-effectiveness of screening, this would suggest that the current lower age limit is too low. Nevertheless, this is a choice for decision-makers; our aim is merely to illustrate the strong impact these factors have if they are included in estimates of the cost-effectiveness of the proposed extension to the screening program.
Our estimate of the cost impact of screening includes a component for changes in treatment. Admittedly, ours is an approximate estimate of this impact, although the plausible bounds approach allows us to represent uncertainty around the estimate. This is a challenging cost to estimate, because the impact of screen detection on treatment pathways is complex. Our model suggests that, in this case, this effort may not be worthwhile in assessing the cost-effectiveness of screening, because it is unlikely to be important relative to the costs of screening itself.
Conclusions
Because the vast majority of women aged 47 to 49 years will test negative when screened for breast cancer and most of those who test positive will actually be free of the disease, the psychological impacts of screening are likely to drive cost-effectiveness for this age group. Therefore, a research priority should be to better understand and quantify these effects. Detailed analysis of the survival benefits of screening will only be necessary for policy-making if decision-makers consider the psychological effects to be irrelevant, or research reveals that they are short-term and minor. In that case, changes in treatment costs and subsequent participation resulting from the additional screening round will not materially affect its cost-effectiveness, and further investigation can be simplified by their exclusion.
Acknowledgments
The authors would like to thank Mrs Julietta Patnick CBE for her support of, and advice on, this work.
Source of financial support: The authors would like to acknowledge funding from the UK Department of Health NHS cancer screening unit for this work. The corresponding author was also funded by a researcher development award from the UK Department of Health National Institute of Health Research Capacity Development program. None of the work presented is proprietary information.




