Value of Information Analyses of Economic Randomized Controlled Trials: The Treatment of Intermittent Claudication
ABSTRACT
Objective: The aim of this study is to design the optimal study comparing endovascular revascularization and supervised exercise training for patients with intermittent claudication and to demonstrate value of information (VOI) analysis of patient-level data from an economic randomized controlled trial to guide future research.
Methods: We applied a net benefit framework to patient-level data on costs and quality-of-life of a previous randomized controlled trial. VOI analyses were performed using Monte Carlo simulation. We estimated the total expected value of perfect information (total EVPI), the total expected value of sample information (total EVSI), the partial expected value of perfect information (partial EVPI), and the partial expected value of sample information (partial EVSI). These VOI analyses identified the key parameters and the optimal sample size of future study designs. Sensitivity analyses were performed to explore the robustness of our assumptions about the population to benefit, the willingness-to-pay threshold, and the study costs. The VOI analyses are demonstrated in statistical software (R) and a spreadsheet (Excel) allowing other investigators to apply VOI analysis to their patient-level data.
Results: The optimal study design for the treatment of intermittent claudication involves a randomized controlled trial collecting data on the quality-adjusted life expectancy and additional admission costs for 525 patients per treatment arm. The optimal sample size remained between 400 and 600 patients for a willingness-to-pay threshold between €30,000 and €100,000/quality-adjusted life-years, for even extreme assumptions about the study costs, and for a range of 3 to 7 years that future patients will benefit from the results of the proposed study.
Conclusions: 1) The optimal study for patients with intermittent claudication collects data on two key parameters for 525 patients per trial arm; and 2) we have shown that value of information analysis provides an explicit framework to determine the optimal sample size and identify key parameters for the design of future clinical trials.
Introduction
The adoption of new medical interventions depends nowadays on evidence of cost-effectiveness in addition to evidence of effectiveness. Consequently, economic data are increasingly collected alongside clinical trials. We performed an economic trial to compare endovascular revascularization and supervised exercise training for patients with intermittent claudication [1]. Considerable uncertainty about the optimal cost-effective medical intervention remained after analysis of the trial. Given this uncertainty, policymakers should address two separate decisions: which intervention should be reimbursed and, is more research—for example, a larger economic trial—justified [2]? More quantitative research could be justified, because a decision based on a trial with a finite sample size can be wrong: that is, the intervention that is identified as optimal may not be the actual optimal intervention. A future study could justify a change in current care which may result in an improvement in quality-adjusted life expectancy (QALE) of future patients and a decrease in health-care costs. However, the actual benefit of a future study is uncertain. Before embarking on an expensive study, funding agencies like to know the expected study cost. Money spent on such a study cannot be spent otherwise, for example, to fund another study or reimburse a new treatment. The cost of a study is usually specified in a grant proposal. The expected benefit of a study typically receives little formal consideration. The challenge of deciding whether more research is justified is to make the cost–benefit trade-off of future clinical research prior to performing it. More research is justified only if the expected benefit exceeds the cost of a proposed study.
Value of Information (VOI) analysis provides a framework to guide the cost–benefit trade-off of future cost-effectiveness research prior to performing it. VOI analysis estimates the expected benefit of a future study using available evidence (e.g., a previous randomized controlled trial) about a decision. VOI analysis can guide the design of a study that maximizes the difference between the expected benefit for future patients and the expected cost of the study. This study is characterized by its design (e.g., randomized or observational), the subset of sampled parameters (e.g., quality-of-life only, or a selection of cost parameters), the sample size, and the associated study costs. Claxton et al. have demonstrated the feasibility of VOI analysis to guide the research priority setting of the National Health Service in the United Kingdom [3].
Most published VOI analyses involve decision models [4]. Economic trials, however, are attractive for VOI analysis because of their high internal validity. VOI analyses can be performed in addition to conventional analyses of economic trials [5]. They offer a sound alternative to significance testing when deciding if more research is needed. Moreover, VOI analysis provides a framework for sample size calculation. Based on patient-level data from an economic trial, VOI analysis can determine the optimal sample size of a future trial. The same methods can be used when patient-level data from a previous trial are not available, using elicited estimates with uncertainty intervals of the outcomes. Ideally, a VOI analysis is performed before and after a clinical trial.
The first objective of this article is to design the optimal study comparing endovascular revascularization and supervised exercise training for patients with intermittent claudication. The second objective is to demonstrate VOI analysis of patient-level data from an economic randomized controlled trial to guide future research. In the following section, we briefly discuss the clinical problem, study design, and results of a previous trial of patients with intermittent claudication. Next, we explain the concepts and demonstrate the methods of the different VOI analyses, focusing on the application of VOI analyses to patient-level data from economic trials. The analyses are explained using mathematical notation (conform Ades [6]) and step-by-step algorithms, specifically for VOI analysis of patient-level data of economic trials. We used Monte Carlo simulation to obtain the VOI estimates. In the appendix, which can be found at: http://www.ispor.org/Publications/value/ViHsupplementary/ViH13i2_Hunink.asp, we present detailed instructions to perform VOI analyses on patient-level data using a spreadsheet such as Excel and statistical software such as R [7,8].
Treatment of Intermittent Claudication
Randomized Controlled Trial
Intermittent claudication is the mildest form of peripheral arterial disease. Patients suffer from a limited walking distance due to inadequate circulation of the legs. The treatment goal for intermittent claudication is to improve health-related quality-of-life. The general consensus is to treat these patients initially with exercise training [9]. Endovascular revascularization seems an attractive alternative with the advantage of immediate clinical success [10]. However, the drawbacks of endovascular revascularization include procedure-related morbidity and mortality as well as increased costs [11,12].
Between September 2002 and September 2005, 150 patients with intermittent claudication were randomly allocated to endovascular revascularization or supervised exercise training [1]. During 12 months of follow-up, all medical and nonmedical costs (11 cost parameters) were assessed from the societal perspective and effects were measured with the EuroQol-5D questionnaire. We transformed the EuroQol-5D values into utilities using the Dutch scoring algorithm [13]. The improvement in quality-adjusted life-years (QALYs) accumulated during the 12-month follow-up period was then used as effect measure in the cost-effectiveness analysis. We refer to the original article for more details on the study design, analyses, and results [1]. The original article presented results with adjustment for age and gender. Here, we used unadjusted data for the VOI analyses. The improvement in QALYs was higher in the revascularization group than in the exercise group (mean difference 0.08; 95% confidence interval [CI] 0.04, 0.12). The total mean cumulative cost per patient was also higher in the revascularization group than in the exercise group (mean difference €4254; 95% CI €1648, €7734).
Cost-Effectiveness Analysis
We adopted the net benefit approach to cost-effectiveness analysis [14]. A decision between two strategies based on both costs and effect can only be made if a trade-off is made between cost and effect by putting a monetary value on health. We used a societal willingness-to-pay threshold (WTP) of 80,000 euros per QALY, as has recently been recommended by a Dutch governmental institute [15]. Cost and effect (in this case, QALE) are combined into a single outcome called net (monetary) benefit: net benefit = WTP*effect − costs.
The net benefit is expressed in euro. The mean net benefit is denoted by B. The difference in mean net benefit between the two interventions is the incremental mean net benefit (IB). The uncertainty interval for the IB was estimated parametrically and non-parametrically [14]. The parametric intervals assume a normal distribution of the IB, justified by the central limit theorem. To check this assumption, we also performed nonparametrical bootstrapping using 1 million bootstraps [16].
The revascularization group had a higher net benefit (€4486 vs. €2316 per patient), but the difference in net benefit was not significant (mean difference €2170; 95% CI €−2818, €6685). Based on these results, we can conclude that revascularization seems cost-effective, but considerable uncertainty remains. Figure 1 presents the incremental net benefit (IB) in euro with 95% uncertainty interval across a range of values for the WTP in euro/QALY. The bootstrapping results showed that assuming normal distributions was justified.
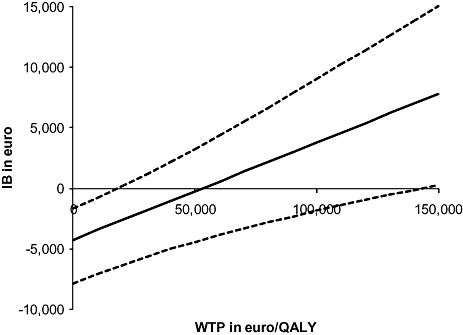
The incremental net benefit (IB) for the revascularization strategy in euro with 95% uncertainty boundaries based on 1 million bootstraps of patient-level net benefits, across a range of values for the willingness-to-pay threshold (WTP) in euro/QALY.
Total Expected Value of Perfect Information (EVPI)—Eliminating Uncertainty
VOI analysis starts with estimating the total EVPI. It is the expected benefit per patient of a study with an infinite sample size, resulting in perfect information about all (total) uncertain cost and effect parameters. Such a study would eliminate uncertainty about the net benefit of each intervention, but is of course hypothetical. However, the total EVPI provides a ceiling level for the expected cost of a future study; studies with a finite sample size or studies that consider a subset of parameters all have a smaller expected benefit. Therefore, if the total EVPI does not exceed the fixed cost of research, more research is not justified. More research is potentially justified if the total EVPI does exceed the fixed cost of research.
Total EVPI—Equations and Algorithm
The net benefit B(a, θ) of intervention a is a function of θ, where θ stands for the set of all unknown distributional cost and effect parameters involved. If all uncertainty about the parameters would be eliminated, the actual net benefit of each intervention would be known. The cost of not knowing the actual net benefit of each intervention is the cost of uncertainty or the opportunity loss. It is defined as the difference between the maximum actual net benefit, and the actual net benefit of the supposedly optimal intervention (a*):
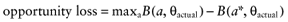
We cannot calculate the opportunity loss, because we do not know the actual parameter values θactual. However, the expected opportunity loss is the expectation over the distribution of the parameters of each intervention. The total EVPI equals the expected opportunity loss:
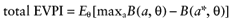
To calculate the total EVPI, the parameters of each intervention must be characterized by a probability distribution based on the data of the initial trial. We can also use the probability distribution of the mean net benefit B(a,θ) of each intervention. Although the net benefit may not be normally distributed in the population, the uncertainty about the mean net benefit typically is (central limit theorem). As the distribution of the mean net benefit, we take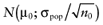 
, for each intervention; µ0 is the estimated mean net benefit in the initial study, for each intervention; σpop is the estimated standard deviation in the initial study, for each intervention; and n0 is the sample size in the initial study, for each intervention. For simplicity, σpop is treated as a known parameter, based on the initial study [6], bj is a random value of the distribution of the mean net benefit for intervention a. The algorithm for the estimation of total EVPI involves the following steps:
- 1
draw a value bj for the net benefit from
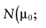
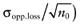, for each intervention a - 2
calculate the opportunity loss:
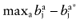
- 3
repeat step 1 and 2 N times
- 4
the total EVPI is estimated by averaging over the opportunity losses at step 2
The standard error of the mean opportunity loss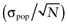 
reflects how precisely the total EVPI was estimated. The process of drawing a random value of each distribution (an iteration) is sometimes referred to as the Monte Carlo simulation.
The Example—Total EVPI
Table 1 presents the results of the Monte Carlo simulation for 10 iterations. Each iteration consists of a random value of the distribution of the mean net benefit of each intervention. For each iteration, the opportunity loss is calculated. For example, exercise was the optimal intervention in the first iteration, and revascularization was the optimal intervention based on the initial trial results. Therefore, the opportunity loss of the first iteration equals €4372 − €3348 = €1024. Based on these 10 iterations alone, the total EVPI is estimated by the mean opportunity loss of €311.
| Iteration | Revascularization | Exercise | opportunity loss |
|---|---|---|---|
| 1 | 3348 | 4372 | 1024 |
| 2 | 7997 | 3198 | 0 |
| 3 | 3129 | 3311 | 182 |
| 4 | 2267 | 2991 | 724 |
| 5 | −466 | 711 | 1177 |
| 6 | 3716 | 2276 | 0 |
| 7 | 3179 | 2220 | 0 |
| 8 | 5204 | 962 | 0 |
| 9 | 3543 | 2435 | 0 |
| 10 | 7679 | 4489 | 0 |
| Mean | 311 |
- EVPI, expected value of perfect information.
A total EVPI of €249 per patient was found with 10 million simulations in R. This means that after eliminating uncertainty, we can expect an improvement in net monetary benefit of €249 per patient. Endovascular revascularization was the optimal intervention given the results of the initial trial, with an expected net benefit of €4486 per patient. With perfect information, the expected net benefit of the optimal intervention (which could be endovascular revascularization or exercise training) is 4486 + 249 = €4735 per patient. The total EVPI per patient should be extrapolated to the entire population that will benefit from the study results, to allow for comparison with the fixed study cost.
Population EVPI and Study Cost
The expected benefit of a study should include the benefit of all future patients from some predetermined perspective: single hospital, health insurance agency, country, or worldwide. The number of years (T) that future patients are expected to benefit from the results of a proposed study is difficult to determine. It depends on the improvement in technology and future evidence. A sensitivity analysis can illustrate the importance of this uncertainty. The expected benefit to future patients is discounted by a discount rate of typically 3% per year, that is, each year further ahead a smaller benefit is assigned on behalf of these patients [17]. The population EVPI equals:
The study costs are typically estimated as fixed cost (e.g., salary of a PhD student) and variable cost per patient in the study [18].
The Example—Population EVPI and Study Cost
Because the initial trial was funded by a national governmental agency, we used the national perspective for the annual population to benefit. This annual population was estimated at 10,000 patients for The Netherlands. We assumed patients would benefit from the results for 5 years and discounted these benefits at 3% per year. We found a discounted population to benefit of about 46,000 patients and a population EVPI of 11 million euros. We estimated the fixed cost of an additional clinical study at 200,000 euros, based on the cost of our previous study. Because the EVPI for the population exceeds the expected costs of an additional study, it is potentially justified to perform some sort of additional study.
Total Expected Value of Sample Information (EVSI)—Reducing Uncertainty
The total EVSI is an estimate of the expected benefit of studies with a finite sample size, collecting information on all cost and effect parameters. Instead of eliminating uncertainty, uncertainty about the mean net benefit of each intervention is only reduced. With increasing sample size, the total EVSI will reach a ceiling which equals the total EVPI, representing an infinite sample size.
Total EVSI—Equations and Algorithm
A proposed study provides data about all cost and effect parameters of n patients for each intervention. The study will improve the mean estimates of the parameter values, and consequently, of the net benefit of each intervention. Once we have observed the actual study data D, the expected benefit of treatment a* is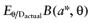 
. The best treatment then has the expected benefit 
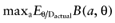. Thus, the current cost of uncertainty about the actual study data D is the opportunity loss:
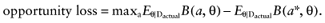
Because B is linear in θ, this simplifies to:
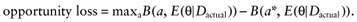
We cannot calculate the opportunity loss, because we do not know the actual data before performing the study. However, the expected opportunity loss is the expectation over all possible values of the new data. The total EVSI equals the expected opportunity loss:
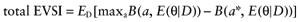
Again, the analysis is simplified using the probability distribution of the mean net benefit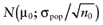 
of each intervention a in the initial study. The data D of the proposed study is characterized by the sample size n1, the sample mean net benefit µ1, and the standard error 
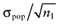for each intervention[6]. The µ1 is unknown, but can be sampled from the distribution of the actual net benefit 
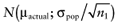for each intervention. The µactual is also unknown, but can be sampled from the distribution of the mean net benefit of the initial trial 
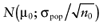for each intervention. The algorithm for the estimation of the total EVSI involves the following steps:
- 1
Choose a sample size n1 per intervention of the proposed study.
- 2
Draw a value µactual,j from
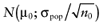, for each intervention. - 3
Draw a value µ1,j from
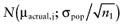, for each intervention. - 4
Calculate the posterior mean net benefit for each intervention a:
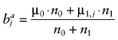
- 5
Calculate the opportunity loss:
- 6
Repeat step 1 to 5 N times.
- 7
The total EVSI is estimated by averaging over the opportunity losses at step 5.
Expected Net Benefit of Sampling (ENBS)—the Optimal Sample Size
The ENBS is defined as the difference between the total EVSI and the study cost. The optimal sample size is reached when the ENBS reaches a maximum. At this maximum, the additional benefit of one more patient in the study equals the additional study costs of one more patient in the study.
In addition to the fixed cost and variable cost per patient, the cost of clinical trials should also include the forgone net benefit of each patient that is randomized to an intervention that is supposedly suboptimal. This amounts to the sample size of the inferior arm of the trial times the difference in net benefit based on the previous trial.
The Example—Total EVSI, Study Costs, and ENBS
For a clinical trial collecting data on all parameters (total EVSI), we estimated a fixed cost of 200,000 euros and a variable cost of €1000 per patient, both based on our previous (identical) study. The difference in net benefit between the revascularization and the exercise group was €2170. The total cost in euro was therefore:
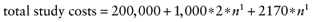
Note that n1 is the sample size per study arm and not the total sample size of the study. We used the same population to benefit about 46,000 patients (see section on total EVPI). Figure 2 presents the study cost, the total EVSI, and the ENBS as a function of the sample size n1 per study arm. A maximum ENBS of €7.3 million is reached for a sample size of about 475 patients per study arm. The study cost of this study would be 2.2 million, of which 1.2 million is accounted for by the forgone net benefit of 475 patients assigned to the supposedly suboptimal intervention (supervised exercise training).
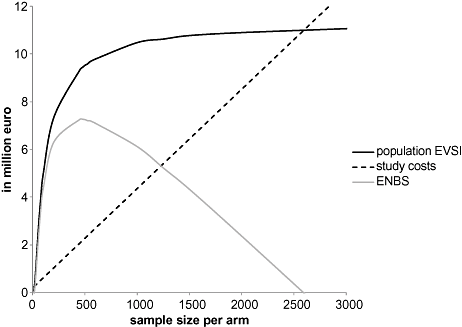
Population EVSI, study costs and ENBS in million Euro for different sample sizes per study arm. The proposed study collects data on all parameters that were considered in the initial trial. The optimal sample size is about 500 patients per study arm with an ENBS of €7.2 million, and total study costs of €2.3 million. Of the total study costs, €1.1 million is accounted for by the forgone net benefit of 500 patients assigned to the supposedly suboptimal intervention (supervised exercise training).
The ENBS of the proposed study is not the actual benefit of the study—which we will only learn after analyzing the results of the study—but the expected benefit, prior to performing the study. The actual benefit to an individual patient is zero if the new study does not lead to a change in current care, because the patient's outcomes remain unchanged. The actual benefit to an individual patient is nonzero if the new study demonstrates that our initial decision was suboptimal and current care is changed accordingly. However, the proposed study will almost always improve the precision of the outcomes and reduce the cost of uncertainty.
Partial EVPI—Eliminating Uncertainty of Some Parameters
The partial EVPI estimates the expected benefit of eliminating uncertainty for individual parameters or subsets of parameters. Typically, it is not justified to consider all parameters in a future study: a few key parameters are the source of most decision uncertainty. Eliminating uncertainty about the other parameters has no additional expected benefit or an expected benefit that does not justify the additional study costs.
Partial EVPI—Equations and Algorithm
For the estimation of partial EVPI, the parameters are divided into two groups: the parameters-of-interest θI are considered in a future study, the parameters-not-of-interest θC are not considered in a future study. If all uncertainty about the parameters-of-interest θI for each intervention would be eliminated, the actual values of these parameters would be known. The current cost of uncertainty of not knowing the actual values of the parameters-of-interest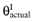 
of each intervention is called the opportunity loss. It is defined as the difference between the maximum expected net benefit given 
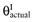and the expected net benefit given 
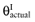of the supposedly optimal intervention (a*). Because B(a, θC, θI) is linear in θC and θI, we get:
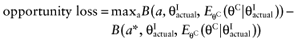
We cannot calculate the opportunity loss, because we do not know the actual values of the parameters-of-interest θI. However, the expected opportunity loss is the expectation over all possible values of the parameters-of-interest θI of each intervention. The partial EVPI equals the expected opportunity loss:
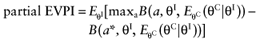
Again, the analysis can be simplified by avoiding the distributions of individual parameters. Instead, we created distributions for the mean net benefit of the parameters-of-interest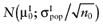 
and the mean net benefit of the parameters-not-of-interest 
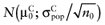, with correlation ρ, for each intervention. The partial EVPI is estimated in the following algorithm. The conditional mean net benefit of the parameters-not-of-interest θC is calculated in step 2 of the algorithm, using the general equation for the conditional mean value of a bivariate normal distribution. [19]
- 1
Draw a value
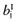from 
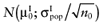, for each intervention. - 2
Calculate the conditional mean net benefit of θC, for each intervention:
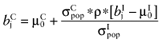
- 3
Calculate the mean net benefit for each intervention:
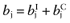. - 4
Calculate the opportunity loss:
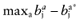. - 5
Repeat step 1 to 4 N times.
- 6
The partial EVPI is estimated by averaging over the opportunity losses at step 4.
Subsets of Parameters
In theory, we could estimate the partial EVPI for each subset of parameters. To evaluate whether more research regarding each subset is potentially justified, the partial EVPI is compared with the subset-specific fixed study costs. The number of required analyses, however, would explode for even a small number of parameters. In practice, investigators typically first estimate the partial EVPI for each individual parameter. Unfortunately, the partial EVPI of individual parameters does not simply sum up to the partial EVPI of a subset of parameters. Even a subset of parameters with individual partial EVPIs of zero, together, may have a nonzero partial EVPI. The subset of parameters with a nonzero EVPI or substantial individual partial EVPI seems a reasonable subset to consider for partial EVPI estimation. Other relevant subsets are found by changing this subset. If the partial EVPI of this subset is close to the total EVPI, we can remove parameters with a small individual partial EVPI or a substantial-associated increase in study costs (e.g., the quality-of-life parameter). If the partial EVPI is much smaller than the total EVPI, we can add parameters with small additional study costs (e.g., a cost parameter that can be collected from administrative records).
The Example—Partial EVPI
Table 2 presents the partial EVPI of each individual parameter with 10 million simulations in R. Of the 12 parameters, only four had a nonzero individual partial EVPI. Together, these four parameters had a partial EVPI of €248 per patient; almost the same as the total EVPI of 249. The partial EVPI of the three parameters with the highest individual EVPI was also €248 per patient. The two parameters with the highest individual partial EVPI together had a partial EVPI of 244. For the subsets with two and three parameters, we identified the optimal sample size in the next section. The partial EVPI of the subset of eight parameters with an individual partial EVPI of zero was still zero. Obtaining more information on these parameters is not justified, even for very small additional study costs.
| Individual parameters | Partial EVPI in euro |
|---|---|
| QALYs | 104 |
| Additional admission costs | 65 |
| Additional treatment costs | 6 |
| Additional imaging costs | 0.007 |
| Subsets of parameters | |
| All 12 parameters = total EVPI | 249 |
| All 4 with nonzero individual pEVPI | 248 |
| All 3 with individual pEVPI > 1 | 248 |
| All 2 with individual pEVPI > 10 | 244 |
| All 8 with zero individual pEVPI | 0 |
| All 11 cost parameters | 69 |
- EVPI, expected value of perfect information; QALYs, quality-adjusted life-years.
Five cost parameters had a similar expected value, ranging from 437 euros to 742 euros per patient: the cost of material, personnel, overhead, treatment, and productivity loss. The partial EVPI of treatment cost was 6 euros per patient. The partial EVPI of the other four parameters together was zero. These results demonstrate that simply selecting the parameters with the highest expected value, or the parameters that differed most between treatments, is not a good alternative for partial VOI analysis.
Partial EVSI—Reducing Uncertainty of Some Parameters
The partial EVSI is an estimate of the expected benefit of studies with a finite sample size, collecting information on a subset of parameters. With increasing sample size, the partial EVSI will reach a ceiling: the partial EVPI, representing an infinite sample size.
Partial EVSI—Equations and Algorithm
A future study provides data D about the parameters-of-interest θI of n patients for each intervention. The study will improve the mean estimates of the parameters-of-interest θI, and consequently, of the net benefit of each intervention. The current cost of not knowing the actual study data Dactual is called the opportunity loss. It is calculated as the difference between the maximum expected net benefit given Dactual, and the expected net benefit given Dactual, of the supposedly optimal intervention (a*):
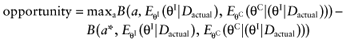
We cannot calculate the opportunity loss, because we do not know the actual data before performing the study. However, the expected opportunity loss is the expectation over all possible values of the new data. The partial EVSI equals the expected opportunity loss:
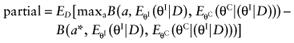
Analogous to estimating the partial EVPI, we used the observed distributions for the mean net benefit of the parameters-of-interest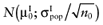 
and the mean net benefit of the parameters-not-of-interest 
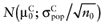, with correlation ρ, for each intervention. The data of the proposed study is characterized by the mean net benefit of the parameters-of-interest 
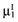and the standard error 
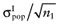for each intervention[6]. The 
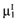is unknown, but can be sampled from the distribution of the actual net benefit of the parameters-of-interest 
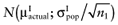, for each intervention. The 
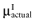is also unknown, but can be sampled from the distribution of the mean net benefit of the parameters-of-interest observed in the initial study 
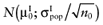, for each intervention. The partial EVSI is estimated in the following algorithm.
- 1
Choose a sample size n1 per intervention of the proposed study.
- 2
Draw a value
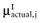from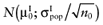 
, for each intervention. - 3
Draw a value
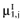from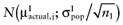 
, for each intervention. - 4
Calculate the posterior mean net benefit of θ1, for each intervention:
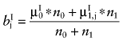. - 5
Calculate the conditional mean net benefit of θC, for each intervention: [19]
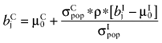. - 6
Calculate the mean net benefit for each intervention:
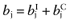. - 7
Calculate the opportunity loss:
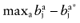. - 8
Repeat step 1 to 7 N times.
- 9
The partial EVSI is estimated by averaging over the opportunity losses at step 7.
Although the proposed data collection sampled only the parameters-of-interest, the net benefit of each intervention is estimated using all available data of all parameters (step 6). The net benefit of the parameters-of-interest is estimated using data from both the initial study and the proposed data collection (step 4). The net benefit of the parameters-not-of-interest is estimated using data from the initial study only, unless a correlation (ρ) exists with the parameters-of-interest (step 5).
The Example—Partial EVSI, Study Costs, and ENBS
We estimated the partial EVSI, for various sample sizes, for two subsets of parameters that were identified with the analysis of partial EVPI. These subsets include, respectively, three and two parameters with the highest individual partial EVPI. We estimated that collecting information on the QALE represents 50% of the fixed and variable study costs: 100,000 euros and 500 euros per patient. Also, collecting hospital admission costs implies searching administrative records: we estimated an increase in study costs of 10,000 euros plus 50 euros per patient. Also, collecting the additional treatment costs requires more resources: we estimated an increase in study costs of 20,000 euros plus 100 euros per patient. We used the same population to benefit of about 46,000 patients (see section on total EVPI).
For the subset of two parameters, the optimal sample size was 525 patients per study arm and the ENBS was 7.6 million euros. For the subset of three parameters, we found an optimal sample size of 500 patients per study arm and an ENBS of also 7.6 million euros. Although the expected benefit of the studies is equal, we prefer the former study because of lower study costs. This optimal study design obtains data on the QALY and additional admission costs for 525 patients per study arm. The required study costs are 690,000 euros. Assigning 525 patients to the supposedly suboptimal arm has an associated cost of 1.1 million euros. To estimate study costs, we assumed a randomized controlled trial as optimal design to reassure validity of the results. Figure 3 presents several sensitivity analyses for the WTP threshold, the population to benefit, and the study costs.
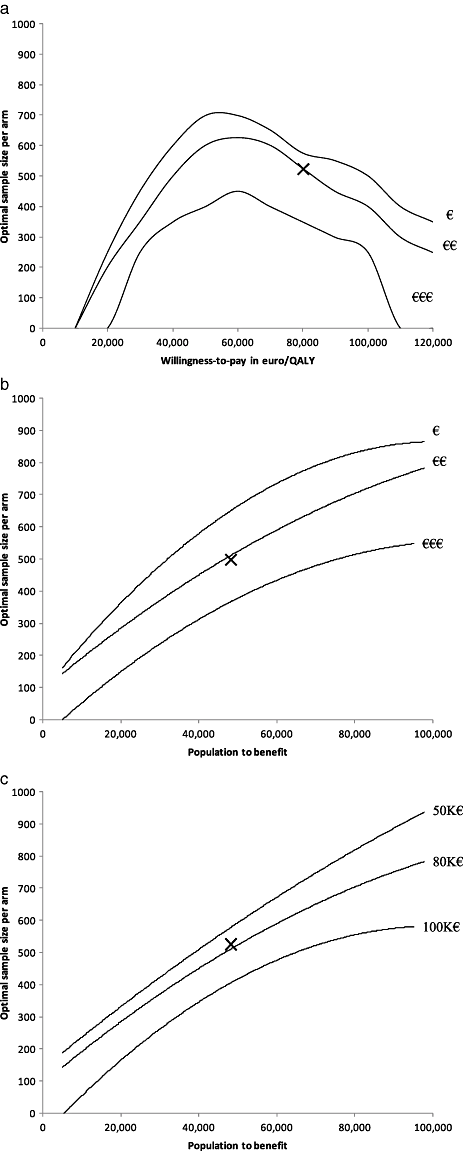
(a) Sensitivity analysis for the willingness-to-pay threshold and the study costs. The proposed study collects information on the quality-adjusted life expectancy (QALE) and the additional admission costs. The population to benefit is about 46,000 patients. The study costs estimates are: fixed 10,000 and variable 100 euro (€); fixed 110,000 and variable 550 (€€: base-case); and fixed 500,000 and variable 2000 (€€€). The X presents the base-case willingness-to-pay threshold and study costs. (b) Sensitivity analysis for the population to benefit and the study costs. The proposed study collects information on the QALE and the additional admission costs. The willingness-to-pay threshold is 80,000 euro/quality-adjusted life-years (QALY). The study costs estimates are: fixed 10,000 and variable 100 euro (€); fixed 110,000 and variable 550 (€€: base-case); and fixed 500,000 and variable 2000 (€€€). The X presents the base-case population to benefit of about 46,000 patients. (c) Sensitivity analysis for the population to benefit and the willingness-to-pay threshold. The proposed study collects information on the QALE and the additional admission costs. The study costs are €110,000 for fixed costs and €550 for the costs per patient. The X presents the base-case population to benefit.
Alternative Methods
We performed VOI analysis assuming a normal distribution of the mean net benefit of each intervention, based on the central limit theorem. The total EVPI can also be estimated using bootstrapping techniques, which do not rely on the normality assumption.[16] With 1 million bootstraps in R, we found a total EVPI of €264 per patient; very close to the €249 that we found, assuming a normal distribution of the mean net benefits. Unfortunately, it is not obvious how bootstrapping should be implemented to estimate partial value of information and sample information. Other nonparametric methods for VOI analysis are being developed [6].
We assessed the total EVPI using unadjusted estimates for the mean net benefit of each intervention. As another alternative, we used regression analysis in the net benefit framework to obtain estimates of the mean net benefit adjusted for potential imbalances of baseline characteristics between the treatment groups. The resulting total EVPI was €119 per patient. The adjusted outcomes probably underestimate the VOI; the unadjusted outcomes may overestimate the VOI. The regression analysis ambiguously decomposes the total variance into components attributable to patient heterogeneity and uncertainty. Both uncertainty and estimates of the VOI will decrease when more variation is attributed to heterogeneity.
Both Claxton and Willan estimated the total EVPI and total EVSI using closed form (analytical) methods that do not rely on simulation [17,18]. Using closed form solutions, Claxton also considered the VOI of trial designs assigning unequal sample sizes to each intervention [20]. Although closed form solutions for estimating the partial EVPI and partial EVSI are not available in the literature, it should be possible to derive such solutions. The advantages of closed form solutions are exact outcomes and negligible calculation time. Simulation, however, also has several advantages as compared with closed form solutions. The simulations that we applied to our example can be easily modified to accommodate more than two comparators, prior distributions other than normal and nonlinear functions of the parameters. Moreover, simulation has educational appeal; by following the steps of the simulation, the reader understands how it works.
Discussion
With VOI analysis, we found that more research is justified regarding the choice between endovascular revascularization and supervised exercise training for patients with intermittent claudication. The optimal study design for a future study involves a randomized controlled trial collecting data on the QALE and additional admission costs for 525 patients per treatment arm. The outcome of this trial could justify a change in current care. As a result, future patients may benefit from an increase in quality-of-life, or cost savings may allow the health care system to reimburse other (unrelated) beneficial interventions. Although we do not know the actual benefit of the proposed study, the VOI analysis estimated an ENBS of 7.6 million euros for The Netherlands, using the results of a previous trial. The study costs of 690,000 euros were accounted for in this estimate. No other study design had a higher ENBS. Sensitivity analyses demonstrated that the optimal sample size was fairly stable. It remained between 400 and 600 patients for a WTP threshold between €30,000 and €100,000/QALY, for extreme assumptions about the study costs, and for a range of 3 to 7 years that future patients will benefit from the results of the proposed study. These results were used for a recent grant proposal. The €7.6 million of the proposed study can be compared with the ENBS of other (unrelated) study proposals. The ENBS can guide a funding agency to set priorities if the research budget is limited: study proposals with a higher ENBS should be reimbursed first. However, funding is justified for any study proposal with an ENBS exceeding zero.
An important assumption of VOI analysis is that health-care costs and research costs are ultimately paid for from the same resources, which is largely true for The Netherlands. The appropriate perspective of the VOI analysis regarding the population to benefit from the results of a study proposal is not obvious. Because the initial trial of our example was funded by a national governmental agency, we used the national perspective. For a European Union or worldwide perspective, the population to benefit would increase at least 20-fold, resulting in an optimal sample size of several thousand patients. The period that patients will benefit from the proposed data collection is also uncertain because of uncertainty about future technological improvements and evidence from future studies. These ambiguities, however, are not drawbacks of VOI analysis in itself, but inherent to setting research priorities.
We demonstrated VOI analysis using patient-level data from a single clinical trial. We may have overestimated uncertainty and the value of information, because we did not consider all available evidence pertaining to the decision. A decision model can bring together evidence from various sources and also extrapolate costs and effects beyond the follow-up period in the initial trial. However, decision models also have several drawbacks. Many assumptions are required when building decision models, to the extent that for the same research question, different models report diverging results [21]. As a consequence, the validity of models is often challenged. Moreover, building models is very time-consuming and requires expertise on both the clinical subject matter as well as the methodology of decision modeling. On the other hand, this investment of time may be worthwhile, because VOI analyses of such a decision model could conclude that more research is not justified. Finally, most decision models are nonlinear and require extremely computer-intensive nested VOI analyses [6]. VOI analysis of patient-level data can avoid these nested analyses because the net benefit is a linear function of the cost and effect parameters. Clinical trials remain attractive because of their high internal validity and timeliness [5]. For many clinical decisions, a trial constitutes the best available evidence, not only to decide what medical intervention should be adopted, but also to address the question whether more research is needed. VOI analysis of trials is aimed at replacing the use of significance testing to determine whether more research is justified; it is not aimed at replacing decision models to guide further research. Advocates for economic trials will emphasize their internal validity, although advocates for models stress their consideration of all available evidence. Whether a decision model is required to guide future research will depend on the methods and results of the initial study, as well as the importance of evidence from other sources.
A limitation of trials as compared with models is that clinical trials rarely have a lifetime follow-up of costs and effects. This is not only a drawback of VOI analysis of trials, but inherent to any analysis of a trial. Sometimes a model is used to extrapolate the trial data beyond the follow-up period [22]. The follow-up of our initial trial was only 12 months. However, both interventions—endovascular revascularization and exercise training—give only temporary relief of symptoms. Improvement of quality-of-life in our study was more immediate after revascularization, but at 12 months, no difference was detected in quality-of-life. Like most interventions in surgery, the costs are largely incurred up front. The base case analysis of a model based on our trial data would assume that no difference in costs and effects is anticipated beyond the follow-up of the trial.
We recommend a randomized controlled trial as the optimal design for the future study. Alternatively, an observational study could collect data on quality-of-life and admission costs. The drawback of a nonrandomized design is that it is more difficult to avoid the differences in (known and unknown) baseline patient characteristics (i.e., confounders) that are responsible for differences between the outcomes of interventions. Moreover, a randomized design is not necessarily associated with additional study costs.
Few applications of VOI analysis to guide the design of clinical trials have been published. In 2005, a guidance document for designing and analyzing cost-effectiveness analyses conducted as part of clinical trials did not mention VOI analysis.[5] However, the philosophy of a formal cost–benefit trade-off prior to experimental studies is not new. VOI analysis was introduced by Grundy [23] in the late fifties and developed by Raiffa and Schlaifer [24]. Howard noted in 1966 that: “Placing a value on the reduction of uncertainty is the first step in experimental design, for only when we know what it is worth to reduce uncertainty do we have a basis for allocating our resources in experimentation designed to reduce the uncertainty.” In 1989, Detsky evaluated the effect of design choices made in the planning stages of a clinical trial on the costs and benefits derived from conducting the trial [25,26]. Claxton introduced VOI analysis to the clinical audience of the Lancet[2]. Moreover, he demonstrated VOI analysis to estimate the optimal sample size of a trial using hypothetical data [17]. More recently, Willan applied VOI analysis to estimate the optimal sample size of a trial using patient-level data from a previous trial [27]. Both studies used closed form solutions that are not available in the literature for partial value of information analyses. Further research could find out closed form solutions for some partial value of information analyses.
Although the VOI analyses are relatively complex and technical, the fundamental ideas of VOI analysis is rather straightforward and may appear familiar to clinicians. A clear analogy exists between the Bayesian framework for VOI analysis and Bayesian diagnostic reasoning. A future trial can change the probability that an intervention is optimal, just as a diagnostic test can change the probability that a patient has a certain disease. Both a trial and a diagnostic test are costly and require a cost–benefit trade-off. The probability and the consequences of implementing a suboptimal intervention or misdiagnosing a patient determine whether more research or a diagnostic test is justified.
Clinical trials often show no statistically significant difference between the treatments compared. We demonstrated that VOI analysis allows for a formal comparison of the expected benefit and the cost of a proposed study, before concluding whether or not more research is justified. Two erroneous conclusions are common about the need for more research when no significant difference is found. Some authors conclude that the decision has been settled: the interventions are assumed to be equivalent and more research is not needed. It has long been demonstrated, however, that a difference is often not found because the study was underpowered to detect even a large difference [28]. In a famous quote, Altman warned that: “Absence of evidence is not evidence of absence”[29]. Other authors conclude the exact opposite—more research is needed—when no significant difference is found. They seem to reason that there must be a difference and because it was not found with the current study, another (larger) study is needed. Phillips pointed out that the conclusion “more research is needed” requires some assessment of the expected benefit for future patients that would come from more research in comparison to the cost of research (e.g., VOI analysis). He observed that studies in health care typically conclude that “more research is needed” without such an assessment [30].
If more research is justified, the investigators should decide on a sample size. We demonstrated VOI analysis as an explicit framework to perform sample size calculations. Classical sample size calculations are based on arbitrary values for the minimal clinically significant difference in treatment effect, a type I error (typically α = 0.05), and a type II error (typically β = 1 − power = 0.2). In practice, the equation is often back-solved after substituting in a sample size that primarily reflects feasibility and cost. VOI analysis considers the actual harm to future patients of making a type I error (i.e., rejecting the null-hypothesis when it is true) and a type II error (not rejecting the null-hypothesis when it is false). The optimal sample size is estimated by considering the marginal cost and benefits of sampling patients. Moreover, VOI analysis can conclude that more research is not justified [31]. We recommend performing VOI analyses before and after an economic trial.
Source of financial support: Financial support for this study was provided entirely by a grant from ZonMW (The Netherlands organization for health research and development), a government agency. The funding agreement ensured the authors' independence in writing and publishing the report.
