Drotrecogin Alfa's Impact on Intensive Care Workload in Real Life Practice: A Propensity Score Approach
ABSTRACT
Objectives: To estimate the impact of drotrecogin alfa (DA) on intensive care workload in an observational study while illustrating the use of propensity score (PS) matching to control for recruitment bias.
Methods: PREMISS is a prospective, multicenter pre–post study. Its goal was to evaluate DA in the treatment of severe sepsis with multiple organ failure. Inclusions took place before (control patients) and after (DA-treated patients) the drug's market authorization. Workload was measured in euros using the French classification of medical procedures. It was compared between the groups via random effects gamma regression using two techniques: 1) regression adjusting for the patients' initial characteristics on the whole population; and 2) PS matching. A structural equation model was used to explore the pathways leading to a workload increase.
Results: Drotrecogin alfa is estimated to increase intensive care unit (ICU) workload by 20% (P = 0.045) according to the multivariate model and 34% (P = 0.002) according to the PS-matched one. In the structural equation model fitted, only DA's direct effect on the occurrence of bleeding events reaches significance (P = 0.024).
Conclusions: We found a significant effect of DA on ICU workload with both standard methods of adjustment and PS matching. This effect appears to be mainly due to DA's effect on bleeding events. The analysis illustrated the usefulness of PS methods in the analysis of observational data, as it leads to conclusions similar to the traditional multivariate regression approaches while avoiding making too many adjustments, allowing focusing on the treatment effect.
Introduction
There has been considerable debate on the role of observational studies for the evaluation of an intervention's effect. Many researchers claim that nonrandomized studies lead to unreliable results and appeal for the exclusive use of randomized clinical trials (RCTs) [1]. The latter are considered the “gold standard” because they imply the equality of the distribution of the variables measurable at the time of randomization [2]. On the contrary, nonrandomized studies cannot guarantee that the populations being compared share the same distribution of prognostic factors. When the populations differ in some baseline characteristic predictive of the outcome of interest, the estimation of the intervention effect can be biased. We will use the term of recruitment bias (a particular case of selection bias) to refer to these situations. Despite the risk of producing biased treatment effect estimates, some authors advocate the use of nonrandomized studies on the basis that, when correctly conducted, they can lead to results similar to those reported in RCTs [3]. There are indeed some arguments in favor of nonrandomized studies. First of all, even if their results are prone to more skepticism than those arising from RCTs, there are some situations where randomization is infeasible (which is sometimes the case in the field of surgery or living habits), not ethical (for example, if the efficacy of the intervention is already acknowledged) or simply too costly. In a recent review of the question, the NHS (United Kingdom's National Health Service) concluded that nonrandomized studies should be used only in these cases [4]. There are however, more possible advantages to nonrandomization. First, some sources of already available observational data can provide valuable information. Moreover, RCTs tend to be conducted under strict protocol-driven conditions, different from what will be the use of the intervention in real practice. Some authors assert that randomized studies do not provide much information relevant to decision-makers [5]. Thus, although most clinical researchers see observational studies as exploratory tools whose results need to be confirmed by RCTs, nonrandomized studies can also be carried after an RCT to assess the external validity of the findings.
The PREMISS study is an example of such an application. It is a study founded by the French ministry of health in 2002 to estimate drotrecogin alfa (DA)'s impact in intensive care practice, in cooperation between the two professional associations of intensive care practitioners in France: the SFAR (French Society of Anesthesia and Intensive Care) and the SRLF (French Speaking Reanimation Society).
Sepsis is a systemic inflammatory response to infection, causing widespread activation of inflammation and coagulation pathways. Severe sepsis (organ dysfunction and perfusion abnormalities) or septic shock affect broadly 15% of French intensive care patients and are associated with high mortality rates (35% at 30 days in 2001) [6]. DA is a recombinant version of human activated protein C, a coagulation factor that as been shown to reduce severe sepsis mortality by 20% [7]. It is indicated in Europe for the treatment of adult severe sepsis with multiple organ failure (MOF).
The main objective of the PREMISS study was to estimate the observational costs of DA's introduction in French intensive care units (ICUs). Because DA's efficacy had already been explored in a large multicenter RCT, it would have been unethical to randomize patients in a control group. Furthermore, some other features of an RCT, like the blinded allocation of treatments or the highly protocoled patterns of care, would have been incompatible with the study's observational objectives. For instance, because DA is known to increase the probability of hemorrhagic events, caregivers aware of the treatment received by their patient may monitor more severely those being administered this product. The PREMISS design was therefore conducted without randomization.
To account for the likely presence of confounding in the PREMISS study, we used the propensity score [8] (PS), an increasingly used method to deal with recruitment bias. It will be illustrated in the estimation of DA's impact on intensive care workload. This impact will subsequently be explored using structural equation modeling [9]. The drugs' “theoretical” (i.e., according to the RCT results) [10] and observational cost-effectiveness [11] have been assessed elsewhere.
Methods
The PREMISS Study
The intervention to be evaluated is the administration of DA at the recommended dosage of 24 μg/kg/h for 96 hours (the physicians were free to use different protocols). The inclusion criteria are those defined in the European indications for DA: adult patients (in practice, 13 patients less than 18 years old at their admission were included and kept for analysis. All were more than 15 years old) with severe sepsis with MOF and without contraindications (active internal bleeding, intracranial pathology, neoplasm or evidence of cerebral herniation, concurrent heparin therapy ≥15 International Units/kg/h, known bleeding diathesis except for acute coagulopathy related to sepsis, chronic severe hepatic disease, platelet count <30,000 × 106/L, even if the platelet count is increased after transfusions, patients at increased risk for bleeding). The PREMISS study follows a quasi-experimental pre–post design. In a “before” phase, from September 2002 to January 2003, before DA's marketing authorization, patients were included in a control group. The “after” phase was carried from January 2003 to December 2004, once DA was available. Among the patients eligible for DA treatment, those actually receiving the drug were included in the study. As physicians were not compelled to treat with DA every patient fulfillling the drug's indication, as they would have been in a clinical trial setting, the study design does not exclude the presence of recruitment bias. The “after” phase lasted longer to include roughly the same number of patients than in the “before” phase (as all patients potentially eligible for DA before it was available were included in this phase). This longer inclusion phase does not affect the length of follow-up (mortality is assessed at 28 days). Analyses were conducted in an intention to treat fashion: all the patients in the “after” phase were considered as treated with DA, even if they did not conform to DA's recommended dosage or if DA infusion was stopped before the 96-hour period. Patients were followed up until their discharge from the hospital.
Data Collection
Use of an Internet database. Information was collected in a decentralized fashion using an online case report form (eCRF). The information was then centralized in a protected server in a single database. The choice of an Internet questionnaire allowed for the inclusion and noninclusion criteria to be automatically validated. The data are checked as they are entered, which substantially reduces the number of errors and queries. Quality controls of the information submitted were also automated, making easier the data-monitoring process. Confidentiality of the data was ensured by the use of unique password-protected identifiers for each participating ward and by the anonymization of patients by an alphanumeric code. The eCRF, its interface, and all associated software were conceived, programmed, and maintained by the authors in cooperation with the intensive care practitioners' societies. We consequently were in possession of a tool entirely customizable to the research needs.
The data collected included information about: the ICU itself; the patients' characteristics at the time of their admission on the ward; their severity at the time of inclusion; the administration of antibiotics, corticoids, DA (in the “after” phase), and other drugs; hemorrhagic and transfusion events; the procedures of care given during their stay on the ICU; their survival status at discharge from the ICU, from the hospital, and 28 days after sepsis initiation.
Initial characteristics. As treatment allocation was not randomized, we needed to take multiple sources of bias into account. We tried to gather as many data as possible on the patients' initial characteristics. They were measured at ICU admission or at enrollment in the study. These included demographic variables (age, gender, weight, prior location, reason for ICU admission), medical conditions (McCabe score, chronic renal failure, chronic liver disease, congestive cardiomyopathy, COPD, diabetes mellitus, immunosuppressive treatment, chemotherapy, metastatic cancer, hematological malignancies, HIV, corticotherapy for more than 3 weeks), infection sites (lung, intraabdominal, urinary tract, central nervous system, etc.), the biological variables used in the SAPS II [12] and LODS [13] scores, and disease severity variables (SAPS II on admission, septic shock at enrollment). On the whole, 46 initial characteristics where measured and considered in the analysis.
Workload measures. The measure of workload used is based on the new French classification of medical procedures, which comprises more than 7000 technical acts. Each is arranged hierarchically according to the material and human resources necessary for its realization. A reimbursement rate linked to the resources (economic or not) required is associated with each act.
The use of this classification in intensive care was troublesome: because severe sepsis is only a syndrome, the range of all potential interventions occurring during a patient's stay is quite important. Only the most important acts were included in the PREMISS eCRF: essentially, those relative to organ support or monitoring (respiratory, cardiovascular, digestive, renal, hematological, nervous system), those relative to medical imagery (ultrasonography, tomography, magnetic resonance image, endoscopy), and, of course, those related with hemorrhage management. In total, 115 different technical acts were included in the eCRF. The ICU workload is estimated as the sum of the number of technical acts multiplied by their reimbursement rate. We use the values from version 10 of the classification. Although this classification serves as the reimbursement classification for private clinics and is measured in euros, it should be considered a workload measure (as the former Omega system) and not as a cost. Reimbursement in French public ICUs is based on the presence of some of these technical acts, and not on their values.
Statistical analysis
Model specification. In econometrics, it is well-known that resource use variables can be particularly skewed. Even if the normality of the explained variable is not a condition of validity of the linear regression model, it can lead to the violation of the hypothesis of normally distributed residuals. There has been large debate over the most appropriate way to deal with such concerns [14,15]. We will first use a classical linear model. If its validity conditions are violated, we will use a generalized linear model (GLM) such as the Gamma model. If we note yi the dependent variable for patient i and xi the vector of his observed covariates, this model is given by:

The gamma distribution further implies that the variance of the variable is proportional to the square of the mean: V[yi|xi] = Φ (E[yi|xi])2, where Φ is the dispersion parameter. We use the procedure described by Manning and Mullahy [16] to select the model to be used.
Adjustments for Recruitment Bias
Identification of unbalanced initial characteristics. To explore the comparability of the “before” and “after” groups, we computed standardized differences. They are a quantitative measure of bias [16,17]. A standardized difference is related to the degree of unbalance in a variable means accounting for its degree of variation. The standardized difference of a variable i is defined as:
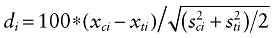
Where xci and xti are the control and treatment sample means of the ith variable and 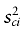 and
and 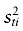 are the corresponding sample variances. For binary variables, the sample means are the sample proportions. For polychotomous variables, we compute a standardized difference contrasting each category with all the others and we retain the highest one. We will consider a variable as balanced between the groups when its absolute value of standardized difference is inferior to 10% [18].
are the corresponding sample variances. For binary variables, the sample means are the sample proportions. For polychotomous variables, we compute a standardized difference contrasting each category with all the others and we retain the highest one. We will consider a variable as balanced between the groups when its absolute value of standardized difference is inferior to 10% [18].
Adjusting for recruitment bias using multivariate regression. Multivariate regression models are the most frequently used methods to assess an intervention effect on a quantitative outcome variable. The model will include an indicator of the PREMISS study phase (“before” or “after”) as a covariate as well as the variables for which we wish to adjust for. Some problems arise in this model. First of all, any parametric model is more or less robust to violations of its validity assumptions. A misspecified model can lead to erroneous conclusions. Furthermore, the model results will depend on the way the relationship between the variable and the outcome is specified. For example, the association between age and workload can be linear or quadratic. Including age as a quantitative variable or as a qualitative one (e.g., by quartiles) might influence the results. Finally, when controlling for too many covariates, more problems are encountered. The sample size may be too small to accurately estimate all model parameters, and multicolinearity issues can arise.
Adjusting for recruitment bias using PS matching methods. An alternative to multiple covariate adjustments is to select a sample of patients comparable in each treatment group. This sample can be obtained with a PS approach. The PS is defined as the conditional probability of belonging to the “after” group given the initial covariates measured [18]. This probability replaces a large number of covariates by a single scalar. The PS can then be used as a stratification variable, as a matching variable or as an adjustment variable in a multivariate regression (or any combination of the three). Although the computation of the PS often uses multivariate regression models, studies have shown that the PS has the advantage of not being too sensitive to assumptions about the functional form of the association of a covariate with the outcome (e.g., linear, quadratic, etc.) [19].
Because there were missing values among the 46 initial covariates, multiple imputation procedures were used [20,21]. We generated 10 imputed data sets, estimated the PS for each and computed each patient PS as the mean of the 10 imputation-based PS estimates.
The PS was estimated using a logistic regression model including all 46 covariates.
Once the PS were estimated for each patient, “after” patients were matched to “before” ones on the basis of their PS using an optimal matching algorithm (the optimality criteria were to minimize the distance between the matched groups. For each pair of matched patients, the absolute value of the difference between their PSs was used as a distance measure). We used Bergstralh and Kosanke's SAS “match” macro [22]. The remaining analyses were performed on the matched sample adjusting only for the treatment group.
Accounting for the Clustering of Patients within the Participating ICUs
PREMISS was a multicenter study. One of the other conditions of validity of the linear regression model is that the residuals are independent and identically distributed (iid). Because some patients share the same ICU, we can expect them to be submitted to similar unobserved treatment procedures. Their outcomes are likely to be correlated. In consequence, so will be the residuals of patients from the same ICU and the iid assumption will not be met. We will use random effects models to take into account the clustering of patients among ICUs. In the traditional multiple regression linear model, the outcome yij observed for patient i from ICU j can be written as:
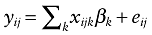
where xijk represents the kth variable observed for patient i from ICU j, βk is the estimated effect of the kth variable on the outcome, and eij is the error assumed to be iid and with null expectation. This model is called the fixed effects model.
The simplest form of a random effects model is the random intercept model, which adds a residual cluster effect:
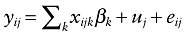
The cluster effect uj is also assumed to have a null expectation. More complex models can be specified when adding random components to the model coefficients.
Random effects models (also called hierarchical or multilevel models) have the advantage of providing a correct modeling of the variation: when fitting fixed effects models to hierarchically structured data, the estimated standard errors associated with the model coefficients will be too small, leading to the overestimation of the significance of the estimates [23].
We will use a penalized quasi-likelihood approach [24] to estimate the random effects. All models were fitted using the R statistical programming language [25].
Further Exploration of DA's Effect on Workload through Structural Equation Modeling
The regression model tests DA's effect on ICU workload as a whole. We tried to explore the path from treatment phase to ICU workload using structural equation modeling. These models use multivariate analysis to test causal relationships between variables in a path diagram.
There are several ways for DA's to affect ICU workload:
- •
Drotrecogin alfa could influence ICU workload through its effect on ICU mortality: patients not surviving ICU hospitalization are known to generate more costs (and therefore more care procedures) [26]. On the other hand, surviving patients have a higher ICU length of stay (LOS), and we expect the LOS to be correlated with workload.
- •
Drotrecogin alfa is associated with adverse events, hemorrhages in particular [7]. The occurrence of an adverse event is expected to lead to additional care and therefore to increase ICU workload. Adverse events could also increase the patients' LOS or mortality.
- •
Finally, DA could directly influence workload; if DA-treated patients are more monitored.
The interpretation of this model should be made with caution, as two of its endogenous variables (treatment phase and ICU mortality) are binary and the others (the number of bleeding events per patient and ICU LOS) have particular distributional shapes (the first is a counting event, and the second is particularly skewed).
These alternative pathways are presented in Figure 1. An arrow represents a specific path from one variable to another.
Model of drotrecogin (DA) treatment, intensive care unit (ICU) survival, bleeding events and ICU length of stay's effect on ICU workload. DA, drotrecogin alfa.
The model was fit using SAS (SAS, Cary, NC) procedure “proc calis,” using its default maximum likelihood estimation method. The model was assessed via a χ2 goodness of fit test, a nonsignificant P-value indicating no differences between the model structure and the observed data. We used the Root Mean Square Error of Approximation (RMSEA) as a secondary model fit indicator (an RMSEA of 0.05 or less indicates a good model fit, an RMSEA of more than 0.10 indicates a poor model fit). The individual regression coefficients were tested using t ratios.
Results
Baseline Characteristics
Once the database was checked for quality, 1096 patients were retained in the analysis: 509 and 587 in the “before” and “after” groups, respectively. These patients are nested within 85 different participating ICUs and 64 different hospitals, including 49 teaching hospitals. The proportion of medical, chirurgical, and general ICUs is broadly balanced. The mean age of the patients was of 60.8 years (range: 15.6–94.8). In total, 62% of the patients were of male sex. A total of 40% of the patients were admitted in the ICU after an internal transfer, 28% entered the ICU from an emergency department, 23% after an external transfer. The remainder entered the ICU directly. In total, 72% of the patients are medical ones. A total of 22% of the patients presented a McCabe and Jackson severity of illness score of 2 (ultimately fatal disease), 6% a score of 3 (fatal disease). The mean SAPS II severity score at the time of admission was of 56.6 (range: 7–131). Due to the specificity of the inclusion criteria (presence of MOF), comparisons with other epidemiological studies [6,26] or RCTs [7], typically focusing on severe sepsis with or without MOF, are difficult. Keeping this limitation in mind, the population recruited in the PREMISS study, compared to other French populations, appears to be similar in terms of admission categories, age or sex. The severity scores are, however, slightly higher in our population, which is not surprising because only patients with MOF were recruited.
Assessment of Recruitment Bias
Among the 46 measured initial covariates, 20 have a standardized difference superior to 10% in absolute value. As expected, there is strong evidence of recruitment bias in the PREMISS study. The first 10 unbalanced covariates are, in decreasing order of unbalance, age (“after” patients are younger), the PaO2/FiO2 (a measure of hypoxemia) ratio (“after” patients are more frequently ventilated), the McCabe score (“after” patients are less severe), the Glasgow coma score (“after” patients are less severe), the delay between hospital admission and ICU admission (shorter for “after” patients), the presence of a neurological infection site (more frequent among “after” patients), urine output (values between 0.75 and 1 L/24 h are less frequent among “after” patients), bilirubin (extreme values are less frequent among “after” patients), the presence of an endo-cardiovascular infection site (less frequent among “after” patients), and the heart rate (extreme low values—<30 bpm—are less frequent among “after” patients). Nevertheless, patient severity did not differ between the groups, at ICU admission (SAPS II of 56.93 vs. 56.24 in the “after” group, P = 0.54) and at the date of severe sepsis with MOF diagnosis (LODS of 8.62 vs. 8.90, P = 0.19). These initial characteristics have been described in more detail elsewhere [11].
Workload and DA Treatment Cost Estimation
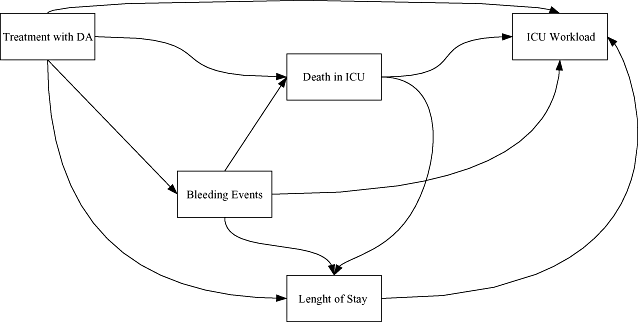
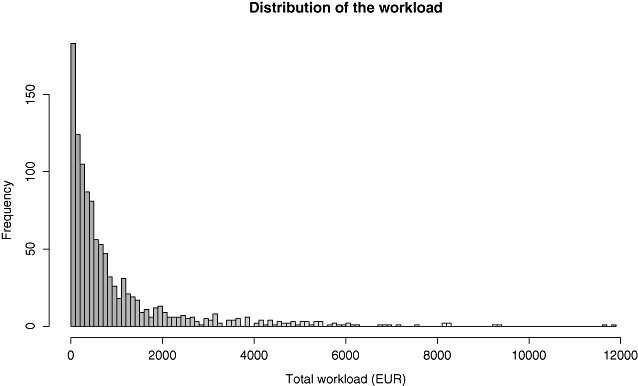
Sixteen patients have a null workload. They stayed between 2 and 7 days in the ICU and left it alive. The distribution of the workload (Fig. 2) is clearly skewed (skewness of 3) and does not fit a normal distribution (P < 0.0001, Shapiro-Wilk normality test). Patients in the “after” group appear to have higher workload measures (Fig. 3).
Distribution of the total workload among the PREMISS study patients. EUR, euros.
Boxplots of the total workload in the “before” and “after” treatment groups.
Among the “after” treatment group, the mean DA cost was of €6668 (95% confidence interval of 6404–6931, for a mean patient weight of 74 kg and a cost of €48.23 per mg of DA). Only 51% of the patients conformed to DA's indications of use (i.e., posology of 24 μg/kg/h, during 96 hours unless the patient dies before or faces an adverse effect or a treatment contraindication). This figure illustrates the gap between the conditions of care in RCTs and in daily practice.
Assessment of Treatment Phase's Impact on Workload
Model specification. Without any covariate adjustments, the linear model assessing the impact of treatment phase on workload is given by:
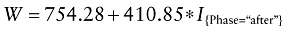
Where I{Phase=“after”} is the indicator variable for the “after” treatment phase (I{Phase=“after”} = 0 if the patient belongs to the “before” group, 1 otherwise).
Adding random effects to the intercept to control for center effects, the model becomes:
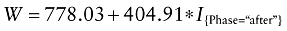
The random effects can be considered statistically significant (P < 0.0001).
As the residuals are non-normally distributed (P < 0.0001, Shapiro-Wilk normality test), the linear model cannot be used. Box-Cox procedures show that a log transformation is suitable (λ = 0.16).
To work on the log scale, we add a constant of 1 to the workload to avoid null values (observed for 16 patients). Because the mean workload is of €974, this constant can be considered negligible.
Nevertheless, even in the log-scale, the residuals obtained from an ordinary least squares (OLS) model (that is a linear model on the log-transformed variable) remain heavy-tailed (kurtosis = 4.5, 95% confidence interval = [3.92–5.13]). Simulation studies have shown that in this case, GLMs could be imprecise [16]. In the case of a kurtosis of 4, the standard errors of the estimates can be two times higher. Nevertheless, we choose to use a GLM model as, despite efficiency losses, they provide unbiased estimates, unlike OLS models if there is heteroscedasticity in the log-scale error.
Using the modified Park test described in Manning and Mullahy [16], we obtain a λ parameter of 2.22 (95% confidence interval of [1.61–2.83]) leading us to use a (mixed effects) Gamma GLM.
The corresponding mixed effects gamma regression model is given by:
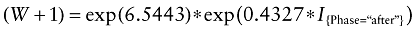
Without any adjustments for covariate unbalance between the two treatment groups, DA is estimated to increase ICU workload by 54% (exp(0.4327) = 1.54). Treatment phase is significant (P < 0.0001).
Full sample multivariate regression. When trying to adjust for all of the 46 covariates used in the PS model, the model fails to converge. To reach convergence, we eliminate the five covariates with the lower standardized differences (and therefore showing good balance between the treatment groups) that are not associated with workload (P > 5% in a nonparametric Mann–Whitney test). These covariates are the presence of an immunosuppressive treatment, diabetes mellitus, COPD, chronic liver disease, lung infection site, and a body temperature >39°C.
In the resulting mixed-effects Gamma GLM model, treatment effect remains statistically significant (P = 0.0445), the estimated increase in ICU workload due to DA treatment is of 20% (coefficient of 0.1822). This value, much lower than the one estimated in the unadjusted model (53%), tends to prove that patients recruited in the “before” phase are less severe than patients in the “after” one. In the random intercept model, the multiplicative effect of ICUs on baseline workload varies from 0.52 to 3.14, indicative of some variability in hospital practices. Nevertheless, because the variance component due to individual variation is of 1.0581 (on the log scale) and the one due to cluster correlation is of 0.1858, only about 15% of the work load variation is due to variation between the participating ICUs.
PS matching. A total of 840 patients remain on the PS-matched sample (77% of the initial sample). Standardized differences were calculated on this matched sample to investigate the performance of the model.
Of the 46 covariates specified in the PS model, only one remains above the 10% threshold: the PaO2/FiO2 ratio, describing the ventilation characteristics of the patients. Its standardized difference between the two treatment groups is of 10.46%. The difference is not statistically significant (P = 0.49, χ2 test. The unbalance is mostly due to a difference in the proportion of patients actually not under ventilation, of 7% vs. 5%). The other issue is age. On the whole, age appears to be balanced in both groups (mean age of 63 in the “before” vs. 63 in the “after” group, standardized difference of 5.12%, P = 0.33). Nevertheless, if focusing specifically on the patients aged 80 years or more, the age category at higher risk according to the SAPS II score, we find a significant difference (10% vs. 6% of the patients, P = 0.04, Fisher's exact test).
Despite these marginal differences, we can consider that we achieve a good balance of the observed patient characteristics in the PS-matched sample.
A mixed-effects Gamma GLM model estimated on the matched sample including only DA treatment as a covariate results in an estimation of this treatment's effect on workload increase of 34.2% (P = 0.0021). Inclusion of the potentially unbalanced covariates (PaO2/FiO2 ratio and age greater or equal to 80) leads to comparable results (33.7% increase, P = 0.0024).
In the random intercept model, the baseline workload varies by a multiplicative constant ranging from 0.53 to 1.98. 8.8% of the workload variation is due to variation between the participating ICUs.
The estimation results of the full sample unadjusted and adjusted models and the matched sample model are summarized in Table 1.
| Model | Full sample analysis | PS-matched sample | ||||
|---|---|---|---|---|---|---|
| Unadjusted (n = 1096) | Adjusted (n = 854*) | (n = 840) | ||||
| Coefficient | 95% CI | Coefficient | 95% CI | Coefficient | 95% CI | |
| Intercept | 6.5443 | (6.39–6.69) | 6.6221 | (5.43–7.82) | 6.5798 | (6.42–6.74) |
| Treatment | 0.4327 | (0.26–0.60) | 0.1822 | (0.01–0.36) | 0.2944 | (0.10–0.49) |
| Variances† | ||||||
| σ2(u) | 0.1437 | (0.07–0.27) | 0.1858 | (0.10–0.33) | 0.1628 | (0.08–0.32) |
| σ2(e) | 1.7148 | (1.57–1.87) | 1.0581 | (0.95–1.17) | 1.6883 | (1.23–1.37) |
- * A total of 242 patients omitted due to the presence of missing values.
- † σ 2(u): estimated variance of the random effect term, σ2(e): within-group error variance.
- DA, drotrecogin alfa.
A sketch of DA's effect on workload through structural equation modeling. All methods used here lead to the same conclusion: DA use in the treatment of patients with severe sepsis and MOF is associated with an increase in ICU workload. We use a structural equation model to assess the mediating roles of ICU LOS, ICU mortality, and hemorrhages on the relationship between DA and ICU workload. We fit the model on the PS-matched sample to control for selection bias.
In the initial model (Fig. 1), the direct effect of DA on ICU LOS is not statistically significant (P = 0.1676). As we have no reason to believe DA has a direct effect on LOS, we remove this path from the model. The resulting model and its estimates are presented in Figure 4.
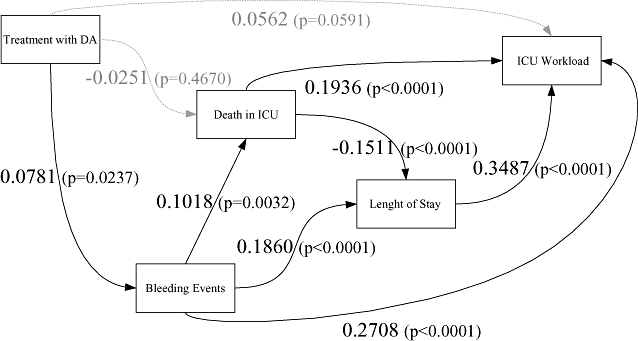
Structural equation modeling of DA's effect on ICU workload. DA, drotrecogin alfa; ICU, intensive care unit.
Two coefficients fail to reach significance. There is no significant association between DA treatment and mortality, and between DA treatment and ICU workload. We keep this first path in the model as DA has been shown to decrease mortality [7]. We also keep the second path as its P-value is close to the 5% threshold. The goodness of fit χ2 indicates that there is no significant difference between the observed data and our hypothesized model (P = 0.1678). The RMSEA criterion, of 0.0329, indicates a good fit.
Discussion
The PREMISS study is illustrative of the role of observational studies in medico-economic research. Its objectives were different from those of an RCT: the question was not to provide evidence in favor of the efficacy of an innovative treatment, but to gather information on the impact of the introduction of this innovation on a local (the French public hospitals) scale. It is our opinion that observational studies are the best suited for these purposes. Of course, the adoption of a nonrandomized design brings its share of methodological issues. Nevertheless, a careful and rigorous analysis can lead to adequate estimates. We developed a PS approach to cope with nonrandomization. There are other methods available [27], and traditional multivariate regression methods can also perform well in the reduction of recruitment bias [28]. Nevertheless, the PS methods are easy to implement and force the analysts to explicitly focus on the recruitment biases. Moreover, the use of PS matching can lead to simpler models. Our analysis of the relationship between DA and ICU workload is illustrative of the strengths and weaknesses of the PS approach. An (inappropriate) crude analysis on the unmatched sample, without adjustments, leads to the conclusion that DA increases ICU workload by 54%. On the opposite, an adjusted analysis on the same unmatched sample leads to an estimation of a 20% increase. Finally, a multivariate analysis on a PS-matched sample estimates this increase at 34%. Adjustment procedures on the unmatched sample divide by two DA's estimated impact. The intermediate figure of 34% could be due to two factors. The first is the presence of residual imbalance between the populations being compared, even after PS matching. The second is due to the matching process itself: it selects a subsample of patients with comparable characteristics on both groups. There is no guarantee that this subsample is representative of the population of treated or potentially treatable patients. Although alternative methods such as weighted PS regression modeling allow keeping all study participants, PS matching has the advantage of being the simplest and the most intuitive method.
What have we learned from this analysis? First of all, the presence of a recruitment bias itself deserves attention. The differences between the “before” and “after” groups are a sign that DA-treated patients were not selected on the basis of just the treatment indications (these corresponded to the study's inclusion criteria). As an example, DA-treated patients are younger. Because DA is a relatively expensive treatment, the physicians could have judged that DA is not cost-effective for older patients. This observation challenges the common view that clinicians base their treatment decisions only on the basis of clinical efficacy and safety. This gap between the theoretical indications and the observed treatment practices could not have been observed in an RCT. One other interesting aspect for decision-makers is that DA's impact on the ICUs will not be limited to its acquisition cost (at present, DA's cost is reported separately and is included in a reimbursement to the ICU).
These conclusions are based on a carefully planned analysis, where not only the issues due to nonrandomization were considered, but also other potential sources of bias. We dealt with recruitment bias using PS methods, we tried to take the skewness of the workload estimate into account by the use of gamma regression and we accounted for the clustering of patients among the ICUs using random effects modeling.
According to the structural equation model presented, the treatment will in particular increase the patients' ICU LOS, as the higher correlation estimate is between ICU LOS and ICU workload. As expected, most of ICU workload is driven by the duration of care in ICU. The second most influential variable on ICU workload is the occurrence of bleeding events. Bleeding events increase ICU workload directly and also indirectly, through an increase in ICU LOS and mortality. The effect of ICU mortality on ICU workload is less obvious: on one hand, deceased patients increase directly the ICU workload; on the other hand, they decrease the ICU LOS. On the whole, mortality remains positively associated with ICU workload (0.1936 − 0.1511 * 0.3487 = 0.1409). This is in agreement with other studies [26]. In conclusion, the structural model leads to the same conclusion as the regression ones: DA increases ICU workload, mostly through its effect on bleeding events.
Nevertheless, the interpretation of this model should be made with caution, as two of its endogenous variables (treatment phase and ICU mortality) are binary and the others (the number of bleeding events per patient and ICU LOS) have particular distributional shapes (the first is a counting event, the second is particularly skewed). Furthermore, we do not take into account the clustering of patients within ICUs.
The authors would like to thank Mark Dusheiko (Center For Health Economics, University of York) and the participants at the second British-French meeting on Health Economics for their substantive input or feedback on an earlier draft. The authors assume full responsibility for the accuracy and completeness of the ideas presented.
Principal investigators contributing data in this multicenter trial were: Djilalli Annane and David Orlikowski (CHU Garches, Hôpital Raymond Poincaré); Pierre-Edouard Bollaert and Aurélie Cravoisy (CHU Nancy, Medical ICU, Hôpital Central); Yves Le Tulzo (CHU Rennes, Medical ICU, Hôpital Pontchaillou); Thierry Boulain (CHR Orléans); Yannick Mallédant, Axelle Maurice, and Philippe Seguin (CHU Rennes, Surgical ICU, Hôpital Pontchaillou); Bernard Regnier and Bruno Mourvillier (CHU Bichat-Claude-Bernard, Medical ICU); François Fourrier and Jacques Mangalaboyi (CHU Lille-Salengro); Jean-François Dhainaut and Nathalie Marin (CHU Cochin); Albert Jaeger and Pascal Bilbault (CHU Strasbourg, Medical ICU); Jean-Michel Boles and Anne Renault (CHU Brest, Medical ICU), Alain Durocher and Fabienne Saulnier (CHU Lille-Calmette); Christian Richard and Jean-Louis Teboul (CHU Bicêtre, Medical ICU); Georges Gbikpi-Benissan (CHU Bordeaux-Tripode, Medical ICU); Claude Martin, François Antonini, and Marc Leone (CHU Marseille-Nord); Benoît Veber (CHU Rouen, Surgical ICU); Michèle Génestal and Olivier Anglès (CHU Toulouse-Purpan); Jean-François Poussel (Hôpital de Metz); Jacques Durand-Gasselin and Isabelle Granier (Hôpital Front Pré, Toulon); Yves Castaing and Odile Pillet (CHU Bordeaux-Pellegrin, Medical ICU); Christian Virenque, Kamran Samii, and Pierre Cougot (CHU Toulouse-Rangueil)
Source of financial support: Health Ministry, DHOS France.




