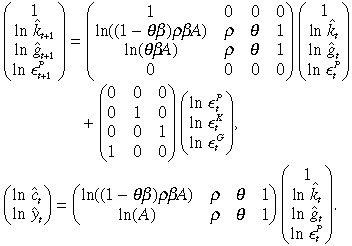Public Capital Spillovers and Growth Revisited: A long-run and Dynamic Structural Analysis*
This paper was originally circulated as ‘Public Infrastructure Spillovers and Growth: Theory and Time Series Evidence for Australia’ by Timothy Kam. We are grateful to David Harris, Robert Dixon, Jim Thomson, Vance Martin, Mark Crosby, Nilss Olekalns, Graeme Wells, John Creedy, Amelia Teng, Kirdan Lees and two anonymous referees for their comments and suggestions. We also thank the Associate Editor, Glenn Otto, Heather Anderson and Farshid Vahid for valuable comments and suggestions that have significantly improved the paper.
Abstract
We extend the deterministic growth model of Glomm and Ravikumar (1994) to a stochastic endogenous growth model which nests both exogenous and endogenous growth factors. By introducing simple shocks to production technology, private capital and public capital investment, we can derive testable time series properties of the analytical model. We find evidence of co-integration between per capita output, per capita private capital and public capital. A nested test of the strictly endogenous growth model is rejected statistically. We find that growth is exogenous even in the presence of significant and sizeable public capital spillover effects. Our long-run elasticity estimates help to inform the short-run dynamic transitions of the model. In particular, we are able to structurally rationalise other empirical findings of bi-directional short-run effects between public and private capital and also aggregate output.
I Introduction
In this paper, we extend the deterministic growth model of Glomm and Ravikumar (1994) to a stochastic growth version with endogenous public capital spillovers. By introducing simple shocks to production technology, private capital and public capital investment, we can derive testable time series properties of the analytical model along the lines of Lau and Sin (1997) who first investigated a similar question for the USA.
We allow growth of per capita income to be generated exogenously via Harrod-neutral technical progress and/or endogenously by aggregate public infrastructure spillovers. The postulation of strict endogenous growth due to public capital spillovers is tested empirically for Australia using annual data for the period 1960/1961–2005/2006.
To the best of our knowledge, there has been no work that takes the approach in Lau and Sin (1997) and Lau (1997), of using a theory-consistent approach to test for endogenous growth effects, with respect to Australian data. We show that the hypothesis of strict endogenous growth due to public capital spillovers is statistically rejected in the Australian data. Instead growth is exogenous even in the presence of significant and sizeable public capital spillover effects. Unlike Lau and Sin (1997), we also explore the short-run causal links between public capital accumulation and growth. Compared to other existing studies based on vector autoregression methods (see Otto and Voss, 1996, 1994b, as Australian examples), we provide an alternative and structurally more coherent study of the long- and short-run effects of public capital investment for the case of Australia.1 Our long-run elasticity estimates help to inform the short-run dynamic transitions of the model. In particular, we are able to provide a purely structural explanation of existing empirical findings or conjectures (e.g. Aschauer, 1989; Otto & Voss, 1996) of bi-directional short-run effects between public and private capital and also private production.
The role of public capital as distinct from private capital in fostering growth has received attention from the economics profession as early as Arrow and Kurz (1970). This hypothesis became known in the empirical literature as the public capital debate, which began with the seminal work of Aschauer (1989). Aschauer's method of estimating a single aggregate production function (which incorporates public capital stock) was first adapted for Australian studies by Otto and Voss (1994a). Both papers found that there was a significantly large elasticity of output (in the order of 0.40) with respect to public capital. Their methodology was not without criticism. The critiques range from claims of possible endogeneity of the public capital variable to the ad hoc nature of imposing a production function.2 However, as earlier works such as Otto and Voss (1996) and Otto and Voss (1994b) have shown, this approach did not suffer from the problem of spurious regression. On the contrary, the production function approach can be interpreted as a long-run relationship between output, and the private and public inputs, as in Flores de Frutos et al. (1998). Furthermore, as Lau and Sin (1997), and we show in this paper, this time series property of the variables can be derived from a stochastic growth framework with sound microfoundations.
The paper is thus arranged. A stochastic growth version of the Glomm and Ravikumar model and the time series (cointegration) basis of the production function framework is derived in Section II. We consider Australian data in Section III. Section IV contains the estimation and test of various growth hypotheses within the co-integrating relationship. The short-run and impulse response analysis, using the structural model which is informed by the long-run parameter estimates, is conducted in Section V. The paper concludes with Section VI.
II A Simple Modified Model
A stochastic growth modification of the Glomm and Ravikumar model is presented in this Section. A representative household-worker chooses an optimal consumption or investment path to maximise expected lifetime utility, given resource constraints and taking government policy as given. The fiscal policy is assumed to be a Ramsey planning problem subject to technological constraints and a periodic balanced budget à la Barro (1990).
(i) Technology and Household Choice
Let Y be aggregate output, K be aggregate private capital stock, L be the total number of workers or population and 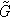 be a measure of congestion-adjusted public capital stock to be defined later. The Harrod-neutral rate of technological progress is denoted by x and some constant level of total factor productivity is given by A > 1. We would like public capital to enter aggregate production so that potentially there would be a spillover effect.3 Assume that the aggregate production function takes the Cobb-Douglas form
be a measure of congestion-adjusted public capital stock to be defined later. The Harrod-neutral rate of technological progress is denoted by x and some constant level of total factor productivity is given by A > 1. We would like public capital to enter aggregate production so that potentially there would be a spillover effect.3 Assume that the aggregate production function takes the Cobb-Douglas form
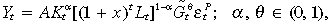 (1)
(1)which yields the production function in per worker terms as
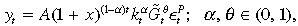 ((1a))
((1a))where the lower case variables, y and k, denote per worker output and private capital, respectively. Thus, the model nests the possibilities of exogenous and/or endogenous growth. The production technology is subject to i.i.d. shocks, 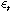 , assumed to be multiplicative in this model. Aggregate public capital,
, assumed to be multiplicative in this model. Aggregate public capital, 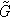 t, enters as an input into production (implying the spillovers or externality effect) and it is taken by the representative agent as given. Furthermore, aggregate public capital is subject to congestion from its use by private production:
t, enters as an input into production (implying the spillovers or externality effect) and it is taken by the representative agent as given. Furthermore, aggregate public capital is subject to congestion from its use by private production:
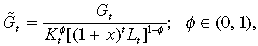 (2)
(2)where Gt is the aggregate stock of public infrastructure investment and φ and (1 – φ) denote the degree of congestion arising from private capital stock and labour force, respectively. This is contrary the usual notion that public goods are nonexclusive and non-rival.
We can further detrend Equation (1a). Let ŷt := yt/(l + x)t, k̂t := kt/(1 + x)t and ĝt := Gt/Lt(1 + x)t. Thus Equation (1a) can be written in per efficiency unit worker terms as
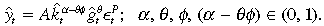 (3)
(3)Assume that there is 100-per cent depreciation at the end of each period for private capital. Then private per capita investment will give the following period's capital stock per efficiency unit worker:
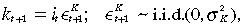 (4)
(4)where i is investment per efficiency unit worker and k0 is given. Similarly, aggregate public infrastructure investment is assumed to depreciate fully at the end of the period such that
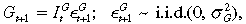 (5)
(5)where IG is aggregate public expenditure on infrastructure and G0 is given.
Let τ be the uniform income tax rate. The household solves
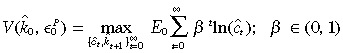 (6)
(6)subject to
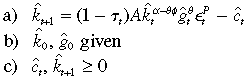
for all 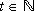 .
.
It is shown in Appendix I, by restating the problem in Equation (6) as a dynamic program, that the solution to the household problem taking government policy  as given, yields the optimal paths of consumption and private capital as
as given, yields the optimal paths of consumption and private capital as
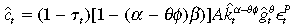 (7)
(7)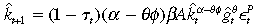 (8)
(8)for all states and dates 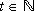 , given k0. The analytical solutions were obtainable by assuming logarithmic utility, Cobb-Douglas technology, 100 per cent depreciation of private and public capital, a uniform tax structure and a balanced budget. This also simplifies the model's restriction on the co-integrating properties of the variables.
, given k0. The analytical solutions were obtainable by assuming logarithmic utility, Cobb-Douglas technology, 100 per cent depreciation of private and public capital, a uniform tax structure and a balanced budget. This also simplifies the model's restriction on the co-integrating properties of the variables.
(ii) Public Sector
The government budget is such that public investment demand each period is exactly financed by income tax revenue:
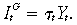 (9)
(9)We assume a government policy to be one that implements a Ramsey optimal fiscal plan. The government maximises the same objective function as households but it also takes into account the optimal behaviour of private agents with respect to the policy plan in a competitive equilibrium. The optimal policy is a sequence of tax functions solving the following problem:
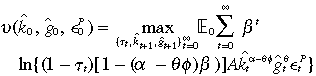 (10)
(10)-
subject to
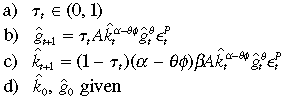
for all 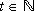 . Notice that we have replaced per period consumption in the objective with the competitive behaviour in Equation (7) and also encoded households’ optimal capital investment decision Equation (8) into constraint (c) above.
. Notice that we have replaced per period consumption in the objective with the competitive behaviour in Equation (7) and also encoded households’ optimal capital investment decision Equation (8) into constraint (c) above.
It is assumed that the benevolent government maximises household welfare when it maximises household consumption growth. A further assumption is that the sequence 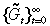 is bounded above by
is bounded above by 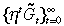 for some value η ≥ 1, to ensure that the infinite horizon household objective is bounded above for all feasible consumption paths. In other words, the optimal paths in Equations (7) and (8) will be unique: Glomm and Ravikumar (1994).
for some value η ≥ 1, to ensure that the infinite horizon household objective is bounded above for all feasible consumption paths. In other words, the optimal paths in Equations (7) and (8) will be unique: Glomm and Ravikumar (1994).
(iii) Optimal Public Policy
Solving the government's problem by dynamic programming (Appendix II), it is found that the optimal tax rate is a function of constants. Specifically, the optimal tax rate is defined by the function
τ = θβ
(11)for all states and dates 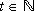 . Thus, the optimal tax rate is equal to the one-period discounted share of public capital in output, where the government faces the same subjective discount rate, β, as the household.
. Thus, the optimal tax rate is equal to the one-period discounted share of public capital in output, where the government faces the same subjective discount rate, β, as the household.
Second, given the optimal choice of public policy, the evolution of private capital per efficiency unit worker in Equation (8) can be described by the first-order stochastic difference equation
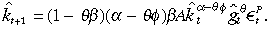 (12)
(12)The evolution of public capital per efficiency unit worker is
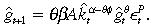 (13)
(13)Consequently, the ratio of the optimal paths for private and public capital stays constant over time. This can be observed by taking the ratio of Equation (13) to Equation (12), which yields
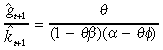 (14)
(14)for all states and dates 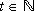 .
.
(iv) Long-Run Growth
Substitution of Equation (14) into (12) gives the essential difference equation for the evolution of private capital:
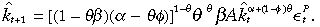 (15)
(15)Under an assumption of constant returns to scale to reproducible factors, where α + (1 – φ)θ = 1, the steady-state ( = 1; ∀t) growth rate of private capital will be given by [(1 – θβ)(α – θφ)]1–θθθβA, which is perpetual and nonexplosive. Also, output and public capital will grow at the same rate as private capital, with constant returns to scale Cobb-Douglas technology.
= 1; ∀t) growth rate of private capital will be given by [(1 – θβ)(α – θφ)]1–θθθβA, which is perpetual and nonexplosive. Also, output and public capital will grow at the same rate as private capital, with constant returns to scale Cobb-Douglas technology.
(v) Testable Time Series Properties of the Model
Equations (12) and (13) can be written in natural logarithm and substitution of these into the stochastic investment equations in (4) and (5) yields
 (16)
(16)and
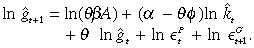 (17)
(17)Multiplying Equation (16) by (1 – θL) on both side, where L is the lag operator, and substituting for (1 – θL) ln ĝt from Equation (17) yields an equilibrium dynamic equation of the log of per capita private capital expressed in terms of its own lags and the external shocks:
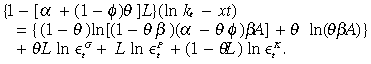 (18)
(18)Multiplying Equation (17) by [1 – (α – θφ)L] and substituting for [1 – (α – θφ)L]ln kt from Equation (16) yields the equilibrium path for aggregate public capital:
 (19)
(19)Also, taking logs of the equation for the private production function in Equation (3), multiplying this by {1 – [α + (1 – φ)θ]L} and expressing this in per worker terms, yields
 (20)
(20)This equation describes the equilibrium path of the log of output per worker, ln yt.
Perpetual and Stable Growth At Steady State
In this growth model, growth in per capita output or income depends on the coefficient of the lagged output variable, α+ (1 – φ)θ. This is also the sum of all the exponents (or the factor shares) of the private and public inputs into production. There will be no perpetual growth in the per capita variables once the economy reaches the steady-state path, if α+ (1 – φ)θ < 1, since the effects of past disturbances decay successively in Equation (20). Conversely, the steady-state growth path will be explosive if α+ (1 – φ)θ > 1. In this case there is increasing returns to all inputs. The model also nests the case of pure exogenous growth, which occurs if α+ (1 – φ)θ < 1 and x > 0. To obtain perpetual endogenous growth with stability in the model, it is a requirement that α+ (1 – φ)θ = 1 and x = 0. This is the strict endogenous growth case. Thus, even if private production displays diminishing returns to private inputs, overall it experiences constant returns to scale due to the spillover effect from public capital. Hence there are two empirical properties to be expected of the variables in the endogenous growth case. First, the sequences of function  and
and  will be exact unit root processes. Second, and consequently, the first difference of the logs of the per capita variables will be stationary, if the linear combinations of the shocks in (18) to (20) are stationary in levels.
will be exact unit root processes. Second, and consequently, the first difference of the logs of the per capita variables will be stationary, if the linear combinations of the shocks in (18) to (20) are stationary in levels.
Derivation of Co-integrating Relationships
If there are three I(1) variables in the system, there can be a maximum of two linearly independent co-integrating vectors. For nonexplosive, perpetual endogenous growth, it was concluded that α+ (1 – φ)θ = 1. Using this fact in Equations (19) and (20), and then subtracting the former from the latter, and performing the same again on Equations (18) and (20) gives the co-integrating space as
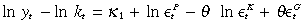 (21)
(21)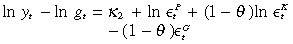 (22)
(22)where κ1 and κ2 are constants.
If the co-integrating space in Equation (21) and (22) is rejected, then there may be at most one co-integrating vector. This co-integrating equation is a linear combination of all the variables. This can be shown by multiplying Equation (21) on both sides by (1 – θ), and and Equation (22) on both sides by θ, and then summing the two equations, to obtain
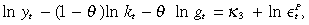 (23)
(23)where κ3 is some constant.
The co-integrating equation in (23) also represents the production function at steady state with nonexplosive, perpetual growth. In general, without assuming α+ (1 – φ)θ = 1, the single unrestricted co-integrating equation can be derived from Equation (3) yielding
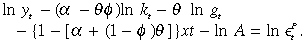 (24)
(24)Note that (23) is a nested case of (24) where (23) was derived under the hypothesis of α+ (1 – φ)θ = 1. These possible co-integrating relationships will be tested in Section IV of this paper.
III Data
The empirical analysis in this part involves annual time series from 1960/61 to 2005/06 for Australia. We measure the model-implied output, Y, as GDP excluding net exports.4 Our proxies for private capital (K) and public capital (G) are obtained from gross private and public capital formation series, respectively. We then deflate the series using a common price deflator, followed by the use of a population measure, to obtain the empirical measures of per capita output, private capital and public capital (y, k, g). All the per capita variables are expressed in logarithms as implied by Equations (23) and (24). Detailed description of the sources and construction of the data is given in Appendix III.
Our choice of data is governed by the model's prescription. Specifically, since the model has 100 per cent depreciation rate of both private and public capital, it would be justified here to treat gross capital formation (investment) at time t to be equivalent to capital stock at time t + 1, subject to small perturbations. Also, since the model is silent on the open-economy sector, an appropriate measure of output for our empirical analysis should be GDP net of trade balance. Finally, the choice of a common price deflator for constructing the real data measures is motivated by the fact that the model is a one-good or one-sector growth model.5
(i) Weak Stationarity of the Series
From Table 1, the augmented Dickey and Fuller (1979, 1981) unit root test reveals that all the variables appear to be non-stationary in levels (contain a unit root), but will be stationary after taking first differences.
| Sample period | Endogenous variables in levels | ||
| ln yt1961–2005 | ln kt1961–2005 | ln gt1962–2005 | |
| Lags of ADF test | 0 | 0 | 1 |
| Exogenous | Constant and trend | Constant and trend | Constant and trend |
| ADF statistics | –2.6933 | –2.2301 | –3.2612 |
| 5 per cent critical value | –3.5131 | –3.5131 | –3.5155 |
| Sample period | Endogenous variables in first differences | ||
| Δln yt1963–2005 | Δln kt1962–2005 | Δln gt1962–2005 | |
| Lags of ADF test | 1 | 0 | 0 |
| Exogenous | Constant | Constant | Constant |
| ADF statistics | –5.3600 | –5.8761 | –4.8639 |
| 5 per cent critical value | –2.9314 | –2.9297 | –2.9297 |
- Notes: (a) The lag length of each dependent variable is optimally determined by Schwarz selection criterion with maximum length 9. (b) Critical values for augmented Dickey–Fuller (ADF) test statistics are from MacKinnon (1991). (c) ADF regression residuals are free of serial correlation problems based on LM tests (at the 5 per cent level of significance).
IV Empirical Evidence for Australia
Since ln yt, ln kt and ln gt are statistically I(1) variables, it may be possible that there is (or are) some long-run relationship(s) between them. As we previously derived in (21) and (22), the theory suggests up to two such long-run or co-integrating relationships. Alternatively (24) suggests one such relationship.
(i) Testing for Two Co-integrating Vectors
We consider first the possibility of two co-integrating relationships. Table 2 shows that we can reject the pairwise co-integrating relationships for Equations (21) and (22) as the residual from each estimated linear combination of the variables fails to be stationary. Therefore, we cannot have a maximum of two linearly independent cointegrating vectors in our sample. Alternatively, we also use the Johansen (1991) cointegration rank test which is fully reported in the next section. Again the conclusion is identical.
| Sample period | Endogenous variables in levels | |
|---|---|---|
| ln yt – ln kt1961–2005 | ln yt – ln gt1961–2005 | |
| Lags of ADF test | 0 | 0 |
| Exogenous | Constant | Constant |
| ADF statistics | –2.8243 | –0.8507 |
| 5 per cent critical value | –2.9281 | –2.9281 |
- Notes: (a) The lag length of each dependent variable is optimally determined by Schwarz selection criterion with maximum length 9. (b) Critical values for augmented Dickey–Fuller (ADF) test statistics are from MacKinnon (1991). (c) ADF regression residuals are free of serial correlation problems based on LM tests (at the 5 per cent level of significance).
(ii) Testing for a Single Cointegrating Vector
Next, we consider whether there exists one cointegrating vector among the three variables in Australia. To motivate this possibility, consider a scatter plot of {ln y, ln k, ln g} in Figure 1. This raw and informal plot suggests that all three series occur along some common vector at least in the long-run. In other words, there is some informal evidence of a single cointegrating vector for all three variables.
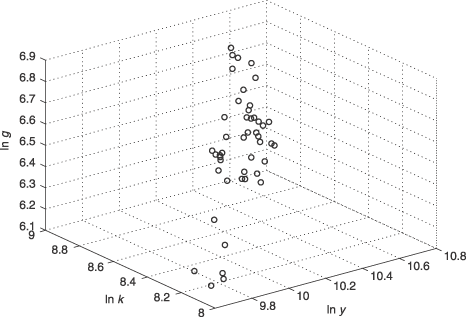
Scatter Plot of Log per Capita Output, Private Capital and Public Capital
Based on the combination of the theoretical relationship in Equations (23) and (24), or more generally on (24), this informal evidence can be tested by the following reduced-form regression:
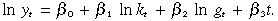 (25)
(25)The reduced-form coefficients β1, β2 and β3 in Equation (25), respectively, denote (α – θφ), θ and {1 – [α + (1 – φ)θ]x} originating from Equation (24). Specifically, if the estimated coefficients follow the conditions that β1 + β2 = 1 and β3 = 0, the engines of economic growth are endogenously determined by both private and public capital. That is, Equation (23) holds such that the production function in Equation (3) exhibits constant returns to scale. Conversely, if β1 + β2 is estimated to be < 1, together with a positive β3, the long-run relationship between the variables {ln y, ln k, ln g} is in favour of Equation (24) and the economy will grow exogenously along the time trend. For completeness, we provide two tests and three alternative estimates of the possible cointegrating relationship.
As one robustness check for the existence of possible cointegrating relationships between {ln y, ln k, ln g} we apply the Johansen (1991) test. Our test is based on a vector autoregressive (VAR) model with lag length 2, which is optimally chosen using the Schwarz information criterion. Johansen's cointegration rank (trace) test indicates that there exists only one cointegrating equation (with an intercept and a time trend) at the usual 5 per cent level of significance. The Trace test statistic for a null hypothesis of no cointegration (against an alternative hypothesis of one cointegrating relationship) is 44.67, and the 5 per cent-significance level critical value is 42.92. There is no further evidence for at most two cointegrating vectors. The estimated single cointegrating relationship is:
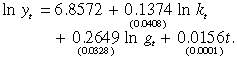 ((25a))
((25a))The cointegration estimators of ln kt, ln gt and time trend are significant even at 1 per cent level of significance.
Alternatively, we can perform the cointegration test amongst {ln y, ln k, ln g} with a time trend based on the Engle and Granger (1987) two-step procedure. In the first step, we estimate the long-run relationship as
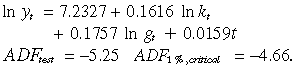 ((25b))
((25b))In the second step of the Engle–Granger procedure, the existence of cointegrating relationship amongst the three variables with a time trend requires the OLS residuals from Equation (25b) to be stationary. Otherwise, we would have a spurious regression. The augmented Dickey–Fuller (ADF) test statistic of the regression residual from Equation (25b) is –5.25 and is beyond the 1 per cent critical value equaling –4.73.6 Therefore, we can conclude that the regression residual from Equation (25b) is a stationary process such that this cointegrating equation holds.
However, the inference on the OLS estimators provided in Equation (25b) is not reliable since the estimators are super-consistent and the distribution of the estimators’t-statistics are non-standard. However, proper inference can be made if we refine the estimation using the dynamic OLS (DOLS) estimation method proposed by Stock and Watson (1993). Specifically, the DOLS method takes into account leads and lags of the first-differenced regressors in Equation (25b). We can further ensure that the estimation errors do not exhibit serial correlation and heteroskedasticity. The estimates of Equation (25b) is refined using DOLS as:
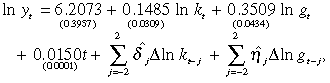 ((25c))
((25c))where the Newey-West heteroskedasticity and autocorrelation consistent (HAC) standard errors are given in parentheses, and 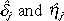 denote the estimated coefficients of the leads and lags of first-differenced regressors.7 The optimal lengths of leads and lags are chosen based on the minimal Schwarz information criterion.
denote the estimated coefficients of the leads and lags of first-differenced regressors.7 The optimal lengths of leads and lags are chosen based on the minimal Schwarz information criterion.
The estimated shares of public and private capital from Equation (25c) suggest that the former is more than double that of the latter. This implies that public capital has dominated the process of economic development in Australia in our sample period. This result is opposite to the findings from Lau and Sin (1997), who used US data for a similar regression and estimated the coefficients of ln gt and ln kt to be 0.11 and 0.43, respectively. They therefore emphasised the dominance of private capital in the process of economic growth in the USA. Another study for Australia was carried out by Otto and Voss (1994a) using a shorter sample period of 1966/1967–1989/1990. Although their findings revealed a higher share of public capital in the production process than Lau and Sin (1997), and which is much closer to our findings here, their share of private capital was estimated to be negative. This negative share does not quite fit well with most growth models.
(iii) Joint Hypothesis Testing of Growth Conjectures
Next, we conduct some hypothesis tests on the long-run relationship based on the DOLS regression result (25c). The tests are reported in Table 3. The first test considers the null hypothesis of β1 + β2 = 1, which is the case of perpetual growth with public capital spillover but not ruling out the existence of exogenous trend growth. The second test is for the hypothesis of no exogenous growth, or β3 = 0. The third joint test is for the hypothesis of strict endogenous growth, or β1 + β2 = 1 and β3 = 0. We can reject all three null hypotheses at the usual 5 per cent level of significance. In particular, the hypothesis of strict endogenous growth due to public capital spillover into aggregate production does not hold in Australia during our sample period. In other words, while there is public capital spillover into aggregate production, there is no endogenous growth effect from it. Instead, growth is driven by an exogenous component. It should also be noted that the trend coefficient estimate of about 0.015, which is the implied annual rate of technical progress, is very close to the Australian Bureau of Statistic's calculations.8
| Null hypothesis | F-test statistic | Critical value | Conclusion |
|---|---|---|---|
| 1. β1 + β2 = 1 | 31.66 | F 1,25 = 4.24 | Rejection of the null |
| 2. β3 = 0 | 584.67 | F 1,25 = 4.24 | Rejection of the null |
| 3. β1 + β2 = 1 and β3 = 0 | 229.60 | F 2,25 = 3.39 | Rejection of the null |
In summary, growth is driven by exogenous factors, along with public capital spillovers that have no endogenous growth effects, when we confront the model with Australian data. Output per capita grows exogenously at a rate about 0.015, and public capital spillovers contribute higher share to the output than private capital in our sample period.
(iv) Economic Relevance of Long-run Estimates
Since one of the parameters {α,φ} cannot be identified from the estimates of β1 and β2 = θ, we perform the following informal exercise to check whether our estimates provide some sensible economic parameterisation. We use the following guideline. Since we know very little about the congestion parameter φ in the model, except that it must be theoretically constrained to be within the open set (0, 1), we set α to two scenarios: α = 1/3 and α = 1/4. The latter parameterisation is motivated by the argument that the usual share of private capital stock in levels is lower than the stylized fact of 1/3 in the presence of endogenous growth effects. Table 4 demonstrates a comparison of estimated results between the two previous studies and our findings based on Equation (25c). It should be noted that when considering the congestion effect of aggregate public infrastructure in Equation (2), the estimated coefficients of ln gt and ln kt from Lau and Sin (1997) result in a theoretically infeasible congestion parameter φ when we set the private capital share α as a reasonable scale (either 1/3 or 1/4). However, in either parameterisation, our regression output indicates that φ can be calculated with reasonable values. The case where α = 1/3 with φ = 0.5267 suggests that private capital, rather than private labour input, has a slightly higher share in creating congestion effects on public capital in Equation (2). In contrast, the congestion effect of private capital is about three times weaker than private labour input when we set α = 1/4.
| Lau and Sin (1997) | Otto and Voss (1994a)† | This paper | ||||
|---|---|---|---|---|---|---|
| Estimated coefficients | US data | Australia data | Australia data | |||
| β 1 = (α – θ φ) | 0.43 | –0.0870 | 0.1485 | |||
| β 2 = θ | 0.11 | 0.4303 | 0.3509 | |||
| Parameterisation | α = 1/3 | α = 1/4 | α = 1/3 | α = 1/4 | α = 1/3 | α = 1/4 |
| Congestion parameter φ | –0.8788 | –1.6364 | 0.9768 | 0.7832 | 0.5267 | 0.2893 |
- Note: † Otto and Voss (1996) and Otto and Voss (1994b) also provide alternative estimates of the parameter similar to θ ranging from 0.39 to 0.45, respectively.
V Public Capital and Transitional Dynamics
In this exercise we will use the point estimates of θ and ρ := α – θφ from the previous DOLS cointegration estimates reported in Equation (25c) for the simulation of the transitional dynamics in the model. Our exercise here differs from Otto and Voss (1996) in the sense that the theoretical model implies a long-run relationship which was estimated and that these estimates also inform the behaviour of the model's short-run dynamics. In this way, we can have a coherent understanding of the role of public capital using an internally consistent model which is also empirically fasifiable. Otto and Voss (1996) considered the short-run impact of public capital using empirical VAR analysis and the mapping of their analysis back to any theoretical structure is unclear.
If one inspects the model again, the short-run dynamics is given by the two stochastic difference Equations (16) and (17), which encode the solutions to the decentralised equilibrium under optimal fiscal policy. More importantly, the unidentified parameters {β, A,φ} are irrelevant towards determining the short-run dynamics. As long as we have obtained the long-run estimate of θ and the composite parameter ρ := α – θφ, we would be able to study the short-run dynamics implied by the model's equilibrium conditions. Since the equilibrium conditions (16) and (17) are already in linear form, it is straightforward to compute the impulse responses of 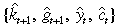 given a shock to any of the following exogenous idependently and identically distributed processes
given a shock to any of the following exogenous idependently and identically distributed processes
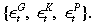
Appendix IV provides the details of the exact log-linear characterisation of equilibrium.
Figure 2 shows the impulse response functions (lines with square markers) of private capital, public capital, consumption and output to a 100 per cent positive shock to public capital investment. From the equilibrium conditions (16) and (17) we can deduce quite readily that the shock has an immediate and equally large impact on public capital. The impact on consumption and output is also immediate, and it has the same magnitude as θ itself. What is interesting is that even without any persistence in the primitive shock, the effect of an increase in public capital investment is felt by private capital, output and consumption (in per unit of efficient worker terms) over several years. To illustrate the role of public capital spillovers, we plot the counterfactual case (solid-line impulse responses) of holding all estimates constant while setting θ = 0, in the same figure. As can be deduced from the equilibrium conditions (16) and (17), when θ = 0, there is no effect on private sector endogenous variables following a public capital investment shock.
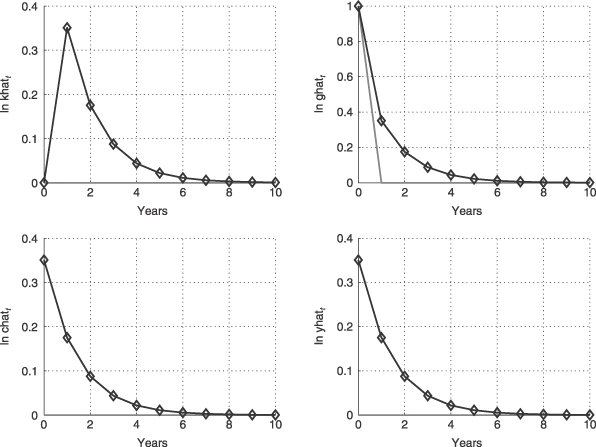
Impulse Response to a One-unit Shock to Public Capital Investment. Estimated Model (
 ). Counterfactual Case with θ = 0 (—)
). Counterfactual Case with θ = 0 (—)
Figure 3 shows the impulse response functions of private capital, public capital, consumption and output to a 100 per cent positive shock to private capital investment. The impulse response profiles look quite similar to the previous case of the public investment shock. The only difference is that private capital responds to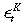 immediately as is evident from (16). This structural exercise also confirms or provides economic intuition for the reverse causality (from private capital to public capital) found in empirical VAR studies, such as Otto and Voss (1996). We have a clean interpretation from the model where the ‘reverse causality’ is a result of optimal fiscal policy that encodes the current state of private capital (and relevant current realised shocks) into the investment in public capital for the following period (see equation 17). Again, comparing the estimated case (lines with square markers) with the counterfactual of θ = 0 (solid lines) in Figure 3, we can see that the existence of public capital spillovers prolong the effect of private capital investment shock on all other endogenous variables.
immediately as is evident from (16). This structural exercise also confirms or provides economic intuition for the reverse causality (from private capital to public capital) found in empirical VAR studies, such as Otto and Voss (1996). We have a clean interpretation from the model where the ‘reverse causality’ is a result of optimal fiscal policy that encodes the current state of private capital (and relevant current realised shocks) into the investment in public capital for the following period (see equation 17). Again, comparing the estimated case (lines with square markers) with the counterfactual of θ = 0 (solid lines) in Figure 3, we can see that the existence of public capital spillovers prolong the effect of private capital investment shock on all other endogenous variables.
Impulse Response to a One-unit Shock to Private Capital Investment. Estimated Model (
 ).Counterfactual Case with θ = 0 (—)
).Counterfactual Case with θ = 0 (—)
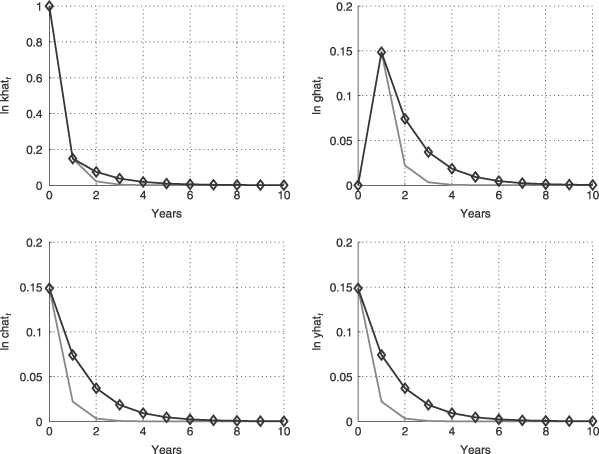
Finally, we can also consider the effect of the total factor productivity shock,  , in Figure 4. Again, the impulse response profiles look quite similar to the previous cases. The only difference is that private and public capital now respond to
, in Figure 4. Again, the impulse response profiles look quite similar to the previous cases. The only difference is that private and public capital now respond to  with a one-period lag. Aschauer (1989) had also pointed out the possibility of reverse causation between the level of public capital expenditure and private production. In this model, this ‘reverse causality’ is actually driven by a total factor productivity shock having a positive symmetric effect on private and public capital accumulation, and also delayed reinforcing feedback of private capital on public capital over the short-run. Comparing the estimated case (lines with square markers) with the counterfactual of θ = 0 (solid lines) in Figure 4, we can see that the responses are more persistent when θ is non-zero.
with a one-period lag. Aschauer (1989) had also pointed out the possibility of reverse causation between the level of public capital expenditure and private production. In this model, this ‘reverse causality’ is actually driven by a total factor productivity shock having a positive symmetric effect on private and public capital accumulation, and also delayed reinforcing feedback of private capital on public capital over the short-run. Comparing the estimated case (lines with square markers) with the counterfactual of θ = 0 (solid lines) in Figure 4, we can see that the responses are more persistent when θ is non-zero.
Impulse Response to a One-unit Shock to Total Factor Productivity. Estimated Model (
 ). Counterfactual Case with θ = 0 (—)
). Counterfactual Case with θ = 0 (—)
VI Conclusions
It was the aim in this paper to study the effect of public infrastructure on the aggregate economy in terms of long-run growth and short-run effects. In particular, the issue was whether growth was determined in the long-run, in part, by the accumulation of the stock of public infrastructure. A simple stochastic growth model nesting exogenous and endogenous growth with public capital spillovers was considered in Section II of the paper.
The long-run implication of this model was tested empirically for Australia in Section IV. It was found that there was evidence of cointegration between per capita output, private capital and public capital around a deterministic trend. A nested test of the strictly endogenous growth model was rejected in favour of the exogenous growth model with public infrastructure spillovers.
Compared to existing studies, we have provided an alternative and, as we argued, a structurally more coherent study of the long- and short-run effects of public capital investment for the case of Australia. Using our long-run elasticity estimates, we were able to work out the short-run dynamic transitions of the model. In particular, we were able to rationalise other empirical findings of bi-directional short-run effects between public and private capital.
We recognise that the model is quite stylized and imposed a lot of restrictions on the data. For example, the assumption of complete per-period capital depreciation, along with the choice of functional forms, facilitated an analytical solution of the model and data choice. But this comes at a cost of unrealistic restrictions on the data. Further work on this issue must relax such an assumption and is not impossible. One could simultaneously estimate, numerically solve the model and infer its long-run properties. We leave that for future work.
Footnotes
REFERENCES
Appendix I
Dynamic Programming for the Household Problem
The method of solving the household's intertemporal utility maximisation problem subject to given constraints and public policy in Equation (6) is as follows. The Bellman (1957) principle of optimality dictates that if the sequence of functions 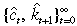 is maximising, then it must also be the case that it is maximal for
is maximising, then it must also be the case that it is maximal for  . Hence, the sequence problem in Equation (6) can be written recursively as
. Hence, the sequence problem in Equation (6) can be written recursively as
 ((A.1))
((A.1))subject to constraints (6) (a)–(c). A guess of the solution to (A.1) is the value function of the form
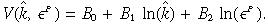 ((A.2))
((A.2))Substituting the form of equation (A.2) into (A.1) gives
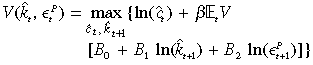 ((A.3))
((A.3))subject to constraints (6) (a)–(c). The optimality conditions for a maximum on the RHS of (A.3) are
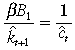 ((A.4))
((A.4))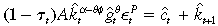 ((A.5))
((A.5))for all states and dates 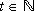 . Substitute equation (A.4) into (A.5) to obtain
. Substitute equation (A.4) into (A.5) to obtain
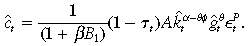 ((A.6))
((A.6))Use the natural constraint (A.5) and (A.6) to derive the stochastic difference equation for private capital per efficiency unit worker
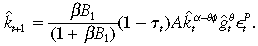 ((A.7))
((A.7))Substitute Equations (A.6) and (A.7) into the RHS of the Bellman Equation (A.3) so that (A.3)
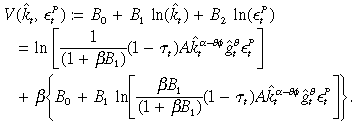
The guess (A.2) is the fixed-point solution of the (A.1), if and only if
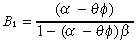 ((A.8))
((A.8))and two similar conditions for B0 and B2 which are not vital for characterising the optimal decision rules. Substitute (A.8) into Equations (A.6) and (A.7) then we can obtain the characterisations of the optimal household consumption (7) and investment (8) plans with given public policy  .
.
Appendix II
The Government's Problem and Optimal Outcomes
The government's Ramsey optimal fiscal policy problem is recursive by assumption:
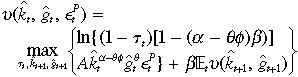 ((B.1))
((B.1))subject to constraints (10)(a)–(d). Guess that the solution is of the form below:
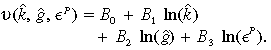 ((B.2))
((B.2))Utilising the guess in (B.2), re-write equation (B.l) as
 ((B.3))
((B.3))subject to (10) (a)–(d). It is also assumed here that ln( ) is i.i.d and therefore,
) is i.i.d and therefore,  ln(
ln( ) = 0.
) = 0.
The optimality conditions for the RHS problem are
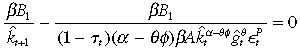 ((B.4))
((B.4))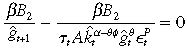 ((B.5))
((B.5))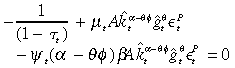 ((B.6))
((B.6))for all states and dates 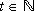 .
.
Substitute Equations (B.4) and (B.5) into equation (B.6) gives
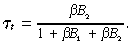 ((B.9))
((B.9))Further substitution of Equation (B.9) back into constraints (B.4) and (B.5) results in
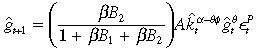 ((B.10))
((B.10))and
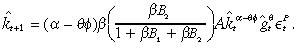 ((B.11))
((B.11))Next, substitute (B.10) and (B.11) into (B.3) and compare with the form of (B.2).
The guess (B.2) is a solution to the government's Bellman equation if and only if B1 = (α – θφ) (1 + βB1 + βB2) and B2 = θ(1 + βB1 + βB2) and a similar condition for B0 holds. Solving for B1 and B2 yields
 ((B.12))
((B.12))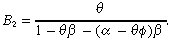 ((B.13))
((B.13))Substitution of equation (B.12) and (B.13) into (B.9), (B.10) and (B.11) gives the optimal tax rate (11), and the evolutions of private capital (12) and public capital (13).
Appendix III
Data Appendix
Population (POP)
Population data in Australia (in 1000 persons) is recovered using GDP and GDP per capita series in the Australian Bureau of Statistics (ABS) National Accounts, 204–01.
GDP deflator (P)
We use a common GDP deflator P constructed by the World Bank World Tables (Table AUS.04), with base year 2000. This is motivated by the one-sector growth model we used.
Domestic output
Domestic output Y is constructed using gross domestic product (GDP) after subtracting out net exports. These original series are available from Table 5204-05 in the ABS National Accounts. This is further deflated using the GDP deflator, P. Finally, to measure real output per worker, y, we divide through by the population data, POP.
Private and public capital
Our proxy for K is given by gross private fixed capital formation (in million AUD), is from Table 5204-05 in the ABS National Accounts. Likewise, G is proxied by gross public fixed capital formation (in million AUD). This series includes the capital formation of national, state and local governments. It is also available from Table 5204-05 in the ABS National Accounts. These two nominal series are converted into real values using the GDP deflator, P. To obtain per capita measures, k and g, we, respectively, divide K and G through by the population data, POP.
Appendix IV
The Exact Log-linear System for Short-run Analysis
Equations (16) and (17) characterise the solutions to the decentralised equilibrium under optimal fiscal policy. Along with (3), (7) and (11), we can re-write the exact log-linear equilibrium conditions in state-space form as: