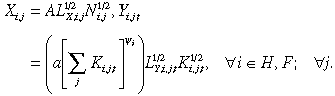Increasing Returns, Financial Capital Mobility and Real Exchange Rate Dynamics*
Thanks are due to Jill Harrison, Centre of Policy Studies, Monash University, for assistance with the modelling software used, to Martin Richardson for useful comments during the research and to two anonymous reviewers for constructive and detailed comments on an earlier draft.
Abstract
The late 1990s saw a US IT investment boom, large capital flows into the USA and an appreciation of the US$. At the time, this appeared to be driven by expectations of continued IT-related knowledge spillover externalities and associated productivity and profit growth. Using a two-region dynamic general equilibrium model with externalities, we find a once-off productivity shock leads to capital inflow and a real appreciation only in the short term. In the long term, capital flows stabilise and the real exchange rate depreciates. For a single shock to trigger long-term growth in capital flows requires unrealistically large externalities.
I Introduction
The late 1990s saw an appreciation of the US Dollar against the Euro and Australian Dollar of around 50 per cent (Figure 1). Then in 2002–2003 it lost all of the ground it had gained over the previous 7 years.1 The late 1990s coincided with the US information technology (IT) boom during which global financial markets funded levels of US investment as a proportion of US gross domestic product (GDP) that had been unseen since the years immediately following World War II.2 This investment was apparently based on the expectation that US productivity growth, and hence the relative rate of return on US capital, would be permanently higher as a result.3 In the language of the day, the ‘internet revolution’ was seen as creating a ‘new economy’, where technological progress could drive the economy faster without inflationary pressures (Brynjolfsson & Hitt, 2000; Oliner & Sichel, 2000; Baily & Lawrence, 2001; Baily, 2002). The particular gains to the US were seen as stemming not only from applications of the new technology, which was taken up almost as quickly in many countries (including Australia), but also from the returns to the US firms that created the associated hardware and software.4
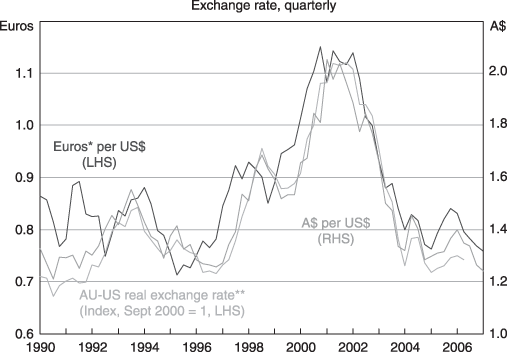
United States Dollar * Deutschmark before 1999; ** Nominal exchange rate deflated by CPI. Source: RBA, Datastream.
The US slowdown of 2001–2002 and the associated stock market crash put an end to these expectations. Yet, as Figure 2 shows, in the late 1990s US labour productivity growth averaged 2.5 per cent: almost double the average of the previous 20 years. There has been much debate about the reasons for this acceleration, however. Gordon (2000) argued, at least initially, that much of the increase was cyclical, while Oliner and Sichel (2000) attributed half of the higher productivity growth to capital deepening as firms invested in information technology. They ascribe the other half to faster total factor productivity growth, of which 40 per cent was due to efficiency gains in computer production. This means that around two-thirds of labour productivity growth was IT related.5 More recent research on this issue confirms the once-off nature of the productivity shock, the associated once-off rise in the IT share of national investment and the marriage in that period of computers with communication technology (Gordon, 2006, 2007; Jorgenson et al., 2007).6 In a very recent review, Oliner et al. (2008) show that the extraordinary US labour productivity growth continued at least through 2005, though the post 2000 growth appeared to depend on organisational efficiencies that, while stemming originally from recent technical changes, are more likely to be once-off gains.
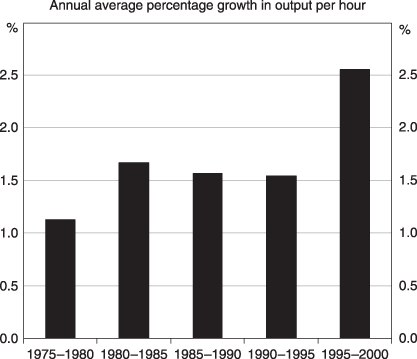
US Non-farm Labour Productivity Source: BLS.
There are several reasons why the initial US advantage in IT might have led to faster long run growth in North America relative to other regions, including Europe. First, high-tech industries might exhibit learning-by-doing, as in Lucas (1988), and Baldwin and Krugman (1992), and so the comparatively large IT sector in the US might have enjoyed falling costs relative to other sectors and other regional economies. Second, technological spillovers may have allowed a sustained increase in relative US technical progress. At the regional level, Saxenian (1994) argues that spillovers from the collaborative culture of Silicon Valley gave it an advantage over older research and development zones such as Route 128 in Boston.7 Third, external economies associated with proximity to specialised labour markets and intermediate input suppliers encourage co-location, regionally and nationally (Krugman & Venables, 1990 and Venables, 1996). All of these factors suggest the presence of increasing returns at the industry level where IT is a significant product or input.
In this paper we consider the hypothesis that the ‘new economy’ expectations were well founded, and the US economy had a unique (or comparatively large) IT productivity externality, conferring on its IT industry increasing returns to scale. We apply a generic two-region growth model, focusing on the effects of a technology shock on financial capital flows into the ‘home’ region and its real exchange rate. In particular, we address the conditions under which financial inflows could cause an agglomeration of the IT industry in the home region. Opposing forces include a rising local real wage and a rising price of local investment goods. At issue is whether these opposing forces are sufficient to bring the global economy to a new stable steady state and whether the residents of the rest of the world are necessarily worse off.
Our simulations suggest that, for a realistic range of externalities, the ‘home’ region enjoys expanded capital inflows and a real appreciation in the short term. In the medium-long-term, however, capital flows stabilise, the home real rate of return on capital declines and its real exchange rate depreciates. A once and for all productivity shock in one region can trigger long-term growth in capital returns and financial inflows but this is shown to require unrealistically large externalities.
The paper is organised as follows. Section II briefly reviews the relevant literature and Section III describes the two-region numerical model adopted. Section IV presents the simulated effects of a once-off IT-related productivity shock in one region without externalities. In the home region, externalities are then added in Section V. Section VI analyses effects of externalities in both regions and considers some extensions. Section VII concludes.
II Externalities and Agglomeration
The economic behaviour exhibited during the US internet boom encompasses the separate literatures on endogenous growth, economic geography and international finance. This paper offers a two-country growth model, though many of our findings relate closely to those found in the other literatures. Beginning with growth, a key antecedent is the work of Grossman and Helpman (1991), who present an international version of Romer's (1990) expanding product variety endogenous growth model with a national knowledge public good. Regions with larger initial stocks of knowledge (which can be thought of as being generated from a larger initial R&D industry) have higher productivity and so tend to dominate the production of the high-tech good in the long term. This suggests that the initial advantage of the US in internet technologies could have given it a permanent advantage in IT. However, Grossman and Helpman (1991) do not include physical capital, so no light is shone on the consequences for the regional distributions of savings and investment.
Lucas (1988) emphasises (human) capital accumulation through learning-by-doing, where high-tech goods generate faster human capital accumulation than low-tech goods. The region that initially specialises in the high tech good grows faster, but faces a decreasing terms of trade.
The ‘new economic geography’ literature suggests that a combination of increasing returns and transportation costs can lead to an agglomeration of industry in one region, the ‘industrial core’, and away from other regions, which become the ‘agricultural periphery’ (Krugman & Venables, 1990; Krugman, 1991). Baldwin (1998) adds internationally immobile (firm-specific) capital and produces broadly similar results. If capital is internationally mobile, however, then where production takes place and where factor income is received become increasingly separate, breaking down the mechanism which attracts firms to a larger market that drives agglomeration.
Caballero et al. (2008) analyse the sources of the large US current account deficit of recent years. Significantly, their focus is on the first decade of the new century, beyond the IT boom, when Gordon (2006) and Oliner et al. (2008) show that US productivity grew more strongly in services than in other sectors. They posit that this has to do with ‘investment efficiency’, whereby a larger proportion of savings generated in the rest of the world is turned into productive assets when invested in the US as compared with other countries. This is not a property of the IT sector but rather a consequence of comparative financial efficiencies that could have stemmed from IT applications in services.
Real exchange rates are approached from two perspectives in the literature. First, in models that incorporate nominal rigidities (such as Fleming, 1962; Mundell, 1963 and Dornbusch, 1976) real exchange rates follow nominal exchange rates in the short term (and hence depart from PPP), but in the long term they tend towards PPP as prices become more flexible (Devereux, 1997). The alternative view, which motivates our approach, is that real exchange rates are driven by real disturbances that affect relative costs on the one hand and the balance of saving and investment in each region (and therefore international financial flows) on the other (Lucas, 1982; Stockman, 1988; Tyers et al., 2008).8
In what follows, we borrow the ‘agglomeration’ nomenclature from the new economic geography literature but use the term to describe whether, ‘in the long term a significant majority of the world's high-tech industry will locate in a particular region, to the point that that region dominates the global high-tech industry’. This might be considered ‘partial agglomeration’– in the model we introduce in the next section, only partial agglomeration can ever occur due to product differentiation by country of origin (which is absent from standard economic geography models).
III The Model
Consider a world with two initially identical regions, Home (H) and Foreign (F), which both produce and freely trade two goods (X and Y).9 There are three primary factors: labour (L), capital (K) and land (N). X is low-tech and uses labour and land. Y uses labour and capital and its firms can enjoy external economies (potentially) in both regions. Saving rates from regional income are fixed and both collective households maintain asset portfolios that include foreign capital. There is no population growth, continuous technical change or money; time is discrete and the two regions are initially in a steady state. In our experiments, this steady state is disturbed by a 10 per cent once-off productivity shock to the Y industry in H. Impulse responses are then calculated for the capital stocks, real rates of return on capital, real exchange rates and real GNP levels.
The technologies in both sectors are Cobb–Douglas:
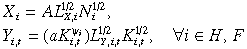 (1)
(1)There is a positive externality in the Y sector if ψi > 0, representing greater localised technological spillovers (Grossman & Helpman, 1991) or learning-by-doing (Lucas, 1988) in country i.10 Importantly, the term in parentheses in Equation (1) refers to the industry wide capital stock in region i, not the capital stock at the firm level. The externality is seen as depending on the size of the Y sector (the level of total capital use by its firms) and it is external to each firm but internal to the sector. For this reason we can use the terms externality and external economy interchangeably. High-tech firms do not perceive the effect of greater sectoral capital use on their productivity and therefore they price competitively – leading to zero pure profits.
Because both goods are traded, departures from PPP require failure of the law of one price for tradable goods. This is justified not only by widespread observation,11 but also by pervasive intra-industry trade. The most widely used approach to this is to assume product differentiation by region of origin, otherwise known as Armington (1969) differentiation.12 Specifically, each region's collective household has separable utility in generic goods and region-specific varieties. Region i's Cobb–Douglas utility in consumption of generic X and Y, 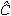 X,i and
X,i and 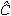 Y,i, is first maximised as in Equation (2).
Y,i, is first maximised as in Equation (2).
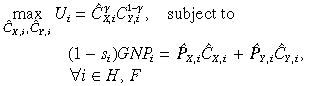 (2)
(2)where si is the regional saving rate. Then, accounting for differences in the prices of the home and foreign varieties, the cost of acquiring these generic volumes is minimised as in Equation (3).
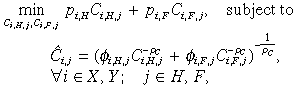 (3)
(3)where the elasticity of substitution between foreign and home varieties is σC = 1/(1 + ρC). Marshallian demands for each variety in each region follow from this, along with regional generic price indices taking the form:
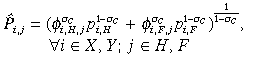 (4)
(4)It follows that each collective household always consumes at least some of all four goods (XH, XF, YH and YF) and hence low productivity and a high price in one region does not preclude exports to the other.
Investment in each region is financed by the issue of ‘bonds’ (B), which are available for sale at home and abroad. For our purpose, these bonds are the single instrument that is traded on capital accounts and are defined to encompass all forms of claims over physical capital. They are imperfectly substitutable between the two regions and yield the net rate of return, r, on regional capital.13 Initially, there is no home-bias in asset portfolios in either region, so the initial portfolios are split 50–50 between bonds issued in each region. In any year, the collective household of each region i allocates new saving, Si = siGNPi, between the bonds of each region, j, to maximise a constant elasticity of substitution (CES) ‘utility’ function as in Equation (5).14
 (5)
(5)This is a standard CES optimisation problem that directs bond holdings according to the weights, αi,H and αi,F with substitutability the more sluggish the larger is ρB. To capture ‘return seeking’ behaviour, however, this is modified by setting αi,H = γi,HrH and αi,F = γi,FrF. The elasticity of substitution between home and foreign bonds is then the conventional σB = 1/(1 + ρB). Our parameterisation sets γi,H = γi,F = 0.5 (no home bias) yielding the following simple and intuitive demand expressions:
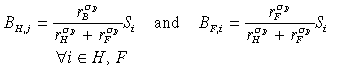 (6)
(6)Initially we set the elasticity of substitution at σB = 1,15 though we show in section IV that the general results of the paper are robust to changes in the sensitivity of savers, as represented by this parameter, unless its value is made very large.
Collective households form expectations over bond yields either myopically, by presuming that future returns will equal those in the present period, or adaptively, projecting yields based on past trends.16
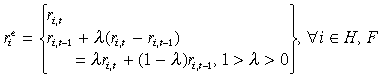 (7)
(7)This system allows imperfect financial capital mobility and differences in yields across regions without the explicit introduction of the practical causes of bond differentiation, namely credit risk, property rights enforcement, systemic (region-wide) risk and fiscal stringency (monetary and nominal exchange rate stability). Moreover, it obviates the need for explicit representation of the smoothing forces on the investment side, which include implementation costs and gestation lags, allowing an analytical focus on the role of the high-tech production externality.
The funds committed to investment in region i finance new purchases of capital goods that add to the capital stock:
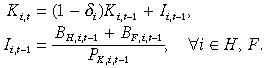 (8)
(8)These new capital goods are constructed from X and Y by a capital goods sector that can only use domestic products, reflecting the importance of local installation costs.17 The composition of capital goods is chosen to minimise cost, subject to a CES installation function:
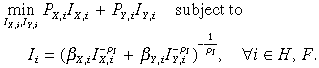 (9)
(9)New capital goods are assumed to be intensive in high-tech Y so that βY,i > βX,i. From the solution to the investment installation problem emerges each region's capital goods price, PK,i, as a weighted average of domestic X and Y prices (with the weight on Y prices being larger).
The yield on each region's bonds is then equal to the net rate of return on regional capital, or the value of the marginal product of capital in the production of high-tech Y, derived from Equation (1) above, as a proportion of its capital goods price, net of depreciation.
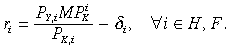 (10)
(10)The level of GNP in region i is the sum of rewards to factors owned by that region's collective household:
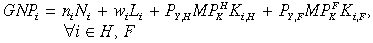 (11)
(11)where ni is the land rental rate, wi is the wage and Ki,H, Ki,F reflect region i's ownership of home and foreign capital. Because there are no intermediate inputs or indirect taxes, GDP is simply the value of regional production (GDP at producers’ prices):
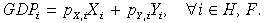 (12)
(12)The GDP price level is constructed from output value weights, θji. Thus, for region i:
 (13)
(13)For welfare interpretations, a consumer price level is also defined, based on the expenditure function from Equation (2), as:
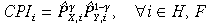 (14)
(14)The real exchange rate is the ratio of the cost of a product bundle in the home region, to the cost of a similar bundle in the foreign region, measured relative to a common global numeraire.18 Appreciations are therefore indicated by increases and depreciations by decreases. The real exchange rate of region H is then the ratio of its output-value weighted GDP price to a similarly weighted Foreign GDP price:
 (15)
(15)The balance on the capital account from the perspective of the home country (the current account is just the negative of this) is:
KA = –CA = BH,F – BF,H
(16)where Bi,j is the real investment (‘bond purchases’) in region H by region F.19 The model is closed by equating demand and supply (at the market clearing price) in all of the represented markets (for goods, factors and bonds).20
The model is calibrated to represent two initially identical large trading regions. The base year steady state and key parameters are detailed in Table 1. When a shock occurs to productivity at home several forces are set in train. These might be summarised as follows:
| Variables and base values | Key parameters | ||
|---|---|---|---|
| Variable | Base value | Parameter | Value |
| Volumes | Rates | ||
| GDP | 2.0 | Saving rate from GNP, s | 0.2 |
| Output, X | 1.0 | ||
| Output, Y | 1.0 | Share parameters | |
| Consn, CX | 0.9 | Home weight in bond portfolio, γiH = γiF | 0.5 |
| Consn, CY | 0.7 | Production share of labour in X | 0.5 |
| Inv goods demand, IX | 0.1 | Production share of labour in Y | 0.5 |
| Inv goods demand, IY | 0.3 | Generic X consumption share γ | 0.562 |
| Exports, X | 0.3 | Home share of X consn, 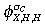 |
0.666 |
| Exports, Y | 0.233 | Home share of Y consn, 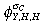 |
0.666 |
| Imports, X | 0.3 | ||
| Imports, Y | 0.233 | Prices | |
| Wage, w | 0.5 | ||
| Factor quantities | Net rate of return on capital, r | 0.025 | |
| Land supply, N | 4.0 | Land rent, n | 0.125 |
| Labour supply, L | 2.0 | pX | 1.0 |
| Capital stock, K | 4.0 | pY | 1.0 |
| Foreign-owned capital | 2.0 | pXforeign | 1.0 |
| Domestically owned capital | 2.0 | pYforeign | 1.0 |
| CPI | 1.0 | ||
| Elasticities of | GDP price | 1.0 | |
| Consumption substitution, σC | 2.0 | ||
| X, Y substitution in investment, σI | 2.0 | Real exchange rate | 1.0 |
| H–F bond substitution, σB | 1.0 | ||
| Other parameters | |||
| Lagged adjustment parameter, λ | 0 (or 0.5) | ||
| Depreciation rate, δ | 0.1 | ||
- † Note that both regions are identical in the initial steady state. The details given here are for a single region.
- •
The investment demand effect increases home prices relative to foreign prices, leading to a real appreciation, when H receives a larger share of world investment and hence is the recipient of an increased share of global financial flows. This effect is dominant in the short run.
- •
The product differentiation effect decreases home prices relative to foreign prices, leading to a real depreciation, when the home industry produces more output. H must lower prices in order to sell the extra goods because products are differentiated. This effect drives real exchange rate movements in the long run.
- •
The fixed factors effect means that the marginal product of home capital (MPK), and hence the rate of return on home bonds, falls with capital accumulation (at least so long as there is no externality in the home high-tech industry). This is because labour, which is fixed in local supply, cannot move into the home high-tech industry in the same quantities as capital. Moreover, because land (N) is also fixed, and employed only in the production of X, as labour moves into the Y industry its marginal product rises in the X industry, ensuring some retention there. Factor prices are not equalised because labour is not mobile internationally and products are differentiated by region of origin and the productivity shock separates the technologies. This effect means that productivity shocks, at least with small production externalities, do not lead to an agglomeration of high-tech industry in the home region.
- •
The capital price effect complements the fixed factors effect in opposing the agglomeration of the high-tech (Y) industry in H. Even if the MPK were to remain constant, the rate of return would tend to fall with capital accumulation in H because its capital goods price rises relative to the price of the home variety of the high-tech product (Y). Capital accumulation increases Y production, which reduces the price of home Y relative to home X. As the price of capital goods is a function of both domestic X and Y prices, the price of new capital falls more slowly than the price of Y, leading to a falling real rate of return, which opposes agglomeration of the Y industry in H.
IV A Boost to Home Productivity with No Externalities (ψ = 0)
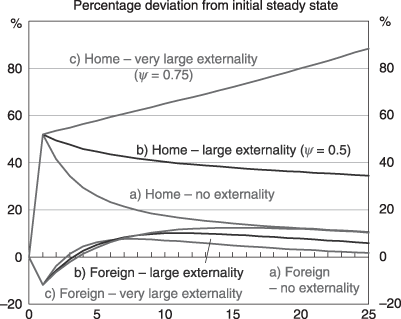
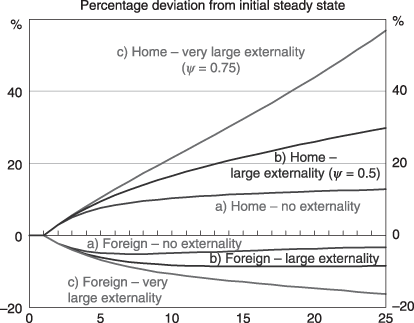
The IT boom is represented by a once-off (but permanent) 10 per cent increase in total factor productivity in the home (but not in the foreign) Y industry.21 The improved productivity in H drives up 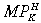 , raising the home relative-to-foreign expected bond yield (Fig. 3, curve (a)). Financial investors are initially assumed to have myopic expectations. Whether their expectations are myopic or adaptive, however, this causes the home and foreign bond portfolios to be rebalanced in favour of home bonds, raising investment in H at the expense of that in F. In turn, this leads to relative accumulation of capital in H (Fig. 4, curve (a)), and the associated net financial inflows necessitate a current account deficit (Fig. 5, curve (a)). In F, falling relative returns lead to a fall in investment below its replacement level, and an absolute fall in its capital stock. Eventually,
, raising the home relative-to-foreign expected bond yield (Fig. 3, curve (a)). Financial investors are initially assumed to have myopic expectations. Whether their expectations are myopic or adaptive, however, this causes the home and foreign bond portfolios to be rebalanced in favour of home bonds, raising investment in H at the expense of that in F. In turn, this leads to relative accumulation of capital in H (Fig. 4, curve (a)), and the associated net financial inflows necessitate a current account deficit (Fig. 5, curve (a)). In F, falling relative returns lead to a fall in investment below its replacement level, and an absolute fall in its capital stock. Eventually, 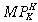 diminishes, increasing F's share of world investment, and allowing some rebounding of its capital stock. After 25 periods a new steady state is approached, with a larger capital stock in H, and a slightly reduced capital stock in F. The latter is due to a decline in global demand for its Y following increased competition from its now more productive counterpart in H.22
diminishes, increasing F's share of world investment, and allowing some rebounding of its capital stock. After 25 periods a new steady state is approached, with a larger capital stock in H, and a slightly reduced capital stock in F. The latter is due to a decline in global demand for its Y following increased competition from its now more productive counterpart in H.22
Net Return on Capital
Capital Stock
Current Account Balance
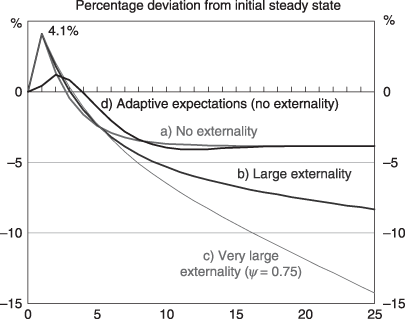
The higher level of productivity in H does not lead to a [partial] agglomeration of high-tech industry in H in the long run because of the fixed factors effect. H's fixed labour supply ensures that its accumulation of capital is greater than the flow of labour from X to Y. The tighter H labour market reduces 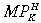 , causing the H bond yield to fall through time. Movements in the real exchange rate in the short run are driven by the investment demand effect, which places upward pressure on the prices of home X and Y (but particularly Y) when capital flows into H in the initial few periods. This leads to a real appreciation for H initially, as shown in Figure 6 (curve (a)).
, causing the H bond yield to fall through time. Movements in the real exchange rate in the short run are driven by the investment demand effect, which places upward pressure on the prices of home X and Y (but particularly Y) when capital flows into H in the initial few periods. This leads to a real appreciation for H initially, as shown in Figure 6 (curve (a)).
Real Exchange Rate
However, higher productivity and capital accumulation in H's Y sector also raises the supply of home relative to foreign Y in the medium-long-term. As savings are rebalanced after the initial capital inflow, investment goods demand falls in H and so the investment demand effect weakens. Eventually, product differentiation by region of origin ensures that the relative price of home Y falls (the product differentiation effect), leading to a real depreciation in the long run. Moreover, instead of approaching its initial level (e = 1, or PPP), the real exchange rate reaches a new steady state below its initial level. That is, in the long run H's permanently more productive Y industry reduces its price and so sells a larger volume at home and abroad.
(i) Welfare Effects23
H's higher Y productivity raises its Y output in both the short and long run. At least one region must therefore always be better off than before. From Figure 7 it is clear that, although F has lower GDP, both regions are net gainers in terms of real income (GNP). This is because both regions share ownership of the newly advantaged home Y industry. These income gains accrue to capital owners in both regions, to home workers and to foreign land owners. Home land owners enjoy a higher X price but lower X employment, with the former dominating, so that home land rents also increase. Foreign workers suffer a wage decline in terms of the numeraire (X in F), but the foreign CPI also falls sufficiently to raise the real purchasing power of the foreign wage in the long term. Of course, because total factor productivity is higher at home and its capital stock rises faster, home workers benefit more than foreign workers.

Welfare – No Externality
(ii) Sensitivity to Elasticities of Substitution
In general, the results are qualitatively similar when elasticities of substitution are changed. If the elasticity of substitution between home and foreign varieties (σC) is increased, price differentials across regions are reduced, weakening movements in the real exchange rate. These price movements lead to slower initial capital accumulation (and hence a smaller home current account deficit), but a larger home (and smaller foreign) capital stock in the long run. This causes real incomes to be more equal in the short run but more unequal in the long run.
Raising the elasticity of substitution between regional bonds (σB) increases the sensitivity of savers to differences in yields and makes financial capital more mobile internationally. Following the productivity shock, H attracts more capital initially and so have a larger current account deficit and a larger initial appreciation (increasing the size of the investment demand effect). The increased capital flow into H increases the speed of adjustment to a new steady state. Changes to the level of international capital mobility do not affect the model in the long run substantially because financial capital flows stabilise in the new steady state. These patterns are always observed when the elasticities of substitution are altered, irrespective of the scale of the IT externality.
(iii) Other Robustness Tests
The model is quite robust to parameter changes that affect the structure of the initial equilibrium, such as factor shares in each industry and the relative sizes of each industry at the outset. This is particularly true for the structure of the X industry. If the X industry is made more labour intensive (0.75 share rather than 0.5 as in Table 1), the simulation results are almost identical (whether there is no externality or a large externality). The initial equilibrium in this case shifts 20 per cent more labour to the X industry, reduces the capital stock by 20 per cent and the quantity of all output goods by also by 20 per cent (at constant prices).
Some short-run results are, however, sensitive to the labour share of the Y industry. The strength of the investment demand effect is positively correlated with the labour share in the Y industry in the neighbourhood of the default parameterisation in Table 1.24 If the labour share is high, then the marginal product of labour in the Y industry is more responsive to total factor productivity shocks, meaning that there must be a higher price of X in order maintain labour in that industry to produce for investment and consumption. If the labour share in the Y industry is 0.55 rather than 0.5, the investment demand effect is four times larger (in terms of the initial appreciation), though the appreciation lasts a similar length of time and in the medium-long-term, the product differentiation effect still dominates (with a larger depreciation). Likewise, if the initial Y industry capital share is 0.67 share (the labour share is 0.33), then there is no investment demand effect – the product differentiation effect dominates from the start. Thus, different structural parameterisations tend to change the relative strengths of the four effects outlined at the end of Section III, but they do not alter the intuition underlying the key results.
V A Productivity Boom in the Presence of a Home Externality (ψ > 0)
Externalities in the US high-tech industry could have been a result of the unique industrial structure of such subregions as Silicon Valley, or they could be a feature of high-tech industries more generally. Saxenian (1994) supports the former, arguing that firms in Silicon Valley were typically smaller, more open and collaborative, and that this allowed skills and ideas to move through the Valley in a way that would not have been possible elsewhere.25 This would have meant knowledge could have been closer to a public good in Silicon Valley than in other regions with larger, more secretive, more inward-looking firms. We therefore begin with the assumption that the externalities operated only in H.
The externality is incorporated into Equation (1) by setting ψ > 0 for H and retaining ψ = 0 in F. The same productivity shock is then applied to the home high-tech industry.26 The  now depends on the size of the externality (ψ).27 For small externalities (0 < ψ < 0.5), it is clear from Equation (1) that the diminishing
now depends on the size of the externality (ψ).27 For small externalities (0 < ψ < 0.5), it is clear from Equation (1) that the diminishing 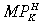 is retained in H (the elasticity of home Y output to capital is less than unity). This means that the rate of return to new units of capital falls over time as capital accumulates in H. The main difference from the results without the externality presented in Section IV is that the higher productivity in H leads to a larger equilibrium capital stock in H (and a smaller one in F). This leads to a lower home Y price in the long run and a larger real depreciation. Because the capital stocks in the initial steady state are the same as before, the initial appreciation is also the same. Real GDP becomes higher in H (and lower in F) in the long run, though real GNP is higher in both regions because investors from F also enjoy the higher returns in H.
is retained in H (the elasticity of home Y output to capital is less than unity). This means that the rate of return to new units of capital falls over time as capital accumulates in H. The main difference from the results without the externality presented in Section IV is that the higher productivity in H leads to a larger equilibrium capital stock in H (and a smaller one in F). This leads to a lower home Y price in the long run and a larger real depreciation. Because the capital stocks in the initial steady state are the same as before, the initial appreciation is also the same. Real GDP becomes higher in H (and lower in F) in the long run, though real GNP is higher in both regions because investors from F also enjoy the higher returns in H.
Despite the fact that ψ > 0 raises the degree of homogeneity of H's Y production function in the long run (Eqn 1), there is no agglomeration of this industry into H. This is because the fixed factors effect opposes the movement of labour into the home Y industry. Indeed, part of the benefit of the home externality is captured by workers, through higher wages. Moreover, the model eventually converges on a new steady state just as it does with no externality.
(i) Large Externality: ψ = 0.5
In this case the 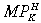 does not depend on the capital stock – there are no longer diminishing returns to capital. The return to capital in H depends on the initial level of total factor productivity, a in Equation (1), the amount of labour in Y production, as well as the home prices of Y and of capital goods. As before, a 10 per cent increase in productivity in H leads to capital accumulation in H, a current account deficit in H and a real appreciation in the short term (due to the investment demand effect). As home Y output increases with the larger capital stock, the product differentiation effect becomes stronger, leading to a larger real depreciation in the long term (Fig. 3, curve (b)).28 Welfare effects are qualitatively similar to the case with no externality presented in Section IV, though H gains a larger share of the welfare gains due to greater ownership of KH and higher factor rewards for LH and NH.
does not depend on the capital stock – there are no longer diminishing returns to capital. The return to capital in H depends on the initial level of total factor productivity, a in Equation (1), the amount of labour in Y production, as well as the home prices of Y and of capital goods. As before, a 10 per cent increase in productivity in H leads to capital accumulation in H, a current account deficit in H and a real appreciation in the short term (due to the investment demand effect). As home Y output increases with the larger capital stock, the product differentiation effect becomes stronger, leading to a larger real depreciation in the long term (Fig. 3, curve (b)).28 Welfare effects are qualitatively similar to the case with no externality presented in Section IV, though H gains a larger share of the welfare gains due to greater ownership of KH and higher factor rewards for LH and NH.
From Figure 6 (curve (b) in blue) it appears that the capital stock in H is increasing without bound. Yet simulations over longer periods reveal that the rate of growth of the capital stock in H is falling. This suggests that the model may be slowly converging to a new steady state.29 It is supported by Figure 5 (curve (b) in blue), which shows a falling real rate of return to capital in H in the long run. The net rate of return to capital in H, from Equation (10), falls because of the capital price effect. In the long term, the price of home Y falls substantially relative to that of home X. Because both home X and Y are required to produce new capital, as in Equation (9), the price of a new unit of capital falls more slowly than that of Y, decreasing PY/PK and thereby reducing the net rate of return to capital.
(ii) A Very Large Externality: ψ = 0.75
Larger externalities can overcome the capital price effect. For ψ > 0.6, the rate of return to capital (and hence the rate of capital accumulation) does not fall over time in H. Consider the case of ψ = 0.75. The externality is so large that an extra unit of capital in H increases total factor productivity more than it crowds existing capital, so the return to capital rises over time (Fig. 5 curve (c) in red). This attracts even more capital, leading to explosive behaviour in the home capital stock (Fig. 6, curve (c) in (red), the home current account deficit (Fig. 4, curve (c)) and GDP (Fig. 8). As H's Y becomes more abundant, its price falls continuously, leading to larger falls in the real exchange rate due to the product differentiation effect (Fig. 3, curve (c)).
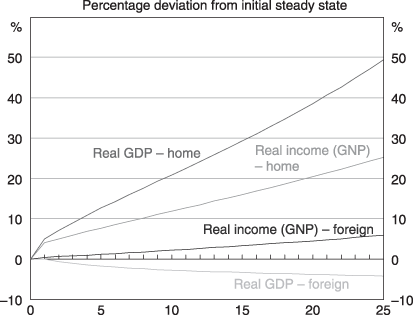
Welfare – Very Large Externality
The foreign Y industry is unable to compete with increasingly productive home Y. Foreign Y production falls (as does foreign GDP). The foreign capital stock declines and its labour moves into the foreign X industry. Because the growth in the home Y industry is now self-sustaining, all of these trends continue in the long term, with foreign Y production contracting asymptotically.30 Despite this, real income in F is higher as a result of the larger externality, due to greater capital income from H and F's more favourable terms of trade. Generally, the majority of the welfare gains accrue to the region with the externality. In the long run, real incomes accruing to all factors rise in both regions, with capital owners enjoying the largest increases.
(iii) Agglomeration and ‘New Economy’ Criteria – How Realistic?
With the parameterisation of Table 1, a one-off productivity shock in H causes a trend towards the agglomeration of the high-tech industry (Y) to the home region if ψ > 0.6. This is therefore ‘knife edge’ externality setting beyond which the model tends to agglomeration. For agglomeration to occur we know that ψ must exceed 0.5 because returns to the internationally mobile factor (capital) must be non-decreasing so that the fixed factors effect will not oppose the movement of labour into the Y industry. If, however, 0.5 ≤ ψ < 0.6 (approximately), the 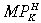 will increase, while the real net rate of return will fall due to the higher relative price of capital in H, so that the externality must be large enough to more than compensate for diminishing capital returns. In other words, an extra unit of capital must add more to output through its indirect effect on total productivity than it does directly. Indeed, an externality yielding ψ > 0.6 implies a long run elasticity of output to capital in the home Y sector of at least 1.1 and long run returns to scale of at least 1.6. These numbers seem high, yet can we generalise from a single parameterisation? We offer two approaches.
will increase, while the real net rate of return will fall due to the higher relative price of capital in H, so that the externality must be large enough to more than compensate for diminishing capital returns. In other words, an extra unit of capital must add more to output through its indirect effect on total productivity than it does directly. Indeed, an externality yielding ψ > 0.6 implies a long run elasticity of output to capital in the home Y sector of at least 1.1 and long run returns to scale of at least 1.6. These numbers seem high, yet can we generalise from a single parameterisation? We offer two approaches.
First, the empirical literature tends to suggest that the impact of spillovers is, at most, approximately equal to the effect of firms’ own R&D. For our model, this suggests a coefficient of ψ equal to or less than 0.5 – which is not large enough to produce agglomeration. Bottazzi and Peri (2003), for example, find that a 10 per cent increase in R&D spending in a European region increases the number of patents in the same region by around 9 per cent, but only leads to a 0.3 per cent increase in the number of patents in neighbouring regions and has no effect on innovation further away. This suggests, further, that any spillovers beyond the sectors undertaking the R&D are small and that spillovers are restricted to the region in which the R&D takes place, which is in line with our assumptions.31
Second, we consider how realistic long run returns to scale of 1.6 are. A useful unitless measure is the elasticity of the long run average cost curve to the level of output. Industries operating with increasing returns to scale have negative elasticities that are readily derived from the technology specification. The specification used here in Equation (1) yields an elasticity of:32
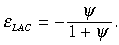 (17)
(17)A value of ψ = 0.6 yields an elasticity of –0.375, while ψ = 0.75 yields –0.429. Larger values of ψ yield larger negative elasticities. ɛLAC can readily be compared with those implied by sectoral studies on imperfectly competitive industries. If ɛLAC calculated here is large by comparison, this lends further support to our claim that the knife-edge value is unrealistic and hence that agglomeration is unlikely. The elasticities of long run average cost curves for manufacturing industries in Australia and Asian economies implied by Tyers (2005) are in the range (0, –0.1). A subsequent study by Tyers and Rees (2008) that focuses on capital-intensive services, which might be expected to be natural monopolies and oligopolies, and hence to have considerable unrealised scale economies, yields elasticities in the range (–0.08, –0.26). Clearly, the ‘knife edge’ value of ψ = 0.6 and its associated long run average cost elasticity, is well outside these ranges and would therefore appear to be unrealistic.
VI Externalities in Both Regions (and Other Extensions)
Many commentators have argued that increasing returns, spillover externalities and/or learning-by-doing are not unique to Silicon Valley or US high-tech industry more generally. For example, productivity could depend on knowledge gained from past research (Romer, 1990) or on the experience of the workforce (Lucas, 1988). Our model does not deal with these issues directly, but we can make positive externalities a feature of the high-tech industries in both regions. This does not complicate the results substantially.33 The foreign externality merely amplifies the effect of any change in the capital stock. When the 10 per cent productivity shock is restricted to H as before, capital is attracted to H, leading to higher productivity in H (as before) and further capital inflow. But it also leads to lower capital in F, which then decreases productivity, leading to an even smaller foreign capital stock. Hence, the presence of externalities in both regions generally amplifies the earlier results and the distributional disparities that stem from the home productivity shock. Nonetheless, agglomeration of capital in H still only occurs with very large externalities, though the ‘knife edge’ externality falls back close to ψ = 0.5, implying a long run average cost elasticity of –0.33, which is still large by comparison with the empirical findings discussed in the previous section.
Further simulations with externalities in both regions reveal that if H starts with a larger high-tech industry (as characterised by a larger initial capital stock), then agglomeration still only occurs with very large externalities. If externalities are not large enough, H's advantage is only temporary. If H were to achieve its productivity gain earlier than F, its advantage would only be temporary unless externalities in both regions were very large.
These simulation results imply that the forces that attract capital to the US are made even stronger by a second externality in Europe. Although this counts against opponents of the ‘new economy’ theory (who might take the view that the US's industrial structure was no different to Europe's), it does not support the ‘new economy’ camp either. Long run predictions of continued capital flows into the US would only be correct if the externalities in both regions were very large or if Europe never‘implemented’ the internet to get the same once-off productivity benefits the US did. Both cases are rather unlikely, meaning that capital inflows into the US would either quickly peter out, or eventually reverse. and as before, even in presence of large externalities, any appreciation of the real exchange rate is short lived, and a real depreciation occurs in the long run – the opposite direction predicted by the ‘new economy’ analysts.
(i) Very Large Externalities and Economic Geography
The results presented here with very large externalities are similar to those in the endogenous growth and economic geography literatures – a small initial advantage in H leads to a tendency toward the agglomeration of the high-tech industry in that region (‘industrial core’), with F becoming the ‘agricultural periphery’. The main difference is that the faster growth in high-tech production in H is at the expense of F, whereas in Lucas's (1988) model of learning by doing, F would continue to ‘learn’ and grow, but just at a slower rate than H. The prediction of a constantly depreciating real exchange rate is, however, the same as is implied by Lucas (1988). In further simulations, a delayed productivity shock in F confirms that history can matter – a ‘head start’ in high-tech industry, or an initially larger industry, leads to a permanently higher growth rate at home – the same result as Grossman and Helpman (1991) and Lucas (1988).34 This behaviour only arises, however, if the externality is very large and, as discussed in the previous section, at a level that is difficult to rationalise empirically.
(ii) Adaptive Expectations over Bond Yields
If agents hold adaptive expectations of the form specified in Equation (7), the key results are little changed. The main effect is that capital flows are more persistent because expected international returns are more persistent, and this smoothes the movement of macroeconomic variables in the wake of the productivity shock.35Figure 1 (curve d in black) shows the response of the real exchange rate to a 10 per cent productivity shock in H when financial investors have adaptive expectations over bond yields and there is no externality. Compared with the case of myopic expectations (Fig. 1– curve (a) in green), the magnitude of the initial real appreciation is reduced by three quarters. This is because it takes time for agents to adjust their expected returns, and so financial capital flows into H are initially not as strong. Adaptive expectations do not substantially affect the new steady state that the model converges to, though adjustment to the new steady state is slower. If savers are made more sensitive to differences in returns between regions (regional bonds are closer substitutes and hence σB is larger), adaptive expectations causes oscillatory convergence in all major variables and particularly in the real exchange rate. This behaviour is akin to the long cycles in real exchange rates that Caballero and Lorenzoni (2007) seek to explain by other means.36
VII Conclusions
There is substantial evidence that the US information technology boom did lead to a pick up in US productivity growth in the late 1990s, and that anticipation of its effects contributed to high levels of investment, financial inflows and a real appreciation of the US dollar. This paper explores the qualitative effects of such a productivity gain on the real exchange rate, financial capital flows and welfare in the short and long runs, and asks under what circumstances might there have emerged a self-sustaining advantage to the US over its foreign trading partners. The effects are examined using a dynamic model of two freely trading regional economies with open capital accounts and imperfectly substitutable financial assets when production technologies exhibit constant returns to scale with external economies (or positive production externalities) of varying sizes.
With small or no externalities, the productivity shock only has significant effects in the short-to-medium term. The increase in productivity in one region attracts investment leading to an inflow of world savings, increasing investment demand for the region's products, raising domestic prices and leading to a real appreciation relative to the other region (the investment demand effect). In the medium term, the return to capital in the advantaged region declines due to the (relative) shortage of labour in the high-tech industry (the fixed factors effect) and savers rebalance their portfolios, leading to a real depreciation towards PPP. Because the advantaged region is now more productive, its prices are lower and hence there is a permanent real depreciation. In the long run, both regions are better off with gains to the disadvantaged region stemming from higher capital returns and an improvement in its terms of trade.
With larger externalities the path of the real exchange rate is similar. If the gains in productivity from the externality exactly balance the losses from diminishing returns to capital in the favoured region, capital inflows are much more persistent, but returns eventually fall due to higher relative capital goods prices (the capital price effect). The exchange rate appreciates by the same amount in the short term, but the larger externality means that it depreciates by more in the long term (due to the product differentiation effect). If the externality is larger than that in the balancing case, then bond yields in the favoured region rise without bound as does that region's capital stock, and the pace of capital accumulation in that region. The real exchange rate continues to depreciate in the long term. Unlike results with smaller values of the externality, F suffers an asymptotic decline in its high technology industry and tends to specialise in low-technology production. However, real GNP rises in both regions, with the majority of the gain accruing to the advantaged region.
Adding externalities in both regions generally produces similar results, though it amplifies differences between regions. So long as the production externalities are not too large, the advantages of starting with a larger high-tech industry, or having an earlier productivity gain, are only temporary. Finally, if investors hold adaptive expectations over regional bond yields, then the real appreciation that follows the productivity improvement takes several periods to peak, and convergence to any new steady state can be oscillatory.
Returning to the perceived ‘new economy’ of the 1990s in the US and the expectation that it would lead to an appreciating dollar and persistently higher returns to capital, our simulations are generally unsupportive. Even if the US IT industry did have positive externalities, sustained increases in real returns would only have occurred if the externalities were large enough to offset diminishing returns to capital and the tendency for financial inflows to raise the relative home price of capital goods. Indeed, the scale of the long run increasing returns that would be required to achieve this would appear to exceed that measured even in industries that are natural monopolies. Moreover, while our results suggest that extreme externalities would have caused the US real rate of return to climb without bound, the US dollar would not have kept appreciating. Indeed, as occurs in all our simulated cases and has been observed in reality because the turn of the century, the long run path would show a US real depreciation.
Footnotes