A Dynamic Incentive-Based Argument for Conditional Transfers*
This paper is based in part on a lecture given by Mookherjee to the Australian Conference for Economists at Hobart, Tasmania in September 2007, and by Mookherjee and Ray at the Latin American Meetings of the Econometric Society at Bogota in October 2007. Authors thank participants at these meetings for useful feedback. Some of the arguments of the paper have been informally discussed in Mookherjee (2006). This research was supported by the National Science Foundation (NSF grant Nos. SES-0617874 and SES-0241070).
Abstract
We compare the long-run effects of replacing unconditional transfers to the poor by transfers conditional on the education of children. Unlike Mirrlees’ income taxation model, the distribution of skill evolves endogenously. Human capital accumulation follows the Freeman–Ljungqvist–Mookherjee–Ray OLG model with missing capital markets and dynastic bequest motives. Conditional transfers (funded by taxes on earnings of the skilled) are shown to induce higher long-run output per capita and (both utilitarian and Rawlsian) welfare, owing to their superior effect on skill accumulation incentives. The result is established both with two skill levels, and a continuum of occupations.
I Introduction
A centrepiece of Mexico's antipoverty program (Progresa, recently renamed Oportunidades) is a system of cash payments made to poor households conditional on sending their children to school and medical clinics for regular checkups.1 Empirical studies of the program have noted its success with respect to increasing school enrolments, family health, reducing child labour, apart from reducing vulnerability of households to indiosyncratic and environmental shocks.2 Similarly, the Food For Education program in Bangladesh transferred food to poor rural households conditional on enrolling their children in school.3 These programs raise the question of relative effectiveness of conditional and unconditional transfers in the design of antipoverty programs. This issue pertains more widely to the design of welfare states in developed as well as developing countries.4
Economists have traditionally favoured unconditional transfers: both Milton Friedman and James Tobin argued on behalf of negative income tax proposals in the 1960s. The theoretical underpinning of this argument is embodied in the Mirrlees (1971) model of optimal income taxation. With a Paretian social welfare function, and an exogenously given distribution of skills, an optimal antipoverty program should seek to maximise the utility of unskilled households for any given expenditure on the program. On the assumption that poor households are the best judge of their own well-being (the postulate of consumer sovereignty), unconditional transfers emerge superior.
While recent advances in behavioural economics may undermine arguments for consumer sovereignty, it can (and has) been argued that the poor are no more inclined to behave against their own self-interest compared to the non-poor (see, e.g. Bertrand et al. (2004) or Mullainathan (2007)). If historical or environmental circumstances are the more proximate causes of differences in earning capacities between the poor and non-poor rather than behavioural traits, it is difficult to make a case for conditional transfers on the basis of denial of consumer sovereignty selectively for the poor.
Nevertheless, the negative income tax has been politically unpopular in the USA: middle class and wealthy voters who pay the taxes that fund antipoverty programs have been uncomfortable with the unconditionality of the transfers, and have worried that the system breeds growing dependence of the poor on the welfare system.5 Accordingly, the 1996 Welfare Reform Act in the US imposed conditionalities on transfers to poor households. In many Western European countries, however, unconditional transfers still remain an important component of their welfare systems. At the same time, most developed countries retain systems of universal public provision of schooling and health, which are essentially conditional transfers. Continuing policy debates concerning design of antipoverty programs in both developed and developing countries frequently include the issue whether transfers should be conditioned on school enrolment or medical checkups of children.6 The conditionality of transfers raises enforcement problems (of verifying that required conditions are being met), as well as administrative problems of coordinating schooling, medical and antipoverty programs.7 These would be justified only if there were substantial benefits of retaining these conditionalities. Yet, there appears to be no clear demonstration of the nature of these benefits, either theoretically or empirically.
In this paper we present a theoretical argument for conditional transfers, from a dynamic perspective that incorporates the concern that they are needed to avoid the problem of long-term welfare dependence. Santiago Levy, one of the principal designers of the Progresa program in Mexico describes this as one of the main motivations of the program:
It was also important, finally, to avoid generating lasting dependence on income transfers. Experience from other countries had shown that making pure income transfers just because the recipients were poor could reduce their incentives to work and invest, inadvertently leading a subset of able and productive citizens to permanent dependence on public welfare. To avoid that outcome, income transfers should be designed to be transitory investments in the human capital of the poor. They should take a life cycle approach, helping poor households in the more critical aspects of each stage of their lives but always with the view that they should have incentives to earn a sufficient level of income through their own efforts to eventually pull themselves out of poverty. Levy (2006, p. 13).
Such concerns cannot be adequately captured in conventional static models of optimal taxation, owing to its assumption that the distribution of abilities is exogenously given.8 The phenomena of poverty alleviation or welfare dependence pertain to the endogenous evolution of skills, itself likely to be affected by the welfare mechanism. As Levy suggests, the long-run purpose of an ‘antipoverty’ scheme can be described as the promotion of incentives for the currently poor (and their descendants) to acquire skills that will enable them to escape poverty. In contrast, the conventional static welfarist purpose is to provide a consumption safety net for those ‘unlucky’ enough to be insufficiently endowed with sufficient earning capacity. The concern for ‘welfare dependence’ reflects the notion that lack of current earning capacities do not result from luck alone, but also from lack of prior investments in skill acquisition.
To address the issue of dynamic investment incentives, we employ a model of skill accumulation in an overlapping generations setting, based on Ray (1990), Ljungqvist (1993), Freeman (1996), Mookherjee and Ray (2003). This model follows Loury (1981) by assuming that all capital markets are missing: parents must pay for their children's education by sacrificing current consumption, and are motivated to do so by a Barro-Becker dynastic bequest motive. In the simplest setting, education decisions and occupations are indivisible: there are two occupations (skilled and unskilled). No education is required to enter the unskilled occupation; education is required to enter the skilled occupation. Education costs are exogenous, and equal throughout the economy: we thus abstract from heterogeneity in learning abilities.9
Investment decisions are subject to pecuniary externalities: the skill premium in wages depends on the proportion of households that are skilled, and both occupations are essential in the production process.10 The only source of heterogeneity in any given generation is differences in skill and earnings across households, the result of past investments by previous generations. Capital market imperfections imply that historical differences can persist indefinitely. The model has a continuum of steady states, each of which is characterised by persistent inequality and absence of mobility. Skilled households invest in the education of their children, unlike unskilled households, and enjoy permanently higher earnings, consumption and utility.
In this setting we compare the long-run effects of unconditional and conditional transfers, funded by taxes collected from skilled households. We focus attention only on steady state outcomes that are eventually reached from non-steady-state initial conditions via a process of gradual skill accumulation. The effects of alternative transfer systems are evaluated in terms of macroeconomic criteria such as per capita output, consumption and skill in the economy in the limiting steady state. We also compare them on the basis of distributive implications, with utilitarian and Rawlsian welfare measures. The major simplification here is that outcomes on the process of transition to the steady state are ignored. This is mainly to keep the analysis simple; we hope to incorporate effects on the transitional process in future work. Nevertheless, the results should be of interest if the concerned ‘social planner’ is presumed to equally weight the welfare of different generations, that is, employ a social discount rate of zero, as persuasively argued by Ramsey, Pigou and many others.
Our principal result is that unconditional transfers tend to reduce investment in human capital, per capita output and consumption in the long run, while the macroeconomic effects of conditional transfers are precisely the opposite. Unconditional transfers create a ‘welfare magnet’ effect that reduces incentives to citizens to engage in costly investments in skill. The deleterious incentive effects of reduced eligibility for transfers, or increased taxes consequent on acquiring skills, turn out to outweigh favourable income effects of the transfers on the ability of citizens to invest.
These adverse incentive effects are avoided by conditional transfers, since they provide investment incentives directly. This is particularly true when there is universal coverage of the population – as in universal public schooling – since eligibility is not phased out as agents accumulate skills and start earning substantially on their own in the market. In the long run, conditional transfers do not result in any direct redistribution from the skilled to the unskilled. But they do result in indirect redistribution via increased supply of skills and the resulting effect on market earnings of the unskilled.
Comparing distributional effects of unconditional and conditional transfers is not straightforward, owing to their respective direct and indirect redistributive effects. However, we show that any system of pure unconditional transfers can be improved (using any welfare measure with inequality aversion anywhere in-between utilitarianism and Rawls) by a system which utilises conditional transfers to a significant degree. In particular, the model is simple enough that the first-best welfare optimum involving maximal per capita consumption and vanishing inequality can be achieved by a system with significant conditional transfers (which effectively subsidise all private costs of investment).
We analyse two specific contexts: one with two occupations varying in skill and training cost, another with a continuum of occupations. In the former case with an occupational indivisibility, there is a continuum of steady states. We focus on a particular selection of steady state in order to carry out the comparative static analysis with respect to tax-welfare policies. This selection is justified as the long-run limit of processes of gradual non-steady-state skill accumulation. In a subsequent section we extend the analysis to the case of a continuum of occupations, where steady state is unique, and show that qualitatively similar conclusions obtain.
It is important to note one key assumption underlying the entire analysis: absence of heterogeneity of private education costs unobserved by the government. This feature implies lack of mobility in steady state, and allows the government to calibrate educational subsidies perfectly. The concluding section describes this and other qualifications of our analysis, which deserve further attention in future research.
II The Basic Model
In this section we use the two occupation skill case in Mookherjee and Ray (2003, Section 4.2) or Ray (1990, 2006), which the reader can consult for additional details. There is a continuum of dynasties. In any dynasty a person is born every new generation (t), and lives two generations (t, t + 1), the first as a child and the second as an adult and parent. There is a single consumption good, and two occupations s, u. To enter the skilled occupation a person needs to acquire education while young: this costs x in units of the consumption good, and must be paid for by the parent as educational loan markets are absent. An important assumption is that there are no differences in these educational costs across households, so x is homogeneous and publicly known by the government.
There is a stationary aggregate production function f(λ, 1 − λ) satisfying constant returns to scale, which provides per capita production of the consumption good as a function of proportions of skilled (λ) and unskilled persons (1 − λ) in the economy. The production function is smooth, strictly increasing, strictly concave and satisfies Inada conditions. The latter imply that allocations will always involve positive proportions in both occupations at every date. The skilled and unskilled wages are denoted by ws and wu, respectively: the former is decreasing and the latter is increasing in λ, going from ∞ to 0 (and vice versa) as λ goes from 0 to 1. These wages equal the corresponding marginal products. Let 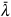 be the skill ratio where the two wages are equalised, and let the skill ratio at date t be denoted λt. In equilibrium it will always be the case that λt ≤
be the skill ratio where the two wages are equalised, and let the skill ratio at date t be denoted λt. In equilibrium it will always be the case that λt ≤ 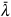 , to provide incentives for skill accumulation.
, to provide incentives for skill accumulation.
Each dynasty has Barro-Becker utility: a parent at t maximises 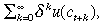 where δ ∈ (0, 1) is a discount rate, and u is a strictly concave, strictly increasing, smooth utility function.
where δ ∈ (0, 1) is a discount rate, and u is a strictly concave, strictly increasing, smooth utility function.
(i) Unconditional Welfare Payments to the Unskilled Funded by Taxes on Skilled Incomes
We start by considering a context in which a welfare program makes cash payments unconditionally to those in unskilled occupations. The program is funded by a linear income tax on the incomes of those in the skilled occupation. The unskilled occupation is not taxed, one reason for which may be that it is in the rural or informal sector and is difficult to tax. Or the unskilled could be poor enough that their incomes always fall below the minimum threshold for agents to be liable to pay income taxes. It turns out the same results obtain even if income taxes are levied on both skilled and unskilled occupations at the same rate, using essentially similar arguments. So we focus on the case where the unskilled sector is untaxed because the arguments are a bit simpler.11
At each date t the government will tax the earnings of the skilled at a constant rate τ and use the proceeds to provide a transfer of Wt to unskilled persons. Like private citizens, the government does not have the ability to borrow and lend, so it is subject to a period-by-period budget constraint:
 (1)
(1)The independent policy instrument here is the tax rate τ. The size of the unskilled transfer Wt will be determined endogenously, along with the skill proportion λt. At each date the government will take the existing skill proportions as given and distribute Wt to the unskilled according to Equation (1). Households will have perfect foresight about the evolution of skill proportions in the future, and will make education decisions for their children accordingly.
A (perfect foresight) competitive equilibrium (CE) given initial skill ratio λ0 and tax rate τ is a sequence λt, t = 1, 2, ... such that:
- (i)
each dynasty in occupation i0 ∈ (0, 1) chooses education decisions it ∈ (0, 1), t = 1, 2, ... (with it = 1 denoting a decision to be in the skilled occupation as an adult in date t) to maximise
 subject to
subject to
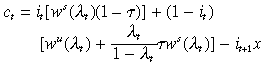 (2)
(2)- (ii)
these investment decisions (i.e. the proportion of households selecting it = 1) aggregate to λt at every t.
A steady state (SS) given tax rate τ is a stationary CE with λ0 = λt, all t.
If there are no taxes and transfers (τ = 0) Ray (1990, 2006) proves that every CE converges to a SS in this model. We shall argue below that this continues to be true in the presence of a positive tax rate. This motivates the restriction to steady states.
In an SS, the investment decision of each dynasty reduces to a stationary dynamic programming problem. Let Vu and Vs denote the value functions of a dynasty that is unskilled and skilled, respectively. Then:
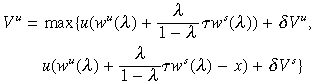
V s = max{u((1 −τ)ws(λ)) + δVu, u((1 − τ)ws(λ) −x) +δVs}
Since both occupations are essential, an SS must have a positive proportion in both skills: λ ∈ (0, 1). This implies Vs > Vu, otherwise no one would choose to be skilled. Therefore skilled people must earn more after taxes: (1 −τ)ws(λ) > wu(λ) +[λ/(1 − λ)]τws(λ).12 The concavity of u then implies that skilled households have a greater incentive to invest in education of their children.
So the arguments of Mookherjee-Ray (2003) continue to apply: every steady state must involve stationary earnings and consumption for every household, and there will be no occupational mobility. Skilled households will educate their children, earn ws(λ) before taxes, and consume (1 − τ)ws(λ) − x at every t. Unskilled households will earn wu(λ) before taxes, and consume wu(λ) +[λ/(1 − λ)]τws(λ) at every date.
This allows us to calculate the value functions explicitly:
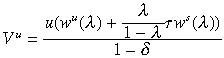

A steady state ratio λ is characterised by the incentive constraints:
C u (λ;τ) ≥B(λ;τ) ≥Cs(λ;τ)
(3)Where,
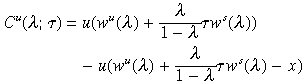
C s (λ; τ) =u((1 −τ)ws(λ)) − u((1 − τ)ws(λ) −x)
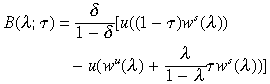
Respectively, denote the utility sacrifice for unskilled and skilled parents, and the benefit associated with investing in education.
Lemma 1. Cu and B are decreasing in λ , while Cs is increasing in λ.
Proof . We first show that wu(λ) +[λ/(1 − λ)]τws(λ) is increasing in λ. This is obvious if λws(λ) is non-decreasing in λ. If it is decreasing instead, then note that
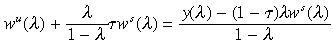
Where, y(λ) denotes per capita output f(λ, 1 − λ). The numerator of this is increasing in λ while the denominator is decreasing in λ. The result then follows upon using the concavity of u. 
These monotonicity properties in turn imply that the convergence arguments of Ray (1990, 2006) also continue to apply:
Proposition 1. (Ray, 2006) Suppose Cu and B are decreasing and Cs is increasing. Starting from any starting skill ratio λ0, there is a unique competitive equilibrium which converges to some steady state. Moreover, if the initial skill ratio λ0 is such that
B(λ0;τ) > Cu(λ0;τ)
(4)then λ t increases monotonically, converging to a steady state λ *(τ) where
B(λ*;τ) =Cu(λ*;τ)
(5)and,
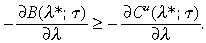 (6)
(6)The dynamics and steady state conditions are illustrated in Figure 1. As explained in Mookherjee-Ray (2003), there is a continuum of steady states varying in skill ratio λ. In general the set of steady states comprises the union of a set of disjoint intervals (such as [λ4, λ3] and [λ2, λ1] in the diagram), in the interior of each of which the incentive constraints hold strictly. The unskilled are indifferent between acquiring and not acquiring skills at each left endpoint (λ4 and λ2 in the diagram), while the same is true for the skilled at each right endpoint (λ3 and λ1 in the diagram).
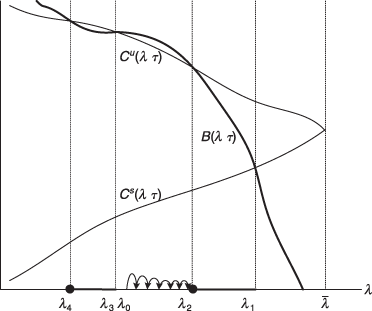
Steady States and Dynamics in the Two-Occupation Model
Efficiency properties of steady states are discussed in detail in Mookherjee-Ray (2003, Section 5). These are complicated by the fact that analysis of Pareto-efficiency requires consideration of non-steady-state allocations as candidate alternative allocations to any given steady state. For if starting with a given steady state a social planner engineers a new dynamic allocation, the new allocation need not constitute a steady state. In that case different generations of different households will realise different levels of utility, and the criterion of Pareto efficiency must keep track of how each such generation of each family is affected. Constructing a Pareto improvement requires that no member of any generation in any family is rendered worse off, while others are better off. In addition, the suitable notion of Pareto efficiency is where the planner is constrained (just as market agents) to not move resources across dates.
An almost complete characterisation of (constrained) efficiency of steady states for a more general setting involving an arbitrary number of occupations is provided in Mookherjee-Ray (2003). It is shown there that (in the current context of two occupations) both efficient and inefficient steady states always exist. Indeed an unconstrained Pareto efficient steady state always exists: it is an interior steady state λ* where the ‘rate of return’ to education (measured by [(ws−wu)/x]) is exactly equal to the discount rate (1/δ). Steady states with higher skill ratios (i.e. with rate of return to education above cost) are also (constrained) efficient. Intuitively, in this situation (with ‘over-investment’) there is no way for the planner to reduce the proportion of households investing in skill without making some members of the current generation in some households worse off.
On the other hand, there also exist steady states with λ < λ* which are Pareto-inefficient, which involve under-investment (a rate of return on education which exceeds cost). This includes steady states such as left end-point states such as λ4 and λ2 in Figure 1. Starting from such states, there exist Pareto improving re-allocations where the children of some unskilled households can be given education, which is financed by some currently skilled parents. In return the children that receive the education in this way are required to compensate the children of the contributing parents in the next generation. This reallocation simulates the effect of the missing capital market, which the social planner can still implement via intraperiod transfers across households (i.e. despite any inability to move resources across different periods).
In this paper, however, we are not concerned with efficiency properties of steady states. Our main interest is in comparing the macroeconomic and utilitarian welfare effects of conditional and unconditional transfers.
The multiplicity of steady states complicates an analysis of such policy interventions. However, if the economy starts at a ‘low’ skill ratio satisfying Equation (4), such as λ0 in Figure 1, it will follow a process of skill accumulation ending at a left endpoint steady state satisfying Equation (5).
We refer to such left-edge steady states as attractors. The terminology is apt. Consider, for instance, the steady state interval [λ2, λ1]. The attractor here is the steady state λ2 which is the long-run limit of a process of skill accumulation starting from an initial condition such as λ0. This is not the case for any other steady state in this interval: Ray (2006) shows that every other steady state (such those in the interior, or the right-edge states) can be reached only if either: (i) the economy starts there, or (ii) resulting from decumulation from one other non-steady-state initial condition with an ‘excess’ of skills to start with (i.e. from some λ > λ1 in the diagram).
Moreover, the long-run limit of any process of gradual skill accumulation must be an attractor. Such a process is initiated by any non-steady-state historical position to the left of λ1. For instance, if the economy starts at some λ to the left of λ4, it will experience gradual accumulation and eventually converge to the attractor λ4.
For every attractor, Equation (6) holds: the benefit function declines faster than the cost function for the unskilled. Indeed, for ease of exposition, we neglect the entirely degenerate case in which (6) holds with equality, and suppose that all attractors are ‘regular’ in the sense that
 (7)
(7)It is easy to see that every regular attractor is locally unique, and admits local comparative statics. It is also easy to see that provided the discount factor δ is high enough so that there is at least one skill ratio λ0 which satisfies Equation (4), an attractor satisfying Equation (7) exists.13
The economic logic for focusing on attractors as a description of the long-run implications of alternative transfer systems, is therefore the following: they constitute long-run outcomes reached from any accumulation path starting from some non-steady state skill ratio. In other words, if transitional growth in this economy results from gradual skill accumulation from a non-steady state skill ratio (as in a Solow model), the limiting steady state must be an attractor. Along this transitional process, the benefit function B exceeds the cost functions Cu, Cs for both types of households. Skilled households therefore always invest, while a fraction of unskilled households invest and the rest do not. Hence unskilled households are indifferent between investing and not all along the transitional process, and the same property obtains in the limit (where B = Cu > Cs). Moreover the benefit function must be falling more steeply than the unskilled cost, since the benefit was higher to start with and becomes equal to the unskilled cost eventually.14
Now consider the effect on an attractor of increasing the tax rate τ on skilled incomes, which funds an expansion of the welfare benefit to the unskilled. The investment cost Cu function shifts downward: this reflects the income effect associated with larger transfers to the poor. On the other hand the investment benefit function B also shifts down: income redistribution reduces the incentive to acquire skill. We now show that the latter effect must outweigh the former.
Proposition 2. A small increase in τ will lower the skill ratio λ in any attractor, causing per capita output and consumption to decline, while wage inequality between skilled and unskilled occupations will rise.
Proof. Using the Implicit Function Theorem, an attractor λ(τ) is locally decreasing if [−∂B(λ*;τ)/∂τ] >[−∂Cu(λ*; τ)/∂τ], which reduces to the condition that
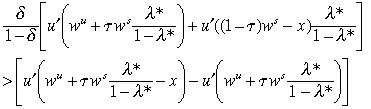 (8)
(8)Recall that by regularity Equation (7) holds:
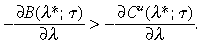
Condition (8) follows from this inequality if
(at λ equal to λ*)
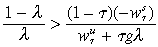 (9)
(9)where g≡[λ/(1 −λ)]ws. Condition (9) reduces to
 (10)
(10)Now 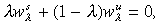 hence Equation (10) reduces to the condition that
hence Equation (10) reduces to the condition that 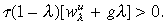 But this is true since
But this is true since 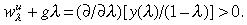
Hence ∂λ*/∂τ < 0 at any attractor, which implies that a small increase in τ will lower λ*, which lowers per capita output y(λ*) and raises ws/wu. Finally, per capita consumption y(λ*) − xλ* must also decline since y −x = (ws − x) − wu, and the requirement that B > 0 in any steady state requires the skilled to consume more than the unskilled: [(1 −τ)ws−x]−[wu+τws(λ/(1 −λ))] > 0, which implies that ws − x − wu > 0. 
This result indicates the power of the ‘welfare magnet’ effect of an increase in redistribution via unconditional transfers: it lowers the steady state benefit from investing by an extent that outweighs the reduction in the steady state cost for unskilled families to invest in their children's education. This reduces net investments in skill in the steady state. The net effect on the welfare of the unskilled is then unclear. The direct effect of the redistribution makes them better off, but in the long run it increases the scarcity of skill and causes a reverse indirect redistribution by lowering the unskilled wage and raising the skilled wage. Conversely the indirect effect on the welfare of the skilled is unclear. The elasticity of substitution in production between skilled and unskilled labour will determine, among other factors, the strength of the indirect redistribution effects.
(ii) Universal Education Subsidy Funded by Taxes on Skilled Incomes
Now consider transfers conditioned on education of children, funded by taxes on the incomes of the skilled. We suppose these education subsidies can be availed of by all households in the economy, both skilled and unskilled. This is akin to a system of universal public schooling, possibly supplemented by additional cash subsidies paid to parents conditional on sending their children to school (to compensate them for other costs privately borne by parents with regard to commuting cost, uniforms or private tuition).
Let the education subsidy per child in generation t be denoted zt. This will be funded by a linear tax at rate τ on skilled incomes. As in the case of unconditional transfers we shall suppose that the primary policy instrument is the tax rate, which is held fixed. Budget balance in generation t requires τλtws(λt) = λt+1zt. Hence in a perfect foresight competitive equilibrium households will correctly anticipate the subsidy rate zt=τ(λt/λt+1)ws(λt). In steady state the subsidy will be constant: z = τws(λ), along with a steady skill ratio of λ.
The steady state value functions are as follows:
V u = max{u(wu(λ)) + δVu, u(wu(λ) +z − x) +δVs}
V s = max{u((1 −τ)ws(λ)) + δVu, u((1 − τ)ws(λ) +z−x) +δVs}
Essentiality of the skilled occupation implies that λ > 0 and thus Vs > Vu, which requires (1 −τ)ws(λ) > wu(λ). Then skilled households have a stronger incentive to invest, implying only they will invest in a steady state. Hence steady states have the same properties as before: zero mobility, with only skilled households educating their children.
The associated education benefit and cost functions are:
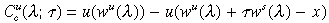
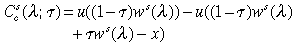
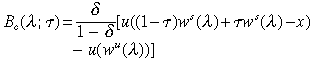
Note the following striking feature of every steady state: the tax rate τ has no effect at all on the expression for steady state consumption of either skilled or unskilled households at any given skill ratio. This follows from using the budget balance condition z = τws(λ), and the property that only the skilled invest and thus avail of the education subsidy. In a steady state, the skilled effectively pay for the education subsidy for their children with their income taxes, and there is no redistribution across occupations. Hence the benefit function is independent of τ, and is exactly the same as in a pure laissez faire economy:
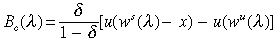
Conditional transfers therefore avoid the ‘welfare magnet’ effect entirely. By subsidising education, it tends to lower the cost to the unskilled of investing. One complication remains, though: since the size of the subsidy is tied (owing to the fiscal balance constraint) to the incomes of the skilled, the investment cost function 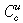 for the unskilled may not be declining in the skill ratio λ. Then Proposition 1 does not apply: we cannot guarantee global convergence to steady states from arbitrary initial conditions. The following Lemma shows this problem can be avoided if the tax rate τ is not too large, relative to the initial skill ratio λ0.
for the unskilled may not be declining in the skill ratio λ. Then Proposition 1 does not apply: we cannot guarantee global convergence to steady states from arbitrary initial conditions. The following Lemma shows this problem can be avoided if the tax rate τ is not too large, relative to the initial skill ratio λ0.
Lemma 2.
With a universal education subsidy funded by a tax on skilled incomes at the rate of τ, and an initial skill ratio λ
0
with
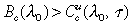 the perfect foresight competitive equilibrium skill ratio sequence converges to an attractor if τ does not exceed a thresholdτ(λ0) which lies between 0 and 1.
the perfect foresight competitive equilibrium skill ratio sequence converges to an attractor if τ does not exceed a thresholdτ(λ0) which lies between 0 and 1.
Proof. Note that
 (11)
(11)so  is upward sloping if
is upward sloping if 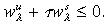 Moreover
Moreover
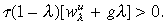 (12)
(12)which is positive if 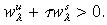 Defining
Defining 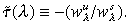 Then
Then  for any τ >
for any τ > 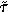 (λ) while
(λ) while  for any τ <
for any τ < 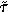 (λ). Since
(λ). Since 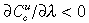 at τ = 0, it follows that there exists τ*(λ) ∈ (0,
at τ = 0, it follows that there exists τ*(λ) ∈ (0, 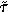 (λ)) such that
(λ)) such that  if and only if τ < τ*(λ).
if and only if τ < τ*(λ).
To complete the proof of the Lemma, suppose that 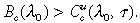 Defining
Defining 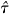 (λ0) as the minimum over τ*(λ) across all λ∈[λ0,
(λ0) as the minimum over τ*(λ) across all λ∈[λ0, 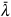 ]; this is easily checked to be well-defined and positive as τ*(λ) is a continuous function. Then τ <
]; this is easily checked to be well-defined and positive as τ*(λ) is a continuous function. Then τ < 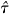 (λ0) implies
(λ0) implies 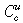 is decreasing in λ over all λ∈[λ0,
is decreasing in λ over all λ∈[λ0, 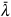 ] Since B is decreasing and
] Since B is decreasing and  is increasing, the result follows from applying the argument underlying Proposition 1.
is increasing, the result follows from applying the argument underlying Proposition 1. 
Given this result, it follows that if the tax rate is not too high then an increase in the tax rate causes an increase in the long-run steady state skill ratio (resulting from an initial skill ratio satisfying 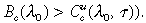 A higher tax rate finances a larger education subsidy, which shifts the unskilled investment cost
A higher tax rate finances a larger education subsidy, which shifts the unskilled investment cost 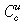 downward. Since it does not affect the steady state benefit function, such a policy raises per capita skill, output and consumption.
downward. Since it does not affect the steady state benefit function, such a policy raises per capita skill, output and consumption.
Proposition 3. The skill ratio in any attractor in a system with a universal education subsidy funded by income taxes on the skilled, is locally increasing in the tax rate τ. Hence a small rise in τ raises per capita income, consumption, at the same time as it reduces inequality of earnings and consumption between the skilled and unskilled. It also raises both utilitarian and Rawlsian measures of welfare (or any intermediate degree of inequality aversion).
The rise in the skill ratio implies that wage inequality declines in the long run, owing (entirely) to the force of indirect redistribution via educational incentives. The absence of direct redistribution enables the ‘welfare magnet’ effect to be avoided. Indirect redistribution raises the consumption of the unskilled, thus raising Rawlsian welfare. Owing to a rise in mean consumption and a decline in consumption inequality, it follows that utilitarian welfare rises in steady state.
Two questions remain. Note that Proposition 1 is known to correctly depict long-run outcomes only when the tax rate is not too high, as described in Lemma 2. Does this restrict the scope for conditional transfers? The problem with ensuring steady state convergence arises partly from the way we formulated the educational subsidy policy. Consider the following alternative: the government commits to a fixed subsidy z, and the tax rate τ is chosen endogenously in order to finance the subsidy. Specifically, in generation t the tax rate is determined by τt=z[λt+1/(λtws(λt))]. The preceding analysis then applies with the following steady state cost and benefit functions parametrized by the subsidy rate z:
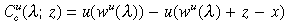
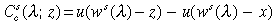
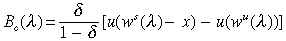
In this formulation, the unskilled cost  is decreasing in λ, since the size of the subsidy is no longer tied to the skilled wage. The conditions of Proposition 1 then apply irrespective of the size of the subsidy. Convergence to an attractor is guaranteed from initial skill ratios where the investment benefit exceeds the cost for the unskilled, and the limiting attractor entails a higher skill ratio if the subsidy rises:
is decreasing in λ, since the size of the subsidy is no longer tied to the skilled wage. The conditions of Proposition 1 then apply irrespective of the size of the subsidy. Convergence to an attractor is guaranteed from initial skill ratios where the investment benefit exceeds the cost for the unskilled, and the limiting attractor entails a higher skill ratio if the subsidy rises:
Proposition 4.
Suppose the government commits to a constant rate z of an education subsidy which is available to everyone in the population, and is funded by a linear tax on skilled incomes at a rate determined endogenously by the government budget constraint. If the economy starts with a skill ratio λ
0
where the steady state benefit Bc(λ0) exceeds the unskilled cost 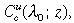 the economy converges to a steady state with a higher macroeconomic (per capita skill ratio, output and consumption) and a higher welfare (Rawlsian, utilitarian, or any intermediate degree of inequality aversion).
the economy converges to a steady state with a higher macroeconomic (per capita skill ratio, output and consumption) and a higher welfare (Rawlsian, utilitarian, or any intermediate degree of inequality aversion).
The other question concerns welfare comparisons between unconditional and conditional transfers. Suppose the welfare function is Rawlsian, so we care only about the consumption standards of the unskilled. Recall that the effect of unconditional transfers on this was ambiguous, owing to the conflicting direct and indirect redistributional effects. Whereas conditional transfers raise the consumption of the unskilled, owing to the absence of a direct effect and the fact that the indirect effect on the poor is positive. It is not clear whether the superior macroeconomic performance of conditional transfers necessarily translates into a welfare improvement.
The following result concerning the welfare superiority of conditional transfers can nevertheless be established.
Proposition 5. Consider any attractor in any system of unconditional cash transfers to the unskilled, funded by a linear tax on incomes of the skilled. Then there exists an educational subsidy z which if the government commits to and funds by a linear tax on incomes of the skilled, every SS entails superior macroeconomic (per capita skill ratio, output and consumption) and welfare (Rawlsian or utilitarian) performance.
To see this, consider a sequence zn converging to x from below. Let the government commit to an education subsidy zn, and fund it by taxing skilled income. As zn tends to x, the unskilled cost 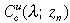 at any given λ <
at any given λ < 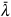 tends to zero. Hence the lowest steady state skill ratio converges to
tends to zero. Hence the lowest steady state skill ratio converges to 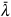 , where the consumption of the skilled and unskilled are equalised, and the per capita consumption and output of the economy is maximised (over the range [0,
, where the consumption of the skilled and unskilled are equalised, and the per capita consumption and output of the economy is maximised (over the range [0, 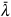 ]). Hence compared to any attractor resulting in a system of unconditional transfers, there must exist a subsidy system of the sort described above which dominates it according to all macro and welfare measures.
]). Hence compared to any attractor resulting in a system of unconditional transfers, there must exist a subsidy system of the sort described above which dominates it according to all macro and welfare measures.
Note also that with unconditional transfers, it is not possible to induce steady state skill ratios close to 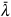 . This owes to the fact that education incentives among the unskilled are promoted indirectly by utilising the income effect associated with transfers. Raising these incentives requires raising the tax in skilled incomes. But this in turn lowers the motivation of the unskilled to invest in education, owing to the welfare magnet effect.
. This owes to the fact that education incentives among the unskilled are promoted indirectly by utilising the income effect associated with transfers. Raising these incentives requires raising the tax in skilled incomes. But this in turn lowers the motivation of the unskilled to invest in education, owing to the welfare magnet effect.
The distinctive feature of the conditional transfer system is that it preserves educational incentives directly through the subsidy. This allows the consumption gap between skilled and unskilled to narrow arbitrarily without destroying human capital investment incentives. In game-theoretic language, it utilises ‘off-equilibrium-path’ educational incentives for the unskilled, which allows ‘equilibrium path’ consumption differentials to vanish. In contrast unconditional transfers utilise ‘equilibrium-path’ incentives: the steady state difference in consumption for their children is the parental reward for undertaking the sacrifice. When consumption inequality narrows, these incentives vanish.
Could one argue that it is infeasible for z to approach x: while public schooling can cover the cost of school resources, some education expenses must inevitably be borne privately by parents, in the form of increased work at home they must do while their children study, or in parental supervision, or in purchasing school uniforms, etc.? Nevertheless, there is nothing that prevents the government from making cash transfers to households to cover these private costs, just as in Progresa. Indeed, it is possible to allow z to exceed x– allow families to earn by schooling their children.15 The key assumption is that all households incur the same educational cost x, thus permitting the government to know what x is and base conditional subsidies on that.
III Continuum of Occupations
We now consider the case of a continuum of occupations, with continuously varying training costs. An occupation is indexed by training cost x, which lies in the interval [0, X]. This is without loss of generality, as long as agents care only about pecuniary costs and returns.16 The occupational distribution λ is now a measure on the interval [0, X]. The production function is given by a function f(λ), which we assume is strictly quasi-concave and satisfies constant returns to scale. The former property means that there is an (almost everywhere) unique measure λ*(w) which solves the unit cost minimisation problem for any given (measurable) wage function w = w(.) defined over [0, X]: minimise  subject to f(λ) = 1. Let c(w) ≡
subject to f(λ) = 1. Let c(w) ≡ *(w) denote the unit cost function. Owing to CRS, profit-maximisation requires c(w) = 1, and the occupational distribution will be a probability measure λ*(w) if the wage function is w.
*(w) denote the unit cost function. Owing to CRS, profit-maximisation requires c(w) = 1, and the occupational distribution will be a probability measure λ*(w) if the wage function is w.
In addition we shall assume that every occupation is essential in the sense that positive production of the consumption good requires the support of the distribution λ to be [0, X].
There is a linear income tax on all wage income, at a constant rate of τ ∈ (0, 1). This finances both an unconditional cash transfer of α and a per unit educational subsidy at the rate of s ∈ (0, 1). We make the simplifying assumption that the entire population is eligible for both kinds of transfers, and liable to the income tax. Introducing forms of means-tested transfers would amount to allowing nonlinearities in the tax-subsidy mechanism, an issue we defer to future work.
In a steady state with occupational distribution λ, fiscal balance requires
 (13)
(13)Any two policy instruments can be chosen independently; Equation (13) will subsequently determine the third (in conjunction with maximising behaviour of households and firms). This formulation allows us to study the effects of unconditional and transfers in isolation, as well as the effect of substituting one by the other. For instance, if we set s = 0, we can study the effect of unconditional transfers by raising τ, with α determined (along with the steady state distribution λ) by Condition (13). Conversely we study the effect of conditional transfers by setting α = 0 and letting τ determine s according to Equation (13), or vice versa. We can study the effect of substituting unconditional by conditional transfers by fixing τ and raising s, with α determined by Equation (13). In what follows we shall suppose that τ and s are chosen independently, with α satisfying Equation (13).
This reduces to the continuum of occupations model of Mookherjee and Ray (2003) if no government policies were considered. We show that arguments similar to that paper ensure that the steady state is unique for any set of policy choices τ, s. In a steady state with wage function (w) an agent that has occupation x at any given date earns w(x) before taxes, and (1 − τ)w(x) after taxes. If this agent were to select an occupation x′ for his child, his payoff would be:
U(x; x′) ≡u((1 −τ)w(x) − (1 −s)x′) +δV(x′)
(14)where V denotes the value function. Note that V(x) ≡ maxx′U(x, x′). Moreover, every steady state wage function w(x) must be strictly increasing – otherwise some high-training cost occupation would be dominated by a lower-training cost occupation, and no agent would choose the former. This in turn implies that V is strictly increasing.
Those in occupations with higher training cost will have a higher incentive to invest, owing to the concavity of u. Hence every steady state must entail no mobility, and a household must select the same occupation in successive generations repeatedly. This implies the first-order condition (∂U(x; x′)/∂x′)|x′=x= 0, which reduces to the condition that
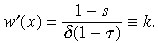 (15)
(15)This means that the wage function is linear in x, with a slope of k that depends on the policy parameters τ, s. Hence the wage function must take the form
w(x; k) =kx+w(0; k)
(16)where the wage w(0; k) of the occupation with zero training cost is pinned down by the profit-maximisation condition that the unit cost of production equals unity. Clearly, w(0; k) is strictly decreasing in k. An increase in k thus increases wage inequality in the sense that wages in the lowest occupations drop, while the wage premium for occupations with higher training cost (as well as the wage in high-x occupations) must rise.
Finally the uniqueness of the steady state follows from the strict quasi-concavity of the production function: with the wage function pinned down uniquely by Equation (16), the occupational distribution λ is determined by the condition that firms maximise profits (i.e. is cost-minimising at the steady state wage function).
Intuitively, the uniqueness follows from the absence of indivisibilities in the occupational structure. Each interval of steady states in the case of two occupations corresponded to a bottom endpoint with indifference for the unskilled occupation, and an upper endpoint for the skilled occupation. When the training costs of the two occupations come closer together, the interval must shrink. In the limit with the elimination of gaps in training costs, every occupation is locally indifferent between itself and neighbouring occupations as a choice, pinning down the slope of the wage function uniquely. The profit-maximisation condition for firms fixes the level of wages, by fixing the wage of the occupation not requiring any training at all.
This uniqueness property enables one to examine the robustness of the results in the previous section, with respect to the selection rule. Moreover, it generates an alternative way of understanding the role of conditionality of transfers. However this comes at some cost: no analysis of non-steady-state dynamics is available in the continuum case.
The discussion above indicates that macroeconomic outcomes depend on policies via their effect on a single parameter k, which is decreasing in the subsidy rate s and increasing in the tax rate τ. An increase in unconditional transfers funded by taxes corresponds to raising τ while holding s fixed: this amounts to an increase in k. A substitution of unconditional by conditional transfers corresponds to raising s while holding τ fixed: this means k falls. We therefore investigate the effects of changes in k on macroeconomic and welfare outcomes. We start with the macroeconomic effects.
Proposition 6. The steady state distribution λ(.; k) with a continuum of occupations has the following properties:
- (i)
Per capita investment a(k) ≡
 (x; k) is decreasing in k.
(x; k) is decreasing in k. - (ii)
Per capita consumption c(k) = f(λ(k)) − a(k) is decreasing in k if k > 1 and increasing in k if k < 1.
- (iii)
Per capita output y(k) ≡ f(λ(k)) is decreasing in k.
Proof. Part (i) follows from the profit-maximisation and strict quasi-concavity of the production function (along with expression in Equation (16) for the steady state wage function). For any given k, λ(x; k) must be the unique maximiser of f(λ) −k (x) −w(0, k), so a standard revealed preference argument implies that given any k′ > k we must have (k′ − k)[
(x) −w(0, k), so a standard revealed preference argument implies that given any k′ > k we must have (k′ − k)[ (x; k′) −
(x; k′) − (x; k)] < 0. Next consider (ii). Suppose k2 ≠ k1, we first claim that
(x; k)] < 0. Next consider (ii). Suppose k2 ≠ k1, we first claim that
(k2−k1)a(k1) +[w(0; k2) − w(0, k1)]≤ 0.
(17)Since firms maximise profits and earn zero profit:
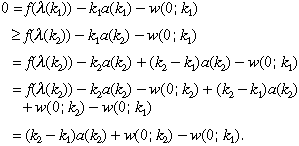
Take first a pair k1, k2 satisfying k2 > k1 > 1; we claim that c(k2) < c(k1). Note that constant returns to scale implies that for any k:
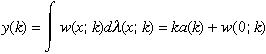 (18)
(18)from which it follows that
c(k) = (k−1)a(k) +w(0; k)
(19)Therefore
c(k2) −c(k1) = (k2− 1)[a(k2) −a(k1)]+ (k2−k1)a(k1) +[w(0; k2) −w(0; k1)]
(20)which is negative, owing to (17), k2 > 1 and the fact established above that a(.) is strictly decreasing.
On the other hand if 1 > k2 > k1, we can reverse this argument:
c(k1) −c(k2) = (k1− 1)[a(k1) −a(k2)]+ (k1−k2)a(k2) +[w(0; k1) −w(0; k2)] < 0.
(21)Finally, to establish (iii), note that if k2 > k1:
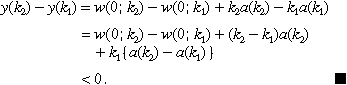
To explain these results intuitively, note that steady state wages are increasing in training cost. An increase in k raises the slope of the wage function. This shifts wages in low-x occupations down, and raises wages in high-x occupations. Firms respond by increasing employment in low-x, low-wage occupations. But these are the less productive occupations, since wages reflect marginal products. Hence an increase in k lowers per capita output.
The effect on consumption is less straightforward because an increase in k lowers per capita investment in skill formation, owing to the shift in favour of low-x occupations. The effect on per capita consumption depends on whether k exceeds or lies below 1. This is because the ‘net’ productivity of an occupation is increasing or decreasing in x depending on the sign of k − 1: using Equation (16) we get
w(x; k) −x= (k− 1)x+w(0; k).
(22)If k > 1 then the shift to low-x occupations lowers per capita consumption (since the latter equals average net productivity).
Proposition 6 shows how results concerning macro effects in the two occupation case extend here. First, suppose there are no conditional transfers at all (s = 0). Then a rise in τ corresponds to an increase in the size of unconditional transfers. In this case k= 1/δ(1 −τ) is always bigger than one. Hence increasing unconditional transfers results in a higher k, which lowers per capita output, consumption and investment in human capital, and raises the skill premium in wages.
Second, suppose we substitute unconditional by conditional transfers (raise s, with τ fixed). This lowers k, raising per capita output and skill investment, just as in the two occupation case. But it will lead to higher per capita consumption only if k > 1. If k < 1, the subsidy rate is already too high: there is over-investment in education. Increasing the subsidy further will encourage greater investment in skill, which raises productivity in the economy by less than it increases the cost of training.17 The ‘golden rule’ in this economy – maximisation of steady state consumption – requires policy parameters be selected to ensure k = 1.
It is not clear, however, whether maximisation of welfare necessarily involves maximisation of per capita consumption, since distributional issues also matter. We turn to this issue next. Note that steady state consumption of an agent in occupation x can be expressed as (where α(k) ≡ τf(λ(k)) − sa(k)):
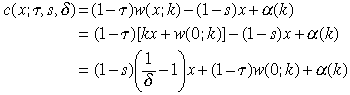 (23)
(23)Hence those in higher-x occupations consume more, irrespective of k.18 It follows that the ‘poorest’ agents in the economy are always those in the occupation with x = 0: a Rawlsian welfare function identifies with the welfare (or consumption c(0; τ, s, δ)) of these agents.
Let us turn to the distributional effects of policy. Note that the steady state unconditional transfer equals
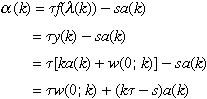
Using the above expression and c(k) = (k − 1) a(k) + w(0; k), Expression (23) is reduced to
 (24)
(24)which shows how the distribution of consumption around its mean depends on the subsidy rate s and distribution of training cost x around its mean a(k). For given k, an increase in s reduces the dispersion of consumption, hence it makes the poor better off. But a rise in s for given τ will raise k and thus have a macroeconomic effect, which will also affect the poor. This is composed of the effect of k on per capita consumption (in a direction that depends on the sign of k − 1), and its effect on per capita training investment a(k). If k > 1 the former effect is positive, while the latter effect is negative. If k < 1 both macro effects are negative, while there is a reduction in inequality. So in either case the overall impact on the poor of a ceteris paribus rise in s (which corresponds to a substitution of unconditional by conditional transfers) is not clear.19
This ambiguity also arose in the case of two occupations. Nevertheless, just as in that case, it pertains to small substitutions of unconditional transfers by conditional transfers. More can be said regarding the improvements that can be made if we consider replacing a system of pure unconditional transfers (with s = 0) with an optimal conditional transfer policy.
Consider the problem of selecting policies to maximise the Rawlsian objective, the consumption of the poorest agents:
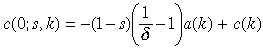 (25)
(25)Note that c(k) is maximised at k = 1. Hence c(0; s, k) ≤ c(k) ≤ c(1). The Rawlsian optimum requires setting k = 1 and then letting s approach 1 in which case c(0; s, k) approaches c(1). This corresponds to selecting for any τ an educational subsidy of s(τ) ≡ 1 − δ (1 − τ) – which ensures that k = 1 irrespective of τ. This ensures the achievement of the maximal level of per capita consumption. Then τ can be selected to achieve the distributional objective without interfering with investment incentives: letting τ approach unity eliminates consumption inequality, raising the consumption of the poorest agents to that of the rest of the population.
Two points are worth noting. First, the Rawlsian optimum is also the utilitarian optimum (more generally the optimum with any intermediate degree of inequality aversion). The Rawlsian optimum involves maximisation of per capita consumption and elimination of inequality. Owing to concavity of the utility function u, this maximises utilitarian welfare as well. This property was also obtained in the case of two occupations. So we can refer to it simply as the welfare optimum.
Second, the welfare optimum does not involve conditional transfers alone, but a mix of conditional and unconditional transfers. Note that if we select a subsidy rate of s(τ) for any given tax rate τ, the unconditional transfer
α(τ) = −(1 − τ)(1 − δ)a(1) + τw(0; 1).
(26)Letting τ approach unity, the unconditional transfer approaches w(0; 1) which is positive. This argument illustrates one important limit to the desirability of substituting unconditional by conditional transfers: if overdone it would result in over-investment in education.
How is this consistent with the results in the two occupation case, where it seemed the welfare optimum could be achieved by conditional transfers alone – for example, the case where the education subsidy z approached x? In that case we had assumed that the subsidy was financed by a tax on skilled income alone. In the current context with a continuum of occupations, transfers are financed by a tax on incomes of all occupations. Approaching the welfare optimum in the current context requires a tax rate τ that approaches unity, as in a perfect socialist state. The role of the unconditional transfer is to return the collected revenues in a lump sum fashion. In the two occupation case this was unnecessary as the incomes of the unskilled were not taxed. Perfect redistribution could be achieved there indirectly through wage movements. Hence unconditional transfers were not needed. This discussion indicates that the desirability of unconditional transfers depends somewhat on how universal the coverage of the income tax is. One can view tax-free treatment of the unskilled or informal sector in less developed countries as a form of unconditional transfers.
IV Conclusion
We conclude by pointing out important assumptions underlying our analysis. Future research could consider the robustness of our results with respect to these.
The assumption that there is no heterogeneity of education costs greatly simplified the argument for conditional transfers. It also enabled us to abstract from steady state mobility. Related to this, we did not allow any randomness in earnings. The presence of either of these would perhaps expand the argument for unconditional transfers: both as a form of insurance against risk, as well as the need to protect those who lack the ability to acquire skills (say, owing to low intelligence or high education costs relative to the rest of the population).
Our model also abstracted from short-run labour supply incentives, since this is already the topic of an extensive literature in the literature on optimal income taxation following Mirrlees (1971). Nevertheless, these incentive considerations may also affect the relative desirability of conditional transfers, and limit the extent to which income tax rates can be raised. Other factors that limit income tax rates are problems with enforcement of taxes. This may limit the practical importance of our results showing that unconditional transfers are dominated by some conditional transfer system, since the latter may need to be accompanied by high rates of income taxation.
Finally, education costs were assumed to be independent of wages. This may be false as a dominant component of educational costs is comprised of teacher salaries. Moreover, foregone earnings of children may constitute an important source of opportunity costs of educating them.
Footnotes
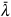 .
.




