Using a Real-Options Approach to Model Technology Adoption Under Carbon Price Uncertainty: An Application to the Australian Electricity Generation Sector*
Abstract
The present climate for investment in electricity generation assets in Australia is uncertain. We develop a real-options model to contrast the timing of the uptake of various electricity generation technologies under two carbon tax simulations: when a carbon tax of known size commences at a certain date in the future; and a carbon tax of known size commences at an uncertain date in the future. We find that uptake in the future varies significantly depending upon an investor's view of uncertainty and whether the technology is primarily designed to be viable in a market with or without carbon taxes.
I Introduction
According to recent projections, gross generation of electricity in Australia is expected to increase by an average 2.1 per cent a year over the long term; from 237 terawatt-hours (TWh) in 2003–2004 to 409 TWh by 2029–2030 (Akmal & Riwoe, 2005). In NSW, a recent estimate indicates that up to 1000 megawatts (MW) of additional generating capacity will be required by 2010, followed by a further 500 MW per year thereafter to meet expected demand (NEMMCO, 2004). However, there currently exists a high level of uncertainty around electricity generation technology investment decisions. This uncertainty is being driven by rapid changes to the environmental, market and political context in which electricity generation projects must operate. The investment risks in this sector are compounded by their highly capital intensive, irreversible and long-term nature.
Since the deregulation of Australia's south-eastern National Electricity Market (NEM), there is an expectation that investment in additional capacity will be made by the private sector (NSW Government, 2004). A number of possible factors could mean that the expected private sector investment in electricity generation assets in NSW is not forthcoming.1 These include, but are not limited to: perceptions that private sector generators will be unable to compete with corporatised State generators because of an unlevel playing field; disparate signals from Federal and State governments in regard to the likelihood of future carbon taxes to address climate change; technology-specific uncertainties relating to new electricity-generation technologies; and community attitudes to any kind of industrial development that may impact upon their local environment.
Although not disputing the significance of other issues, our focus in this paper is on what we consider to be the key factor; the effect of carbon price uncertainty on the uptake of a subset of electricity-generation technologies. The combination of the need for additional generating capacity and carbon price uncertainty, introduces considerable risk into the investment decision-making process. The primary uncertainty relates to the possible introduction (timing) of a price charged to major emitters of carbon dioxide (CO2) via a national emissions trading scheme or carbon tax. The size of the carbon penalty under either measure is also uncertain.
Given the long-lived largely irreversible nature of electricity-generation assets, and their chief role in the accumulation of greenhouse gas (GHG) emissions in the atmosphere, this paper seeks to employ a real-options approach to model technology adoption under carbon price uncertainty. We also use a partial equilibrium model of the electricity sector to generate key market-dependent project revenue and costs streams.
The paper proceeds as follows. Section II briefly discusses real-options theory and its application to the energy sector. The modelling framework is then described in Section III. This is followed by a discussion of the simulation design and results in Section IV. Section V concludes the paper.
II Real-Options Theory and Past Approaches
The real-options (RO) theory of investment received a detailed treatment in the seminal publication of Dixit and Pindyck (1994). RO theory recognises that, although conditions change as new information arrives, as long as an option to invest remains open it has an economic value (referred to as strategic value in the literature) that should be priced (i.e. the option has value).
RO analysis is well suited to investment in electricity-generation assets. Investment in such assets is capital intensive and given their long life and specific use, largely irreversible. That is, investment in electricity-generation assets once incurred are best viewed as sunk. Accordingly, the pricing of any options (‘flexibility’) related to the investment can have a significant impact on its value. Second, this ‘asset inertia’ amplifies the impact of multiple uncertainties (such as market prices, exchange rates, carbon prices, technological change, resource availability, etc.) impacting on future costs and revenue flows. Third, given the considerable lags in these investment decisions, there are a number of potential flexibilities in the project that allow an investor to deal with those multiple uncertainties. Common types of project flexibility or options include: the option to defer investment in the project (also called an option to wait); the option to temporarily or permanently shutdown; the option to switch fuels or outputs; and multiple sequential options where one option to invest in a project provides the option to invest in another project (so-called, ‘compound option’).
Accordingly, there are an increasing number of case studies applying the RO approach to energy industry investment problems. An example of this coverage is provided in Ronn (2003). A notable difference from previous studies is the method we employ for handling uncertainty in the key variables. We obtain projections for electricity and fuel prices from output of CSIRO's Electricity Market Model (EMM); a partial equilibrium model of the centralised electricity generation market in Australia (for details, see Graham & Williams, 2003; Graham et al., 2003; Reedman & Graham, 2004). As part of its reporting parameters, the EMM estimates shadow prices for key resources (brown coal, black coal, gas, biomass) as well as wholesale and retail electricity prices by State, out to 2050 (discussed further below).
We consider our approach to have a number of advantages over previous studies. First, previous studies have typically assumed that uncertain variables track a stochastic process, such as a geometric Brownian motion (GBM) with drift and volatility parameters estimated from historical data. This presumes that future electricity prices (ignoring carbon taxes) will track a similar path to past movements, which may not be the case. Instead, our use of the EMM projects the future path of electricity prices based on underlying drivers such as technological change and turnover of installed generating capacity. Second, the projection of prices based on historical data is problematic in the case where carbon taxes are imposed. In this case, future electricity prices will make a substantial break from GBM-based projections. Third, the use of the EMM price estimates has considerable flexibility as the structure of the EMM can be modified to include additional technologies to examine their impact on electricity market outcomes and to gauge the sensitivity of price projections. Fourth, our method can be used to understand how model outcomes under perfect foresight and investment under uncertainty perspectives will diverge. The limits of perfect foresight models have long been recognised but they remain useful as long as these limits are well understood.
In developing our prototype ‘wait’ model of investment in electricity generation assets, we posit that a modelling approach incorporating real options has considerable value in assessing the uptake of different generation technologies under alterative carbon tax scenarios. Such value may be demonstrated by the model selecting a favoured technology under each scenario. It also provides information about the optimal timing of investments that may reflect current observations about the industry. Such information is useful to the stakeholders making these investment expenditure decisions and Federal and State government policy-makers.
III Model Description
As mentioned above, our approach obtains projections for electricity and fuel prices from the output of an existing model (EMM), which are then inputs into our RO model. This section briefly describes the EMM and provides more detail on the RO model.
Consistent with most bottom–up models of energy systems, the EMM is constructed as a mathematical program that represents the electricity market. Electricity generators are assumed to be profit maximising and forward looking. They have perfect advance knowledge of factors such as the growth in electricity demand and the potential for technological change. Accordingly, the EMM takes the form of an intertemporal optimisation problem where generators optimise their investment and output for the entire period being studied. It should be remembered that this is a stylised representation of that market. The EMM does ignore that some electric utilities are not fully privatised and decision-makers’ information is in reality imperfect.
The mathematical structure of the EMM has been previously outlined in Graham and Williams (2003) with further refinements detailed in Reedman and Graham (2004). The EMM version we use here includes the following amendments: (i) the addition of a retrofit option (post-combustion carbon capture and storage) for black and brown coal pulverised fuel; (ii) the inclusion of a representative nuclear technology; and (iii) for the purposes of this paper, the replacement of Kyoto-style GHG emission targets with a carbon tax.
Although the EMM is a model of the Australian electricity market the RO model is not. Rather, the RO model takes the perspective of an individual generator (an investor) evaluating what type of electricity-generation technology to invest in and when to invest in it, if at all. It also seeks to explicitly incorporate carbon price uncertainty which the EMM, a perfect foresight model, does not.
The RO model focuses on the uptake of a subset of the technologies featured in the EMM. The generating technologies of interest are:
- •
A natural gas-fuelled combined cycle power plant (NGCC).
- •
A supercritical pulverised-fuel black-coal power plant (SCPF).
- •
A black-coal-fuelled integrated gasification combined-cycle power plant (IGCC).
- •
A supercritical pulverised-fuel black coal power plant fitted with post-combustion capture of carbon dioxide (POCSCPF).
- •
A black-coal-fuelled integrated gasification combined-cycle power plant fitted with precombustion capture of carbon dioxide (PRCIGCC).
Both NGCC and SCPF plants are currently deployed in Australia. NGCC plants utilise the waste heat from the gas turbine to generate more electricity from a steam turbine resulting in higher thermal efficiencies compared with a ‘single-cycle’ gas-fired plant. SCPF plants employ elevated steam conditions that improve fuel efficiency and lower emissions when compared with subcritical coal-fired plants. IGCC plants use coal to create a clean-burning gas (syngas), which after cleaning generates power in a combined-cycle configuration. They are not currently deployed in Australia but have been piloted elsewhere. Both carbon-capture plants (POCSCPF and PRCIGCC) use different processes to capture CO2 to significantly reduce GHG emissions, and are currently under development.
We initially examine the uptake of these technologies as a single investment decision. With respect to the last two options we then contrast this single investment decision with the multiple investment decision of retro-fitting an existing SCPF or IGCC power plant with CO2 capture at a later date. Examination of this compound option is of considerable interest in the current climate of carbon price uncertainty, capturing a key flexibility of existing coal-fired power plants: the ‘bolt-on’ of carbon capture and sequestration in anticipation of a penalty for GHG emissions in the future.
Although the RO approach is an alternative to standard net present value (NPV) analysis, calculating the real-option value (ROV) of a project is not very different from calculating its expected net present value (ENPV). The important difference between the ENPV and the ROV of an investment opportunity or project is that the ROV includes any additional strategic value (SV) inherent in a project. That is:
ROV = ENPV + SV
(1)It follows from (1) that:
- •
The ROV of a project can never be less than its ENPV.
- •
The ROV of a project is equal to its ENPV if there is no SV in the project.
- •
A project can still have value even if its ENPV is less than or equal to zero.
However, the existence of uncertainty does not provide any strategic value to the investor unless there are flexibilities in the project, which allows one to deal with those uncertainties. In this paper, we are assuming that an investor has the flexibility (option) to defer an investment for a period of time without relinquishing exclusive rights to that investment. Whether the investor knows that the net return from the project is rising with certainty or not, as long as there is a possibility of the net return from the project rising in the future, then the option to defer the investment until such a time has value. Of course, the degree of carbon price uncertainty will be crucial in determining the size of the strategic value gained by the option to defer (wait).
Although the RO approach is an alternative to standard NPV analysis, we still need to calculate the ENPV for each investment option. To do so requires the estimation of various parameters. The principal data assumptions used to estimate these parameters are shown in Table 1. Although coal-fired plant typically have a slightly higher capacity factor than 85 per cent (typically around 90 per cent) and a 660 MW unit size for NGCC is atypically large (usually around 385 MW), we employed identical unit size, auxiliary power consumption and capacity factors for the non-capture technology options (NGCC, SCPF and IGCC) to simplify the understanding of results as being driven by a small number of plant differences.2 These assumptions mean that within the RO model the annual output and gross revenue for the non-capture technologies are the same. Output of CO2 capture plants is lower because of higher auxiliary power consumption (electricity used to run the capture plant). Note the actual asset life may be much longer than the payback period (economic life of the plant) that is assumed here.
| Assumptions | NGCC | SCPF | IGCC | POCSCPF (new) | PRCIGCC (new) | POCSCPF (‘bolt-on’) | PRCIGCC (‘bolt-on’) | |
|---|---|---|---|---|---|---|---|---|
| Unit size | MWe | 660 | 660 | 660 | 660 | 660 | 660 | 660 |
| Auxiliary power consumption | rate | 0.05 | 0.05 | 0.05 | 0.20 | 0.16 | 0.20 | 0.16 |
| Capacity factor† | rate | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 |
| Capital cost | AUD/MW | 0.8 m | 1.1 m | 1.5 m | 1.5 m | 1.7 m | 0.7 m | 0.6 m |
| Operating & maintenance cost | AUD/MWh | 4.0 | 4.0 | 5.0 | 6.2 | 6.6 | 2.2 | 1.6 |
| CO2 transport and storage cost | AUD/t | N/A | N/A | N/A | 12 | 12 | 12 | 12 |
| Fuel cost‡ | AUD/GJ | 2.76 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Construction time | years | 2 | 4 | 4 | 4 | 4 | 1 | 1 |
| Net fuel efficiency HHV§ | rate | 0.53 | 0.41 | 0.43 | 0.32 | 0.36 | 0.32 | 0.36 |
| CO2 intensity¶ | t/MWh | 0.41 | 0.88 | 0.84 | 0.13 | 0.11 | 0.13 | 0.11 |
| Economic life of plant | years | 25 | 30 | 30 | 30 | 30 | 30 | 30 |
- Notes:
- † Capacity factor is defined as the ratio of expected electricity output in a year to its technical optimum.
- ‡ Fuel price shown is 2005. Coal and gas prices increase by up to $0.13 and $1.17, respectively, to 2030.
- § Net fuel efficiency for capture technologies includes compression energy but not energy used in pipelining (estimated at 0.4 per cent).
- ¶ The CO2 intensity for the capture technologies assume an 88 per cent capture efficiency.
- Sources: Allinson et al. (2003); Cottrell et al. (2003); Graham et al. (2003); Wibberley and Palfreyman (2004); and CSIRO estimates.
- Abbreviations in table not already defined: AUD is 2005 Australian dollars; GJ is gigajoule; HHV is higher heating value; m is million; MWe is megawatt electric; MWh is megawatt hour; N/A is not applicable; t is tonnes.
The data for the capture technologies, POCSCPF new and PRCIGCC new in Table 1, are figures for the whole plant, whereas the ‘bolt-on’ figures reflect the additional costs of ‘bolting-on’ carbon capture to an existing SCPF or IGCC plant at a later date (compound option).
Using the data in Table 1 a number of key parameters are estimated. The constant annual output (q) of a power plant in MWh for a technology (n) is:
qn = uzn × hyr ×cfn(1 − apcn) ∀n
(2)where uz is unit size, hyr is hours in the year (set at 8766), cf is capacity factor and apc is auxiliary power consumption. The annual output figure is the quantity of electricity generated that is actually sold on the market.
The total investment cost (ic) of a power plant in million Australian dollars (AUD) is:
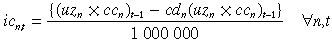 (3)
(3)where cc is capital cost and cd is the annual rate of decline in capital cost reflecting technical improvement. The assumed declines in capital costs calculated from Cottrell et al. (2003) are as follows: 1 per cent per year (NGCC); 0.75 per cent per year (SCPF); and 2 per cent per year (IGCC, POCSCPF, PRCIGCC). The first term in the numerator is the investment cost in the previous time period with the second term reducing that cost by the decline in capital cost to the current time period. In regard to the capture technologies, these equations assume that we are constructing a new plant rather than adding-on carbon capture.
Another calculated value that is significant for the POCSCPF and PRCIGCC technologies is the annual cost of CO2 transport and storage in AUD per MWh (acst). This calculation requires two steps. First, annual emissions of CO2 in tonnes (ae) for the base plant must be calculated:
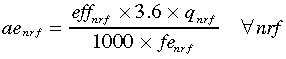 (4)
(4)where eff is the CO2 emission factor in kilo tonnes per petajoule of fuel combusted, 3.6 is a general conversion factor for energy (watt hours to joules), and fe is the rate of net fuel efficiency of the fuel (already incorporating auxiliary power consumption). q is as defined earlier. Thus, the numerator calculates the mass of emissions and the denominator adjusts this for the fuel efficiency of the technology.
In (5), we then calculate the volume of CO2 captured as the capture rate (cr) multiplied by the annual emissions of the base plant. Multiplying the amount of emissions captured by the cost of transport and storage (cst) and dividing by the sent-out output of the capture plant gives the annual cost of CO2 transport and storage in AUD per MWh (acst). We note that the cost of CO2 capture is a component of the operating and maintenance cost for the capture technologies.
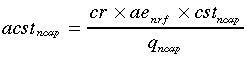 (5)
(5)Other significant costs are annual emissions cost and fuel costs. However, to calculate these values for each time period we need to know the size of the carbon penalty (permit price or carbon tax) and the time period in which the penalty commences. We discuss these issues in the following section.
IV Simulation Design and Results
We use the models described in Section III to conduct two main simulation runs:
- •
The first simulation assumes a carbon tax of known size that commences at certain dates in the future.
- •
The second simulation posits the introduction of a carbon tax of known size at an uncertain date in the future.
As such the calculation for the first simulation is an ordinary NPV. The second simulation involves the calculation of a ROV and ENPV.
With respect to the first simulation, three scenarios of a carbon tax per tonne of carbon dioxide equivalent (CO2e) are calculated: $15/t (REG1), $30/t (REG2) and $45/t (REG3): with the tax commencing in 2014. The selected date reflects the premise that following on from the Kyoto Protocol (with its commitment period ending in 2012) an international agreement (including Australia) is reached for the post-Kyoto period. Allowing for a 2-year lag before commencement, carbon pricing would begin in 2014.
The three tax rates used are intended to represent lower and upper bounds ($15/t and $45/t respectively) and a mid-point estimate ($30/t). Although the selection of the different carbon tax rates was somewhat arbitrary, other studies have employed similar estimates (see AGO, 1999; Graham et al., 2003; Simshauser & Docwra, 2004). In this prototype model, the three tax rates are implemented in the model as a fixed tax rather than emission trading. Emission trading, including options such as grandfathering would lead to a different impact and will be investigated in future research.
Figure 1 charts the impact of a carbon tax on NSW wholesale electricity prices for the period 2005 to 2030 as estimated in the EMM. In the first simulation run, prior to 2014, all investors receive the ‘business-as-usual’ (BAU) price for their output following construction of the plant. From 2014 onwards, there is an immediate known ‘jump’ in the electricity price with the size of the jump increasing with the size of the carbon tax. For the scenario with the most stringent carbon tax of $45/t (REG3) this equates to an approximate doubling in wholesale electricity prices over the period. Resource prices are also estimated in the EMM. In the base period, black coal is $1/GJ and natural gas is $2.70/GJ with the fuel prices tracking a linear trend out to 2030. Black coal and natural gas prices, respectively, in that year (and carbon tax regime) are: $1.12/GJ and $3.80/GJ (BAU); $1.13/GJ and $3.73/GJ (REG1); $1.06/GJ and $3.93/GJ (REG2); and $1.06/GJ and $3.91/GJ (REG3).
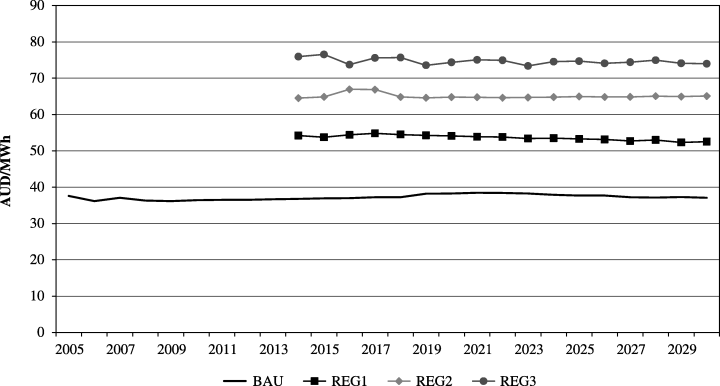
Wholesale Electricity Prices, NSW: 2005 to 2030
In the second simulation, investors are uncertain about the starting date on which the tax is introduced. We limit this uncertainty by assuming that the tax is expected to arrive once in the next 10 years. This is again, another simplifying assumption as it means we can assume the probability of the carbon tax event is 0.1 throughout. Future work could include a more complex treatment, for example where the probability increases over time.
(i) Known Carbon Tax Arrives in 2014
Annual CO2e emissions tax and fuel costs are sensitive to the size and timing of a carbon penalty (permit price or carbon tax). Given that this simulation assumes that the carbon tax is known to arrive in the year 2014, we can now calculate these costs as inputs into our NPV calculation.
The annual cost of emitting CO2e in AUD per MWh (ec) is:
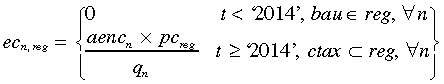 (6)
(6)As shown, the emissions cost is dependent on the level of the carbon tax (pc for ‘price of carbon’) and the greenhouse signature of each technology represented by the annual emissions of CO2e that are not captured (aenc). Clearly, there is no emissions cost prior to the introduction of the carbon tax in 2014. Table 2 summarises the emissions cost in AUD per MWh by technology and carbon tax regime (ctax).
| Carbon tax regime (ctax) | Emission cost by technology ($/MWh) | ||||
|---|---|---|---|---|---|
| NGCC | SCPF | IGCC | POCSCPF | PRCIGCC | |
| Regime 1 ($15/t CO2e) | 6.11 | 13.16 | 12.54 | 1.88 | 1.70 |
| Regime 2 ($30/t CO2e) | 12.23 | 26.32 | 25.09 | 3.75 | 3.41 |
| Regime 3 ($45/t CO2e) | 18.34 | 39.47 | 37.64 | 5.63 | 5.11 |
Similarly, fuel cost is also dependent on the level of the carbon tax as resource prices are sourced from the output of the EMM. The fuel cost (fc) in AUD per MWh for all technologies prior to the carbon tax in (7) is a function of resource prices (fl), the rate of net fuel efficiency (fe) and the general conversion factor for energy (watt hours to joules).
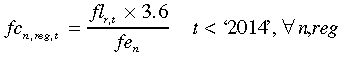 (7)
(7)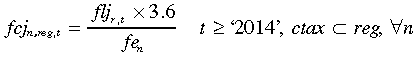 (8)
(8)Once the carbon tax is introduced, Equation (8), fuel costs after the ‘jump’ (fcj) are dependent on the projected resource prices (flj) prevailing in each carbon regime, as estimated by the EMM. For ‘business as usual’ (bau) (7) now holds in all time periods.
Previous equations articulating the calculation of output and costs are inputs into the net revenue (nr) stream calculation (aomc is the annual operating and maintenance cost from Table 1). Equation (9) shows the nr calculation for the ‘business-as-usual’ (bau) scenario with the divergence because of the cost of CO2 transport and storage (acst) for capture (ncap) technologies:
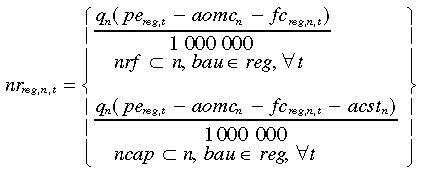 (9)
(9)Equation (10) shows the nr calculation for the three carbon tax regimes (ctax):
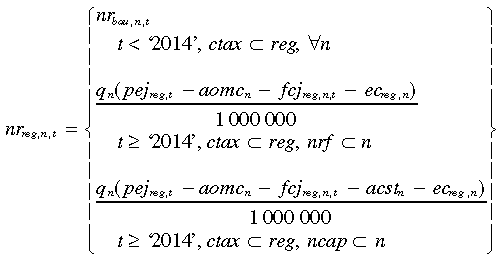 (10)
(10)From (9) and (10) we calculate the net present value (npv) for each technology (n) and carbon regime (reg) in (11). We use the subscript (w) to denote a time within the ‘waiting’ period when the investment decision can be made.
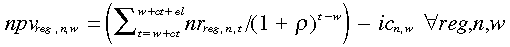 (11)
(11)The bracketed term in (11) is the net revenue earned by the asset over its economic life in present value terms. In a given decision period, this is the discounted sum (the real discount rate (ρ) is 5 per cent) of net revenue that flows after the plant has been built (construction time represented by ct) to the end of its economic life (el). Subtracting the investment cost for the corresponding decision period gives the net present value of operating the asset. Given that the carbon tax commences in 2014, we are mainly interested in those decision periods (years) preceding the tax to ascertain the relative profitability of each technology. Thus, in this simulation, w ∈ {2005, 2006, ... , 2013}.
Although we are more interested in technology uptake during the ctax regimes, to provide some context we make some brief comments on the bau regime. Under bau, no matter when (w) the decision is evaluated the only technologies with a positive npv are the black coal-fired non-capture plants. The most profitable is a SCPF plant. The IGCC plant has a lower npv but narrows the gap nearing the end of w because of declines in its capital cost. The negative npv result for the NGCC plant reflects its higher fuel cost compared with the coal-fired plant. The negative npv result for the capture technologies in a non-carbon constrained world is intuitive as they require a greater capital outlay and incur additional operating costs (acst and aomc) and do not receive a lower tax offset (no carbon tax in place) compared with the non-capture technologies.
Turning our attention to technology uptake in the carbon tax (ctax) regimes, the introduction of a carbon tax in 2014 has improved the profitability of all technologies. SCPF continues to have the highest npv indicating that the size of the carbon penalty ($15/t) does not sufficiently erode its profitability, providing no incentive for the investor to select a less GHG intensive technology. However, as the size of the carbon tax increases, PRCIGCC has the highest npv by 2009 because of its lower emission signature for a $30/t carbon tax. The increased capital cost of the capture technologies is more than offset by the tax penalty imposed on the non-capture technologies and the comparatively low cost of capturing and storing CO2. PRCIGCC remains the optimal choice (highest npv) in regime 3 ($45/t) with POCSCPF also performing better surpassing NGCC in 2008. With regard to the capture technologies, the superiority of PRCIGCC over POCSCPF reflects greater declines in the capital cost of the base plant and higher energy efficiency (lower fuel and emission costs). Overall, the reversal of fortune between regimes 1 and 2 suggests the crossing of a threshold where the economics of capturing and storing CO2 become favourable to the investor.3 These results are consistent with the perfect foresight simulations of the EMM where PRCIGCC is taken up after the imposition of a carbon tax.
(ii) Carbon Tax Arrives in Unknown Time Period
We noted earlier that in this simulation, although we impose the three levels of the carbon tax, we do not fix the starting date at which the tax is introduced. Instead we posit that although the actual arrival date of a carbon tax is uncertain, we limit this uncertainty by assuming that the tax is expected to arrive once in the next 10 years. If we represent this mean arrival rate by the symbol lambda (λ), in our case, the value of λ is 1/10 or 0.1. Thus, in contrast to the first simulation, here we must apply probability weights to our net revenue flows.
To avoid confusion, re-define (10) as (12) and (13), with nr and nrj representing our net revenue stream calculations for the no carbon tax (‘non-jump’) and carbon tax worlds (‘jump’), respectively:
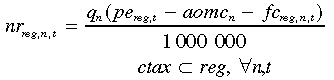 (12)
(12)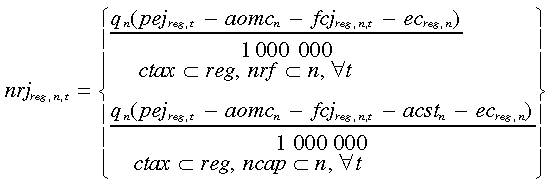 (13)
(13)Accordingly, the expected net present value (enpv) for each technology (n) and carbon tax regime (ctax) over each decision period (w) now becomes:
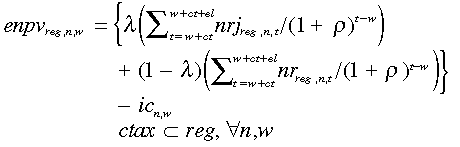 (14)
(14)There is a stark contrast in the results when the introduction of a carbon tax is uncertain, compared with the case when its timing is known in advance. Evaluating technology uptake on the basis of enpv, SCPF has the highest enpv in all carbon tax regimes, peaking in regime 1 (the lowest carbon tax regime). IGCC is the next most profitable followed by NGCC in all carbon tax regimes. The capture technologies (POCSCPF and PRCIGCC) have negative epnv's over each decision period (w). The reasons for these outcomes can be inferred from Equation (14). Because the mean arrival rate of a carbon tax is 0.1 (λ), the continuation of ‘business as usual’ enters the enpv calculation with a very high weighting of 0.9 (1 –λ). This explains the strong resemblance with the ‘business-as-usual’ results from the first simulation.
However, the examination of technology uptake based on enpv does not account for any flexibility inherent in any of the technologies. The specific flexibility in our case is the option to defer the investment to a future time period (the option to wait) if this would result in greater project value.
In qualitative terms and in the context of our problem the rov calculation based on the ‘Bellman equation’ (see Dixit & Pindyck, 1994: 98–101) amounts to an algorithm that searches, from the end of our decision (wait) period (the year 2013) backwards, for the optimal investment timing (with any delay in enpv received properly discounted if the optimal timing is not immediate). The search must begin at the end and work backwards to rule out the possibility that a decision to invest now forgoes higher present value-adjusted benefits. Thus, even if a project has a positive enpv in the year 2005 (SCPF and IGCC above), the algorithm may choose a later time period between 2006 and 2013 as the optimal time to commence construction of the plant.
Evaluating technology uptake on the basis of a rov, the optimal timing of investment in a SCPF plant is 2005 for all carbon tax regimes. Thus, there is no value in waiting (strategic value) to build these plants at a later date and the optimal timing is identical to that indicated on an enpv basis. However, the optimal timing of an investment in an IGCC plant diverges from that indicated by the enpv framework. Our algorithm selects 2011 as the optimal time in regimes 1 and 2, and 2012 for regime 3. Thus, even though an IGCC plant has a positive enpv in 2005 in all regimes, the investor gains greater value by waiting 6 (regimes 1 and 2) or 7 (regime 3) years, presumably to take advantage of declining capital costs. In contrast, the value of building a NGCC or new capture plant is composed entirely of strategic value as the option to wait avoids any losses that would be incurred if the investment took place. In all ‘wait’rov evaluations the lowest value is zero as the investment can always be avoided altogether by waiting indefinitely.4
However, the optimal timing of investment based on a ro analysis above ignores an additional flexibility of the SCPF and IGCC technologies: the option to ‘bolt-on’ CO2 capture and sequestration at a later date. We can, however, apply the same principle outlined above to value this compound option. In the case of our two CO2 capture technologies (POCSCPF and PRCIGCC), the algorithm searches for the optimal timing of two investments with the provision that they take place in the correct order. That is, valuing the option to ‘bolt-on’ CO2 capture and sequestration at a later date after the SCPF or IGCC plant has already been built.
In applying this algorithm, however, we find that the option to retrofit CO2 capture to either a SCPF or IGCC plant is not taken up at any time. This is not surprising as we discovered earlier that the enpv for capture technologies were negative. This reflected the fact that although such technologies were economically viable when carbon taxes were certain, when the carbon taxes are only expected with a 10 per cent probability (λ = 0.1) they are not expected to be viable. Upon further investigation of this issue we found that carbon taxes need to be expected with a probability of around 55 per cent in order for the POCSCPF and PRCIGCC options to be taken up prior to carbon taxes being imposed with certainty.
V Conclusion
The present climate for investment in electricity generation assets in Australia is uncertain. The principle drivers are the long-lived largely irreversible nature of electricity-generation assets and the risk that investors in such assets may need to pay carbon taxes on the emissions from generation at some unknown time in the future. One could restate this last driver as the risk that investors may not need to pay carbon taxes on emissions in the future as such an outcome would reduce the value of low emission technology investments. Indeed, using real options analysis, we find that the technologies that can be expected to be taken up in the future vary significantly depending upon an investor's view of this uncertainty and whether the technology is primarily designed to be viable in a market with or without carbon taxes.
Viewing the reported results as preliminary, we have shown that an investor's view of carbon price uncertainty does affect the uptake of different technologies. When the imposition of a carbon tax is known with certainty, super-critical coal-fired plant (SCPF) was the optimal investment choice at low carbon prices. However, at higher carbon prices, combined cycle gas plant (NGCC) and carbon capture technologies (POCSCPF and PRCIGCC) become more viable because of their lower emission signature. In contrast, when both the timing and imposition of a carbon tax is uncertain neither of our two carbon capture technologies are taken up. Our real-options analysis indicates that the timing of investment in IGCC should be delayed, whereas investment in SCPF plant should proceed immediately (no value in waiting). We also find that the option to retrofit CO2 capture to coal-fired plants is not taken up at any time.
All of these results should be regarded as preliminary. Further work will be undertaken to consider whether there are more appropriate ways to represent the shape and spread of the notional probability distribution of future carbon taxes over time and with the size of the carbon tax. Additional compound options could be a retrofit combining partial carbon capture and carbon taxes. These alternative specifications could result in some changes to the optimal timing of investment in the technologies considered here.




