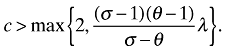Trade Liberalization, Firm Selection, and Variety Growth
Abstract
Recent empirical findings indicate that when trade is liberalized both firm selection takes place and product variety increases. Each of these two stylized facts has its own seminal theory. But how can they arise together? This paper presents a model of heterogeneous, multi-variety firms that provides an intuitive explanation. When trade is liberalized efficient foreign exporters enter and push out the least efficient domestic firms. Fewer firms remain in total. But exporters endogenously offer more variety than domestic firms. The entry of variety-rich foreign firms unambiguously dominates the decrease in the number of firms. Thus, total variety increases.
1. Introduction
According to Feenstra (2006) firm selection and rising product variety are the two key empirical regularities that emerge from recent microeconometric work in international trade. First, when barriers to trade are lowered, efficient foreign exporters enter the domestic market and push out the least efficient domestic firms (Tybout, 2003; Greenaway and Kneller, 2007). This is known as firm selection. Firm selection raises the average productivity of the firms that are active on the domestic market. Second, opening up the domestic market broadens the available choice of product varieties, to the benefit of domestic consumers (Broda and Weinstein, 2006).
For each of these stylized facts there exists a seminal theory: Melitz (2003) for firm selection and Krugman (1980) for product variety. But how are the two connected? The purpose of this paper is to present an intuitive mechanism that links the two stylized facts. When trade is liberalized, firm selection leaves a market with fewer, larger firms. But exporters endogenously offer more variety than purely domestic firms. Upon liberalization, the efficient foreign exporters that enter the domestic market are more variety-rich than those domestic firms that are pushed out. This more than compensates for the fact that fewer firms remain. Thus, total variety increases.
The model is based on the contributions of Melitz (2003) and Allanson and Montagna (2005). In the Melitz model, firms produce a single horizontally differentiated variety and differ in their productivity. Exporting involves a sunk cost, which leads to a scale ranking: only the most productive firms export. Allanson and Montagna (2005), instead, present a closed-economy model of multi-variety firms. They work with a nested CES, in which the varieties of a single firm are closer substitutes than the varieties of different firms. This bounds a firm's optimal variety, because additional varieties cannibalize on the demand for the firm's existing line.
Bringing these together, we obtain a model of international trade with heterogeneous, multi-variety firms. We assume that a firm's efficiency parameter is applicable to all its varieties. That is, we abstract from efficiency differences within a firm. This allows us to parameterize the productivity distribution and obtain a closed-form solution. As is common in both the theoretical and the empirical literature on firm heterogeneity, we apply a Pareto distribution (Helpman et al., 2004; Baldwin and Forslid, 2006; Melitz and Ottaviano, 2008).
As proven by Baldwin and Forslid (2006), applying a Pareto distribution in the standard Melitz model leads it to predict that trade liberalization reduces the total number of firms that sell to domestic consumers. Market concentration rises. This property of the model not only seems fairly intuitive, but is also consistent with Mirza's (2006) empirical work.1 However, given that it is a single-variety model, fewer firms necessarily imply less variety.
In our multi-variety setting, instead, trade liberalization always increases total variety available to domestic consumers. The mechanism comes about because more productive firms choose to offer more variety. The reason is the presence of a firm-wide fixed cost. This generates an economy of scope, which is stronger for firms that have a lower marginal cost per variety. As only the most productive firms self-select into export, exporters offer more variety than purely domestic firms. Firm selection still leaves a more concentrated market. But, quite remarkably, the variety gap between entering exporters and exiting domestic firms unambiguously dominates the reduction in the number of firms. Thus, firm heterogeneity in productivity is the driving force behind both firm selection and variety growth.
However, the welfare implications of our model are less straightforward than those in a model with single-variety firms. Consumers value more variety. But due to the difference between the intrafirm and interfirm elasticities of substitution, they also value being able to buy from different firms. We prove that, on the whole, consumers sometimes prefer the variety offering they could choose from before trade was liberalized. Gains from lower prices always more than compensate in this case, though.
Our work also relates to that of Bernard et al. (2006), Nocke and Yeaple (2006) and Eckel and Neary (2010) on multi-product firms in trade. The latter develop a model with firms that differ in organizational capability, while overall productivity declines in the number of product categories that firms choose to be active in. The model explains why larger firms have lower market-to-book values. In Bernard et al. (2006) firms are heterogeneous in both managerial ability and expertise in each product category. Trade liberalization results in higher average productivity due to not only firm selection, but also product selection within firms. Eckel and Neary (2010) consider trade with homogeneous multi-product firms under oligopolistic competition. Optimal variety offering depends on both core competencies (increasing marginal costs for additional products) and cannibalization (additional products decrease demand for the firm's existing line). These three models have richer structures than our own. For this reason, they cannot be parameterized with a single distribution to obtain a simple mechanism that matches the stylized facts described above.
2. The Model
In this section we present our model. We first describe demand and then the decision problem that firms face. At the end of the section we demonstrate how the presented model nests the models of Melitz (2003) and Allanson and Montagna (2005).
Demand
Preferences are given by a nested CES, in which the domestic representative consumer optimizes over three stages. In the first stage, the consumer optimally allocates expenditure, E, between the quantity index of a differentiated good q (defined below), and an outside composite good, z, which is used as a numéraire. We assume that the numéraire good is produced with identical constant-returns-to-scale technology everywhere and is freely traded. This is a common assumption (Helpman et al., 2004), which brings about international wage equalization. First-stage utility is given by:
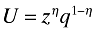 (1)
(1)with η ∈ (0, 1). By optimization, the consumer spends y = (1 − η)E on q, so that we can write the consumer's budget constraint for the differentiated good as
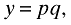 (2)
(2)where p is the price index associated with the differentiated good. Second- and third-stage utility are given by
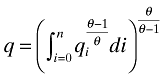 (3)
(3)and
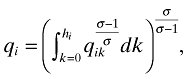 (4)
(4)where qik is the demand for each variety k of a given firm i, which produces a number (= mass) hi of varieties. Then, qi is the quantity index associated with the sales of a given firm, while n is the number of firms. Importantly, σ is the elasticity of substitution between different varieties of a given firm and θ is the interfirm elasticity of substitution. We assume that σ > θ > 1.
It is well known that minimizing expenditure subject to the CES aggregator gives the following solutions for the welfare-based price indices (Allanson and Montagna, 2005; Obstfeld and Rogoff, 1996, pp. 227–28):
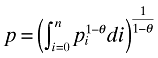 (5)
(5)and
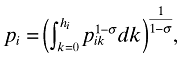 (6)
(6)and that the final demand for varieties can then be expressed as
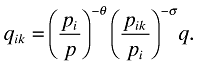 (7)
(7)Firms
The firm's problem consists of an entry stage and, subsequently, for as many periods as it stays active, sales decisions. To start operating, firms have to pay a one-time cost Fe, which entails, among other things, plant set-up, initial market research, and setting up a distribution network. Only after incurring this cost, do firms discover their productivity. Firms draw their productivity, ϕ, from a time-invariant distribution, g(ϕ). This is an essential building block of the model of Melitz (2003), based on empirical evidence that firms differ widely in their productivities, even within narrowly defined industries.2
Once firms know their productivity, they must decide whether to produce or to exit. Those who stay set their prices and variety offering. However, each period active firms face an exogenous probability, δ, of being hit by a death shock. These industry dynamics of the Melitz model are essentially a simplified version of Hopenhayn's (1992) work on endogenous entry, exit, and long-run stationary equilibria.
Being active on the domestic market brings about the following costs each period:
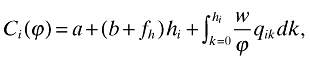 (8)
(8)where a and b are firm-wide and variety-specific fixed costs, respectively. These represent, for instance, advertisement, management time, and maintenance of the distribution network. They are the fixed costs required to maintain activity on the domestic market. Both are necessary elements of the model: a generates increasing returns to scale, while a positive b, in conjunction with σ > θ, keeps optimal variety bounded. That is, the marginal benefit of variety is decreasing due to σ > θ, while its marginal cost is constant and positive.
Distinct from these is fh, which is the cost of creating a new variety. Once we introduce exports, it will be clear why these must be kept distinct. In fact, it costs Fh to set up a new variety. But firms are indifferent between paying this Fh up front, or paying the amortized fixed cost δFh = fh each period.3 The last term in the equation captures the variable costs of production. Here, marginal costs are inversely proportional to the productivity parameter, ϕ, and w is the wage. We normalize w = 1.
Simultaneously with its domestic sales decision a firm also chooses whether to become an exporter, how many of its varieties to export, and which prices to charge abroad. Yet, in order to export, firms face an additional hurdle. As in Melitz (2003), they must pay a so-called beachhead cost, fx, associated to setting up a new trade line.4 For simplicity, we let the fixed costs of maintaining activity on a market, a and b, be the same in the domestic and foreign markets. To export a good, furthermore, a firm pays tariff and transport costs τ > 1 per shipped unit. The firm's per-period profit function becomes:
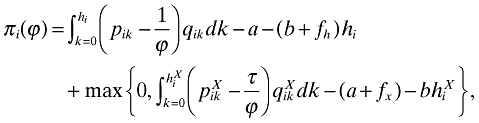 (9)
(9)where the second term in the max operator represents the profits from exporting. If these are smaller than zero, the firm will not export. The terms 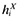 ,
, 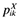 , and
, and 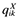 stand for, respectively, the number of varieties exported, the price of variety k charged in the foreign market, and the quantity of variety k sold abroad. Countries are identical and the trading cost τ is the same to each destination.5 In the above equation, it is implicit that firms do not develop new varieties only for export. That is,
stand for, respectively, the number of varieties exported, the price of variety k charged in the foreign market, and the quantity of variety k sold abroad. Countries are identical and the trading cost τ is the same to each destination.5 In the above equation, it is implicit that firms do not develop new varieties only for export. That is, 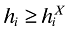 , and firms export a subset of their domestic varieties. Equation (13) below states the required parameter restriction for this to hold. This condition is necessary for an interior solution.
, and firms export a subset of their domestic varieties. Equation (13) below states the required parameter restriction for this to hold. This condition is necessary for an interior solution.
The first-stage decision of the firm can now be summarized by a free-entry condition:
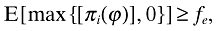 (10)
(10)where we have rewritten δFe = fe. Firms will enter as long as the expected net present value of positive future profits covers the entry cost. After having drawn ϕ, moreover, firms have a cutoff productivity level, 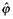 , for which they are indifferent between continuing and ceasing production:
, for which they are indifferent between continuing and ceasing production:
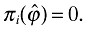 (11)
(11)Similarly, the model contains a cutoff productivity for exporting, 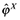 , which is the productivity draw for which a firm is indifferent between exporting and not exporting.
, which is the productivity draw for which a firm is indifferent between exporting and not exporting.
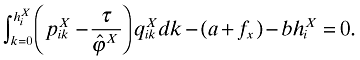 (12)
(12)As in Melitz (2003), however, we require a condition that ensures 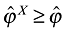 :
:
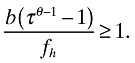 (13)
(13)After all, the fact that only the most productive fraction of active firms become exporters is the driving force of firm selection. The above condition is also necessary and sufficient for 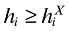 . This is verifiable in the next section.
. This is verifiable in the next section.
Finally, if we set σ = θ and fix 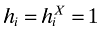 we obtain a model with heterogeneous, single-variety firms that is equivalent to Melitz's. An alternative way to put it is that in the standard Melitz model fh = 0 for hi ∈ [0, 1] and fh → ∞ for hi > 1: the R&D cost function is discontinuous at one variety. In addition, the model presented above nests the contribution of Allanson and Montagna (2005). Their closed-economy model of homogeneous, multi-variety firms is obtained by fixing
we obtain a model with heterogeneous, single-variety firms that is equivalent to Melitz's. An alternative way to put it is that in the standard Melitz model fh = 0 for hi ∈ [0, 1] and fh → ∞ for hi > 1: the R&D cost function is discontinuous at one variety. In addition, the model presented above nests the contribution of Allanson and Montagna (2005). Their closed-economy model of homogeneous, multi-variety firms is obtained by fixing  for all firms and taking away firms' possibility to export.
for all firms and taking away firms' possibility to export.
3. Equilibrium
In this section we compute a closed-form equilibrium solution for the Pareto distribution. As discussed in the introduction, this is a common parameterization, both in theoretical and quantitative work on firm heterogeneity.
To solve for the price setting of the firms, we replace qik from equation (7) into equation (9) and set ∂πi(ϕ)/∂pik = 0. Likewise, noting that
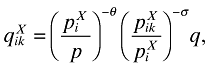
where 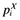 is the price index of domestic consumers' purchases from a foreign firm, we set
is the price index of domestic consumers' purchases from a foreign firm, we set 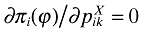 to obtain prices charged by exporters. Subsequently,
to obtain prices charged by exporters. Subsequently,
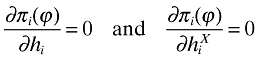
give us equations for hi and 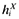 . It should be noted that in solving for firms' decisions on pricing and variety offering we have ruled out strategic interactions. This follows Allanson and Montagna's (2005) approach in extending the standard single-variety per firm Dixit–Stiglitz monopolistic competition model to the multi-variety case.
. It should be noted that in solving for firms' decisions on pricing and variety offering we have ruled out strategic interactions. This follows Allanson and Montagna's (2005) approach in extending the standard single-variety per firm Dixit–Stiglitz monopolistic competition model to the multi-variety case.
Replacing terms, equations (11) and (12) provide solutions for the cutoff productivity levels for activity on the domestic and foreign markets, 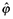 and
and 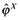 . To solve for the firms' free-entry condition in equation (10), we rewrite the max operators in the profit function to probabilistic terms. That is, with the probability that
. To solve for the firms' free-entry condition in equation (10), we rewrite the max operators in the profit function to probabilistic terms. That is, with the probability that 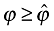 the firm will remain active in the domestic market after discovering its productivity. This probability is simply
the firm will remain active in the domestic market after discovering its productivity. This probability is simply 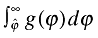 . Similarly, before entering the market, the firm has a chance of
. Similarly, before entering the market, the firm has a chance of 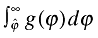 becoming an exporter. Finally, we rewrite the aggregate price level from equation (5) to
becoming an exporter. Finally, we rewrite the aggregate price level from equation (5) to
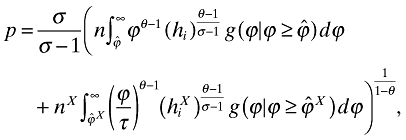 (14)
(14)where 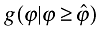 is the conditional distribution of ϕ, while
is the conditional distribution of ϕ, while 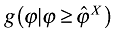 is that distribution among exporters. Furthermore, nX is the number of foreign firms from which domestic consumers purchase. By the symmetry of countries this is equal to the number of domestic exporters. Formally,
is that distribution among exporters. Furthermore, nX is the number of foreign firms from which domestic consumers purchase. By the symmetry of countries this is equal to the number of domestic exporters. Formally,
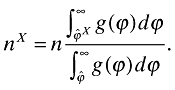 (15)
(15)This gives us enough to solve the free-entry condition and obtain an equation for n. For the Pareto distribution, the probability density function takes the form
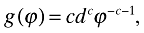 (16)
(16)where g(ϕ) has support on [d, ∞), and c is the parameter that measures heterogeneity. A smaller c implies a wider distribution and, thus, a more heterogeneous population of firms. As is common in the literature, we normalize d = 1. Moreover, as in Helpman et al. (2004) and Chaney (2008), we require a parameter restriction
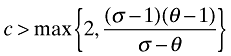 (17)
(17)to ensure finite variance of the distribution of productivity draws g(ϕ) and the conditional productivity distribution of active firms 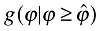 . If this condition is violated, productivity cutoffs are indeterminate. Implementing the Pareto distribution and solving algebraically, gives us the closed-form solution:
. If this condition is violated, productivity cutoffs are indeterminate. Implementing the Pareto distribution and solving algebraically, gives us the closed-form solution:
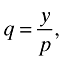 (18)
(18)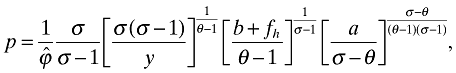 (19)
(19)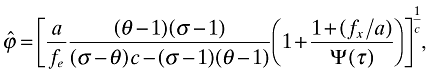 (20)
(20) (21)
(21)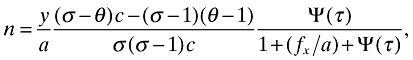 (22)
(22)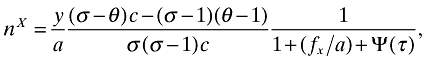 (23)
(23)where we have defined
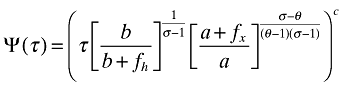 (24)
(24)to make things visually easier to absorb. Moreover, for a given firm with productivity draw ϕ we also have the following equations governing price setting and the optimal scope at home and abroad:
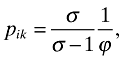 (25)
(25)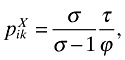 (26)
(26)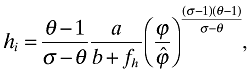 (27)
(27)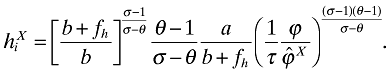 (28)
(28)It is interesting to observe here that the interfirm elasticity of substitution, θ, does not affect price setting. Rather, as in Allanson and Montagna (2005), firms set markups purely according to their intrafirm elasticity, σ, and adjust for θ completely along the variety margin.
4. Results
As discussed in the introduction, the purpose of our model is to explain how trade liberalization simultaneously leads to an increase in the average industry productivity and variety growth. With our closed-form solution in hand, we can now show that the model indeed matches these stylized facts, and observe the mechanism through which it does so.
The way that trade liberalization raises the average productivity of the firms that are active in an industry, is identical to the Melitz model: firm selection. The least efficient firms are pushed out of the market. Formally, we have that
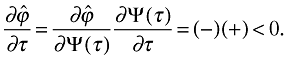
Hence, a tariff reduction raises the productivity cutoff, 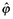 , and the average remaining firm is more productive.
, and the average remaining firm is more productive.
Moreover, our equilibrium solution allows us to derive a closed-form expression for the number of firms that are active on the domestic market:
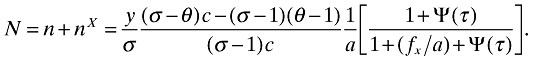 (29)
(29)Taking the derivative of this expression towards tariffs and replacing
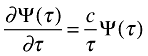
yields
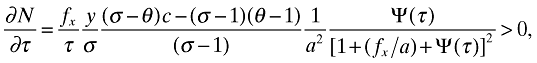 (30)
(30)from which we get:
Proposition 1. The number of firms that sell to consumers on the domestic market unambiguously decreases when trade is liberalized: ∂N/∂τ > 0.
Finally, we can obtain a similar expression for the total variety available to domestic consumers:
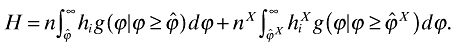 (31)
(31)That is, total variety is the sum of the variety offered by domestic firms and the variety offered by foreign firms. The former equals the number of domestic firms times the average amount of variety per domestic firm. Likewise, the latter equals the number of foreign firms on the domestic market times the average amount of variety that such firms offer to domestic consumers. Thus, H is an unweighted variety measure. Each variety counts equally. Section 6 extends to a general measure of variety.
Solving in closed form gives:
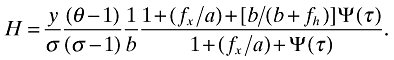 (32)
(32)And taking the derivative towards tariffs:
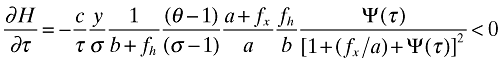 (33)
(33)so that we get:
Proposition 2. Total variety available to domestic consumers unambiguously rises when trade is liberalized: ∂H/∂τ < 0.
Thus, on the one hand, each foreign entrant pushes out more than one local firm when trade is liberalized. But, on the other hand, foreign entrants offer more variety than the firms that exit: 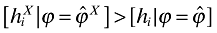 by equations (27) and (28). This unambiguously dominates the decrease in the number of firms. In this manner, both market concentration and total variety increase.
by equations (27) and (28). This unambiguously dominates the decrease in the number of firms. In this manner, both market concentration and total variety increase.
The result on variety growth is quite surprising when one considers that, due to trade costs, firms export only a part of their domestic varieties (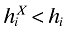 ). Hence, the productivity gap between the marginal foreign entrant and the marginal exiting domestic firm (
). Hence, the productivity gap between the marginal foreign entrant and the marginal exiting domestic firm (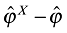 ) is large enough to overcome the effect of the trade costs: the foreign entrant always offers more variety to domestic consumers than the exiting domestic firm (
) is large enough to overcome the effect of the trade costs: the foreign entrant always offers more variety to domestic consumers than the exiting domestic firm (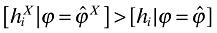 ). And, in turn, this difference is large enough to more than compensate for variety lost from the decrease in the number of firms.
). And, in turn, this difference is large enough to more than compensate for variety lost from the decrease in the number of firms.
5. Welfare Implications
On the whole, consumers always gain from trade liberalization in our model. From our closed-form solution it is apparent that
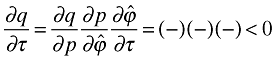
and total welfare unambiguously increases in liberalization. It should be noted, however, that this outcome depends crucially on the assumption of monopolistic competition. Long et al. (2007) show that, depending on trade costs, trade liberalization can reduce welfare in oligopolistic markets.
In our model the total welfare gain of liberalization comes about through both prices and variety. We have seen that trade liberalization gives consumers the choice between more varieties, but from fewer firms. Thus, the question remains whether consumers prefer the available choice after liberalization to that before. After all, by σ > θ consumers care about how many firms they can buy from. We ask, therefore, whether the variety effect of trade liberalization is positive in welfare terms.
Proposition 3. There exist parameterizations for which the variety effect of trade liberalization is positive in welfare terms. There also exist parameterizations for which it is negative.
Proof. It suffices to consider the cases fx → 0 and fh → 0 (neither of which violates the condition in equation (13)). When entry costs to export vanish, fx → 0, all firms export at least some varieties and liberalization ceases to affect the number of firms:
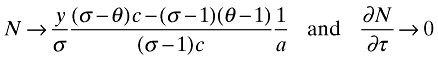
from equations (29) and (30). But by equation (33)∂H/∂τ, does not go to zero, since exporters expand their variety offering when tariffs are lower, 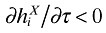 (equation (28)). More variety with the same number of firms implies an unambiguous welfare gain. Conversely, for fh → 0 economies of scope from exporting domestically developed varieties vanish, and
(equation (28)). More variety with the same number of firms implies an unambiguous welfare gain. Conversely, for fh → 0 economies of scope from exporting domestically developed varieties vanish, and
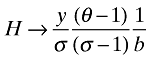
so that ∂H/∂τ → 0. At the same time, ∂N/∂τ does not go to zero. The same amount of variety from fewer firms implies an unambiguous welfare loss.□
Overall, therefore, the outcomes of our model are straightforward in the nominal sense (i.e. fewer firms, more variety), but more intricate when it comes to consumers' welfare. Yet, even when the variety effect of trade liberalization is negative in welfare terms, lower prices more than compensate the consumer.
6. Generalized Variety Index
The measure for total variety we have used thus far, H, is a simple unweighted sum of all final varieties on the market. However, as consumers value receiving variety from different firms, this section considers the implications of a generalized (weighted) measure of total variety. Determining this measure is not straightforward. The optimization problem itself gives no direct solution, as the quantity index q in equation (3) measures both price and variety effects. Hence, ∂q/∂τ measures liberalization's impact on welfare, not variety.6
We propose the following general measure of variety:
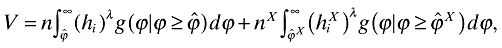 (34)
(34)where λ > 0 represents consumers' relative weight of the final variety offering, hi (and 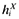 ), versus the number of firms they can choose from n (and nX). A natural value for λ might be
), versus the number of firms they can choose from n (and nX). A natural value for λ might be
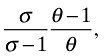
for instance. The higher is σ for a given θ (firms are more differentiated from the consumer's point of view)—the lower is λ—the greater the value that the consumer attaches to the number of firms from which he can buy.
In fact,
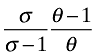
is exactly the value for λ that comes out of equations (3) and (4) if all firms set the same prices (qik in equation (7) is a constant). That is, if one simplifies the model by assuming that firms can only adjust for their productivity differences along the variety margin (cutting out the price margin), then it is straightforward to show that q can be written to a constant times V where
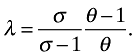
When firms adjust along both price and variety margins, however, there is no obvious solution for λ. Nonetheless, we use
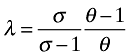
as a benchmark, since it has both an intuitive and a formal basis, and allows for a discussion of λ in terms of elasticities.
It is straightforward to see that the results of Propositions 2 and 3 will not always hold. In particular, for λ → 0 consumers put an extreme weight on the number of firms that offer them varieties. Therefore, as liberalization always reduces the number of firms on the domestic market (Proposition 1), it must be that V goes down (τ↓⇒V↓): limλ→0(∂V/∂τ) > 0. However, we can prove the following:7
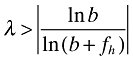
is a sufficient condition for Proposition 2 to hold. Moreover, the derivative ∂V/∂τ now directly measures the variety channel. Proposition 3 is then replaced by the statement that the variety channel's effect on welfare is positive if and only if
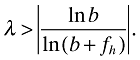
Proof. Applying the solutions from section 3, consider that
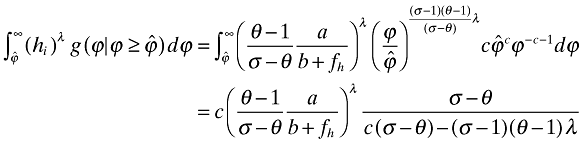
so that in any derivative towards τ(∂V/∂τ) the term λ only affects the constant term. This happens because when integrating

all terms  fall off, and λ only affects the constant of integration. Thus,
fall off, and λ only affects the constant of integration. Thus,
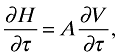
where A is a constant. As can be seen from equation (32), this constant can only alter the sign of the derivative if
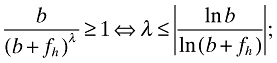
it follows that when this is not the case, ∂V/∂τ < 0 and Proposition 2 carries through unaltered for the generalized variety measure. Moreover, as V represents variety weighted by consumer preferences on substitutability, Proposition 3 becomes a direct extension of Proposition 2: whenever ∂V/∂τ < 0 holds, the variety channel of liberalization raises welfare. Whenever it does not hold, the opposite is true.□
Proposition 4 provides us with a sufficient condition for the results in the paper to go through in a general variety formulation. This can be given an interpretation in terms of elasticities if we apply
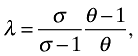
namely
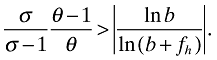
Thus, for instance, take b = 2 and fh = 2. Then the condition becomes
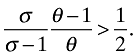
In this case an example of a sufficient parameter restriction on the elasticities is θ > 2, as this implies σ/(σ − 1) > 1, which always holds. Proposition 4 in conjunction with our benchmark for λ allow us, for any given parameterization of costs, to derive conditions on elasticities such that the main result of the paper holds, therefore.
References
Notes