Technology Diffusion through Trade with Heterogeneous Firms
Abstract
I investigate the long-run implications of trade and technology diffusion through trade, when firms are heterogeneous and trade is costly. This paper integrates firm heterogeneity and trade into a product innovation growth model from endogenous growth theory. I find that although exposure to trade increases average productivity, it has an ambiguous effect on economic growth and consumer welfare.
1. Introduction
In endogenous growth models, technological progress is driven by new designs that result from the research and development efforts of profit-maximizing agents (Romer, 1990; Grossman and Helpman, 1991a, GH hereafter; Aghion and Howitt, 1992). An important assumption in these models is that firms that use these designs to produce goods face a “common” production technology. Firm-level empirical studies, however, find the existence of large and persistent productivity differences across firms even in the same industries (Bernard and Jensen, 1999; Bernard et al., 2003).
The same production technology assumption has an important consequence in trade context. Since firms face the same technology, when exposed to trade all firms will sell their products in foreign markets. Empirical studies, on the other hand, show that even in traded sectors only some firms participate in trade and, more importantly, there is a strong correlation between firms' foreign market participation and the firms' productivity levels (Clerides et al., 1998; Bernard and Jensen, 1999).
These findings restrict the implications of these models in yet another important dimension: technology diffusion through trade. There is an influential literature in which these endogenous growth models are used to address the effects of technology diffusion through trade on growth (GH, 1991a; Rivera-Batiz and Romer, 1991, RR hereafter; Aghion and Howitt, 1998). Since the above empirical findings state that not all firms participate in trade, the technology diffusion through trade will be more limited than what these models imply. Moreover, given the strong correlation between firms' productivity levels and foreign market participation, the effects of the diffusion process may be more complicated than what these models predict.
This paper investigates the long-run effects of trade and technology diffusion through trade when firms are heterogeneous in their productivity levels and trade is costly.1 Toward this goal, I integrate Melitz's (2003) work on firm heterogeneity and trade into the product innovation (i.e. variety-expansion) endogenous growth model developed by Romer (1990). In the R&D process, labor and available technology are used. To capture the positive effects of trade on product innovation, I assume that foreign contribution to local technology increases through trade.
I find that exposure and further exposure to trade increase average productivity.2 Although trade facilitates the technology diffusion and increases average productivity, I also find that these positive effects may not be high enough to overcome its costs. Thus, exposure and further exposure to trade has an ambiguous effect on economic growth and consumer welfare.
In a recent paper, Baldwin and Robert-Nicoud (2008, BR hereafter) also study the long-run implications of trade when firms are heterogeneous. They find that greater openness produces anti- and pro-growth effects. Although their results are qualitatively similar to mine, the two papers are still different.3
The main difference is the way I formulate the technology diffusion (the knowledge flow).4 They assume that, as in RR (1991), the amount of the knowledge flow is proportional to the level of foreign knowledge. To that end, they consider different specifications for technology diffusion, but in none of them do they relate the knowledge flow to the trade volume as I did. There are several reasons to think that foreign contribution to the local knowledge stock increases with (the volume of) trade. First, the foreign knowledge is embodied in imported goods and the local producers will gain new insights from using these goods. Second, foreign purchasing agents may suggest new ways to develop new products (i.e. learning by exporting). Finally, exposure to trade increases the number of personal contracts between domestic and foreign producers, which then enhances the exchange of knowledge between countries. Indeed, based on these insights, GH (1991b) develop a technology diffusion model for a small open economy, in which the extent of spillovers from the rest of the world increases with the volume of trade.
Using trade volume is also consistent with the previous empirical studies on international R&D spillovers (Coe and Helpman, 1995; Keller, 2004). In this literature, foreign R&D spillovers are measured as the weighted average of foreign R&D stocks, where weights are constructed by using the volume of bilateral trade between countries.
2. Specification of the Model
Consumer Behavior
I assume that there is a representative agent who is endowed with fixed quantities of labor, L. His intertemporal utility is given by
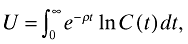(1)where ρ is the subjective discount rate and C(t) represents total consumption at time t. The agent maximizes the above utility subject to his budget constraint
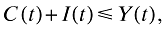(2)where I denotes investment, and Y is total output. To simplify the notation, I suppress the time arguments and I shall do so in subsequent analysis as long as it causes no confusion. I also hereafter normalize the price of final good Y to one for all t. I further assume that a no-Ponzi game condition is satisfied. The intertemporal optimization problem yields that the consumption, C, must grow according to
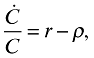(3)where r is the real interest rate.
Producer Behavior
Following Romer (1990), the production function for consumption goods is given by
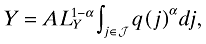(4)where Y is the final output, LY denotes labor input, q(j) represents the amount of intermediate good j used in production,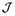 
denotes the mass of available intermediate goods; and A and α are constants with 0 < α < 1.
For expositional simplicity, it is more convenient to write the above production function as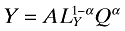 
, where Q denotes the aggregate manufacturing index for intermediate goods and is given by
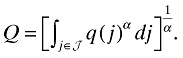
I further assume that the product market for consumption goods is competitive. The profit-maximizing strategy yields that
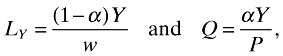(5)where w is wage rate and P denotes the aggregate price index associated with Q, and is given by
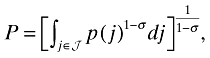(6)where p(j) is the price of brand j intermediate good and σ = 1/(1 − α) > 1 is the elasticity of substitution between any two brands. With these aggregates Q and P, the optimal quantity and expenditure levels for individual brands are
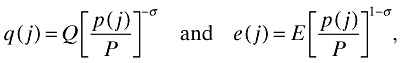(7)where E = PQ is the aggregate expenditure on intermediate goods.
Intermediate goods are produced by a continuum of monopolists, each choosing to produce a different variety. Following Melitz (2003), I assume that firms have different productivity levels indexed by ϕ > 0. More specifically, for a firm with productivity ϕ to produce q units of intermediate goods, q/ϕ units of final goods must be forgone. I also assume that goods are nondurables, i.e. they depreciate fully after use.5 Regardless of its productivity level, each firm faces a residual demand curve described in (7). Profit-maximizing behavior yields the following price rule:
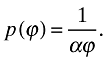(8)Given this pricing rule, firm profit is then
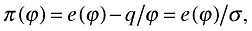(9)where e(ϕ) is expenditure on the firm's product (i.e. firm's revenue). Using this pricing rule in (7) and (9):
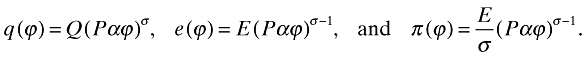(10)These equations further imply that
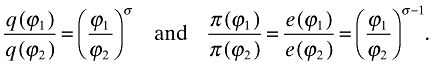(11)Hence, a more productive firm has a lower price, produces more output, and earns a higher profit than a less productive firm.
A main concern for the monopolists is the net present discounted value of profits. These net present discounted values can be found by solving the following dynamic programming problem:
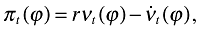(12)where ν(t) denotes the expected value of a claim to the stream of profits that accrues to a typical firm operating at time t. In steady-state, where all variables have constant growth rates, this equation further implies that
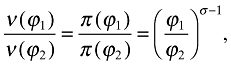(13)where the third equality follows from (11).
Aggregation
Let µ(ϕ) denote the distribution of productivity levels over a subset of (0, ∞) and n be the mass of firms. Note that µ(ϕ)dϕ is the fraction of firms who have a productivity level of ϕ, and nµ(ϕ)dϕ is the total number of firms at that productivity level. Thus, aggregate price P is given by
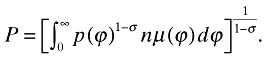(14)Using the pricing rule (8), this can be written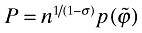 
, where
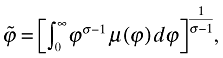(15)where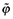 
is a weighted average of the firm productivity levels ϕ and is independent of the number of firms n. By using (11) it is straightforward to show that other aggregate variables are given by
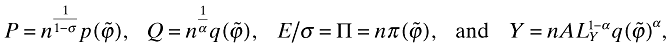(16)where Π denotes the aggregate profit of the intermediate-good sector.
Innovator Behavior and Equilibrium Dynamics
In formulating the R&D process, I will follow Romer (1990) and, to some extent, use insights provided by BR (2005). Labor and available technology (or stock of knowledge) are used in the innovation process and I assume that the stock of knowledge is approximated by the number of products, n. I also assume that the R&D sector is perfectly competitive and finances the up-front product development costs by issuing equity. This perfectly competitive sector makes and sells blueprints for new varieties.
The variety–innovation process, however, is stochastic. To develop a new variety, innovators first invest fe/n units of labor, which is sunk. Each variety is associated with a productivity level ϕ, which is randomly drawn from a common distribution φ(·), which has positive support over (0, ∞) and has a continuous cumulative distribution Φ. After learning the associated productivity level, the innovator checks the expected value of the firm that may produce this variety. With the associated productivity level ϕ, if its expected value is greater than the cost of adapting the product into the market, denoted by wfd/n, then the innovator will spend fd additional units of labor.
With this interpretation, there are two conditions. First, among the observed productivity levels, there is now a cutoff productivity level ϕ* where
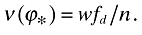(17)Only firms with a productivity level of ϕ ≥ ϕ* stay in the market, others will not be introduced. Hence, the ex-post distribution of firms productivity, ν(·), is the conditional distribution of φ(·) on [ϕ*, ∞):
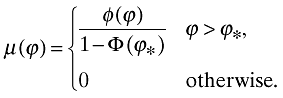
The aggregate productivity index is now given by
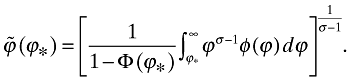(18)Second, since the R&D sector is competitive, the expected cost should equal expected profit. Note that fd/n (wfd/n) occurs if the productivity level is greater than ϕ*. Thus, expected cost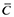 
is given by
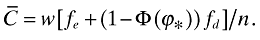(19)The ex-ante value of a firm, on the other hand, is
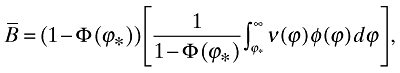(20)where 1 − Φ(ϕ*) is the ex-ante probability of successfully entering into the market and the term in square brackets is the average value of a successful firm. Thus, in competitive equilibrium
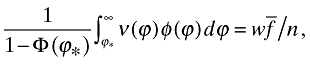(21)where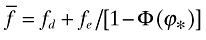 
. The left-hand side of (21) is the average value of a successful entrant, and the right-hand side is its average development cost. Thus, to expect to “produce” a new variety an innovator has to use 
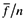units of labor.
Let Le denote the total amount of labor used by entrepreneurs in R&D, then the expected number of changes in the number of products is
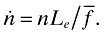(22)The dynamic evolution of this economy is now described by (3), (12), and (22), together with the two other conditions described in (17) and (21). Given the stochastic nature of the problem, analysis of this system is quite complex. I therefore confine myself to the steady-state equilibrium analysis, where the variables have constant growth rates. The steady-state analysis yields that the equilibrium cutoff level ϕ* is (see the Appendix for details):
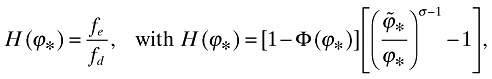(23)where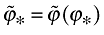 
. Using the definition of 
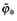in (18) implies that H(ϕ*) is a decreasing function with respect to ϕ* (Melitz, 2003). Thus, there exists a unique ϕ* that satisfies this equation. Hence, the cutoff level ϕ* is constant.
The growth rate of the economy, ga, on the other hand, is given by (see again the Appendix for details):
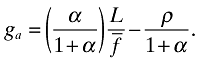(24)3. Open Economy
I now consider the impact of trade in intermediate goods in a world that is composed of two countries of the kind just analyzed. Firms wishing to export face per-unit costs (such as transport and tariffs) that do not depend on firm characteristics such as productivity. Per-unit trade costs are modeled in the standard iceberg formulation, whereby τ > 1 units of a good must be shipped in order for one unit to arrive at its destination. Because countries are symmetric, they have the same prices for final goods, which is again normalized to one, and the same mass of firms n.
Each firm's pricing rule in its domestic market is still given by pd(ϕ) = 1/αϕ. Firms who export will set higher prices in the foreign markets that reflect the increased marginal cost τ of serving these markets: px(ϕ) = τ /αϕ = τpd(ϕ). Thus, revenues earned from domestic sales and export sales to any given country are ed(ϕ) = E(Pαϕ)σ−1 and ex(ϕ) = τ1−σed(ϕ), respectively. Since π(ϕ) = e(ϕ)/σ, the combined profit of a firm, π(ϕ), is given by:
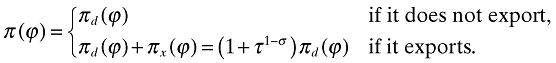(25)Innovator Behavior
The technology for product development is similar to that in the closed economy. Note that now a firm may serve in the foreign market too; in this case, however, the inventor should devote additional labor for modifying the product to meet the foreign market specifications.6 Specifically, developing a new variety now requires fe/Kn units of labor, where Kn denotes the available stock of knowledge. After developing the new variety, the innovator checks the associated productivity level ϕ. If the firm's expected value is greater than wfd/Kn with this productivity level, then the innovator will spend fd/Kn units of labor to serve this into the domestic market. If the productivity level is high enough to also cover the foreign market adaptation costs, the innovator will spend fx/Kn units of labor, in addition to fd, to serve this product into the foreign market.
In section 2, I assumed that the two countries are completely isolated and, therefore, indexed the available technology by n, i.e. Kn = n. Now they engage in trade and, as discussed in the introduction, it is plausible to think that the foreign contribution to local technology increases with trade. I will assume that the amount of technology transferred from the other country is a function of total trade (import plus export) with the other country. Thus,
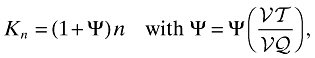(26)where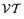 
is the value of total trade (imports plus exports) of the home country and 
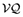is the value of intermediate goods produced at the home country (symmetry assumption ensures that these will be identical across countries). Ψ is assumed to be an increasing function.
Notice that a firm with productivity ϕ will serve in the domestic market if νd(ϕ) ≥ wfd/Kn, where νd is the value generated by domestic sales. And it will export to the other country if νx(ϕ) ≥ wfx/Kn, where νx is the value generated by foreign sales. Thus, there are two cutoff levels:
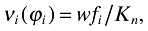(27)where i = d, x. Using πx(ϕ) = τ1−σπd(ϕ) and (11) implies the following relationship between ϕd and ϕx:
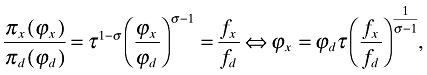(28)where ϕx > ϕd further implies that τ(fx/fd)1/σ−1 > 1 and I assume that this is the case. With these cutoffs, the value of a firm is now given by
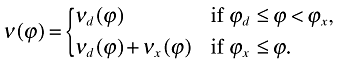(29)Since the R&D sector is competitive, it easily follows that
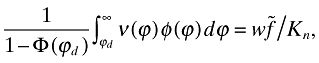(30)where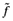 
is
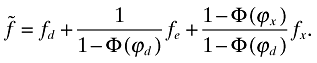(31)As in the closed-economy case, the left-hand side of (30) represents the average value of a successful entrant, and the right-hand side represents its average development cost. With this interpretation, the expected number of new products is
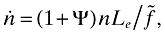(32)where Le again denotes the total amount of labor devoted to R&D.
Aggregation and Equilibrium Dynamics
Consider the aggregate price index P. Note that when trade is allowed in a given country, not only domestic but also foreign producers will sell their goods. Then P is
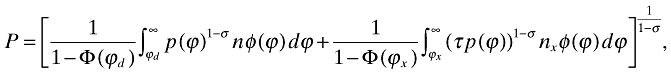
where nx is the mass of foreign firms who have sales at the home market, i.e. nx = ζxn with ζx = [1 − Φ(ϕx)]/[1 − Φ(ϕd)]. Thus, N = (1 + ζx)n represents the total mass of varieties available to consumers in each country.
Using the same function defined in (17), let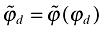 
and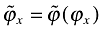 
denote the average productivity levels of all firms and exporting firms, respectively. Let 
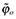be the average productivity defined as
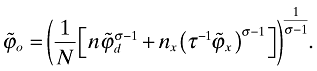
Similar to the closed-economy case, the aggregate variables are
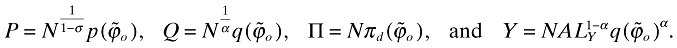(33)Furthermore, using the definitions of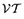 
and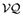 
it is straightforward to show that
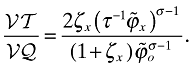(34)I will again only consider the steady-state equilibrium and let go denote the growth rate of the number of products produced in any country. In the steady-state, the cutoffs ϕd and ϕx will be related to each other as follows (see the Appendix):
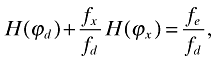(35)where H(·) is defined as in (23). Equations (28) and (35) constitute a system of two equations with two unknowns, ϕd and ϕx. H(ϕ) is a monotone-decreasing function (Melitz, 2003). Moreover, since, according to (28), ϕx is an increasing function of ϕd, equation (35) together with (28) immediately yields a unique solution for (ϕd, ϕx). Hence, the cutoff levels ϕd and ϕx are constant. To show that ϕd > ϕ*, notice that the right-hand sides of (23) and (35) are identical. For each ϕ, the left-hand side of (35), however, is greater than that of (23). Thus, ϕd > ϕ*, i.e. the cutoff level for domestic market entry is now higher than that in the closed economy. This will further imply that the average productivity will be higher in an open economy.
If there was no technology transfer through trade (i.e. Kn = n), then the intuition behind this result would be similar to that in Melitz (2003). The open economy offers new profit opportunities to firms. However, only more productive firms can benefit from such profit opportunities, since selling a new variety in the foreign market requires an additional market adaptation cost. Furthermore, the new profit opportunities induce more entry into the R&D process. Increased labor demand by the exporting firms and the R&D sector bids up the real wage and, hence, domestic market adaptation cost. Since firm value is increasing with its productivity level, an increase in the domestic market adaptation cost will yield a higher zero cutoff productivity level in equilibrium.
Existence of spillovers through trade makes the intuition behind this result more subtle. However, notice that the average value of a successful entrant is given by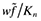 
, while the value of the firm with domestic cutoff productivity level is given by wfd/Kn. These imply that the average value of a successful entrant relative to the value of the domestic cutoff firm is 
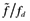. In the closed economy, on the other hand, this ratio is 
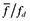. Since exposure to trade offers new profit opportunities to more productive firms, it increases the average value of a successful entrant relative to the value of the domestic cutoff firm. Thus, 
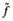will be greater than 
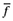. Moreover, because the relative value of firms is increasing with their relative productivity levels (see equation (16)), the previous conclusion yields that the ratio of the average productivity to the domestic cutoff productivity in the open economy is greater than that in the closed economy. Given that the average productivity is increasing with the domestic cutoff level, it follows that the domestic cutoff level in the open economy is greater than that in the closed.
The growth rate, go, is given by (see the Appendix):
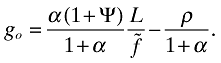(36)Subtracting (24) from this equation yields that
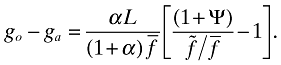(37)The sign of go − ga, then, depends on the sign of the expression in square brackets. Since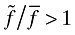 
and 1 + Ψ > 1, the ratio 
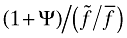may be greater than, less than, or equal to one. Thus, the sign of the expression in square brackets is ambiguous; hence, go − ga is ambiguous.
The result simply follows from the two conflicting effects of trade on the marginal productivity of labor in R&D. To see these, notice that in the open economy, the marginal product of labor in R&D is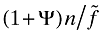 
, while in the autarky it is 
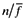. The possibility of selling a new variety in the other country, which requires additional labor, increases the demand for labor in the product development process (this is captured by 
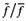). Trade, on the other hand, increases the foreign contribution to the local stock of knowledge, which then reduces the amount of labor needed to develop a new variety (this is captured by 1 + Ψ). The net effect depends on which of these two factors is dominant.
RR (1991) consider a similar specification with no firm heterogeneity or trade costs. They find that exposure to trade does not contribute to economic growth, unless there is an economic integration through which ideas can flow across countries. Specifically, they assume that after exposure to trade, the total available technology will be given by Kn = (1 + λ)n, where λ measures the degree of integration between two countries.7 This paper, however, explicitly links the degree of integration with trade and shows that exposure to trade has an ambiguous effect on growth. In addition, this paper shows that trade contributes to productivity gain. The differences stem from the firm heterogeneity and the foreign market adaptation costs of the R&D sector.
BR (2008) also study the long-run implications of trade on economic growth when firms are heterogeneous. They find that exposure to trade has an ambiguous effect on economic growth. They assume that knowledge flow is proportional to foreign knowledge stock as in RR (1991). They consider several specifications for λ, but in none of them do they link the degree of knowledge flow with trade volume. In one case, for example, they assume that λ equals the fraction of the foreign firms that engage in trade (i.e. λ = ζx). As argued in the introduction, relating knowledge flow to the volume of bilateral trade is more reasonable than relating it to the fraction of the foreign firms that engage in trade. Moreover, my approach is more consistent with the literature on international R&D spillovers (Keller, 2004).
Another important question now is how further exposure to trade affects average productivity and economic growth. Although I can analyze this problem in a general setting, I examine a specific case where productivity levels are drawn from a Pareto distribution. This will also provide more intuition about the model.
An Example: Pareto Distribution and Closed-Form Solutions
Following Helpman et al. (2004), Melitz and Ottaviano (2008), and many others in this literature, I assume that the productivity levels are drawn from a Pareto distribution:
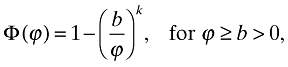
where k is the shape parameter and b is a scale parameter that bounds the support [b, +∞) from below. This distribution has a finite variance if and only if k > 2. I assume that k + 1 > σ, which ensures that the integrals in the aggregate variables converge. With this distributional assumption, I can get closed-form solutions for the variables. Using (18) with φ(ϕ) = kbkϕ−k−1, I get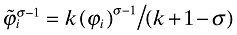 
, where i = *, d, x. Also, note that Pareto distribution implies that ζx = (ϕd/ϕx)k, and with (11) this will imply that ζx = τ−k (fx/fd)−k/(σ−1). Using these equations together with the reduced-form equilibrium conditions for cutoffs described by (23), (28), and (35), it is straightforward to show that the equilibrium cutoffs are given by
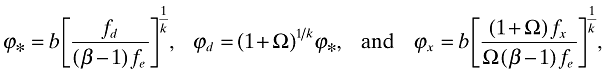
where, following BR (2005), I define β = k/(σ − 1) > 1, Ω = τ−kT1−β, with T = fx/fd. Notice that when τ and/or T decrease, Ω increases; hence, a higher value of Ω corresponds to a more open economy. Using these cutoff levels and (34):
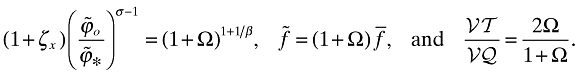
With these equations, (37) becomes
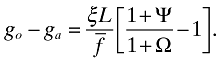
The sign of go − ga depends on the functional form of Ψ and I consider the following simple specification:
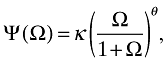
where κ and θ are positive constants. Since Ψ(Ω) is the fraction of foreign technology transferred to the home country, it must be the case that Ψ ≤ 1. Furthermore, notice that Ψ is an increasing function of Ω. Thus, κ cannot be greater than 2θ; i.e. κ ∈ (0, 2θ]. With this specification:
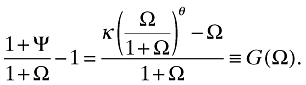
The sign of G(Ω) depends on κ[Ω/(1 + Ω)]θ − Ω: if it is positive (negative), then G(Ω) will also be positive (negative). Figure 1 represents the graph of G(Ω) for different values of (κ, θ) over Ω ∈ [0, 1]. This figure clearly shows that exposure and further exposure to trade has an ambiguous effect on growth.
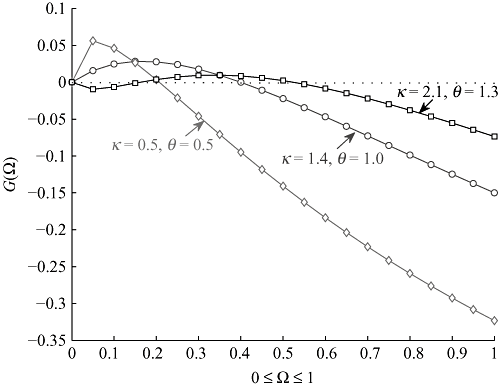
The Graphs of G(Ω) under Different (κ, θ)
4. Welfare Analysis
I begin with the welfare implications of trade and then investigate whether the growth rate of the decentralized economy is optimal.
Consumptions in the autarky and the open economy are (see the Appendix):
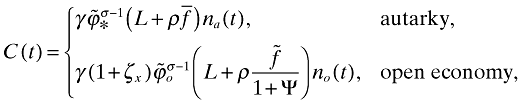(38)where γ ≡ ασ/(1 − α), and the subscripts a and o represent the autarky and the open economy, respectively. Note that except for na(t) and no(t), all other terms on the right-hand side of this equation are time-invariant in equilibrium. Thus, the coefficient in front of na relative to that in front of no measures the combined static (or level) effect of trade on welfare.
From the analyses in sections 2 and 3, it easily follows that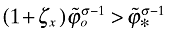 
. This basically reflects the productivity gain through trade, as in Melitz (2003) and BR (2008). The term 
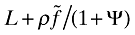relative to 
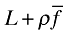, on the other hand, represents the effect of trade on LY. Since the ratio 
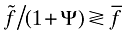, this second effect of trade is ambiguous. The first effect may not be large enough to overcome this ambiguity. As a result, the overall static effect of trade on welfare is ambiguous.
Since consumption is linear in the number of products, the dynamic (or growth) effect of trade on consumption (welfare) is measured by the changes in the growth rate of n. Since exposure to trade has an ambiguous effect on growth, the dynamic effect of trade on consumption (and welfare) is also ambiguous. Using equation (38) together with the analysis in section 3, it is easy to see that the static and dynamic effects of further exposure to trade on welfare are also ambiguous. To sum up, exposure and further exposure to trade has an ambiguous effect on welfare.
I now turn to address the second question. To do so, I will compare the market growth rate with that obtained under a social planner. The solution to the planner's problem yields the following optimum growth rates (see the Appendix):
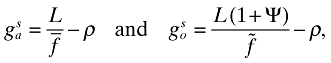
where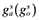 
denotes the growth rate in autarky (open economy) under the social planner.
Comparing these growth rates to those under the market economy, it is easy to see that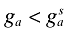 
and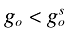 
. Thus, like the previous endogenous growth models (Romer, 1990; Aghion and Howitt, 1992), the growth rate of the market economy is suboptimal. Note that total labor allocated to R&D under the market economy is less than that in the centralized economy. As originally explained by Romer (1990), there are two reasons for this. First, a new design raises the productivity of all future researchers, but because this benefit is nonexcludable it is not reflected in the market price for designs. Second, research produces an input that is purchased by a sector that engages in monopolistic competition (Romer, 1990).
5. Concluding Remarks
I investigated the long-run effects of trade and technology diffusion through trade when firms are heterogeneous in their productivity levels. In the model, trade plays an important role as a conduit of technology diffusion. I find that although exposure to trade increases average productivity, it has an ambiguous effect on economic growth and welfare.
The present work can be extended in several ways. For example, here I only consider one single channel through which technology is diffused. Extending the model to include other channels, especially foreign direct investment, would broaden understanding of the process of technology diffusion. Another interesting avenue is to extend the model to two sectors and two factors of production, as in GH (1991a). Such an extension would give a better picture of the dynamic comparative advantage of trade.
Appendix
In the steady-state C and Y grow at the same rate and let ga (go) denote this growth rate in a closed (open) economy. By (3), ra = ga + ρ (ro = go + ρ).
Equilibrium Analysis of Section 2
To calculate the growth rate ga, first note that perfect competition in final goods implies that
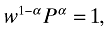((A1))and recall that the price of final good is normalized to one. This equation further implies that w = P1−σ. Second, using the optimal quantity function described in (7) together with the equations in (5), the profit equation in (9) will be π(ϕ) = αLYw[p(ϕ)/P]1−σ. Inserting w = P1−σ into this equation implies that π(ϕ) = αLYp(ϕ)1−σ = ασLYϕσ−1. Third, since the total labor supply is fixed, in the steady-state LY will be time-invariant. Moreover, since each firm's productivity level ϕ does not change over time, this implies that π(ϕ) is also time-invariant. Together with (12) implies that ν(ϕ) is time-invariant (since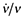 
must be constant in the steady-state). Hence, 
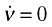in (12), which further ensures that
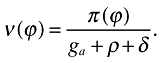((A2))Combining this with (17) implies that
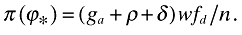((A3))As indicated in the text, only firms with ϕ ≥ ϕ* stay in the market, others will not be introduced, and the aggregate productivity index will be given by (18). Using (A2) and (A3) together with (11) in equation (21), I obtain the cutoff equation in the main text:
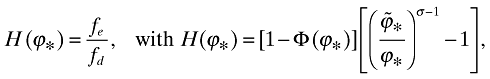((A4))where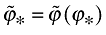 
.
To calculate the growth rate ga, first note that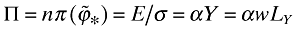 
, which implies that 
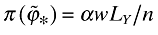. Combining this with the second equation in (A3) further implies that 
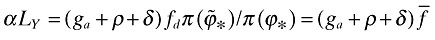, where I used (11) together with (A4). Second, 
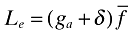from (22). These two equations together with LY + Le = L yield the expression in (24).
Equilibrium Analysis of Section 3
Note that (A1) still holds. Thus, the profit is still given by πd(ϕ) = ασLYϕσ−1. Since πx(ϕ) = τ1−σπd(ϕ), I have πx(ϕ) = ασLY(τ-1ϕ)σ−1. Productivity level ϕ is time-invariant and in the steady-state LY will be a constant function of L. Thus, profits πd(ϕ) and πx(ϕ) are also time-invariant which together with (12) imply that
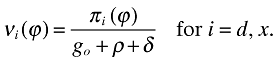((A5))Combining these with equations in (27) yields that
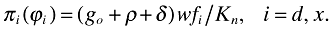((A6))Using πx(ϕ) = τ1−σπd(ϕ) and (11) yields
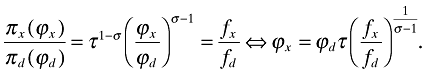((A7))Using equations (A5) and (A6) together with (11) in (29), implies (upon simplifications) the equation (35) in the main text.
To find the growth rate go, note that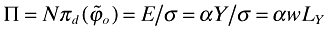 
, which further implies that 
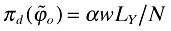. Combining this with the second equation in (A6) ensures that
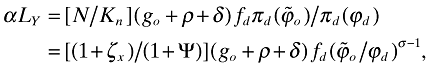
where I use N = (1 + ζx)n, Kn = (1 + Ψ)n, and (11). Notice that the definition of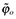 
from the main text implies that 
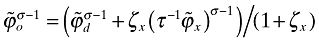. Using this together with equations (A7) and (35), I obtain that 
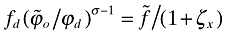; hence, 
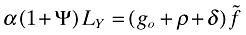. Notice that 
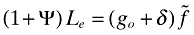from the second equation in (31). Again these equations together with LY + Le = L yield (36).
Welfare Analysis
It is easy to show that using (16) and (33) in PQ = αY implies
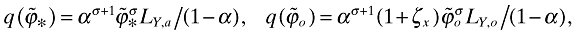
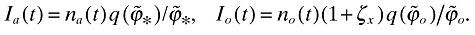
Since C = Y − I, using these equations together with Y's in (16) and (33) easily yields
where γ ≡ ασ/(1 − α). Using the growth equations in sections 2 and 3, it is easy to show that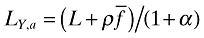 
and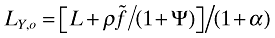 
. Inserting these into the above equation yields equation (38) in the text.
I now turn to the social planner's problem. For the sake of brevity, I will only present analysis for the closed economy (the open-economy analysis is straightforward and it is available upon request). Given the total investment I, the static allocation problem of the social planner is
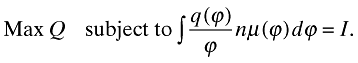
The first-order conditions imply that q(ϕ1)/q(ϕ2) = (ϕ1/ϕ2)σ. As in the previous analysis, this implies that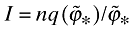 
and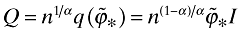 
. Thus, Y can be written as
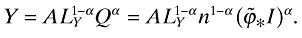
The social planner's problem is:
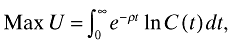
subject to
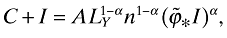
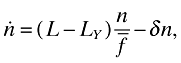
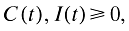
where n(0) is given. Since capital fully depreciates, I is a control variable. Thus in this problem, C, LY, and I are control variables, while n is the state variable. The corresponding Hamiltonian is given by
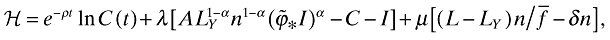((A8))where λ and µ are the time-dependent Lagrange multipliers. The optimality conditions are given by
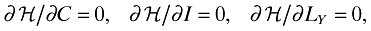((A9))
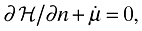((A10))
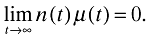((A11))The last condition represents the transversality condition.
Again, I will only consider the steady-state equilibrium. The second equation in (A9) ensures that
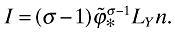((A12))This together with the third equation in (A9) implies that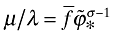 
. That is, λ and µ grow at the same rate (since 
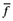and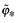 
are time-invariant in the steady-state). Furthermore, using (A12) in the production function yields
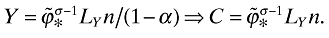((A13))Since C, I, Y, and n have the same rate (denoted by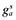 
), the first equation in (A9) implies that 
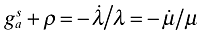. This together with (A13) and (A11) yields
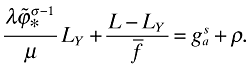
Inserting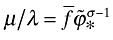 
into this equation implies 
.
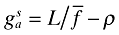