Payment Limitations and Acreage Decisions under Risk Aversion: A Simulation Approach
Abstract
Payment limits have played an important role in U.S. farm policy deliberations for the last thirty years. Current limits are largely nonbinding. Proposals to strengthen and enforce limits are currently in discussion. We evaluate the likely effects of such proposals on acreage for corn, soybeans, wheat, cotton, and rice in several important producing states. Our results generally indicate that payment limits are unlikely to significantly affect acreage in most cases; exceptions occur for cotton and rice, where the probability that limits would be binding is much greater and thus more likely to affect production.
The 2002 Farm Bill was scored by the Congressional Budget Office at $190 billion in costs to U.S. taxpayers over the ten-year period following 2002. Competing versions of the 2007 Farm Bill are scored at about $285 billion. Critics of U.S. farm programs raise a number of issues pertaining to the distortions and inefficiencies that are believed to result from government support, especially those support mechanisms which are tied to market prices or production. One complaint that is often raised about U.S. farm support pertains to its significant concentration among a relatively small number of producers. The Environmental Working Group (EWG) reports that between 1995 and 2004, the top 1% of U.S. farmers received 23% of all farm subsidies while the top 10% received 72% of subsidies (EWG 2007).
The concentration of payments is a natural consequence of the mechanisms used to distribute farm program benefits. Support is generally tied to units of production (e.g., $/bushel). Even in the case of decoupled support, which is not tied to current production, payments are based on a farmer's base acreage and yield, which in turn reflect historical patterns of production. Larger farms naturally tend to have more base acreage and thus receive larger decoupled payments.
Supporters of U.S. farm programs often make a persuasive argument advocating that support should not discriminate against large farmers who in many cases are believed to have substantial efficiency advantages arising from scale economies. At the same time, such supporters are grappling with the best means to explain very large payouts to individual farmers. For example, Kenneth Hood, then Chairman of the National Cotton Council, was quoted in 2002 as saying, “The core of our dilemma is finding a way to make the public feel good about six- and seven-figure payments to farmers” (Wahlquist 2005). The underlying rationale for such support is often rooted in a belief that U.S. agriculture is made up of large numbers of “family farms” with limited wealth and lower incomes than is the case for nonfarm households. However, although most farms remain family-run businesses, the typical commercial farm has a higher household income and substantially more wealth than the typical nonfarm household.1 In addition to questions about the merits and efficiency losses associated with such programs, the transfer of taxpayer-funded benefits to a group that tends to be relatively wealthy and in upper-income strata has been subject to considerable debate.
This debate led to discussions about legislative limits on the total amount of payments that could be made to a single farmer. Debate over payment limits characterized the 2002 Farm Bill discussions. Most recently, the Administration's 2007 Farm Bill proposal contained a rather radical proposal to exclude any producer with an adjusted gross income (AGI) over $200,000 from being eligible for any farm program payments. This “means-testing” restriction represents a significant tightening of the previous restriction, which limited AGI to $2.5 million.
Disagreements over payment limits also framed the 2007 Farm Bill debates in the Senate and House. On the Senate side provisions to tighten limits on direct payments (from $80,000 to $40,000) and counter-cyclical payments (from $130,000 to $60,000) were included in the proposed legislation, although limits on loan deficiency payments and marketing loan gains were removed. Senate debate also included reference to a “means-testing” requirement that would limit payments to only those households with adjusted gross incomes less than $750,000 per year.2 The House version of the 2007 Farm Bill proposed limiting direct payments to $60,000 per farmer and counter-cyclical payments to $65,000 per farmer, though the bill also lifted any limits on loan deficiency payments and marketing loan gains. The House version also mandated tracking of payments to individuals, eliminated the three-entity rule and made farm households with an AGI in excess of $1 million ineligible for farm program payments. Senators Grassley and Dorgan proposed an amendment to the Senate legislation that would place an overall cap of $250,000 on farm payments. This amendment, which was narrowly defeated in a vote, is identical to the binding limits considered in this analysis. A similar measure was passed as an amendment to the 2002 Senate Farm Bill but was later removed in conference negotiations.
The relative merits or shortcomings of binding payment limits aside, a very important question involves the extent to which such payments may actually have an effect on the farm economy. Existing evidence on this issue is very sparse. A recent study by the Food and Agricultural Policy Research Institute (FAPRI) concluded that for most crops changes in acreage as a result of binding payment limits would be minor (FAPRI 2003). However, their results did suggest that the cotton and rice acreage could decrease by 4–10% if payment limits were made binding. The objective of this paper is to offer empirical evidence regarding the likely effects that tighter and more strongly enforced payment limits could conceivably have on the acreage of important program crops in the United States.
An Overview of Legislative Limits on Farm Program Payments
Limits on farm payments have been in place in varying forms since the 1938 Agricultural Adjustment Act. After considerable debate during the 1960s, the 1970 Farm Bill set the limit for payments at $55,000 for wheat, feed grains, and upland cotton, implying a per-farmer limit of $165,000. Payment limits were adjusted in farm legislation throughout the 1970s and 1980s. In 1987, Congress enacted the Farm Program Payments Integrity Act, which established guidelines that required a farmer or farm operation to be “actively engaged in farming” in order to be eligible for farm program payments. This act also established the “three-entity rule,” which allows farmers to operate as three entities, collecting 100% of allowable payments on one farm entity and 50% of allowable payments on the other two farm entities. In order to be eligible for farm program payments, an individual entity must make a significant contribution of land, capital, or equipment, and this contribution must be “at risk” of financial loss. In addition an entity must be actively engaged by providing a significant service contribution to the entity's operation through labor and/or “active personal management.” One goal of the 1987 legislation was to prevent payment limits from being circumvented through the construction of financial schemes or devices.3
The provision requiring significant service contributions through active personal management has proven to be the focus of much debate over current payment limit guidelines. A recent U.S. General Accounting Office (US-GAO) report (2004) concluded that the lack of a measurable standard for “active personal management” is a weak point in legislation limiting farm program payments. In contrast to federal tax regulations, which establish a firm hour requirement for active involvement, a precise definition of the contribution necessary to establish active management involvement for payment eligibility is lacking. In addition, the US-GAO report argues that current legislation is vague in terms of defining the characteristics that an entity must display in order to be considered to be a “scheme or device” established for the purposes of evading payment limits.
The 2002 Farm Bill established a “Commission on the Application of Payment Limitations for Agriculture” to evaluate payment limit issues. The Commission released a report in 2003 that provided a comprehensive discussion of the issues and a set of broad recommendations regarding how payment limits should be implemented. The report did not, however, offer strong conclusions regarding the merits of changes to payment limit legislation.
Under current farm legislation, there are three distinct forms in which farm program payments are made. The first is through fixed direct payments (FDP), which are paid on the basis of a landowner's or farmer's holding of base acreage. In this case, there is no requirement for production—the payments can be made on idled land.4 A second form of payment, also made upon base acreage, is in the form of counter-cyclical payments (CCPs), which are triggered when market prices fall beneath a predefined target price. Again, it is important to note that such payments do not require current production. Finally, market prices are supported directly through the use of a “loan deficiency payment” (LDP) program. The LDP program pays benefits whenever market prices fall below a predetermined loan rate. These payments involve a given level of support (determined by the difference in loan rates and market prices) for each unit produced, such that more production naturally implies larger total payments.
Under current payment limit guidelines, FDP payments are limited to $40,000, CCPs to $65,000 and LDPs to $75,000. An important qualification exists on LDP limits, however. If these payments are taken in the form of generic commodity certificates or loan forfeiture gains, no limit applies.5 The use of commodity certificates has created an obvious loophole in any efforts to restrict LDPs. Under the three-entity rule, the limits on each individual form of payment imply an overall limit of $360,000 per individual, ignoring the aforementioned loophole.
Recent budgetary pressures have made payment limits the focus of discussion once again. The Administration's 2006 budget for the USDA included a proposal for binding limits on farm program payments of $250,000. As we noted above, the Administration's 2007 Farm Bill proposal advocated a means-testing limit of $200,000 in adjusted gross income to be eligible for any farm program payments. In February 2005, Senators Grassley, Dorgan, Hagel, and Johnson introduced Senate Bill 385, which called for an amendment to the 1985 legislation that would limit FDP, CCP, and LDPs to $40,000, $60,000, and $150,000 per farmer, respectively. As noted, the same general terms of this proposed legislation were included in an unsuccessful amendment to the Senate version of the 2007 legislation. The likelihood of such binding payment limits becoming law remains unclear, as supporters of farm programs in the Senate have voiced strong opposition. It is clear, however, that the issue of payment limits remains central to farm policy discussions and will undoubtedly play an important role in deliberations over the next farm bill.
Modeling Framework
Our goal is to derive inferences regarding the likely effects of strictly enforced payment limits. To do so, we apply a combination of empirical models and simulation techniques to consider the likely effects of payment limits under various market conditions. Our basic model assumes a representative agent acting to choose acreage to maximize her/his expected utility of profits. We adopt a modeling framework similar to that used by Hennessy (1998) in a consideration of the effects of decoupled program payments on production. In contrast to his analysis, our focus here is on the acreage effects of payments, and thus, we focus on acreage as the relevant decision variable. We assume that technology is linear in acreage and marginal yields are constant in the neighborhood of recommended levels of variable inputs, such that an additional acre will yield a constant addition to total output. We also assume that the recommended variable input levels reflected in extension crop budgets are optimal. This approach allows us to focus on the question of acreage impacts of payment limitations.6
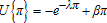(1)We assume that there are two sources of risk—prices and yields. In order to focus on single crop effects and maintain the tractability of our analysis, we focus on single crop farms. It is important to acknowledge that most farms produce multiple crops in any given year, and therefore our simulations may not perfectly mirror reality. However, the results can be extended to consider multiple crop farms. For example, a finding that neither corn nor soybeans are likely to be affected by payment limits suggests that farms producing a mix of corn and soybeans are unlikely to be impacted. Further to this point, we should also acknowledge that multiple enterprises may significantly alter the overall risk associated with total farm profits through the portfolio effects brought about by diversification. To the extent that such diversification lowers risk, acreage decisions may be altered. In this light, our analysis of optimal acreage levels may not perfectly reflect actual acreage patterns but does allow us to make crop-specific inferences about the effects of payment limits. Following convention, we assume that crop prices are log-normally distributed. We assume mean values for prices (which are adjusted in the simulations) and adopt the historical volatility measures taken from commodity exchange markets for each crop in question.7
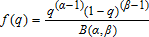(2)
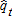and deviations from the trend 
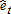. We then recenter the yields on the predicted 2004 yield by using:
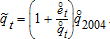(3)Simulation Analysis
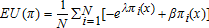(4)
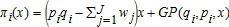(5)We chose values for the utility function that reflected estimates of risk aversion coefficients that are common in the empirical literature, λ = 1 × 10−4 and β = 5 × 10−7. In a similar exercise Hennessy (1998) chose values of about λ = 1.5 × 10−4 to λ = 6.4 × 10−5 and a value of β = 1.2 × 10−8, which implied risk aversion parameters of about 6 × 10−5. Babcock, Chalfant, and Collender (1987) estimated risk aversion parameters that ranged from 3 × 10−3 to 3 × 10−5. Kramer and Pope (1981) found values that ranged from 3 × 10−2 to 1 × 10−3. McSweeny and Kramer (1986) used absolute risk aversion parameters that ranged from 0 to 6 × 10−4. Rister, Skees, and Black (1984) obtained estimates of 1 × 10−5 to 1 × 10−8.10Meyer and Meyer (2005) have emphasized the difficulties associated with comparing measures of risk aversion across studies. They argue in favor of using relative risk aversion coefficients rather than absolute measures, but also note the problems that may arise from different definitions of outcome variables (i.e., wealth or profits). For typical Arrow-Pratt definitions of wealth such as that adopted in this study, they conclude that relative risk aversion coefficients tend to be close to but generally greater than one. Using reported profits and absolute risk aversion values, the aforementioned studies yield relative risk aversion parameter values of about 2.5–11.5 for McSweeny and Kramer (1986), 0.5–7.8 for Babcock, Choi, and Feinerman (1993), 64–1,525 for Kramer and Pope (1981), 0.01–0.11 for Rister, Skees, and Black (1984), and 4.1–9.7 for Hennessy (1998). In our simulations relative risk aversion parameters range from zero to almost 15. In order to provide results that are fully comparable across individual crops, we consider a simulation where preferences are assumed to be CARA, and absolute risk aversion parameters are adjusted to yield relative risk aversion values close to 1.0.
Prior to simulating acreage choices, we consider a simple analysis that derives the relationship between acreage and the probability of hitting the constraints imposed by strictly enforced payment limits. This is conducted in three parts. In the first, we consider the base acreage necessary to reach the proposed $40,000 fixed, direct payment limit. Fixed payments are evaluated over a range of base yields (ranging from 25% to 125% of the 2004 trend-adjusted, average yield). In a second segment of the analysis, we consider the relationship between acreage and the likelihood that the $150,000 limit on LDPs would be reached. Finally, we repeat the analysis for CCPs, deriving the relationship between acreage and the probability of hitting the $60,000 limit on CCPs. Because LDPs and CCPs depend upon market prices and, in the case of LDPs, on production, we consider four different scenarios—average prices and yields, high prices and average yields, low prices and average yields, and low prices and high yields. In the case of CCPs the yield corresponds to the base yield pertinent to direct and counter-cyclical payments. “Low” prices and yields are set at 60% of the 2004 average values, while “high” prices and yields are set at 140% of the 2004 averages.
The second segment of our analysis considers how binding payment constraints would affect the acreage decisions of representative producers. We assume that producers choose acreage levels that maximize their expected utility of profits using the aforementioned risk preference parameters. We also assume that producers follow the input recommendations implicit in the crop budgets reported by state extension services and thus limit our consideration of production decisions to the level of acreage. This simulation exercise allows us to derive the expected utility maximizing acreage as well as estimates of the probability that payment limits would be binding for representative producers of each commodity in each state of interest. We alter various parameters of the model in order to see how acreage choices and the relevant probability estimates vary under alternative estimates of price and yield variability, costs of production, and producers' attitudes toward risk.
Discussion of Data
We consider the effects of payment limits on five crops observed in six different states. In particular, we consider corn and soybeans in Indiana and Iowa, rice and cotton in Arkansas and California, and wheat in Kansas and Nebraska. This yielded a total of ten state/crop comparisons. We limit crop acreage for our individual farm to 2,000 acres for all crops except for wheat, which we limit to 4,000 acres. For conventional levels of risk aversion, these extremes were rarely reached in our simulations, and the results are not sensitive to these acreage limits.
We use unpublished crop yield data from the National Agricultural Statistics Service (NASS) of the USDA. State average crop yields for each state under consideration were collected for the period covering 1970–2004. The yields were aggregated across all practice types. In the case of wheat, we only considered winter wheat. In the case of cotton, our consideration was limited to upland cotton. Corn yields pertained to corn produced for grain (thus omitting sweet corn and silage). It is important to recognize that individual-level yields will likely be subject to considerably more variability than is the case for state-average yields. To represent such variability, we added normally-distributed random shocks to each replicated state-average yield. These random shocks had a mean of zero and a standard deviation equal to 75% of the standard deviation of the detrended state average yield.11
An example of the resulting yield distributions for Iowa corn is presented in figure 1. The light density represents the Beta density estimated for the state, while the dark density represents a kernel estimate of the state density with the adjustment to account for the additional variation likely to be experienced by an individual farm. Maximum likelihood methods were used to estimate the Beta function parameters describing yields. Table 1 presents estimates of the Beta parameters, the assumed maximum yield, assumed price volatilities, and χ2 specification tests of the Beta distribution with associated p-values. The specification tests rejects the Beta in four of the ten cases at the α = 0.05 level. In lieu of an obvious alternative and in light of the prevalence of the Beta assumption, we maintain use of the Beta for all simulations.
Production costs are also important factors influencing production decisions. We collected empirical production costs from the State Extension Services of Arkansas, California, Indiana, Iowa, Kansas, and Nebraska. Collection of crop budgets and related cost and returns data is an ongoing effort in most state extension services. The resulting production costs are presented in table 2. Of course, crop budgets and production costs are notoriously difficult to measure and thus are subject to considerable judgment on the part of the specialist constructing the measures. In addition the budgets are constructed for a representative farm using recommended production practices. It is likely that production costs and other factors (e.g., yields) vary substantially across individual producers. Two production cost issues merit special discussion. The first concerns the time-span of the production decision. What are considered to be fixed costs (e.g., machinery and managerial labor) may actually be variable if the decision is viewed to be one of a long-run choice. In contrast fixed costs are sunk in the short run, and thus are not relevant to production decisions. The treatment of rents in crop budgeting is also an important issue. In some cases rents are omitted, and the excess of revenues over the sum of other costs is viewed as a “return to land.” We do not adopt such an approach and instead view all costs as relevant to the production decision, including rents. Rents also play a key role in considerations of changes to farm programs, since rents will be expected to vary directly with government payments. In Arkansas, where rents were not reported in the budgets, average farm land rental rates from unpublished NASS data were used.
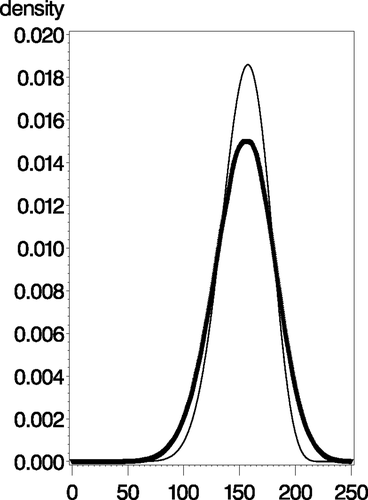
Example of estimated Beta density: Iowa corn
| Crop | State | Average Yield | Maximum Yield | α | β | χ2 Test of Beta(·) | p-value | Price Volatility |
|---|---|---|---|---|---|---|---|---|
| Corn | Indiana | 146 | 219 | 19.44 | 9.78 | 10.71 | 0.013 | 0.18 |
| Corn | Iowa | 154 | 232 | 17.35 | 8.75 | 4.50 | 0.212 | 0.18 |
| Cotton | Arkansas | 892 | 1,338 | 13.79 | 6.90 | 1.84 | 0.607 | 0.28 |
| Cotton | California | 1,365 | 2,047 | 25.04 | 12.56 | 14.39 | 0.002 | 0.28 |
| Rice | Arkansas | 63 | 94 | 52.33 | 26.17 | 5.21 | 0.157 | 0.22 |
| Rice | California | 86 | 129 | 56.12 | 28.13 | 0.28 | 0.964 | 0.22 |
| Soybeans | Indiana | 46 | 68 | 34.21 | 16.90 | 6.63 | 0.085 | 0.19 |
| Soybeans | Iowa | 46 | 69 | 30.76 | 15.63 | 11.87 | 0.008 | 0.19 |
| Wheat | Kansas | 40 | 60 | 13.95 | 7.08 | 3.72 | 0.590 | 0.21 |
| Wheat | Nebraska | 38 | 58 | 21.41 | 10.86 | 14.11 | 0.015 | 0.21 |
- a Note: The minimum and maximum possible yields are set at zero and at 150% of the trend-adjusted mean. α and β are the two shape parameters of the beta distribution. The χ2 test statistics and associated p-values consider the appropriateness of the beta distribution. The price volatilities are based on historical price data and reflect the volatility (the standard deviation of returns) implied by a Black-Scholes option pricing model.
Issues related to the measurement of costs are highlighted by a consideration of crop budgets in particular states. For example, the 2005 crop budgets and returns (which include government payments) in Iowa projected net returns of −$81 and −$43 per acre for corn and soybeans. Yet, an examination of NASS statistics indicates that 12.6 million acres of corn and 10.2 million acres of soybeans were planted in 2005 in Iowa. Some farms clearly have cost advantages, depart from recommended practices, or are motivated by other factors (such as incentives to build future base acreage). In light of these issues, several of our simulations, including our baseline case, are carried out under an assumption that costs are 60% of the levels implied by the budgets.
| Year of Budget | State | Commodity | Practice | Fixed Costs | Variable Costs | Rents | Total Costs | Expected Revenues |
|---|---|---|---|---|---|---|---|---|
| 2005 | Indiana | Corn | Following soybeans | 98.30 | 184.00 | 129.00 | 411.30 | 274.27 |
| 2005 | Iowa | Corn | Following soybeans | 63.24 | 210.86 | 140.00 | 414.10 | 333.44 |
| 2005 | Arkansas | Cotton | Roundup ready, non-irrigated | 70.48 | 313.22 | 55.00 | 438.70 | 402.42 |
| 2004 | California | Cotton | 40-in row, acala variety | 42.00 | 730.00 | 125.00 | 897.00 | 765.62 |
| 2005 | Arkansas | Rice | Silt loam soils | 64.39 | 348.52 | 78.00 | 490.91 | 475.58 |
| 2004 | California | Rice | Rice only rotation | 182.00 | 648.00 | 147.00 | 977.00 | 652.22 |
| 2005 | Indiana | Soybeans | Herbicide tolerant after corn | 98.30 | 114.00 | 129.00 | 341.30 | 238.63 |
| 2005 | Iowa | Soybeans | Herbicide tolerant after corn | 46.86 | 113.46 | 140.00 | 300.32 | 257.28 |
| 2005 | Kansas | Wheat | Wheat-fallow rotation | 102.76 | 41.91 | 59.80 | 204.47 | 119.37 |
| 2004 | Nebraska | Wheat | No-till after row crop | 72.18 | 31.82 | 55.00 | 159.00 | 116.50 |
- a Note: All costs and revenues are on a per-acre basis and, in cases where land quality is specified, represent average quality land. Expected revenues given by product of average yields and 2004 state average prices. Rental rates Arkansas were taken from National Agricultural Statistics' Service estimates.
We used state average prices for October 2004 (representing expectations of typical harvest time prices) for each commodity in each state. National prices were represented in the same manner. County loan rates for 2005 were collected from the Farm Service Administration (FSA) of the USDA. We selected representative counties which corresponded to important counties for the pertinent crop in each state. National loan rates, direct payment rates and counter-cyclical payment rates were also collected. We assumed fixed base acreage levels and adopted base yields that corresponded to 75% of the detrended state average yields over the 1970–2004 period. Relevant price and policy parameters are presented in table 3. Note that fixed, direct payments are determined by the product of the fixed payment rate, the base acreage and the base yield. Counter-cyclical payments are determined by the difference between target prices, the direct payment rate and the greater of the national loan rate or the national price. Of course, if prices exceed the target price, no counter-cyclical payments are made. Finally, LDPs are given by the difference between local loan rates and local prices.
We used the well-recognized result that rank correlation is preserved by monotonic distributional transformations and thus used draws from a correlated multivariate normal distribution to construct correlated yields (taken from a Beta marginal distribution) and prices (taken from a log-normal marginal distribution). Inverse cumulative distribution functions were used to transform correlated draws from the multivariate normal distributions to corresponding draws from the Beta and log-normal distributions. The results were not found to be especially sensitive to the assumed level of correlation (−0.20), although risk is naturally lowered by the “natural hedge” provided by negative correlation between prices and yields. Slightly lower levels of acreage would be implied by correlation coefficients that were closer to zero.12
| State | County | Local Loan Rate | National Loan Rate | 2004 Harvest National Price | 2004 Harvest State Price | Target Price | Fixed- Direct Payment Rate | Assumed Base Acreage | Assumed Base Yield |
|---|---|---|---|---|---|---|---|---|---|
| Corn | |||||||||
| Indiana | Allen | 1.950 | 1.950 | 2.150 | 1.880 | 2.630 | 0.280 | 500 | 109 |
| Iowa | Sioux | 1.830 | 1.950 | 2.150 | 2.160 | 2.630 | 0.280 | 500 | 116 |
| Cotton | |||||||||
| Arkansas | Mississippi | 0.524 | 0.520 | 0.444 | 0.451 | 0.724 | 0.067 | 650 | 669 |
| California | Fresno | 0.505 | 0.520 | 0.444 | 0.561 | 0.724 | 0.067 | 650 | 1024 |
| Rice | |||||||||
| Arkansas | Poinsett | 6.610 | 6.500 | 7.590 | 7.590 | 10.500 | 2.350 | 400 | 47 |
| California | Colusa | 6.040 | 6.500 | 7.590 | 7.590 | 10.500 | 2.350 | 400 | 64 |
| Soybeans | |||||||||
| Indiana | Montgomery | 5.110 | 5.000 | 5.560 | 5.240 | 5.800 | 0.440 | 500 | 34 |
| Iowa | Pottawattamie | 5.000 | 4.955 | 5.560 | 5.620 | 5.800 | 0.440 | 500 | 34 |
| Wheat | |||||||||
| Kansas | Reno | 2.890 | 2.750 | 3.190 | 3.000 | 3.920 | 0.520 | 500 | 30 |
| Nebraska | Cheyenne | 2.640 | 2.750 | 3.190 | 3.030 | 3.920 | 0.520 | 500 | 29 |
Two points are relevant to our treatment of counter-cyclical payments and fixed direct payments. First, these are largely determined by our assumed values for base yield and acreage. Although our assumptions are entirely consistent with typical farm conditions in the states under consideration, the degree to which limits on each of these programs are binding is largely dependent upon the values assumed for base parameters. Second, this issue is not likely to be of much consequence for acreage decisions since FDP and CCPs are decoupled from production and thus do not directly influence acreage decisions. The only avenue for fully decoupled payments to influence production would be through wealth-induced changes in risk preferences, which would be implied by declining absolute risk aversion.13
Empirical Results
Direct and Counter-Cyclical Payment Limits and Base Acreage
Table 4 presents the base acreage levels that at current direct payment rates would be required to attain the direct payment limit of $40,000. Note that direct and counter-cyclical payments are only paid on 85% of the base acreage. In our analysis, “base acreage” refers to the acreage actually eligible for earning payments (i.e., the 85% proportion) rather than the larger amount (by 17.6%) that would include base not eligible for payments. The results are, of course, dependent on base yields (which we varied from 25–125% of the state average), and thus we consider various proportions of the state average yield to represent base yields. California and Arkansas rice reach the direct payment limit with the smallest amount of acreage. With base yields set at 75% of the average, 264 acres of California rice will result in the $40,000 limit being binding. For Arkansas rice the limit is reached with 362 acres. The case is similar for cotton, where the limit is reached (at 75% of average yields) at 586 and 896 acres. In the case of corn at 75% of average yields, it takes about 1,200–1,300 acres of base to reach the direct payment limit. For soybeans much higher levels of acreage, at about 2,600 acres, are required to trigger direct payment limits. In a later section, we compare these acreage statistics to the distribution of acreage reported in the 2002 Agricultural Census. However, it is worth noting here that most production occurs on farms with less acreage than what would be required to reach the payment limits. For wheat it takes about 2,600 acres of wheat base to earn enough direct payments (paid at 75% of average yields) to trigger the $40,000 limit.
We next consider the likelihood that the $60,000 limitation on counter-cyclical payments would be triggered at alternative base acreage levels. Recall that counter-cyclical payments are triggered by market price movements and thus are not known to farmers when planting decisions are made. Therefore, we consider the probability that the proposed CCP limit would be binding at given base acreage levels and yields, conditional on the distribution of prices around the October 2004 level. Probabilities of LDP and CCP limits being binding for acreage levels ranging from 500 to 2,500 acres are presented for all of the state/crop combinations in table 5. We consider four scenarios comprised of combinations of average/high yields and low/average/high prices.
| Base Acreage to Attain Direct Payment Limit of $60,000 Yield % of Average Yield | ||||||||
|---|---|---|---|---|---|---|---|---|
| State | Crop | Payment Rate | Average Yield | At 25% | At 50% | At 75% | At 100% | At 125% |
| Indiana | Corn | 0.280 | 145.89 | 3,917 | 1,958 | 1,306 | 979 | 783 |
| Iowa | Corn | 0.280 | 154.37 | 3,702 | 1,851 | 1,234 | 925 | 740 |
| Arkansas | Cotton | 0.667 | 892.28 | 2,688 | 1,344 | 896 | 672 | 538 |
| California | Cotton | 0.667 | 1,364.74 | 1,758 | 879 | 586 | 439 | 352 |
| Arkansas | Rice | 2.350 | 62.66 | 1,087 | 543 | 362 | 272 | 217 |
| California | Rice | 2.350 | 85.93 | 792 | 396 | 264 | 198 | 158 |
| Indiana | Soybeans | 0.440 | 45.54 | 7,985 | 3,992 | 2,662 | 1,996 | 1,597 |
| Iowa | Soybeans | 0.440 | 45.78 | 7,943 | 3,972 | 2,648 | 1,986 | 1,589 |
| Kansas | Wheat | 0.520 | 39.79 | 7,733 | 3,866 | 2,578 | 1,933 | 1,547 |
| Nebraska | Wheat | 0.520 | 38.45 | 8,002 | 4,001 | 2,667 | 2,001 | 1,600 |
It is again the case that a relatively small level of cotton and rice base acreage is needed to trigger the cap on counter-cyclical payments. In the case of Arkansas cotton and rice farms with average yields and prices, the probabilities that CCP limits would be binding for a farm with 1,000 acres of base are 86% and 45%. These probabilities rise to 91% and 56% for farms with 2,000 acres of base. For cotton and rice farms with high base yields, the probability that the $60,000 limit on CCP will be binding is nearly 100%, even for farms with only 500 acres. In contrast an Iowa corn farm with 1,000 acres of base and average yields has a 24% chance of having CCP being constrained by the proposed $60,000 limit. For an Indiana corn farm with 1,000 acres of corn base, the probability of binding CCP limits is 18% at average yields and prices. The situation is similar for other crops, with the likelihood that the proposed CCP payment limit would restrict total payments remaining relatively low for farms with less than 1,000 acres of base. In the case of wheat farms, the likelihood that the proposed payment limits would be binding for farms of 2,500 base acres with average base yields is less than 25% at average prices.
| Average Price/Average Yield | Low Price/Average Yield | High Price/Average Yield | Low Price/High Yield | |||||
|---|---|---|---|---|---|---|---|---|
| Acreage | LDP | CCP | LDP | CCP | LDP | CCP | LDP | CCP |
| Indiana corn | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0086 | 0.0008 |
| 1,000 | 0.0013 | 0.1784 | 0.2257 | 0.4374 | 0.0000 | 0.0080 | 0.6327 | 0.9409 |
| 1,500 | 0.0302 | 0.4349 | 0.6991 | 0.9669 | 0.0002 | 0.0253 | 0.9005 | 0.9966 |
| 2,500 | 0.1619 | 0.5685 | 0.9446 | 0.9982 | 0.0028 | 0.0484 | 0.9806 | 0.9992 |
| Iowa corn | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0009 | 0.0081 |
| 1,000 | 0.0001 | 0.2448 | 0.0542 | 0.5683 | 0.0000 | 0.0119 | 0.2828 | 0.9554 |
| 1,500 | 0.0021 | 0.4656 | 0.3432 | 0.9737 | 0.0000 | 0.0291 | 0.6153 | 0.9969 |
| 2,500 | 0.0203 | 0.5732 | 0.7177 | 0.9981 | 0.0001 | 0.0490 | 0.8416 | 0.9991 |
| Arkansas cotton | ||||||||
| 500 | 0.0139 | 0.4552 | 0.2068 | 0.5438 | 0.0005 | 0.2214 | 0.5647 | 0.9347 |
| 1,000 | 0.2469 | 0.8584 | 0.8163 | 0.9932 | 0.0373 | 0.4707 | 0.9185 | 0.9983 |
| 1,500 | 0.4182 | 0.8926 | 0.9306 | 0.9985 | 0.0882 | 0.5236 | 0.9629 | 0.9991 |
| 2,500 | 0.5654 | 0.9113 | 0.9728 | 0.9993 | 0.1540 | 0.5657 | 0.9821 | 0.9994 |
| California cotton | ||||||||
| 500 | 0.0187 | 0.7942 | 0.3277 | 0.9878 | 0.0008 | 0.3631 | 0.5817 | 0.9971 |
| 1,000 | 0.1389 | 0.8566 | 0.7455 | 0.9979 | 0.0122 | 0.4514 | 0.8284 | 0.9985 |
| 1,500 | 0.2169 | 0.8745 | 0.8391 | 0.9984 | 0.0245 | 0.4783 | 0.8796 | 0.9988 |
| 2,500 | 0.2872 | 0.8851 | 0.8932 | 0.9988 | 0.0406 | 0.5017 | 0.9110 | 0.9987 |
| Arkansas rice | ||||||||
| 500 | 0.0000 | 0.0219 | 0.0020 | 0.0494 | 0.0000 | 0.0023 | 0.0923 | 0.9292 |
| 1,000 | 0.0078 | 0.4447 | 0.4029 | 0.9834 | 0.0001 | 0.0496 | 0.6581 | 0.9901 |
| 1,500 | 0.0427 | 0.5220 | 0.6954 | 0.9912 | 0.0006 | 0.0728 | 0.8174 | 0.9934 |
| 2,500 | 0.1129 | 0.5837 | 0.8565 | 0.9941 | 0.0031 | 0.0943 | 0.8999 | 0.9950 |
| California rice | ||||||||
| 500 | 0.0000 | 0.3291 | 0.0166 | 0.9186 | 0.0000 | 0.0272 | 0.1670 | 0.9840 |
| 1,000 | 0.0081 | 0.5077 | 0.4370 | 0.9899 | 0.0001 | 0.0682 | 0.6278 | 0.9932 |
| 1,500 | 0.0306 | 0.5644 | 0.6548 | 0.9929 | 0.0004 | 0.0868 | 0.7588 | 0.9949 |
| 2,500 | 0.0708 | 0.6070 | 0.7937 | 0.9950 | 0.0014 | 0.1049 | 0.8402 | 0.9961 |
| Indiana soybeans | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1,000 | 0.0000 | 0.0000 | 0.0242 | 0.0000 | 0.0000 | 0.0000 | 0.3001 | 0.0000 |
| 1,500 | 0.0043 | 0.0000 | 0.3840 | 0.0000 | 0.0000 | 0.0000 | 0.7331 | 0.0000 |
| 2,500 | 0.0637 | 0.0000 | 0.8354 | 0.0000 | 0.0007 | 0.0000 | 0.9314 | 0.3571 |
| Iowa soybeans | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1,000 | 0.0000 | 0.0000 | 0.0072 | 0.0000 | 0.0000 | 0.0000 | 0.1485 | 0.0000 |
| 1,500 | 0.0009 | 0.0000 | 0.2073 | 0.0000 | 0.0000 | 0.0000 | 0.5328 | 0.0000 |
| 2,500 | 0.0195 | 0.0000 | 0.6699 | 0.0001 | 0.0001 | 0.0000 | 0.8302 | 0.3802 |
| Kansas wheat | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1,000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0004 | 0.0001 |
| 1,500 | 0.0000 | 0.0004 | 0.0014 | 0.0009 | 0.0000 | 0.0000 | 0.0711 | 0.2958 |
| 2,500 | 0.0026 | 0.2364 | 0.1943 | 0.6424 | 0.0000 | 0.0176 | 0.5195 | 0.9419 |
| Nebraska wheat | ||||||||
| 500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1,000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1,500 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0065 | 0.1736 |
| 2,500 | 0.0001 | 0.2185 | 0.0406 | 0.5988 | 0.0000 | 0.0150 | 0.2579 | 0.9597 |
In short the results again suggest that cotton and rice farms are the most likely to be constrained by limits on the total amount of counter-cyclical payments that can be received. Limits on CCPs become binding at lower levels of cotton and rice acreage than is the case for corn, wheat, and soybeans. It is important again to note that the likelihood that counter-cyclical payment limits will be relevant depends on the price level as well as the base yield. If we set the mean of prices at 140% of the October 2004 level, the probabilities that the CCP limit will be binding fall considerably. Naturally, any policy based upon the deviation of market prices from target prices will be less likely to trigger payments when market prices are expected to be high.
Loan Deficiency Payments
We also considered the likelihood that the proposed $150,000 limit on LDPs would be binding. Note that LDPs are paid on the basis of market prices, actual acreage, and actual yields. Because LDPs are based upon both current yields and prices (both of which are uncertain), the variability of LDPs will be higher than is the case for CCPs. Again, we evaluate the probability that payment limits will be attained for different yield and price conditions. For prices centered around the October 2004 levels and with yields at average levels, there is little likelihood that the $150,000 cap on payments will be binding, even for farms with substantial acreage. The largest probabilities occur for Arkansas and California cotton, at 57% and 29%. In the case of high yields and low prices (the “worst-case” scenario in terms of triggering payments), the likelihood that LDP limits will be binding becomes substantially larger at lower acreage levels. In the case of corn, the likelihood that LDP limits will hit the $150,000 cap reaches 50% at about 1,000 acres. In particular for 1,000 acres of production, the probability of reaching the LDP limit ranges from 28% for Iowa corn to 63% for Indiana corn. In the case of soybeans, the equivalent probabilities are much smaller for 1,000 acres of production, ranging from 15% to 30%. The probability of binding LDP limits at low prices and high yields reaches 50% at about 1,200–1,500 acres of soybeans. In the case of wheat, it takes 2,500 or more acres to result in a 50% probability of binding LDP limits.
For cotton and rice, it is again the case that a much smaller level of acreage results in nontrivial probabilities of limits constraining LDPs. In the case of high yields and low prices, the probability that the LDP limit will be binding reaches 50% at about 250–300 acres of cotton. The situation is similar for rice, although it takes approximately 750 acres to result in a 50% probability that the limits would be binding. For 1,000 acres of cotton or rice, the probability that LDPs would be limited by the proposed payment restrictions ranges from 63% to 90%.
In all, our results illustrate the relationship between acreage (both current and base) and the probability that payment limits will be relevant. Of course, this relationship depends critically on other important policy parameters and market conditions. This simple exercise demonstrates that among the crop-state combinations that we considered, the likelihood that payment limits would be binding is highest for cotton and rice in Arkansas and California. In every case, it takes less acreage to trigger payment limits for these crops. It appears that under typical price conditions the limit on counter-cyclical payments is met at smaller levels of base acreage than the limit on direct payments. However, the likelihood that CCPs will be received is intimately tied to the distribution of prices. The likelihood that payment limits will be binding is small in high-price years. Finally, we derive the relationships between LDP limit probabilities and acreage. Again, this probability depends on current yields and market prices.
Acreage Decisions under Uncertainty
In the second segment of our analysis, we defined utility of profit functions for each of the 10 state/crop combinations. Our simulations adopted the costs taken from the state crop budgets and the 2004 harvest-time prices to represent expected prices. The maximum available acreage was limited to 2,000 acres in all cases except for wheat, in which case we allowed 4,000 acres which restricted the search domain for the expected utility maximizing level of acreage. As we have noted, these limits were rarely reached and thus the results are not sensitive to our choice of maximum farm size.14 Of course, a smaller amount of available acreage would result in the size constraint being met more frequently and therefore would imply less acreage and a smaller likelihood of payment limits being binding.
We considered a number of simulation scenarios. In our baseline scenario (Scenario 1), we assumed that all production costs, rents, and market prices were 60% of the levels reported in the crop budgets.15 This could represent farms with substantial efficiency advantages or lower rents operating in low price conditions. It could also represent farms that are only operating to cover their variable production costs (assuming that actual fixed costs are 40% of total costs).16 It is in such a low price situation that we expect payments to be high since LDPs and CCPs are triggered by low prices. In Scenario 2, we maintain assumptions regarding low costs and rents and examine a high price environment—where prices are expected to be 140% of 2004 harvest-time levels. In Scenario 3, we assume low prices, rents and production costs and examine a farm with above average yields—at 140% of the state average. In such a case the combination of high yields and low prices should result in the largest payment outlays. In Scenario 4, we again assume low prices, rents, and costs with normal yields but CARA preferences and a high degree of risk aversion. Scenario 5 repeats this CARA analysis, although with risk preferences adjusted to result in relative risk aversion coefficients of about 1.0 for each of the crops. Finally, in Scenario 6 we repeat the same experiment under the assumption that producers are risk neutral and thus choose to maximize profits.
Following the procedures outlined above, we simulated correlated prices and yields for each state/crop combination and then estimated the expected utility maximizing level of acreage for each of the seven scenarios outlined above. Results are presented in table 6. In each case, we present the optimal acreage level, expected payment receipts under each of the three programs (i.e., LDP, FDP, and CCP), and absolute (ρA) and relative (ρR) risk aversion coefficients at the expected utility maximizing level of production. Perhaps of greatest interest are estimates of the probabilities that payment limits will be binding. These estimates are calculated by considering the proportion of replications for which each respective payment limit is found to be binding at the expected utility maximizing acreage. Our simulations are conducted under the payment limits recently proposed in the Senate—$150,000 for LDP and marketing loan gains, $60,000 for counter-cyclical payments, and $40,000 for fixed direct payments.
The first scenario considers production at average yields and with prices and costs set at 60% of the values reported in table 2. This represents the actions of a typical producer (having risk preferences similar to those reported elsewhere in the literature), with advantages over the production costs reported in state budgets (or a producer covering only her/his variable costs), operating in a low price environment. This represents a rather extreme low price environment, with corn prices averaging about $1.25 per bushel. The fact that mean prices are 40% lower than those realized in 2004 suggests that expected policy benefits should play an important role in determining production. In the case of corn in Iowa and Indiana, about 186–213 acres of corn would be planted by the representative producer. In comparison, Agricultural Census statistics, which are discussed below, suggest an average of about 240 acres of corn on the typical farm in these states. Total farm payments on the order of $55,000–$63,000 would be anticipated by the representative farmer. Although loan deficiency payments figure prominently in making up total payments, there is very little probability that the proposed payment limits would be binding and affect production.
| Variable | Indiana Corn | Iowa Corn | Arkansas Cotton | California Cotton | Arkansas Rice | California Rice | Indiana Soybeans | Iowa Soybeans | Kansas Wheat | Nebraska Wheat |
|---|---|---|---|---|---|---|---|---|---|---|
| Baseline Scenario: low costs, rents, and prices | ||||||||||
| Acres | 213 | 186 | 609 | 437 | 1,241 | 0 | 343 | 546 | 0 | 265 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 21,737 | 23,141 | 59,452 | 59,876 | 30,547 | 41,896 | 6,066 | 6,070 | 9,626 | 9,306 |
| LDPs | 25,727 | 15,644 | 123,192 | 97,489 | 123,976 | 0 | 30,977 | 40,239 | 0 | 8,567 |
| Total payments | 62,725 | 55,025 | 211,779 | 197,365 | 194,523 | 81,896 | 44,523 | 53,789 | 17,426 | 25,414 |
| Profits | 44,942 | 45,739 | 196,805 | 161,181 | 181,493 | 81,896 | 23,102 | 39,218 | 17,426 | 18,549 |
| LDP limit | 0.0000 | 0.0000 | 0.4228 | 0.2158 | 0.5812 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.9962 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 6.91E−05 | 6.74E−05 | 5.67E−11 | 2.00E-09 | 2.62E−10 | 5.26E−06 | 9.52E−05 | 7.98E−05 | 9.72E−05 | 9.69E−05 |
| ρR(profit) | 3.1048 | 3.0809 | 0.0000 | 0.0003 | 0.0000 | 0.4307 | 2.1994 | 3.1313 | 1.6942 | 1.7974 |
| Scenario 2: low costs and rents with high prices | ||||||||||
| Acres | 385 | 476 | 455 | 655 | 2,000 | 616 | 815 | 1,508 | 364 | 1,107 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 983 | 1,000 | 28,003 | 26,968 | 1,965 | 2,704 | 121 | 128 | 517 | 503 |
| LDPs | 485 | 27 | 10,402 | 3,980 | 1,231 | 169 | 503 | 216 | 173 | 134 |
| Total payments | 16,728 | 17,268 | 67,540 | 70,948 | 43,196 | 42,873 | 8,104 | 7,823 | 8,490 | 8,177 |
| Profits | 68,456 | 119,620 | 201,144 | 414,280 | 779,907 | 241,621 | 112,041 | 276,261 | 24,178 | 82,087 |
| LDP limit | 0.0000 | 0.0000 | 0.0002 | 0.0031 | 0.0018 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.3618 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 1.75E−05 | 1.27E−07 | 3.68E−11 | 2.04E−20 | 2.69E−36 | 6.42E−13 | 2.72E−07 | 2.01E−14 | 9.47E−05 | 5.16E−06 |
| ρR(profit) | 1.2013 | 0.0152 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0304 | 0.0000 | 2.2894 | 0.4239 |
| Scenario 3: low costs, rents, and prices with high yields | ||||||||||
| Acres | 576 | 518 | 646 | 600 | 1,799 | 622 | 1,000 | 1,225 | 408 | 1,088 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 21,738 | 23,142 | 59,452 | 59,876 | 30,543 | 41,893 | 6,066 | 6,069 | 9,627 | 9,307 |
| LDPs | 96,689 | 60,903 | 139,138 | 126,081 | 138,158 | 101,802 | 118,423 | 114,413 | 25,125 | 49,258 |
| Total payments | 133,687 | 100,285 | 227,725 | 225,956 | 208,701 | 183,695 | 131,969 | 127,963 | 42,552 | 66,105 |
| Profits | 123,280 | 115,688 | 273,720 | 285,388 | 394,362 | 158,353 | 126,666 | 170,413 | 33,099 | 68,173 |
| LDP limit | 0.0467 | 0.0015 | 0.7655 | 0.6783 | 0.8575 | 0.3334 | 0.2968 | 0.3389 | 0.0000 | 0.0000 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.9962 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 8.84E−08 | 1.89E−07 | 2.59E−14 | 8.07E−15 | 1.49E−19 | 2.65E−09 | 6.31E−08 | 7.95E−10 | 8.80E−05 | 1.80E−05 |
| ρR(profit) | 0.0109 | 0.0218 | 0.0000 | 0.0000 | 0.0000 | 0.0004 | 0.0080 | 0.0001 | 2.9113 | 1.2245 |
| Scenario 4: low costs, rents, and prices with CARA preferences and high risk aversion | ||||||||||
| Acres | 169 | 143 | 236 | 153 | 652 | 0 | 333 | 514 | 0 | 258 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 21,738 | 23,141 | 59,448 | 59,879 | 30,543 | 41,903 | 6,066 | 6,070 | 9,625 | 9,306 |
| LDPs | 20,436 | 11,983 | 54,071 | 36,386 | 84,838 | 0 | 30,080 | 37,878 | 0 | 8,335 |
| Total payments | 57,433 | 51,365 | 142,654 | 136,265 | 155,382 | 81,903 | 43,627 | 51,429 | 17,425 | 25,182 |
| Profits | 43,322 | 44,256 | 136,892 | 123,581 | 148,637 | 81,903 | 22,845 | 37,742 | 17,425 | 18,503 |
| LDP limit | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0541 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.9963 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 | 1.00E−04 |
| ρR(profit) | 4.3382 | 4.4257 | 13.6957 | 12.2968 | 14.9047 | 8.2537 | 2.2881 | 3.7660 | 1.7550 | 1.8558 |
| Scenario 5: low costs, rents, and prices with CARA preferences and comparable relative risk aversion | ||||||||||
| Acres | 884 | 947 | 806 | 510 | 1,235 | 0 | 1,149 | 1,689 | 0 | 514 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 21,738 | 23,141 | 59,452 | 59,879 | 30,549 | 41,894 | 6,066 | 6,070 | 9,626 | 9,307 |
| LDPs | 105,010 | 78,945 | 135,861 | 106,742 | 123,805 | 0 | 102,160 | 113,325 | 0 | 16,626 |
| Total payments | 142,009 | 118,326 | 224,448 | 206,622 | 194,354 | 81,894 | 115,706 | 126,874 | 17,426 | 33,473 |
| Profits | 68,277 | 71,272 | 204,801 | 164,378 | 181,401 | 81,894 | 44,074 | 81,789 | 17,426 | 20,152 |
| LDP limit | 0.1035 | 0.0356 | 0.6880 | 0.3445 | 0.5774 | 0.0000 | 0.0946 | 0.3234 | 0.0000 | 0.0000 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.9962 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 1.45E−05 | 1.40E−05 | 4.90E−06 | 6.10E−06 | 5.50E−06 | 1.21E−05 | 2.23E−05 | 1.23E−05 | 5.70E−05 | 5.00E−05 |
| ρR(profit) | 0.9900 | 0.9978 | 1.0035 | 1.0027 | 0.9977 | 0.9909 | 0.9828 | 1.0060 | 0.9933 | 1.0076 |
| Scenario 6: low costs, rents, and prices with risk neutrality | ||||||||||
| Acres | 993 | 1,350 | 928 | 569 | 1,771 | 0 | 1,300 | 1,947 | 0 | 2,878 |
| Direct payments | 15,260 | 16,240 | 29,135 | 40,000 | 40,000 | 40,000 | 7,480 | 7,480 | 7,800 | 7,540 |
| CCPs | 21,737 | 23,139 | 59,453 | 59,882 | 30,545 | 41,889 | 6,066 | 6,070 | 9,626 | 9,307 |
| LDPs | 115,045 | 105,006 | 139,749 | 112,490 | 133,453 | 0 | 112,655 | 121,721 | 0 | 90,809 |
| Total payments | 152,042 | 144,385 | 228,337 | 212,372 | 203,998 | 81,889 | 126,201 | 135,271 | 17,426 | 107,656 |
| Profits | 69,276 | 77,101 | 205,633 | 165,203 | 185,520 | 81,889 | 45,131 | 83,327 | 17,426 | 33,082 |
| LDP limit | 0.2140 | 0.2514 | 0.7802 | 0.4358 | 0.7665 | 0.0000 | 0.2110 | 0.4654 | 0.0000 | 0.1083 |
| CCP limit | 0.0000 | 0.0000 | 0.0000 | 0.9963 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| FDP limit | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| ρA(profit) | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| ρR(profit) | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
- a Note: ρA and ρR represent absolute and relative risk aversion coefficients evaluated at expected profits.
Scenario 2 considers a high price environment characterized by low costs of production. In particular, prices are set at 140% of the 2004 harvest values and production costs are again lowered by 40%. In this case, corn producers again find it profitable to engage in significant levels of corn production. The levels of corn production implied by low costs and low prices, with deficiency payments, are quite similar to those implied by low costs in a high market price environment, with 385–476 acres being produced in the latter case. Again, there is little chance that payment limits would influence corn production since market prices are high.
The third scenario considers a low price environment together with high yields and low production costs. This represents the “worst case” scenario in terms of the effect of payment limits. Production is higher in both states and the probability that limits on LDPs would affect production rises slightly, although it still remains very small. In the case of Indiana corn, 576 acres of corn would maximize expected utility, and the likelihood that LDP limits would be binding is 5%. In Iowa, 518 acres of corn are produced, and there is less than a 1% chance that LDP limits would be binding. These results are driven by the combination of very low prices and very high yields.
The fourth and fifth scenarios maintain the low price and cost conditions and examine how risk aversion assumptions affect corn production. In Scenario 4, we assume that absolute risk aversion is constant across levels of income (wealth) and that agents are considerably more averse to risk. The implied coefficient of absolute risk aversion is at the larger end of the spectrum of what is typically found in empirical studies. The effects of this stronger aversion to risk are apparent in the much smaller acreage levels that maximize expected utility. Corn acreage in Indiana and Iowa falls to about 150 acres. Note that the relative risk aversion coefficients are about 4.3, representing a strong degree of relative risk aversion. There is almost no likelihood that the proposed payment limits would be binding.
In Scenario 5, we adjust the absolute risk aversion parameters to yield relative risk aversion coefficients at the expected utility maximizing levels of production that are approximately 1.0. This significantly raises the level of corn production, resulting in 880–950 acres. The probability that loan deficiency payment limits will be binding also rises, ranging from 4% for Iowa to 10.4% for Indiana. Total profits range from $68,000 to $71,000.
In Scenario 6, we assume that agents are risk neutral. In such a case, the only items that limit production are production costs and the limit on payments. As expected in such a case, larger acreage levels are chosen by agents—993 acres in Iowa and 1,350 acres in Indiana, and the likelihood that LDP limits will be binding is about 25%.
In all, the results do not suggest that enforcement of payment limits would have a significant effect on corn producers in the states considered. The limits have very modest effects on acreage, even in cases of very low expected prices. Likewise, the probability that payment limits will be binding is small even for large corn farms. In short our results would seem to imply that binding payment limits would have little effect on corn production in the major producing states of Iowa and Indiana.
Table 6 also presents simulation results for cotton and rice production in Arkansas and California. Many observers have noted that these crops and states are the most likely to be affected by limits on payments. This is implied by the substantial payments that are typically made on these crops. Our baseline scenario suggests that there is a significant likelihood that payment limits would be binding on production, at least for cotton and Arkansas rice. The simulations suggest production of about 400–600 acres of cotton and 1,241 acres of rice in Arkansas. The probability that loan deficiency payment limits will be binding ranges from 22% for California cotton to 42% for Arkansas cotton. In the case of Arkansas rice, the probability that LDP limits will be binding is over 58%. No production of rice in California is implied for the baseline scenario, which reflects the high production costs. Under our assumed direct payment levels, the limits are binding for California cotton and rice and for Arkansas rice.17 The likelihood that CCP limits will be binding is very high for California cotton.
In a production environment characterized by low production costs and high prices, similar levels of cotton and rice acreage are implied, with the exception that California rice production is now profitable. The likelihood that LDP and CCPs will affect production falls dramatically in light of the high market prices. A situation of low costs of production, low prices, and high yields corresponds to similar levels of acreage. The likelihood that cotton and rice acreage will be constrained by binding payment limits becomes very significant. In particular, the probability that LDP limits will be met is 33% for California rice, 68% for California cotton, 86% for Arkansas rice, and 77% for Arkansas cotton. Lower acreage levels occur when producers have CARA preferences with a higher degree of risk aversion, and the likelihood that LDP limits will be binding falls accordingly. However, when the parameters underlying the CARA preferences are adjusted to yield relative risk aversion coefficients of 1.0, higher acreage levels are suggested, with an exception occurring for California rice, which is again unprofitable. The probability that LDP limits will be binding ranges from 34% for California cotton to 69% for Arkansas cotton. In the case of risk neutral producers with low costs and prices, high levels of acreage occur and the probability that LDPs will be constrained becomes substantial. An exception occurs for California rice, which is again not profitable to produce.
In short the likelihood that payment limits will have an effect on the acreage of cotton and rice is substantially higher than was the case for corn. An exception occurs for California rice production. In a result that largely reflects the relatively high costs of production, the simulation results suggest that it is not optimal to produce substantial amounts of rice in California unless prices and yields are far above the average. In this case, there is a significant chance that production decisions will be influenced by LDP limits.
In the case of soybeans, the results are very similar to those obtained for corn. In situations characterized by very low costs and prices, acreage allocations range from 343 to 546 acres, although there is little chance that payment limits will be binding. In a case of high yields combined with low prices and costs of production, acreage rises to about 622–1,000 acres, and the probability that LDP limits will be binding rises to about 30%. Thus, it is only in cases of very high yields combined with very low prices that production decisions would be affected by LDP limits. There appears to be little likelihood that CCP limits will be binding, at least given our assumed levels of base.
Finally, table 6 presents simulation results for Kansas and Nebraska wheat. Dryland wheat production in these states is often undertaken on large farm operations. In this light, we allow the maximum farm size to be 4,000 acres in these two cases. The simulation results suggest that in a low cost and price environment, 265 acres of wheat will be produced in Nebraska although production in Kansas is unprofitable. In a case of low costs and high prices, production is profitable in both states, and there is little likelihood of payment limits being binding. In the case of greatest interest, with low costs and prices and high yields, acreage rises significantly in both states, but is much larger in Nebraska. In this case, with 1,088 acres of wheat being produced, the likelihood that LDP limits will be binding remains very low. The largest level of wheat acreage occurs for Nebraska under the risk neutrality scenario, where 2,878 acres of wheat are produced. Even in this case, the likelihood that LDP limits will be binding remains very low at only 11%.
Perhaps the most direct means of summarizing the potential impacts of binding payment limits lies in a simple consideration of how expected utility maximizing acreage choices might differ when payment restrictions are binding in comparison to when there are no binding limits on payments. To consider this point, we reran the simulations for the case most relevant to binding payment limits—low prices and costs with high yields—without any restriction on payment benefits and compared expected utility maximizing acreages to those implied under payment limits. We also considered the risk neutral case, which essentially eliminates the curvature implied by the risk aversion parameters. Table 7 summarizes the results. As we noted above, for a risk neutral farmer, no limits on payments should imply either zero production or production on all available acres. Table 7 presents expected utility maximizing acreage with the payment restrictions (repeated from the previous table) and without restrictions on payments, along with the absolute and percentage differences between the two.
For conventional levels of risk aversion based on estimates in the empirical literature, the imposition of payment limits does not tend to have a substantial impact on acreage. The increases in acreage implied by the removal of binding limits are modest in most cases. Of course, this demonstrates the importance of risk aversion and price and yield risk as factors determining acreage. Consistent with our earlier simulation findings, the removal of payment limits tends to have the most significant impact on cotton and rice acreage in Arkansas and California. In the case of Arkansas cotton and rice under the risk averse case, removal of binding payment limits increases acreage by 7–10%. For California cotton and rice, acreage would increase by about 24%. These increases are substantially higher under risk neutrality.
| State/Crop | Scenario | With Limits | Without Limits | Difference | Percentage Difference |
|---|---|---|---|---|---|
| Indiana corn | Low costs, prices, and high yields with risk aversion (No. 3) | 576 | 582 | 6 | 1.03 |
| Low costs and prices with risk neutrality (No. 6) | 993 | 2,000 | 1,007 | 50.35 | |
| Iowa corn | Low costs, prices, and high yields with risk aversion (No. 3) | 518 | 518 | 0 | 0.00 |
| Low costs and prices with risk neutrality (No. 6) | 1,350 | 2,000 | 650 | 32.50 | |
| Arkansas cotton | Low costs, prices, and high yields with risk aversion (No. 3) | 646 | 697 | 51 | 7.32 |
| Low costs and prices with risk neutrality (No. 6) | 928 | 2,000 | 1,072 | 53.60 | |
| California cotton | Low costs, prices, and high yields with risk aversion (No. 3) | 600 | 761 | 161 | 21.16 |
| Low costs and prices with risk neutrality (No. 6) | 569 | 2,000 | 1,431 | 71.55 | |
| Arkansas rice | Low costs, prices, and high yields with risk aversion (No. 3) | 1,799 | 2,000 | 201 | 10.05 |
| Low costs and prices with risk neutrality (No. 6) | 1,771 | 2,000 | 229 | 11.45 | |
| California rice | Low costs, prices, and high yields with risk aversion (No. 3) | 622 | 814 | 192 | 23.59 |
| Low costs and prices with risk neutrality (No. 6) | 0 | 0 | 0 | — | |
| Indiana soybeans | Low costs, prices, and high yields with risk aversion (No. 3) | 1,000 | 1,082 | 82 | 7.58 |
| Low costs and prices with risk neutrality (No. 6) | 1,300 | 2,000 | 700 | 35.00 | |
| Iowa soybeans | Low costs, prices, and high yields with risk aversion (No. 3) | 1,225 | 1,293 | 68 | 5.26 |
| Low costs and prices with risk neutrality (No. 6) | 1,947 | 2,000 | 53 | 2.65 | |
| Kansas wheat | Low costs, prices, and high yields with risk aversion (No. 3) | 408 | 408 | 0 | 0.00 |
| Low costs and prices with risk neutrality (No. 6) | 0 | 0 | 0 | — | |
| Nebraska wheat | Low costs, prices, and high yields with risk aversion (No. 3) | 1,088 | 1,088 | 0 | 0.00 |
| Low costs and prices with risk neutrality (No. 6) | 2,878 | 4,000 | 1,122 | 28.05 |
Overall, several important conclusions emerge from our simulation analysis. The payment limits recently considered in the Senate would not be likely to have a significant effect on the acreage (and by implication on production) of corn, soybeans, or wheat. The situation is different in the case of cotton and rice. For such commodities payment limits could have a more significant effect on acreage decisions and thus on output. An exception occurs for California rice, which has a very high cost of production due to high rents. These results are conditional on our estimates of risk aversion, which are based on results presented elsewhere in the professional literature as well as on our own estimates of price and yield risks.
Framing the Results
Our simulation analysis has revealed that for most state/commodity combinations that were considered, the probabilities that the typical producer would be constrained by policy changes that made payment restrictions binding are quite low. Exceptions occurred for cotton and rice in Arkansas and California. In an analogous fashion, the results also suggested that a considerable level of acreage would need to be in production in order for payment restrictions to be binding. In order to place these results into a proper perspective, it is important that we consider the size distribution of farms for the crops and states considered.
We collected acreage and size distribution statistics from the 2002 Agricultural Census. Figure 2 presents the cumulative distributions of acreage for each crop-state combination considered. The size distribution data, along with other relevant Census statistics, are presented in table 8. We calculated the proportions of total acreage and total production in the state that were represented by farms of each size category as well as the proportion of total farms in each category. The table includes the share of total production in 2002 that came from farms in each size category.18
The figures demonstrate that total acreage tends to be concentrated on smaller farms for corn and soybeans than is the case for other crops. About 50–60% of corn and soybean acreage (and production) tends to be on farms of 500 acres or less. The size distribution of California rice farms tends to be similar, with about 49% of the acreage being on farms of 500 acres or less. Likewise for Nebraska wheat farms, about 49% of the acreage is on farms of 500 or fewer acres. In contrast, Kansas wheat farms tend to be larger, with only 37% of the acreage being on farms of 500 or less acres and 67% of the total acreage on farms of 1,000 or fewer acres. Arkansas rice and cotton farms in both Arkansas and California tend to be the largest. In the case of Arkansas cotton farms, only 12.5% of the total state acreage in 2002 was on farms of 500 or fewer acres, and only 35% of the total acreage was on farms of 1,000 or fewer acres. In the case of Arkansas rice farms, 35% of the acreage was on farms of 500 or fewer acres while 67% of the acreage was on farms of 1,000 acres or less. This is very similar to the size distribution of Kansas wheat farms, although recall that it takes far fewer acres of rice to result in binding payment limits than is the case for wheat. California cotton acreage is also relatively concentrated among larger farms, with 30% of the total acreage being on farms of 500 or fewer acres and 53% of the acreage on farms of 1,000 or fewer acres. Put differently, only about 10–25% of the acreage of corn and soybeans tends to be on farms over 1,000 acres, while 65% of Arkansas cotton acreage and 47% of California cotton acreage is on farms of 1,000 or more acres. This suggests that the largest effects of binding payment limits would likely be realized by rice farms in Arkansas and cotton farms in Arkansas and California.
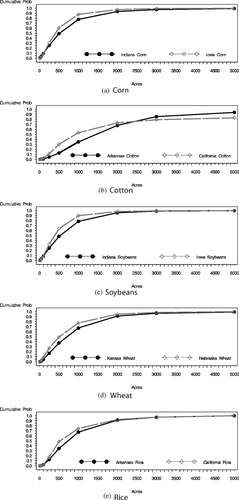
Implied cumulative distribution functions (cdf) of farm size
| State/Crop (Units) | Acreage Size Category | Implied Average Size | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Variable | 1–100 | 100–249.9 | 250–500 | 500–1,000 | 1–2,000 | 2–3,000 | 3–5,000 | >5,000.0 | ||
| Arkansas | Farms | 621 | 934 | 941 | 745 | 281 | 39 | 11 | 1 | |
| Rice | Acres | 32,092 | 154.78 | 334.10 | 494.76 | 358.67 | 87.33 | (D) | (D) | |
| (cwt) | Production | 2 | 9.72 | 21.38 | 31.86 | 23.60 | 5.81 | (D) | (D) | |
| Proportion | 0.02 | 0.10 | 0.22 | 0.33 | 0.24 | 0.06 | 0.03 | (—) | 429 | |
| Arkansas | Farms | 182 | 196 | 202 | 289 | 223 | 70 | 21 | 9 | |
| Cotton | Acres | 8.70 | 33.07 | 73.45 | 206.28 | 302.51 | 164.53 | 76.38 | 56.41 | |
| (bales) | Production | 0.01 | 0.05 | 0.13 | 0.36 | 0.54 | 0.30 | 0.14 | 0.11 | |
| Proportion | 0.01 | 0.03 | 0.08 | 0.22 | 0.33 | 0.18 | 0.09 | 0.07 | 643 | |
| California | Farms | 240 | 460 | 481 | 207 | 71 | 10 | 4 | 0 | |
| Rice | Acres | 13.27 | 79.57 | 165.78 | 138.20 | 94.17 | 25.81 | 14.52 | 0.00 | |
| (cwt) | Production | 1.04 | 6.51 | 13.59 | 11.42 | 7.95 | 2.10 | 0.97 | 0.00 | |
| Proportion | 0.02 | 0.15 | 0.31 | 0.26 | 0.18 | 0.05 | 0.02 | 0.00 | 371 | |
| California | Farms | 274 | 385 | 362 | 235 | 104 | 19 | 7 | 7 | |
| Cotton | Acres | 13.95 | 63.70 | 130.86 | 161.41 | 135.80 | 45.34 | 24.57 | 119.03 | |
| (bales) | Production | 0.04 | 0.18 | 0.40 | 0.49 | 0.42 | 0.14 | 0.07 | 0.32 | |
| Proportion | 0.02 | 0.09 | 0.19 | 0.24 | 0.20 | 0.07 | 0.04 | 0.16 | 431 | |
| Indiana | Farms | 12,499 | 5,328 | 3,417 | 2,160 | 637 | 82 | 27 | 6 | |
| Corn | Acres | 472.30 | 847.48 | 1,195.53 | 1,458.11 | 821.05 | 189.48 | 98.53 | 40.81 | |
| (bushels) | Production | 47.36 | 93.56 | 139.42 | 178.86 | 104.54 | 24.87 | 13.41 | 4.14 | |
| Proportion | 0.08 | 0.15 | 0.23 | 0.30 | 0.17 | 0.04 | 0.02 | 0.01 | 226 | |
| Indiana | Farms | 12,146 | 5,789 | 3,876 | 2,538 | 765 | 77 | 18 | 3 | |
| Soybeans | Acres | 504.62 | 927.11 | 1,353.08 | 1,724.02 | 1,000.82 | 173.74 | 61.97 | 16.00 | |
| (bushels) | Production | 18.60 | 36.23 | 54.74 | 72.66 | 42.13 | 7.44 | 3.00 | 0.64 | |
| Proportion | 0.08 | 0.15 | 0.23 | 0.31 | 0.18 | 0.03 | 0.01 | 0.00 | 243 | |
| Iowa | Farms | 20,391 | 16,414 | 10,115 | 4,855 | 917 | 89 | 22 | 3 | |
| Corn | Acres | 978.81 | 2,646.46 | 3,497.90 | 3,195.03 | 1,131.82 | 203.57 | 82.68 | 25.13 | |
| (bushels) | Production | 145.65 | 408.51 | 550.72 | 511.71 | 184.18 | 33.13 | 13.09 | 4.29 | |
| Proportion | 0.08 | 0.22 | 0.30 | 0.28 | 0.10 | 0.02 | 0.01 | 0.00 | 242 | |
| Iowa | Farms | 19,280 | 15,183 | 9,371 | 4,140 | 700 | 64 | 10 | 4 | |
| Soybeans | Acres | 955.01 | 2,434.32 | 3,246.45 | 2,706.24 | 866.86 | 147.00 | 33.25 | 29.48 | |
| (bushels) | Production | 43.82 | 113.90 | 152.13 | 127.04 | 40.38 | 7.06 | 1.55 | 1.51 | |
| Proportion | 0.09 | 0.23 | 0.31 | 0.26 | 0.08 | 0.01 | 0.00 | 0.00 | 233 | |
| Kansas | Farms | 8,062 | 6,180 | 4,677 | 3,544 | 1,519 | 182 | 64 | 8 | |
| Wheat | Acres | 381.44 | 990.79 | 1,645.21 | 2,415.52 | 1,960.36 | 420.37 | 218.79 | 48.38 | |
| (bushels) | Production | 12.83 | 32.96 | 53.84 | 78.91 | 62.47 | 13.69 | 6.80 | 1.48 | |
| Proportion | 0.05 | 0.13 | 0.20 | 0.30 | 0.24 | 0.05 | 0.03 | 0.01 | 343 | |
| Nebraska | Farms | 3,073 | 1,761 | 967 | 631 | 213 | 22 | 6 | 1 | |
| Wheat | Acres | 135.88 | 279.05 | 336.66 | 428.90 | 270.13 | 49.96 | (D) | (D) | |
| (bushels) | Production | 5.34 | 10.63 | 11.59 | 12.76 | 7.59 | 1.56 | (D) | (D) | |
| Proportion | 0.11 | 0.21 | 0.23 | 0.25 | 0.15 | 0.03 | 0.02 | (—) | 245 | |
- a Note: “(D)” indicates reporting withheld to preserve anony. Acres given in thousands and production given in millions. Proportions are given by farms in each size category of production applies to farms of 3,000 or more acres.
This size distribution provides perspective on the preceding simulation results. A comparison of the acreages relevant to binding payment limits to the actual size distributions of farms suggests that payment limits are not likely to be relevant to substantial proportions of the overall acreage of corn, wheat, and soybeans in these states. In contrast, binding payment limits are much more likely to constrain acreage and thus affect producer decisions for rice and cotton producers in Arkansas and California. The greatest effect probably exists for Arkansas cotton, where for example 65% of the acreage is concentrated on farms that could realize a 90% likelihood of experiencing binding LDP limits under high yield and low price conditions. Similar conditions exist for cotton in California and for Arkansas rice farms, where about 30–40% of the acreage is concentrated on farms having a 60% or greater probability of experiencing binding LDPs when yields are high and prices are low.
Concluding Remarks
The issue of limiting payments to farmers continues to be an important part of U.S. farm policy deliberations. Current policy guidelines formally limit payments to total no more than $360,000. However, these limits are generally not binding in that benefits paid through commodity certificates are not subject to any limit. In addition considerable concern has been raised over the degree to which the complex business arrangements used by some farms make it difficult to accurately monitor payments to individuals.
While the relative merits of payment limits may be open to debate, central to the issue is the question of what effect such payments might be expected to have on acreage. The objective of this study was to evaluate the extent to which representative farms might be expected to be affected by binding limits on payments. To this end, we collected cost of production data for a number of different state/crop combinations from several state extension services. We used empirical measures of price volatility and empirical models of yield distributions to stochastically simulate producer decisions under uncertainty and with varying degrees of risk aversion.
Our results generally suggest that any effects from current proposals to limit payments would be modest. An exception occurs for rice and cotton, which exhibit higher probabilities of being affected by binding payment limits. In most cases, it is only in an environment of very low market prices that a typical farm would be likely to be affected by payment limits. Likewise, farms with above-average yields are naturally more likely to be affected by payment limits. In general, our results suggest that with the exception of cotton and rice, there are not likely to be significant acreage effects from payment limits. This is not to imply that payment limits would not affect producers. Depending on the level of base acreage that an individual farmer possesses, limits on fixed direct and counter cyclical payments could be binding. Although such decoupled payments do not seem to have a large impact on acreage and production decisions, the welfare of those receiving the benefits certainly could be affected.
The direct policy implications of the analysis are clear—strictly enforced payment limits of the form being debated among legislators would not have a significant impact on production of corn, soybeans, and wheat. In contrast, cotton and rice acreage may be affected by binding payment limits. This could bring about a number of more general structural adjustments that lie beyond the scope of this analysis. Land values could be negatively impacted in important cotton and rice growing regions and acreage could be reallocated across producers. Rental arrangements might also adjust in response to changes in payment limits that could impact tenants and landlords. These longer-term adjustments remain important topics for future research.
