Characteristics of failed U.S. commercial banks: an exploratory study
We acknowledge the excellent research assistance of Ty Dattaray and Chen Zhou, both graduate students at California State University Fullerton. Fatima Alali acknowledges the generous research grant support of Mihaylo College of Business & Economics at California State University Fullerton. We thank the editor and anonymous reviewers for their valuable comments.
Abstract
This study uses survival analysis to determine how early the indications of bank failure can be observed. We find that banks with high loan to asset and high personal loan to assets ratios are more likely to survive. Older banks and banks with high real estate and agricultural loans, loan loss allowance, loan charges off and non-performing loans to assets ratio are more likely to fail. It is possible to predict survival functions of <50% for failed banks, 3 years or less before failure. Moreover, we find that most of the variables present a behaviour that departs from Benford’s Law.
1. Introduction
This study examines the characteristics of failed commercial banks relative to non-failed commercial banks in years leading to the bank’s failure. Using historical data of a sample of U.S. commercial banks that failed from 2000 to 2012, this study uses 6,069 failed bank-year observations to examine the characteristics of the failed banks from 1984 to 2010, in an attempt to explore the basic financial characteristics of these failed banks compared to non-failed U.S. commercial banks. The study uses a comprehensive set of financial variables over a long period of time prior to failure, to differentiate between failed banks and non-failed banks and to determine how early the indications of failure can be observed.
Seminal work by Secrist (1938) and Pettway and Sinkey (1980) suggests that bank accounting data can be used to distinguish sound from unsound banking. As such, U.S. regulatory bank examinations and capital regulations have focused on different qualities of banks including, earnings quality, capital ratio, default risk and management competence. Because those banks that fail tend to decay over time instead of failing all-at-once, identifying banks with financial difficulties is the first step towards achieving failure prevention goal (Pettway and Sinkey, 1980). This is specially required given the current financial crisis that propagated internationally.
Using a sample of failed and non-failed banks, we conduct a survival analysis and find that banks with high loan to asset ratio, agricultural loan to asset, non-performing loans to loan, loan to deposit ratio, loan loss allowance to asset ratio, loan charge offs to loan ratio and older banks have shorter window of survival (are more likely to fail sooner). We also find that as loan variables increase, bank failure increases and survival likelihood decreases. The same effect is found when real estate loans and agricultural loans increase and personal loans decrease in the pre-global financial crisis period. Loan variables are significant at the 1% level. Moreover, we find that as equity to assets increase, bank failure decreases and survival likelihood increases. Equity to assets is significant at the 1% level. The study of bank failure is important for at least two reasons. First, an understanding of factors related to a bank’s failure enables regulatory authorities to detect an unhealthy bank before the bank becomes problematic and may threaten the financial system. As such, developing a model that can be used to predict a bank’s failure not only protects from a potential future financial crisis but also reduces the costs to depositors and the deposit insurance funds (Thomson, 1991). Second, the study’s results are relevant to the current financial crisis as the economic downturn was initiated by financial institutions’ failure. Hence, it is even more important to develop models that explain and predict bank failures in up and down economic periods.
We include an additional analysis based on Benford’s law to evaluate whether some variables could have been manipulated years before failure to conceal the real situation of the bank. Benford (1938) conducted a study looking at the digital frequencies in tabulated data. He also formulated the expected digital frequencies for first and second digits as well as their combinations. If the digital frequency in the data for failed banks departs from the expectations of Benford, we can assume that the data were altered to conceal the real economic or financial situation of the bank. In the pre-financial crisis period, the mean values for first two digits in liabilities are lower than expected, and in operating revenues and interest revenue are higher than expected, indicating that failed banks might have manipulated these numbers in that period. These results are statistically significant. For the post-financial crisis period, the manipulation is not observed, which may be explained by the increased regulatory scrutiny during this period.
The study contributes to existing literature in the following ways. The study uses a large sample of commercial banks that failed between years 2000 and 2012 and tracks their financial characteristics over a long period of time (1984–2010) to allow for better evaluation of financial stability of the bank well before it actually fails. Prior published studies use data up to 2003 to examine the characteristics of high default risk banks, Ravi Kumar and Ravi (2007). In addition, our study uses survival analysis with time variant covariates to determine how long before the bank actually fails, it can be determined to be suspect to failure. The study, as such, has regulatory and policy implications.
2. Literature review
The prediction of bankruptcy has been extensively researched since late 1960s starting with Altman. Ravi Kumar and Ravi (2007) present a comprehensive survey of research studies published during 1968–2005, where various statistical and intelligent techniques were applied to solve the bankruptcy prediction problem. They indicate that the most precise way of monitoring banks is by conducting on-site examinations. The Federal Deposit Insurance Corporation Improvement Act of 1991 (FDICIA) mandates these examinations every 12–18 months. For that purpose, regulators utilize a six-part rating system to indicate the safety and soundness of an institution. This rating, referred to as CAMELS, evaluates banks in the following areas: Capital adequacy, Asset quality, Management expertise, Earnings strength, Liquidity and Sensitivity to market risk. While CAMELS ratings clearly provide regulators with important information, Cole and Gunther (1995) show that CAMELS ratings decay rapidly.
Prior studies have established the usefulness of accounting data in identifying problem/failed banks (e.g. Bell 1997, Boyacioglu et al., 2009, Kolari et al., 2002, Martin 1977, Olmeda and Fernandez 1997, Swicegood and Clark 2001, Shumway 2001, Alam et al., 2000, Varetto 1998, Ravi Kumar and Ravi 2007). In these studies, a sample of distressed banks is compared with a paired or random sample of healthy banks. Using data from several years before a defined critical date (e.g. failure), financial characteristics are identified, sample banks are reclassified, and predictions are made. These studies use different classification techniques including discriminant analysis, logit, probit, fuzzy logic, neural systems and support vector machine.
Most of the studies use an ex-post empirical approach and compare characteristics of failed and non-failed banks to predict failure in the future. However, those studies do not indicate how early the determinants of failure can be predicted. Bell (1997) looks at the usefulness of financial statement data to predict the regulator’s decisions to close commercial banks. He compares logistic regression and neural network computing and shows that neither the logit nor the neural network model dominates the other in terms of predictive ability, but for complex decision-making, the latter method performs better. Using Turkish data, Boyacioglu et al. (2009) compares the classification performance of neural networks, support vector machines and multivariate statistical methods. They find that the performance of different techniques varies with respect to the format of the data set. They also find different performance in training and validation data sets. Kolari et al. (2002) uses logit analysis and trait recognition to develop and test a classification model. They find satisfactory performance in classification, but the trait recognition outperformed logit in most tests in minimizing type I and II errors. Martin (1977) compares independent variables in 1974 to predict failure in 1975 and 1976. They found that 87% of the failed banks and 88.6% of the non-failed banks were correctly classified, but 12% of non-failed banks were classified as failed as well. Olmeda and Fernandez (1997) used data from Spain and found that an additive aggregation of combining classifiers is better than a single classifier in terms of predicting bankruptcy. Swicegood and Clark (2001) compare discriminant analysis, neural networks and human judgment to predict bank underperformance. They find the neural network and human judgment to be significantly better than the discriminant analysis, and the neural networks to be slightly better than the human judgment. Shumway (2001) develops a hazard model for forecasting bankruptcy that uses all the information available for a firm. He finds that while half of the accounting ratios used previously are poor predictors, several market-driven variables are related with bankruptcy. Cole and Wu (2009) use Shumway’s model and test its accuracy relative to a simple one-period probit model. Their model outperforms the one-period probit model with and without including macroeconomic variables. In this study, we consider all the information available for each firm and we use a regression method with survival data that does not assume independence of the errors. Afifi et al. (2004) indicates that survival analysis examines and models the time it takes for events to occur. This is appropriate for our study because our interest is not only on the variables that discriminate between failed and non-failed banks, but also in determining the probability of a bank’s survival given its financial history. Wheelock and Wilson (2000) use a hazard model with time-varying covariates to identify the characteristics that make banks more likely to fail or being acquired. They estimate the model with emphasis on management quality measures and find that inefficiency increases the risk of failure while reducing the probability of acquisition. We use variables identified in these studies and using a large sample of banks to examine bank’s survival over a recent time period. Predicting when failure happens can be used to schedule on-site examinations, early interference programmes or simply to help regulatory supervisors look closely at risk banks and potentially require correct actions before they signify into bank failures. We also examine susceptibility of banks to manipulation using Benford’s Law. Nigrini and Mittermaier (1997) present a comprehensive discussion. Carslaw (1988) hypothesized that when income is below psychological boundaries, managers would round them up. For example, 798,000 would be rounded up to 800,000. This manipulation would deal an increase of second digits = 0 and a decrease of second digits = 9. He found that effect using New Zealand data. Thomas (1989) found excess second digit 0 in quarterly US net income data and the opposite effect for net losses. He also found that earnings per share are multiples of five cents more often than expected. Christian and Gupta (1993) found more individual taxpayers have incomes in the upper dollars of the tax tables, indicating that taxpayers reduce taxable income when they are a few dollars above a table step boundary. Benford’s law was also studied as an aid for auditors (Durtschi et al., 2004; Nigrini and Mittermaier, 1997; Busta and Weinberg, 1998; Nigrini, 2001). Finally, Hill (1988) shows that when people make up numbers they do not conform to Benford’s Law. Therefore, if the tested variables were manipulated years before failure to conceal the financial troubles of the banks, those variables are not expected to conform to the law.
On the basis of above literature, we identify factors that are significant in determining bank failure, and then we use these variables on a sample of three banks that failed in January 2011. Furthermore, we match the three healthy banks, based on bank’s size, age and fiscal year-end, with the three failed banks and compare their survival functions. Finally, we compare the likelihood of survival for Citibank, Bank of America, Wachovia and Wells Fargo 6 years before 2007 and in 2007. We select these banks to illustrate our results because they are the most publicized “at risk” banks, and they received Troubled Assets Relief Program (TARP) funds.
3. Data collection
A sample of failed U.S. commercial banks is obtained from the Federal Deposit Insurance Corporation website including their FDIC’s certificate number, on 26 February 2012, for banks that failed from 15 October 2000 to 26 February 2012. We use FDIC certificate numbers of 452 failed banks to obtain the annual balance sheet, income statement and capital ratio data from the quarterly call reports available on Wharton Database, that is, 31 December of each year. The failed bank sample includes banks that failed and subsequently either liquidated or were acquired by another bank over the period 13 October 2000 until 26 February 2012. The study looks retrospectively at the characteristics of these failed banks compared to non-failed banks. Similarly, the non-failed banks’ annual data are retrieved from the quarterly call reports available on Wharton Database for all the banks excluding the failed ones. We hand-collected data for the missing observations of risk-weighted assets, capital ratios and loan portfolio variables from both the bank’s annual reports and the FDIC website. Our initial sample of banks’ observations included 418,092 observations. We delete observations with missing values including return on assets (ROA), loan loss allowance, total loans, non-performing loans and total deposits. This resulted in 279,165 observations. We deleted additional 1,583 observations for which risk-weighted assets were missing. We deleted 19,396 observations for which lagged variables were missing. This resulted in a final 258,186 observations covering the period 1984–2010. Our remaining sample includes 400 different failed banks representing a pooled 6,065 failed bank-year observations.1 The sample of non-failed banks includes 252,117 bank-year observations.
4. Selection of variables
We identify a comprehensive set of predictor variables that are chosen based on previous studies. These variables are classified into four groups following the CAMEL2 ratings:
- C.
CAPITAL ADEQUACY: These variables were found to be significantly different between failed and non-failed banks by Boyacioglu et al. (2009). C1 was also found significant by Kolari et al. (2002), and C3 by Martin (1977).
- C1.
Shareholders Equity/Total Assets
- C2.
Shareholders Equity/Total Loans
- C3.
Gross Capital/Risk Assets
- C1.
- A.
ASSET QUALITY AND LIQUIDITY: Bell (1997) found A1, A2 and A3 significant variables in their model to classify failed and non-failed banks. Martin (1977) found A1 and A11 significant. Kolari et al. (2002) found A7, A10 and A11 to be significant.
- A1.
Total Loans/Total Assets
- A2.
Non-performing Loans/Total Assets
- A3.
Agricultural Loans/Total Assets
- A4.
Personal Loans/Total Assets
- A5.
Real Estate Loans/Total Assets
- A6.
Non-performing Loans/Total Loans
- A7.
Total Loan and Leases/Total Assets
- A8.
Total Loans/Total Deposits
- A9.
Allowance for Loan Losses/Total Assets
- A10.
Net Loan Charge offs/Total Assets
- A11.
Provision for Loan Losses/Total Assets
- A1.
- E.
EARNINGS: Boyacioglu et al. (2009) found E1 and E2 significant variables in the classification between failed and non-failed banks. Kolari et al. (2002) found E3 and E4 significant, and Bell (1997) found E5 significant.
- E1.
Net Profit/Total Assets
- E2.
Net Profit/Total Equity
- E3.
Income before Extraordinary Items/Total Assets
- E4.
Interest Income/Total Operating Income
- E5.
Non-interest Expense/Total Operating Income
- E6.
Salary and Wages Expense/Total Assets
- E1.
- O.
Other Characteristics.
- O1.
Size is included to control for the probability of small bank failure compared to large bank failure. O2 represents bank’s age, and according to Shumway (2001), age of bank is defined as reporting year relative to the year it was included in the database = 1976. For example, if a bank is reporting in year 2000, then age of the bank is 2000–1976 = 24. To avoid heteroscedasticity, we take the log of age. O3 to O14 are dummy variables included to capture regional geographic location, regardless of whether a bank is insured or not by a federal agency.3 O3-O14 dummy variables identify banks by one of the Federal Reserve bank regions as defined by FED1-12 as follows: Chicago, New York, Boston, Philadelphia, Cleveland, Richmond, Atlanta, St. Louis, Kansas City, Minneapolis, Dallas and San Francisco, respectively. The dependent variable (GAP) is the gap in years between the year of failure and the reporting year. For example, if a bank failed in 2008 and it is reporting year 2000, then GAP equals to 8 years.
- O1.
5. Research design
Following prior studies (e.g. Bell, 1997; Kolari et al., 2002; Martin, 1977; Olmeda and Fernandez, 1997), we compile a comprehensive set of variables that are used to determine the characteristics of failed banks compared to those of the non-failed banks. We obtain coefficients of the variables using the GAP variable where GAP of zero (representing non-failed banks) is a reference category.
We use the Cox method with survival data because our interest not only on the variables that discriminate between failed and non-failed banks, but also in the probability of survival of the bank years before failure, based on their financial characteristics. Afifi et al. (2004) indicates that survival analysis examines and models the time it takes for events to occur. Therefore, this methodology allows us to examine explanatory variables that may predict the time leading to bank failure. The non-failed banks represent censored observations because we know that these banks still survive but may possibly fail in future. Afifi et al. (2004) discuss two survival regression methods, log linear and Cox regression. We use the latter because it allows testing for the relationship between survival time (t) and a set of explanatory variables (Xi) that change over time.
The Cox regression does not require the specification of a baseline hazard rate or the estimation of absolute risk, but it requires the definition of an indicator and a time variable. The dependent variable is the status variable (failed versus non-failed), which is analysed in relation with the time variable (GAP) with hazard or survival rates. The time variable measures the duration to the event; therefore, it indicates the number of periods until failure.
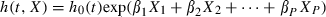 ()
()where the hazard rate h0(t) does not depend on the Xi variables (covariates) and exp(β1X1 + β2X2 + … + βPXP) does not depend on t (time). In the basic model, an explicit assumption is that the explanatory variables do not change over time. Cox regression implements a proportional hazard ratio h(t, 1)/h(t, 0) = exp(β1), which is the ratio of two hazard functions. The hazard ratio (HR) is the estimated effect that group 1 has relative to group 2. The maximum likelihood method is used to estimate the model parameters and their standard errors (Afifi et al., 2004).
The Cox regression model assumes that the hazard rate increases linearly with time, conditional on the covariates. When small time intervals are used, the power of the model increases because there are less chances of type II error. The covariates can be categorical or continuous, time-fixed or time-dependent. In our study, because the Xi variables are time-dependent, we estimate time-dependent covariates. The status variable is defined as an indicator variable that is equal to one if a bank fails and zero otherwise. The time variable (GAP) equals the gap between the year of failure and the reporting year. To estimate time-dependent covariates Cox regression and to avoid simultaneity, we use lag form of time-dependent covariates (Box-Steffensmeier et al., 2004). We centre the lagged variables (Box-Steffensmeier et al., 2004: p65), so that the baseline functions are estimated for points that exist in the data set; otherwise, the baselines functions would be misleading.
6. Results
6.1. Descriptive statistics
Table 1 presents descriptive statistics of the independent variables used as predictors of bank failure. The total number or observations is 258,186. Besides the mean, descriptive statistics of the 25th and 75th percentiles are included. Overall, our sample consists of large banks with average log of total assets of 11.28. The sample banks are on average profitable (average ROA = 0.8%) and average gross capital ratio of about 13%. Average leverage (LEV) is 9.6%. The banks, on average, have non-performing loans to assets ratios (NPLTOASST) of 0.30% and average loan loss allowance (LLATOASSET) of 0.9%, while average percentage of non-performing loans to loans (NPLTOLOAN) is 0.50%. Average net charge offs to assets (NCOFFTOASST) is 0.0005%. The average total loan portfolio to assets (LOANTOASST) is 58.3%, with real estate loans (RETOASST) representing an average of 33.1%, personal loans including credit cards (PERSONTOASST) 8.4% and agricultural loans (AGRTOASST) 5.0%.4 Interest revenue to total operating income (operating income is sum of interest and non-interest revenues, as defined in the literature) represents average of 90.5%, and non-interest expense to operating income (NONINTEXPTOOPINC) is 40.2%. The average loan to deposits (LOANTODPST) ratio is 68.5%, and average employee salaries and benefits to assets (SALARIESTOASST) is 1.6%. In addition, we find that the different Federal Reserve regions are represented in the sample with 21.3% banks in Chicago Federal Reserve region, about 14.8% in the Kansas City Federal Reserve region and about 13% in Minneapolis Federal Reserve region.
| Variables | Mean | SD | 25th Pctl | Median | 75th Pctl | |
|---|---|---|---|---|---|---|
| GAP | 0.249 | 1.930 | 0.000 | 0.000 | 0.000 | |
| FD | 0.024 | 0.152 | 0.000 | 0.000 | 0.000 | |
| C1 | LEV | 0.096 | 0.033 | 0.075 | 0.089 | 0.109 |
| C2 | EQTOLAN | 0.189 | 0.125 | 0.118 | 0.152 | 0.212 |
| C3 | GCAPTORISK | 0.129 | 0.067 | 0.090 | 0.090 | 0.144 |
| A1 | LOANTOASST | 0.583 | 0.157 | 0.483 | 0.598 | 0.696 |
| A2 | NPLTOASST | 0.003 | 0.005 | 0.000 | 0.001 | 0.003 |
| A3 | AGRTOASST | 0.050 | 0.081 | 0.000 | 0.009 | 0.067 |
| A4 | PERSONTOASST | 0.084 | 0.073 | 0.034 | 0.065 | 0.112 |
| A5 | RETOASST | 0.331 | 0.177 | 0.195 | 0.312 | 0.450 |
| A6 | NPLTOLOAN | 0.005 | 0.008 | 0.000 | 0.001 | 0.006 |
| A7 | LOANLEASETOASST | 0.583 | 0.157 | 0.483 | 0.598 | 0.696 |
| A8 | LOANTODPST | 0.685 | 0.204 | 0.553 | 0.689 | 0.813 |
| A9 | LLATOASST | 0.009 | 0.005 | 0.006 | 0.008 | 0.011 |
| A10 | NCOFFTOASST | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| A11 | LLPTOASST | 0.004 | 0.007 | 0.001 | 0.002 | 0.004 |
| E1 | ROA | 0.008 | 0.010 | 0.006 | 0.010 | 0.013 |
| E2 | ROE | 0.054 | 6.225 | 0.062 | 0.104 | 0.142 |
| E3 | NIBTX | 0.008 | 0.010 | 0.006 | 0.010 | 0.013 |
| E4 | INTREVTOOPINC | 0.905 | 0.068 | 0.881 | 0.920 | 0.948 |
| E5 | NONINTEXTOOPINC | 0.402 | 0.132 | 0.310 | 0.380 | 0.470 |
| E6 | SALARIESTOASST | 0.016 | 0.005 | 0.013 | 0.015 | 0.019 |
| O1 | SIZE | 11.275 | 1.308 | 10.378 | 11.125 | 11.976 |
| O2 | AGE | 2.969 | 0.372 | 2.639 | 2.996 | 3.296 |
- All continuous variables are winsorized at top and bottom 1%. GAP: the difference between the failure year and the reporting year; C1. LEV: equity to total assets; C2. EQTOLOAN: equity to total loans; C3. GCAPTORISK: ter1 + tier 2 divided by risk-weighted assets; A1. LOANTOASST: total loans to total assets; A2. NPLTOASST: non-performing loans to total assets; A3. AGRTOASST: agricultural loans to total assets; A4. PERSONTOASST: personal loans to total assets; A5. RETOASST: real estate in mortgages, industrial and commercial loans to total assets; A6. NPLTOLOAN: non-performing loans to total loans; A7. LOANLEASETOASST: total loans and leases to total assets; A8. LOANTODPST: total loans to total deposits; A9. LLATOASST: loan loss allowance to total assets; A10. NCOFFTOASST: charge offs recoveries to total assets; E1. ROA: net income to total assets; E2. ROE: net income before extraordinary items to equity; E3: NIBTX: net income before extraordinary items to total assets; E4. INTREVTOOPINC: interest revenue to operating income; E5. NONINTEXTOOPINC: non-interest expense to operating income; E6. SALARIESTOASST: employees salaries and benefits to total assets; O1. SIZE: the log of total assets; O2. AGE: the log of age of bank in year of reporting, starting from 1976; and O3–O14: indicator variables for Federal Reserve Bank Region are also included in test model but are unreported for brevity.
Correlations5 among variables show that there is a significant positive association between SIZE, AGE, ROA, loan to assets (LOANTOASST), real estate loans to assets (RETOASST), loans to deposits (LOANTODPST), loan loss allowance to assets (LLATOASST) and net charge offs to assets (NCOTOASST). We find that size is negatively and significantly correlated with LEV, non-performing loans to assets (NPLTOASST), agricultural loans (AGRTOASST), personal loans including credit card debt (PERSONTOASST), non-interest expense to operating income (NONINTEXPTOOPINC) and interest revenue to operating income (INTREVTOOPINC). LEV and gross capital ratio to risk-weighted assets (GCAPTORISK) are positively and significantly correlated as expected. These two variables are negatively and significantly correlated with non-performing loans to assets (NPLTOASST), total loans to deposit (LOANTODPST), loan loss allowance to total assets (LLATOASST) and loan charge offs (NCOTOASST). We find that (GCAPTORISK) is positively and significantly correlated with real estate loans (RETOASST), AGE and non-interest expense to operating income (NONINTEXPTOOPINC). We also find that leverage (LEV) is negatively and significantly related to real estate loans (RETOASST), where leverage is measured by equity to asset ratio. Spearman’s correlation coefficients are smaller in magnitude and less significant than Pearson’s correlation coefficients.
Table 2 presents the differences in means of the variables between failed and non-failed banks. Similar to Bell (1997) and Martin (1977), we find that the variables AGRTOASST and NONINTEXTOOPINC are significantly different between failed and non-failed banks. Similar to Kolari et al. (2002), we find INTREVTOOPINC are significantly lower for failed banks than non-failed banks. In addition, we find that PERSONTOASST, RETOASSTLOANTODPST, LLATOASST, SALARIESTOASST and AGE are significantly different between failed and non-failed banks. Consistent with expectations, failed banks have higher proportion of their total assets in loans, especially real estate loans. The proportion of agricultural and personal loans is lower for failed banks compared to non-failed banks. Because our sample includes failures until February 2012, this effect might be related to the recent crisis. Relative to non-failed banks, failed banks have lower equity to loans (EQTOLOAN) and lower equity to total assets (LEV), and the difference is statistically significant at <1% level. Failed banks also have higher non-performing loans to total loans (NPLTOLOAN), higher non-performing loans to assets (NPLTOASST) and higher net charge offs (NCOFFTOASST), with differences only statistically significant for net loan charge offs.
| Variables | Failed banks (N = 6,069) | Non-failed banks (N = 252,117) | Mean Diff. | t-value | Pr > |t| | |||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | |||||
| C1 | LEV | 0.092 | 0.034 | 0.097 | 0.033 | −0.005 | −10.590 | <0.0001 |
| C2 | EQTOLOAN | 0.154 | 0.104 | 0.190 | 0.125 | −0.036 | −26.400 | <0.0001 |
| C3 | GCAPTORISK | 0.121 | 0.054 | 0.129 | 0.067 | −0.007 | −10.650 | <0.0001 |
| A1 | LOANTOASST | 0.666 | 0.154 | 0.581 | 0.156 | 0.085 | 42.480 | <0.0001 |
| A2 | NPLTOASST | 0.003 | 0.005 | 0.003 | 0.005 | 0.000 | 0.880 | 0.380 |
| A3 | AGRTOASST | 0.023 | 0.057 | 0.051 | 0.081 | −0.028 | −37.040 | <0.0001 |
| A4 | PERSONTOASST | 0.060 | 0.067 | 0.085 | 0.073 | −0.025 | −28.200 | <0.0001 |
| A5 | RETOASST | 0.454 | 0.207 | 0.328 | 0.175 | 0.126 | 46.990 | <0.0001 |
| A6 | NPLTOLOAN | 0.005 | 0.009 | 0.005 | 0.008 | 0.000 | −2.750 | 0.006 |
| A7 | LOANLEASETOASST | 0.666 | 0.154 | 0.581 | 0.156 | 0.085 | 42.480 | <0.0001 |
| A8 | LOANTODPST | 0.795 | 0.206 | 0.683 | 0.203 | 0.112 | 41.810 | <0.0001 |
| A9 | LLATOASST | 0.011 | 0.007 | 0.009 | 0.005 | 0.002 | 18.470 | <0.0001 |
| A10 | NCOFFTOASST | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 6.410 | <0.0001 |
| A11 | LLPTOASST | 0.007 | 0.011 | 0.004 | 0.007 | 0.003 | 19.770 | <0.0001 |
| E1 | ROA | 0.004 | 0.016 | 0.008 | 0.010 | −0.005 | −22.620 | <0.0001 |
| E2 | ROE | −0.143 | 13.856 | 0.059 | 5.921 | −0.202 | −1.130 | 0.258 |
| E3 | NIBTX | 0.003 | 0.016 | 0.008 | 0.010 | −0.005 | −22.580 | <0.0001 |
| E4 | INTREVTOOPINC | 0.899 | 0.079 | 0.905 | 0.068 | −0.006 | −5.840 | <0.0001 |
| E5 | NONINTEXTOOPINC | 0.451 | 0.159 | 0.401 | 0.132 | 0.050 | 24.470 | <0.0001 |
| E6 | SALARIESTOASST | 0.017 | 0.006 | 0.016 | 0.005 | 0.001 | 15.780 | <0.0001 |
| O1 | SIZE | 11.585 | 1.383 | 11.268 | 1.305 | 0.317 | 17.680 | <0.0001 |
| O2 | AGE | 3.121 | 0.340 | 2.965 | 0.372 | 0.156 | 35.260 | <0.0001 |
- *Assuming unequal variances. All continuous variables are winsorized at top and bottom 1%. GAP: the difference between the failure year and the reporting year; C1. LEV: equity to total assets; C2. EQTOLOAN: equity to total loans; C3. GCAPTORISK: ter1 + tier 2 divided by risk-weighted assets; A1. LOANTOASST: total loans to total assets; A2. NPLTOASST: non-performing loans to total assets; A3. AGRTOASST: agricultural loans to total assets; A4. PERSONTOASST: personal loans to total assets; A5. RETOASST: real estate in mortgages, industrial and commercial loans to total assets; A6. NPLTOLOAN: non-performing loans to total loans; A7. LOANLEASETOASST: total loans and leases to total assets; A8. LOANTODPST: total loans to total deposits; A9. LLATOASST: loan loss allowance to total assets; A10. NCOFFTOASST: charge offs recoveries to total assets; E1. ROA: net income to total assets; E2. ROE: net income before extraordinary items to equity; E3: NIBTX: net income before extraordinary items to total assets; E4. INTREVTOOPINC: interest revenue to operating income; E5. NONINTEXTOOPINC: non-interest expense to operating income; E6. SALARIESTOASST: employees salaries and benefits to total assets; O1. SIZE: the log of total assets; O2. AGE: the log of age of bank in year of reporting, starting from 1976; and O3-O14: indicator variables for Federal Reserve Bank Region are also included in test model but are unreported for brevity.
Salaries and wages (SALARIESTOASST), non-interest expense to total operating revenue (NONINTEXTOOPINC) and loans to deposits (LOANTODPST) are higher for failed banks than non-failed banks; and interest revenue to total operating revenue (INTREVTOOPINC) is lower for failed than for non-failed banks, and the differences are statistically significant. We also find that the size of failed banks is on average larger than the size of non-failed banks with means of 11.59 and 11.27, respectively. Moreover, we find that Chicago, Atlanta, Minneapolis, Dallas and San Francisco Federal Reserve regions have significantly higher percentage of bank failure compared to the other Federal Reserve regions.
Table 3 shows the frequency distribution of GAP variables for failed banks. The sample includes banks data between 1 and 27 years before failure. More than 91% of failed banks have data prior to failure, between 2 and 24 years. There are four bank-year observations for 27 years prior to failure, 36 bank-year observations for 26 years prior to failure and 87 bank-year observations for 25 years prior to failure.
| GAP | No. of Obs. | % of Obs. |
|---|---|---|
| 1 | 384 | 6.33 |
| 2 | 390 | 6.43 |
| 3 | 382 | 6.29 |
| 4 | 363 | 5.98 |
| 5 | 346 | 5.70 |
| 6 | 323 | 5.32 |
| 7 | 311 | 5.12 |
| 8 | 296 | 4.88 |
| 9 | 281 | 4.63 |
| 10 | 264 | 4.35 |
| 11 | 240 | 3.95 |
| 12 | 228 | 3.76 |
| 13 | 220 | 3.62 |
| 14 | 207 | 3.41 |
| 15 | 202 | 3.33 |
| 16 | 192 | 3.16 |
| 17 | 187 | 3.08 |
| 18 | 178 | 2.93 |
| 19 | 175 | 2.88 |
| 20 | 170 | 2.80 |
| 21 | 161 | 2.65 |
| 22 | 156 | 2.57 |
| 23 | 149 | 2.46 |
| 24 | 137 | 2.26 |
| 25 | 87 | 1.43 |
| 26 | 36 | 0.59 |
| 27 | 4 | 0.07 |
| Total | 6069 | 100.00 |
- GAP is defined as difference between reporting year and failure year.
6.2. Cox regression analysis
We estimate the Cox regression model using the comprehensive set of variables discussed earlier. We use a backward elimination method to retain in the model only those variables that are significant at the 10% level. The results of the estimated model and the eliminated variables are provided in Table 4. Table 4 shows that LEV, EQTOLOAN, LOANTOASST, AGRTOASST, PERSONLOAN, NPLTOLOAN, LOANTODPST, LLATOASST, NCOFFTOASST, ROA, NONINTEXTOOPINC and AGE are significant at the 10% level or better. The coefficients of LEV, LOANTOASST, LOANTOASST, PERSONTOASST, ROA and NONINTEXTOOPINC are negative and significant at the 1% level, suggesting that hazard (bank failure) decreases and survival likelihood increases as these variables increase. Therefore, an increase in these covariates appears to be associated with a decrease in risk of failure. In addition, the coefficients of EQTOLOAN, AGRTOASST, NPLTOASST, LOANTODPST, LLATOASST, NCOFFTOASST and AGE are positive and significant at 10% or better. This indicates that for each of these time-varying covariates, hazard (bank failure) increases and survival likelihood decreases as the covariate increases. The corresponding hazard ratio shows the rate of the failure for an increase in one unit of the covariate. We find that the hazard ratio for ROA is zero. The hazard ratios for EQTOLOAN, AGRTOASST, NPLTOLOAN, LOANTODPST, LLATOASST, NCOFFTOASST and AGE are larger than 1.0, indicating an increase in the rate of the bank failure occurring for a one-unit increase in the covariate, after controlling for other covariates in the model. The hazard ratio for LEV, LOANTOASST, PERSONTOASST and NONINTEXTOOPINC is <1.0, indicating that after controlling for other covariates in the model, an increase in the rate of bank failure occurs for one-unit decrease in the covariate. The overall model fit statistics show that the model is significant at <1%, using partial likelihood test ratio and Wald ratio.
| Variables | Coef. | Pr > χ2 | Hazard ratio | Step | Variable removed | Wald | Pr > χ2 |
|---|---|---|---|---|---|---|---|
| LEV | −3.07 | <0.0001 | 0.046 | 1 | RETOASST | 0.004 | 0.952 |
| EQTOLOAN | 0.773 | 0.000 | 2.167 | 2 | SIZE | 0.009 | 0.923 |
| LOANTOASST | −0.425 | 0.048 | 0.654 | 3 | INTREVTOOPIN | 0.153 | 0.696 |
| AGRTOASST | 0.579 | 0.006 | 1.784 | 4 | SALARIESTOASST | 1.479 | 0.224 |
| PERSONTOASST | −0.521 | 0.027 | 0.594 | 5 | NPLTOASST | 2.225 | 0.136 |
| NPLTOLOAN | 7.93 | <0.0001 | 2780.454 | ||||
| LOANTODPST | 0.686 | <0.0001 | 1.986 | ||||
| LLATOASST | 13.698 | <0.0001 | 889281.100 | ||||
| NCOFFTOASST | 647.112 | 0.013 | 109000 + E9 | ||||
| ROA | −9.233 | <0.0001 | 0.000 | ||||
| NONINTEXTOOPINC | −0.331 | 0.003 | 0.718 | ||||
| AGE | 13.751 | <0.0001 | 937977.400 | ||||
| Criterion | Without covariates | With covariates | |||||
| −2 LOG L | 94484.779 | 80164.94 | |||||
| AIC | 94484.779 | 80188.94 | |||||
| SBC | 94484.779 | 80269.471 | |||||
| Testing global null hypothesis: BETA = 0 | |||||||
| Test | χ2 | Pr > χ2 | |||||
| Likelihood ratio | 14319.839 | <0.0001 | |||||
| Wald | 6347.029 | <0.0001 | |||||
- Variables used in the Cox regression are mean-centred lagged variables (Box-Steffensmeier et al., 2004). GAP: the difference between the failure year and the reporting year; C1. LEV: equity to total assets; C2. EQTOLOAN: equity to total loans; C3. GCAPTORISK: ter1 + tier 2 divided by risk-weighted assets; A1. LOANTOASST: total loans to total assets; A2. NPLTOASST: non-performing loans to total assets; A3. AGRTOASST: agricultural loans to total assets; A4. PERSONTOASST: personal loans to total assets; A5. RETOASST: real estate in mortgages, industrial and commercial loans to total assets; A6. NPLTOLOAN: non-performing loans to total loans; A7. LOANLEASETOASST: total loans and leases to total assets; A8. LOANTODPST: total loans to total deposits; A9. LLATOASST: loan loss allowance to total assets; A10. NCOFFTOASST: charge offs recoveries to total assets; E1. ROA: net income to total assets; E2. ROE: net income before extraordinary items to equity; E3: NIBTX: net income before extraordinary items to total assets; E4. INTREVTOOPINC: interest revenue to operating income; E5. NONINTEXTOOPINC: non-interest expense to operating income; E6. SALARIESTOASST: employees salaries and benefits to total assets; O1. SIZE: the log of total assets; O2. AGE: the log of age of bank in year of reporting, starting from 1976; and O3–O14: indicator variables for Federal Reserve Bank Region are included but are not reported. Indicator variables for years are also included but are not reported.
Figure 1 shows the baseline survival function. The survival function represents the probability of surviving plotted against time. The graph shows that at GAP = 0, by definition, all banks are surviving, and thus survival probability is 100%. When a bank fails, the percentage of banks that are surviving declines. The baseline survival function shows that as time increases, the probability of surviving decreases. When GAP = 12, the probability of surviving decreases to 85%, at GAP = 13, probability of surviving is down to 73%, at GAP = 14, the probability of surviving is <55% and probability of surviving falls to 30% at GAP = 15.
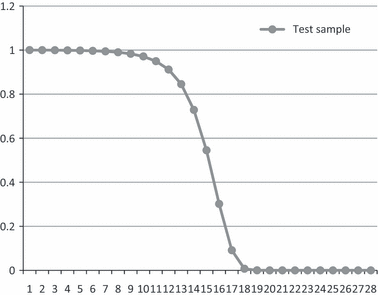
Predicted survival function for the pooled sample.
As a following step, we use the Cox proportional hazards regression results to obtain the predicted survival curves for specific covariate values.6 In particular, we identify three banks that failed in January 2011 according to the FDIC failed banks list. For each of these banks, we compute the survival estimates. The specific covariate values used are from year 2007 owing to data availability.7
We find that the probability of bank A’s survival is decreased to 35% at GAP = 3, and to 15% at GAP = 4. The probability of bank B’s survival is decreased to about 39% at GAP = 3 and to 18% at GAP = 4. Bank C’s survival function is marginally better than that of bank A and is comparable to bank B. In particular, we note that the probability of bank C’s survival is decreased to 40% at GAP = 3, to 18% at GAP = 4 and to <10% at GAP = 5. For the three banks, the predicted survival function is about or <5% at GAP = 6. These results suggest that it is possible to predict bank failures between 3 and 4 years before the actual failure. Comparing these predicted banks’ survival functions to the Cox survival function estimation, only at GAP = 15, survival function decreases to <50% for the latter.
To obtain confidence in the results documented earlier, we identify three healthy banks that are matched with the three failed banks (A, B and C) in terms of size, age and fiscal year-end. Because we cannot predict that those healthy banks are going to survive in the future, we assume that they failed 6 years ago and estimate the predicted survival functions. We find that compared to the failed banks, the potential failure of the three matched healthy banks is lower until GAP = 4, after that, the probability of survival falls also below 10% for the three healthy banks. The probability of the first healthy bank’s survival at GAP = 3 is higher than 42%, and 20% at GAP = 5 (compared with 35% and 15%, respectively, for bank A). The probability of the second healthy bank’s survival was 35% at GAP = 3 and falls to 15% at GAP = 4 compared with failed bank B above. Lastly, the survival function for the third healthy bank is 84% at GAP = 1 and 65% at GAP = 2.
Finally, we study the likelihood of failure for Bank of America (BAO), Citibank (Citi), Wachovia (WAC) and Wells Fargo (WF) 6 years before 2007 and in 2007. Figure 2 presents the likelihood of failure of BAO, Citi, WAC and WF 6 years before 2007. The likelihood of survival for BOA was higher than 80% for GAP = 4, and over 80% for GAP = 5. This likelihood drops to 70% for GAP = 6. The likelihood of survival is lower for WAC and Citi when compared to BOA. WF shows likelihood of failure, with 76% survival rate at GAP = 4, 61% at GAP = 5 and under 50% at GAP = 7, while both Wachovia and Citi Bank have <50% survival likelihood at GAP = 4. However, log rank tests show statistically insignificant differences between survival functions of WF, Citi and BOA. Our results comparing the predicted survival functions of Citi and BOA in 2007 show that the predicted survival function of Citi is lower than that of BOA. Retrospectively speaking, Citi was on the verge of failure without government bailout in 2008.
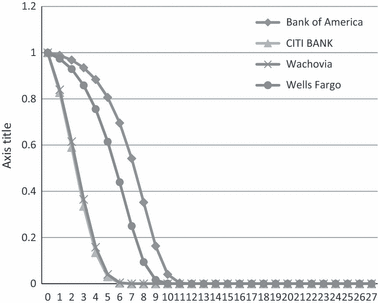
Predicted survival functions for BOA v.s. Citi Bank, Wachovia & Wells Fargo.
6.3. Benford’s law results
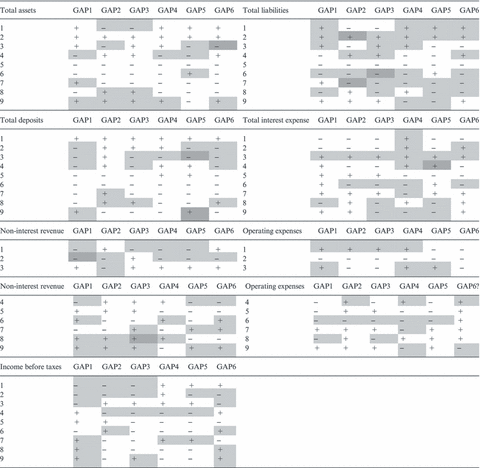
To complement our Cox regression analyses, two additional analyses were produced. First, we look at the behaviour of the first digit in the list of variables. Benford’s Law is an expected distribution of digits in tabulated data on the basis that when the data are ranked from smallest to largest, they form a geometric sequence. Raimi (1976) observed that almost all sequences defined by linear recursions will follow Benford’s Law. He also observed that if a sequence does not conform to Benford’s Law, there is no constant that multiplication would cause it to become a Benford set. As pointed by Nigrini (1996), “conformity of a data set to Benford’s Law does not necessarily imply naturalness, but non-conformity should raise some level of suspicion.” Indeed, Hill (1988) showed that invented numbers did not conform to this law.8 If manipulation occurs on variables representing total assets, total deposits and revenues, it is expected that the numbers reported will be larger than the real ones. In this scenario, the percentage of large numbers expected according to Benford’s Law will be less than the observed, and the percentage of small numbers expected will be more than observed. Therefore, the difference between observed and expected will have a negative sign for small numbers and a positive sign for large numbers. Opposite is the behaviour expected for liabilities and expenses. Therefore, the observed small numbers will be more than the expected according to Benford’s Law (positive sign), and the observed large numbers will be less than the expected (negative sign).We observe that for years 1–6 before a bank’s failure, most of the observed variables present a behaviour that departs from Benford’s Law and could indicate manipulation, although very few are statistically significant as shown in Table 5.
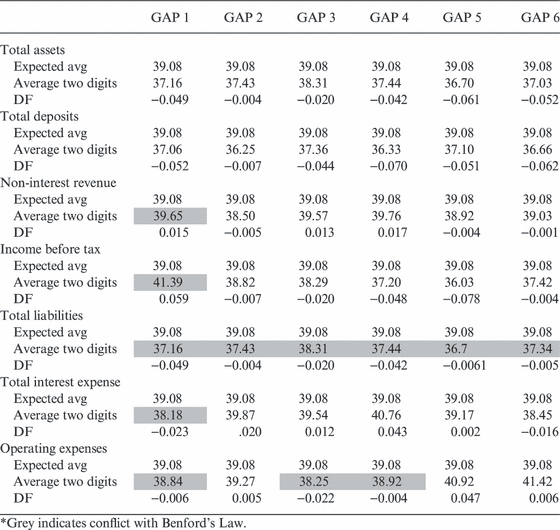
Second, we follow Nigrini (1996) and we compute the distortion factor model (DF). The DF is calculated as the difference in the mean of the observed first two digits and compared with the expected mean according to Benford’s Law. The expected mean is 39.08. If the expenses and liabilities were manipulated, we expect the mean observed to be lower than the mean expected. Contrary, if the revenues and assets accounts were manipulated, we expect the mean observed to be higher than the expected according to Benford’s Law. The results of the years 1–6 before bank’s failure indicate that non-interest revenue has mean values higher than expected during three of those 6 years. Total liabilities have mean values lower than expected in all 6 years, and operating expenses have mean values lower than expected in three of the 6 years as reported in Table 6, although these results are not statistically significant. This analysis indicates that failed banks might increase their revenue and decrease their liabilities years before failure to conceal their financial difficulties.
6.4. Sensitivity analysis9
6.4.1. Size effect
The political cost hypothesis dictates that large banks are more visible and historically have been “too big to fail”. To test whether large banks are more likely to survive, we estimate the survival functions for large and small banks subsamples. We use the log of total assets of higher than or equal to sample median (11.125) to classify a bank as large; otherwise, a bank is classified as small. Our sample includes 129,065 bank-year observations classified as small banks of which 3,754 bank-year observations failed, and 129,121 bank-year observations classified as large banks of which 2,315 bank-year observations failed. Survival functions for small and large banks provide that large banks have higher rates of survival than small banks. As a small bank fails, the survival probability of another small bank declines more than when a large bank fails. Significance tests of log rank, Wilcoxon rank and -2 log likelihood ratio (chi-square values of 72.33, 82.57 and 21.17, respectively) indicate statistically significant difference in the survival functions of large and small banks at less than 1% level.
6.4.2. Partitioning the data by pre- and post-periods of the recent global financial crisis
We examine the effect of the global financial crisis (GFC) on identifying the characteristics of failed commercial banks. This is important because the variables that explain bank failure in the post-GFC period may be different from the variables that explain bank failure in the pre-GFC period.10 As such, we break down the total sample and run survival analyses on the subsamples of the two periods. We identify post-GFC period as 2008–2010 and pre-GFC period as 2004–2007.11 The post-GFC subsample includes a total of 21,413 bank-year observations of which 674 bank-year observations represent failed banks (i.e. event). The pre-GFC subsample includes a total of 30,730 bank-year observations of which 1,348 bank-year observations represent failed banks (i.e. event). The estimated Cox survival models deal different variables for these periods. In the pre-GFC period, LOANTOASST, AGRTOASST, PERSONLOAN, LOANTODPST, NONINTEXTOOPINC, AGE, TETTOASST and NPLTOASST are significant at the 10% level or better. LOANTOASST, PERSONTOASST and NONINTEXTOOPINC are negative, suggesting that bank failure decreases and survival increases as these variables increase. The coefficients of AGRTOASST, LOANTODEPST, RETTOASST, NPLTOASST and AGE are positive, indicating that for each of these covariates, bank failure increases and survival likelihood decreases as the variable increases. The hazard ratio for AGRTOASST, LOANTODPST, RETTOASST and AGE are larger than 1.0, indicating an increase in the rate of failure for a one-unit increase in the covariate, after controlling for other covariates in the model. The hazard ratio for LOANTOASST, PERSONTOASST, NONINTEXTOOPINC, NPLTOASST and AGE are smaller than 1.0, indicating an increase in the rate of bank failure for one-unit decrease in the covariate, after controlling for other covariates in the model. For the post-GFC period, LEV, LOANTOASST, LOANTODPST, LLATOASST and AGE are significant at 10% level or better. LEV and LOANTOASST have negative coefficients, indicating a decrease in bank failure or an increase in the likelihood of survival with an increase in these variables. LOANTOASST, LLATOASST and AGE are positive, indicating an increase in bank failure or a decrease in likelihood of survival when these variables increase. The hazard ratio for LOANTODPST and AGE is larger than 1.0, indicating, after controlling for other covariates in the model, an increase in the rate of failure for a one-unit increase in the covariate. The hazard ratio for LEV, LOANTOASST and LLATOASST is smaller than 1.0, indicating an increase in the rate of failure for one-unit decrease in the covariate, after controlling for other covariates in the model. The overall model fit statistics show that both models are significant at <1% level using partial likelihood test ratio and Wald ratio.
Moreover, we apply Benford’s law to the data of failed and non-failed banks in the pre- and post-GFC period to study whether the data conform to it, or whether we find signs of manipulation in those periods. In pre-GFC period, the average of the first two digits of operating revenue and interest revenue of failed banks are higher than expected according to Benford’s law. On the contrary, the average of the first two digits of total liabilities is lower than expected. These results, which are statistically significant, indicate that banks may have manipulated those figures to disguise their poor financial performance. The same effect is not observable for non-failed banks. This group presents small departures from Benford’s law, but the results are not significant, except for interest expense, which indicates evidence of manipulation. In the post-GFC period, the only significant departure from Benford’s law is in the average of the first two digits of total liabilities. Both failed and non-failed banks have averages that are significantly lower than would be expected of data conforming to Benford’s law. In terms of financial statements information disclosed in the pre- and post-GFC periods, as measured by conformation to Benford’s law, we do not find evidence that indicates manipulation after crisis, except for interest expense, and we do find evidence of manipulation in the pre-GFC period. Lack of evidence of manipulation may indicate the increased bank regulatory scrutiny that may be a deterrent to manipulate in the post-crisis period.
7. Conclusions
The study uses survival analysis to identify variables that discriminate between failed and non-failed banks and the survivorship of the banks. We find that large banks, banks with higher loan to asset ratio, ROA, higher equity to assets, higher non-interest expense to operating income and higher personal loan to asset ratio are more likely to survive and that older banks and banks with high loan loss allowance, high loan loss charge offs, high non-performing loans to asset, high loan to deposit ratio and high equity to loan ratio are more likely to fail. In addition, we find that the survivor function for large banks is higher than for small banks, using large–small subsamples. We also find that it is possible to predict survival functions for failed banks with <50% probability of survival, 3 years or earlier before actual failure. We find that our model is significant at conventional levels. Our pre- and post-GFC results show that variables that predict bank failure are different in these two periods. We find that high agricultural loans to assets, real estate loans to assets, non-performing loans to assets and loan to deposit ratios increase probability of bank failure. Moreover, we find that high loan to deposit ratio and loan loss allowance to asset ratio increase probability of bank failure in post-GFC. We find that high equity to asset ratio improves bank survivability in post-GFC period but does not affect bank’s survivability in pre-GFC period. We find that older banks are more likely to fail in both the pre- and post-GFC.
Our Benford’s Law results show that for years 1–6 before failure, most of the observed variables present a behaviour that departs from Benford’s Law and could indicate manipulation. Non-interest revenue has mean values higher than expected during three of those 6 years, total liabilities have mean values lower than expected in all 6 years and operating expenses have mean values lower than expected in three of the 6 years, showing that failed banks might increase their revenue and decrease their liabilities years before failure to conceal their financial difficulties. In the pre-GFC period, the mean values for first two digits in liabilities are lower than expected, and in operating revenue and interest revenue are higher than expected, indicating that failed banks might have manipulated there disclosures in that period. These results are statistically significant. For the post-GFC period, the manipulation is not observed.
Our results are limited given the model specification. In this analysis, we used CAMEL indicators as explanatory variables. Further analyses may be carried out to test whether there are relationships between CAMEL ratings and the model predicting ability. We yet believe that our large sample is representative of the population of failed banks and the results presented are relevant and potentially may have regulatory implications.